В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дроби
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь ![]() . Чтобы решить этот пример, нужно число 2 представить в виде дроби
. Чтобы решить этот пример, нужно число 2 представить в виде дроби ![]() . Затем сложить дроби с разными знаменателями:
. Затем сложить дроби с разными знаменателями:
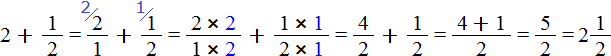
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: ![]() , а конец так:
, а конец так: ![]() . Различие в том, что в первом случае число 2 и дробь
. Различие в том, что в первом случае число 2 и дробь ![]() соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что
соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что ![]() это свёрнутая форма записи смешанного числа, а
это свёрнутая форма записи смешанного числа, а ![]() — развёрнутая.
— развёрнутая.
Когда перед нами смешанное число вида ![]() , мы должны понимать, что знак сложения опущен.
, мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения ![]() равно
равно ![]()
![]()
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
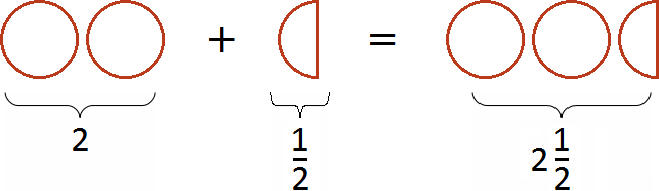
Пример 2. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем сложим дроби с разными знаменателями:
. Затем сложим дроби с разными знаменателями:
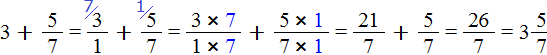
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
![]()
Пример 3. Найти значение выражения ![]()
Можно записать вместе число 2 и дробь ![]() , но этот ответ не будет окончательным, поскольку в дроби
, но этот ответ не будет окончательным, поскольку в дроби ![]() можно выделить целую часть.
можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби ![]() . Пять вторых это две целых и одна вторая:
. Пять вторых это две целых и одна вторая:
![]()
Теперь в главном выражении ![]() вместо дроби
вместо дроби ![]() запишем смешанное число
запишем смешанное число ![]()
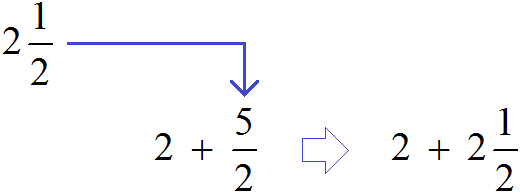
Получили новое выражение ![]() . В этом выражении смешанное число
. В этом выражении смешанное число ![]() запишем в развёрнутом виде:
запишем в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
![]()
Теперь свернём полученное смешанное число:
![]()
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
![]()
Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения ![]() . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
. Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
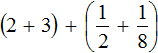
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
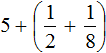
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
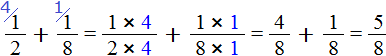
Получили ![]() . Теперь в главном выражении
. Теперь в главном выражении 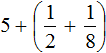 заменяем дробные части на полученную дробь
заменяем дробные части на полученную дробь ![]()
![]()
Теперь свернем полученное смешанное число:
![]()
Таким образом, значение выражения ![]() равно
равно ![]() . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
. Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
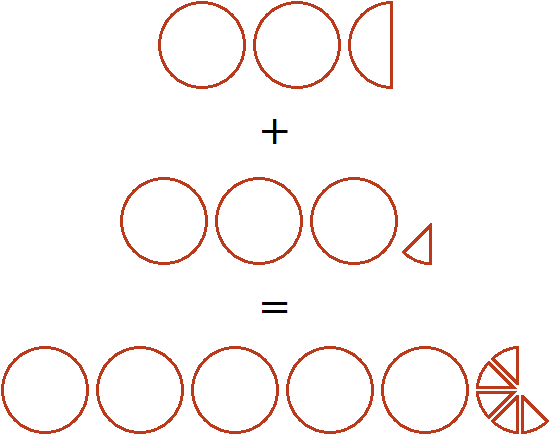
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
![]()
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
![]()
Сгруппируем целые и дробные части по отдельности:
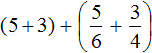
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
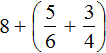
Теперь вычислим дробные части:
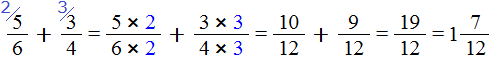
Получили смешанное число ![]() . Теперь в главном выражении
. Теперь в главном выражении 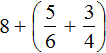 заменяем выражение в скобках на полученное смешанное число
заменяем выражение в скобках на полученное смешанное число ![]()
![]()
Получили выражение ![]() . В данном случае число 8 надо прибавить к целой части смешанного числа
. В данном случае число 8 надо прибавить к целой части смешанного числа ![]() . Для этого смешанное число
. Для этого смешанное число ![]() можно временно развернуть, чтобы было понятнее, что с чем складывать:
можно временно развернуть, чтобы было понятнее, что с чем складывать:
![]()
Сложим целые части. Получаем 9
![]()
Сворачиваем готовый ответ:
![]()
Таким образом, значение выражения равно
![]() .
.
Полное решение этого примера выглядит следующим образом:
![]()
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения ![]()
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
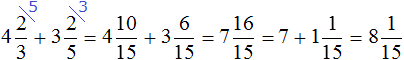
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число ![]() . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
. В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
![]()
Здесь смешанная дробь ![]() была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ
была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ ![]() .
.
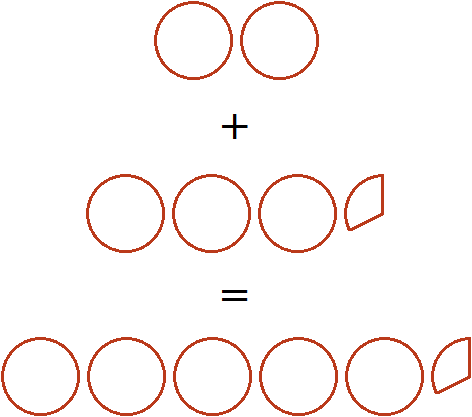
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
Пример 2. Найти значение выражения ![]()
В этом примере, как и в предыдущем, нужно сложить целые части:
![]()
Осталось свернуть целую и дробную части, но дело в том, что дробная часть ![]() представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
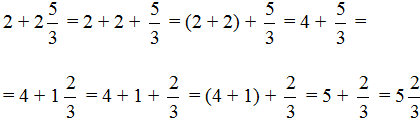
Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь ![]() . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби
. Чтобы решить такой пример, нужно целое число 1 представить в виде дроби ![]() , и выполнить вычитание дробей с разными знаменателями:
, и выполнить вычитание дробей с разными знаменателями:
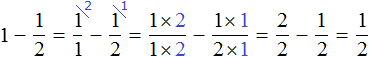
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
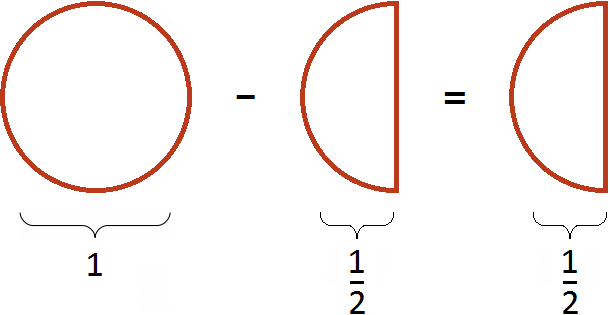
Пример 2. Найти значение выражения ![]() .
.
Представим число 2 в виде дроби ![]() , и выполним вычитание дробей с разными знаменателями:
, и выполним вычитание дробей с разными знаменателями:
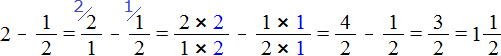
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
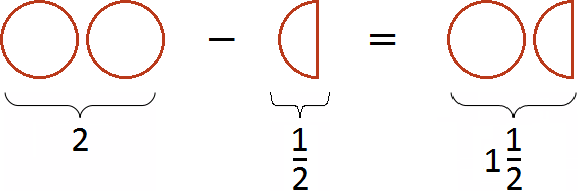
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения ![]() , не приводя на бумаге никаких вычислений.
, не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:

Нужно вычесть из них ![]() . Мы помним, что треть выглядит следующим образом:
. Мы помним, что треть выглядит следующим образом:

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

Получилось ![]() (две целых и две трети пиццы).
(две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения ![]() обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
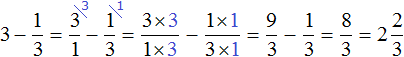
Пример 3. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем выполним вычитание дробей с разными знаменателями:
. Затем выполним вычитание дробей с разными знаменателями:
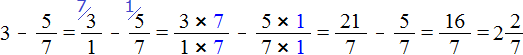
Вычитание смешанного числа из целого числа
Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа
в неправильную дробь, получим дробь
![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
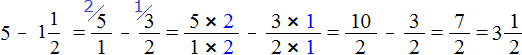
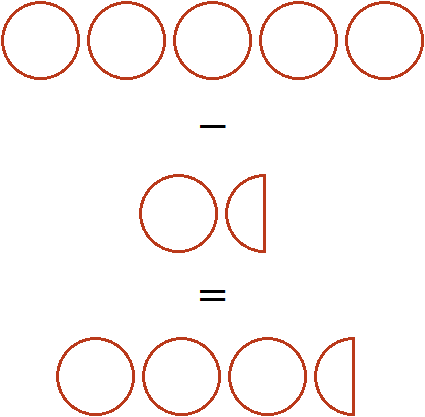
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
Пример 2. Найти значение выражения ![]()
Представим 6 в виде дроби ![]() , а смешанное число
, а смешанное число ![]() , в виде неправильной дроби. После перевода смешанного числа
, в виде неправильной дроби. После перевода смешанного числа ![]() в неправильную дробь, получим дробь
в неправильную дробь, получим дробь ![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
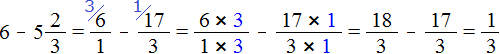
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения ![]() , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
, то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)

Тогда от той пиццы, от которой отрезали останется
![]() пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
![]()
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения: ![]()
Чтобы решить этот пример, нужно смешанные числа ![]() и
и ![]() перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
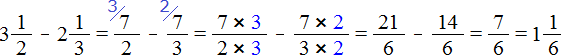
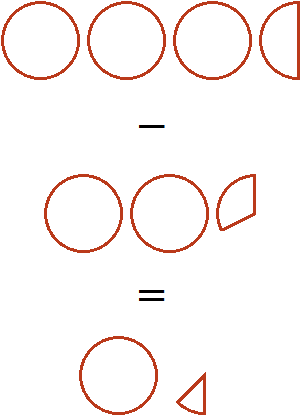
Если от трёх целых и половины пиццы вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа ![]() и
и ![]() в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
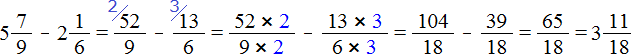
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробь
Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь ![]() . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби
. Чтобы решить этот пример, нужно число 5 умножить на числитель дроби ![]() , а знаменатель оставить без изменения:
, а знаменатель оставить без изменения:
![]()
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
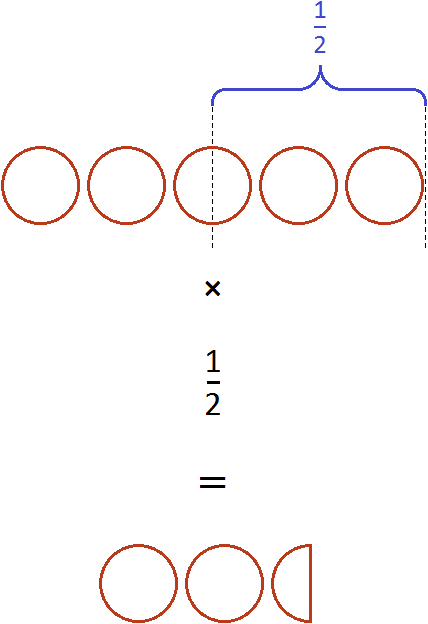
Пример 2. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
В ответе получилась неправильная дробь ![]() , но мы выделили её целую часть и получили 2.
, но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
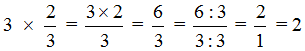
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
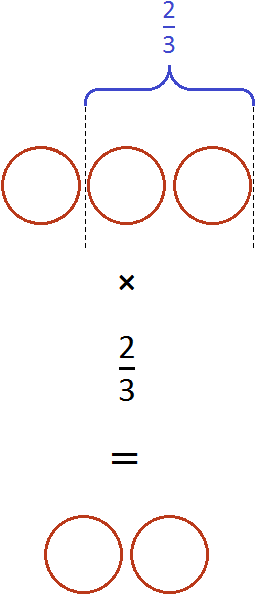
Пример 3. Найти значение выражения ![]()
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
![]()
Пример 4. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения ![]()
Переведём смешанное число ![]() в неправильную дробь. После перевода это число превратится в дробь
в неправильную дробь. После перевода это число превратится в дробь ![]() . Затем можно будет умножить эту дробь на
. Затем можно будет умножить эту дробь на
![]()
Допустим, имеются одна целая и половина пиццы:

Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
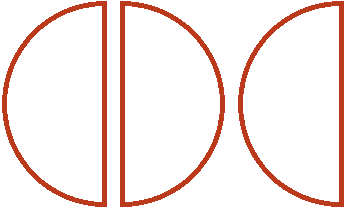
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
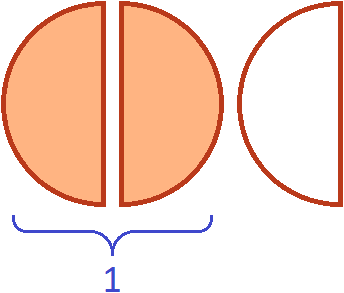
Поэтому значение выражения ![]() было равно 1
было равно 1
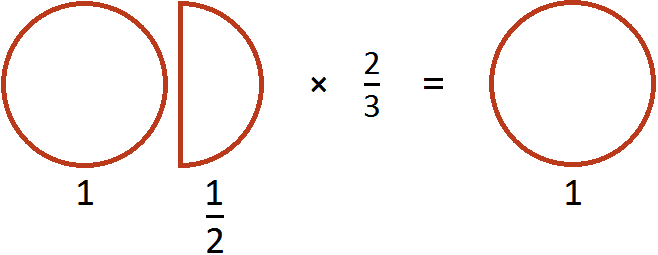
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить ![]() и
и ![]() . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
. Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
![]()
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
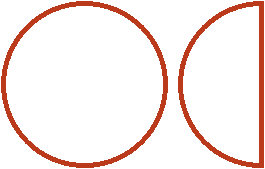
Теперь разберемся со смешанным множителем ![]() . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще
. Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще ![]() раза.
раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
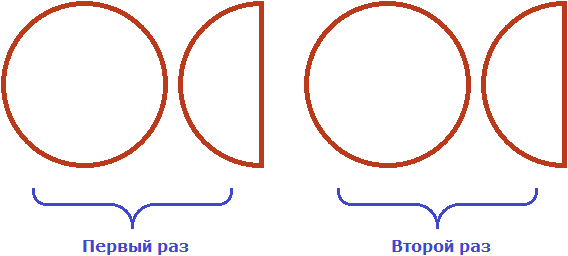
Но ещё осталось взять ![]() от изначальной целой пиццы и половины, ведь множителем было смешанное число
от изначальной целой пиццы и половины, ведь множителем было смешанное число ![]() . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
. Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
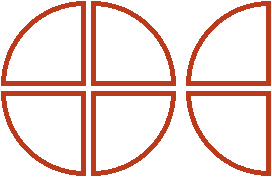
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
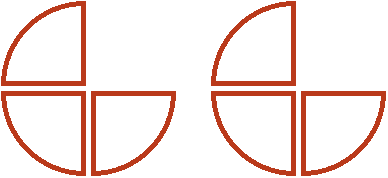
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения ![]() равно
равно ![]()
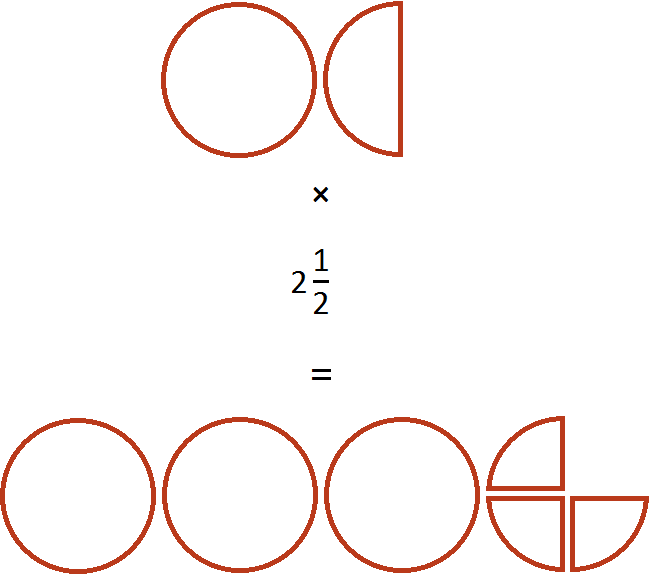
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
![]()
Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь ![]() . Здесь число 3 — это делимое, а дробь
. Здесь число 3 — это делимое, а дробь ![]() — делитель.
— делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 3 на дробь
. Поэтому умножаем число 3 на дробь ![]()
![]()
Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз ![]() (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
(половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
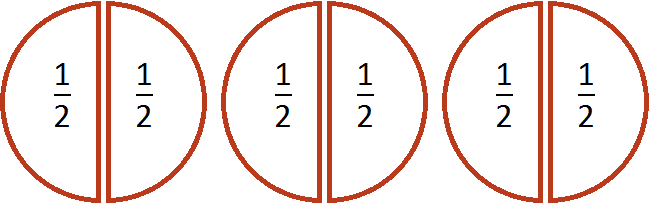
Поэтому значение выражения ![]() равно 6.
равно 6.
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби
пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби ![]() . После выделения целой части в этой дроби получим
. После выделения целой части в этой дроби получим ![]()
Теперь поставим вопрос так: «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух пиццах?».
(одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
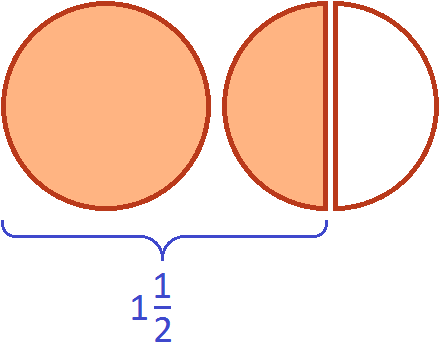
А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
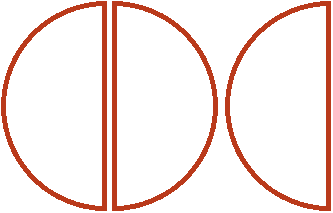
Поэтому значение выражения ![]() равно
равно ![]()
Пример 3. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 5 на
. Поэтому умножаем число 5 на ![]()
![]()
Дробь ![]() это 2 целых и
это 2 целых и ![]() . Проще говоря, две целые и четверть пиццы:
. Проще говоря, две целые и четверть пиццы:

А выражение ![]() определяет сколько раз
определяет сколько раз ![]() содержится в пяти целых пиццах. Ответом было смешанное число
содержится в пяти целых пиццах. Ответом было смешанное число ![]() .
.
То есть ![]() пиццы содержится в пяти целых пиццах
пиццы содержится в пяти целых пиццах ![]() раза.
раза.
Давайте нащупаем в пяти пиццах два раза по ![]()
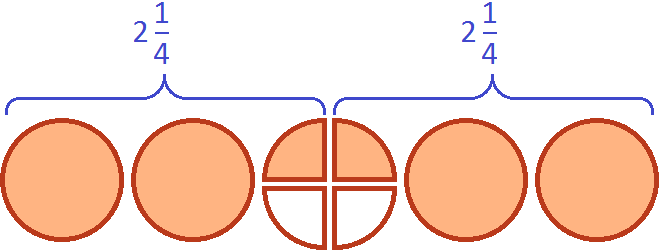
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой ![]() от
от ![]() , которые не вместились. Двумя девятыми они являются по той причине, что в
, которые не вместились. Двумя девятыми они являются по той причине, что в ![]() пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
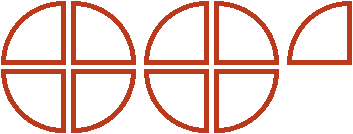
Поэтому значение выражения ![]() равно
равно ![]()
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь ![]() на число 2
на число 2
Чтобы разделить дробь ![]() на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь ![]()
![]()
Пусть имеется половина пиццы:

Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
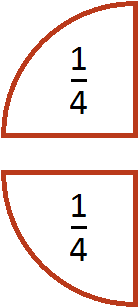
Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно дробь ![]() умножить на число, обратное числу 2. Обратное числу 2 это дробь
умножить на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Пример 3. Найти значение выражения ![]()
Умножаем первую дробь ![]() на число, обратное числу 3. Обратное числу 3 это дробь
на число, обратное числу 3. Обратное числу 3 это дробь ![]()
![]()
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на ![]() .
.
Чтобы решить этот пример, нужно делитель ![]() перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Затем умножим 2 на дробь, обратную дроби
. Затем умножим 2 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
(одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:

Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Переводим делитель ![]() в неправильную дробь, получаем
в неправильную дробь, получаем ![]() . Теперь умножаем число 5 на дробь, обратную дроби
. Теперь умножаем число 5 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь ![]()
![]()
Сначала мы получили ответ ![]() , затем сократили эту дробь на 5, и получили
, затем сократили эту дробь на 5, и получили ![]() , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
, но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ ![]()
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим ![]() на 2. Чтобы решить этот пример, нужно делимое
на 2. Чтобы решить этот пример, нужно делимое ![]() перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() .
.
Теперь умножаем ![]() на число, обратное числу 2. Обратное числу 2 это дробь
на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
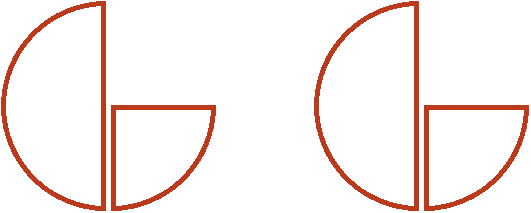
Поэтому значение выражения ![]() равно
равно
Пример 2. Найти значение выражения ![]()
Переведём делимое ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Теперь умножаем
. Теперь умножаем ![]() на число, обратное числу 4. Обратное числу 4 это дробь
на число, обратное числу 4. Обратное числу 4 это дробь ![]() .
.
![]()
Деление смешанных чисел
Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Как решать дальше мы уже знаем. Первую дробь ![]() нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь
нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь ![]() .
.
Дорешаем данный пример до конца:
![]()
Допустим, имеются две целые и половина пиццы:
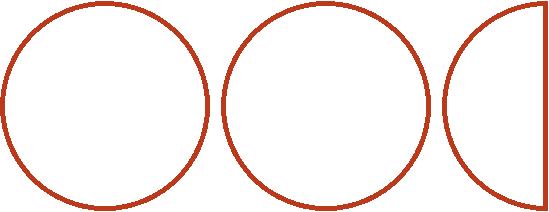
Если зададим вопрос «Сколько раз ![]() (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
(одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
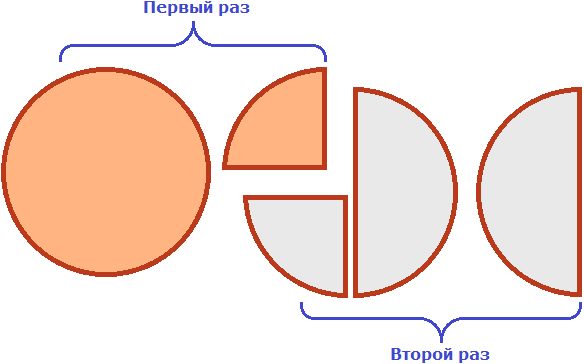
Пример 2. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь ![]()
![]()
Сначала мы получили дробь![]() . Эту дробь мы сократили на 9. В результате получили дробь
. Эту дробь мы сократили на 9. В результате получили дробь ![]() , но такой ответ нас тоже не устроил и мы выделили в дроби
, но такой ответ нас тоже не устроил и мы выделили в дроби ![]() целую часть. В результате получили окончательный ответ
целую часть. В результате получили окончательный ответ ![]() .
.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:

Решение:
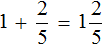
Задание 2. Найдите значение выражения:
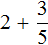
Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:
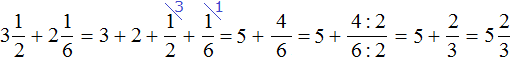
Задание 5. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Смешанные дроби в математике можно получить одним из способов, например, из неправильной дроби или путем сложения дробей и еще много вариантов, когда вы сможете столкнуться со смешанной дробью.
Как сделать из неправильной дроби правильную дробь?
Рассмотрим неправильную дробь (frac{21}{9})
Дробная черта — это деление, поэтому число 21 поделим на 9 столбиком.
 После деления столбиком у нас появились неполное частное, его записываем в целую часть дроби. Остаток записываем в числитель, а делитель записываем в знаменатель.
После деления столбиком у нас появились неполное частное, его записываем в целую часть дроби. Остаток записываем в числитель, а делитель записываем в знаменатель.
Получаем дробь (2frac{3}{9}), такие дроби называются смешанными. В этой смешанной дроби число 2 – целая часть, а (frac{3}{9}) – правильная дробь.
Смешанные дроби состоят из целой и дробной части.
Рассмотрим еще одну неправильную дробь (frac{76}{5})
Разделим ее столбиком:
 Получили смешанную дробь (15frac{1}{5})
Получили смешанную дробь (15frac{1}{5})
Как смешанную дробь перевести в неправильную дробь?
Чтобы из смешанной дроби сделать неправильную дробь нужно знаменатель умножить на целую часть и сложить с числителем, получим числитель неправильной дроби. А знаменатель остается без изменения. Рассмотрим пример:
(color{blue} {3}frac{color{green} {2}}{color{red} {5}} = frac{color{red} {5} times color{blue} {3} + color{green} {2}}{color{red} {5}} = frac{17}{5})
Вопросы по теме:
Смешанная дробь может быть меньше единицы?
Ответ: нет, потому что смешанную дробь можно представить в виде неправильной дроби, а неправильная дробь всегда больше или равна единицы.
Что показывает целая часть у смешанной дроби?
Ответ: целая часть показывает сколько полных знаменателей содержит дробь.
Как представить смешанное число в виде неправильной дроби?
Ответ: к произведению знаменатели и целой части прибавить числитель получим числитель искомой неправильной дроби, а знаменатель не меняется.
Как перевести неправильную дробь в смешанное число? И как выделить целую часть?
Ответ: делим в столбик числитель на знаменатель, неполное частное – это целое, делитель – это знаменатель, а остаток – это числитель. Смотрите пример выше.
Что такое смешанные дроби или смешанные числа?
Ответ: Смешанные дроби – это числа, которые состоят из целой и дробной части.
Пример №1:
Представьте дробь в виде смешанного числа: (frac{508}{17})
Решение:
Разделим дробь столбиком:

Ответ: Получили смешанную дробь (29frac{15}{17})
Пример №2:
Представьте число в виде неправильной дроби: а) (9frac{2}{3}), б) (1frac{3}{7})
Решение:
а) (9frac{2}{3} = frac{9 times 3 +2}{3} = frac{29}{3}\\)
б) (1frac{3}{7} = frac{1 times 7 +3}{7} = frac{10}{7}\\)
Задача №1:
Миша готовился к экзамену. За месяц он решил 120 задач. За первую неделю Миша решил (frac{2}{5}) от этого числа. Сколько задач решил Миша за первую неделю?
Решение:
У нас есть дробь (frac{2}{5}), знаменатель равен 5 это значит, что общее число 120 надо разделить на 5 и получим сколько составляет одна часть.
(120 div 5 = 24) задачи это одна часть или (frac{1}{5})
В числителе стоит 2, значит нам надо взять две части, поэтому 24 умножаем на 2.
(24 times 2 = 48) задач
Ответ: за неделю Миша решил 48 задач.
На чтение 7 мин. Опубликовано 25.05.2020 Обновлено 25.05.2020
Очень часто при решении числовых выражений используется в математике 5 класса «правило смешанного числа». Это определенная методика, позволяющая производить различные операции над величинами заданного типа. Она включает в свой состав два алгоритма, которые называются прямым и обратным.
Содержание
- Общие сведения
- Основные термины и деление
- Классификация обыкновенных дробей
- Работа со смешанными числами
- Методики конвертации
- Арифметические операции
- Пример решения
Общие сведения
Для работы со смешанными числами требуются определенные знания. Специалисты разработали специальную методику, которая позволяет добиться успехов в изучении этой темы. Она имеет следующий вид:
- Определения математических терминов.
- Характеристика элементов операции деления.
- Классификация дробных величин.
- Работа со смешанными дробями.
Специалисты рекомендуют досконально изучить каждый из пунктов, поскольку именно такой способ позволит полностью разобраться в теме и добиться отличных результатов. Следует придерживаться последовательности, поскольку каждый предыдущий шаг вносит основные понятия и алгоритмы, необходимые для дальнейшего продвижения в процессе обучения.
Основные термины и деление

Наиболее качественные формулировки терминов с примерами можно найти в книгах советского математика В. Я. Виленкина. Автор делает основной акцент на практическом применении материала в жизни. Это объясняется особенностью строения головного мозга человека, который лучше запоминает эмоции, а не цифры.
Делением называется арифметическая операция для нахождения определенной величины, характеризующей определенное количество частей, которые получаются при распределении искомого числа между элементами. Математическая запись деления имеет следующий вид: W/Q=R, где W — искомое значение (делимое), Q — элементы (делитель) и R — количество частей (частное или результат).
Делимое — искомая величина, подлежащая дроблению на равные части. Делитель — число, показывающее, на сколько одинаковых компонентов требуется поделить искомое значение. Частное — результат, полученный при осуществлении операции деления и характеризующий общее количество равных частей.
Чтобы понять принцип деления, необходимо привести пример — требуется поделить один пирог на семь человек. Для этого его нужно разрезать на 7 равных частей, т. е. целый пирог составляет 7/7. Он состоит из семи равных частей. Значит, знаменатель обыкновенной дроби эквивалентен значению 7, и указывается под чертой дроби. Над ней отображается числитель.

Если один человек не придет на праздник, то один кусок пирога достанется кому-то еще. У этого человека будет уже не 1/7, а 2/7. Еще один пример — общее число акций какого-либо предприятия. Например, один собственник может иметь 2/3 от общего количества. Далее требуется разобрать классификацию дробных величин.
Классификация обыкновенных дробей
Дробные величины отличаются между собой. Они бывают обыкновенными и десятичными. Первые представлены в виде неполной операции деления, а вторые считаются результатом операции деления, т. е. частным. Обыкновенные дроби W/Q можно классифицировать на два вида:

- Правильные: W<Q.
- Неправильные: W>Q.
Исходя из условий классификации, математики сформулировали два определения. Они звучат следующим образом:
- Правильной является дробь, знаменатель которой больше числителя.
- Неправильной называется обыкновенное дробное выражение, удовлетворяющее условию: числитель больше знаменателя.
Следует отметить, что любое дробное выражение неправильного вида можно перевести в смешанное число. Для этих целей математики предлагают воспользоваться специальными методиками.
Работа со смешанными числами
Для работы со смешанными представлениями дробных тождеств существуют определенные правила, которыми нужно руководствоваться при выполнении заданий различного типа по математике. К ним относятся следующие:
- Преобразование в неправильное дробное тождество.
- Конвертация неправильного дробного выражения в смешанную величину.
- Арифметические операции, требующие конвертации смешанных обыкновенных дробей.
В первом и втором случаях применяются специальные алгоритмы для прямой и обратной операций. Однако их не всегда нужно применять, т. к. это влияет на оптимизацию расчетов. Последний пункт необходимо разобрать более подробно, чтобы не делать лишних вычислений. Например, не имеет смысла преобразовывать смешанную дробную форму в неправильную дробь при сравнении двух величин.
Методики конвертации
Для ознакомления с методиками конвертации неправильной дроби в смешанную величину нужно записать величину в общем виде, т. е. W/Q. Алгоритм конвертации выглядит таким образом:
- Пишется исходное значение: W/Q.
- Выделяется целое «С» при делении W/Q: W/Q=C.
- Рассчитывается новое значение числителя W’ по следующему соотношению: W’=W-CQ.
- Записывается результат: C[W’/Q].
Чтобы преобразовать смешанное дробное выражение в неправильную дробь, используется обратная методика. Она имеет такой вид:

- Записывается cмешанная дробная величина: С[W’/Q].
- Осуществляется расчет числителя W по такой формуле: W=QC+W’.
- Получается результат в виде неправильной дроби: W/Q.
Для демонстрации работы двух методик требуется произвести операции прямого и обратного конвертирования на примере величины «73/15».
Чтобы преобразовать последнее значение в смешанное дробное выражение, нужно воспользоваться соответствующим алгоритмом:
- Записать число: 73/15.
- Выделить целое значение: 4.
- Рассчитать числитель: 73−15*4=13.
- Записать искомый результат: 4[13/15].
Обратное преобразование осуществляется по обратной методике. Решать задачу нужно следующим образом:

- Смешанное число: 4[13/15].
- Новый числитель: 15*4+13=73/15.
- Результат: 73/15.
Если обратить внимание на оба преобразования, то можно сделать вывод, что они отличаются между собой обратными действиями. Далее нужно разобрать все арифметические операции, в которых необходимо применять конвертацию смешанного числа в неправильную форму.
Арифметические операции
Не всегда рекомендуется использовать преобразование смешанного значения. Существует ряд арифметических операций, представленных в виде отдельных задач. К ним относятся следующие:
- Сравнение дробей.
- Сложение.
- Вычитание.
В первом случае оба числа должны быть с одинаковыми знаменателями. Допускается также и одинаковые числители, но разные знаменатели. При сравнении необходимо сначала учитывать целые части. Например, при сравнении величин 4[2/3] и 5[7/11] сразу можно сделать вывод, что вторая больше первой, поскольку ее целая часть больше, чем у первой.
Если требуется сравнить два дробных тождества 4[2/3] и 5[7/11], то нужно выполнять конвертацию в неправильную дробь. Это объясняется тем, что следует приводить первоначальные значения к общему знаменателю.

Операции сложения и вычитания осуществляются по такому же принципу, как и в первом случае. Однако обязательным условием является равенство знаменателей. В противном случае дроби смешанного типа необходимо преобразовывать в неправильные, а затем выполнять операцию приведения к единому знаменателю.
При вычитании необходимо учитывать знак. Правила операции распространяются и на смешанные числа. Например, 4−6=-2. За знаками необходимо постоянно следить, поскольку невнимательность со стороны ученика может привести к некорректным вычислениям. Далее для закрепления теоретического материала необходимо решить математический ребус.
Пример решения
Очень часто для закрепления теоретического материала после объяснения используется практика решения задач в игровой форме. Основная задача преподавателя — заинтересовать ученика, и доказать ему, что математика может быть нескучной дисциплиной. Одним из таких примеров является такая задача нахождения искомой неправильной дроби по следующим условиям:
- Числитель примерно в семь раз больше знаменателя.
- Знаменатель представлен двузначным числом 11.
- В смешанной форме числитель меньше знаменателя на 10.
- У неправильной дроби числитель больше знаменателя на 67.
Чтобы найти решения задачи, необходимо учитывать все условия. Для начала требуется обозначить числитель литерой «t». После этого необходимо составить выражения с учетом новой введенной переменной:
- Числитель — t, а знаменатель — t/7.
- Смешанная форма: t-10=0.
- Неправильная: t’-67.
Далее необходимо составить систему уравнений. Она имеет такой вид:
- Правильная: 11-t=10.
- Неправильная: t’-11=67.
- Целая часть: 7.
Искомые уравнения будут решаться следующим образом: t=1 и t’=67+11=78. На основании вычислений можно сделать следующие выводы:
- Неправильная дробь: 78/11.
- Смешанная величина: 7[1/11].
Чтобы выполнить проверку результата, достаточно осуществить конвертацию второго значения в первое, т. е. 7[1/11]=(11*7+1)/11=78/11. Из этого следует, что решение выполнено правильно.
Таким образом, конвертация смешанных дробных выражений осуществляется при помощи специальных алгоритмов, предложенных специалистами. Математик Виленкин В. Я. в своих книгах рекомендует совмещать задачи с фактическими примерами из различных жизненных ситуаций, что позволит сделать обучение более продуктивным.
Сложение смешанных чисел
- Калькулятор сложения смешанных чисел
Чтобы сложить смешанные числа, надо сложить отдельно их целые и их дробные части и полученные результаты сложить.
Пример.

Условились считать, что любое натуральное число имеет дробную часть, равную нулю, а любая правильная дробь имеет целую часть, равную нулю. Поэтому складывать правильные дроби и натуральные числа со смешанными числами можно по правилу сложения смешанных чисел.
Так как натуральное число имеет дробную часть, равную нулю, то при сложении смешанного числа с натуральным числом, складывается только целая часть c натуральным числом, а дробная часть остаётся без изменений:

Так как правильная дробь имеет целую часть, равную нулю, то при сложении смешанного числа с правильной дробью, складывается только дробная часть с правильной дробью, а целая часть остаётся без изменений:

При сложении дробных частей двух смешанных чисел или дробной части смешанного числа с правильной дробью может получиться неправильная дробь. В этом случае неправильную дробь нужно представить в виде смешанного числа:


Если дробные части смешанных чисел имеют разные знаменатели, то сначала их нужно привести к общему знаменателю:

Также, смешанные числа можно записать в виде неправильных дробей и выполнить сложение, а в конце (если требуется по условию задания) записать результат в виде смешанного числа:

Калькулятор сложения смешанных чисел
Данный калькулятор поможет вам выполнить сложение смешанных чисел. Просто введите слагаемые и нажмите кнопку Вычислить
. Данный калькулятор позволяет также выполнять сложение: натурального числа и дроби, смешанного числа и дроби, натурального и смешанного числа, натуральных чисел.
Содержание материала
- Основное свойство дроби
- Видео
- Деление смешанного числа на целое число
- Вычитание дроби из целого числа
- Умножение смешанных чисел
- Умножение смешанного числа на смешанное число
- Умножение смешанного числа на обыкновенную дробь
- Умножение целого числа на дробь
- Арифметические действия с обыкновенными дробями
- Сложение и вычитание дробей
- Умножение дробей
- Деление дробей
- Нахождение целого по его части (числа по его дроби)
Основное свойство дроби
Дроби a/b и c/d называются равными, если ad = bc.
Из этого определения следует, что одну и ту же дробь можно записать по-разному. Например, 1/2 = 2/4, поскольку 1 · 4 = 2 · 2. Разумеется, существует множество дробей, которые не равны друг другу. Например, 1/3 ≠ 5/4, поскольку 1 · 4 ≠ 3 · 5.
Возникает резонный вопрос: как найти все дроби, равные данной? Ответ дадим в форме определения:
Основное свойство дроби — числитель и знаменатель можно умножать на одно и то же число, отличное от нуля. При этом получится дробь, равная данной.
Примеры:

Это очень важное свойство — запомните его. С помощью основного свойства дроби можно упрощать и сокращать многие выражения. В будущем оно постоянно будет «всплывать» в виде различных свойств и теорем.
Видео
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим  на 2. Чтобы решить этот пример, нужно делимое
на 2. Чтобы решить этот пример, нужно делимое  перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число  в неправильную дробь, получим
в неправильную дробь, получим  .
.
Теперь умножаем  на число, обратное числу 2. Обратное числу 2 это дробь
на число, обратное числу 2. Обратное числу 2 это дробь 

Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по  пиццы в каждой группе:
пиццы в каждой группе:

Поэтому значение выражения  равно
равно 
Пример 2. Найти значение выражения 
Переведём делимое  в неправильную дробь, получим
в неправильную дробь, получим  . Теперь умножаем
. Теперь умножаем  на число, обратное числу 4. Обратное числу 4 это дробь
на число, обратное числу 4. Обратное числу 4 это дробь  .
.

Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь  . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби
. Чтобы решить такой пример, нужно целое число 1 представить в виде дроби  , и выполнить вычитание дробей с разными знаменателями:
, и выполнить вычитание дробей с разными знаменателями:

Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:

Пример 2. Найти значение выражения  .
.
Представим число 2 в виде дроби  , и выполним вычитание дробей с разными знаменателями:
, и выполним вычитание дробей с разными знаменателями:

Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:

Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения  , не приводя на бумаге никаких вычислений.
, не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:

Нужно вычесть из них  . Мы помним, что треть выглядит следующим образом:
. Мы помним, что треть выглядит следующим образом:

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

Получилось  (две целых и две трети пиццы).
(две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения  обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:

Пример 3. Найти значение выражения 
Представим число 3 в виде дроби  . Затем выполним вычитание дробей с разными знаменателями:
. Затем выполним вычитание дробей с разными знаменателями:

Умножение смешанных чисел
Давайте разберемся как выполнять умножение в примерах, где есть смешанные числа.
Умножение смешанного числа на смешанное число
Запоминаем
Чтобы умножить одно смешанное число на другое, нужно перевести оба смешанных числа в неправильные дроби, а затем выполнить умножение по правилу умножения дробей.
Пример. Выполните умножение смешанного числа и
Как решаем:
Запишем выражение
Следуя правилу, переведем смешанные числа в неправильные дроби.
Выполним умножение: .
Из полученной неправильной дроби выделяем целую часть .
Ответ: .
Умножение смешанного числа на обыкновенную дробь
Запоминаем
Чтобы выполнить умножение смешанного числа и обыкновенной дроби, представьте смешанное число в виде неправильной дроби и выполните умножение дробей.
Пример. Умножьте смешанное число на обыкновенную дробь
Как решаем:
Запишем выражение
Представим смешанное число в виде неправильной дроби.
.
Выполним умножение дробей
Выделим из полученной неправильной дроби целую часть
Ответ: .
Умножение целого числа на дробь
Запоминаем
Чтобы умножить целое число на дробь, просто умножьте это число на числитель дроби.
Пример. Выполните умножение числа 7 на обыкновенную дробь
Как решаем:
Запишем выражение:
Выделим из получившейся неправильной дроби целую часть .
Ответ:
Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.

Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!

Общий случай сложения (вычитания) дробей.

Умножение дробей
- Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

- При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.

Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.

При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.

Нахождение целого по его части (числа по его дроби)
Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.
Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.

Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Десятичная дробь
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
