Как найти смешанное произведение двух векторов

Как найти смешанное произведение двух векторов

Сме́шанное произведе́ние ({mathbf {a}},{mathbf {b}},{mathbf {c}}) векторов {mathbf {a}},{mathbf {b}},{mathbf {c}} — скалярное произведение вектора {mathbf {a}} на векторное произведение векторов {mathbf {b}} и {mathbf {c}}:

({mathbf {a}},{mathbf {b}},{mathbf c})={mathbf {a}}cdot left({mathbf {b}}times {mathbf c}right).

Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).

Геометрический смысл: модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами {mathbf a},{mathbf b},{mathbf c}.

Свойства[править | править код]

  • Смешанное произведение кососимметрично по отношению ко всем своим аргументам:
({mathbf a},{mathbf b},{mathbf c})=({mathbf b},{mathbf c},{mathbf a})=({mathbf c},{mathbf a},{mathbf b})=-({mathbf b},{mathbf a},{mathbf c})=-({mathbf c},{mathbf b},{mathbf a})=-({mathbf a},{mathbf c},{mathbf b});
т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что
langle {mathbf a},[{mathbf b},{mathbf c}]rangle =langle [{mathbf a},{mathbf b}],{mathbf c}rangle
({mathbf {a}},{mathbf {b}},{mathbf {c}})={begin{vmatrix}a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}\c_{x}&c_{y}&c_{z}end{vmatrix}}.
({mathbf {a}},{mathbf {b}},{mathbf {c}})=-{begin{vmatrix}a_{x}&a_{y}&a_{z}\b_{x}&b_{y}&b_{z}\c_{x}&c_{y}&c_{z}end{vmatrix}}.
В частности,

Три вектора, определяющие параллелепипед.

  • Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивита:
({mathbf a},{mathbf b},{mathbf c})=sum _{{i,j,k}}varepsilon _{{ijk}}a^{i}b^{j}c^{k}

(в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).

Обобщение[править | править код]

В n-мерном пространстве естественным обобщением смешанного произведения, имеющего смысл ориентированного объема, является определитель матрицы ntimes n, составленной из строк или столбцов, заполненных координатами векторов. Смысл этой величины — ориентированный n-мерный объем (подразумевается стандартный базис и тривиальная метрика).

В произвольном базисе произвольной размерности смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивиты соответствующей размерности:

({mathbf a},{mathbf b},{mathbf c},ldots )=sum _{{i,j,k,ldots }}varepsilon _{{ijkldots }}a^{i}b^{j}c^{k}ldots

В двумерном пространстве таковым служит псевдоскалярное произведение.

См. также[править | править код]

  • Двойное векторное произведение
  • Векторное произведение
  • Скалярное произведение
  • Псевдоскалярное произведение

Примечания[править | править код]

  1. ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.

Ссылки[править | править код]

  • Смешанное произведение векторов и его свойства. Примеры решения задач
Источник
Автор статьи

Марина Николаевна Ковальчук

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Предварительные сведения

Для того чтобы мы могли ввести понятие смешанного произведения векторов, нужно сначала вспомнить понятия скалярного и векторного произведений этих векторов.

Определение 1

Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.

Математически это может выглядеть следующим образом:

$overline{α}overline{β}=|overline{α}||overline{β}|cos⁡∠(overline{α},overline{β})$

Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.

Теорема 1

Скалярное произведение двух данных векторов $overline{α}$ и $overline{β}$ равняется сумме произведений их соответствующих координат.

Математически выглядит следующим образом

$overline{α}overline{β}=α_1 α_2+β_1 β_2$

Обозначение: $overline{α}cdot overline{β}$.

Определение 2

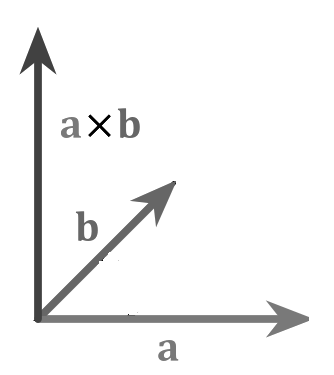
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.

Обозначение: $overline{α}хoverline{β}$.

Математически это выглядит следующим образом:

  1. $|overline{α}хoverline{β}|=|overline{α}||overline{β}|sin⁡∠(overline{α},overline{β})$
  2. $overline{α}хoverline{β}⊥overline{α}$, $overline{α}хoverline{β}⊥overline{β}$
  3. $(overline{α}хoverline{β},overline{α},overline{β})$ и $(overline{i},overline{j},overline{k})$ одинаково ориентированы (рис. 1)

«Как найти смешанное произведение векторов» 👇

Понятие смешанного произведения векторов

Определение 3

Смешанным произведением векторов $overline{α}$, $overline{β}$ и $overline{γ}$ будем называть такой скаляр (или число), которое будет равняться скалярному произведению первого вектора $overline{α}$ на вектор векторного произведения $overline{β}хoverline{γ}$ двух других векторов.

Обозначение: $(overline{α},overline{β},overline{γ})$.

Математически это выглядит следующим образом:

$(overline{α},overline{β},overline{γ})=overline{α}cdot (overline{β}хoverline{γ})$

Очевидно, что смешанное произведение будет равняться нулю в двух случаях:

  1. Если длина одного или нескольких векторов равняется нулю.
  2. Если эти векторы будут являться компланарными.

Пример 1

Найти значение смешанного произведения векторов $overline{α}$, $overline{β}$ и $overline{γ}$, которые имеют координаты $(0,0,5)$, $(0,4,0)$ и $(3,0,0)$, соответственно.

Решение.

Из определений 1, и 3 будем получать

$(overline{α},overline{β},overline{γ})=overline{α}cdot (overline{β}хoverline{γ})=|overline{a}||overline{β}хoverline{γ}|cos∠(overline{α},overline{β}хoverline{γ})$

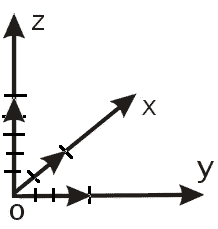
Изобразим эти векторы в декартовом координатном пространстве (рис. 2):

Найдем вначале длину вектора векторного произведения векторов $overline{β}$ и $overline{γ}$

Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^0$. Найдем длины этих векторов:

$|overline{β}|=sqrt{0+16+0}=4$

$|overline{γ}|=sqrt{9+0+0}=3$

Тогда, по определению 2, получим

$|overline{β}хoverline{γ}|=|overline{α}||overline{β}|sin90^circ=4cdot 3cdot 1=12$

Из 3 части определения 2 очевидно, что вектор $overline{β}хoverline{γ}$ принадлежит оси $Oz$ и направлен в туже сторону, что и сама ось, следовательно, угол между векторами $overline{α}$ и $overline{β}хoverline{γ}$ равняется $0^circ$.

Длина вектора $overline{α}$

$|overline{α}|=sqrt{0+0+25}=5$

Получим

$(overline{α},overline{β},overline{γ})=|overline{a}||overline{β}хoverline{γ}|cos∠(overline{α},overline{β}хoverline{γ})=5cdot 12cdot cos0^circ=60$

Ответ: $60$.

Вычисление смешанного произведения по координатам векторов

Из определения 1 сразу же вытекает и способ нахождения смешанного произведения для трех данных векторов. Но существует еще способ нахождения с помощью координат данных нам векторов.

Пусть нам даны векторы $overline{α}$, $overline{β}$ и $overline{γ}$, которые будут иметь координаты $(α_1,α_2,α_3)$, $(β_1,β_2,β_3)$ и $(γ_1,γ_2,γ_3)$, соответственно. Тогда значение смешанного произведения можно найти по следующей формуле:

$(overline{α},overline{β},overline{γ})=begin{vmatrix}α_1&α_2&α_3\β_1&β_2&β_3\γ_1&γ_2&γ_3end{vmatrix}$

Иначе, получим

$overline{α}хoverline{β}=α_1 β_2 γ_3+α_3 β_1 γ_2+α_2 β_3 γ_1-α_3 β_2 γ_1-α_2 β_1 γ_3-α_1 β_3 γ_2$

Пример 2

Найти значение смешанного произведения векторов $overline{α}$, $overline{β}$ и $overline{γ}$ с координатами $(1,1,0)$, $(0,3,3)$ и $(-1,2,6)$.

Решение.

Воспользуемся формулой, приведенной выше. Получим

$(overline{α},overline{β},overline{γ})=begin{vmatrix}1&1&0\0&3&3\-1&2&6end{vmatrix}=18+(-3)+0-0-6-0=18-9=9$

Ответ: $9$.

Свойства смешанного произведения векторов

Для произвольных четырех векторов $overline{α}, $overline{β}$, $overline{γ}$ и $overline{δ}$, а также $r∈R$ справедливы следующие свойства: справедливы следующие свойства:

1) При перестановке местами знаков произведений в смешанном произведении можно менять между собой

$(overline{α},overline{δ},overline{γ})=overline{α}cdot (overline{δ}хoverline{γ})=(overline{α}хoverline{δ})cdot overline{γ}$

2) Векторы в смешанном произведении можно менять только циклически

$(overline{α},overline{δ},overline{γ})=(overline{δ},overline{γ},overline{α})=(overline{γ},overline{α},overline{δ})$

3) Перемещение только одного вектора на другое место меняет знак

$(overline{α},overline{δ},overline{γ})=-(overline{β},overline{α},overline{γ})=-(overline{γ},overline{δ},overline{α})=-(overline{α},overline{γ},overline{δ})$

4) Из формулы выше, очевидны следующие равенства:

$(roverline{α},overline{δ},overline{γ})=r(overline{α},overline{δ},overline{γ})$

$(overline{α},roverline{δ},overline{γ})=r(overline{α},overline{δ},overline{γ})$

$(overlie{α},overline{δ},roverline{γ})=r(overline{α},overline{δ},overline{γ})$

5) Справедливы равенства:

$(overline{α}+overline{β},overline{δ},overline{γ})=(overline{α},overline{δ},overline{γ})+(overline{β},overline{δ},overline{γ})$

$(overline{α},overline{δ}+overline{β},overline{γ})=(overline{α},overline{δ},overline{γ})+(overline{α},overline{β},overline{γ})$

$(overline{α},overline{δ},overline{γ}+overline{β})=(overline{α},overline{δ},overline{γ})+(overline{α},overline{δ},overline{β})$

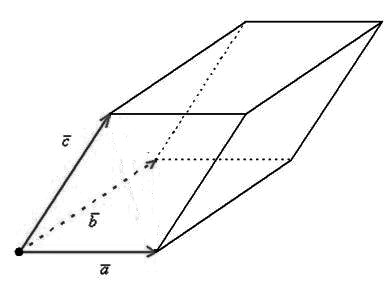
6) Геометрический смысл – площадь параллелепипеда (рис. 3):

$S=|(overline{α},overline{β},overline{c})|$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Смешанное произведение векторов.

Определение. Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.

Формулы вычисления смешанного произведения векторов

Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.

Смешанное произведение векторов a = {ax; ay; az}, b = {bx; by; bz} и c = {cx; cy; cz} в декартовой системе координат можно вычислить, используя следующую формулу:

a · [b × c] =  ax   ay   az 
 bx   by   bz 
 cx   cy   cz 

Свойства смешанного произведения векторов

  • Геометрический смысл смешанного произведения.

    Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами:

    Vпарал = |a · [b × c]|

  • Геометрический смысл смешанного произведения.

    Объем пирамиды образованной тремя векторами a, b и с равен одной шестой части от модуля смешанного произведения этих векторов:

  • Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.

  • a · [b × c] =
    b · (a · c) –
    c · (a · b)

  • a · [b × c] =
    b · [c × a] =
    c · [a × b] =
    –a · [c × b] =
    –b · [a × c] =
    –c · [b × a]

  • a · [b × c] + b · [c × a] + c · [a × b] = 0 – тождество Якоби.

Примеры задач на вычисления смешанного произведения векторов

Пример 1. Найти смешанное произведение векторов a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.

Решение:

a · [b × с] =    1     2     3    =
  1     1     1  
  1     2     1  

= 1·1·1 + 1·1·2 + 1·2·3 – 1·1·3 – 1·1·2 – 1·1·2 = 1 + 2 + 6 – 3 – 2 – 2 = 2

пирамида построенная на векторах

Пример 2.

Найти объем пирамиды построенной на векторах a = {1; 2; 3}, b = {1; -1; 1}, c = {2; 0; -1}.

Решение: Найдем смешанное произведение этих векторов:

a · [b × с] =    1     2     3    =
  1     -1     1  
  2     0     -1  

= 1·(-1)·(-1) + 2·1·2 + 3·1·0 – 3·(-1)·2 – 2·1·(-1) – 1·1·0 =

= 1 + 4 + 0 + 6 + 2 – 0 = 13

Найдем объем пирамиды воспользовавшись свойствами:

Vпир =  1 |a · [b × c]| =  13  = 2 1
6 6 6
Источник

Содержание:

  • Формула
  • Примеры вычисления смешанного произведения векторов

Формула

Для того чтобы найти смешанное произведение
$(bar{a}$, $bar{b}$, $bar{c})$ трех векторов, заданных своими координатами
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right), b=left(b_{x} ; b_{y} ; b_{z}right)$ и $bar{c}=left(c_{x}, c_{y}, c_{z}right)$ необходимо
вычислить следующий определитель, где по
строкам записаны координаты заданных векторов, то есть

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{lll}a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z} \ c_{x} & c_{y} & c_{z}end{array}right|$$

Примеры вычисления смешанного произведения векторов

Пример

Задание. Вычислить смешанное произведение векторов
$bar{a}=(1 ; 3 ; 1)$, $bar{b}=(2 ; 1 ; 3)$, и $bar{c}=(3 ; 1 ; 2)$

Решение. Для нахождения смешанного произведения заданных векторов воспользуемся формулой

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{lll}a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z} \ c_{x} & c_{y} & c_{z}end{array}right|$$

Подставляя координаты заданных векторов, получим:

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{ccc}1 & 3 & 1 \ 2 & 1 & 3 \ 3 & 1 & 2end{array}right|$$

Определитель вычисляем по правилу треугольника:

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{ccc}1 & 3 & 1 \ 2 & 1 & 3 \ 3 & 1 & 2end{array}right|=1 cdot 1 cdot 2+3 cdot 3 cdot 3+2 cdot 1 cdot 1-$$
$$-1 cdot 1 cdot 3-3 cdot 2 cdot 2-3 cdot 1 cdot 1=2+27+2-3-12-3=13$$

Ответ. $(bar{a}, bar{b}, bar{c})=13$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Даны три вектора $bar{a}=(1 ;-2 ; 3), bar{b}=(3 ;-5 ; 6)$ и $bar{c}=(5 ;-4 ; 1)$. Проверить, являются ли они компланарными, если нет,
определить левую или правую тройку они образуют.

Решение. Найдем смешанное произведение этих векторов. Для этого воспользуемся формулой

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{lll}a_{x} & a_{y} & a_{z} \ b_{x} & b_{y} & b_{z} \ c_{x} & c_{y} & c_{z}end{array}right|$$

Подставляя координаты заданных векторов, получим

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{ccc}1 & -2 & 3 \ 3 & -5 & 6 \ 5 & -4 & 1end{array}right|$$

Определитель вычисляем по правилу треугольника:

$$(bar{a}, bar{b}, bar{c})=left|begin{array}{ccc}1 & -2 & 3 \ 3 & -5 & 6 \ 5 & -4 & 1end{array}right|=1 cdot(-5) cdot 1+(-2) cdot 5 cdot 6+$$
$$+3 cdot 3 cdot(-4)-3 cdot(-5) cdot 5-3 cdot(-2) cdot 1-1 cdot 6 cdot(-4)=$$
$$-5-60-36+75+6+24=4 neq 0$$

Смешанное произведение заданных векторов не равно нулю, следовательно, векторы некомпланарные. Так как смешанное
произведение положительно, то делаем вывод, что заданные векторы образуют правую тройку.

Ответ. Векторы некомпланарны и образуют правую тройку.

Читать дальше: как найти вектор коллинеарный вектору.

Источник

Смешанное произведение векторов и его свойства

Смешанным произведением векторов vec{a},vec{b},vec{c} называется число bigllanglevec{a},[vec{b},vec{c}]biglrangle, равное скалярному произведению вектора vec{a} на векторное произведение векторов vec{b} и vec{c}. Смешанное произведение обозначается (vec{a},vec{b},vec{c}).

Геометрические свойства смешанного произведения

1. Модуль смешанного произведения некомпланарных векторов vec{a},vec{b},vec{c} равен объему V_{*vec{a},vec{b},vec{c}} параллелепипеда, построенного на этих векторах. Произведение (vec{a},vec{b},vec{c}) положительно, если тройка векторов vec{a},vec{b},vec{c} — правая, и отрицательно, если тройка vec{a},vec{b},vec{c} — левая, и наоборот.

2. Смешанное произведение (vec{a},vec{b},vec{c}) равно нулю тогда и только тогда, когда векторы vec{a},vec{b},vec{c} компланарны:

(vec{a},vec{b},vec{c})=0~Leftrightarrow векторы vec{a},vec{b},vec{c} компланарны.

Докажем первое свойство. Найдем по определению смешанное произведение: (vec{a},vec{b},vec{c})=|vec{a}|cdotbigl|[vec{b},vec{c}]bigl|cospsi, где psi — угол между векторами vec{a} и [vec{b},vec{c}]. Модуль векторного произведения (по геометрическому свойству 1) равен площади S_{*vec{b}vec{c}} параллелограмма, построенного на векторах vec{b} и vec{c}: bigl|[vec{b},vec{c}]bigl|,=|vec{b}|cdot|vec{c}|cdotsinvarphi=S_{*vec{b}vec{c}}. Поэтому (vec{a},vec{b},vec{c})=S_{*vec{b}vec{c}}|vec{a}|cospsi. Алгебраическое значение |vec{a}|cospsi длины проекции вектора vec{a} на ось, задаваемую вектором [vec{b},vec{c}], равно по модулю высоте h=|vec{a}|cdot|cospsi| параллелепипеда, построенного на векторах vec{a},vec{b},vec{c} (рис. 1.47). Поэтому модуль смешанного произведения равен объему V_{*vec{a}vec{b}vec{c}} этого параллелепипеда:

Параллелепипед, построенный на векторах

bigl|vec{a},vec{b},vec{c}bigl|,=S_{*vec{b}vec{c}}cdot|vec{a}|cdot|cospsi|=S_{*vec{b}vec{c}}cdot h=V_{*vec{a}vec{b}vec{c}}.

Знак смешанного произведения определяется знаком косинуса угла psi. Если тройка vec{a},vec{b},vec{c} правая, то psi<frac{pi}{2} и смешанное произведение (vec{a},vec{b},vec{c}) положительно. Если же тройка vec{a},vec{b},vec{c} левая, то psi>frac{pi}{2} и смешанное произведение (vec{a},vec{b},vec{c}) отрицательно.

Докажем второе свойство. Равенство (vec{a},vec{b},vec{c})=|vec{a}|cdotbigl|[vec{b},vec{c}]bigl|cospsi=0 возможно в трех случаях: vec{a}=vec{o} или [vec{b},vec{c}]=vec{o} (т.е. vec{b}parallelvec{c}),или cospsi=0 (т.е. вектор vec{a} принадлежит плоскости векторов vec{b} и vec{c}). В каждом случае векторы vec{a},vec{b},vec{c} компланарны (см. разд. 1.1).

Алгебраические свойства смешанного произведения

1. При перестановке двух множителей смешанное произведение изменяет знак на противоположный:

(vec{a},vec{b},vec{c})=-(vec{b},vec{a},vec{c}),qquad (vec{a},vec{b},vec{c})=-(vec{c},vec{a},vec{a}),qquad (vec{a},vec{b},vec{c})=-(vec{a},vec{c},vec{b}).

При циклической (круговой) перестановке множителей смешанное произведение не изменяется:

(vec{a},vec{b},vec{c})=(vec{b},vec{c},vec{a})=(vec{c},vec{a},vec{b}).

2. Смешанное произведение линейно по любому множителю.

Первое свойство следует из геометрического свойства 1 и свойств ориентации троек векторов (см. разд. 1.9), поскольку от перестановки двух множителей модуль смешанного произведения не изменяется, а меняется только ориентация тройки. При циклической перестановке векторов ориентация тройки не изменяется.

Второе свойство следует из линейности скалярного произведения и свойства 1.

Пример 1.21. Объем параллелепипеда, построенного на векторах vec{a},vec{b},vec{c}, равен V. Найти объем параллелепипеда, построенного на векторах

vec{p}=vec{a}+vec{b}+vec{c},qquad vec{q}=vec{a}+vec{b}-vec{c},qquad vec{r}=vec{a}-vec{b}+vec{c},.

Решение. Используя алгебраические и геометрические свойства, найдем смешанное произведение

begin{aligned} (vec{p},vec{q},vec{r})=,&(vec{a}+vec{b}+vec{c},vec{a}+vec{b}-vec{c},vec{a}-vec{b}+vec{c})=\[3pt] =,&(vec{a},vec{a}+vec{b}-vec{c},vec{a}-vec{b}+vec{c})+(vec{b},vec{a}+vec{b}-vec{c},vec{a}-vec{b}+vec{c})+(vec{c},vec{a}+vec{b}-vec{c},vec{a}-vec{b}+vec{c})=\[3pt] =,&underbrace{(vec{a},vec{a},vec{a}-vec{b}+vec{c})}_0+(vec{a},vec{b},vec{a}-vec{b}+vec{c})-(vec{a},vec{c},vec{a}-vec{b}+vec{c})+\[3pt] phantom{=,}&+(vec{b},vec{a},vec{a}-vec{b}+vec{c})+underbrace{(vec{b},vec{b},vec{a}-vec{b}+vec{c})}_0-(vec{b},vec{c},vec{a}-vec{b}+vec{c})+\[3pt] phantom{=,}&+(vec{c},vec{a},vec{a}-vec{b}+vec{c})+(vec{c},vec{b},vec{a}-vec{b}+vec{c})-underbrace{(vec{c},vec{c},vec{a}-vec{b}+vec{c})}_0=\[3pt] =,&underbrace{(vec{a},vec{b},vec{a})}_0-underbrace{(vec{a},vec{b},vec{b})}_0+(vec{a},vec{b},vec{c})-underbrace{(vec{a},vec{b},vec{a})}_0+(vec{a},vec{c},vec{b})-underbrace{(vec{a},vec{c},vec{c})}_0+\[3pt] phantom{=<br />,}&+underbrace{(vec{b},vec{a},vec{a})}_0-underbrace{(vec{b},vec{a},b)}_0+(vec{b},vec{a},vec{c})-(vec{b},vec{c},vec{a})+underbrace{(vec{b},vec{c},vec{b})}_0-underbrace{(vec{b},vec{c},vec{c})}_0+\[3pt] phantom{=,}&+underbrace{(vec{c},vec{a},vec{a})}_0-(vec{c},vec{a},vec{b})+underbrace{(vec{c},vec{a},vec{c})}_0-(vec{c},vec{b},vec{a})+underbrace{(vec{c},vec{b},vec{b})}_0-underbrace{(vec{c},vec{b},vec{c})}_0=\[3pt] =,&(vec{a},vec{b},vec{c})+underbrace{(vec{a},vec{c},vec{b})}_{-(vec{a},vec{b},c)}+underbrace{(vec{b},vec{a},vec{c})}_{-(vec{a},vec{b},c)}-underbrace{(vec{b},vec{c},a)}_{(vec{a},vec{b},c)}-underbrace{(vec{c},vec{a},vec{b})}_{(vec{a},vec{b},c)}+underbrace{(vec{c},vec{b},vec{a})}_{-(vec{a},vec{b},c)}=-4cdot(vec{a},vec{b},vec{c}), end{aligned}

а затем его модуль |(vec{p},vec{q},vec{r})|=|-4|{cdot}|(vec{a},vec{b},vec{c})|=4V. По первому геометрическому свойству смешанного произведения искомый объем равен 4V.

Формула вычисления смешанного произведения

Теорема 1.9 (формула вычисления смешанного произведения). Если векторы vec{a},vec{b},vec{c} в правом ортонормированном базисе vec{i},vec{j},vec{k} имеют координаты x_a,y_a,z_a; x_b,y_b,z_b; x_c,y_c,z_c соответственно, то смешанное произведение этих векторов находится по формуле

(vec{a},vec{b},vec{c})= begin{vmatrix} x_a&y_a&z_a\ x_b&y_b&z_b\ x_c&y_c&z_c end{vmatrix}.

(1.17)

В самом деле, учитывая (1.10) и (1.15), по определению находим:

begin{gathered}left(x_a,vec{i}+y_a,vec{j}+z_a,vec{k},~begin{vmatrix}y_b&z_b\y_c&z_cend{vmatrix}vec{i}-begin{vmatrix}x_b&z_b\x_c&z_cend{vmatrix}vec{j}+begin{vmatrix}x_b&y_b\x_c&y_cend{vmatrix}vec{k}right)=\=x_abegin{vmatrix}y_b&z_b\y_c&z_cend{vmatrix}-y_abegin{vmatrix}x_b&z_b\x_c&z_cend{vmatrix}+z_abegin{vmatrix}x_b&y_b\x_c&y_cend{vmatrix}=begin{vmatrix}x_a&y_a&z_a\x_b&y_b&z_b\x_c&y_c&z_cend{vmatrix},end{gathered}

что и требовалось доказать.

Замечания 1.13

1. Используя свойства смешанного произведения, можно доказать линейность векторного произведения по первому множителю (см. п.1 замечаний 1.12 в разд.1.15):

bigl[alphacdotvec{a}+betacdotvec{b},,vec{c}bigl],=alphacdot[vec{a},vec{c}]+betacdot[vec{b},vec{c}].

Для этого найдем скалярное произведение вектора в левой части равенства и единичного вектора vec{i} стандартного базиса. Учитывая линейность смешанного произведения по второму множителю, получаем

begin{gathered}bigl(vec{i},[alphacdotvec{a}+betacdotvec{b},vec{c}]bigr),=bigl(vec{i},alphacdotvec{a}+betacdotvec{b},vec{c}bigr),=alphacdotbigl(vec{i},vec{a},vec{c}bigr)+betacdotbigl(vec{i},vec{b},vec{c}bigr),=\[3pt]=alphacdotbigl(vec{i},[vec{a},vec{c}]bigr)+betacdotbigl(vec{i},[vec{b},vec{c}]bigr),=bigl(vec{i},alphacdot[vec{a},vec{c}]+betacdot[vec{b},vec{c}]bigr),end{gathered}

т.е. абсцисса вектора, стоящего в левой части доказываемого равенства равна абсциссе вектора в правой его части (см. пункт З замечаний 1.10). Аналогично доказываем, что ординаты, а также и аппликаты, векторов в обеих частях равенства соответственно равны. Следовательно, это равные векторы, так как их координаты относительно стандартного базиса совпадают.

2. Из первого алгебраического свойства смешанного произведения и коммутативности скалярного произведения следует, что

bigl(vec{a},[vec{b},vec{c}]bigr),=bigl(vec{a},vec{b},vec{c}bigr),=bigl(vec{c},vec{a},vec{b}bigr),=bigl(vec{c},[vec{a},vec{b}]bigr),=bigl([vec{a},vec{b}],vec{c}bigr)

т.е. bigl(vec{a}, vec{b},vec{c} bigr),=bigl([vec{a},vec{b}],vec{c}bigr). Последнее равенство можно взять в качестве эквивалентного определения смешанного произведения.

3. Если тройка векторов vec{e}_1,vec{e}_2,vec{e}_3 является базисом пространства, то тройка векторов

vec{e}_1,!!^*=frac{[vec{e}_2,vec{e}_3]}{(vec{e}_1,vec{e}_2,vec{e}_3)};qquad vec{e}_2,!!^*=frac{[vec{e}_3,vec{e}_1]}{(vec{e}_1,vec{e}_2,vec{e}_3)};qquad vec{e}_3,!!^*=frac{[vec{e}_1,vec{e}_2]}{(vec{e}_1,vec{e}_2,vec{e}_3)}

образует взаимный базис.

В самом деле, указанный вектор vec{e}_1,!!^* по определению векторного произведения ортогонален векторам vec{e}_2 и vec{e}_3,т.е. bigl(vec{e}_2,vec{e}_1,!!^*bigr)=0 и bigl(vec{e}_3,vec{e}_1,!!^*bigr)=0, а скалярное произведение bigl(vec{e}_1,vec{e}_1,!!^*bigr) равно единице, так как bigl(vec{e}_1,vec{e}_1,!!^*bigr)=frac{(vec{e}_1,[vec{e}_2,vec{e}_3])}{(vec{e}_1,vec{e}_2,vec{e}_3)}=frac{(vec{e}_1,vec{e}_2,vec{e}_3)}{(vec{e}_1,vec{e}_2,vec{e}_3)}=1. Поэтому вектор vec{e}_1,!!^* содержится во взаимном базисе. Аналогичные рассуждения проводятся относительно векторов vec{e}_2,!!^* и vec{e}_3,!!^*. Поэтому базисы vec{e}_1,vec{e}_2,vec{e}_3 и vec{e}_1,!!^*,vec{e}_2,!!^*,vec{e}_3,!!^* взаимные.

4. Если a=begin{pmatrix} x_a&y_a&z_a end{pmatrix}^T,~ b=begin{pmatrix}x_b&y_b&z_bend{pmatrix}^T,~ c=begin{pmatrix} x_c&y_c&z_c end{pmatrix}^T — координатные столбцы векторов vec{a},vec{b},vec{c} в стандартном базисе, то их смешанное произведение находится по формуле

bigl(vec{a},vec{b},vec{c}bigr),=begin{pmatrix}x_a&y_a&z_aend{pmatrix}!cdot!begin{pmatrix}0&-z_b&y_b\z_b&0&-x_b\-y_b&x_b&0end{pmatrix}!cdot!begin{pmatrix}x_c\y_c\z_cend{pmatrix}.

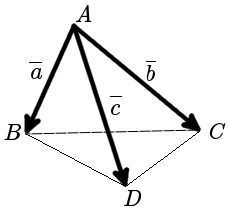
Пример 1.22. Параллелепипед ABCDA_1B_1C_1D_1 построен на векторах overrightarrow{AB}=vec{i}+2vec{j}+2vec{k}, overrightarrow{AD}=3vec{i}-2vec{j}+vec{k}, overrightarrow{AA_1}=2vec{i}-vec{j}+3vec{k} (рис.1.48). Требуется найти:

Треугольная пирамида, вписанная в параллелепипед

а) смешанное произведение bigl(overrightarrow{AB}, overrightarrow{AD}, overrightarrow{AA_1}bigr), а также ориентацию тройки overrightarrow{AB},overrightarrow{AD},overrightarrow{AA_1};

б) объем треугольной пирамиды ABDA_1;

в) высоту h параллелепипеда (расстояние между плоскостями оснований ABCD и A_1B_1C_1D_1).

Решение. а) Смешанное произведение bigl(overrightarrow{AB},overrightarrow{AD},overrightarrow{AA_1}bigr) находим по формуле (1.17):

bigl(overrightarrow{AB},overrightarrow{AD},overrightarrow{AA_1}bigr)=begin{vmatrix}1&2&2\3&-2&1\2&-1&3end{vmatrix}=-17.

Поскольку произведение отрицательно, то тройка векторов overrightarrow{AB},overrightarrow{AD},overrightarrow{AA_1} — левая (см. первое геометрическое свойство смешанного произведения).

Для нахождения смешанного произведения можно использовать матричную запись формулы (1.17) (см. пункт 4 замечаний 1.13). Векторам vec{a}=overrightarrow{AB}, vec{c}=overrightarrow{AA_1}, vec{a}=overrightarrow{AB} соответствуют координатные столбцы

a=begin{pmatrix}1\2\2end{pmatrix}!,qquad b=begin{pmatrix}3\-2\1end{pmatrix}!,qquad c=begin{pmatrix}2\-1\3end{pmatrix}

По формуле пункт 4 замечаний 1.13 получаем

bigl(vec{a},vec{b},vec{c}bigr)=begin{pmatrix}1&2&2end{pmatrix}!cdot!begin{pmatrix}0&-1&-2\1&0&-3\2&3&0end{pmatrix}!cdot!begin{pmatrix}2\-1\3end{pmatrix}=begin{pmatrix}1&2&2end{pmatrix}!cdot!begin{pmatrix}-5\-7\1end{pmatrix}

Результаты совпадают.

б) Объем V треугольной пирамиды ABDA_1 составляет шестую часть объема V_{*} параллелепипеда. Действительно, их высоты совпадают, а площадь S_{text{osn}} основания пирамиды составляет половину площади S_{*} параллелограмма ABCD.

Поэтому V=frac{h}{3}cdot S_{text{osn}}=frac{1}{3}cdotfrac{1}{2}cdot S_{*}cdot h=frac{1}{6}cdot V_{*}. Поскольку V_{*}=Bigl|bigl(overrightarrow{AB},overrightarrow{AD},overrightarrow{AA_1}bigr)Bigl|,=17, то V=frac{1}{6}cdot V_{*}=frac{17}{6}.

в) Высоту h параллелепипеда найдем по формуле h=frac{V_{*}}{S_{*}}, где S_{*} — площадь параллелограмма ABCD. Поскольку V_{*}=17 и S_{*}=5sqrt{5} (см. пример 1.20), то h=frac{17}{5sqrt{5}}.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Добавить комментарий