Как найти смешанную частную производную первого порядка - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 февраля 2016 года; проверки требуют 4 правки.

Определение[править | править код]

Пусть функция , и её частные производные

${displaystyle {frac {partial f}{partial x}},;{frac {partial f}{partial y}}}$

определены в некоторой окрестности точки $(x_{0},;y_{0})$ .
Тогда предел

${displaystyle lim _{Delta yto 0}{frac {displaystyle {{frac {partial f(x_{0},y_{0}+Delta y)}{partial x}}-{frac {partial f(x_{0},;y_{0})}{partial x}}}}{Delta y}},}$

если он существует, называется смешанной (смежной) производной функции f(x,;y) в точке $(x_{0},;y_{0})$ и обозначается ${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial ypartial x}}}$ .

Аналогично определяется ${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial xpartial y}}}$ как

${displaystyle lim _{Delta xto 0}{frac {displaystyle {{frac {partial f(x_{0}+Delta x,;y_{0})}{partial y}}-{frac {partial f(x_{0},;y_{0})}{partial y}}}}{Delta x}},}$

если он существует.

Смешанные частные производные порядка большего двух определяются индуктивно.^{[уточнить]}

Обозначение[править | править код]

${displaystyle {frac {partial ^{2}f}{partial ypartial x}}={frac {partial ^{2}z}{partial ypartial x}}=f''_{yx}=z''_{yx}}$
${displaystyle {frac {partial ^{2}f}{partial xpartial y}}={frac {partial ^{2}z}{partial xpartial y}}=f''_{xy}=z''_{xy}}$

Свойства[править | править код]

Если смешанные производные непрерывны в точке, то имеет место равенство ${displaystyle {frac {partial ^{2}f}{partial xpartial y}}={frac {partial ^{2}f}{partial ypartial x}}}$ .

Пример Шварца[править | править код]

${displaystyle f(x,;y)={begin{cases}displaystyle {xy{frac {x^{2}-y^{2}}{x^{2}+y^{2}}}},quad x^{2}+y^{2}>0\0,quad x=y=0end{cases}}Rightarrow {frac {partial ^{2}f(0,;0)}{partial xpartial y}}=-1neq 1={frac {partial ^{2}f(0,;0)}{partial ypartial x}}}$

То есть смешанные производные в примере Шварца не равны.

Имеет место теорема о равенстве смешанных производных

Теорема Шварца[править | править код]

Пусть выполнены условия:

функции ${displaystyle z=f(x,;y),;{frac {partial f}{partial x}},;{frac {partial f}{partial y}},;{frac {partial ^{2}f}{partial xpartial y}},;{frac {partial ^{2}f}{partial ypartial x}}}$ определены в некоторой окрестности точки $(x_{0},;y_{0})$ .
${displaystyle {frac {partial ^{2}f}{partial xpartial y}},;{frac {partial ^{2}f}{partial ypartial x}}}$ непрерывны в точке $(x_{0},;y_{0})$ .

Тогда ${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial xpartial y}}={frac {partial ^{2}f(x_{0},;y_{0})}{partial ypartial x}}}$ , то есть смешанные производные второго порядка равны в каждой точке, где они непрерывны.

Теорема Шварца о равенстве смешанных частных производных индуктивно распространяется на смешанные частные производные высших порядков, при условии, что они непрерывны.

Тем не менее, условие непрерывности смешанных производных отнюдь не является необходимым в теореме Шварца.

Пример[править | править код]

${displaystyle f(x,;y)={begin{cases}displaystyle {frac {x^{2}y^{2}}{x^{2}+y^{2}}},quad x^{2}+y^{2}>0\0,quad x=y=0end{cases}}Rightarrow }$ смешанные производные второго порядка равны всюду (в том числе и в точке ), однако частные производные второго порядка не являются непрерывными в точке

Доказательство

Так как ,
то ${displaystyle {frac {partial f}{partial x}}(0,;0)={frac {partial f}{partial y}}(0,;0)=0}$

В остальных точках

${displaystyle {frac {partial f}{partial x}}(x,;y)={frac {2xy^{4}}{(x^{2}+y^{2})^{2}}}}$

${displaystyle {frac {partial f}{partial y}}(x,;y)={frac {2x^{4}y}{(x^{2}+y^{2})^{2}}}}$

Таким образом,

${displaystyle {frac {partial f}{partial x}}(x,;0)=0;forall xin mathbb {R} }$

${displaystyle {frac {partial f}{partial x}}(0,;y)=0;forall yin mathbb {R} }$

Следовательно,

${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial xpartial y}}={frac {partial ^{2}f(x_{0},;y_{0})}{partial ypartial x}}=0}$

При

${displaystyle {frac {partial ^{2}f(x_{0},;y_{0})}{partial xpartial y}}={frac {partial ^{2}f(x_{0},;y_{0})}{partial ypartial x}}={frac {8x^{3}y^{3}}{(x^{2}+y^{2})^{3}}}}$

Легко видеть, что вторая смешанная производная имеет разрыв в точке , так как

${displaystyle lim _{xto 0}{frac {partial ^{2}f}{partial xpartial y}}(x,;x)=1}$ , а, например,

${displaystyle lim _{xto 0}{frac {partial ^{2}f}{partial xpartial y}}(x,;-x)=-1}$

^[1].

Примечания[править | править код]

↑ Тер-Крикоров А. М., Шабунин М. И. Глава 5. Функции многих переменных // Курс математического анализа. — 2-е изд. — М.: МФТИ, 1997. — С. 283. — 716 с. — ISBN 5-89155-006-7.

Источник

Смешанная частная производная

Изучаем производные

Что такое производная?

Геометрический смысл производной

Физический смысл производной

Обобщённая таблица производных

Как найти производную?

Производная сложной функции

Что такое дифференциал функции?

Источник

Частные производные

Частной производной по x функции z = f(x,y) в точке A(x₀,y₀) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.

Частные производные функции z(x,y) находятся по следующим формулам:

Вторые частные производные функции z(x,y) находятся по формулам:

Смешанные частные производные функции z(x,y) находятся по формулам:

Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word.

Решение онлайн
Видеоинструкция
Также решают

Правила ввода функции, заданной в явном виде

Примеры

x²+xy ≡ x^2+x*y.

cos²(2x+y) ≡ (cos(2*x+y))^2

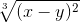≡ (x-y)^(2/3)

Правила ввода функции, заданной в неявном виде

Все переменные выражаются через x,y,z

Примеры

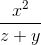≡ x^2/(z+y)

cos²(2x+zy) ≡ (cos(2*x+z*y))^2

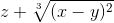≡ z+(x-y)^(2/3)

Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.

Частные производные функции нескольких переменных

Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δ_xz=f(x+Δ_x,y)-f(x,y) – это частное приращение функции z по аргументу x; Δ_yz=f(x,y+Δ_y)-f(x,y) – это частное приращение функции z по аргументу у.

Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:

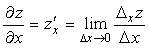– это частная производная функции z по аргументу x;

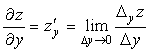– это частная производная функции z по аргументу у.

Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.

Пример 1. z=2x⁵+3x²y+y²–4x+5y-1

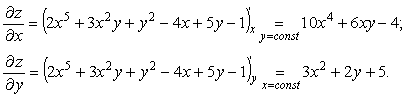
Пример 2. Найти частные производные функции z = f(x;y) в точке A(x₀;y₀).

Находим частные производные:

Найдем частные производные в точке А(1;1)

Находим вторые частные производные:

Найдем смешанные частные производные:

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Источник

Частной
производной функции z=f(x;
y)
по переменным x
и y
называется предел отношения
соответствующего частного приращения

или

к приращению данной переменной при
условии, что приращение переменной
стремится к нулю:

,
(1)

.
(2)

Из
определения следует, что производная
функции нескольких переменных определяется
как производная функции одной из
переменных при фиксированных значениях
всех других переменных. Поэтому все
правила и формулы дифференцирования,
выведенные для функции одной переменной,
сохраняются и для частных производных
функции нескольких переменных. Следует
помнить только одно правило: если
по одной переменной дифференцируем, то
остальные считаются постоянными.

Полным
дифференциалом функции z=z(x;
y)
называется выражение

,
(3)

а
полный дифференциал функции u=u(x;
y;
z)
будет определяться по формуле

.
(4)

При
малых

и

полное приращение

отличается от полного дифференциала

на бесконечно малую величину высшего
порядка от
.
Этим пользуются в приближенных
вычислениях:

Отсюда,
можно записать следующую формулу

.
(5)

Пример
3.1.

Найти
частные производные и полный дифференциал
функции

Решение.

;

Пример
3.2.

Найти
частные производные и полный дифференциал
функции
.

Решение.

;

Пример
3.3.

Найти
приближенное значение числа
.

Решение.

Число

есть частное значение функции
.
Известно, что
.
Поэтому, принимаем
,
.
Тогда
,

Значение

вычислим при помощи формулы (5). Найдем
частные производные в точке (2;0):

;

Ответ:
4,24.

Задачи
для самостоятельного решения:

Найти
частные производные и полный дифференциал
функций:

10.

Вычислить
приближенно:

11.

15.

12.

16.

13.

17.

14.

Показать,
что функция удовлетворяет уравнению

18.

;

19.

;

4 Частные производные высших порядков. Дифференциалы высших порядков

Частными
производными
второго порядка от функции z
= f(x;
y) называются
частные производные от ее частных
производных первого порядка, также
являющихся дифференцируемыми функциями.

–
вторая частная производная по x;

–
вторая частная производная по y;

– смешанные частные производные второго
порядка.

Аналогично
определяются и обозначаются частные
производные третьего и высших порядков,
например:

Теорема
Шварца. Если
смешанные частные производные второго
порядка непрерывны, то они равны между
собой. Другими словами, результат
смешанного дифференцирования не зависит
от порядка:

.
(6)

Вторым
дифференциалом или дифференциалом
второго порядка для функции z
называется выражение

,
где
,

.
(7)

Дифференциалы
высших порядков определяются по аналогии:

.
(8)

Выражение
для

формально можно записать в виде,
напоминающем формулу бинома Ньютона:

.
(9)

Пример
4.1.

Найти
частные произвольные второго порядка
функции
.

Решение.

;

Пример
4.2.

Проверить,
что

для функции z=ln(x²
– y²
+ 3).

Решение.
Найдем частные
производные:

Действительно,
смешанные частные
производные второго порядка равны между
собой.

Задачи
для самостоятельного решения:

Дана
функция z=f(x;
y).
Проверить, удовлетворяет ли она данному
уравнению:

;

Дана
функция z=f(x;
y),
найти значения указанных выражений:

;

Найти
:

10.

11.

12.

13.

Дана
функция u.
Найти
.

14.

.
15.
.
16.
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Смешанная производная

Содержание:

Теорема 10.4 (о равенстве смешанных производных):
Доказательство:

Пусть функция определена и имеет частные производные и во всех точках множества . Тогда и сами являются функциями двух переменных, и, стало быть, можно определить их частные производные:

Они называются частными производными второго порядка функции .

Точно таким же образом можно определить частные производные -го порядка для произвольного натурального . Они называются частными производными высших порядков. — примеры частных производных высших порядков. Здесь возникает естественный вопрос: равны ли между собой частные производные второго порядка и , которые называются смешанными производными?

Ответ на этот вопрос в общем случае отрицательный. Однако справедлива следующая теорема.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Теорема 10.4 (о равенстве смешанных производных):

Пусть функция и ее частные производные

определены в некоторой окрестности точки , причем и непрерывны в точке . Тогда в точке .

Доказательство:

Составим смешанные частные приращения функции :

(109)

Учитывая последнее равенство и применяя теорему Лагранжа по переменной к функции на промежутке , получим , (10.10)

где .

Применение теоремы Лагранжа правомерно, поскольку по предположению теоремы существует частная производная в достаточно малой окрестности точки . Так как такое же предположение верно и для частной смешанной производной то, снова применяя теорему Лагранжа на промежутке , из (10.10) получим , (10.11) где . Поскольку по условию теоремы функция непрерывна в точке , то последнее равенство можно записать в следующей форме: , (10.12) где при и . Из (10.12) следует, что . (10.13) Совершенно аналогично можно доказать, что

. (10.14) Из последних двух равенств в силу (10.9) следует утверждение теоремы.

Возможно вам будут полезны данные страницы:

Замечание 10.2.

В последней теореме условие непрерывности смешанных производных является существенным. То есть при отсутствии этого условия смешанные производные могут быть различными в данной точке .

Действительно, рассмотрим функцию и докажем, что ее смешанные частные производные в точке (0,0) не равны друг другу. Действительно,

Теперь вычислим вторые производные: Осталось заметить, что смешанные частные производные разрывны в точке (0,0). В самом деле, например, при . Следовательно, . А это значит, что не является непрерывной в точке (0,0).