Как найти смешанную дробь в квадрате - Сайт, где вы сможете решить свои вопросы

Как выполнить возведение дроби в квадрат? Как возвести в квадрат смешанное число?

Чтобы найти квадрат дроби, нужно найти произведение двух множителей, каждый из которых равен этой дроби:

$[{(frac{a}{b})^2} = frac{a}{b} cdot frac{a}{b}]$

Например,

$[{(frac{1}{4})^2} = frac{1}{4} cdot frac{1}{4} = frac{1}{{16}};]$

$[{(frac{2}{9})^2} = frac{2}{9} cdot frac{2}{9} = frac{4}{{81}};]$

$[{(frac{7}{{16}})^2} = frac{7}{{16}} cdot frac{7}{{16}} = frac{{49}}{{256}};]$

$[{(frac{5}{{11}})^2} = frac{5}{{11}} cdot frac{5}{{11}} = frac{{25}}{{121}}.]$

Другой способ найти дробь в квадрате — возвести в квадрат отдельно числитель, отдельно — знаменатель:

$[{(frac{a}{b})^2} = frac{{{a^2}}}{{{b^2}}}]$

Например,

$[{(frac{3}{{10}})^2} = frac{{{3^2}}}{{{{10}^2}}} = frac{9}{{100}};]$

$[{(frac{5}{{12}})^2} = frac{{{5^2}}}{{{{12}^2}}} = frac{{25}}{{144}};]$

$[{(frac{6}{{17}})^2} = frac{{{6^2}}}{{{{17}^2}}} = frac{{36}}{{289}};]$

$[{(frac{{19}}{{30}})^2} = frac{{{{19}^2}}}{{{{30}^2}}} = frac{{361}}{{900}}.]$

Чтобы найти квадрат смешанного числа (смешанной дроби), надо сначала перевести это число в неправильную дробь, возвести ее в квадрат, а затем из полученной неправильной дроби выделить целую часть.

Например,

$[{(1frac{2}{3})^2} = {(frac{5}{3})^2} = frac{5}{3} cdot frac{5}{3} = frac{{25}}{9} = 2frac{7}{9};]$

$[{(2frac{3}{5})^2} = {(frac{{13}}{5})^2} = frac{{13}}{5} cdot frac{{13}}{5} = frac{{169}}{{25}} = 6frac{{19}}{{25}};]$

$[{(7frac{1}{2})^2} = {(frac{{15}}{2})^2} = frac{{15}}{2} cdot frac{{15}}{2} = frac{{225}}{4} = 56frac{1}{4};]$

$[{(4frac{1}{6})^2} = {(frac{{25}}{6})^2} = frac{{25}}{6} cdot frac{{25}}{6} = frac{{625}}{{36}} = 17frac{{13}}{{36}}.]$

Источник

Загрузить PDF

Возведение в квадрат дробей – это одна из самых простых операций с дробями. Она похожа на возведение в квадрат целых чисел – нужно умножить числитель и знаменатель на себя.^[1] В некоторых случаях дробь можно упростить, а потом возвести ее в квадрат, чтобы упростить процесс. Эта статья научит вас возводить в квадрат дроби.

1
Уясните, как возводить в квадрат целые числа. Если показатель степени равен 2, то число нужно возвести в квадрат. Для этого нужно умножить число на себя.^[2] Например:
- 5² = 5 × 5 = 25
2
Возведение в квадрат дробей похоже на возведение в квадрат целых чисел. Чтобы возвести в квадрат дробь, нужно умножить ее на себя, то есть нужно умножить числитель на себя, а затем умножить знаменатель на себя.^[3] Например:
- (⁵/₂)² = ⁵/₂ × ⁵/₂ = (^5²/_2²).
- Возведя каждое число в квадрат, вы получите: (²⁵/₄).
3
Умножьте числитель на себя и умножьте знаменатель на себя. Не имеет значения, какое число умножать в первую очередь – главное возвести в квадрат и числитель, и знаменатель. Чтобы упростить процесс, начните с числителя: умножьте его на себя. Затем умножьте знаменатель на себя.
- Числитель записывается над чертой, а знаменатель – под чертой.
- Например: (⁵/₂)² = (^{5 x 5}/_{2 x 2}) = (²⁵/₄).
4
Сократите дробь. В конце вычислений нужно сократить дробь до наименьших значений числителя и знаменателя, или преобразовать неправильную дробь в смешанное число.^[4] В нашем примере дробь ²⁵/₄ является неправильной, потому что числитель больше знаменателя.
- Чтобы преобразовать дробь в смешанное число, разделите 25 на 4. Вы получите 6 (6 х 4 = 24) и остаток 1. Таким образом, смешанное число: 6 ¹/₄.
Реклама

1
Обратите внимание на знак «минус» перед дробью. Если дана отрицательная дробь, перед ней стоит знак «минус». В некоторых случаях отрицательные дроби (и числа) заключают в круглые скобки, чтобы не перепутать отрицательную дробь (или число) с операцией вычитания.^[5]
- Например: (–²/₄)
2
Умножьте дробь на себя. То есть умножьте числитель на себя, а затем умножьте знаменатель на себя. Или просто умножьте дробь на себя.
- Например: (–²/₄)² = (–²/₄) x (–²/₄)
3
Помните, что при перемножении двух отрицательных чисел получается положительное число. Если перед дробью стоит знак «минус», то дробь отрицательная. Возводя в квадрат дробь, вы перемножаете два отрицательных числа. При перемножении двух отрицательных чисел получается положительное число.^[6]
- Например: (-2) x (-8) = (+16)
4
После возведения в квадрат избавьтесь от знака «минус» (-). Возведя в квадрат дробь, вы перемножили два отрицательных числа. То есть теперь дробь стала положительной. Не забудьте записать окончательный ответ без знака «минус».^[7]
- В нашем примере конечная дробь будет положительной.
- (–²/₄) x (–²/₄) = (+⁴/₁₆)
- В подавляющем большинстве случаев знак «плюс» (+) перед положительными дробями (и числами) не пишут.^[8]
5
Сократите дробь. В конце вычислений нужно сократить дробь до наименьших значений числителя и знаменателя, или преобразовать неправильную дробь в смешанное число, которое затем сокращается.
- Например: у числителя и знаменателя дроби (⁴/₁₆) есть общий делитель 4.
- Разделите дробь на 4: 4/4 = 1, 16/4 = 4
- Запишите сокращенную дробь: (¹/₄)
Реклама

1
Проверьте, можно ли сократить дробь перед тем, как возвести ее в квадрат. Как правило, легче сократить дробь до ее возведения в квадрат. Чтобы сократить дробь до наименьших значений числителя и знаменателя, нужно разделить и числитель, и знаменатель на общий делитель.^[9] Сокращение дроби до возведения в квадрат означает, что сокращать дробь после возведения в квадрат уже не нужно.
- Например: (¹²/₁₆)²
- Числа 12 и 16 можно разделить на 4: 12/4 = 3 и 16/4 = 4. Таким образом, дробь ¹²/₁₆ сокращается до ³/₄.
- Теперь возведите в квадрат дробь ³/₄.
- (³/₄)² = ⁹/₁₆. Эту дробь сократить нельзя.
- Чтобы доказать это, возведите в квадрат исходную дробь:
  - (¹²/₁₆)² = (^{12 x 12}/_{16 x 16}) = (¹⁴⁴/₂₅₆)
  - У числителя и знаменателя дроби (¹⁴⁴/₂₅₆) есть общий делитель 16. Разделив числитель и знаменатель на 16, вы сократите дробь до (⁹/₁₆), то есть получается такая же дробь, как при сокращении до возведения в квадрат.
2
Научитесь определять, когда нужно повременить с сокращением дроби. Работая с более сложными уравнениями, можно сократить один из множителей. В этом случае с сокращением дроби лучше подождать. Дробь, которая участвовала в приведенном выше примере, умножим на число:
- Например: 16 × (¹²/₁₆)²
- Степень запишите в виде произведения дроби на себя, а затем сократите множитель:16 * ¹²/₁₆ * ¹²/₁₆
  - Так как множитель равен 16, и один из знаменателей равен 16, можно сократить и множитель, и один из знаменателей – просто зачеркните их.
- Упрощенное уравнение запишется так: 12 × ¹²/₁₆
- Сократите дробь ¹²/₁₆, разделив числитель и знаменатель на 4. Вы получите дробь: ³/₄
- Перемножьте: 12 × ³/₄ = 36/4
- Разделите: 36/4 = 9
3
Научитесь упрощать степень. Упрощение степени – это другой способ решить ту же задачу. Вы получите тот же ответ, но процесс вычисления немного изменится.
- Например: 16 * (¹²/₁₆)²
- Запишите числитель и знаменатель в виде степеней: 16 * (^12²/_16²)
- Сократите множитель и показатель степени у знаменателя:16 * ^12²/_16²
  - Показатель степени множителя 16 равен 1: 16¹. По правилу деления степеней их показатели вычитаются: 16¹/16² = 16^1-2 = 16^-1 = 1/16.
- Вы получили дробь:^12²/₁₆
- Перепишите дробь в следующем виде и сократите ее: ^12*12/₁₆ = ¹² * ³/₄.
- Перемножьте: 12 × ³/₄ = 36/4
- Разделите: 36/4 = 9
Реклама

Что вам понадобится

Бумага или доска
Карандаш/ручка или мел

Об этой статье

Эту страницу просматривали 90 874 раза.

Была ли эта статья полезной?

Источник

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Возведение дроби в степень

Поддержать сайт

Запомните!

При возведении в степень дроби нужно
возвести в степень и числитель, и знаменатель.

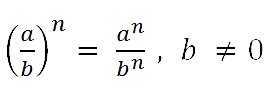
Данное свойство соответствует другой записи свойства № 5
«Степень частного», расмотренного на предыдущей странице.

Примеры возведения в степень дроби.

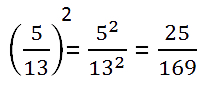
()² =

=

=

Как возвести в степень смешанное число

Чтобы возвести в степень смешанное число, сначала избавляемся от целой
части, превращая смешанное число в неправильную дробь. После этого
возводим в степень и числитель, и знаменатель.

Пример.

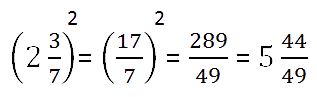
Формулу возведения в степень дроби применяют как
слева направо, так и справа налево, то есть, чтобы
разделить друг на друга степени
одинаковыми показателями, можно разделить одно основание на другое,
а показатель степени оставить неизменным.

Пример. Найти значение выражения рациональным способом.

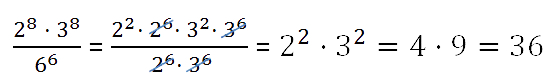
На нашем сайте вы также можете проверить свои вычисления и
возвести число в степень онлайн.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

A mixed fraction expresses the combination of an integer (whole number) and a fraction. For example, 3 2/3 is a mixed fraction. Squaring a number means multiplying it by itself; for example, 3^2 = 3*3 = 9.

Mixed fractions are often used in regular speech. For instance, if you asked a child how old he is, he might say “five and a half,” which would be written 5 1/2. He is unlikely to say “5.5,” “66 months” or “11 halves.”

Convert the Mixed Fraction to an Improper Fraction

Find the denominator of the fractional part. For example, in the mixed fraction 5 2/3, 3 is the denominator.

Multiply the integer portion by the denominator found in Step 1. In the example, 5*3 = 15.

Find the numerator of the fractional part. In 5 2/3, 2 is the numerator.

Add the result in Step 2 to the result in Step 3. In the example, 15 + 2 = 17.

Write a fraction with the denominator from Step 1 and the result from Step 4 as numerator. In the example, you would write “17/3.”

Square the Fraction

Square the numerator of the fraction in Section 1. In the example, 17*17 = 289.

Square the denominator of the fraction in Section 1. In the example 3*3 = 9.

Write a fraction with the numerator from Step 1 and the denominator from Step 2. In the example, you would write “289/9.”

Convert Back to a Mixed Fraction

Divide the numerator of the fraction in Section 2 by its denominator, write the result as quotient and remainder. In the example, 289/9 = 32 with a remainder of 1.

Write the whole number of the result in Step 1. In the example, you would write “32.” This is the numerator of the mixed fraction result.

Write a fraction with the remainder from Step 1 as the numerator and the denominator from the fraction in Section 2 as the denominator. In the example, you would write “1/9.”

Write the result of Step 2 and then Step 3. This is the mixed-fraction result, 32 1/9.

Источник

Смешанная дробь выражает комбинацию целого числа (целое число) и дроби. Например, 3 2/3 – смешанная фракция. Квадрат числа означает его умножение; например, 3 ^ 2 = 3 * 3 = 9.

Смешанные фракции часто используются в обычной речи. Например, если вы спросите ребенка, сколько ему лет, он может сказать «пять с половиной», что будет написано 5 1/2. Он вряд ли скажет «5, 5», «66 месяцев» или «11 половин».

Преобразовать смешанную дробь в неправильную дробь

Найдите знаменатель дробной части. Например, в смешанной фракции 5 2/3, 3 – знаменатель.

Умножьте целую часть на знаменатель, найденный на шаге 1. В примере 5 * 3 = 15.

Найдите числитель дробной части. В 5 2/3 2 – числитель.

Добавьте результат в шаге 2 к результату в шаге 3. В примере 15 + 2 = 17.

Запишите дробь со знаменателем из шага 1 и результат из шага 4 в качестве числителя. В этом примере вы должны написать «17/3».

Квадрат Фракция

Возведите в квадрат числитель дроби в разделе 1. В примере 17 * 17 = 289.

Квадрат знаменателя дроби в разделе 1. В примере 3 * 3 = 9.

Напишите дробь с помощью числителя из шага 1 и знаменателя из шага 2. В этом примере вы должны написать «289/9».

Конвертировать обратно в смешанную дробь

Разделите числитель дроби в Разделе 2 на ее знаменатель, запишите результат как частное и остаток. В примере 289/9 = 32 с остатком 1.

Запишите полное число результата на шаге 1. В этом примере вы должны написать «32». Это числитель результата смешанной дроби.

Запишите дробь с остатком от шага 1 в качестве числителя и знаменатель от дроби в разделе 2 в качестве знаменателя. В этом примере вы должны написать «1/9».

Запишите результат шага 2, а затем шага 3. Это результат смешанной дроби, 32 1/9.

Источник

Что вам понадобится

Об этой статье

Была ли эта статья полезной?

Возведение дроби в степень

Как возвести в степень смешанное число

Ваши комментарии

Convert the Mixed Fraction to an Improper Fraction

Square the Fraction

Convert Back to a Mixed Fraction

Преобразовать смешанную дробь в неправильную дробь

Квадрат Фракция

Конвертировать обратно в смешанную дробь

Вам также может понравиться

Как найти хорошего юриста по недвижимости

Как найти размерность калькулятор

Синий значок в хамачи как исправить

Добавить комментарий Отменить ответ