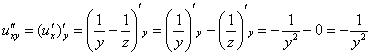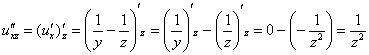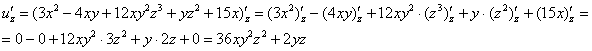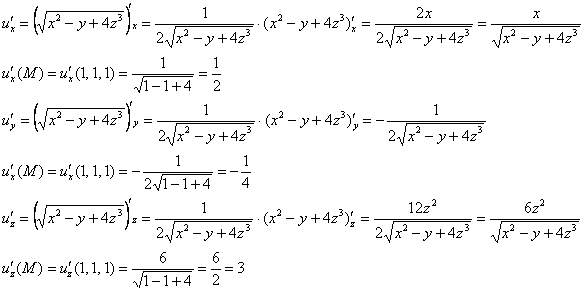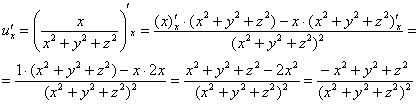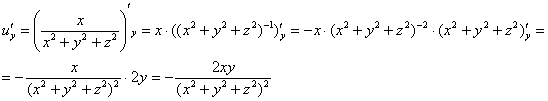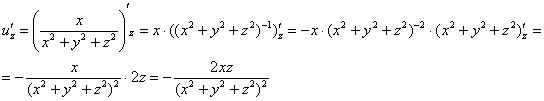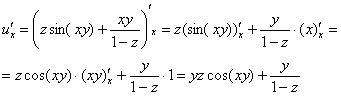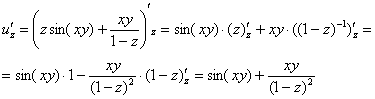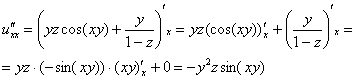Смешанная частная производная
Как найти?
Постановка задачи
Найти смешанную частную производную второго порядка функции $ z = f(x_1,x_2) $
План решения
Смешанная частная производная второго порядка функции $ z = f(x_1,x_2) $ по переменным $ x_1 $ и $ x_2 $ обозначается: $ frac{partial^2 z}{partial x_1 partial x_2} $ или $ z”_{x_1 x_2} $
Порядок дифференцирования не имеет значения, то есть выполняется свойство:
$$ frac{partial^2 z}{partial x_1 partial x_2} = frac{partial^2 z}{partial x_1 partial x_2} $$
$$ z”_{xy} = z”_{yx} $$
- Фиксируем $ x_2 $. Считая функцию $ z = f(x_1,x_2) $ одной переменной от $ x_1 $ находим её производную $ z’_{x_1} $
- Фиксируем $ x_1 $ и по правилу дифференцирования функции одной переменной находим производную функции $ z = f(x_1,x_2) $ по $ x_2 $ и получаем $ z”_{x_1 x_2} $
Примеры решений
| Пример 1 |
| Найти смешанную частную производную функции $ z(x,y) = ln (x+y) $ |
| Решение |
|
Фиксируем переменную $ x $ и находим производную по $ y $: $$ z’_y = frac{1}{x+y} cdot (x+y)’_y = frac{1}{x+y} $$ Считая переменную $ y $ постоянной дифференцируем функцию $ z’_y $ по $ x $: $$ z”_{yx} = -frac{1}{(x+y)^2} cdot (x+y)’_x = -frac{1}{(x+y)^2} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ z”_{xy} = z”_{yx} = -frac{1}{(x+y)^2} $$ |
| Пример 2 |
| Найти смешанную производную функции $ z(x,y) = sin x cos y $ |
| Решение |
|
Фиксируем переменную $ y $ и выполняем дифференцирование по $ x $: $$ z’_x (y = const) = cos x cos y $$ Считаем постоянной $ x $ и находим производную по $ y $: $$ z’_{xy} (x = const) = -cos x sin y $$ |
| Ответ |
| $$ z’_{xy} = z’_{yx} = -cos x sin y $$ |
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 февраля 2016 года; проверки требуют 4 правки.
Определение[править | править код]
Пусть функция 
определены в некоторой окрестности точки 
Тогда предел
если он существует, называется смешанной (смежной) производной функции 


Аналогично определяется 
если он существует.
Смешанные частные производные порядка большего двух определяются индуктивно.[уточнить]
Обозначение[править | править код]
Свойства[править | править код]
- Если смешанные производные непрерывны в точке, то имеет место равенство
.
Пример Шварца[править | править код]
То есть смешанные производные в примере Шварца не равны.
- Имеет место теорема о равенстве смешанных производных
Теорема Шварца[править | править код]
Пусть выполнены условия:
- функции
определены в некоторой окрестности точки
.
непрерывны в точке
.
Тогда 
Теорема Шварца о равенстве смешанных частных производных индуктивно распространяется на смешанные частные производные высших порядков, при условии, что они непрерывны.
- Тем не менее, условие непрерывности смешанных производных отнюдь не является необходимым в теореме Шварца.
Пример[править | править код]



Доказательство
Так как 
то 
В остальных точках


Таким образом,


Следовательно,

При 

Легко видеть, что вторая смешанная производная имеет разрыв в точке 


[1].
Примечания[править | править код]
- ↑ Тер-Крикоров А. М., Шабунин М. И. Глава 5. Функции многих переменных // Курс математического анализа. — 2-е изд. — М.: МФТИ, 1997. — С. 283. — 716 с. — ISBN 5-89155-006-7.
Смешанная производная
Содержание:
- Теорема 10.4 (о равенстве смешанных производных):
- Доказательство:
Пусть функция 






Они называются частными производными второго порядка функции 
Точно таким же образом можно определить частные производные
-го порядка для произвольного натурального
. Они называются частными производными высших порядков.
— примеры частных производных высших порядков. Здесь возникает естественный вопрос: равны ли между собой частные производные второго порядка
и
, которые называются смешанными производными?
Ответ на этот вопрос в общем случае отрицательный. Однако справедлива следующая теорема.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Теорема 10.4 (о равенстве смешанных производных):
Пусть функция 







Доказательство:
Составим смешанные частные приращения функции 

Учитывая последнее равенство и применяя теорему Лагранжа по переменной 



где 
Применение теоремы Лагранжа правомерно, поскольку по предположению теоремы существует частная производная 












. (10.14) Из последних двух равенств в силу (10.9) следует утверждение теоремы.
Возможно вам будут полезны данные страницы:
Замечание 10.2.
В последней теореме условие непрерывности смешанных производных является существенным. То есть при отсутствии этого условия смешанные производные могут быть различными в данной точке 
Действительно, рассмотрим функцию 

Теперь вычислим вторые производные: 




Лекции:
- Предел функции
- Знакочередующиеся ряды
- Производная неявной функции
- Неопределенный интеграл
- Формула Байеса
- Значения случайной величины
- Площади поверхностей круглых фигур
- Интегралы для чайников
- Метод координат на прямой и его применение
- Системы счисления
Частные производные второго порядка функции трёх переменных
Общий
принцип нахождения частных производных
порядка второго порядка функции трёх
переменных аналогичен принципу нахождения
частных производных 2-го порядка функции
двух переменных. Поэтому, если вы хорошо
проработали урок Частные
производные функции двух переменных,
то будет всё очень просто.
Для
того чтобы найти частные производные
второго порядка, необходимо сначала
найти частные производные первого
порядка
или
в другой записи:
.
Частных
производных второго порядка девять
штук.
Первая
группа – это вторые производные по тем
же переменным:
или
–
вторая производная по «икс»;
или
–
вторая производная по «игрек»;
или
–
вторая производная по «зет».
Вторая
группа – это смешанные частные
производные 2-го порядка, их
шесть:
или
– смешанная производная
«икс по игрек»;
или
– смешанная производная
«игрек по икс»;
или
– смешанная производная
«икс по зет»;
или
– смешанная производная
«зет по икс»;
или
– смешанная производная
«игрек по зет»;
или
– смешанная производная
«зет по игрек».
Как и
для случая функции двух переменных, при
решении задач можно ориентироваться
на следующие равенства смешанных
производных второго порядка:
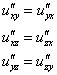
Примечание:
строго говоря, это не всегда так
На
всякий случай несколько примеров, как
правильно читать сиё безобразие
вслух:
–
«у два штриха дважды по игрек»;
–
«дэ два у по дэ зет квадрат»;
–
«у два штриха по икс по зет»;
–
«дэ два у по дэ зет по дэ игрек».
Примеры на нахождение
частных производных 2-го прядка для
функции трёх переменных на практике
встречаются реже. Обычно они не очень
сложные, но довольно большие по объему.
Пример 10
Найти
все частные производные первого и
второго порядка функции трёх переменных
Решение: Сначала
найдем частные производные первого
порядка:
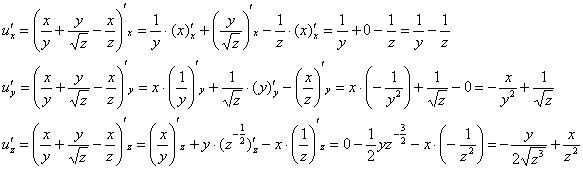
Частные производные
второго порядка рекомендую начинать
искать со смешанных производных,
поскольку это позволит выяснить, а
правильно ли вообще найдены производные
первого порядка.
Берём
найденную производную
и
дифференцируем её по «игрек»:
Берём
найденную производную
и
дифференцируем её по «икс»:
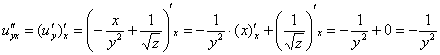
Равенство
выполнено.
Гуд.
Разбираемся
со второй парой смешанных производных.
Берём
найденную производную
и
дифференцируем её по «зет»:
Берём
найденную производную
и
дифференцируем её по «икс»:
–
всё путём.
Аналогично
разбираемся с третьей парой смешанных
производных:
Нормалёк.
После проделанных
трудов гарантированно можно утверждать,
что, во-первых, мы правильно нашли все
частные производные 1-го порядка,
во-вторых, правильно нашли и смешанные
частные производные 2-го порядка.
Осталось
найти ещё три частные производные
второго порядка, вот здесь уже во
избежание ошибок следует максимально
сконцентрировать внимание:

Готово.
Повторюсь, задание не столько сложное,
сколько объемное. Решение можно сократить
и сослаться на равенства смешанных
частных производных, но в этом случае
не будет проверки. Поэтому лучше таки
потратить время и найти все производные
(к тому же это может потребовать
преподаватель), или, в крайнем случае,
выполнить проверку на черновике.
Пример 11
Найти
все частные производные первого и
второго порядка функции трёх переменных
Это пример для
самостоятельного решения.
Решения и ответы:
Пример
2: Решение:
Пример
4: Решение: Найдем
частные производные первого
порядка.
Составим
полный дифференциал первого порядка:
Пример
6: Решение: Вычислим
частные производные первого порядка в
точке
:
Пример
7: Решение: Вычислим
частные производные первого порядка в
точке
:
Пример
9: Решение: Найдем
частные производные первого порядка:
Пример
11: Решение: Найдем
частные производные первого
порядка:
Найдем
частные производные второго
порядка:
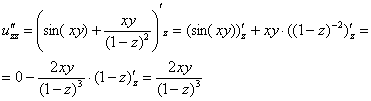
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
08.02.20157.31 Mб91.rtf
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Смешанная частная производная
Изучаем производные
Что такое производная?
Геометрический смысл производной
Физический смысл производной
Обобщённая таблица производных
Как найти производную?
Производная сложной функции
Что такое дифференциал функции?










 -го порядка для произвольного натурального
-го порядка для произвольного натурального  . Они называются частными производными высших порядков.
. Они называются частными производными высших порядков.  — примеры частных производных высших порядков. Здесь возникает естественный вопрос: равны ли между собой частные производные второго порядка
— примеры частных производных высших порядков. Здесь возникает естественный вопрос: равны ли между собой частные производные второго порядка  и
и  , которые называются смешанными производными?
, которые называются смешанными производными? . (10.14) Из последних двух равенств в силу (10.9) следует утверждение теоремы.
. (10.14) Из последних двух равенств в силу (10.9) следует утверждение теоремы.