Смешанные числа: определения, примеры
Смешанное число — это число, состоящее из натурального числа и обыкновенной дроби. Пишут в виде
.
Где n — целая часть,
— дробная часть.
Смешанное число равно сумме своей целой и дробной части. То есть
.
Примеры смешанных чисел
Каждое такое смешанное число содержит целую и дробную части.
Чтобы точно определять, какая именно перед вами дробь, запомните:
-
Дробь вида
называется правильной дробью. В ней числитель всегда меньше знаменателя.
-
Дробь вида
называется неправильной. В таких дробях числитель больше знаменателя или равен ему.
-
Дробь вида
называется смешанной дробью/смешанным числом. Такая дробь состоит из целой части (натуральное число) и дробной части.
Смешанные числа можно складывать, вычитать, умножать и делить. Давайте узнаем, как именно это делать.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.

Сложение смешанных чисел
Всего мы рассмотрим три типа сложения со смешанными числами. В каждом подпункте приведено необходимое правило и примеры выполнения решений.
Сложение смешанного числа и натурального числа
Запоминаем
Чтобы сложить смешанное число и натуральное число, прибавьте натурально число к целой части смешанного числа, а дробную часть оставьте нетронутой.
Представим первое правило в виде буквенных выражений.
Выполним сложение смешанного числа
и натурального числа d.
Известно, что любое смешанное число равное сумме целой и дробной частей.
Это значит, что
.
Тогда
.
Рассмотрим примеры сложения смешанных чисел с натуральными числами.
Пример 1. Выполните сложение смешанного числа
и натурального числа 18.
Как решаем:
Записываем выражение
Согласно правилу, прибавляем к натуральному числу целую часть смешанного числа и вычисляем:
.
Ответ:
.
Пример 2. Выполните сложение смешанного числа
и натурального числа 10.
Как решаем:
Записываем выражение:
.
.
Ответ:
.
Пример 3. Выполните сложение смешанного числа
и натурального числа 2.
Как решаем:
Записываем выражение:
.
Ответ:
.
Сложение смешанного числа со смешанным числом
Запоминаем
Чтобы сложить смешанное число с другим смешанным числом, сложите сначала целые части этих чисел, а затем — дробные части.
Представим правило в виде буквенных выражений.
Выполним сложение смешанного числа
и смешанного числа
.
Следуя правилу, запишем выражение в виде:
.
Рассмотрим примеры сложения смешанных чисел.
Пример 1. Сложите смешанное число
и смешанное число
.
Как решаем:
Записываем выражение:
.
Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:
Решаем: складываем целые части 2 + 7 = 9.
Чтобы выполнить сложение дробных частей, воспользуемся правилом сложения дробей с разными знаменателями: приведем дроби к наименьшему общему знаменателю и выполним сложение.
.
Наименьшее общее кратное 5 и 15 — 15.
.
Если в результате сложения получилась сократимая дробь, сокращайте, не задумываясь:
сокращаем на 3, получим дробь
.
.
Ответ:
.
Пример 2. Сложите смешанное число
и смешанное число
.
Как решаем:
Записываем выражение:
.
Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:
.
Решаем: складываем целые части 13 + 2 = 15.
Складываем дробные части
Наименьшее общее кратное 12 и 20 равно 60.
.
Сокращаем дробь
на
.
.
Ответ:
Таким же образом можно складывать три, четыре и больше натуральных чисел. Не забывайте сокращать дроби и выделять целые части из неправильных дробей.
Сложение смешанного числа и правильной дроби
Запоминаем
Чтобы выполнить сложение смешанного числа и правильной дроби, прибавьте к дроби дробную часть смешанного числа, а целую часть оставьте без изменений.
Представим правило в виде буквенного выражения.
Если нам нужно сложить смешанное число
и правильную дробь
, то запишем следующее выражение:
.
Рассмотрим примеры сложения смешанных чисел с обыкновенными дробями.
Пример 1. Выполните сложение обыкновенной дроби
и смешанного числа
Как решаем:
Записываем выражение:
Согласно правилу, складываем дробь с дробной частью смешанного числа:
.
Складываем дроби
.
Наименьшее общее кратное 5 и 20 равно 20.
, сокращаем на 5, получается
.
.
Ответ:
.
Пример 2. Выполните сложение правильной дроби
и смешанного числа
.
Как решаем:
Записываем выражение:
.
Следуя правилу, складываем дробь с дробной частью смешанного числа:
.
Складываем дроби
.
Наименьшее общее кратное 4 и 2 равно 4.
.
.
Ответ:
.
Чтобы выполнить сложение смешанного числа и неправильной обыкновенной дроби, выделите целую часть из неправильной дроби и выполните сложение смешанных чисел.
Вычитание смешанных чисел
Рассмотрим три типа вычитания со смешанными числами. В каждом подпункте вы найдете правила и решение примеров с разбором.
Вычитание одного смешанного числа из другого
Запоминаем
Любое смешанное число можно представить в виде суммы целой и дробной части.
Это значит, что
.
Исходя из значения дробных частей, вычитание можно выполнять тремя способами.
Если дробная часть уменьшаемого больше дробной части вычитаемого
, то выполняем вычитание целой части вычитаемого из целой части уменьшаемого, затем выполняем вычитание дробных частей. Вот так:
-
.
Пример. Выполните вычитание
.
Как решаем:
Чтобы решить пример, нужно выяснить, какая из дробных частей больше:
или
.
Чтобы сравнить две дроби, приведем их к общему знаменателю — 8:
.
По правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, чей числитель больше.
Это значит, что
.
.
Следуя правилу, выполняем вычитание
.
Вычитаем дробные части
.
НОК = 8
.
.
Ответ:
.
Запоминаем
Если дробные части смешанных чисел равны, то есть
, то разность этих смешанных чисел будет равна разности их целых частей.
Пример. Выполните вычитание:
Как решаем:
Дробные части смешанных чисел равны. Это значит, что
.
Следуя правилу, выполним вычитание:
.
Ответ:
.
Запоминаем
Если дробная часть уменьшаемого меньше дробной части вычитаемого
, то вычитание выполняется вот так
.
Пример. Найдите значение разности смешанных чисел
и
Как решаем:
Запишем выражение
Сначала выясним, как из дробных частей больше. Для этого приведем их к НОЗ.
НОК 5 и 15 = 15.
Следуя правилу, решаем:
.
Представим число 21 в виде смешанной дроби
и выполним вычитание дроби из натурального числа:
Ответ:
.
Вычитание смешанного числа из натурального числа
Запоминаем
Чтобы из целого числа вычесть смешанное число, сначала отнимите от натурального числа целую часть смешанного числа, а затем отнимите от этой разности дробную часть смешанного числа.
Представим правило в виде буквенного выражения:
.
Пример. Отнимите от натурального числа 15 смешанное число
Как решаем:
Запишем выражение:
.
Следуя правилу, выполним вычитание целой части смешанного числа из натурального числа:
Ответ:
Умножение смешанных чисел
Давайте разберемся как выполнять умножение в примерах, где есть смешанные числа.
Умножение смешанного числа на смешанное число
Запоминаем
Чтобы умножить одно смешанное число на другое, нужно перевести оба смешанных числа в неправильные дроби, а затем выполнить умножение по правилу умножения дробей.
Пример. Выполните умножение смешанного числа
и
Как решаем:
Запишем выражение
Следуя правилу, переведем смешанные числа в неправильные дроби.
Выполним умножение:
.
Из полученной неправильной дроби выделяем целую часть
.
Ответ:
.
Умножение смешанного числа на обыкновенную дробь
Запоминаем
Чтобы выполнить умножение смешанного числа и обыкновенной дроби, представьте смешанное число в виде неправильной дроби и выполните умножение дробей.
Пример. Умножьте смешанное число
на обыкновенную дробь
Как решаем:
Запишем выражение
Представим смешанное число в виде неправильной дроби.
.
Выполним умножение дробей
Выделим из полученной неправильной дроби целую часть
Ответ:
.
Умножение целого числа на дробь
Запоминаем
Чтобы умножить целое число на дробь, просто умножьте это число на числитель дроби.
Пример. Выполните умножение числа 7 на обыкновенную дробь
Как решаем:
Запишем выражение:
Выделим из получившейся неправильной дроби целую часть
.
Ответ:
Деление смешанных чисел
Вы уже рассмотрели три типа арифметических действий со смешанными числами. Осталось разобраться, как выполнять деление в примерах, где есть смешанные числа. Давай научимся это делать.
Деление смешанного числа на смешанное число
Запоминаем
Чтобы разделить одно смешанное число на другое, переведите оба числа в неправильные дроби и выполните деление, следуя правилу деления дробей.
Пример. Найдите результат деления смешанного числа
на смешанное число
Как решаем:
Запишем выражение:
Следуя правилу, переведем оба смешанных числа в неправильные дроби.
Пользуясь правилом деления дробей, находим частное:
Ответ:
.
Деление смешанного числа на целое число
Запоминаем
Чтобы разделить смешанное число на целое число, переведите смешанное число в неправильную дробь и выполните деление.
Пример. Разделите смешанное число
на натуральное число 15
Как решаем:
Запишем выражение
Следуя правилу, переведем смешанное число в неправильную дробь
Выполним деление
Ответ:
.
Деление целого числа на смешанное число
Запоминаем
Чтобы разделить целое число на смешанное число, переведите смешанное число в неправильную дробь и выполните деление.
Пример. Выполните деление натурального числа 30 на смешанное число
Запишем выражение
Представим смешанное число в виде неправильной дроби
.
Выполним деление
.
Выделим из полученной неправильной дроби целую часть
.
Ответ:
.
Деление смешанного числа на обыкновенную дробь
Запоминаем
Чтобы разделить смешанное число на обыкновенную дробь, представьте смешанное число в виде неправильной дроби и выполните деление.
Пример. Разделите смешанное число
на обыкновенную дробь
Как решаем:
Запишем выражение
.
Представим смешанное число в виде неправильной дроби
.
Выполним деление, следуя правилу деления дробей:
.
Ответ:
.
Мы можем использовать неправильные дроби и смешанные числа для представления одних и тех же значений. Рассмотрим на примере равенство неправильной дроби и смешанного числа 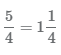 :
:
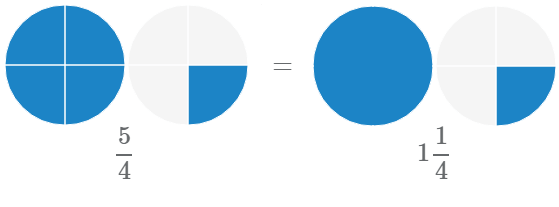
Перевод неправильной дроби в смешанное число
Для перевода неправильной дроби 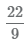 в смешанное число выполните следующие шаги:
в смешанное число выполните следующие шаги:
- 1 Разделим числитель на знаменатель 22 ÷ 9, получим 2 целых и 4 в остатке.
- 2 Число 2 будет целой частью смешанного числа.
-
3 Остаток от деления 4 будет числителем дроби, а знаменатель останется прежним, равным 9. В результате получаем
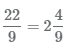
Перевод смешанного числа в неправильную дробь
Для перевода смешанного числа 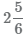 в неправильную дробь выполните следующие шаги:
в неправильную дробь выполните следующие шаги:
- 1 Умножим целую часть на знаменатель 2×6 и прибавим числитель 5. Полученное число 17=2×6+5запищем в числитель неправильной дроби.
- 2 Запищем в знаменатель неправильной дроби число 6, знаменатель при преобразование в неправильную дробь остается неизменным.
-
3 В результате шагов 1-2 получаем неправильную дробь
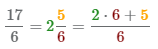
Рассмотрим на примерах как переводить смешанные числа в неправильные дроби.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Обыкновенные дроби
- Смешанное число
Пусть у нас есть 7 яблок:

Нам необходимо разделить их поровну между тремя детьми. Как это возможно сделать?
1 способ:
Можно каждое яблоко разделить на три доли, то есть мы получим по 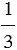 яблока, и дать всем детям долю от каждого яблока. Тогда каждый ребенок получит семь таких долей, значит, один ребенок получит
яблока, и дать всем детям долю от каждого яблока. Тогда каждый ребенок получит семь таких долей, значит, один ребенок получит 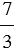 яблока:
яблока:
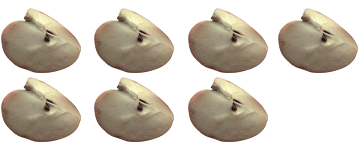
2 способ:
Так как у нас семь яблок, то мы можем каждому ребенку дать по два целых яблока, а седьмое поделить между ними поровну, то есть по 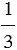 яблока каждому:
яблока каждому:

В этом случае каждый ребенок получит по  яблока.
яблока.
Такую сумму, как  , принято записывать так:
, принято записывать так: 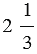 . Число
. Число 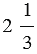 читают: “две целых одна третья”. Число
читают: “две целых одна третья”. Число 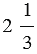 называют смешанным числом. В нем число 2 называют целой частью, а число
называют смешанным числом. В нем число 2 называют целой частью, а число 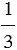 – его дробной частью, при этом дробная часть смешанного числа – это всегда правильная дробь.
– его дробной частью, при этом дробная часть смешанного числа – это всегда правильная дробь.
Вернемся к задаче, которую мы рассматривали. В обоих случаях дети получили одинаковые части яблок, то есть мы можем сказать, что: 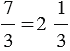 .
.
Данное равенство показывает, что неправильную дробь 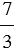 можно записать в виде смешанного числа
можно записать в виде смешанного числа 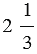 . Говорят, что из неправильной дроби
. Говорят, что из неправильной дроби 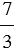 выделена целая часть. При этом из любой неправильной дроби, числитель которой нацело не делится на знаменатель, можно выделить целую часть, то есть записать ее в виде смешанного числа. При этом, если числитель делится нацело на знаменатель, то эта дробь равна натуральному числу.
выделена целая часть. При этом из любой неправильной дроби, числитель которой нацело не делится на знаменатель, можно выделить целую часть, то есть записать ее в виде смешанного числа. При этом, если числитель делится нацело на знаменатель, то эта дробь равна натуральному числу.
Чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
Пример 1: Выделим целую часть из неправильной дроби 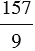 .
.
Для этого разделим 157 на 9 с остатком, имеем: 157: 9 = 17 (ост. 4)
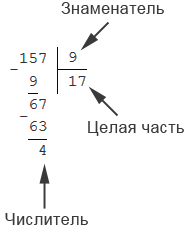
То есть получили, что неполное частное равно 17, а остаток – 4. Значит, 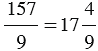 .
.
Мы выделили целую часть неправильной дроби, или по-другому, представили неправильную дробь в виде смешанного числа. На практике часто приходится выполнять обратное, то есть смешанное число представлять в виде неправильной дроби.
Чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в ее знаменатель записать знаменатель дробной части смешанного числа.
Пример 2: Преобразуем в смешанную дробь число 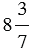 :
:
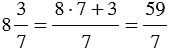 .
.
Стоит отметить, что переместительное и сочетательное свойство сложения натуральных чисел выполняются и для смешанных чисел. На их основе мы можем записать:
Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
Пример 3: Найдем сумму чисел 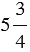 и
и  :
:

Обратите внимание, что число 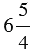 не является смешанным, так как дробь
не является смешанным, так как дробь 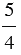 является неправильной.
является неправильной.
Со смешанными числами можно также проводить операцию вычитания. При этом, если дробная часть уменьшаемого больше или равна дробной части вычитаемого, то можно воспользоваться следующим правилом.
Чтобы найти разность двух смешанных чисел, надо из целой и дробной частей уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Пример 4: Найдем разность чисел 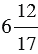 и
и 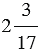 :
:
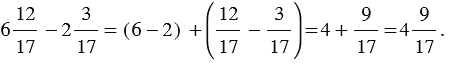
В случае, если дробная часть уменьшаемого меньше дробной части вычитаемого, данное правило использовать нельзя, но уменьшаемое можно преобразовать так, чтобы данное правило было применимо.
Пример 5: Найдем разность чисел 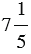 и
и 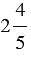 :
:
Мы видим, что дробная часть уменьшаемого меньше дробной части вычитаемого, выполним преобразование уменьшаемого:
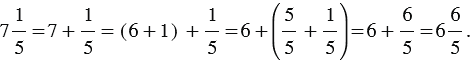
Тогда имеем:
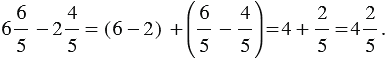
Советуем посмотреть:
Доли. Обыкновенные дроби
Сравнение дробей
Делители и кратные
Признаки делимости на 10, на 5 и на 2
Четные и нечетные числа
Признаки делимости на 9 и на 3
Простые и составные числа
Разложение на простые множители
Наибольший общий делитель
Наименьшее общее кратное
Деление и дроби
Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание смешанных чисел
Основное свойство дроби
Решето Эратосфена
Приведение дробей к общему знаменателю
Сравнение, сложение и вычитание дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Обыкновенные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1087,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1089,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1090,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1148,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1205,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1465,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1726,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1821,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 1139,
Мерзляк, Полонский, Якир, Учебник
Номер 9,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 316,
Мерзляк, Полонский, Якир, Учебник
Номер 383,
Мерзляк, Полонский, Якир, Учебник
Номер 451,
Мерзляк, Полонский, Якир, Учебник
Номер 466,
Мерзляк, Полонский, Якир, Учебник
Номер 1048,
Мерзляк, Полонский, Якир, Учебник
Номер 1118,
Мерзляк, Полонский, Якир, Учебник
Задание 88,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 486,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1245,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1589,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 530,
Мерзляк, Полонский, Якир, Учебник
Номер 539,
Мерзляк, Полонский, Якир, Учебник
Номер 580,
Мерзляк, Полонский, Якир, Учебник
Номер 582,
Мерзляк, Полонский, Якир, Учебник
Номер 583,
Мерзляк, Полонский, Якир, Учебник
Номер 873,
Мерзляк, Полонский, Якир, Учебник
Номер 1146,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 9,
Мерзляк, Полонский, Якир, Учебник
Номер 66,
Мерзляк, Полонский, Якир, Учебник
Номер 118,
Мерзляк, Полонский, Якир, Учебник
Номер 193,
Мерзляк, Полонский, Якир, Учебник
Номер 207,
Мерзляк, Полонский, Якир, Учебник
Номер 272,
Мерзляк, Полонский, Якир, Учебник
Номер 281,
Мерзляк, Полонский, Якир, Учебник
Номер 282,
Мерзляк, Полонский, Якир, Учебник
Номер 379,
Мерзляк, Полонский, Якир, Учебник
Номер 380,
Мерзляк, Полонский, Якир, Учебник
В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.
Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.
Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.
Сложение целого числа и правильной дроби
Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь ![]() . Чтобы решить этот пример, нужно число 2 представить в виде дроби
. Чтобы решить этот пример, нужно число 2 представить в виде дроби ![]() . Затем сложить дроби с разными знаменателями:
. Затем сложить дроби с разными знаменателями:
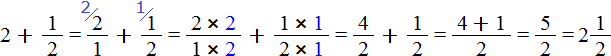
А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: ![]() , а конец так:
, а конец так: ![]() . Различие в том, что в первом случае число 2 и дробь
. Различие в том, что в первом случае число 2 и дробь ![]() соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что
соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что ![]() это свёрнутая форма записи смешанного числа, а
это свёрнутая форма записи смешанного числа, а ![]() — развёрнутая.
— развёрнутая.
Когда перед нами смешанное число вида ![]() , мы должны понимать, что знак сложения опущен.
, мы должны понимать, что знак сложения опущен.
Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.
Значит значение выражения ![]() равно
равно ![]()
![]()
Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:
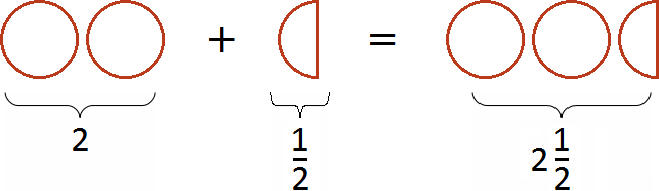
Пример 2. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем сложим дроби с разными знаменателями:
. Затем сложим дроби с разными знаменателями:
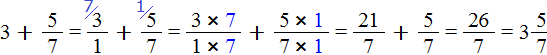
Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:
![]()
Пример 3. Найти значение выражения ![]()
Можно записать вместе число 2 и дробь ![]() , но этот ответ не будет окончательным, поскольку в дроби
, но этот ответ не будет окончательным, поскольку в дроби ![]() можно выделить целую часть.
можно выделить целую часть.
Поэтому в данном примере сначала нужно выделить целую часть в дроби ![]() . Пять вторых это две целых и одна вторая:
. Пять вторых это две целых и одна вторая:
![]()
Теперь в главном выражении ![]() вместо дроби
вместо дроби ![]() запишем смешанное число
запишем смешанное число ![]()
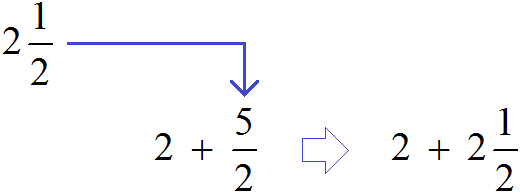
Получили новое выражение ![]() . В этом выражении смешанное число
. В этом выражении смешанное число ![]() запишем в развёрнутом виде:
запишем в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сложим две двойки, получим 4:
![]()
Теперь свернём полученное смешанное число:
![]()
Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:
![]()
Сложение смешанных чисел
Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения ![]() . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
. Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.
Для начала запишем смешанные числа в развёрнутом виде:
![]()
Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:
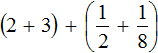
Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:
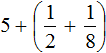
Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:
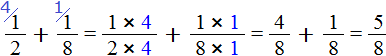
Получили ![]() . Теперь в главном выражении
. Теперь в главном выражении 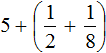 заменяем дробные части на полученную дробь
заменяем дробные части на полученную дробь ![]()
![]()
Теперь свернем полученное смешанное число:
![]()
Таким образом, значение выражения ![]() равно
равно ![]() . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
. Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:
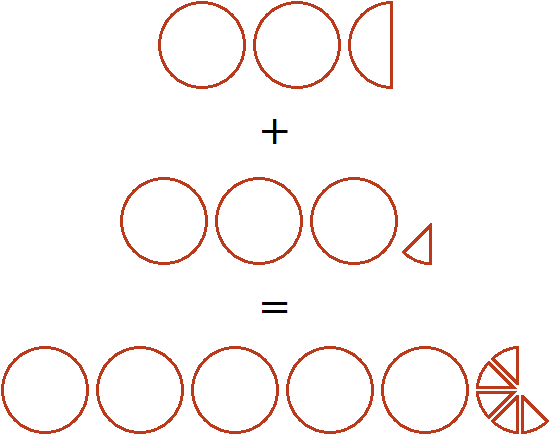
Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:
![]()
Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.
Пример 2. Найти значение выражения
Запишем смешанные числа в развёрнутом виде:
![]()
Сгруппируем целые и дробные части по отдельности:
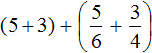
Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8
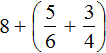
Теперь вычислим дробные части:
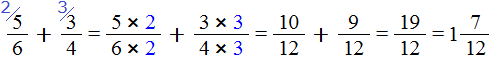
Получили смешанное число ![]() . Теперь в главном выражении
. Теперь в главном выражении 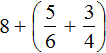 заменяем выражение в скобках на полученное смешанное число
заменяем выражение в скобках на полученное смешанное число ![]()
![]()
Получили выражение ![]() . В данном случае число 8 надо прибавить к целой части смешанного числа
. В данном случае число 8 надо прибавить к целой части смешанного числа ![]() . Для этого смешанное число
. Для этого смешанное число ![]() можно временно развернуть, чтобы было понятнее, что с чем складывать:
можно временно развернуть, чтобы было понятнее, что с чем складывать:
![]()
Сложим целые части. Получаем 9
![]()
Сворачиваем готовый ответ:
![]()
Таким образом, значение выражения равно
![]() .
.
Полное решение этого примера выглядит следующим образом:
![]()
Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:
Чтобы сложить смешанные числа, надо:
- привести дробные части этих чисел к общему знаменателю;
- отдельно выполнить сложение целых и дробных частей.
Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.
Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.
Пример 3. Найти значение выражения ![]()
Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:
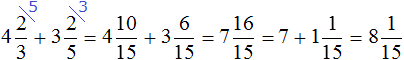
Сложение целого и смешанного числа
Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число ![]() . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
. В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:
![]()
Здесь смешанная дробь ![]() была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ
была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ ![]() .
.
Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:
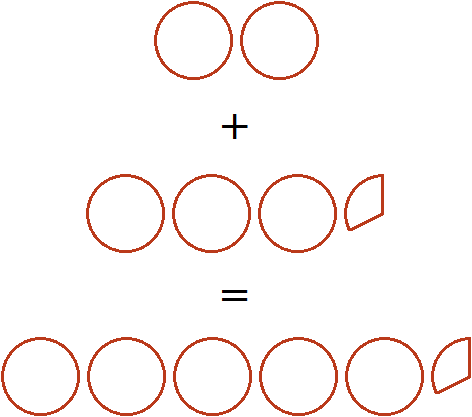
Пример 2. Найти значение выражения ![]()
В этом примере, как и в предыдущем, нужно сложить целые части:
![]()
Осталось свернуть целую и дробную части, но дело в том, что дробная часть ![]() представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:
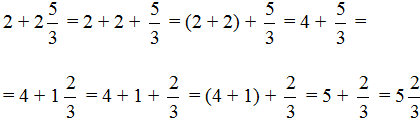
Вычитание дроби из целого числа
Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь ![]() . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби
. Чтобы решить такой пример, нужно целое число 1 представить в виде дроби ![]() , и выполнить вычитание дробей с разными знаменателями:
, и выполнить вычитание дробей с разными знаменателями:
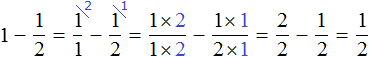
Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:
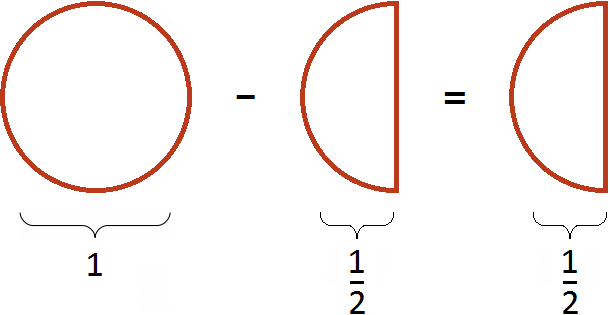
Пример 2. Найти значение выражения ![]() .
.
Представим число 2 в виде дроби ![]() , и выполним вычитание дробей с разными знаменателями:
, и выполним вычитание дробей с разными знаменателями:
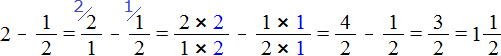
Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:
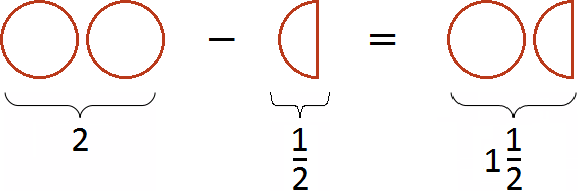
Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения ![]() , не приводя на бумаге никаких вычислений.
, не приводя на бумаге никаких вычислений.
Представим, что число 3 это три пиццы:

Нужно вычесть из них ![]() . Мы помним, что треть выглядит следующим образом:
. Мы помним, что треть выглядит следующим образом:

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

Получилось ![]() (две целых и две трети пиццы).
(две целых и две трети пиццы).
Чтобы убедиться в правильности решения, можно найти значение выражения ![]() обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:
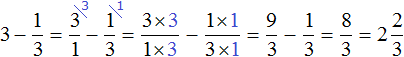
Пример 3. Найти значение выражения ![]()
Представим число 3 в виде дроби ![]() . Затем выполним вычитание дробей с разными знаменателями:
. Затем выполним вычитание дробей с разными знаменателями:
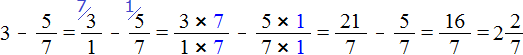
Вычитание смешанного числа из целого числа
Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .
Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа
в неправильную дробь, получим дробь
![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
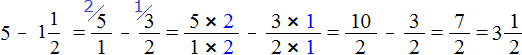
Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:
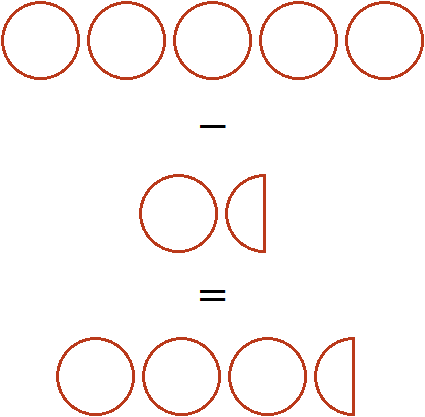
Пример 2. Найти значение выражения ![]()
Представим 6 в виде дроби ![]() , а смешанное число
, а смешанное число ![]() , в виде неправильной дроби. После перевода смешанного числа
, в виде неправильной дроби. После перевода смешанного числа ![]() в неправильную дробь, получим дробь
в неправильную дробь, получим дробь ![]() . Теперь выполним вычитание дробей с разными знаменателями:
. Теперь выполним вычитание дробей с разными знаменателями:
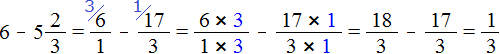
Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.
К примеру, если нужно быстро найти значение выражения ![]() , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)
, то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)

Тогда от той пиццы, от которой отрезали останется
![]() пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:
![]()
Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.
Вычитание смешанных чисел
Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения: ![]()
Чтобы решить этот пример, нужно смешанные числа ![]() и
и ![]() перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:
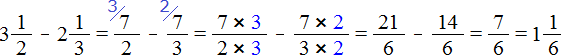
Если от трёх целых и половины пиццы вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:
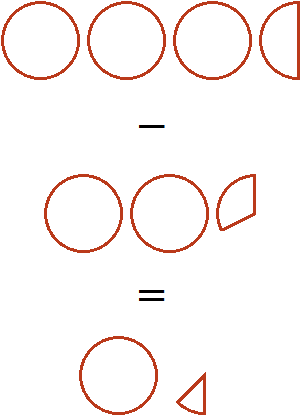
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа ![]() и
и ![]() в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
в неправильные дроби и выполняем вычитание дробей с разными знаменателями:
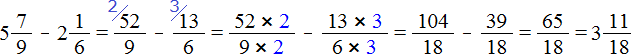
К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.
А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.
Умножение целого числа на дробь
Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.
Например, умножим число 5 на дробь ![]() . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби
. Чтобы решить этот пример, нужно число 5 умножить на числитель дроби ![]() , а знаменатель оставить без изменения:
, а знаменатель оставить без изменения:
![]()
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:
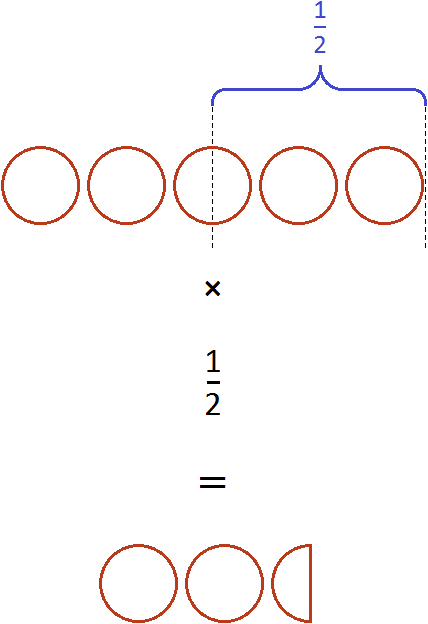
Пример 2. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
В ответе получилась неправильная дробь ![]() , но мы выделили её целую часть и получили 2.
, но мы выделили её целую часть и получили 2.
Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:
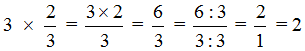
Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:
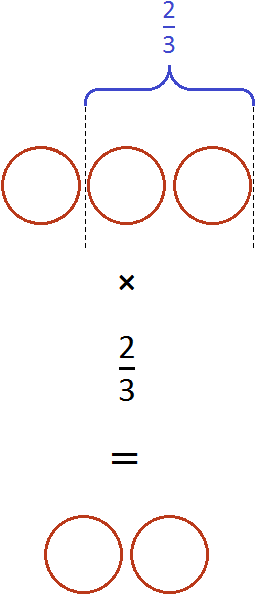
Пример 3. Найти значение выражения ![]()
Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:
![]()
Пример 4. Найти значение выражения ![]()
Умножим число 3 на числитель дроби ![]()
![]()
Умножение смешанного числа на дробь
Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.
Пример 1. Найти значение выражения ![]()
Переведём смешанное число ![]() в неправильную дробь. После перевода это число превратится в дробь
в неправильную дробь. После перевода это число превратится в дробь ![]() . Затем можно будет умножить эту дробь на
. Затем можно будет умножить эту дробь на
![]()
Допустим, имеются одна целая и половина пиццы:

Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:
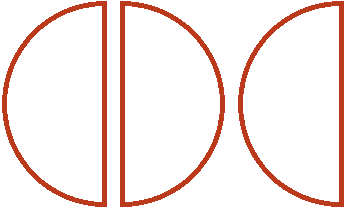
Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:
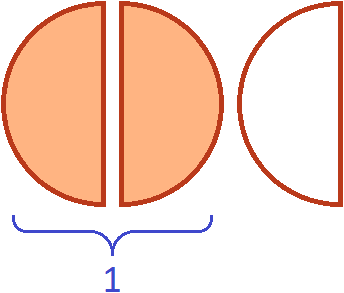
Поэтому значение выражения ![]() было равно 1
было равно 1
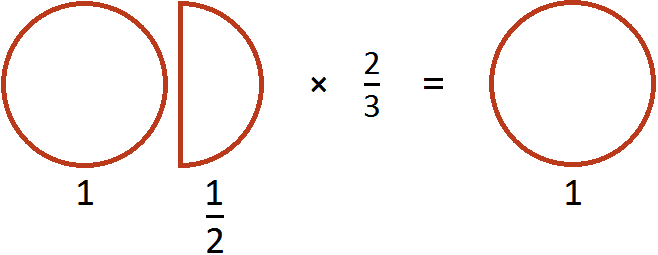
Умножение смешанных чисел
Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить ![]() и
и ![]() . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
. Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:
![]()
Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:
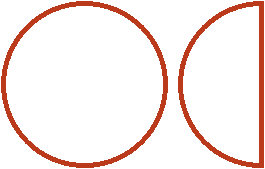
Теперь разберемся со смешанным множителем ![]() . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще
. Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще ![]() раза.
раза.
С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:
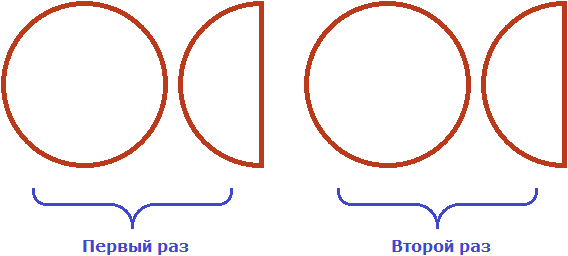
Но ещё осталось взять ![]() от изначальной целой пиццы и половины, ведь множителем было смешанное число
от изначальной целой пиццы и половины, ведь множителем было смешанное число ![]() . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
. Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:
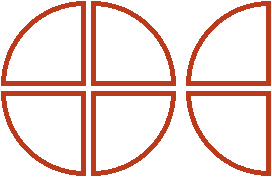
Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:
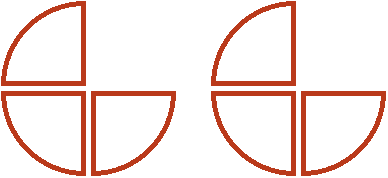
А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.
Поэтому значение выражения ![]() равно
равно ![]()
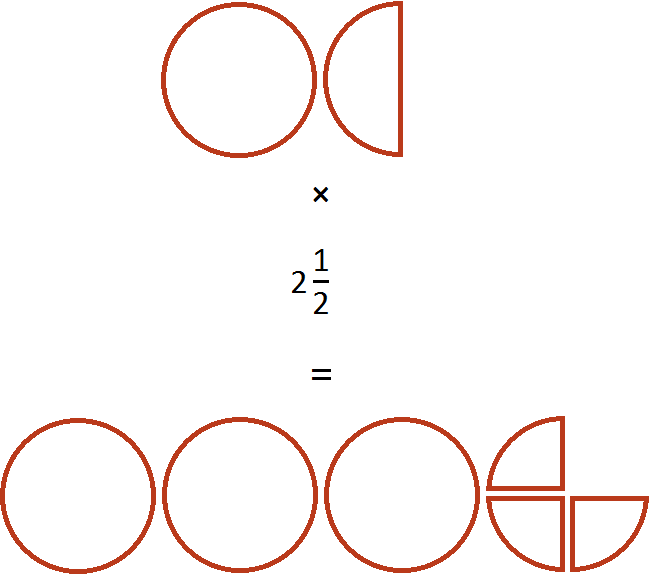
Пример 2. Найти значение выражения ![]()
Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:
![]()
Деление целого числа на дробь
Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.
Например, разделим число 3 на дробь ![]() . Здесь число 3 — это делимое, а дробь
. Здесь число 3 — это делимое, а дробь ![]() — делитель.
— делитель.
Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 3 на дробь
. Поэтому умножаем число 3 на дробь ![]()
![]()
Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз ![]() (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
(половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».
Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:
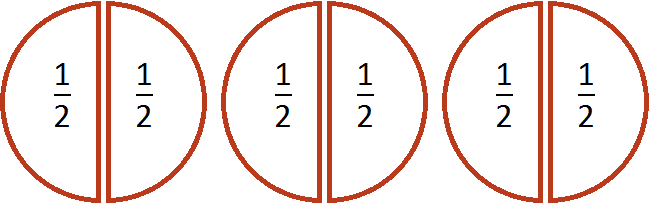
Поэтому значение выражения ![]() равно 6.
равно 6.
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби
пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби ![]() . После выделения целой части в этой дроби получим
. После выделения целой части в этой дроби получим ![]()
Теперь поставим вопрос так: «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух пиццах?».
(одна целая и половина пиццы) содержится в двух пиццах?».
Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:
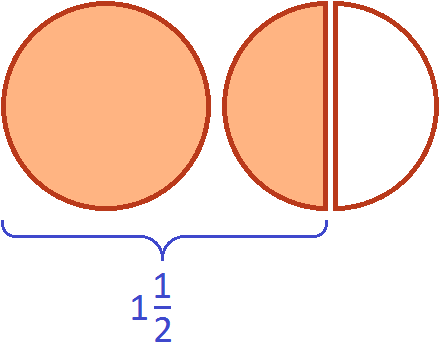
А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
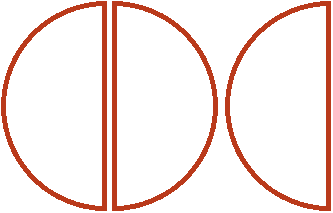
Поэтому значение выражения ![]() равно
равно ![]()
Пример 3. Найти значение выражения ![]()
Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби ![]() . А обратная дробь для дроби
. А обратная дробь для дроби ![]() это дробь
это дробь ![]() . Поэтому умножаем число 5 на
. Поэтому умножаем число 5 на ![]()
![]()
Дробь ![]() это 2 целых и
это 2 целых и ![]() . Проще говоря, две целые и четверть пиццы:
. Проще говоря, две целые и четверть пиццы:

А выражение ![]() определяет сколько раз
определяет сколько раз ![]() содержится в пяти целых пиццах. Ответом было смешанное число
содержится в пяти целых пиццах. Ответом было смешанное число ![]() .
.
То есть ![]() пиццы содержится в пяти целых пиццах
пиццы содержится в пяти целых пиццах ![]() раза.
раза.
Давайте нащупаем в пяти пиццах два раза по ![]()
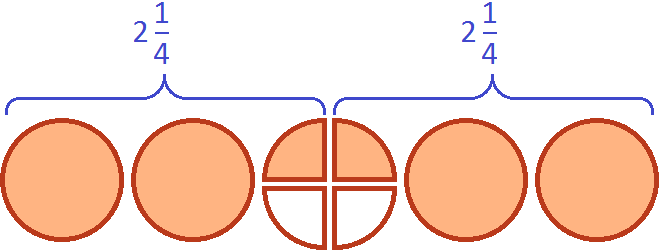
Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой ![]() от
от ![]() , которые не вместились. Двумя девятыми они являются по той причине, что в
, которые не вместились. Двумя девятыми они являются по той причине, что в ![]() пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:
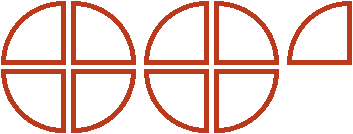
Поэтому значение выражения ![]() равно
равно ![]()
Деление дроби на целое число
Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.
Пример 1. Разделим дробь ![]() на число 2
на число 2
Чтобы разделить дробь ![]() на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь
на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь ![]()
![]()
Пусть имеется половина пиццы:

Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:
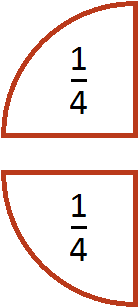
Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Чтобы решить этот пример, нужно дробь ![]() умножить на число, обратное числу 2. Обратное числу 2 это дробь
умножить на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Пример 3. Найти значение выражения ![]()
Умножаем первую дробь ![]() на число, обратное числу 3. Обратное числу 3 это дробь
на число, обратное числу 3. Обратное числу 3 это дробь ![]()
![]()
Деление целого числа на смешанное число
Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на ![]() .
.
Чтобы решить этот пример, нужно делитель ![]() перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.
Переведём делитель ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Затем умножим 2 на дробь, обратную дроби
. Затем умножим 2 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь
![]()
Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз ![]() (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
(одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.
В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от ![]() , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:
, которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:

Поэтому значение выражения ![]() равно
равно ![]()
Пример 2. Найти значение выражения ![]()
Переводим делитель ![]() в неправильную дробь, получаем
в неправильную дробь, получаем ![]() . Теперь умножаем число 5 на дробь, обратную дроби
. Теперь умножаем число 5 на дробь, обратную дроби ![]() . Обратная для дроби
. Обратная для дроби ![]() это дробь
это дробь ![]()
![]()
Сначала мы получили ответ ![]() , затем сократили эту дробь на 5, и получили
, затем сократили эту дробь на 5, и получили ![]() , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ
, но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ ![]()
Деление смешанного числа на целое число
Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.
Например, разделим ![]() на 2. Чтобы решить этот пример, нужно делимое
на 2. Чтобы решить этот пример, нужно делимое ![]() перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.
Переведём смешанное число ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() .
.
Теперь умножаем ![]() на число, обратное числу 2. Обратное числу 2 это дробь
на число, обратное числу 2. Обратное числу 2 это дробь ![]()
![]()
Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:
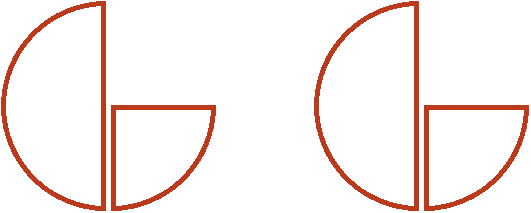
Поэтому значение выражения ![]() равно
равно
Пример 2. Найти значение выражения ![]()
Переведём делимое ![]() в неправильную дробь, получим
в неправильную дробь, получим ![]() . Теперь умножаем
. Теперь умножаем ![]() на число, обратное числу 4. Обратное числу 4 это дробь
на число, обратное числу 4. Обратное числу 4 это дробь ![]() .
.
![]()
Деление смешанных чисел
Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.
Пример 1. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Как решать дальше мы уже знаем. Первую дробь ![]() нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь
нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь ![]() .
.
Дорешаем данный пример до конца:
![]()
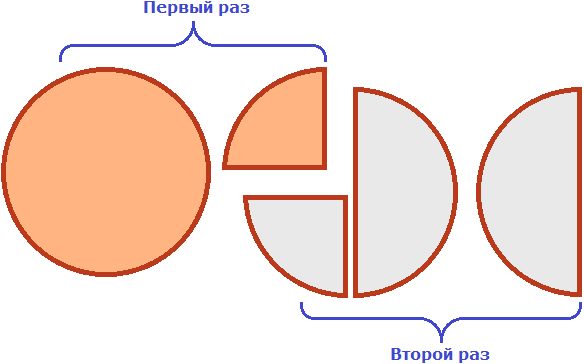
Допустим, имеются две целые и половина пиццы:
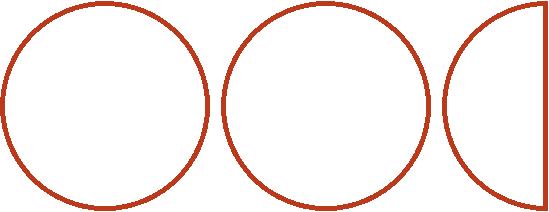
Если зададим вопрос «Сколько раз ![]() (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
(одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:
Пример 2. Найти значение выражения ![]()
Переведём смешанные числа в неправильные дроби. Получим следующее выражение:
![]()
Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь ![]()
![]()
Сначала мы получили дробь![]() . Эту дробь мы сократили на 9. В результате получили дробь
. Эту дробь мы сократили на 9. В результате получили дробь ![]() , но такой ответ нас тоже не устроил и мы выделили в дроби
, но такой ответ нас тоже не устроил и мы выделили в дроби ![]() целую часть. В результате получили окончательный ответ
целую часть. В результате получили окончательный ответ ![]() .
.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения:

Решение:
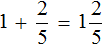
Задание 2. Найдите значение выражения:
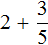
Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:
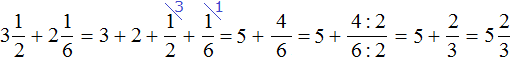
Задание 5. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Сумму натурального числа правильной дроби принято записывать без знака «+». Такую сумму называют смешанным числом. Можно сказать немного иначе: запись числа, которая содержит целую и дробную части, называют смешанной. Для краткости вместо «число в смешанной записи» говорят смешанное число.
 Натуральное число называют целой частью смешанного числа, а дробь – дробной частью смешанного числа.
Натуральное число называют целой частью смешанного числа, а дробь – дробной частью смешанного числа.
Например,
![]()
целая часть этого смешанного числа равна 31, дробная – ![]()
Смешанное число можно представить в виде неправильной дроби. Чтобы представить смешанное число в виде неправильной дроби, нужно:
1) умножить его целую часть на знаменатель дробной части;
2) к полученному произведению прибавить числитель дробной части;
3) записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.
Например,
![]()
Неправильную дробь можно представить в виде смешанного числа.
Запись неправильной дроби в виде смешанного числа называют выделением целой части дроби.
Чтобы выделить целую часть неправильной дроби, надо разделить её числитель на знаменатель и записать смешанное число в виде:
- целая часть – частное от деления;
- числитель дробной части – остаток от деления;
- знаменатель дробной части – знаменатель данной неправильной дроби.
Если остаток от деления числителя неправильной дроби на её знаменатель равен 0, неправильная дробь равна получившемуся при делении натуральному числу.
Например, выделим целую часть неправильной дроби ![]()
131 : 8 = 16 (и 3 в остатке);
![]()
Выделим целую часть неправильной дроби ![]()
13104 : 13 = 1008.
 Сложение смешанных чисел
Сложение смешанных чисел
Чтобы найти сумму смешанных чисел, нужно сложить отдельно целые и дробные части.
Если при сложении дробных частей получилась неправильная дробь, выделяют целую часть этой дроби и добавляют к уже имеющейся целой части.
Например,
![]()
Вычитание смешанных чисел
Чтобы найти разность смешанных чисел, нужно найти отдельно разность целых частей и отдельно разность дробных частей.
Если дробная часть уменьшаемого меньше дробной части вычитаемого, то одну единицу целой части уменьшаемого необходимо предварительно прибавить к его дробной части.
Например,
![]()
Остались вопросы? Хотите знать больше о смешанных числах?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
