Как найти смещение колеблющейся точки при фазах

§
6. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные
формулы

• Уравнение
гармонических колебаний

где х
— смещение
колеблющейся точки от положения
равновесия;
t
— время; А,
ω,
φ—
соответственно амплитуда, угловая
частота,
начальная фаза колебаний;
—
фаза колебаний в момент t.

• Угловая частота
колебаний

, или
,

где ν
и
Т — частота и период колебаний.

• Скорость точки,
совершающей гармонические колебания,

• Ускорение при
гармоническом колебании

• Амплитуда
А
результирующего
колебания, полученного при сложении
двух колебаний с одинаковыми частотами,
происходящих по одной прямой, определяется
по формуле

где
a₁
и
А₂—
амплитуды
составляющих колебаний; φ₁
и
φ₂—
их
начальные фазы.

•
Начальная фаза φ
результирующего колебания может быть
найдена
из формулы

•
Частота биений,
возникающих при сложении двух колебаний,
происходящих
по одной прямой с различными, но близкими
по зна­чению
частотами ν₁
и
ν₂,

•
Уравнение траектории
точки, участвующей в двух взаимно
перпендикулярных
колебаниях с амплитудами A₁
и A₂
и начальны­ми
фазами φ₁
и φ₂,

Если
начальные фазы φ₁
и
φ₂
составляющих колебаний одинако­вы,
то уравнение траектории принимает вид

т. е. точка движется
по прямой.

В том
случае, если разность фаз
,
уравнение
принимает вид

т. е. точка движется
по эллипсу.

• Дифференциальное
уравнение гармонических колебаний
ма­териальной точки

, или
,
где
m
—
масса точки; k
—
коэффициент
квазиупругой силы (k=тω²).

•
Полная энергия
материальной точки, совершающей
гармони­ческие
колебания,

• Период
колебаний тела, подвешенного на пружине
(пружин­ный
маятник),

где
m
—
масса тела; k
—
жесткость
пружины.
Формула справедлива для упругих
колебаний в пределах, в ко­торых
выполняется закон Гука (при малой массе
пружины в срав­нении
с массой тела).

Период колебаний
математического маятника

где
l
— длина маятника; g
—
ускорение
свободного падения. Период
колебаний физического маятника

где J
— момент инерции колеблющегося тела
относительно оси

колебаний;
а
— расстояние центра масс маятника от
оси колебаний;

— приведенная
длина физического маятника.

Приведенные
формулы являются точными для случая
бесконеч­но малых амплитуд. При
конечных амплитудах эти формулы дают
лишь приближенные результаты. При
амплитудах не более
ошибка в значении периода не превышает
1 %.

Период
крутильных колебаний тела, подвешенного
на упругой нити,

где J
—
момент
инерции тела относительно оси, совпадающей
с упругой нитью; k
—
жесткость
упругой нити, равная отношению упругого
момента, возникающего при закручивании
нити, к углу, на который нить закручивается.

• Дифференциальное
уравнение затухающих колебаний

, или
,

где r
— коэффициент сопротивления; δ
— коэффициент
затухания:

; ω₀—
собственная угловая частота колебаний
*

• Уравнение
затухающих колебаний

где A
(t) —
амплитуда
затухающих колебаний в момент t;
ω
— их угловая частота.

• Угловая частота
затухающих колебаний

О Зависимость
амплитуды затухающих колебаний от
времени

I

где
А₀
— амплитуда
колебаний в момент t=0.

• Логарифмический
декремент колебаний

где
A
(t) и
A
(t+T) —
амплитуды
двух последовательных колеба­ний,
отстоящих по времени друг от друга на
период.

• Дифференциальное
уравнение вынужденных колебаний

, или

,

где

—
внешняя периодическая сила, действующая
на
колеблющуюся
материальную точку и вызывающая
вынужденные
колебания;
F₀
—
ее
амплитудное значение;

•
Амплитуда вынужденных
колебаний

•
Резонансная частота
и резонансная амплитуда

и

Примеры решения
задач

Пример
1. Точка
совершает колебания по закону
x(t)= ,
где
А=2
см.
Определить начальную фазу φ,
если

x(0)= см
и х^,(0)<0.
Построить векторную диаграмму для
мо-­
мента t=0.

Решение.
Воспользуемся уравнением движения и
выразим смещение в момент t=0
через начальную фазу:

Отсюда
найдем начальную фазу:

*
В приведенных ранее формулах
гармонических колебаний та же
величина
обозначалась просто ω
(без индекса 0).

Подставим
в это выражение заданные значения x(0)
и А:
φ=
= .
Значению аргумента

удовлетворяют
два
значения угла:

Для
того чтобы решить, какое из этих значений
угла φ
удовлет-­
воряет
еще и условию
,
найдем сначала
:

Подставив
в это выражение значение t=0
и поочередно значения
начальных
фаз
и
,
найдем

Так
как всегда A>0
и ω>0,
то условию удовлетворяет
толь­
ко
первое значение начальной фазы.
Таким
образом, искомая начальная
фаза

По
найденному значению φ
постро-­
им
векторную диаграмму (рис. 6.1).
Пример
2. Материальная
точка
массой т=5
г совершает гармоничес-­
кие колебания
с частотой ν
=0,5 Гц.
Амплитуда
колебаний A=3
см. Оп-­
ределить: 1) скорость υ
точки
в мо-­
мент времени, когда смещение
х=
=
1,5 см; 2) максимальную силу
F_max,
действующую
на точку; 3)
Рис.
6.1 полную
энергию Е
колеблющейся
точ­
ки.

Решение.
1. Уравнение гармонического колебания
имеет вид

(1)

а
формулу скорости получим, взяв первую
производную по времени от смещения:

(2)

Чтобы
выразить скорость через смещение, надо
исключить из формул (1) и (2) время. Для
этого возведем оба уравнения в квад­рат,
разделим первое на А²,
второе
на A²
ω
²
и сложим:

, или

Решив
последнее уравнение относительно υ,
найдем

Выполнив вычисления
по этой формуле, получим

см/с.

Знак
плюс соответствует случаю, когда
направление скорости совпадает
с положительным направлением оси х,
знак
минус — ког­да
направление скорости совпадает с
отрицательным направлением оси
х.

Смещение при
гармоническом колебании кроме уравнения
(1) может быть определено также уравнением

Повторив
с этим уравнением такое же решение,
получим тот же ответ.

2.
Силу действующую на точку, найдем по
второму закону Нью­тона:

(3)

где а
— ускорение
точки, которое получим, взяв производную
по времени
от скорости:

, или

Подставив выражение
ускорения в формулу (3), получим

Отсюда максимальное
значение силы

Подставив
в это уравнение значения величин π,
ν,
т
и
A,
найдем

3.
Полная энергия колеблющейся точки есть
сумма кинетической и
потенциальной энергий, вычисленных для
любого момента вре­мени.

Проще
всего вычислить полную энергию в момент,
когда кинети­ческая
энергия достигает максимального
значения. В этот момент потенциальная
энергия равна нулю. Поэтому полная
энергия E
колеблющейся точки равна максимальной
кинетической энергии

T_max:

(4)

Максимальную
скорость определим из формулы (2),
положив

:
.
Подставив выражение скорости в фор­-
мулу
(4), найдем

Подставив
значения величин в эту формулу и произведя
вычис­ления, получим

или

мкДж.

Пример
3.
На концах тонкого стержня длиной l
=
1 м и массой m₃=400
г
укреплены шарики малых размеров массами
m₁=200
г
и
m₂=300г.
Стержень
колеблется около горизонтальной оси,
перпен-

дикулярной
стержню и проходящей через его середину
(точка О на рис. 6.2). Определить период Т
колебаний,
совершаемых стержнем.

Решение.
Период колебаний физического маятника,
каким является стержень с шариками,
определяется соотношением

(1)

где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; l_С
— расстояние
от центра масс ма­ятника
до оси.

Момент
инерции данного маятника равен сумме
моментов
инерции шариков J₁
и
J₂
и
стержня J₃:

(2)

Принимая
шарики за материальные точки, вы­разим
моменты их инерции:

Так
как ось проходит через середину стержня,
то
его
момент инерции относительно этой оси
J₃=
= .
Подставив
полученные выражения
J₁
,
J₂
и

J₃
в формулу (2), найдем общий момент инерции
фи-­
зического маятника:

Произведя
вычисления по этой формуле, найдем

Рис.
6.2 Масса маятника состоит из масс шариков
и массы
стержня:

Расстояние
l_С
центра
масс маятника от оси колебаний найдем,
исходя
из следующих соображений. Если ось х
направить
вдоль стержня
и начало координат совместить с точкой
О,
то
искомое рас­стояние
l
равно координате центра масс маятника,
т. е.

, или

Подставив
значения величин m₁,
m₂,
m,
l
и произведя вычисле­ния,
найдем

см.

Произведя
расчеты по формуле (1), получим период
колебаний физического
маятника:

Пример
4. Физический
маятник представляет собой стержень
длиной
l=
1 м и массой 3т₁
с прикрепленным
к одному из его концов
обручем
диаметром
и
массой т₁.
Горизонтальная
ось Oz

маятника
проходит через середину стержня
перпендикулярно ему (рис. 6.3). Определить
период Т
колебаний
такого маятника.

Решение.
Период
колебаний физического маятника
опреде­ляется
по формуле

(1)

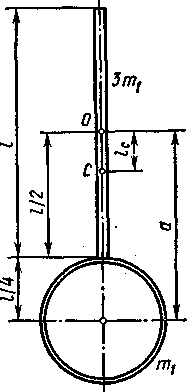
где
J
—
момент
инерции маятника относительно оси
колебаний; т
— его
масса; l_C
— расстояние
от центра масс
маятника до оси колебаний.

Момент
инерции маятника равен сумме мо­ментов
инерции стержня J₁
и
обруча J₂:

(2).

Момент
инерции стержня относительно
оси,
перпендикулярной
стержню и проходящей
через
его центр масс, определяется по форму-­
ле
.
В данном случае т=3т₁
и

Момент
инерции обруча найдем, восполь-­
зовавшись
теоремой Штейнера
,
где
J
—
момент
инерции относительно про-­
извольной
оси;
J₀
—
момент
инерции отно-­
сительно
оси, проходящей через центр масс
параллельно
заданной оси; а
— расстояние
между
указанными осями. Применив эту фор-­
мулу
к обручу, получим

Рис. 6.3

Подставив
выражения J₁
и
J₂
в форму­лу
(2), найдем момент инерции маятника
относительно оси вра­щения:

Расстояние
l_С
от
оси маятника до его центра масс равно

Подставив
в формулу (1) выражения J,
l_с
и массы маятника

, найдем период его колебаний:

После
вычисления по этой формуле получим
T=2,17
с.

Пример
5. Складываются
два колебания одинакового направле-­
ния,
выражаемых уравнениями
;
х₂=
=,
где А₁=1
см,
A₂=2
см,

с,

с, ω
=
=.
1. Определить начальные фазы φ₁
и φ
₂
составляющих коле-

баний.
2. Найти амплитуду А
и
начальную фазу φ
результирующего колебания.
Написать уравнение результирующего
колебания.

Решение.
1. Уравнение гармонического колебания
имеет вид

(1)

Преобразуем
уравнения, заданные в условии задачи,
к такому же
виду:

(2)

Из
сравнения выражений (2) с равенством (1)
находим начальные фазы
первого и второго колебаний:

рад и

рад.

2.
Для определения амплитуды А
результирую­щего
колебания удобно воспользоваться
векторной диаграммой,
представленной на рис.
6.4.
Согласно теореме косинусов, получим

(3)

где

— разность фаз составляющих колебаний.
Так
как
,
то, подставляя найденные
значения
φ₂
и φ₁
получим

рад.

Рис. 6.4

Подставим
значения А₁
,
А₂
и

в формулу (3)
и
произведем вычисления:

A=2,65
см.

Тангенс
начальной фазы φ
результирующего колебания опреде-­
лим
непосредственно из рис. 6.4:

, отку-­
да
начальная фаза

Подставим
значения А₁,
А₂,
φ
₁,
φ
₂
и произведем вычисления:

= рад.

Так
как угловые частоты складываемых
колебаний одинаковы,
то
результирующее колебание будет иметь
ту же частоту ω.
Это
позволяет
написать уравнение результирующего
колебания в виде

, где A=2,65
см,
,

рад.

Пример
6. Материальная
точка участвует одновременно в двух
взаимно перпендикулярных гармонических
колебаниях, уравне­ния
которых

(1).

(2)

где
a₁=1
см,
A₂=2
см,
.
Найти уравнение траектории точ-­
ки.
Построить траекторию с соблюдением
масштаба и указать
направление
движения точки.

Решение.
Чтобы
найти уравнение траектории точки,
ис­ключим
время t
из
заданных уравнений (1) и (2). Для этого
восполь-

зуемся
формулой
.
В данном случае

, поэтому

Так
как согласно формуле (1)
,
то уравнение траекто-­
рии

(3)

Полученное
выражение представляет собой уравнение
параболы, ось которой совпадает с осью
Ох.
Из
уравнений (1) и (2) следует, что смещение
точки по осям координат ограничено и
заключено в пределах от —1 до +1 см по
оси Ох
и
от —2 до +2 см по оси Оу.

Для
построения траектории найдем по уравнению
(3) значения у,
соответствующие
ряду значений х,
удовлетворяющих
условию

см, и составим таблицу:

X , СМ	-1	—0,75	—0,5	0	+0,5	+ 1
у, см	0	±0,707	±1	±1,41	±1,73	±2

Начертив
координатные оси и выбрав масштаб,
нанесем на пло­скость
хОу
найденные
точки. Соединив их плавной кривой,
получим траекторию точки, совершающей
колеба­ния
в соответствии с уравнениями движе­ния
(1) и (2) (рис. 6.5).

Рис. 6.5

Для
того чтобы указать направление движения
точки, проследим за тем, как из­меняется
ее положение с течением времени. В
начальный момент t=0
координаты точ­ки
равны x(0)=1
см и y(0)=2
см. В по­следующий
момент времени, например при t₁=l
с,
координаты точек изменятся и ста­нут
равными х
(1)=
—1
см, y(t)=0.
Зная
положения
точек в начальный и последую­щий
(близкий) моменты времени, можно указать
направление движения точки по траектории.
На рис. 6.5 это направление движения
указано стрелкой (от точки А
к
началу
координат). После того как в мо­мент
t₂
= 2 с колеблющаяся точка достиг­нет
точки D,
она
будет двигаться в обратном направлении.

Задачи

Кинематика
гармонических колебаний

6.1.
Уравнение колебаний точки имеет вид
,
где
ω=π
с^-1,
τ=0,2
с. Определить период Т
и
начальную фазу φ
колебаний.

6.2.
Определить
период Т,
частоту
v
и
начальную фазу φ
коле­баний,
заданных уравнением
,
где ω=2,5π
с^-1,
τ=0,4
с.

6.3.
Точка
совершает колебания по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

;
2)
х(0)
=см
и
;
3) х(0)=2см
и
;
4)
х(0)=
и
.
Построить векторную диаграмму
для
момента
t=0.

6.4.
Точка
совершает колебания .по закону
,
где
A=4
см. Определить начальную фазу φ,
если: 1) х(0)=2
см
и

; 2) x(0)=
см и
;
3) х(0)=
см и
;
4)
x(0)=см
и
.
Построить векторную диаграмму для
момента
t=0.

Основные формулы

Гармонические колебания происходят по закону:

X = A cos(ωT + φ0),

Где X – смещение частицы от положения равновесия, А – амплитуда колебаний, ω – круговая частота, φ0 – начальная фаза, T – время.

Период колебаний T = .

Скорость колеблющейся частицы:

υ = = – A ω sin (ωT + φ0),

Ускорение A = = – Aω2 cos (ωT + φ0).

Кинетическая энергия частицы, совершающей колебательное движение: EK = = sin2(ωT + φ0).

Потенциальная энергия:

EN = cos2(ωT + φ0).

Периоды колебаний маятников

– пружинного T = ,

Где M – масса груза, K – коэффициент жесткости пружины,

– математического T = ,

Где L – длина подвеса, G – ускорение свободного падения,

– физического T = ,

Где I – момент инерции маятника относительно оси, проходящей через точку подвеса, M – масса маятника, L – расстояние от точки подвеса до центра масс.

Приведенная длина физического маятника находится из условия: LNp = ,

Обозначения те же, что для физического маятника.

При сложении двух гармонических колебаний одной частоты и одного направления получается гармоническое колебание той же частоты с амплитудой:

A = A12 + A22 + 2A1 A2 cos(φ2 – φ1)

И начальной фазой: φ = arctg .

Где А1, A2 – амплитуды, φ1, φ2 – начальные фазы складываемых колебаний.

Траектория результирующего движения при сложении взаимноперпендикулярных колебаний одной частоты:

+ – cos (φ2 – φ1) = sin2 (φ2 – φ1).

Затухающие колебания происходят по закону:

X = A0 E— βT Cos(ωT + φ0),

Где β – коэффициент затухания, смысл остальных параметров тот же, что для гармонических колебаний, А0 – начальная амплитуда. В момент времени T амплитуда колебаний:

A = A0 E — βT.

Логарифмическим декрементом затухания называют:

λ = ln = βT,

Где Т – период колебания: T = .

Добротностью колебательной системы называют:

D = .

Уравнение плоской бегущей волны имеет вид:

Y = Y0 cos ω(T ± ),

Где У – смещение колеблющейся величины от положения равновесия, У0 – амплитуда, ω – круговая частота, T – время, Х – координата, вдоль которой распространяется волна, υ – скорость распространения волны.

Знак «+» соответствует волне, распространяющейся против оси X, знак «–» соответствует волне, распространяющейся по оси Х.

Длиной волны называют ее пространственный период:

λ = υT,

Где υ–скорость распространения волны, T–период распространяющихся колебаний.

Уравнение волны можно записать:

Y = Y0 cos 2π ( + ).

Стоячая волна описывается уравнением:

Y = (2Y0 cos ) cos ω T.

В скобки заключена амплитуда стоячей волны. Точки с максимальной амплитудой называются пучностями,

XП = N,

Точки с нулевой амплитудой – узлами,

XУ = (N + ) .

Примеры решения задач

Задача 20

Амплитуда гармонических колебаний равна 50 мм, период 4 с и начальная фаза . а) Записать уравнение этого колебания; б) найти смещения колеблющейся точки от положения равновесия при T=0 и при T = 1,5 с; в) начертить график этого движения.

Решение

Уравнение колебания записывается в виде X = A cos(wT + j0).

По условию известен период колебаний. Через него можно выразить круговую частоту w = . Остальные параметры известны:

А) X = 0,05 cos(T + ).

Б) Смещение X при T = 0.

X1 = 0,05 cos= 0,05 = 0,0355 м.

При T = 1,5 c

X2 = 0,05 cos( 1,5 + )= 0,05 cos p = – 0,05 м.

В) график функции X=0,05cos (T + ) выглядит следующим образом:

Определим положение нескольких точек. Известны Х1(0) и Х2(1,5), а также период колебаний. Значит, через DT = 4 c значение Х повторяется, а через DT = 2 c меняет знак. Между максимумом и минимумом посередине – 0 .

Задача 21

Точка совершает гармоническое колебание. Период колебаний 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда ее смещение от положения равновесия равно 25 мм.

Решение

1 способ. Записываем уравнение колебания точки:

X = 0,05 cos p T, т. к. w = = p.

Находим скорость в момент времени T:

υ = = – 0,05 cos p T.

Находим момент времени, когда смещение равно 0,025 м:

0,025 = 0,05 cos p t1,

Отсюда cos pT1 = , pT1 = . Подставляем это значение в выражение для скорости:

υ = – 0,05 p sin = – 0,05 p = 0,136 м/c.

2 способ. Полная энергия колебательного движения:

E = ,

Где А – амплитуда, w – круговая частота, M – масса частицы.

В каждый момент времени она складывается из потенциальной и кинетической энергии точки

EK = , EП = , но K = MW2, значит, EП = .

Запишем закон сохранения энергии:

= + ,

Отсюда получаем: A2w2 = υ 2 + w2X2,

υ = w = p = 0,136 м/c.

Задача 22

Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия Е = 3∙10-7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F = 2,25∙10-5 Н?

Решение

Полная энергия точки, совершающей гармонические колебания, равна: E = . (13)

Модуль упругой силы выражается через смещение точек от положения равновесия X следующим образом:

F = K X (14)

В формулу (13) входят масса M и круговая частота w, а в (14) – коэффициент жесткости K. Но круговая частота связана с M и K:

W2 = ,

Отсюда K = MW2 и F = MW2X. Выразив MW2 из соотношения (13) получим: MW2 = , F = X.

Откуда и получаем выражение для смещения X: X = .

Подстановка числовых значений дает:

X = = 1,5∙10-2 м = 1,5 см.

Задача 23

Точка участвует в двух колебаниях с одинаковыми периодами и начальными фазами. Амплитуды колебаний А1 = 3 см и А2 = 4 см. Найти амплитуду результирующего колебания, если: 1) колебания происходят в одном направлении; 2) колебания взаимно перпендикулярны.

Решение

1) Если колебания происходят в одном направлении, то амплитуда результирующего колебания определится как:

A = ,

Где А1 и А2 – амплитуды складываемых колебаний, j1 и j2–начальные фазы. По условию начальные фазы одинаковы, значит j2 – j1 = 0, а cos 0 = 1.

Следовательно:

A = == А1+А­2 = 7 см.

2) Если колебания взаимно перпендикулярны, то уравнение результирующего движения будет:

Cos(j 2 – j 1) = sin2(j 2 – j 1).

Так как по условию j2 – j1 = 0, cos 0 = 1, sin 0 = 0, то уравнение запишется в виде: =0,

Или =0,

Или .

Полученное соотношение между X и У Можно изобразить на графике. Из графика видно, что результирующим будет колебание точки на прямой MN. Амплитуда этого колебания определится как: A = = 5 см.

Задача 24

Период затухающих колебаний Т=4 с, логарифмический декремент затухания l = 1,6 , начальная фаза равна нулю. Смещение точки при T = равно 4,5 см. 1) Написать уравнение этого колебания; 2) Построить график этого движения для двух периодов.

Решение

1) Уравнение затухающих колебаний с нулевой начальной фазой имеет вид:

X = A0E — bT cos2p.

Для подстановки числовых значений не хватает величин начальной амплитуды А0 и коэффициента затухания b.

Коэффициент затухания можно определить из соотношения для логарифмического декремента затухания:

L = bТ.

Таким образом b = = = 0,4 с-1.

Начальную амплитуду можно определить, подставив второе условие:

4,5 см = A0 cos 2p = A0 Cos = A0 .

Отсюда находим:

A0 = 4,5∙ (см) = 7,75 см.

Окончательно уравнение движения:

X = 0,0775 CosT.

2) Для построения графика сначала рисуем огибающую X = 0,0775 , а затем колебательную часть.

Задача 25

Чему равен логарифмический декремент затухания математического маятника, если за T = 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника L = 1 м.

Решение

Логарифмический декремент затухания можно найти из соотношения: l= bТ,

Где b – коэффициент затухания, Т – период колебаний. Собственная круговая частота математического маятника:

W0 = = 3,13 с-1.

Коэффициент затухания колебаний можно определить из условия: A0 = A0 E-bT,

BT = ln2 = 0,693 ,

B = = 0,0116 c-1.

Поскольку b << w0, то в формуле w = можно пренебречь b по сравнению с w0 и период колебаний определить по формуле: T = = 2 c.

Подставляем b и Т в выражение для логарифмического декремента затухания и получаем:

L = bT = 0,0116 с-1 ∙ 2 с = 0,0232.

Задача 26

Уравнение незатухающих колебаний дано в виде x = 4 sin600 pT см.

Найти смещение от положения равновесия точки, находящейся на расстоянии L = 75 см от источника колебаний, через T = 0,01 с после начала колебаний. Скорость распространения колебаний υ = 300 м/с.

Решение

Запишем уравнение волны, распространяющейся от данного источника: X = 0,04 sin 600 p(T – ).

Находим фазу волны в данный момент времени в данном месте:

T – = 0,01 – = 0,0075 ,

600p ∙ 0,0075 = 4,5p,

Sin 4,5p = sin = 1.

Следовательно, смещение точки X = 0,04 м, т. е. на расстоянии L =75 см от источника в момент времени T = 0,01 c смещение точки максимально.

В
рамках прошлой темы говорилось о новом виде механического движения –
колебательном движении.

Механическое колебательное движение —это движение, при котором состояния
тела с течением времени повторяются, причем тело проходит через положение
устойчивого равновесия поочередно в противоположных направлениях.

Если колебания происходят в системе только под действием
внутренних сил, то такие колебания называют свободными.

Колебательной системой называют такую физическую систему, в которой при отклонении
от положения равновесия возникают и существуют колебания.

Маятник – это твердое тело, совершающее под действием приложенных сил колебания
около неподвижной точки или вокруг оси.

В
рамках данной темы будет рассмотрен простейший вид колебательного движения —
гармонические колебания.

Гармонические
колебания — это колебания, при которых смещение колеблющейся
точки от положения равновесия изменяется с течением времени по закону синуса
или косинуса.

Смещение
от положения равновесия при гармонических колебаниях описывается уравнениями
вида:

Эти
уравнения называют кинематическим законом гармонического движения.

Покажем,
что гармонические колебания действительно подчиняются закону синуса или
косинуса. Для этого рассмотрим следующую установку.

Возьмем
нитяной маятник, а в качестве груза к нему выберем небольшой массивный сосуд с
маленьким отверстием снизу и насыплем в него песок.А под полученную систему
положим длинную бумажную ленту.

Если
ленту перемещать с постоянной скоростью в направлении, перпендикулярном
плоскости колебаний, то на ней останется волнообразная дорожка из песка, каждая
точка которой соответствует положению колеблющегося груза в тот момент, когда
он проходил над ней. Из опыта видно, что след, который оставляет песок на листе
бумаги, есть некая кривая.

Она
называется синусоидой. Из курса математики старших классов вы узнаете о том,
что аналогичные графики имеют функции типа

Значит,
графически зависимость смещения колеблющейся точки от времени изображается
синусоидой или косинусоидой.

Через
точки, соответствующие положению равновесия маятника, проведена ось времени t,
а перпендикулярно ей — ось смещения икс. График дает возможность приблизительно
определить координату груза в любой момент времени.

Теперь
разберемся с величинами, входящими в уравнение колебательного движения.

Смещение
— величина, характеризующая положение колеблющейся точки в некоторый момент
времени относительно положения равновесия и измеряемая расстоянием от положения
равновесия до положения точки в данный момент времени.

Амплитуда
колебаний — максимальное смещение тела от положения равновесия.

Циклическая,
или круговая частота, показывающая, сколько колебаний совершает
тело за 2p секунд.

j0
— это начальная фаза колебаний.

Фаза
колебаний — это аргумент периодической функции, который при
заданной амплитуде колебаний определяет состояние колебательной системы в любой
момент времени.

Промежуток
времени, в течение которого тело совершает одно полное колебание, называется периодом
колебаний.

Период
колебаний обычно обозначается буквой Т и в системе СИ измеряется в
секундах.

Число
колебаний в единицу времени называется частотой колебаний.  Обозначается
частота буквой ν. За единицу частоты принято одно колебание в
секунду. Эта единица названа в честь немецкого ученого Генриха Герца.

Период
колебания и частота колебаний связаны следующей зависимостью:

Т.е.
частота — это величина обратная периоду и равная числу полных колебаний, совершаемых
за 1 секунду.

Циклическая
частота также связана с периодом колебаний или частотой. Эту связь
математически можно записать в следующем виде:

Таким
образом, любое колебательное движение характеризуется амплитудой, частотой
(или периодом) и фазой колебаний.

При
совершении телом гармонических колебаний не только его координата, но и такие
величины, как сила, ускорение, скорость, тоже изменяются по закону синуса или
косинуса.

Это
следует из известных вам законов и формул, в которых указанные величины попарно
связаны прямо пропорциональной зависимостью, например законом Гука или вторым
законом Ньютона. Из этих формул видно, что сила и ускорение достигают
наибольших значений, когда колеблющееся тело находится в крайних положениях,
где смещение наиболее велико, и равны нулю, когда тело проходит через положение
равновесия.

Что
же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при
прохождении телом положения равновесия достигает наибольшего значения.

Колебания,
практически близкие к гармоническим, совершает тяжелый шарик, подвешенный на
легкой и малорастяжимой нити, длина которой значительно больше диаметра шарика.
Такую колебательную систему называют математическим маятником.

Математический
маятник — это материальная точка, подвешенная на невесомой нерастяжимой
нити, прикрепленной к подвесу и находящейся в поле силы тяжести.

Также
гармонические колебания может совершать груз подвешенный на пружине,
совершающий колебания в вертикальной плоскости. Такую колебательную систему
называют пружинным маятником — это система, состоящая из материальной
точки массой m и пружины.

Основные
выводы:

– Гармонические колебания
— это колебания, при которых смещение колеблющейся точки от положения
равновесия изменяется с течением времени по закону синуса или косинуса.

– Любое колебательное движение характеризуется
амплитудой, частотой (или периодом) и фазой колебаний.

– Амплитуда колебаний
— максимальное смещение тела от положения равновесия.

– Промежуток времени, в течение которого тело
совершает одно полное колебание, называется периодом колебаний.

– Число колебаний в единицу времени называется частотой
колебаний.

– Фаза колебаний — это аргумент
периодической функции, который при заданной амплитуде колебаний определяет
состояние колебательной системы в любой момент времени.

– Математический и пружинный маятники
— это простейшие идеализированные колебательные системы, подчиняющиеся закону синуса
или косинуса.

– Математический маятник
— это материальная точка, подвешенная на невесомой нерастяжимой нити,
прикрепленной к подвесу и находящейся в поле силы тяжести.

– Пружинный маятник
— это система, состоящая из материальной точки массой m
и пружины, которая совершает колебания в вертикальной плоскости.