Как найти смещение параболы

Как найти смещение параболы

Смещение по горизонтали параболы

Если мы прибаляем к функции (y=x^2) число 3 (y=(x+3)^2), то график смещается по оси (0X) на (-3) еденицы, если вычитаем число (2)  (y=(x-2)^2), то график сместится (+2)  относительно  (0X):

Чтение графиков функций: парабола

Если мы отнимем от (y=(x+3)^2) 3 , то (y=(x+3)^2-3), то график начнет смещаться уже по вертикали вниз на (3) единицы, а именно по оси (0Y):

Чтение графиков функций: парабола

Напомним, графиком квадратичной функции (y = ax^2 + bx + c ) является парабола, если забыл что такое парабола, то повтори в этой статье https://myalfaschool.ru/articles/parabola. Вершину параболы можно вычислить по формуле: (x=frac{ – b}{2a}.)

Задача 

Чтение графиков функций: парабола

Здесь нам пригодятся знания нахождения формулы вершины параболы  (x=frac{ – b}{2a}), она не такая  и тяжелая, так что запомните ее. Если мы видим на графике параболу, то сразу представляем уранение вида (y = ax^2 + bx + c ). По графику выше определяем вершина равна -1:

(frac{-b}{2a}=-1)  (–>) (b=2a)

Как видно из рисунка парабола пересекает (OY) в точке 3, поэтому (с=3)  и (y = ax^2 + 2ax + 3), так как (b=2a). Находим любую точку проходящую через параболу, возьмем вершину параболы ((-1; 2)) и подставим в уравнение:

(2 = (-1)x^2 + 2(-1)x + 3) (–>) (2=-a+3) (–>) (a=1)

Ответ: 2)1.

Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!


Запишитесь на бесплатное тестирование знаний!

Источник

Парабола в математике: уравнение, построение, виды

Содержание:

  • Что такое парабола в математике
  • Алгоритм построения параболы

    • Примеры решения задач на построение параболы
  • Смещение параболы

Что такое парабола в математике

Парабола – график квадратичной функции вида (f(x)=ax^2+bx+c). Состоит данный график из вершины и ветвей.

Парабола

Источник: tutomath.ru

При этом (aneq0), иначе функция уже будет не квадратичной, а линейной.

Формула параболы может рассказать нам о многом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

  1. Коэффициент (a) говорит о направлении ветвей параболы. Если (а>0), то ветви смотрят вверх, если (а<0), вниз.
  2. От параметра (b) зависит вершина параболы. Она рассчитывается по формуле: (x_в=frac{-b}{2a})
  3. Свободный член (с) отвечает за пересечение параболы с осью (y).

Алгоритм построения параболы

Построим график функции (f(x)=ax^2+bx+c.)

  1. Определим куда смотрят ветви параболы.
  2. Найдем вершину по формуле (x_в=frac{-b}{2a}). Подставим (x_в) в формулу функции и получим значение (y_в). Таким образом мы имеем обе координаты вершины. Нанесем их на систему координат.
  3. Найдем точку пересечения с осью y по параметру с и нанесем на чертеж точку, симметричную ей, относительно оси симметрии параболы, т.е. прямой (y=frac{-b}{2a}.)
  4. Далее решаем уравнение (ax^2+bx+c=0). Получаем корни – они являются точками пересечения параболы с осью (x). Если они рациональны, наносим их на чертеж, в обратном случае, они не пригодятся.
  5. Затем считаем значения функции в дополнительных симметричных точках и соединяем все найденные точки.

Примеры решения задач на построение параболы

Пример задачи

Источник: egemaximum.ru

Пример задачи 2

Источник: egemaximum.ru

Смещение параболы

Свободный член с смещает параболу по оси y. Например, если c=2, то парабола f(x)=ax^2+bx сместится вверх на 2 единичных отрезка, а если с=-2, то график сместится вниз так же на 2 единичных отрезка.

Смещение параболы

Источник: egemaximum.ru

В случае, когда к аргументу x прибавляется или вычитается какое-либо число, график смещается по оси x. Например, для построения графика функции (y={(x+4)}^2) достаточно сместить график (y=x^2 )на 4 единичных отрезка влево, а для построения графика (y={(x-3)}^2) нужно сместить график (y=x^2) на 3 единичных отрезка вправо.

Смещение параболы 2

 

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Как смещается график параболы?

График квадратичной функции – парабола. Если коэффициент displaystyle a<0, ветви параболы направлены вниз, если displaystyle a>0 – ветви параболы направлены вверх. Чем больше значение displaystyle a (по модулю), тем у́же становится парабола (ветви становятся более крутыми).

Что отвечает за ширину параболы?

Построение квадратичной функции Квадратичная функция задается формулой y = ax2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение: a — старший коэффициент, который отвечает за ширину параболы.

Что такое D в параболе?

Чем больше |a|, тем у́же парабола (больше прижата к оси Y ). Наоборот, чем меньше |a|, тем шире парабола (больше прижата к оси X). где D = b2 − 4ac — дискриминант.

Чему равен коэффициент b в параболе?

1) Коэффициент а влияет на направление ветвей параболы: при а > 0 – ветви направлены вверх, при а < 0 – вниз. 2) Коэффициент b влияет на расположение вершины параболы. При b = 0 вершина лежит на оси оу. 3) Коэффициент с показывает точку пересечения параболы с осью ОУ.

Как найти х вершины?

Воспользуйтесь формулой для вычисления значения координаты x вершины. Вершина также является точкой симметрии параболы. Формула для нахождения координаты x параболы: x = -b/2a.

Как определить А в параболе?

Нахождение коэффициента a :

  1. По графику параболы определяем координаты вершины (m;n).
  2. По графику параболы определяем координаты любой точки А (х1;у1).
  3. Подставляем эти значения в формулу квадратичной функции, заданной в другом виде: у=a(х-m)2 +n.
  4. Решая полученное уравнение, находим а.

31 янв. 2022 г.

Как найти y0 в параболе?

то абсциссу вершины параболы ( x o ; y o ) можно вычислить по формуле: x o = − b 2 a . Ординату можно вычислить, подставив полученное значение x o в формулу данной функции: y o = a x o 2 + b x o + c .

Какая зависимость называется квадратичной?

Квадратичной функцией называется функция, которую можно задать формулой вида y=ax²+bx+c. Рассмотрим случай, когда a=1,b=0 и c=0. Формула примет вид y=x². Вы, наверно, уже знаете, какая зависимость между площадью квадрата и длиной его стороны.

Что означает D в графике функции?

Область определения функции — это множество всех значений переменной x, которые имеют соответствующие им значения функции. Обозначают: D(f). На графике область определения — это промежутки на оси ОX, над которыми (или под которыми) имеются части графика. Для нашего примера D(f) = [-8; 9,4].

Как в параболе найти B?

нахождение коэффициента b: 1) Сначала находим значение коэффициента a (шаг I, смотри выше). 1) В формулу для абсциссы вершины параболы m= —b/2a подставляем значения m и a. 2) Вычисляем значение коэффициента b.

Что означают коэффициенты k и b?

Понятие линейной функции Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат. Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Как выглядит парабола?

Парабола — кривая второго порядка. Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.

Как найти коэффициенты параболы по графику?

Нахождение коэффициента a :

  1. По графику параболы определяем координаты вершины (m;n).
  2. По графику параболы определяем координаты любой точки А (х1;у1).
  3. Подставляем эти значения в формулу квадратичной функции, заданной в другом виде: у=a(х-m)2 +n.
  4. Решая полученное уравнение, находим а.

31 янв. 2022 г.

Как определить коэффициент?

Числовой множитель в произведении, где есть хотя бы одна буква, называется коэффициентом. Если чисел несколько, нужно их перемножить, упростить выражение и таким образом будет получен коэффициент.

Как найти x0 и y0?

то абсциссу вершины параболы ( x o ; y o ) можно вычислить по формуле: x o = − b 2 a . Ординату можно вычислить, подставив полученное значение x o в формулу данной функции: y o = a x o 2 + b x o + c .

Какие преобразования графиков вы знаете?

Преобразование графика функции

Общий вид функции Преобразования
y = f(x + b) влево, если b > 0; вправо, если b < 0.
y = f(x) + m Параллельный перенос графика вдоль оси ординат на | m | единиц вверх, если m > 0, вниз, если m < 0.
Отражение графика
y = f( — x) Симметричное отражение графика относительно оси ординат.

Что называется квадратичной функции?

Квадратичной функцией называют функцию, которую можно задать формулой вида у=ах²+bх+c, где а, b и с – некоторые числа, причем а≠0.

Источник

Преобразование графиков функций

Анна Малкова

В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.

Очень жаль, что эта тема — полезная и очень интересная — выпадает из школьной программы. На нее постоянно не хватает времени. Из-за этого многим старшеклассникам не даются задачи с параметрами — которые на самом деле похожи на конструктор, где вы собираете решение из знакомых элементов. Хотя бы для того, чтобы решать задачи с параметрами, стоит научиться строить графики функций.

Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.

Начнем со сдвигов графиков по Х и по Y.

1. Сдвиг по горизонтали.

Пусть функция задана формулой y = f(x) и a textgreater 0. Тогда график функции y = f(x - a) сдвинут относительно исходной на а вправо. График функции y = f(x + a) сдвинут относительно исходной на а влево.

2. Сдвиг по вертикали.

Пусть функция задана формулой y = f(x) и С — некоторое положительное число. Тогда график функции y = f(x) + C сдвинут относительно исходного на С вверх. График функции y = f(x) - C сдвинут относительно исходного на С вниз.

Теперь растяжение графика. Или сжатие.

3.  Растяжение (сжатие) по горизонтали.

Пусть функция задана формулой y = f(x) и k textgreater 0. Тогда график функции y = f(kx) растянут относительно исходного в k раз по горизонтали, если 0 textless k textless 1, и сжат относительно исходного в k раз по горизонтали, если k textgreater 1.

4.  Растяжение (сжатие) по вертикали.

Пусть функция задана формулой y = f(x) и M textgreater 0. Тогда график функции y = Mcdot f(x) растянут относительно исходного в М раз по вертикали, если M textgreater 1, и сжат относительно исходного в М раз по вертикали, если 0 textless M textless 1.

И отражение по горизонтали.

5. Отражение по горизонтали.

График функции y = f(-x) симметричен графику функции y = f(x) относительно оси Y.

6. Отражение по вертикали.

График функции y = - f(x) симметричен графику функции y = f(x) относительно оси Х.

Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.

И еще два интересных преобразования. Здесь в формулах присутствует знак модуля. Если не помните, что такое модуль, — срочно повторите эту тему.

7. Графики функций y= f(|x|) и y=|f(x)|.

На рисунке изображен график функции y= f(|x|). Она специально взята такая — несимметричная относительно нуля.

Построим график функции y= f(|x|).

Конечно же, мы пользуемся определением модуля.

Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.

Теперь график функции y= |f(x)|. Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.

Как определить по формуле функции, будет график преобразован по горизонтали (по Х) или по вертикали (по Y)? Разница очевидна. Если сначала мы что-либо делаем с аргументом х (прибавляем к нему какое-либо число, умножаем на какое-либо число или берем модуль) — преобразование по Х. Если сначала мы нашли функцию, а затем уже к значению функции что-то прибавили, или на какое-нибудь число умножили, или взяли модуль, — преобразование по Y.

Вот самые простые задачи на преобразование графиков.

1. Построим график функции  y={left(x+3right)}^2-1.

Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.

Вершина в точке (-3; -1).

2. Построим график функции y=x^2-4x-1.

Выделим полный квадрат в формуле.

y=x^2-4x+4-4-1=x^2-4x+4-5={left(x-2right)}^2-5.

График — квадратичная парабола, сдвинутая на 2 вправо по x и на 5 вниз по y.

Обратите внимание: график функции y=ax^2+bx+c пересекает ось y в точке (0; c). На нашем графике это точка (0; -1).

Продолжение — в статье «Построение графиков функций».

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Преобразование графиков функций» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Цели урока:

Образовательная: исследовать смещение
графика квадратичной функции, определить
положение графика в зависимости от значений
коэффициентов b, c.

Воспитательная: умение работать в группе,
организованности.

Развивающая: навыки исследовательской
работы, умение выдвигать гипотезы, анализировать
полученные результаты, систематизировать
полученные данные.

Структура урока


  1. Организационный момент – 3 минуты.
  2. Исследовательская работа – 20 минут.
  3. Закрепление изученного материала – 15 минут.
  4. Рефлексия – 2 минут.
  5. Итог урока – 3 минуты.
  6. Домашнее задание – 2 минуты.

Ход урока

1. Организационный момент.

Цель урока провести исследовательскую работу.
Объектом исследования будут квадратичные
функции разного вида. Вам предстоит определить,
как влияют коэффициенты b, c на график
функций вида y=x2+с, y=(x-b)2, y=(x-b)2+c.

Для выполнения задания необходимо разделиться
на группы (4 группы по 5 человек, одна группа
“эксперты” наиболее подготовленные ученики).

Каждая группа получает план исследования
<Приложение>, лист формата А3 для оформления
результатов.

2. Исследовательская работа.

Две группы (уровень А) исследуют функции вида y= x2+с,
одна группа (уровень В) исследует функцию вида
y=(x-b)2, одна группа (уровень С) исследует
функцию y=(x-b)2+c. Группа “Экспертов”
исследует все функции.

План работы

  1. Для того чтобы выдвинуть гипотезу сделайте
    предположение, как может выглядеть ваша функция.
  2. Постройте график исследуемых функций
    (определите вершину параболы (х0, y0),
    задайте таблицей 4 точки).
  3. Сравните получившийся график с контрольным
    образцом y=x2.
  4. Сделайте вывод (как изменилось положение
    графика вашей функции относительно контрольного
    образца).
  5. Результаты оформите на листе формата А3 и
    представьте “экспертной” группе.

“Экспертная” группа сверяет результаты свои с
результатами остальных групп, систематизирует и
обобщает результаты, выступает с выводами. В
случае неточностей или ошибок учитель вносит
коррекционные замечания.

Сверка полученных результатов со слайдами
№2-5.

Любую квадратичную функцию y=ax2+bx+c, можно
записать в виде y=a(x-x0)2+y0, где x0
и y0 выражаются через коэффициенты a, b, c.
Таким образом, ваши коэффициенты b=x0, c=y0
являются координатами вершины параболы.

3. Закрепление изученного материала.

Фронтальная работа с классом.

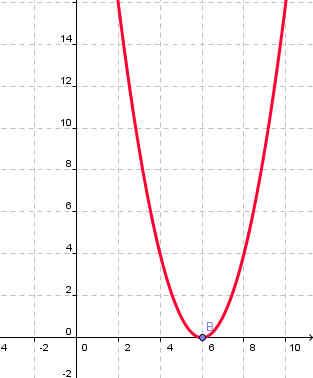
1. Найти ошибку в графиках функций (Слайды№6-9).

y=(х+6)2

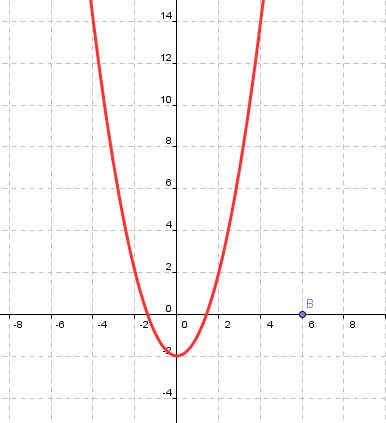
у=х2-2

Коэффициент b

Нет ошибки

Рисунок 1

Рисунок 2
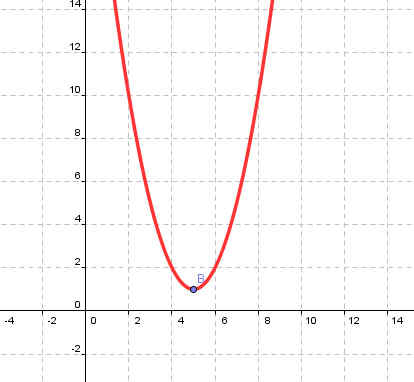
у=(х+5)2-1 у=(х-2)2+2
Коэффициент b и с Коэффициент b
Рисунок 3 Рисунок 4

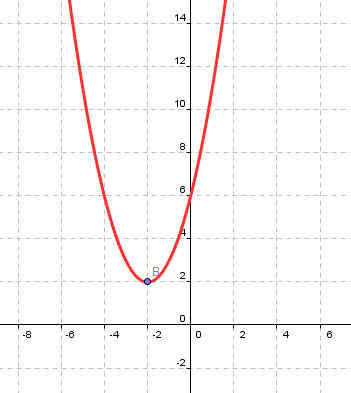Результаты

<Рисунок 7>

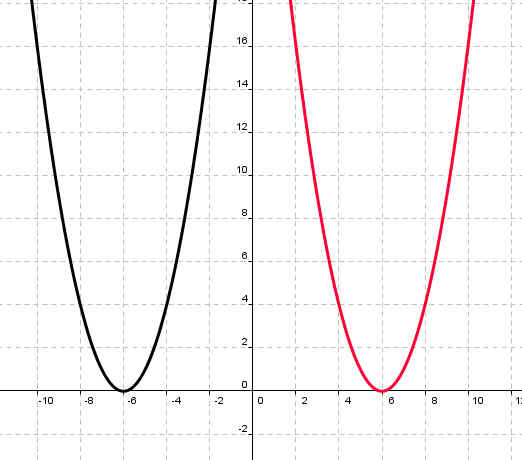
<Рисунок 2>

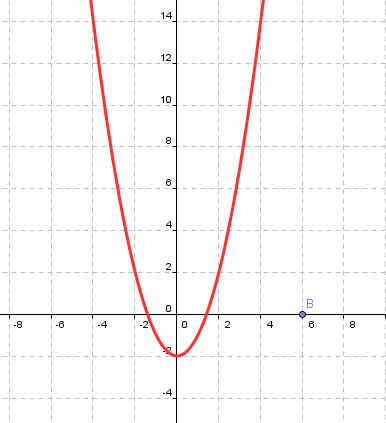
<Рисунок 8>

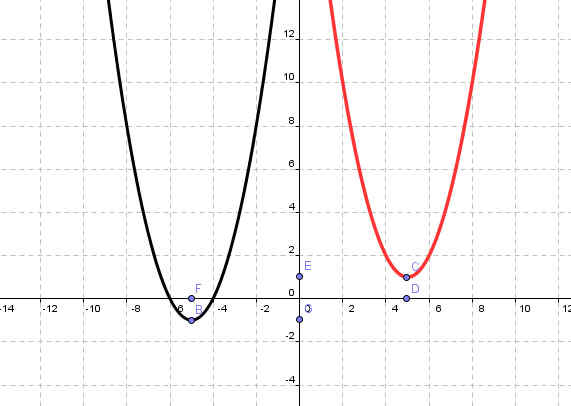
<Рисунок 9>

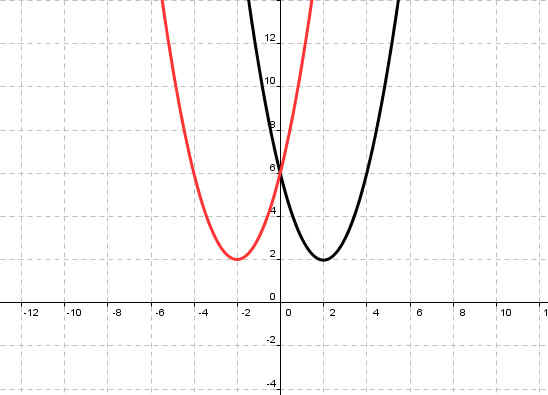
Какой коэффициент вам помог найти ошибку?

2. Соотнесите графики функций согласно цветам (слайд
№10).

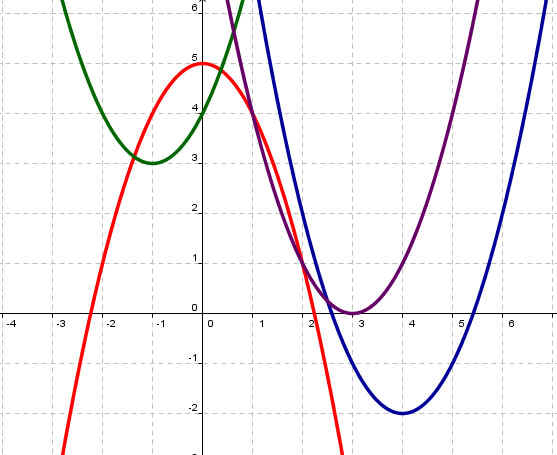
Рисунок 5

y=(х-4)2-2 синий
y=-x2+5 красный
y=(x+1)2+3 зеленый
y=(x-3)2 фиолетовый

4. Рефлексия.

Группа “Экспертов” отвечают на вопросы:

– Какие ошибки допустили группы?

– Достигнута ли цель занятия?

– Соответствуют ли полученные результаты
исследования поставленной гипотезе?

5. Итог урока (слайд №11):

На положение графика функции y=(x-b)2+c
влияют коэффициенты b и c,

“+b” парабола сдвинута вправо по оси абсцисс на
b единичных отрезков,

“–b” парабола сдвинута влево по оси абсцисс на
b единичных отрезков,

“+с” парабола сдвинута вверх по оси ординат на
с единичных отрезков,

“-с” парабола сдвинута вниз по оси ординат на с
единичных отрезков.

6. Домашнее задание

  1. Построить график квадратичной функции, имеющую
    вершину в точке А(1;-2), коэффициент a=1.
  2. Подумайте, в какой области можно использовать
    знания по данной теме (практическое применение).

Приложение

Источник

Добавить комментарий