Смежные углы в геометрии
15 июня 2022
Два угла называются смежными, если у них общая вершина, общая сторона, а две других стороны образуют прямую.
В этом уроке:
- Что такое смежные углы
- Основное свойство смежных углов
- Биссектрисы смежных углов
- Тренировочные задачи
Это довольно простая, но очень важная тема.
1. Что такое смежные углы
Возьмём прямую $AB$ и отметим на ней точку $M$. Получим развёрнутый угол $AMB:$
Проведём из точки $M$ луч $MN$, не совпадающий с лучами $MA$ и $MB$.
Получим два новых угла: $angle AMN$ и $angle BMN$. Эти углы и называются смежными.
Определение. Два угла называются смежными, если у них одна общая сторона, а две других образуют прямую (или, что то же самое, являются дополнительными лучами).
Обратите внимание: чтобы углы стали смежными, им недостаточно просто иметь общую сторону. Вот эти углы — не смежные, хотя они и имеют общую сторону:
А вот дальше — смежные, хотя и расположены немного непривычно:
Часто смежные углы возникают в точке пересечения прямых. Например, при пересечении двух прямых
образуется четыре пары смежных углов: $angle ASM$ и $angle ASN$; $angle BSM$ и $angle MSN$; $angle ASN$ и $angle BSN$; наконец, $angle ASM$ и $angle BSM$.
2. Основное свойство внешних углов
У смежных углов есть замечательное свойство, которое будет преследовать нас на протяжении всей геометрии, до конца 11 класса.
Теорема. Сумма смежных углов равна 180°.
Доказательство. Рассмотрим смежные углы $AMN$ и $BMN$ с общей стороной $MN$:
Поскольку луч $MN$ делит угол $AMB$ на смежные углы $AMN$ и $BMN$, по основному свойству углов
[angle AMB=angle AMN+angle BMN]
Но угол $AMB$ — развёрнутый, поэтому
[angle AMN+angle BMN={180}^circ ]
Другими словами, если один угол равен $alpha $, то смежный с ним равен ${180}^circ -alpha $. Или если известно, что углы $alpha $ и $beta $ — смежные, то $alpha +beta ={180}^circ $.
Казалось бы, элементарные рассуждения, но их вполне достаточно, чтобы решать большой класс задач.
Задача 1. Найдите угол, смежный с углом $ABC$, если:
- $angle ABC={36}^circ $.
- $angle ABC={121}^circ $.
Решение
1) Обозначим смежный угол $DBC=x$. Он будет тупым:
Тогда $x=180-36=144$.
2) Обозначим смежный угол $DBC=x$. Он будет острым:
Тогда $x=180-121=59$.
Немного усложним задачу.
Задача 2. Найдите смежные углы, если:
- один из них на 68° больше другого.
- один из них в 5 раз больше другого.
- их градусные меры относятся как 5 : 4.
Решение.
1) Пусть один из углов равен $x$. Тогда другой (очевидно, больший) будет равен $x+68$.
Поскольку углы смежные, их сумма равна 180 градусов:
[begin{align}2x+68&=180 \ 2x&=112 \ x&=56 end{align}]
Итак, один угол равен 56 градусов. Тогда другой равен $x+68=124$ градуса.
2) Пусть меньший угол равен $x$. Тогда смежный с ним равен $5x$.
Сумма смежных углов равна 180 градусов, поэтому
[begin{align}5x+x&=180 \ 6x&=180 \ x&=30 end{align}]
Мы нашли меньший угол — он равен 30 градусов. Тогда второй угол равен $5x=150$ градусов.
3) В задачах с отношениями величинам удобно обозначать их кратными некоторой переменной. Например, если углы относятся как 5 к 4, то пусть величина одного угла будет $5x$, а другого — $4x$.
Сумма смежных углов вновь равна 180 градусов:
[begin{align}5x+4x&=180 \ 9x&=180 \ x&=20 end{align}]
Поэтому сами углы равны $4x=80$ и $5x=100$ градусов.
3. Биссектрисы смежных углов
Вновь рассмотрим смежные углы $AMN$ и $BMN$:
Построим биссектрису $MC$ угла $AMN$ и биссектрису $MD$ угла $BMN$:
Если $angle AMC=x$ и $angle BMD=y$, то $angle AMN=2x$ и $angle BMN=2y$. Это смежные углы, поэтому
[begin{align}2x+2y&={180}^circ \ x+y&={90}^circ end{align}]
Получается, что биссектрисы смежных углов всегда пересекаются под углом 90°. Этот факт известен далеко не всем ученикам. Хотя он вполне может встретиться, например, на ЕГЭ.
Задача 3. Углы $ABC$ и $MBC$ смежные, $angle ABC={70}^circ $. Луч $BD$ принадлежит углу $ABC$, причём $angle ABD={40}^circ $. Найдите угол между биссектрисами углов $CBD$ и $MBC$.
Решение. Изобразим все углы на рисунке:
Видим, что углы $ABD$ и $MBD$ — смежные. Следовательно
[begin{align}angle MBD&={180}^circ -angle ABD= \ &={180}^circ -{40}^circ ={140}^circ end{align}]
Синим цветом отмечены биссектрисы углов $CBD$ и $MBC$. Обозначим величину углов переменными: $angle CBD=2x$, $angle MBD=2y$. Но $angle MBD=angle MBC+angle CBD$, поэтому
[begin{align}2x+2y&=140 \ x+y&=70 end{align}]
Это и есть искомый угол между биссектрисами. Он равен 70 градусов.
Задача 4. Дан треугольник $ABC$. Лучи $AM$ и $CN$ лежат на одной прямой со стороной $AB$ (см. рисунок). Известно, что $angle MAC+angle ABC={180}^circ $. Докажите, что $angle MAC=angle NBC$.
Пусть $angle ABC=x$. Тогда из условия следует, что $angle MAC={180}^circ -x$.
С другой стороны, углы $ABC$ и $NBC$ смежные, поэтому $angle NBC={180}^circ -x$.
Получается, что углы $MAC$ и $NBC$ равны одному и тому же выражению. Следовательно, $angle MAC=angle NBC$, что и требовалось доказать.
Смотрите также:
- Что такое вертикальные углы

- Перпендикулярные прямые — определение и свойства

- Правила комбинаторики в задаче B6

- Метод координат в пространстве

- Четырехугольная пирамида: как найти координаты вершин

- Задача B4 про три дороги — стандартная задача на движение

Как найти смежный угол
Плоским углом называют фигуру, образованную двумя лучами, исходящими из одной точки. Эта точка называется вершиной угла, а лучи – его сторонами. Если один из лучей продолжить за его начальную точку, то есть сделать прямой линией, то его продолжение образует со вторым лучом еще один угол – он называется смежным. Так как стороны угла равнозначны и продолжить можно любую из них, у каждого угла есть по два смежных.
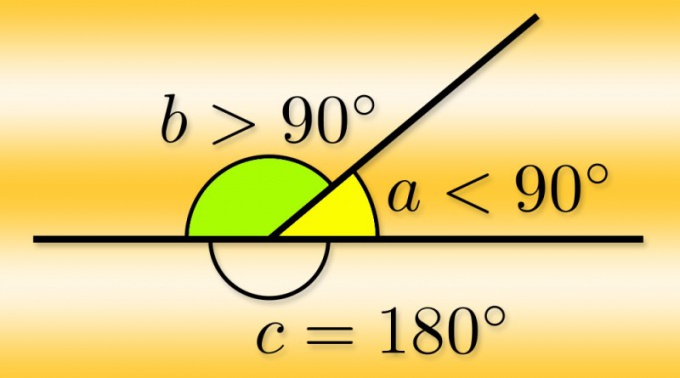
Инструкция
Если вам известна величина основного угла (α) в градусах, рассчитать градусную меру любого из пары смежных (α₁ и α₂) будет очень просто. Каждый из них дополняет основной угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого числа известную величину основного угла α₁ = α₂ = 180°-α.
Величина исходного угла может быть приведена в радианах. Если и результат нужно получить в этих единицах, исходите из того, что развернутому углу соответствует количество радиан, равное числу Пи. Значит, формулу вычисления можно записать в таком виде: α₁ = α₂ = π-α.
Вместо градусной или радианной меры основного угла в условиях может быть дано соотношение величин основного и смежного углов. В этом случае составьте уравнение пропорции. Например, обозначьте через Y величину доли пропорции, относящуюся к основному углу, через X – относящуюся к смежному, а количество градусов, приходящееся на каждую единицу пропорции, обозначьте через k. Тогда общую формулу можно будет записать так: k*X+k*Y=180° или k*(X+Y)=180°. Выразите из нее общий множитель: k=180°/(X+Y). Затем рассчитайте величину смежного угла, умножив полученный коэффициент на долю этого угла в заданной пропорции: k*X = 180°/(X+Y)*X. Например, если это соотношение равно 5/13, величина смежного угла должна составлять 180°/(5+13)*13 = 10°*13 = 130°.
Если в исходных условиях ничего не сказано об основном угле, но дана величина вертикального угла, для вычисления смежных углов используйте формулы двух предыдущих шагов. Согласно определению вертикальный угол образуется двумя лучами, исходящими из той же точки, что и лучи основного угла, но направленными в строго противоположные стороны. Это значит, что градусная или радианная мера основного и вертикального угла равны, а значит, равны и величины смежных им углов.
Видео по теме
Источники:
- как найти смежный угол в треугольнике если
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Смежные углы. Свойства смежных углов
Определение 1. Смежными называются два угла, у которых одна сторона общая, а другие стороны являются продолжениями друг друга.
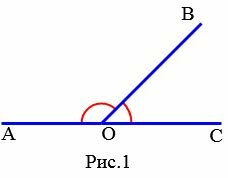
На Рис.1 углы AOB и BOC смежные, так как сторона OB общая для этих углов, а стороны OA и OC являются продолжениями друг друга. Поскольку угол AOC является развернутым углом, то сумма смежных углов равна 180°:
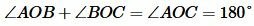 . . |
(1) |
Свойства смежных углов
1. Сумма смежных углов равна 180°
2. Если оба смежных угла равны между собой, то они являются прямыми.
3. В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
4. Синусы смежных углов равны.
5. Косинусы, тангенсы и котангенсы смежгых углов равны, но имеют противоположный знак.
Справедливость пунктов 2 и 3 очевидны и следуют из (1).
Доказательство пункта 4. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но (см. статью Формулы приведения тригонометрических функций онлайн)
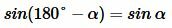 .
.
То есть синусы смежных углов равны.
Доказательство пункта 5. Обозначим через α один из смежных углов. Тогда величина другого угла будет равна 180°−α. Но
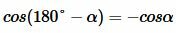 ,
,
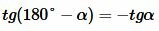 ,
,
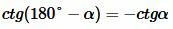 .
.
То есть косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.
Углы. Смежные углы.
Какие углы называются смежными?
Смежными углами называется пара углов с общей вершиной и одной
общей стороной. 2 оставшиеся стороны делают продолжение друг
другу, образовывая прямую линию. Для угла 135 градусов смежным
будет угол равный 45 градусам. Для угла x градусов смежным
является угол (180 – x) градусов.

Два смежных угла — это углы, с одной общей стороной, а остальные стороны находятся на одной прямой.
При пересечении 2-х прямых получается 4-ре пары смежных углов:
Но, так как ∠1 =∠4, ∠2 = ∠3 (как вертикальные), то достаточно рассматривать
только одну из этих пар.

Свойство смежных углов.
Чему равна сумма смежных углов?
Смежные углы равны: сумма смежных углов 180º.
Следствия из теоремы о смежных углах.
- Если 2 угла равны, то смежные им углы тоже равны.
- Если угол не развернутый, значит он ≠180°.
- Смежный угол для прямого угла (т.е. угла, у него градусная мера = 90°), тоже прямой.
- Смежный угол для острого угла (градусная мера меньше 90°), будет тупым (градусная мера больше
90°), а смежный тупому – острым.
Тригонометрические соотношения.
- Синусы смежных углов одинаковы. Их косинусы и тангенсы равны по величине, но имеют
противоположные знаки (исключение неопределенные значения).
- Чтобы построить угол, смежный существующему, необходимо одну из сторон нашего угла продлить

Задание. Чему будет равна градусная мера угла α, когда градусная мера смежного ему угла = 70°?
Как найти смежный угол?
Решение. Из теоремы о смежных углах находим:
Смежные и вертикальные углы. Треугольник. Равнобедренный треугольник. Медиана, биссектриса, высота, средняя линия
Готовиться с нами – ЛЕГКО!
Эффективное решение существует!
Вы ищете теорию и формулы для ЕГЭ по математике ? Образовательный проект «Школково» предлагает вам заглянуть в раздел «Теоретическая справка». Здесь представлено пособие по подготовке к ЕГЭ по математике, которое фактически является авторским. Оно разработано в соответствии с программой школьного курса и включает такие разделы, как арифметика, алгебра, начала анализа и геометрия (планиметрия и стереометрия). Каждое теоретическое положение, содержащееся в пособии по подготовке к ЕГЭ по математике, сопровождается методически подобранными задачами с подробными разъяснениями.
Таким образом, вы не только приобретете определенные знания. Полный справочник для ЕГЭ по математике поможет вам научиться логически и нестандартно мыслить , выполнять самые разнообразные задачи и грамотно объяснять свои решения. А это уже половина успеха при сдаче единого государственного экзамена.
После того, как вы нашли необходимые формулы и теорию для ЕГЭ по математике, рекомендуем вам перейти в раздел «Каталоги» и закрепить полученные знания на практике. Для этого достаточно выбрать задачу по данной теме и решить ее. Кроме того, справочные материалы по математике для ЕГЭ пригодятся вам и для других естественнонаучных дисциплин, таких как физика, химия и т. д.
Факт 1.
(bullet) Смежные углы – два угла, имеющие общую сторону, а две другие стороны являются продолжениями одна другой.
Смежные углы: (angle AOB) и (angle BOC) .
Теорема: Сумма смежных углов равна (180^circ) : (angle AOB+angle BOC=180^circ) .
Факт 2.
(bullet) Вертикальные углы – два угла, у которых стороны одного угла являются продолжениями сторон другого (образуются, например, при пересечении двух прямых).
Вертикальные углы: (angle 1) и (angle 2) , (angle 3) и (angle 4) .
Теорема: Вертикальные углы равны: (angle 1=angle 2) и (angle 3=angle 4) .
Факт 3.
(bullet) Сумма углов (angle A, angle B, angle C) треугольника (ABC) равна (180^circ) .
(bullet) Внешний угол (angle BCD) треугольника (ABC) равен сумме двух углов треугольника, не смежных с ним.
Факт 4.
(bullet) Биссектрисы смежных углов взаимно перпендикулярны.
(bullet) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.
Факт 5.
(bullet) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
(bullet) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Факт 6.
(bullet) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:
Второе свойство равнобедренного треугольника: углы при основании равны.
Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.
Факт 7.
(bullet) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Факт 8.
(bullet) Медианы в треугольнике точкой пересечения делятся в отношении (2:1) , считая от вершины.
Факт 9.
(bullet) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Факт 10.
(bullet) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
(bullet) Квадрат этой высоты равен произведению отрезков, на которые она делит гипотенузу.
Факт 11.
(bullet) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
(bullet) 1. Средняя линия треугольника параллельна третьей стороне.
(bullet) 2. Средняя линия треугольника равна половине третьей стороны.
(bullet) 3. Средняя линия отсекает от треугольника подобный ему треугольник.
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, – на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор . Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.
- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
[spoiler title=”источники:”]
http://www.calc.ru/Ugly-Smezhnyye-Ugly.html
http://shkolkovo.net/theory/smezhnye_i_vertikalnye_ugly_treugolnik_ravnobedrennyj_treugolnik_mediana_bissektrisa_vysota_srednyaya_liniya
[/spoiler]
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
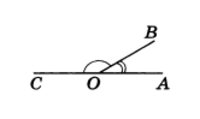
Сумма смежных углов равна 180°
Рис.1
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Рис.2
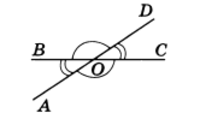
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1
∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
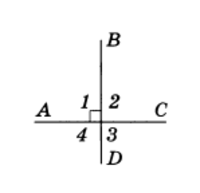
Рис.3
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
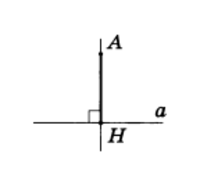
АН — перпендикуляр к прямой
Рис.4
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
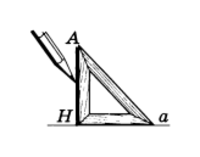
Чертежный угольник
Рис.5
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x, тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° – ∠ COD = 180° – 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° – 50° = 130°.
В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°.
Найдите величину угла ABC . Ответ дайте в градусах.
Отыскание смежных углов треугольника.

Смежные углы
Определение
Смежные углы — это два угла, у которых есть общая вершина и одна сторона, а две другие стороны являются продолжением друг друга и лежат на одной прямой.
Свойства и виды смежных углов в геометрии
- Так как две стороны смежных углов образуют прямую линию, то вместе они составляют развернутый угол. Его градусная мера составляет 180^circ. Следовательно — сумма смежных углов тоже равна (180^circ.)
- Если две прямые пересекаются, то они образуют две пары смежных углов: (angle1) и (angle2), (angle3) и (angle4), а также (angle1) и (angle3), ( angle2) и (angle4). При этом объединение пар, которые обозначены обозначениями 1 и 4, 2 и 3, представляют из себя вертикальные углы, а значит — они равны. Поэтому рассматривать можно только одну из пар смежных углов, другая окажется идентична по всем показателям.
- У смежных углов одинаковые синусы.
- Для косинусов и тангенсов тоже распространяется равенство, но их значения противоположны по знаку.
- Чтобы построить смежный угол уже заданному, требуется продлить одну из сторон существующего угла дальше вершины.
Примечание
В паре, если один угол тупой, то по правилу другой обязательно острый.
Если один из углов является прямым, то второй тоже прямой.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти, чему равна сумма
Сумма смежных углов всегда составляет 180 градусов.
Отсюда следует формула:
(anglealpha+anglebeta=180^circ)
(anglealpha=180^circ-anglebeta)
(anglebeta=180^circ-anglealpha)
Примеры решения задач
Задача №1
Дано: (anglealpha) и (anglebeta) — смежные, (anglebeta=60^circ).
Найти: чему равен (anglealpha).
Решение
Так как углы смежные, значит:
(anglealpha+anglebeta=180^circ.)
(anglealpha=180^circ-anglebeta.)
(anglealpha=180^circ-60^circ=120^circ.)
Ответ: (;anglealpha=120^circ).
Задача №2
Дано: ( anglealpha) и (anglebeta) — смежные, (anglealpha) на (30^circ) больше, чем (anglebeta.)
Найти: чему равны (anglealpha) и (anglebeta.)
Решение
Допустим,( anglebeta=x), тогда (anglealpha=x+30^circ.)
Так как сумма смежных углов равна 180 градусов, то получаем уравнение, которое выглядит, как:
(x+x+30^circ=180^circ)
(2x=180^circ-30^circ)
(2x=150^circ)
(x=75^circ)
Значит, величина (anglebeta=75^circ.)
Чтобы найти (anglealpha), нужно выполнить стандартные вычисления согласно теореме о сумме:
(anglealpha=180^circ-anglebeta=180^circ-75^circ=105^circ.)
Ответ: (anglealpha=105^circ.)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так













