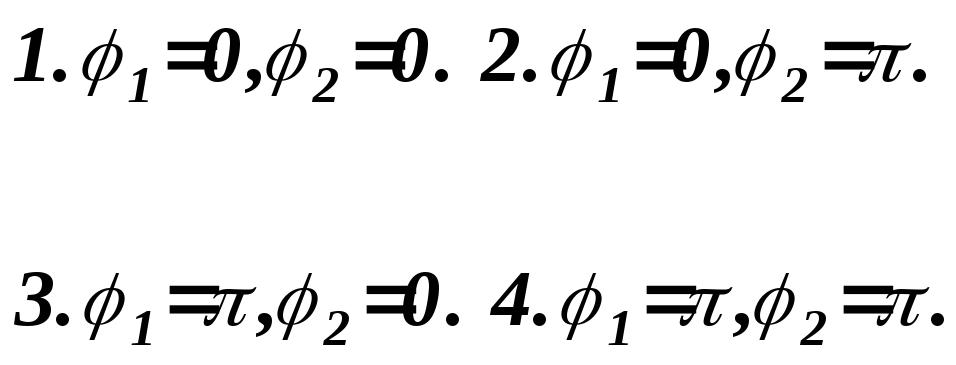Богдан Новах
Эксперт по предмету «Архитектура и строительство»
Задать вопрос автору статьи
Собственные колебания
Собственные или свободные колебания – это колебания, происходящие в системе при отсутствии переменных внешних воздействий. Такие колебания возникают по причине начального отклонения одного из параметров от состояния равновесия.
В целом колебания представляют собой повторяющийся во времени процесс изменения состояния системы около точки равновесия (при колебании маятника все углы его отклонения от вертикали повторяются с определенной периодичностью.
В реальных макроскопических системах собственные колебания затухают по причине потерь энергии. Любой колебательный процесс связан с переходом энергии из одной формы в другую.
Следует заметить, что колебания различной физической природы имеют ряд общих закономерностей и тесно связаны с волнами. В этой связи исследованием таких закономерностей занимается теория колебаний и волн. Принципиальное отличие колебаний от волн заключается в том, что распространение последних сопровождается переносом, а не переходом энергии.
По характеру взаимодействия с окружающей средой колебания разделяют на:
- вынужденные;
- автоколебания;
- параметрические;
- собственные.
В настоящей статье речь пойдет о собственных колебаниях, т.е. о колебаниях системы под действием внутренних сил после выведения системы из равновесия.
При небольших отклонениях от состояния равновесия движение любой системы будет удовлетворять принципу суперпозиции. Согласно данному принципу сумма произвольных движений составляет допустимое движение системы. Подобные движения описываются линейными (дифференциальными) уравнениями.
В случае, если в системе нет потерь энергии (она консервативна), а ее параметры не изменяются во времени, то любое собственное колебание может быть представлено, как совокупность нормальных колебаний, изменяющихся во времени по закону синуса с определенными частотами собственных колебаний.
Если положение системы в любой момент времени описывается единственным параметром, то такая система имеет одну степень свободы. Идеальным примером такой системы является маятник, колеблющийся в плоскости. И действительно, положение маятника в любой момент может определяться лишь углом его отклонения от вертикали.
«Как определить собственную частоту колебаний» 👇
В природе существует большое количество весьма интересных систем, имеющих две степени свободы. Например, молекулы и элементарные частицы (наиболее примечательны нейтральные К-мезоны). Более простым и понятным примером является двойной маятник (один маятник подвешивается к опоре, второй – к гире первого маятника; два маятника, объединенные пружиной).
Чтобы описать состояние системы с двумя степенями свободы необходимо уже две переменные. Например, в случае со сферическим маятником роль таких переменных будут выполнять положения маятника в двух взаимно перпендикулярных плоскостях. В случае объединенных маятников эти переменные соответствуют положению каждого из маятников.
В общем виде движение системы, имеющей две степени свободы, может иметь весьма сложный вид, не напоминающий простое гармоническое движение.
Для двух степеней свободы, а также при линейных уравнениях движения общий вид движения представляет собой суперпозицию двух простейших гармонических зависимостей, происходящих в один момент. Эти два элементарных движения называют нормальными (собственными) колебаниями или гармониками.
Колебательные системы с сосредоточенными параметрами, состоящими из N связанных осцилляторов (например, цепочка из связанных между собой пружинками шариков), число гармоник будет равно N. В системах с распределенными параметрами (мембрана или резонатор) таких колебаний существует бесчисленное множество. Например, для закрепленной струны длиной L гармоники будут отличаться количеством полуволн, которые возможно уложить по всей длине струны. Если скорость распространения волн струны равна v, то спектр собственных частот определяется по формуле:
Рисунок 1. Формула 1. Автор24 — интернет-биржа студенческих работ
Наличие дисперсии волн искажает данное простое распределение частот, спектр которых определяется уже из дисперсионных уравнений.
Что касается реальных систем, то в них собственные колебания затухают из-за потерь энергии, поэтому их следует считать лишь приближенно гармоническими в интервале времени, меньшем $1/δ$. Затухающие колебания могут быть представлены в виде нескольких гармонических колебаний, непрерывно заполняющих определенный интервал частот, тем меньшим, чем меньше $δ$. В таком случае следует говорить о расширении спектральной линии, характеризуемой добротностью $Q$ и равной отношению запасенной энергии $W$ к потерям $P$. Отсюда следует, что отношение сгущение спектра из-за потерь энергии может повлечь за собой превращение дискретного спектра в сплошной при приближении ширины линий к интервалу между ними.
Колебания в нелинейных системах
Собственные колебания нелинейных систем не поддаются простой классификации. Нелинейность систем с дискретным спектром частот собственных колебаний приводят к переходу энергии по спектральным компонентам. При этом возникает явление конкуренции гармоник – выживание одних и подавление других.
Подобный процесс может стабилизировать дисперсия. Она может привести к появлению устойчивых пространственно-временных образований (например, солитоны).
Большое значение при возбуждении колебаний может иметь явление резонанса, которое заключается в резком увеличении амплитуды колебаний (отклика). Данное явление наблюдается при приближении частоты внешних воздействий на систему к некоторой резонансной частоте, которая характеризует настоящую систему.
Если система линейна и ее параметры находятся вне зависимости от времени, то резонансные частоты совпадают с частотой собственных ее колебаний. Отклик системы в данном случае будет усиливаться с увеличением добротности колебательной системы $Q$.
Раскачка будет происходить до тех пор, пока энергия, поступающая извне (например, полученная при отклонении маятника от положения равновесия) будет превышать потери за время осцилляции. Что касается линейных колебаний, то энергия, вносимая извне будет пропорциональна амплитуде, а потери будут расти пропорционально ее квадрату. Отсюда следует, что баланс энергии достижим во всех случаях.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Будем
рассматривать колебательные движения
механических систем относительно
положения устойчивого равновесия,
которые описываются системой линейных
дифференциальных уравнений ( 6.1 ). Решение
будем искать в виде
(
6.5 )
где
– амплитудаj–
ой обобщенной координаты,
–
частота
и
– начальная фаза колебаний.
Подставляя
решения ( 6.5 ) в систему дифференциальных
уравнений и сокращая их на общий множитель
,
получим систему линейных однородных
алгебраических уравнений относительно
неизвестных амплитуд
(
6.6 )
Система
линейных однородных уравнений ( 6.6 )
может иметь отличное от нуля решение
только в том случае, если ее определитель,
составленный из коэффициентов при
неизвестных амплитудах, будет равен
нулю, т.е.
(
6.7 )
Раскрывая
данный определитель, получаем
алгебраическое уравнение порядка s
относительно квадрата неизвестной
частоты колебаний
.
Это уравнение называетсяхарактеристическим
или частотным.
Для
колебательной механической системы
все корни
характеристического уравнения будут
положительными. Этим свойством можно
воспользоваться для проверки полученных
значений коэффициентов
и
.
Если хотя бы один из корней характеристического
уравнения будет отрицательным, это
значит, что коэффициенты определены
неправильно.
Совокупность
полученных значений
определяет набор частот, на которых
возможно существование колебаний в
консервативной механической системе.
Такие частоты называютсясобственными
или главными
частотами. Если среди корней
характеристического уравнения будут
кратные, то решение уравнения будет
иметь иной вид1.
Для
механической системы с двумя степенями
свободы характеристическое уравнение
имеет следующий вид
Учитывая,
что коэффициенты характеристического
уравнения не зависят от порядка индексов,
полученное уравнение можно переписать
в более простом виде:
(
6.8 )
Решением
его будет являться пара значений
и
, определяющих две собственные частоты
исследуемой механической системы.
Принято считать первой собственной
частотой меньшую.
Подставляя
в уравнения ( 6.6 ) значения собственных
частот, получаем систему из s
уравнений относительно амплитуд
колебаний, из которых независимыми
будут только s
– 1.
Следовательно, решая эти уравнения,
нельзя найти значения амплитуд, можно
лишь выразить s
– 1 амплитуду
через какую-либо одну, например
.
применяя для этого известные формулы
алгебры, получаем
—
( 6.9 )
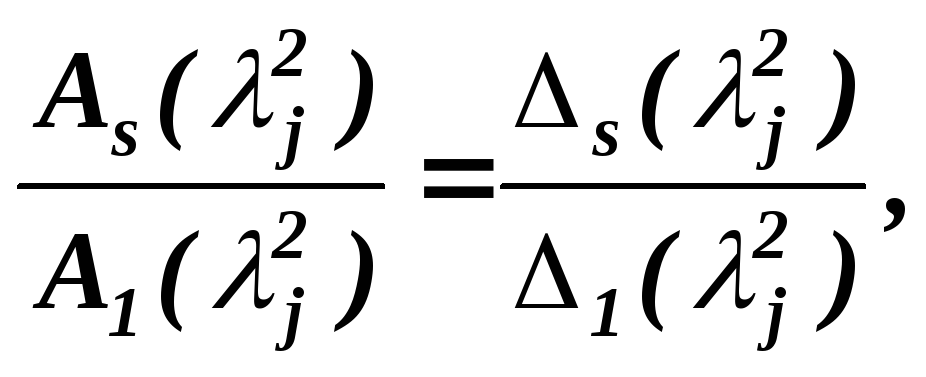
где
–
алгебраическое дополнение элемента
определителя системы уравнений ( 6.6 ).
Из соотношений ( 6.9 ) видно, что при
колебании с каждой из собственных частот
отношения амплитуд отдельных обобщенных
координат остаются постоянными. Они
определяется свойствами только самой
механической системы и не зависит от
начальных условий. Эти отношения
называютсяформами
колебаний.
Для
системы с двумя степенями свободы формы
колебаний определяют отношение амплитуд
изменения обобщенных координат в каждом
из главных колебаний ( колебаний с одной
из собственных частот )
Выражение
( 6.9 ) можно переписать в другом виде
Если ввести
обозначение
получим
Каждому
корню
частотного уравнения можно поставить
в соответствие систему частных решений
дифференциального уравнения, которые
будут описывать движение механической
системы с одной из собственных частот
– главное колебание с частотой
.
. . .
Общее
решение рассматриваемой системы является
суммой всех ее частных решений и имеет
следующий вид
(
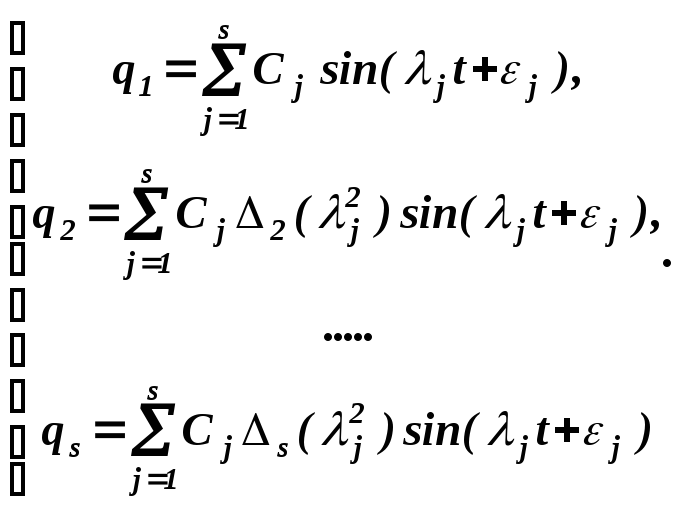
6.10 )
Решения
( 6.10 ) содержат 2s
постоянных интегрирования
и
,
которые определяются из начальных
условий.
Если
обобщенные координаты являются
нормальными, то отдельно для каждой из
них решение можно найти из соответствующего
уравнения, причем изменения различных
координат не зависят друг от друга и
каждое главное колебание будет связано
только с одной обобщенной координатой.
Пример.
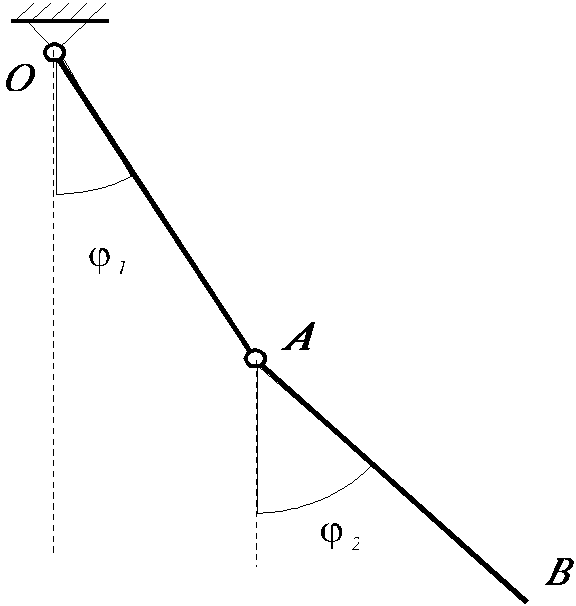
Рассмотрим малые колебания двойного
физического маятника, состоящего из
двух однородных стержней 1 и 2 одинаковой
длины L
и массы m,
соединенных в точке А
шарниром ( рис. 6.1 ). Трением и сопротивлением
воздуха пренебрегаем.
-
Выберем
обобщенные координаты. В данном случае
за них удобно принять углы
и, которые стержни образуют с вертикалью.
На рис. 6.1 показано положение системы
при положительных обобщенных координатах
.
и
, которые стержни образуют с вертикалью.
Рис.
6.1
2.
Составим выражение для кинетической
энергии системы как функцию обобщенных
скоростей и координат. При выполнении
данного раздела курсовой работы можно
воспользоваться полученными ранее
выражениями.
-
Составим
выражение для потенциальной энергии
системы как функцию обобщенных координат.
Пользуясь полученным
выражением, из условия равенства нулю
обобщенных сил можно найти все положения
равновесия системы, если они не были
найдены ранее.
Из
этих условий следует, что в данной
механической системе возможны четыре
положения равновесия
При
этом, как нетрудно убедиться, только
для первого положения равновесия
потенциальная энергия имеет изолированный
минимум и только это положение равновесия
будет устойчивым.
4.
Определим обобщенные коэффициенты
инерции
и жесткости
.
Для определения обобщенных коэффициентов
инерции, приведем кинетическую энергию
системы к квадратичной форме ее обобщенных
скоростей. Для этого разложим выражение
в ряд Тейлора и оставим члены только
второго порядка малости:
Откуда
Приведем
потенциальную энергию системы в
окрестности первого положения равновесия
к квадратичной форме. Для этого разложим
потенциальную энергию в ряд Тейлора по
и
в точке
.
Тогда, учитывая, что
получим
с точностью до членов второго порядка
малости
или
Полученная
квадратичная форма будет положительно
определенной, так как выполняются
условия критерия Сильвестра
5.
Пользуясь полученными значениями
обобщенных коэффициентов инерции и
жесткости, запишем дифференциальные
уравнения малых колебаний системы в
развернутом виде ( 6.2 )
6.
Составим характеристическое уравнение:
Или
в развернутом виде
7. Найдем корни
характеристического уравнения
Два
полученных значения определяют две
собственные частоты колебаний исследуемой
механической системы
Таким
образом, движение рассматриваемой
системы при собственных колебаниях в
общем случае будет происходить по
следующему закону:
где
–
коэффициенты формы, соответствующие
каждой из собственных частот:
8.
Определим коэффициенты форм колебаний
С
учетом полученных значений коэффициентов
форм перепишем общее решение
9.
Найдем значения постоянных интегрирования
для следующих начальных условий:
Для
этого подставим начальные значения
координат, скоростей и времени в
уравнения движения и уравнения,
определяющие зависимости скоростей от
времени
Решая
полученную систему уравнений, получаем
С
учетом полученных значений постоянных
интегрирования запишем окончательный
вид уравнений колебаний
ЛИТЕРАТУРА
-
Бать М.И., Джанелидзе
Г.Ю., Кельсон А.С. Теоретическая механика
в примерах и задачах. Т. II. Динамика.-
М.: Наука.- 1991.- 640 с. -
Бутенин
Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической
механики. Т. I
и II.- М.: Наука.- 1985. -
Бухгольц
Н.Н. Основной курс теоретической
механики. Ч. I
и II. М.: Наука. – 1966. -
Кильчевский
Н.А. Курс теоретической механики. Т.
II. М.:
1977. -
Меркин Д.В. Введение
в теорию устойчивости движения. – М.:
Наука, 1976. – 320 с. -
Мещерский Н.В.
Сборник задач по теоретической механике.
М.: Наука, 1986. – 448 с. -
Сборник заданий
для курсовых работ по теоретической
механике./ Под ред. А.А. Яблонского.- М.:
Высш. шк.- 1985.-367 с. -
СТП СГАУ 6.1.4. – 97.
Общие требования к оформлению учебных
текстовых документов: методические
указания. -
Яблонский А.А.
Курс теоретической механики, Ч. II.
Динамика .- М.: Высш. шк.- 1971.- 488 с.
1Гантмахер Ф.Р. Лекции по аналитической
механике. -М., Наука. 1966.
84
Уравнения собственных колебаний
Как уже говорилось, колебательные движения системы вызываются консервативными силами. Поэтому изучение колебательных движений системы с двумя степенями свободы начнем с изучения движения ее под действием сил, принадлежащих потенциальному силовому полю. Эти движения, так же как и в случае прямолинейного колебания точки, называются собственными движениями системы. Дифференциальные уравнения движения в этом случае имеют вид:
Уравнения частот
Полагая, что движение, описываемое этими уравнениями, является колебательным (в дальнейшем это будет доказано), будем искать частные решения дифференциальных уравнений в тригонометрической форме
где 
и 
— постоянные величины.
Определяя 
и подставляя найденные значения в исходные уравнения, придем к уравнениям вида:
которые являются линейными однородными уравнениями относительно 
Решение этих уравнений будет отлично от нуля, если детерминант, составленный из коэффициентов при 
будет равен нулю
Полученное соотношение есть квадратное уравнение относительно 
Оно носит название характеристического уравнения или уравнения частот
Докажем, что оба корня этого квадратного уравнения действительные и положительные. Тем самым будет доказано, что решение исходных уравнений можно искать в тригонометрической форме. Запишем уравнение частот в виде
Найдем значения функции 
при 
равных:
Положим для определенности, что
При 
имеем:
В силу условия, связывающего 
имеем:
Следовательно, при 
положительно.
Далее при 
имеем.
Отсюда имеем, что при 
отрицательно.
При 
имеем.
Следовательно, при 
отрицательно
Рис. 140
Наконец, при 
Следовательно, график функции 
будет вида, указанного на рис 140. Функция 
проходит через нуль один раз в промежутке между 
второй раз в промежутке между 
Эти нули соответствуют двум положительным корням 
и кг уравнения частот. Уравнению частот можно придать вид
Откуда 
определяются по формуле:
Частные решения уравнений
Так как уравнения, определяющие 
зависимы, то из них можно найти только отношение их. Взяв, например, 
найдем отношение 
которое обозначим 
в виде:
где 
будет определенное число.
В этом отношении, например, 
может принимать любое постоянное значение. Обозначая его как произвольную постоянную 
можем, например, принять:
Однако в целях большей симметрии формул, определяющих 
целесообразнее записать 
например, в виде:
Таким же образом для корня 
можем найти 
где 
— произвольная постоянная.
Так как никаких ограничений на постоянные а не накладывается, то исходные дифференциальные уравнения движения допускают два частных независимых решения вида:
где 
— произвольные постоянные.
Причем:
— определенные постоянные величины.
Главные колебания и собственные частоты системы
Двум полученным частным решениям уравнений движения соответствует некоторое гармоническое колебательное движение системы. Эти два движения носят название главных колебаний системы.
Частота главных колебаний 
носит название собственных частот системы.
Если система совершает какое-либо главное колебание, то обе обобщенные координаты ее изменяются по гармоническому закону, имея одинаковые частоты и фазы. Это значит, что обе обобщенные координаты одновременно приходят в положение равновесия, одновременно достигают максимальных отклонений от положения равновесия и т. д.
Амплитуды колебаний обеих обобщенных координат различны, но отношение их остается постоянным, не зависит от начальных условий и определяется только структурой движущейся системы. Амплитуда и начальная фаза главного колебания определяются начальными условиями системы. Частота колебаний системы зависит только от характеристик движущейся системы.
Общее решение уравнений движения
В силу линейности дифференциальных уравнений движения сумма частных решений этих уравнений дает новое решение. Следовательно, имеем:
В это решение входят четыре произвольных постоянных 
Так как уравнения движения представляют собой систему двух дифференциальных уравнений второго порядка, то общее решение этой системы должно содержать четыре произвольных постоянных. Следовательно, найденное решение есть общее решение уравнений движения. Произвольные постоянные этого решения 
определяются из начальных условий вида: при 
Принцип наложения малых колебаний
Полученное решение уравнений движения системы указывает, что каждая из обобщенных координат системы совершает сложное колебательное движение, которое является результатом наложения двух главных колебаний системы различных частот 
Последний результат носит название принципа наложения малых колебаний. Так как частоты наложенных колебаний 
в общем случае несоизмеримы, то движение механической системы не будет периодическим. Смысл принципа наложения заключается в том, что
сложное результирующее движение можно представить в виде суммы простых главных колебаний, которые представляют собой гармонические движения.
Все рассуждения настоящего параграфа относились к случаю, когда уравнения частот 
были различны и не равны нулю. Если эти корни равны между собой или один из них равен нулю, то эти случаи требуют специального исследования.
Как определить собственную частоту колебаний
Для лучшего понимания вопроса рассмотрим, что собой представляют собственные колебания и колебания в нелинейных системах.
Собственные колебания
Колебания очень схожи по природе с волнами, они подчиняются общим закономерностям, единственное их отличие в том, что в процессе распространения волн энергия не переходит из одной формы в другую, а всего лишь переносится. Исследованием закономерностей физической природы волн и колебаний занимается теория колебаний и волн. На практике в реальных условиях без воздействия внешних факторов любые колебания со временем затухают, это связано с потерей энергии.
Колебания, по характеру взаимодействия с внешней средой, разделают на:
- автоколебания;
- собственные;
- вынужденные;
- параметрические.
Рассмотрим подробнее собственные колебания.
Причиной возникновения таких колебаний является отклонение от равновесия одного или нескольких параметров системы. Такие колебания возникают под воздействием внутренних сил после выведения системы из равновесия.
Рассмотрим принцип суперпозиции, который гласит о том, что допустимое движение системы равно сумме ее произвольных движений. При незначительных отклонениях характеристик системы от положения равновесия, ее движение будет соответствовать принципу суперпозиции. Подобные движения описываются дифференциальными уравнениями линейного характера. Если рассмотреть консервативную систему, т.е. такую, в которой отсутствуют потери энергии и ее параметры постоянны во времени, то любое свободное колебание такой системы представляет собой сумму простых колебаний, меняющихся во времени с определенными частотами свободных колебаний по закону синуса.
Не нашли что искали?
Просто напиши и мы поможем
Системы бывают с одной или несколькими степенями свободы. Если состояние системы в любой конкретный момент времени описывается одним параметром, то такая система имеет одну степень свободы, если двумя – то две, тремя – три, и так далее. Как пример системы с одной степенью свободы, можно рассмотреть маятник, который совершает колебательные движения в плоскости. В этом случае любое конкретное его положение характеризуется углом его отклонения от оси вертикали. Для описания колебательной системы с двумя степенями свободы нужны два переменных параметра. Примером таких колебаний является маятник, колеблющийся в сфере. В этом случае переменными параметрами будут являться углы положения маятника относительно двух перпендикулярных плоскостей. Но зачастую движения системы с двумя степенями свободы имеют сложный негармоничный характер. Они описываются линейными уравнениями суперпозиций двух простых переменных параметров, которые происходят одновременно. Так вот, каждое из этих двух простых элементарных колебаний называют собственной или свободной, так называемой гармоникой.
Для колебательных систем, состоящих из определенного количества осцилляторов (к примеру вереница шариков, соединенных между собой маленькими пружинками), число гармоник будет равняться их числу. Для более сложных систем, таких как мембрана, например, гармоники будут различные по длине волн и их будет бесконечное множество. При заданной скорости распространения таких волн, спектр собственных частот определяется простой линейной формулой. При наличии волн с разной скоростью распространения такой линейный закон уже не действует, здесь в силу вступают различные дисперсионные уравнения.
Если рассмотреть реальные существующие системы, в которых собственные колебания затухают со временем, то их считают лишь относительно гармоничными в небольшом конкретном отрезке времени. Свободные колебания, затухающие во времени, могут состоять из нескольких гармоник в определенном диапазоне частот. В таком случае имеет место так называемая добротность, то есть расширение спектральной линии, которое равно отношению запасенной энергии к потерям системы. Соответственно, сгущение спектра за счет потерь влечет за собой трансформацию его дискретной формы в сплошную в том случае, если ширина линий приближается к ширине между ними.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Колебания в нелинейных системах
Свободные или собственные колебания в нелинейных системах сложно поделить на какие-либо классы. В нелинейных системах спектр частоты свободных колебаний дискретен, что приводит к движению энергии по различным компонентам спектра. В таких колебательных системах наблюдается явление конкуренции гармоник, т.е. выживание одних за счет подавления других. Лишь дисперсия может уравновесить подобный процесс, приводя к образованию устойчивых в пространстве и времени форм колебаний.
В колебательных системах частым явлением, имеющим большое значение, является процесс резонанса. Его суть заключается в резком возрастании амплитуды колебаний. Это происходит из-за приближения частоты внешнего воздействия к частоте колебания внутреннего собственного параметра системы.
Если линейная система и ее параметры находятся вне времени, то частота резонанса совпадает с частотой ее собственных колебаний. Амплитуда колебаний системы будет усиливаться с ростом параметра ее добротности. В таком случае раскачка амплитуды будет происходить до того момента, пока поступающая энергия будет больше потерь при осцилляции.
Если говорить о линейных колебаниях, то поступающая внешняя энергия пропорциональна амплитуде, а потери пропорциональны амплитуде в квадрате. Таким образом можно сказать, что баланс энергии достигается во всех известных случаях.
Как определить собственную частоту колебаний
Вы будете перенаправлены на Автор24
Собственные колебания
Собственные или свободные колебания – это колебания, происходящие в системе при отсутствии переменных внешних воздействий. Такие колебания возникают по причине начального отклонения одного из параметров от состояния равновесия.
В целом колебания представляют собой повторяющийся во времени процесс изменения состояния системы около точки равновесия (при колебании маятника все углы его отклонения от вертикали повторяются с определенной периодичностью.
В реальных макроскопических системах собственные колебания затухают по причине потерь энергии. Любой колебательный процесс связан с переходом энергии из одной формы в другую.
Следует заметить, что колебания различной физической природы имеют ряд общих закономерностей и тесно связаны с волнами. В этой связи исследованием таких закономерностей занимается теория колебаний и волн. Принципиальное отличие колебаний от волн заключается в том, что распространение последних сопровождается переносом, а не переходом энергии.
По характеру взаимодействия с окружающей средой колебания разделяют на:
- вынужденные;
- автоколебания;
- параметрические;
- собственные.
В настоящей статье речь пойдет о собственных колебаниях, т.е. о колебаниях системы под действием внутренних сил после выведения системы из равновесия.
При небольших отклонениях от состояния равновесия движение любой системы будет удовлетворять принципу суперпозиции. Согласно данному принципу сумма произвольных движений составляет допустимое движение системы. Подобные движения описываются линейными (дифференциальными) уравнениями.
В случае, если в системе нет потерь энергии (она консервативна), а ее параметры не изменяются во времени, то любое собственное колебание может быть представлено, как совокупность нормальных колебаний, изменяющихся во времени по закону синуса с определенными частотами собственных колебаний.
Если положение системы в любой момент времени описывается единственным параметром, то такая система имеет одну степень свободы. Идеальным примером такой системы является маятник, колеблющийся в плоскости. И действительно, положение маятника в любой момент может определяться лишь углом его отклонения от вертикали.
Готовые работы на аналогичную тему
В природе существует большое количество весьма интересных систем, имеющих две степени свободы. Например, молекулы и элементарные частицы (наиболее примечательны нейтральные К-мезоны). Более простым и понятным примером является двойной маятник (один маятник подвешивается к опоре, второй – к гире первого маятника; два маятника, объединенные пружиной).
Чтобы описать состояние системы с двумя степенями свободы необходимо уже две переменные. Например, в случае со сферическим маятником роль таких переменных будут выполнять положения маятника в двух взаимно перпендикулярных плоскостях. В случае объединенных маятников эти переменные соответствуют положению каждого из маятников.
В общем виде движение системы, имеющей две степени свободы, может иметь весьма сложный вид, не напоминающий простое гармоническое движение.
Для двух степеней свободы, а также при линейных уравнениях движения общий вид движения представляет собой суперпозицию двух простейших гармонических зависимостей, происходящих в один момент. Эти два элементарных движения называют нормальными (собственными) колебаниями или гармониками.
Колебательные системы с сосредоточенными параметрами, состоящими из N связанных осцилляторов (например, цепочка из связанных между собой пружинками шариков), число гармоник будет равно N. В системах с распределенными параметрами (мембрана или резонатор) таких колебаний существует бесчисленное множество. Например, для закрепленной струны длиной L гармоники будут отличаться количеством полуволн, которые возможно уложить по всей длине струны. Если скорость распространения волн струны равна v, то спектр собственных частот определяется по формуле:
Рисунок 1. Формула 1. Автор24 — интернет-биржа студенческих работ
Наличие дисперсии волн искажает данное простое распределение частот, спектр которых определяется уже из дисперсионных уравнений.
Что касается реальных систем, то в них собственные колебания затухают из-за потерь энергии, поэтому их следует считать лишь приближенно гармоническими в интервале времени, меньшем $1/δ$. Затухающие колебания могут быть представлены в виде нескольких гармонических колебаний, непрерывно заполняющих определенный интервал частот, тем меньшим, чем меньше $δ$. В таком случае следует говорить о расширении спектральной линии, характеризуемой добротностью $Q$ и равной отношению запасенной энергии $W$ к потерям $P$. Отсюда следует, что отношение сгущение спектра из-за потерь энергии может повлечь за собой превращение дискретного спектра в сплошной при приближении ширины линий к интервалу между ними.
Колебания в нелинейных системах
Собственные колебания нелинейных систем не поддаются простой классификации. Нелинейность систем с дискретным спектром частот собственных колебаний приводят к переходу энергии по спектральным компонентам. При этом возникает явление конкуренции гармоник – выживание одних и подавление других.
Подобный процесс может стабилизировать дисперсия. Она может привести к появлению устойчивых пространственно-временных образований (например, солитоны).
Большое значение при возбуждении колебаний может иметь явление резонанса, которое заключается в резком увеличении амплитуды колебаний (отклика). Данное явление наблюдается при приближении частоты внешних воздействий на систему к некоторой резонансной частоте, которая характеризует настоящую систему.
Если система линейна и ее параметры находятся вне зависимости от времени, то резонансные частоты совпадают с частотой собственных ее колебаний. Отклик системы в данном случае будет усиливаться с увеличением добротности колебательной системы $Q$.
Раскачка будет происходить до тех пор, пока энергия, поступающая извне (например, полученная при отклонении маятника от положения равновесия) будет превышать потери за время осцилляции. Что касается линейных колебаний, то энергия, вносимая извне будет пропорциональна амплитуде, а потери будут расти пропорционально ее квадрату. Отсюда следует, что баланс энергии достижим во всех случаях.
Собственная частота незатухающих гармонических колебаний, формула
Отличительным признаком гармонических колебаний является пропорциональность восстанавливающей силы отклонению (линейный закон силы). Отношение восстанавливающей силы к отклонению наряду с массой колебательной системы определяет собственную частоту.
| D | жесткость, | Ньютон / метр |
|---|---|---|
| F | сила вызывающая отклонение y, и равная по величине восстанавливающей силе | Ньютон |
| y | отклонение, | Метр |
Частота гармонических колебаний получается из формулы
источники:
http://spravochnick.ru/arhitektura_i_stroitelstvo/kak_opredelit_sobstvennuyu_chastotu_kolebaniy/
http://www.fxyz.ru/%D1%84%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D1%8B_%D0%BF%D0%BE_%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B5/%D0%BA%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D1%8F_%D0%B8_%D0%B2%D0%BE%D0%BB%D0%BD%D1%8B/%D0%BD%D0%B5%D0%B7%D0%B0%D1%82%D1%83%D1%85%D0%B0%D1%8E%D1%89%D0%B8%D0%B5_%D0%B3%D0%B0%D1%80%D0%BC%D0%BE%D0%BD%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BA%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D1%8F/%D1%81%D0%BE%D0%B1%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D0%B0%D1%8F_%D1%87%D0%B0%D1%81%D1%82%D0%BE%D1%82%D0%B0/
Собственная частота незатухающих гармонических колебаний, формула
Отличительным признаком гармонических колебаний является пропорциональность восстанавливающей силы отклонению (линейный закон силы).
Отношение восстанавливающей силы к отклонению наряду с массой колебательной системы определяет собственную частоту.
Если
| D | жесткость, | Ньютон / метр |
|---|---|---|
| F | сила вызывающая отклонение y, и равная по величине восстанавливающей силе | Ньютон |
| y | отклонение, | Метр |
то
[
D = frac{F}{y}
]
Частота гармонических колебаний получается из формулы
[
frac{D}{m} = ω^2
]
, использованной при выводе уравнения колебаний (7).
Если
| ω | угловая частота, | радиан / секунда |
|---|---|---|
| f | линейная частота, | Герц |
| T | период полного колебания, | секунда |
| m | масса колебательной системы, | кг |
| D | жесткость, | Ньютон / метр |
то справедливы следующие соотношения:
Вычислить, найти собственную круговую частоту незатухающих гармонических колебаний по формуле
[
ω = sqrt{frac{D}{m}}
]
Вычислить, найти собственную линейную частоту незатухающих гармонических колебаний по формуле
[
f = frac{1}{2π} sqrt{frac{D}{m}}
]
Вычислить, найти период незатухающих гармонических колебаний по формуле
[
T = 2π sqrt{frac{m}{D}}
]
Собственная частота незатухающих гармонических колебаний |
стр. 542 |
|---|
