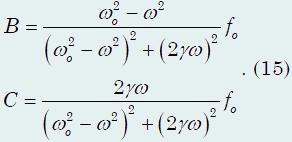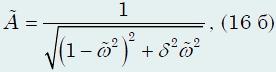Уравнение вынужденных колебаний и его решение. Резонанс.
Потери
механической энергии в любой колебательной
системе из-за
наличия сил трения неизбежны, поэтому
без «подкачки» энергии извне колебания
будут затухающими. Существует несколько
принципиально различных способов
создания колебательных систем незатухающих
колебаний. Остановимся более подробно
на рассмотрении незатухающих
колебаний под действием внешней
периодической силы.
Такие колебания называются
вынужденными.
Продолжим изучение
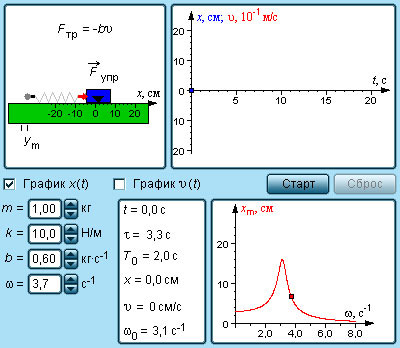
движения гармонического маятника (рис.
6.9 ).
рис.
6.9
Помимо
рассмотренных ранее сил упругости и
вязкого трения, на шарик действует
внешняя
вынуждающая
периодическая сила, изменяющаяся по
гармоническому закону
частота,
которой может отличаться от собственной
частоты колебаний маятника ωo.
Природа
этой сил в данном случае нам не существенна.
Создать такую силу можно различными
способами, например, сообщить шарику
электрический заряд и поместить его во
внешнее переменное электрическое
поле.
Уравнение движения шарика в
рассматриваемом случае имеет вид
Разделим
его на массу шарика и используем прежние
обозначения параметров системы. В
результате получим
уравнение
вынужденных колебаний:
где
fo
= Fo/m
− отношение амплитудного значения
внешней вынуждающей силы к массе
шарика.
Общее решение уравнения (3)
достаточно громоздко и, конечно, зависит
от
начальных условий. Характер движения
шарика, описываемого уравнением (3),
понятен: под действием вынуждающей силы
возникнуть колебания, амплитуда которых
будет возрастать. Этот переходный режим
достаточно сложен и зависит от начальных
условий. По прошествии некоторого
промежутка времени колебательный режим
установится, их амплитуда перестанет
изменяться. Именно установившийся
режим колебаний,
во многих случаях представляет основной
интерес. Мы не будем рассматривать
переход системы к установившемуся
режиму, а сконцентрируем внимание на
описании и изучении характеристик этого
режима.
При такой постановке задачи
нет необходимости задавать начальные
условия, так как интересующий нас
установившийся режим не зависит от
начальных условий, его характеристики
полностью определяются самим уравнением.
С
аналогичной ситуацией мы сталкивались
при изучении движения тела под действием
постоянной внешней силы и силы вязкого
трения
По
прошествии некоторого времени тело
движется с постоянной установившейся
скоростью
v
= Fo/β,
которая не зависит от начальных условий,
и полностью определяется уравнением
движения. Начальные условия определяют
режим, переходный к установившемуся
движению.
На основании здравого смысла
разумно предположить, что в установившемся
режиме колебаний шарик будет колебаться
с частотой внешней вынуждающей силы.
Поэтому решение уравнения (3) следует
искать в гармонической функции с частотой
вынуждающей силы.
Для начала решим
уравнение (3), пренебрегая силой
сопротивления
Попробуем
найти его решение в виде гармонической
функции
Для
этого вычислим зависимости скорости и
ускорения тела от времени, как производные
от закона движения
и
подставим их значения в уравнение (4)
Теперь
можно сократить на
cosωt.
Следовательно, это выражение обращается
в верное тождество в любой момент
времени, при выполнении условия
Таким
образом, наше предположение о решении
уравнения (4) в виде (5)
оправдалось: установившийся режим
колебаний описывается функцией
Отметим,
что коэффициент A
согласно полученному выражению (6) может
быть, как положительным (при ω
< ωo),
так и отрицательным (при ω
> ωo).
Изменение знака соответствует изменению
фазы колебаний на π
(причина такого изменение будет выяснена
чуть позже), поэтому амплитудой колебаний
является модуль этого коэффициента
|A|.
Амплитуда
установившихся колебаний, как и следовало
ожидать,
пропорциональна
величине вынуждающей силы. Кроме того,
эта амплитуда сложным образом зависит
от частоты вынуждающей силы. Схематический
график этой зависимости показан на рис.
6.10
Рис.
6.10 Резонансная кривая
Как
следует из формулы (6) и хорошо видно на
графике, при приближении
частоты вынуждающей силы к собственной
частоте системы амплитуда резко
возрастает. Причина такого возрастания
амплитуды понятна: вынуждающая сила
«во время» подталкивает шарик, при
полном совпадении частот установившейся
режим отсутствует − амплитуда возрастает
до бесконечности. Конечно, на практике
такого бесконечного возрастания
наблюдать невозможно: во-первых,
это может привести к разрушению самой
колебательной системы, во-вторых,
при больших амплитудах колебаний нельзя
пренебрегать силами сопротивления
среды.
Резкое
возрастание амплитуды вынужденных
колебаний при приближении частоты
вынуждающей силы к собственной частоте
колебаний системы называется явлением
резонанса.
Приступим
теперь к поиску решения уравнения
вынужденных колебаний с учетом силы
сопротивления
Естественно,
что и в этом случае решение следует
искать в виде
гармонической функции с частотой
вынуждающей силы. Легко заметить, что
поиск решения в форме (5) в данном случае
не приведет к успеху. Действительно,
уравнение (8), в отличие от уравнения
(4), содержит скорость частицы, которая
описывается функцией синуса. Поэтому,
временная часть в уравнении (8) не
сократится. Следовательно, решение
уравнения (8) следует представить в общей
форме гармонической функции
в
которой два параметра Ao
и φ
необходимо найти с помощью уравнения
(8). Параметр Ao
является амплитудой вынужденных
колебаний, φ
− сдвиг фаз между изменяющейся координатой
и переменной вынуждающей силой. Используя
тригонометрическую формулу для косинуса
суммы, функцию (9) можно представить в
эквивалентной форме
которая
также содержит два параметра B
= Aocosφ
и C
= −Aosinφ,
подлежащих определению. Используя
функцию (10), запишем явные выражения для
зависимостей скорости и ускорения
частицы от времени
и
подставим в уравнение (8):
Перепишем
это выражение в виде
Для
того чтобы равенство (13) выполнялось в
любой момент времени
необходимо, чтобы коэффициенты при
косинусе и синусе были равны нулю. На
основании этого условия получаем два
линейных уравнения для определения
параметров функции (10):
Решение
этой системы уравнений имеет вид
На
основании формулы (10) определяем
характеристики вынужденных колебаний:
амплитуду
сдвиг
фаз
При
малом затухании эта зависимость имеет
резкий максимум при приближении частоты
вынуждающей силы ω
к собственной частоте системы ωo.
Таким образом, и в этом случае возможно
возникновения резонанса, поэтому
построенные зависимости часто называют
резонансной кривой. Учет слабого
затухания показывает, что амплитуда не
возрастает до бесконечности, ее
максимальное значение зависит от
коэффициента затухания − с возрастанием
последнего максимальная амплитуда
быстро убывает.
Полученная зависимость
амплитуды колебаний от частоты вынуждающей
силы (16) содержит слишком много независимых
параметров ( fo,
ωo,
γ)
для того, чтобы построить полное семейство
резонансных кривых. Как и во многих
случаях, эту зависимость можно существенно
упростить, перейдя к «безразмерным»
переменным. Преобразуем формулу (16) к
следующему виду
и
обозначим
− относительная
частота (отношение частоты вынуждающей
силы к собственной частоте колебаний
системы);
− относительная
амплитуда (отношение амплитуды колебаний
к величине отклонения Ao
= f/ωo2
при нулевой частоте);
−
безразмерный параметр,
определяющий величину затухания.
Используя эти обозначения, функция (16)
существенно упрощается
так
как содержит всего один параметр −
δ.
Однопараметрическое
семейство резонансных кривых, описываемых
функцией
(16 б) может быть построено, особенно
легко с помощью компьютера. Результат
такого построения показан на рис. 629.
рис.
6.11
Отметим,
что переход к «обычным» единицам
измерения может быть проведен элементарным
изменением масштаба осей координат.
Следует
отметить, что частота вынуждающей силы,
при которой амплитуда
вынужденных колебаний максимальна,
также зависит от коэффициента затухания,
слегка убывая с ростом последнего.
Наконец, подчеркнем, что увеличение
коэффициента затухания приводит к
существенному увеличению ширины
резонансной кривой.
Возникающий сдвиг
фаз между колебаниями точки и вынуждающей
силой также
зависит от частоты колебаний и коэффициента
их затухания. Более подробно с ролью
этого сдвига фаз мы познакомимся при
рассмотрении преобразования энергии
в процессе вынужденных колебаний.
частота
свободных незатухающих колебаний
совпадает с собственной частотой,
частота затухающих колебаний немного
меньше собственной, а частота вынужденных
колебаний совпадает с частотой вынуждающей
силы, а не собственной частотой.
Вынужденные
электромагнитные колебания
Вынужденными
называются
такие колебания, которые происходят в
колебательной системе под влиянием
внешнего периодического воздействия.
Рис.6.12.
Контур с вынужденными электрическими
колебаниями
Рассмотрим
процессы, протекающие в электрическом
колебательном контуре (рис.6.12),
присоединенном к внешнему источнику,
ЭДС которого изменяется по гармоническому
закону
,
г
– амплитуда внешней ЭДС,
– циклическая
частота ЭДС.
Обозначим
через UC
напряжение на конденсаторе, а через i
–
силу тока в контуре. В этом контуре кроме
переменной ЭДС (t)
действует еще ЭДС самоиндукции L
в катушке индуктивности.
ЭДС
самоиндукции прямо пропорциональна
скорости изменения силы тока в контуре
.
Для
вывода дифференциального
уравнения вынужденных колебаний
возникающих
в таком контуре используем второе
правило Кирхгофа
.
Напряжение
на активном сопротивлении R
найдем по закону Ома
.
Cила
электрического тока равна заряду
протекающему за единицу времени через
поперечное сечение проводника
.
Следовательно
.
Напряжение
UC
на конденсаторе прямо пропорционально
заряду на обкладках конденсатора
.
ЭДС
самоиндукции можно представить через
вторую производную от заряда по времени
.
Подставляя
напряжения и ЭДС во второе правило
Кирхгофа
.
Разделив
обе части этого выражения на L
и распределив слагаемые по степени
убывания порядка производной, получим
дифференциальное уравнение второго
порядка
.
Введем
следующие обозначения и получим
–коэффициент
затухания,
–циклическая
частота собственных колебаний контура.
.
(1)
Уравнение
(1) является неоднородным
линейным дифференциальным уравнением
второго порядка. Такого типа уравнения
описывают поведение широкого класса
колебательных систем (электрических,
механических) под влиянием внешнего
периодического воздействия (внешней
ЭДС или внешней силы).
Общее
решение уравнения (1) складывается из
общего решения q1
однородного
дифференциального уравнения (2)
(2)
и
любого частного решения q2
неоднородного
уравнения (1)
.
Вид
общего решения однородного
уравнения
(2) зависит от величины коэффициента
затухания .
Нас будет интересовать случай слабого
затухания
<< 0.
При этом общее решение уравнения (2)
имеет вид
,
(3)
где
B
и 0
– постоянные, задаваемые начальными
условиями.
Решение
(3) описывает затухающие колебания в
контуре. Входящие в (3) величины:
–циклическая
частота затухающих колебаний;
–амплитуда
затухающих колебаний;
–фаза
затухающих колебаний.
Частное
решение уравнения (1) ищем в виде
гармонического колебания, происходящего
с частотой, равной частоте
внешнего периодического воздействия
– ЭДС, и отстающего по фазе на
от него
,
(4)
где
– амплитуда вынужденных колебаний,
зависящая от частоты.
Подставим
(4) в (1) и получим тождество
Чтобы
сравнить фазы колебаний, используем
тригонометрические формулы приведения
,
.
Тогда
наше уравнение перепишется в виде
Представим
колебания в левой части полученного
тождества в виде векторной
диаграммы
(рис.6.13)..
Третье
слагаемое, соответствующее колебаниям
на емкости С,
имеющее фазу (t
– )
и амплитуду
,
изобразим горизонтальным вектором,
направленным вправо.
Рис.6.13.
Векторная диаграмма
Первое
слагаемое левой части, соответствующие
колебаниям на индуктивности L,
изобразится на векторной диаграмме
вектором, направленным горизонтально
влево (его амплитуда
).
Второе
слагаемое, соответствующие колебаниям
на сопротивлении R,
изобразим вектором, направленным
вертикально вверх (его амплитуда
),
т. к. его фаза на/2
отстает от фазы первого слагаемого.
Так
как сумма трех колебаний слева от знака
равно дает гармоническое колебание
,
то векторная сумма на диаграмме (диагональ
прямоугольника) изображает колебание
с амплитудойи фазойt,
которая на
опережает фазу колебаний третьего
слагаемого.
Из
прямоугольного треугольника по теореме
Пифагора можно найти амплитуду A()
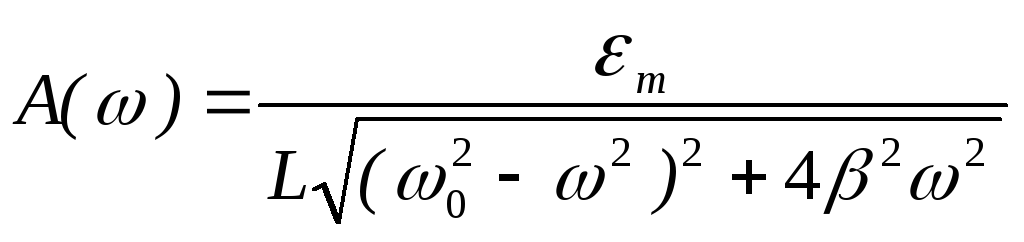
и
tg
как отношение противолежащего катета
к прилежащему катету.
.
(6)
Следовательно,
решение (4) с учетом (5) и (6) примет вид

(7)
Общее
решение дифференциального уравнения
(1) является суммой q1
и q2

(8)
Формула
(8) показывает, что при воздействии на
контур периодической внешней ЭДС в нем
возникают колебания двух частот, т.е.
незатухающие колебания с частотой
внешней ЭДС
и затухающие колебания с частотой
.
Амплитуда затухающих колебанийсо временем становится пренебрежимо
малой, и в контуре остаются только
вынужденные колебания, амплитуда которых
не зависит от времени. Следовательно,
установившиеся вынужденные колебания
описываются функцией (4). То есть в контуре
возникают вынужденные гармонические
колебания, с частотой, равной частоте
внешнего воздействия, и амплитудой,
зависящей от этой частоты (рис.3а)
по закону (5). При этом по фазе вынужденное
колебание отстает на
от вынуждающего воздействия.
Продифференцировав
выражение (4) по времени, найдем силу
тока в контуре
,
где
– амплитуда силы тока.
Запишем
это выражение для силы тока в виде
,
(9)
где
–сдвиг
по фазе между током и внешней ЭДС.
В
соответствии с (6) и рис.2
.
(10)
Из
этой формулы следует, что сдвиг по фазе
между током и внешней ЭДС зависит, при
постоянном сопротивлении R,
от соотношения между частотой вынуждающей
ЭДС
и собственной частотой контура 0.
Если
< 0,
то сдвиг по фазе между током и внешней
ЭДС
< 0. Колебания силы тока опережают
колебания ЭДС по фазе на угол .
Если
> 0,
тогда
> 0. Колебания силы тока отстают от
колебаний ЭДС по фазе на угол .
Если
= 0
(резонансная
частота),
то
= 0, т. е. сила тока и ЭДС колеблются в
одинаковой фазе.
Резонанс
– это
явление резкого возрастания амплитуды
колебаний при совпадении частоты
внешней, вынуждающей силы с собственной
частотой колебательной системы.
При
резонансе
= 0
и период колебаний
.
Учитывая,
что коэффициент затухания
,
получим
выражения для добротности при резонансе
Т
= Т0
,
с
другой стороны
.
Амплитуды
напряжений на индуктивности и емкости
при резонансе можно выразить через
добротность контура
,
(15)
.
(16)
Из
(15) и (16) видно, что при
= 0,
амплитуда напряжения на конденсаторе
и индуктивности в Q
раз больше амплитуды внешней ЭДС. Это
свойство последовательного RLC
контура используется для выделения
радиосигнала определенной частоты
из спектра радиочастот при перестройке
радиоприемника.
На
практике RLC
контура связаны с другими контурами,
измерительными приборами или усилительными
устройствами, вносящими дополнительное
затухание в RLC
контур. Поэтому реальная величина
добротности нагруженного RLC
контура оказывается ниже величины
добротности, оцениваемой по формуле
.
Реальная
величина добротности может быть оценена
как
Рис.6.14.
Определение добротности по резонансной
кривой
,
где
f
– ширина полосы частот, в которых
амплитуда составляет 0,7 от максимального
значения (рис.4).
Напряжения
на конденсаторе UC,
на активном сопротивлении UR
и на катушке индуктивности UL
достигают максимума при различных
частотах, соответственно
,
,

Если
затухание мало 0
>> ,
то все эти частоты практически совпадают
и можно считать что
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вынужденные колебания, теория и онлайн калькуляторы
Вынужденные колебания
Определение вынужденных колебаний
Для того чтобы в реально существующей колебательной системе получать незатухающие колебания, следует каким-либо образом компенсировать потери энергии, которые происходят в результате существования сил сопротивления. Самым простым способом реализации незатухающих колебаний является воздействие на систему при помощи внешней периодической силы. Работа внешней силы обеспечить приток энергии в систему извне. Эта энергия не даст колебаниям затухнуть, при действии сил трения.
Определение
Колебания, которые возникают под действием периодически меняющейся силы (периодически изменяющейся ЭДС),
называют вынужденными механическими (электромагнитными) колебаниями.
Дифференциальное уравнение вынужденных колебаний
Допустим, на механическую колебательную систему действует гармонически изменяющаяся внешняя сила:
[F=F_0{cos left(omega tright) }left(1right).]
Рассмотрим колебания груза на пружине (пружинный маятник). Уравнение незатухающих гармонических колебаний для этой системы можно записать как:
[ddot{x}+2delta dot{x}+{omega }^2_0x=frac{F_0}{m}{cos left(omega tright) }left(2right),]
где $x$ – координата; $delta $ – коэффициент затухания; ${omega }_0$ – циклическая частота свободных незатухающих колебаний (если $delta $=0, то ${omega }_{0 }$называют собственной частотой колебаний).
Если рассматривается, например, электрический колебательный контур, то роль периодически действующей силы может играть внешняя ЭДС или переменное напряжение. Их подводят к контуру извне и изменяются они по гармоническому закону. Уравнение колебаний в электрическом контуре можно представить как:
[ddot{q}+2delta dot{q}+{omega }^2_0q=frac{U_m}{L}{cos left(omega tright) }left(3right),]
где $q$ – заряд; $delta =frac{R}{2L}$ – коэффициент затухания; ${omega }_0=frac{1}{sqrt{LC}}$; $U=U_m{cos left(omega tright) }$ – внешнее переменное напряжение.
Уравнения (2) и (3) можно свести к линейному неоднородному дифференциальному уравнению вида:
[frac{d^2s}{dt^2}+2delta frac{ds}{dt}+{omega }^2_0s=x_0{cos left(omega tright) }left(4right),]
где $s$ – колеблющийся параметр; $x_0=frac{F_0}{m}$ если колебания механические ($x_0=frac{U_m}{L}- в случае электрических колебаний$).
Решением уравнения (4) является сумма общего решения однородного уравнения и частного решения неоднородного уравнения. Однородное уравнение при этом имеет вид:
[frac{d^2s}{dt^2}+2delta frac{ds}{dt}+{omega }^2_0s=0 left(5right).]
Его общее решение:
[s_1=A_0e^{-delta t}{cos left({omega }_1t+{varphi }_1right)left(6right), }]
где $A_0$ – начальная амплитуда колебаний.
Частное решение уравнения (4) в представлено выражением:
[s=A{cos (omega t-varphi ) }left(7right),]
где $A=frac{x_0}{sqrt{{left({omega }^2_0-{omega }^2right)}^2+4{delta }^2{omega }^2}} (8)$; $varphi =arc tg frac{2delta omega }{{omega }^2_0-{omega }^2} (9)$.
Слагаемое $s_1$ в решении уравнения (5) играет значительную роль в начальной стадии установления колебаний, пока амплитуда вынужденных колебаний не будет определяться выражением (8).
Установившись, вынужденные колебания происходят с частотой $omega $ и являются гармоническими. Амплитуда и фаза этих колебаний определяются равенствами (8) и (9), и они зависят от частоты $omega $.
Резонанс вынужденных колебаний
Если частота вынуждающей силы приближается к собственной частоте колебаний, то возникает резкое увеличение амплитуды колебаний. Такое явление называют резонансом.
Из выражения (8) видно, что амплитуда имеет максимум. Для нахождения резонансной частоты (частоты при которой $A=max$), следует найти максимум функции $A(omega )$. Взяв производную $frac{dA}{domega }$ и приравняв ее к нулю получим:
[-4left({omega }^2_0-{omega }^2right)omega +8{delta }^2omega =0 left(10right).]
Равенство (10) справедливо при:
[left{ begin{array}{c}
{omega }_1=0;; \
{omega }_2=sqrt{{omega }^2_0-2{delta }^2;;} \
{omega }_3=-sqrt{{omega }^2_0-2{delta }^2.} end{array}
right.]
Получается, что резонансная частота (${omega }_r$) равна:
[{omega }_r=sqrt{{omega }^2_0-2{delta }^2}left(11right).]
При ${delta }^2ll {omega }^2_0$ резонансная частота совпадает с собственной частотой колебаний ${omega }_0.$ Подставим вместо частоты правую часть выражения (11) в формулу (8), получим выражение для резонансной амплитуды вынужденных колебаний:
[A_r=frac{x_0}{2delta sqrt{{omega }^2_0-{delta }^2}}left(12right).]
При небольшом затухании колебаний (если ${delta }^2ll {omega }^2_0$) амплитуда при резонансе равна:
[A_r=frac{x_0}{2delta {omega }_0}=Qfrac{x_0}{{omega }^2_0}left(13right),]
где $Q=frac{{omega }_0}{2delta }$ – добротность колебательной системы, величина, характеризующая резонансные свойства колебательной системы. С увеличением добротности увеличивается амплитуда резонанса.
Примеры задач с решением
Пример 1
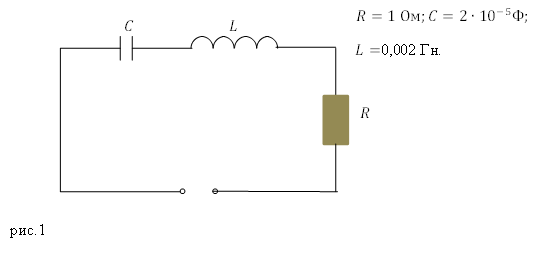
Задание. Какова добротность колебательного контура, представленного на рис.1?
Решение. Добротность электрического колебательного контура найдем как:
[Q=frac{{omega }_0}{2delta } left(1.1right).]
При этом собственная частота колебаний в таком контуре равна:
[{omega }_0=frac{1}{sqrt{LC}}left(1.2right).]
коэффициент затухания находим как:
[delta =frac{R}{2L}left(1.3right).]
Подставляет правые части выражений (1.2) (1.3) вместо соответствующих величин в (1.1), в результате, добротность представленного на рис. 1 контура найдем при помощи формулы:
[Q=frac{1}{2sqrt{LC}}cdot frac{2L}{R}=frac{1}{R}sqrt{frac{L}{C}}.]
Вычислим добротность:
[Q=frac{1}{1}sqrt{frac{2cdot {10}^{-3}}{2cdot {10}^{-5}}}=10.]
Ответ. $Q=10$
Пример 2
Задание. Пружинный маятник выполняет вынужденные колебания в вязком веществе. Масса груза на пружине
равна $m$, коэффициент упругости пружины $k$. Коэффициент сопротивления среды равен $r$. Систему заставляет совершать
колебания сила $F={cos left(omega tright)(Н). }$Чему равна резонансная амплитуда заданных колебаний ($A_r$)?
Решение. Допустим, что груз совершает колебания вдоль прямой X, тогда уравнением данных механических колебаний
будет выражение:
[ddot{x}+2delta dot{x}+{omega }^2_0x=frac{F_0}{m}{cos left(omega tright) }left(2.1right),]
где коэффициент затухания равен $delta =frac{r}{2m}$. Из функции, которая задает вынуждающую силу:
[F={cos left(omega tright)(2.2) }]
мы видим, что амплитуда силы равна единице:
[F_0=1 left(Нright).]
Собственная частота колебаний груза на пружине:
[{omega }_0=sqrt{frac{k}{m}}to {omega }^2_0=frac{k}{m}left(2.3right).]
Амплитуда при резонансе таких колебаний равна:
[A_r=frac{frac{F_0}{m}}{2delta sqrt{{omega }^2_0-{delta }^2}}=frac{F_0}{2(frac{r}{2m})msqrt{frac{k}{m}-{(frac{r}{2m})}^2}}=frac{F_0}{rsqrt{frac{k}{m}-{(frac{r}{2m})}^2}}.]
Ответ. $A_r=frac{F_0}{rsqrt{frac{k}{m}-{(frac{r}{2m})}^2}}$
Читать дальше: гидростатическое давление.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Если колебания совершаются под воздействием внешней силы, они называются вынужденными. Работа внешней силы, которая обеспечивает колебательную систему энергией, при этом является положительной. Благодаря ей колебания не затухают и могут противодействовать силам трения.
Внешняя сила не обязательно должна быть постоянной. С течением времени она может изменяться по разным законам. Особый случай – воздействие на колебательную систему внешней силы, которая изменяется по гармоническому закону с частотой, равной ω, в то время как сама система совершает собственные колебания с той же самой частотой.
Установившиеся вынужденные колебания всегда происходят с частотой внешней силы. Частоту свободных колебаний определяют параметры системы.
Когда внешняя сила начинает воздействовать на колебательную систему, должно пройти некоторое время Δt , прежде чем вынужденные колебания установятся. Это время будет равно тому времени τ, за которое затухают свободные колебания в данной системе.
В момент начала воздействия в системе начинают происходить два процесса одновременно – свободные колебания с собственной частотой ω0 и вынужденные с частотой ω. Однако из-за сил трения свободные колебания в определенный момент затухают, поэтому по прошествии времени в системе сохраняются лишь стационарные колебания с той частотой, которая соответствует внешней (вынуждающей) силе.
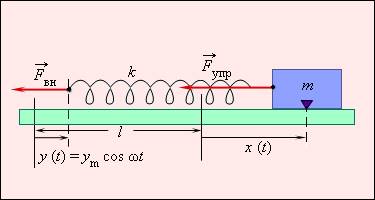
Разберем пример. У нас есть тело на пружине, совершающее вынужденные колебания (см. иллюстрацию ниже). Приложим внешнюю силу, обозначенную F→вн, к свободному концу пружины, после чего этот конец начнет перемещаться по закону, выражаемому формулой:
y=ymcos ωt.
Здесь буквой ω обозначена круговая частота, а ym – амплитуда колебаний.
Перемещения такого рода обеспечиваются шатунным механизмом, который преобразует круговые движения в возвратно-поступательные.
Рисунок 2.5.1. Груз на пружине, совершающий вынужденные колебания. Перемещение свободного конца выражено формулой y=ym cos ωt, где l означает длину недеформированной пружины, а k –ее жесткость.
При смещении левого конца пружины на некоторое расстояние y и правого – на x по сравнению с первоначальным положением недеформированной пружины будет происходить ее удлинение. Найти величину этого удлинения можно по следующей формуле:
∆l=x-y=x-ymcos ωt.
В таком случае мы можем переформулировать второй закон Ньютона для этого случая следующим образом:
ma=-k(x-y)=-kx+kymcos ωt.
Здесь сила, которая действует на тело, показана как сумма двух слагаемых, первым из которых является упругость, стремящаяся к равновесию тела, а вторым – внешнее воздействие, совершающееся с определенными интервалами. Внешнюю силу также называют вынуждающей.
Теперь выразим эту зависимость в строгой математической формуле, учитывающей связь между координатой тела a=x¨ и его ускорением. У нас получится следующее:
x¨+ω02x=A cos ωt.
Эта зависимость называется уравнением внешних колебаний. Здесь ω0=km является собственной круговой частотой свободного колебания, а ω – циклической частотой внешней (вынуждающей) силы.
Чтобы найти величину A для вынужденного колебания груза на пружине, нужно воспользоваться следующей формулой:
A=kmym-ω02ym.
То уравнение, что мы записали перед этим, не учитывает, что на тело действуют также и силы трения. В уравнении вынужденных колебаний, в отличие от уравнения свободных, учитываются сразу обе частоты – частота вынуждающей силы и частота свободных колебаний.
Вынужденные колебания груза на пружине, которые устанавливаются со временем, имеют частоту внешнего воздействия. Это определяется следующим законом:
x(t)=xmcos (ωt+θ).
Здесь xm обозначает амплитуду вынужденного колебания, а буква θ – его начальную фазу. Значения обоих этих показателей будут зависеть от амплитуды внешней силы и соотношения частот.
Если частоты очень низкие, т.е. ω≪ω0, то тело, прикрепленное к правому концу пружины, движется точно так же, как и левый конец этой пружины. Тогда получается, что x(t)=y(t). Сама пружина при этом практически не деформируется, а модуль внешней силы F→вн, приложенной к ее левому концу, стремится к нулю. Работа при этом не совершается.
Понятие резонанса
Резонанс – это резкое возрастание амплитуды вынужденных колебаний при сближении частоты внешней силы с собственной частотой колебания тела.
С помощью резонансной кривой (резонансной характеристики) можно описать зависимость, существующую между амплитудой внешних колебаний xm и частотой вынуждающей силы ω.
Когда происходит резонанс, амплитуда xm может оказаться значительно больше, чем амплитуда колебаний левого (свободного) конца пружины.. Если мы не будем учитывать силы трения, то получится, что при резонансной частоте амплитуда вынужденных колебаний будет возрастать неограниченно. В реальности она будет зависеть от следующего условия: работа внешней силы в течение всего времени колебаний должна совпадать с потерями механической энергии, происходящими из-за трения. При уменьшении трения (и, соответственно, повышении добротности Q колебательной системы) амплитуда вынужденных колебаний при резонансе возрастет.
Рисунок 2.5.2. Моделирование вынужденных колебаний.
Если добротность колебательной системы невысока (менее 10), то частота резонанса будет находиться ближе к низким частотам. Это показано на иллюстрации 2.5.2.
Явление резонанса имеет большое практическое значение. Именно из-за него зачастую разрушаются здания, мосты и другие сооружения. Это происходит в тот момент, когда их собственные частоты совпадают с частотой внешней силы, например, колебаниями мотора.
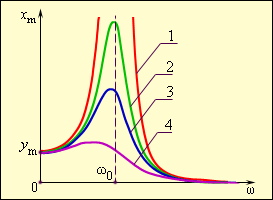
Рисунок 2.5.3. Изображение затухания различных колебаний при помощи резонансных кривых: 1 – условная система без учета трения (бесконечное возрастание амплитуды вынужденных колебаний), 2,3,4 – резонансные колебания в реальных условиях, происходящих в системах разной степени добротности (Q2>Q3>Q4). Если частоты низкие, то (ω≪ω0) xm≈ym, а если высокие, то (ω≫ω0) xm→0.
Вынужденные колебания являются незатухающими. При трении неизбежно теряется часть энергии, однако воздействие внешних периодически действующих сил компенсирует ее.
Что такое автоколебательные системы
Автоколебательные системы – это системы, в которых могут возникать незатухающие колебания безотносительно внешнего воздействия, а лишь за счет способности самостоятельно регулировать подвод энергии от внешнего источника. Процесс колебаний в таких системах называют автоколебаниями.
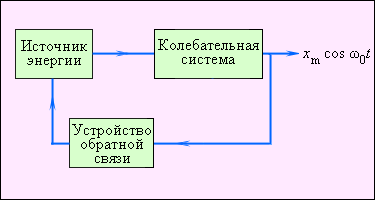
Внутри этой системы можно выделить три составляющих – саму систему, источник внешней постоянной энергии и обратную связь между ними. Первым элементом выступает любая механическая система, которая может совершать затухающие колебания, например, часовой маятник. В качестве источника можно использовать потенциальную энергию груза в поле тяжести или энергию деформации пружины. Система обратной связи – это, как правило, особый механизм, функцией которого является регулирование поступлений энергии. На иллюстрации показано, как эти компоненты взаимодействуют между собой.
Рисунок 2.5.4. Автоколебательная система со всеми основными составляющими.
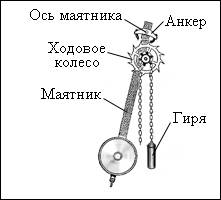
Какие можно привести примеры таких систем? Ярким примером является часовой механизм с так называемым анкерным ходом. В нем есть ходовое колесо с косыми зубчиками, прочно сцепленное с зубчатым барабаном, через который перекинута цепочка с грузом. В верхней части маятника закреплен якорек (анкер), состоящий из двух твердых пластинок, дугообразно изогнутых по окружности с центром на основной оси. В механизме ручных часов вместо гири используется пружина, а вместо маятника – маховичок-балансир, соединенный со спиральной пружиной, который совершает круговые колебания вокруг своей оси. В качестве источника внешней энергии выступает заведенная пружина или поднятая гиря. Обратная связь осуществляется с помощью анкера: он позволяет ходовому колесу совершать поворот только на один зубец за полупериод. Когда анкер взаимодействует с ходовым колесом, происходит передача энергии. Когда маятник колеблется, зубец ходового колеса передает анкерной вилке энергию по направлению движения маятника, и именно этим компенсируются силы трения. Таким образом, энергия поднятой гири или заведенной пружины поступает маленькими порциями к маятнику.
Существует также много других автоколебательных систем, которые широко применяются в технике. Автоколебания происходят внутри двигателей внутреннего сгорания, паровых машин, электрических звонков, музыкальных инструментов, голосовых связок и т.д.
Рисунок 2.5.5. Схема маятникового часового механизма.
Механические колебания.
-
Гармонические колебания.
-
Уравнение гармонических колебаний.
-
Пружинный маятник.
-
Математический маятник.
-
Свободные и вынужденные колебания.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания – это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания – это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия – это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела – это величина его наибольшего отклонения от положения равновесия.
Период колебаний – это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний – это величина, обратная периоду:
. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
к оглавлению ▴
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение
. Основная задача механики в данном случае состоит в нахождении функции
, дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них – синус и косинус – являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания – это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому
– амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина
, равная значению фазы при
, называется начальной фазой. Начальная фаза отвечает начальной координате тела:
.
Величина называется циклической частотой. Найдём её связь с периодом колебаний
и частотой
. Одному полному колебанию отвечает приращение фазы, равное
радиан:
, откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
 |
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить
. Мы получаем закон косинуса:
.
График гармонических колебаний в этом случае представлен на рис. 2.
 |
| Рис. 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить
. Получаем закон синуса:
.
График колебаний представлен на рис. 3.
 |
| Рис. 3. Закон синуса |
к оглавлению ▴
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы
определяются из начальных условий – по начальным значениям координаты и скорости.
к оглавлению ▴
Пружинный маятник.
Пружинный маятник – это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна
.
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
 |
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось
имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и
. Наоборот, если
, то
. Знаки
и
всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
к оглавлению ▴
Математический маятник.
Математический маятник – это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
 |
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство
. Воспользуемся им в формуле (11):
,
или
.
Это – уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
к оглавлению ▴
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
 |
| Рис. 6. Затухающие колебания |
Вынужденные колебания – это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
 |
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс – явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы:
, и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний,
, а амплитуда колебаний возрастает до бесконечности при
.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Механические колебания.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Содержание книги
Предыдующая страница
§17. Механические колебания
17.6 Вынужденные колебания. Резонанс.
17.6.1 Уравнение вынужденных колебаний и его решение.
Потери механической энергии в любой колебательной системе из-за наличия сил трения неизбежны, поэтому без «подкачки» энергии извне колебания будут затухающими. Существует несколько принципиально различных способов создания колебательных систем незатухающих колебаний. Остановимся более подробно на рассмотрении незатухающих колебаний под действием внешней периодической силы. Такие колебания называются вынужденными.
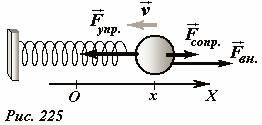
Продолжим изучение движения гармонического маятника (Рис. 225). Помимо рассмотренных ранее сил упругости и вязкого трения, на шарик действует внешняя вынуждающая периодическая сила, изменяющаяся по гармоническому закону
(~F_{vn} = F_0 cos omega t) , (1)
частота, которой может отличаться от собственной частоты колебаний маятника ω0.
Природа этой сил в данном случае нам не существенна. Создать такую силу можно различными способами, например, сообщить шарику электрический заряд и поместить его во внешнее переменное электрическое поле.
Уравнение движения шарика в рассматриваемом случае имеет вид
(~ma = -kx – beta upsilon + F_0 cos omega t) . (2)
Разделим его на массу шарика и используем прежние обозначения параметров системы. В результате получим уравнение вынужденных колебаний:
(~a = -omega^2_0 x – 2 gamma upsilon + f_0 cos omega t) . (3)
где (~f_0 = frac{F_0}{m}) – отношение амплитудного значения внешней вынуждающей силы к массе шарика.
Общее решение уравнения (3) достаточно громоздко и, конечно, зависит от начальных условий. Характер движения шарика, описываемого уравнением (3), понятен: под действием вынуждающей силы возникнуть колебания, амплитуда которых будет возрастать. Этот переходный режим достаточно сложен и зависит от начальных условий. По прошествии некоторого промежутка времени колебательный режим установится, их амплитуда перестанет изменяться. Именно установившийся режим колебаний, во многих случаях представляет основной интерес. Мы не будем рассматривать переход системы к установившемуся режиму, а сконцентрируем внимание на описании и изучении характеристик этого режима. При такой постановке задачи нет необходимости задавать начальные условия, так как интересующий нас установившийся режим не зависит от начальных условий, его характеристики полностью определяются самим уравнением.
С аналогичной ситуацией мы сталкивались при изучении движения тела под действием постоянной внешней силы и силы вязкого трения
(~ma = F_0 – beta upsilon) .
По прошествии некоторого времени тело движется с постоянной установившейся скоростью (~upsilon = frac{F_0}{beta}), которая не зависит от начальных условий, и полностью определяется уравнением движения. Начальные условия определяют режим, переходный к установившемуся движению.
На основании здравого смысла разумно предположить, что в установившемся режиме колебаний шарик будет колебаться с частотой внешней вынуждающей силы. Поэтому решение уравнения (3) следует искать в гармонической функции с частотой[1] вынуждающей силы.
Для начала решим уравнение (3), пренебрегая силой сопротивления
(~a = -omega^2_0 x + f_0 cos omega t) . (4)
Попробуем[2] найти его решение в виде гармонической функции
(~x = A cos omega t) . (5)
Для этого вычислим зависимости скорости и ускорения тела от времени, как производные от закона движения
(~begin{matrix} upsilon(t) = x'(t) = -A omega sin omega t \ a(t) = upsilon'(t) = -A omega^2 cos omega t end{matrix}) ,
и подставим их значения в уравнение (4)
(~-A omega^2 cos omega t = – A omega^2_0 cos omega t + f_0 cos omega t) .
Теперь можно сократить на cos ωt. Следовательно, это выражение обращается в верное тождество в любой момент времени, при выполнении условия
(~A = frac{f_0}{omega^2_0 – omega^2}) . (6)
Таким образом, наше предположение о решении уравнения (4) в виде (5) оправдалось: установившийся режим колебаний описывается функцией
(~x(t) = frac{f_0}{omega^2_0 – omega^2} cos omega t) . (7)
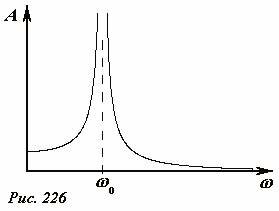
Отметим, что коэффициент A согласно полученному выражению (6) может как положительным (при ω0 < ω), так и отрицательным (при ω0 > ω). Изменение знака соответствует изменению фазы колебаний на π (причина такого изменение будет выяснена чуть позже), поэтому амплитудой колебаний является модуль этого коэффициента A. Амплитуда установившихся колебаний, как и следовало ожидать, пропорциональна величине вынуждающей силы. Кроме того, эта амплитуда сложным образом зависит от частоты вынуждающей силы. Схематический график этой зависимости показан на Рис. 226.
Как следует из формулы (6) и хорошо видно на графике, при приближении частоты вынуждающей силы к собственной частоте системы амплитуда резко возрастает. Причина такого возрастания амплитуды понятна: вынуждающая сила «во время» подталкивает шарик, при полном совпадении частот установившейся режим отсутствует – амплитуда возрастает до бесконечности. Конечно, на практике такого бесконечного возрастания наблюдать невозможно: во-первых, это может привести к разрушению самой колебательной системы, во-вторых, при больших амплитудах колебаний нельзя пренебрегать силами сопротивления среды.
Резкое возрастание амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к собственной частоте колебаний системы называется явлением резонанса.
Приступим теперь к поиску решения уравнения вынужденных колебаний с учетом силы сопротивления
(~a = -omega^2_0 x – 2 gamma upsilon + f_0 cos omega t) . (8)
Естественно, что и в этом случае решение следует искать в виде гармонической функции с частотой вынуждающей силы. Легко заметить, что поиск решения в форме (5) в данном случае не приведет к успеху. Действительно, уравнение (8), в отличие от уравнения (4), содержит скорость частицы, которая описывается функцией синуса. Поэтому, временная часть в уравнении (8) не сократится. Следовательно, решение уравнения (8) следует представить в общей форме гармонической функции
(~x(t) = A_0 cos (omega t + varphi)) , (9)
в которой два параметра A0 и φ необходимо найти с помощью уравнения (8). Параметр A0 является амплитудой вынужденных колебаний, φ – сдвиг фаз между изменяющейся координатой и переменной вынуждающей силой. Используя тригонометрическую формулу для косинуса суммы, функцию (9) можно представить в эквивалентной форме
(~x(t) = A_0 cos (omega t + varphi) = A_0 cos varphi cdot cos omega t – A_0 sin varphi cdot sin omega t = B cos omega t + C sin omega t) , (10)
которая также содержит два параметра (B = A_0 cos varphi) и (C = -A_0 sin varphi), подлежащих определению. Используя функцию (10), запишем явные выражения для зависимостей скорости и ускорения частицы от времени
(~begin{matrix} x(t) = B cos omega t + C sin omega t \ upsilon(t) = x'(t) = -B omega sin omega t + C omega cos omega t \ a(t) = upsilon'(t) = -B omega^2 cos omega t – C omega^2 sin omega t end{matrix}) (11)
и подставим в уравнение (8):
(~-B omega^2 cos omega t – C omega^2 sin omega t = -omega^2_0 (B cos omega t + C sin omega t) – 2 gamma (-B omega sin omega t + C omega cos omega t) + f_0 cos omega t) . (12)
Перепишем это выражение в виде
(~(B (omega^2_0 – omega^2) + 2 gamma omega C – f_0) cos omega t + (C (omega^2_0 – omega^2) + 2 gamma omega B) sin omega t = 0) . (13)
Для того чтобы равенство (13) выполнялось в любой момент времени необходимо, чтобы коэффициенты при косинусе и синусе были равны нулю. На основании этого условия получаем два линейных уравнения для определения параметров функции (10):
(~begin{matrix} B (omega^2_0 – omega^2) + 2 gamma omega C = f_0 \ C (omega^2_0 – omega^2) + 2 gamma omega B = 0 end{matrix}) . (14)
Решение этой системы уравнений имеет вид
(~begin{matrix} B = frac{omega^2_0 – omega^2}{(omega^2_0 – omega^2)^2 + (2 gamma omega)^2} f_0 \ C = frac{2 gamma omega}{(omega^2_0 – omega^2)^2 + (2 gamma omega)^2} f_0 end{matrix}) . (15)
На основании формулы (10) определяем характеристики вынужденных колебаний:
амплитуду
(~A_0 = sqrt{B^2 + C^2} = frac{f_0}{sqrt{(omega^2_0 – omega^2)^2 + (2 gamma omega)^2}}) , (16)
сдвиг фаз
(~operatorname{tg} varphi = -frac{C}{B} = – frac{2 gamma omega}{omega^2_0 – omega^2}) . (17)
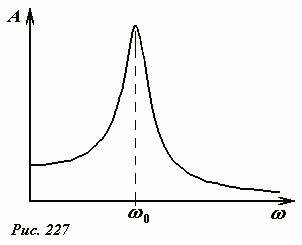
На Рис. 227 показана схематическая зависимость амплитуды вынужденных колебаний A от частоты вынуждающей силы ω. При малом затухании эта зависимость имеет резкий максимум при приближении частоты вынуждающей силы ω к собственной частоте системы ω0. Таким образом, и в этом случае возможно возникновения резонанса, поэтому построенные зависимости часто называют резонансной кривой. Учет слабого затухания показывает, что амплитуда не возрастает до бесконечности, ее максимальное значение зависит от коэффициента затухания – с возрастанием последнего максимальная амплитуда быстро убывает.
Полученная зависимость амплитуды колебаний от частоты вынуждающей силы (16) содержит слишком много независимых параметров (f0, ω0, γ0) для того, чтобы построить полное семейство резонансных кривых. Как и во многих случаях, эту зависимость можно существенно упростить, перейдя к «безразмерным» переменным. Преобразуем формулу (16) к следующему виду
(~A_0 = frac{f_0}{sqrt{(omega^2_0 – omega^2)^2 + (2 gamma omega)^2}} = frac{f_0}{omega^2_0} cdot frac{1}{sqrt{left(1 – left(frac{omega}{omega_0}right)^2 right)^2 + left(frac{2 gamma}{omega_0}right)^2 left(frac{omega}{omega_0}right)^2}}) , (16а)
и обозначим (~tilde{omega} = frac{omega}{omega_0}) – относительная частота (отношение частоты вынуждающей силы к собственной частоте колебаний системы); (~tilde{A} = frac{A}{A_0}) – относительная амплитуда (отношение амплитуды колебаний к величине отклонения (~A_0 = frac{f}{omega^2_0}) при нулевой частоте); (~delta = frac{2 gamma}{omega_0} = frac{gamma T}{pi}) – безразмерный параметр[3], определяющий величину затухания. Используя эти обозначения, функция (16) существенно упрощается
(~tilde{A} = frac{1}{sqrt{(1 – tilde{omega}^2)^2 + delta^2 tilde{omega}^2}}) , (16б)
так как содержит всего один параметр – δ. Однопараметрическое семейство резонансных кривых, описываемых функцией (16 б) может быть построено, особенно легко с помощью компьютера. Результат такого построения показан на Рис. 227а. Отметим, что переход к «обычным» единицам измерения может быть проведен элементарным изменением масштаба осей координат.
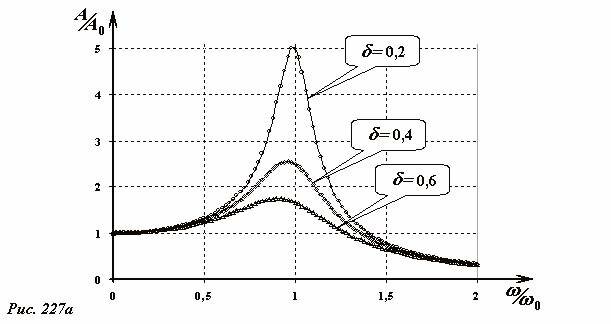
Следует отметить, что частота вынуждающей силы, при которой амплитуда вынужденных колебаний максимальна, также зависит от коэффициента затухания, слегка убывая с ростом последнего. Наконец, подчеркнем, что увеличение коэффициента затухания приводит к существенному увеличению ширины резонансной кривой.
Возникающий сдвиг фаз между колебаниями точки и вынуждающей силой также зависит от частоты колебаний и коэффициента их затухания. Более подробно с ролью этого сдвига фаз мы познакомимся при рассмотрении преобразования энергии в процессе вынужденных колебаний.
17.6.2 Векторное описание колебаний. Векторное сложение колебаний.
Решение уравнения вынужденных колебаний потребовало от нас достаточно громоздких тригонометрических преобразований. Аналогичные проблемы возникают и при решении других задач, связанных со сложением нескольких тригонометрических функций. Поэтому для упрощения подобных математических выкладок разработан специальный математический метод – метод векторных диаграмм, с которым мы сейчас познакомимся.
Этот метод применяется для нахождения суммы гармонических функций одинаковой частоты вида
(~x(t) = A cos (omega t + varphi)) . (1)
Каждая такая функция определяется двумя параметрами[4] A и φ. Сумма произвольного числа слагаемых вида (1) также является гармонической функцией того же вида.
Суммирование функций вида (1) может быть проведено аналитически в самом общем случае:
(~X(t) = A_1 cos (omega t + varphi_1) + A_2 cos (omega t + varphi_2) + A_3 cos (omega t + varphi_3) + ldots = sum_k^N A_k cos (omega t + varphi_k) = sum_k^N A_k (cos omega t cdot cos varphi_k – sin omega t cdot sin varphi_k) = left( sum_k^N A_k cos varphi_k right) cos omega t – left( sum_k^N A_k sin varphi_k right) sin omega t = A_0 cos (omega t + varphi_0)) ,
где амплитуда результирующей функции равна
(~A_0 = sqrt{left( sum_k^N A_k cos varphi_k right)^2 + left( sum_k^N A_k sin varphi_k right)^2}) , (2)
а ее фаза удовлетворяет условию
(~operatorname{tg} varphi_0 = -frac{left( sum_k^N A_k sin varphi_k right)}{left( sum_k^N A_k cos varphi_k right)}) . (3)
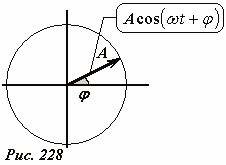
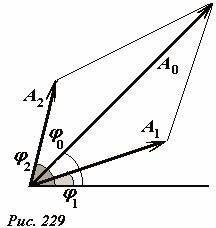
Поведенным преобразованиям можно дать наглядное геометрическое, векторное истолкование. Изучение колебаний мы начали с рассмотрения связи между равномерным вращением вектора и закона движения его проекции. На рис. 228 восстановлена эта связь. Теперь мы скажем, что вектор длиной A, направленный под углом φ к одной из осей может представлять функцию (1). Теперь вместо аналитического сложения функций этого вида можно геометрически сложить векторы, изображающие отдельные слагаемые. При этом важно подчеркнуть, что все функции имеют одинаковые частоты, следовательно, изображающие их векторы вращаются с одной и той же угловой скоростью, поэтому углы между ними не изменяются. Можно сделать следующий шаг – «забыть» об их вращении[5], а складывать неподвижные векторы. Окончательным результатом суммирования будет являться проекция суммарного вектора на исходную ось. Так Рис. 229 иллюстрирует сложение двух гармонических функций с разными амплитудами и разными начальными фазами. Амплитуду A0 и фазу φ0 результирующего колебания можно найти геометрически.
Полезно также запомнить геометрическое представление других тригонометрических функций (Рис. 230). Для этого следует воспользоваться тригонометрическими формулами приведения и «привести» эти функции к виду (1):
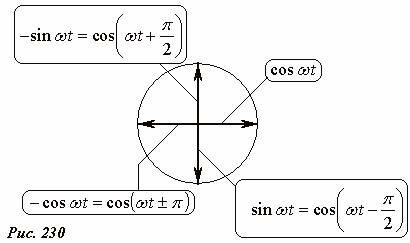
(~begin{matrix} sin omega t = cos left(omega t – frac{pi}{2} right) \ -cos omega t = cos (omega t pm pi) \ -sin omega t = cos left(omega t + frac{pi}{2} right) end{matrix}) .
Продемонстрируем применение метода векторных диаграмм для решения уравнения вынужденных колебаний.
(~a = -omega^2_0 x – 2 gamma upsilon + f_0 cos omega t) . (4)
Зависимости координаты, скорости и ускорения частицы запишем в виде
(~begin{matrix} x(t) = A cos (omega t + varphi) \ upsilon(t) = x'(t) = -A omega sin (omega t + varphi) = A omega cos left(omega t + varphi + frac{pi}{2} right) \ a(t) = upsilon'(t) = -A omega^2 cos (omega t + varphi) = A omega^2 cos (omega t + varphi + pi) end{matrix}) . (5)
Подставим эти выражения в уравнение (4), которое запишем в виде
(~begin{matrix} a + 2 gamma upsilon + omega^2_0 x = f_0 cos omega t \ A omega^2 cos (omega t + varphi + pi) + 2 gamma A omega cos left(omega t + varphi + frac{pi}{2} right) + omega^2_0 A cos (omega t + varphi) = f_0 cos omega t end{matrix}) . (6)
Теперь формально это уравнение имеет следующий смысл: сумма трех гармонических функций с разными амплитудами и фазами равна известной гармонической функции (вынуждающей силе). Изобразим векторную диаграмму суммы трех слагаемых. Пока неизвестное направление оси, от которой отсчитываются углы, можно выбрать произвольно (на рис. 231 она выбрана горизонтально).

Рис. 231
Геометрическая сумма этих трех векторов (найти которую в данном случае можно элементарно) должна быть равна вектору, изображающему вынуждающую силу. Так как в исходном уравнении именно эта функция имеет нулевую фазу, то отсчет угла сдвига фаз должен проводится именно от этого вектора. Так на приведенном рисунке этот угол отрицателен, так поворот от вектора, изображающего вынуждающую силу, к вектору, изображающему зависимость x(t), осуществляется в отрицательном направлении («по часовой стрелке»).
Используя построенную диаграмму легко записать уравнение, связывающее амплитуду колебаний и амплитуду вынуждающей силы (на основании теоремы Пифагора):
(~A^2 (omega^2_0 – omega^2)^2 + A^2 (2 gamma omega)^2 = f^2_0) ,
из которого следует выражение для амплитуды вынужденных колебаний
(~A_0 = frac{f_0}{sqrt{(omega^2_0 – omega^2)^2 + (2 gamma omega)^2}}) , (7)
естественно, совпадающее с полученным ранее аналитическим методом. Векторная диаграмма дает такое же выражение и для сдвига фаз
(~operatorname{tg} varphi = – frac{2 gamma omega}{omega^2_0 – omega^2}) . (8)
Таким образом, метод векторных диаграмм позволяет получать точные формулы гораздо быстрее, чем традиционный аналитический метод, основанный на громоздких преобразованиях тригонометрических формул.
17.6.3 Превращения энергии при вынужденных колебаниях.
Внешняя сила, действующая на колебательную систему, совершает работу, следовательно, в систему поступает энергия. Полезно рассмотреть превращения энергии в ходе вынужденных колебаний. Для этого поступим уже традиционным образом:
динамическое уравнение[6] колебаний
(~a = -omega^2_0 x – 2 gamma upsilon + f_0 cos omega t) , (1)
умножим на скорость
(~a cdot upsilon = -omega^2_0 x cdot upsilon – 2 gamma upsilon cdot upsilon + f_0 cos omega t cdot upsilon)
и перепишем в виде
(~f_0 cos omega t cdot upsilon = a cdot upsilon + omega^2_0 x cdot upsilon + 2 gamma upsilon cdot upsilon ) . (2)
В этом уравнении каждое слагаемое имеет наглядный физический смысл. Так функция (P_0(t) = f_0 cos omega t cdot upsilon(t)) описывает мгновенную мощность, развиваемой внешней вынуждающей силой. Величина (2 gamma upsilon cdot upsilon = f_{sopr}(t) cdot upsilon(t) = P_{poteri}(t)) является мощностью силы сопротивления и описывает потери механической энергии в единицу времени.
Слагаемое (a(t) cdot upsilon(t)) преобразовывается следующим образом
(~a(t) cdot upsilon(t) = upsilon frac{Delta upsilon}{Delta t} = frac{Delta left(frac{upsilon^2}{2} right)}{Delta t} = frac{Delta E_{kin}}{Delta t})
и равно скорости изменения кинетической энергии колеблющегося тела ΔEkin. Наконец,
(~ omega^2_0 x cdot upsilon = omega^2_0 x frac{Delta x}{Delta t} = frac{Delta left(frac{omega^2_0 x^2}{2} right)}{Delta t} = frac{Delta U}{Delta t})
есть мощность силы упругости, равная скорости изменения потенциальной энергии системы U. С учетом проведенных преобразований, уравнение (2) приобретает смысл закона сохранения и превращения энергии:
(~P_0 Delta t = Delta (E_{kin} + U) + P_{poteri} Delta t) , (3)
энергия, переданная посредством работы внешней силы, расходуется на увеличение механической энергии системы и работу против сил сопротивления (равную в свою очередь, потерям механической энергии).
Полученное уравнение (3) справедливо для любого промежутка времени, в том числе и на стадии переходного режима. Применим его к режиму установившихся колебаний. В этом режиме колебания являются гармоническими, поэтому за время равное периоду колебаний все характеристики движения (координата, скорость, кинетическая и потенциальная энергия) возвращаются к исходным значениям. Если в уравнении (3) интервал времени Δt положить равным периоду колебаний, то изменение полной энергии будет равно нулю, что приводит к очевидному результату: работа внешней силы за период колебаний равна работе против силы сопротивления. Иными словами, вся энергия, поступающая в систему, превращается в теплоту, выделяющуюся из-за наличия сил сопротивления.
Не составляет труда получить точные значения механической энергии и мощностей всех сил в процессе вынужденных колебаний. Зависимости координаты и скорости от времени нам известны и описываются формулами
(~begin{matrix} x(t) = A_0 cos (omega t + varphi) \ upsilon(t) = -A_0 omega sin (omega t + varphi) end{matrix}) . (4)
В этом режиме полная механическая энергия системы равна
(~E + U = frac{upsilon^2}{2} + frac{omega^2_0 x^2}{2} = frac{A^2_0}{2} (omega^2 sin^2 (omega t + varphi) + omega^2_0 cos^2 (omega t + varphi)) = frac{A^2_0 omega^2_0}{2} left(1 + frac{omega^2 – omega^2_0}{omega^2_0} sin^2 (omega t + varphi) right) ) . (5)
Ее значение колеблется вокруг некоторого среднего значения.
Мощности внешней силы и силы сопротивления описываются формулами
(~begin{matrix} P_0 = f_0 cos omega t cdot upsilon = -A_0 omega f_0 cos omega t sin (omega t + varphi) \ P_{poteri} = 2 gamma upsilon^2 = 2 gamma A^2_0 omega^2 sin^2 (omega t + varphi) end{matrix}) . (6)
Причем первая принимает как положительные, так и отрицательные значения, а вторая все время положительна.
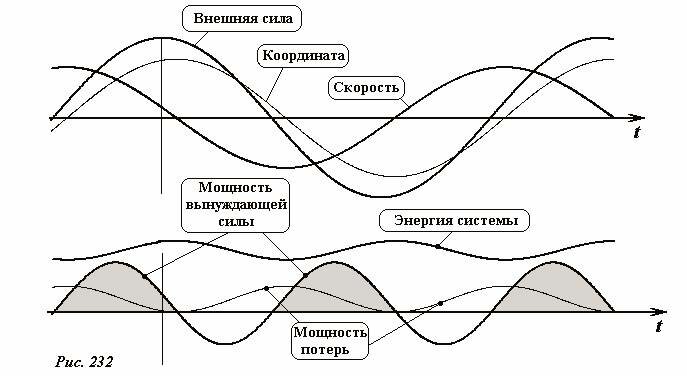
На рисунке 232 показаны графики зависимостей от времени внешней силы, координаты и скорости частицы, ниже построены графики зависимости от времени мощностей внешней силы и силы сопротивления, а также механической энергии. Графики построены для случая, когда частота вынуждающей силы меньше собственной частоты системы ω < ω0, а затухание незначительно. На графиках выделены интервалы времени, когда работа внешней силы положительна, то есть когда энергия поступает в систему.
Эти графики показывают, что мгновенные значения энергетических характеристик даже в установившемся режиме достаточно сложно взаимосвязаны между собой – энергия, сообщаемая внешней силой, расходуется на изменение энергии системы (как кинетической, так и потенциальной), кинетическая энергия переходит в потенциальную и обратно, часть энергии теряется из-за наличия сопротивления.
Более проста ситуация в случае точного резонанса, когда частота вынуждающей силы совпадает с собственной частотой колебаний системы. В этом случае механическая энергия системы остается постоянной, поэтому в любой момент времени мощность внешней силы в точности равна мощности потерь. Сдвиг фаз между вынуждающей силой и координатой точки равен ±π, что приводит к тому, что изменение скорости точки синфазно с изменением внешней силы.
Следует отметить, что рассмотрение мгновенных энергетических характеристик представляет скорее академический интерес, с точки зрения практических применений более важно рассмотрение этих характеристик, усредненных по промежутку времени, значительно превышающему период колебаний. Тем более, это справедливо в тех случаях, когда частота колебаний настолько велика, что различить отдельное колебание не представляется возможным[7].
Проведем расчет усредненных энергетических характеристик в установившемся режиме вынужденных колебаний.
Для начала получим одну важную математическую формулу, которую неоднократно будем использовать в дальнейшем. Пусть две функции изменяются по гармоническому закону с одной и той же частотой
(~begin{matrix} X_1(t) = A_1 cos (omega t + varphi_1) \ X_2(t) = A_2 cos (omega t + varphi_2) end{matrix}) . (7)
Найдем среднее значение произведения этих функций, используя тригонометрическую формулу для произведения косинусов
(~<X_1(t) cdot X_2(t)> = A_1 A_2 <cos (omega t + varphi_1) cdot cos (omega t + varphi_2)> = frac{A_1 A_2}{2} <cos (varphi_1 – varphi_2) + cos (2 omega t + varphi_1 + varphi_2)>) .
Первое слагаемое (косинус разности фаз) не зависит от времени, второе – является переменной функцией времени, очевидно, что ее среднее значение равно нулю. Таким образом, мы получаем, что среднее произведение двух функций равно половине произведения амплитуд, умноженной на косинус сдвига фаз между ними
(~<X_1(t) cdot X_2(t)> = frac{A_1 A_2}{2} cos (varphi_1 – varphi_2)) . (8)
Частные случаи этой формулы, очевидны, и ранее уже применялись нами. Так при сдвиге фаз равном нулю среднее произведение равно половине произведения амплитуд – ранее мы показали, что среднее значение квадрата косинуса (и синуса) равно 0,5; при сдвиге фаз равном (~pm frac{pi}{2}) среднее произведение равно нулю.
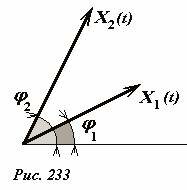
Полученная формула имеет красивую геометрическую интерпретацию на языке векторного представления колебаний. Если гармонические функции представить в векторной форме (в виде вращающихся векторов), то их среднее произведение в соответствии с полученной формулой (8) равно половине скалярного произведения векторов, изображающих функции-сомножители (рис. 233). Обратимся еще раз к рис. 231, на котором построена векторная диаграмма, иллюстрирующая процесс вынужденных колебаний. С ее помощью легко получить те же энергетические характеристики, которые мы нашли аналитически. Убедитесь в этом самостоятельно.
В заключение данного раздела получим явное выражение для средней мощности внешней силы (и равной ей мощности потерь) при вынужденных колебаниях. Эту величину разумно назвать средней мощностью поглощаемой системой. Проще всего это сделать, усредняя мгновенную мощность потерь (6)
(~<P_{poteri}> = <2 gamma A^2_0 omega^2 sin^2 (omega t + varphi)> = 2 gamma A^2_0 omega^2 frac{1}{2} = frac{gamma f^2_0 omega^2}{sqrt{(omega^2_0 – omega^2)^2 + (2 gamma omega)^2}}) , (9)
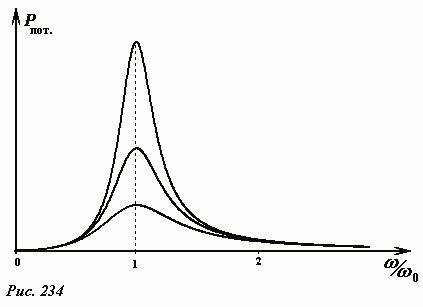
при выводе этой функции использовано явное выражение для амплитуды вынужденных колебаний. Схематические графики зависимости поглощенной энергии от частоты вынуждающей силы при различных значениях параметра затухания показаны на рис. 234. Эти графики похожи на зависимости амплитуды от частоты вынуждающей силы (Рис. 227а), но следует помнить, что это, все-таки, разные функции.
Примечания
- ↑ В последовательности нашего изучения колебаний мы все время уходим от частоты собственных колебаний: частота свободных незатухающих колебаний совпадает с собственной частотой, частота затухающих колебаний немного меньше собственной, а частота вынужденных колебаний совпадает с частотой вынуждающей силы, а не собственной частотой.
- ↑ Строгое решение этого уравнения изобилует простыми, но объемными, математическими выкладками, которые затуманивают физический смысл получаемых результатов. Поэтому, мы фактически, будем стараться угадать его решение, основываясь на здравом физическом смысле. Во-первых, такой подход является физическим, а, во-вторых, полученные нами результаты могут быть строго обоснованы математически.
- ↑ Для любителей новых слов укажем, что эта величина называется декрементом затухания и очень часто встречается в теории колебаний.
- ↑ Частоту колебаний ω считаем заданной.
- ↑ Для физиков можно сказать о переходе во вращающуюся систему отсчета.
- ↑ Напомним, что уравнение следует из второго закона Ньютона, которое мы разделили на массу движущегося тела. Слагаемые, стоящие в правой части этого уравнения имеет смысл «удельных» сил, то есть отношений сил к массе тела. Для упрощения изложения в дальнейшем эти слагаемые мы также будем называть «силами»[-omega^2_0 x] – сила упругости, (2 gamma upsilon) – сила сопротивления, (+f_0 cos omega t) – вынуждающая сила. Аналогично, энергетические характеристики так же относятся единице массы, поэтому величину (~frac{upsilon^2}{2}) будем называть кинетической энергией, а величину (~frac{omega^2_0 x^2}{2}) – потенциальной энергией системы. Кому такие переименования не нравятся, может все выражения этого раздела умножить на массу тела и любоваться знакомыми формулами.
- ↑ Наиболее ярким примером такого положения является изучение взаимодействие света с веществом, где ни один прибор не в состоянии выделить отдельное колебание электромагнитной волны.
Следующая страница