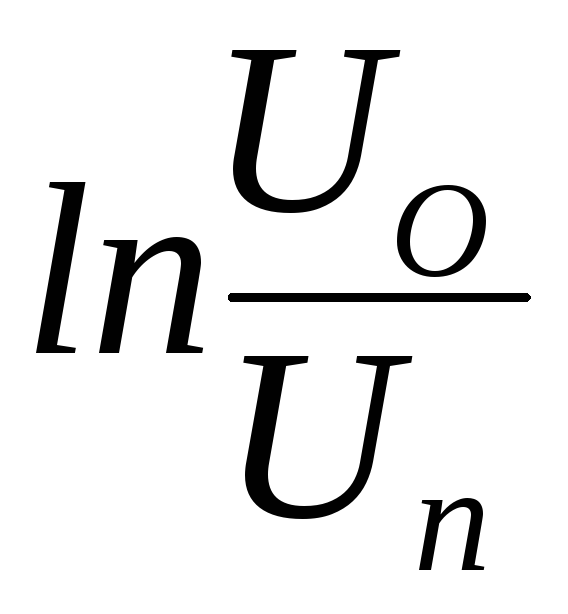Собственная частота затухающих колебаний, формула
В любой колебательной системе затухание приводит к уменьшению частоты и соответственно увеличению периода колебаний.
Если
| ωзат | угловая частота затухающих колебаний, | радиан/сек |
|---|---|---|
| ω0 | угловая частота незатухающих колебаний, | радиан/сек |
| δ | коэффициент затухания, | радиан/сек |
то выражение отклонения будет решением дифференциального уравнения затухающих колебаний только при условии
[
ω_{зат} = sqrt{ ω_{0}^2 – δ^2 }
]
Вычислить, найти собственную частоту затухающих колебаний по формуле (1)
Собственная частота затухающих колебаний |
стр. 553 |
|---|
ТОМСКИЙ
МЕЖВУЗОВСКИЙ ЦЕНТР ДИСТАНЦИОННОГО
ОБРАЗОВАНИЯ (ТМЦДО)
ТОМСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
ОТЧЕТ
Лабораторная
работа по курсу “Общая физика”
ИЗУЧЕНИЕ
ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
1.
ЦЕЛЬ РАБОТЫ
Целью
данной работы является изучение работы
колебательного контура, свободных
затухающих электромагнитных колебаний
и их характеристик.
2.
ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
С
хема
установки представлена на рис. 2.1.
Колебания в контуре II возбуждаются с
помощью генератора импульсного
напряжения, вырабатываемого в контуре
I, собранного на резисторе R1
, емкости
C1
и диоде VD1
(в качестве генератора импульсного
напряжения можно использовать стандартный
генератор импульсов или генератор
релаксационных колебаний).
Схема
смонтирована на съемной панели
лабораторного макета. В качестве
резистора RP1
в колебательном контуре II используется
переменное сопротивление, максимальное
значение которого RP1 = 400 Ом
устанавливается поворотом ручки
потенциометра по часовой стрелке в
крайнее положение. При повороте ручки
против часовой стрелки в крайнее
положение значение сопротивления
RP1 = 0.
В этом случае активное сопротивление
колебательного контура R
складывается из сопротивления
соединительных проводов контура и
активного сопротивления катушки
индуктивности. Возбуждение контура
производится периодически от генератора
импульсного напряжения I, регистрируются
колебания на осциллографе III. Каждый
импульс, подаваемый с генератора на
колебательный контур, возбуждает один
цуг колебаний.
Измерения
амплитуды и периода колебаний
осуществляются непосредственно с
помощью осциллографа.
3.
ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Значения
логарифмического декремента затухания:
![]() ,
,
n –
номер измерений амплитуды (3.1)
Коэффициент
затухания (угловой коэффициент):
 (3.2)
(3.2)
Индуктивность
колебательного контура:
![]() ,
,
отсюда
![]() (3.3)
(3.3)
Суммарное
активное сопротивление проводников:
![]() (3.4)
(3.4)
Частота
собственных колебаний:
![]() (3.5)
(3.5)
Частота
свободно затухающих колебаний:
![]() (3.6)
(3.6)
Период
колебаний:
![]() (3.7)
(3.7)
Критическое
сопротивление:
![]() (3.8)
(3.8)
Добротность
колебательного контура:
![]() (3.9)
(3.9)
4.
РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ
Экспериментальные
данные и результаты их обработки
представлены в следующей таблице.
Таблица
Результаты
прямых и косвенных измерений.
|
Значение R |
Номер n |
Значение Un, мм (дел.) |
Значение |
Среднее <> |
|
Период T, |
|
R |
1 2 3 4 5 |
29,1 25,9 23,1 20,6 18,3 |
0,1165 0,1144 0,1145 0,1184 |
0,11595 |
0,116 0,2325 0,3469 0,4615 0,5799 |
|
|
R |
1 2 3 4 5 |
26,8 17,2 11,0 7,0 4,5 |
0,4435 0,447 0,452 0,4418 |
0,446075 |
0,4459 0,8894 1,3364 1,7884 2,2303 |
|
Произведем
расчеты значений амплитуды
![]()
для каждой из приведенных амплитуд. Так
как цена деления по оси
![]() равна
равна
![]() ,
,
то расчеты будут выглядеть следующим
образом:
Для
значений активного сопротивления
контура
![]()
![]()
![]()
![]()
![]()
![]()
Для
значений активного сопротивления
контура
![]()
![]()
![]()
![]()
![]()
![]()
Переходим
к следующему шагу – вычисление значений
логарифмического декремента затухания
![]() .
.
Для этого воспользуемся выражением
(3.1).
Рассчитаем
значение логарифмического декремента
для
![]() .
.
![]()
![]()
![]()
![]()
Аналогичные
вычисления проведем для значений
![]() .
.
![]()
![]()
![]()
![]()
Рассчитаем
среднее значение
![]() .
.
Для расчета значений среднего результата
измерений, то есть среднее арифметическое
из требуемых значений воспользуемся
выражением
![]() .
.
Для
значений
![]() .
.
![]()
Для
значений
![]() .
.
![]()
Заполним
следующую колонку нашей таблицы. Для
начала следует найти значение напряжения
при
![]() .
.
Для
![]() .
.
![]()
e
=
2,718
Для
![]() .
.
![]()
Теперь
когда мы знаем чему равно значение
![]()
для каждого из представленных сопротивлений
без труда можем рассчитать
![]() .
.
Для
![]() .
.
![]()
![]()
![]()
![]()
![]()
Аналогично
для
![]() .
.
![]()
![]()
![]()
![]()
![]()
Найдем
период затухающих колебаний для каждого
из представленных сопротивлений.
Для
![]() .
.
![]()
Для
![]() .
.
![]()
Построим
графики зависимостей
![]()
для случаев
![]()
и
![]() .
.
Сначала
найдем время для каждой из представленных
амплитуд опираясь на выражение
![]() .
.
Для
![]() .
.
![]()
![]()
![]()
![]()
![]()
Для
![]() .
.
![]()
![]()
![]()
![]()
![]()
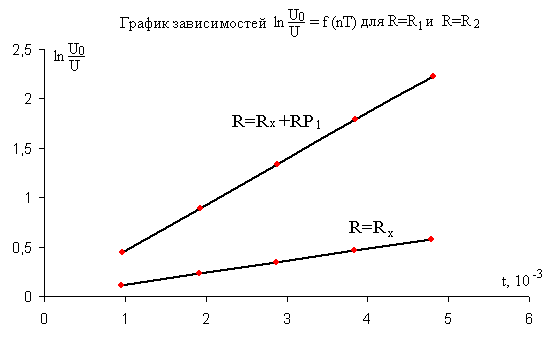
Рис.4.1
Из
построенных графиков определяем значение
коэффициентов затухания
![]()
и
![]() .
.
Используем выражение (3.2).
Для
![]() .
.
![]()
Для
![]() .
.
![]()
Определяем
индуктивность колебательного контура,
применяя выражение 3.3.
![]()
Произведем
расчет суммарного сопротивления по
выражению (3.4).
![]()
Оперируя
со значениями емкости конденсатора и
индуктивности можно рассчитать
собственную частоту контура и частоту
затухающих колебаний. Для этого
воспользуемся формулами (3.5) – (3.6).
![]()
Для
![]() .
.
![]()
C
=
0,04
мкФ
Для
![]() .
.
![]()
По
выражению 3.7 определяем периоды колебаний.
Для
![]() .
.
![]()
Для
![]() .
.
![]()
Отличие
периодов очень незначительно, поэтому
справедливость экспоненциального
закона убывания амплитуды со временем
подтверждается.
Критическое
сопротивление можно рассчитать используя
выражение (3.8), что мы сейчас и проделаем.
![]()
Теперь
вычисляем добротность контура. Для
этого стоит воспользоваться формулой
(3.9).
Для
![]() .
.
![]()
Для
![]() .
.
![]()
5.
ВЫВОДЫ
Согласно
поставленной цели настоящей работы мне
в полном объеме удалось изучить работу
колебательного контура и процессы,
происходящие во время явления. Так же
на практике убедились в справедливости
экспоненциального закона убывания
амплитуды с течением времени.
В
результате проделанной работы нам
удалось получить следующие значения
для приведенных ниже характеристик:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
6.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Вопрос
1. Какова
цель работы?
Ответ.
Целью настоящей работы является изучение
работы колебательного контура, свободных
затухающих электромагнитных колебаний
и их характеристик.
Вопрос
2. С помощью
какой системы можно получить свободные
электромагнитные колебания?
Ответ.
Свободные электромагнитные колебания
можно получить используя колебательный
контур, который представляет собой
замкнутую цепь, состоящую из последовательно
соединенных конденсатора емкостью C,
катушки индуктивностью L
и омического сопротивления R.
Омическое сопротивление включает в
себя сопротивление соединенных проводов,
сопротивление провода катушки
индуктивности и сопротивление включенного
в контур резистора.

Рис.6.1
Вопрос
3. К изменению
каких характеристик колебаний приведет
увеличение активного сопротивления в
колебательном контуре?
Ответ.
В результате увеличения активного
сопротивления в колебательном контуре
увеличатся значения коэффициента
затухания колебаний, логарифмический
декремент затухания и период затухающих
колебаний. Уменьшению подвергнуться
такие характеристики как добротность
контура и частота свободных затухающих
колебаний.
Вопрос
4. Какое
условие необходимо выполнить, чтобы
при подборе элементов (R,
L,
C)
для колебательного контура, чтобы
изменение напряжения на предварительно
заряженном конденсаторе осуществлялось
по колебательному закону?
Ответ.
Для того, чтобы изменение напряжения
на предварительно заряженном конденсаторе
осуществлялось по колебательному закону
необходимы следующие условия:
![]()
или
![]() .
.
Вопрос
5. Каким
образом в данной работе подтверждается
правильность вывода об экспоненциальном
уменьшении амплитуды напряжения со
временем?
Ответ.
Для подтверждения правильности вывода
об экспоненциальном уменьшении амплитуды
напряжения со временем необходимо
воспользоваться методом линеаризации.
В результате его логарифмирования
получаем уравнение прямой. Истинность
закона проверяется построением графика
этой прямой по экспериментальным точкам.
Вопрос
6. Как в данной
работе определяется коэффициент
затухания?
Ответ.
В настоящей лабораторной работе
коэффициент затухания определяется
как угловой коэффициент зависимости
![]() .
.
Вопрос
7. Какими
параметрами контура определяется
частота собственных колебаний?
Ответ.
Частоту собственных колебаний можно
выразить через следующее выражение:
![]() ,
,
где L
– индуктивность катушки, C
– емкость конденсатора.
Вопрос
8. Как
соотносится между собой частота
собственных колебаний контура и частота
затухающих колебаний?
Ответ.
Частота собственных колебаний и частота
затухающих колебаний контура представлена
в виде
![]() ,
,
где
![]()
– частота собственных колебаний,
![]() –
–
коэффициент затухания,
![]() –
–
частота свободных затухающих колебаний.
Вопрос
9. Изменение
каких физических величин осуществляется
в контуре по колебательному закону?
Ответ.
В колебательном контуре по колебательному
закону изменяется энергия электрического
поля конденсатора, энергия магнитного
поля катушки индуктивности, напряжение
и ток на элементах контура.
Вопрос
10. Как
образуются в контуре электромагнитные
колебания?
Ответ.
Электромагнитные колебания в контуре
возникают следующим путем. В начальный
момент с помощью генератора одиночных
импульсов конденсатор заряжается до
некоторой разности потенциалов U
на его обкладках. При этом обкладкам
конденсатора сообщен заряд
![]() .
.
Энергия электрического поля конденсатора
![]() .
.
Если теперь генератор отключить, а
конденсатор замкнуть на катушку с
индуктивностью L,
то начнется его разрядка и в катушке
возникнет ток. Это возрастающий от нуля
ток приводит к возникновению магнитного
поля. Следовательно, энергия электрического
поля между обкладками конденсатора
постепенно переходит в энергию магнитного
поля катушки. В момент разрядки
конденсатора ток в катушке достигает
максимального значения и энергия
магнитного поля
![]() .
.
В результате самоиндукции ток в катушке
продолжает существовать. Этот убывающий
ток продолжает переносить заряды от
одной обкладки конденсатора к другой
в том же направлении и перезаряжает
конденсатор. Перезарядка заканчивается,
когда ток становиться равным нулю. В
этот момент энергия магнитного поля
катушки переходит в энергию электрического
поля конденсатора. В следующий момент
начинает разряжаться конденсатор, при
этом ток течет в обратном направлении.
Разрядный ток возрастает, пока конденсатор
не разрядится полностью, а затем убывает,
но вследствие явления самоиндукции
снова перезаряжается конденсатор и
контур возвращается в исходное состояние.
Этим завершается один период колебаний
в контуре.
Вопрос
11. Как влияет
коэффициент затухания на условный
период затухающих колебаний контура?
Ответ.
Коэффициент затухания влияет на условный
период затухающих колебаний контура.
Чем больше коэффициент затухания, тем
больше и условный период затухающих
колебаний.
Вопрос
12. Как
изменяется логарифмический декремент
затухания и добротность контура, если
известно, что при изменении параметров
контура (R,
L,
C)
число колебаний, за которое амплитуда
уменьшиться в e
раз, увеличилось на десять колебаний?
Ответ.
Логарифмический декремент затухания
и добротность контура изменяются
следующим образом. Происходит уменьшение
логарифмического декремента затухания
и увеличение добротности контура.
Вопрос
13. Чем
обусловлено затухание колебаний в
контуре?
Ответ.
Затухание колебаний в контуре обусловлено
потерями энергии на нагрев и на излучение
электромагнитных колебаний в установке.
Вопрос
14. К изменению
каких характеристик колебаний и
колебательного контура приведет
изменение индуктивности в цепи?
Ответ.
В результате изменения индуктивности
в цепи будут происходить изменения
логарифмического декремента затухания,
добротности контура, коэффициента
затухания, частоты собственных колебаний
контура, частоты свободных затухающих
колебаний, условного периода колебания
и критического сопротивления контура.
Вопрос
15. Выполняется
ли в реальном колебательном контуре
закон сохранения электромагнитной
энергии?
Ответ.
Закон сохранения электромагнитной
энергии в колебательном контуре не
выполняется по причине расхода энергии
на нагревание проводников и на
электромагнитное излучение.
Вопрос
16. Почему
при выводе основного уравнения свободных
затухающих колебаний в контуре, где
протекают переменные токи, используют
закон Ома и правила Кирхгофа, полученные
для постоянного тока?
Ответ.
В данном случае в цепи протекает
переменный ток, но, учитывая, что размеры
контура l
не слишком велики (т.е.
![]() ,
,
где с
– скорость света, с которой распространяются
электромагнитные колебания, l
– длина контура и ν
– частота контура), можно считать, что
мгновенное значение тока будет практически
одинаково во всех точках контура. Токи,
удовлетворяющие такому условию, называют
квазистанционарными.
Вопрос
17. Как нужно
изменить параметры контура, чтобы при
однократной зарядке конденсатора
разрядка его осуществлялась по
апериодическому закону?
Ответ.
Для того, чтобы разрядка конденсатора
осуществлялась по апериодическому
закону необходимо увеличить коэффициент
затухания, при этом условный период T
затухающих колебаний возрастает и
обращается в бесконечность при
![]() .
.
Благодаря этому в контуре не происходит
свободных колебаний, и процесс переходит
в апериодический.

Рис.6.2.
Вопрос
18. Какие
колебания называют непериодическими
и являются ли затухающие колебания
периодическими?
Ответ.
Непериодические колебания – колебания,
имеющие не повторяющиеся через равные
промежутки времени значения физических
величин, характеризующих колебательную
систему. Вследствие этого, затухающие
колебания не являются периодическими,
так как максимальное
значение амплитуды колебаний, достигаемое
в некоторый момент времени, не повторяется.
Вопрос
19. Какая
характеристика является количественной
характеристикой убывания амплитуды
затухающих колебаний? Какими параметрами
контура она определяется?
Ответ.
Количественной характеристикой убывания
амплитуды затухающих колебания является
логарифмический декремент затухания.
Данная характеристика обусловлена
параметрами контура, а именно R,
L,
C.
Вопрос
20. Чему равно
время релаксации затухающих колебаний?
Ответ.
Время релаксации затухающих колебаний
равно промежутку времени τ,
в течение которого амплитуда затухающих
колебаний уменьшается в e
раз.
3.1. Механические затухающие колебания
3.2. Электромагнитные затухающие колебания
3.3. Характеристики затухающих колебаний
Затуханием колебаний называется постепенное уменьшение амплитуды колебаний с течением времени, обусловленное потерей энергии колебательной системой.
Собственные колебания без затухания – это идеализация. Причины затухания могут быть разные. В механической системе к затуханию колебаний приводит наличие трения. В электромагнитном контуре к уменьшению энергии колебаний приводят тепловые потери в проводниках, образующих систему. Когда израсходуется вся энергия, запасенная в колебательной системе, колебания прекратятся. Поэтому амплитуда затухающих колебаний уменьшается, пока не станет равной нулю.
Затухающие колебания, как и собственные, в системах, разных по своей природе, можно рассматривать с единой точки зрения – общих признаков. Однако, такие характеристики, как амплитуда и период, требуют переопределения, а другие – дополнения и уточнения по сравнению с такими же признаками для собственных незатухающих колебаний. Общие признаки и понятия затухающих колебаний следующие:
Дифференциальное уравнение должно быть получено с учетом убывания в процессе колебаний колебательной энергии.
Уравнение колебаний – решение дифференциального уравнения.
Амплитуда затухающих колебаний зависит от времени.
Частота и период зависят от степени затухания колебаний.
Фаза и начальная фаза имеют тот же смысл, что и для незатухающих колебаний.
3.1. Механические затухающие колебания
Механическая система: пружинный маятник с учетом сил трения. Силы, действующие на маятник:
Упругая сила. ![]() , где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
, где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.
Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): ![]() . Знак “минус” показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
. Знак “минус” показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:
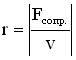 Закон движения пружинного маятника – это второй закон Ньютона: ma = Fупр. + Fсопр.
Закон движения пружинного маятника – это второй закон Ньютона: ma = Fупр. + Fсопр.
Учитывая, что ![]() и
и 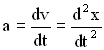 , запишем второй закон Ньютона в виде:
, запишем второй закон Ньютона в виде:
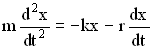 .
.
Разделив все члены уравнения на m, перенеся их все в правую часть, получим дифференциальное уравнение затухающих колебаний:
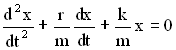
Обозначим ![]() , где β – коэффициент затухания,
, где β – коэффициент затухания, ![]() , где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
, где ω0 – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.
В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:
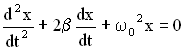 . Это линейное дифференциальное уравнение второго порядка. Уравнение затухающих колебаний есть решение такого дифференциального уравнения:
. Это линейное дифференциальное уравнение второго порядка. Уравнение затухающих колебаний есть решение такого дифференциального уравнения: ![]()
![]() .
.
В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных.
Частота затухающих колебаний:
![]() (физический смысл имеет только вещественный корень, поэтому
(физический смысл имеет только вещественный корень, поэтому ![]() ).
).
Период затухающих колебаний: 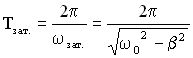 .
.
Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: ![]() .
.
Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.
Для механической системы пружинного маятника имеем:
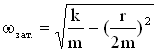 ,
, 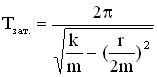 . Амплитуда затухающих колебаний:
. Амплитуда затухающих колебаний: ![]() , для пружинного маятника
, для пружинного маятника ![]() .
.
Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить.
При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.
Графики зависимости смещения от времени ![]() и амплитуды от времени
и амплитуды от времени ![]() представлены на Рисунках 3.1 и 3.2.
представлены на Рисунках 3.1 и 3.2.
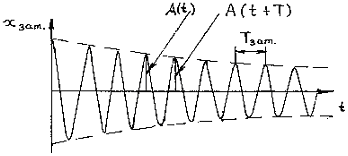
Рисунок 3.1 – Зависимость смещения от времени для затухающих колебаний

Рисунок 3.2 – Зависимости амплитуды от времени для затухающих колебаний
3.2. Электромагнитные затухающие колебания
Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).
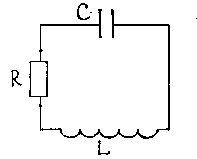
Рисунок 3.3.
Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура: ![]()
Падение напряжения:
– на активном сопротивлении: ![]() , где I – сила тока в контуре;
, где I – сила тока в контуре;
– на конденсаторе (С): ![]() , где q – величина заряда на одной из обкладок конденсатора.
, где q – величина заряда на одной из обкладок конденсатора.
ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: ![]() (закон Фарадея).
(закон Фарадея).
Подставим значения UR, UC, ![]() в уравнение, отражающее закон Кирхгофа, получим:
в уравнение, отражающее закон Кирхгофа, получим:
![]() .
.
Сила тока определяется как производная от заряда ![]() , тогда
, тогда 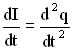 , и дифференциальное уравнение примет вид:
, и дифференциальное уравнение примет вид:
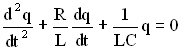 .
.
Обозначим ![]() ,
, ![]() , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
, получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:
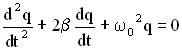
Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:
![]() или
или
![]() .
.
Амплитуда затухающих колебаний заряда имеет вид:
![]() , где
, где ![]() .
.
Частота затухающих колебаний в LCR – контуре:
 .
.
Период затухающих электромагнитных колебаний:
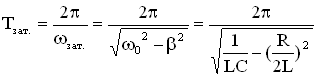 .
.
Возьмем уравнение для заряда в виде ![]() , тогда уравнение для напряжения на обкладках конденсатора можно записать так
, тогда уравнение для напряжения на обкладках конденсатора можно записать так 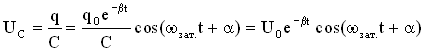 .
.
Величина 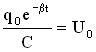 называется амплитудой напряжения на конденсаторе.
называется амплитудой напряжения на конденсаторе.
Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение ![]() и векторную диаграмму.
и векторную диаграмму.
Окончательное уравнение для силы тока таково:
![]() ,
,
где 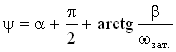 – начальная фаза.
– начальная фаза.
Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.
Энергия колебаний в контуре складывается из энергии электрического поля
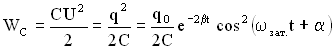
и энергии магнитного поля
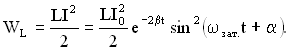
Полная энергия в любой момент времени:
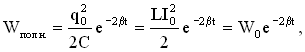
где W0 – полная энергия контура в момент времени t=0.
1. Коэффициент затухания β. Изменение амплитуды затухающих колебаний происходит по экспоненциальному закону: ![]() .
.
Пусть за время τ амплитуда колебаний уменьшится в “e ” раз (“е” – основание натурального логарифма, е ≈ 2,718). Тогда, с одной стороны, 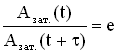 , а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем
, а с другой стороны, расписав амплитуды Азат.(t) и Азат.(t+τ), имеем 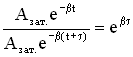 . Из этих соотношений следует βτ = 1, отсюда
. Из этих соотношений следует βτ = 1, отсюда
![]() .
.
Промежуток времени τ, за который амплитуда уменьшается в “е” раз, называется временем релаксации.
Коэффициент затухания β – величина, обратно пропорциональная времени релаксации.
2. Логарифмический декремент затухания δ – физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период .
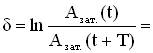
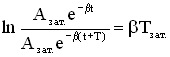
Если затухание невелико, т.е. величина β мала, то амплитуда незначительно изменяется за период, и логарифмический декремент можно определить так:
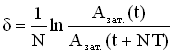 ,
,
где Азат.(t) и Азат.(t+NT) – амплитуды колебаний в момент времени е и через N периодов, т.е.в момент времени (t + NT).
3. Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) νа отношение энергии W(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
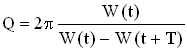 . Так как энергия пропорциональна квадрату амплитуды, то
. Так как энергия пропорциональна квадрату амплитуды, то 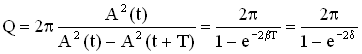 .
.
При малых значениях логарифмического декремента δ добротность колебательной системы равна
![]() ,
,
где Ne – число колебаний, за которое амплитуда уменьшается в “е” раз.
Так, добротность электромагнитной системы LCR – контура при малом затухании колебаний равна 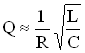 , а добротность пружинного маятника –
, а добротность пружинного маятника – 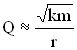 .Чем больше добротность колебательной системы, тем меньше затухание, тем дольше будет длиться периодический процесс в такой системе.
.Чем больше добротность колебательной системы, тем меньше затухание, тем дольше будет длиться периодический процесс в такой системе.
4. При увеличении коэффициента β, частота затухающих колебаний уменьшает-ся, а период увеличивается. При ω0 = β частота затухающих колебаний становится равной нулю ωзат. = 0, а Тзат. = ∞. При этом колебания теряют периодический характер и называются апериодическими.
При ω0 = β параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими. Для пружинного маятника условие ω0 = β запишется так: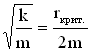 , откуда найдем величину критического коэффициента сопротивления:
, откуда найдем величину критического коэффициента сопротивления:
![]() .
.
Для LCR – контура условие 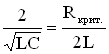 позволяет вычислить критическое сопротивление контура, при котором колебания потеряют свою периодичность:
позволяет вычислить критическое сопротивление контура, при котором колебания потеряют свою периодичность:
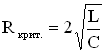 .
.
Богдан Новах
Эксперт по предмету «Архитектура и строительство»
Задать вопрос автору статьи
Собственные колебания
Собственные или свободные колебания – это колебания, происходящие в системе при отсутствии переменных внешних воздействий. Такие колебания возникают по причине начального отклонения одного из параметров от состояния равновесия.
В целом колебания представляют собой повторяющийся во времени процесс изменения состояния системы около точки равновесия (при колебании маятника все углы его отклонения от вертикали повторяются с определенной периодичностью.
В реальных макроскопических системах собственные колебания затухают по причине потерь энергии. Любой колебательный процесс связан с переходом энергии из одной формы в другую.
Следует заметить, что колебания различной физической природы имеют ряд общих закономерностей и тесно связаны с волнами. В этой связи исследованием таких закономерностей занимается теория колебаний и волн. Принципиальное отличие колебаний от волн заключается в том, что распространение последних сопровождается переносом, а не переходом энергии.
По характеру взаимодействия с окружающей средой колебания разделяют на:
- вынужденные;
- автоколебания;
- параметрические;
- собственные.
В настоящей статье речь пойдет о собственных колебаниях, т.е. о колебаниях системы под действием внутренних сил после выведения системы из равновесия.
При небольших отклонениях от состояния равновесия движение любой системы будет удовлетворять принципу суперпозиции. Согласно данному принципу сумма произвольных движений составляет допустимое движение системы. Подобные движения описываются линейными (дифференциальными) уравнениями.
В случае, если в системе нет потерь энергии (она консервативна), а ее параметры не изменяются во времени, то любое собственное колебание может быть представлено, как совокупность нормальных колебаний, изменяющихся во времени по закону синуса с определенными частотами собственных колебаний.
Если положение системы в любой момент времени описывается единственным параметром, то такая система имеет одну степень свободы. Идеальным примером такой системы является маятник, колеблющийся в плоскости. И действительно, положение маятника в любой момент может определяться лишь углом его отклонения от вертикали.
«Как определить собственную частоту колебаний» 👇
В природе существует большое количество весьма интересных систем, имеющих две степени свободы. Например, молекулы и элементарные частицы (наиболее примечательны нейтральные К-мезоны). Более простым и понятным примером является двойной маятник (один маятник подвешивается к опоре, второй – к гире первого маятника; два маятника, объединенные пружиной).
Чтобы описать состояние системы с двумя степенями свободы необходимо уже две переменные. Например, в случае со сферическим маятником роль таких переменных будут выполнять положения маятника в двух взаимно перпендикулярных плоскостях. В случае объединенных маятников эти переменные соответствуют положению каждого из маятников.
В общем виде движение системы, имеющей две степени свободы, может иметь весьма сложный вид, не напоминающий простое гармоническое движение.
Для двух степеней свободы, а также при линейных уравнениях движения общий вид движения представляет собой суперпозицию двух простейших гармонических зависимостей, происходящих в один момент. Эти два элементарных движения называют нормальными (собственными) колебаниями или гармониками.
Колебательные системы с сосредоточенными параметрами, состоящими из N связанных осцилляторов (например, цепочка из связанных между собой пружинками шариков), число гармоник будет равно N. В системах с распределенными параметрами (мембрана или резонатор) таких колебаний существует бесчисленное множество. Например, для закрепленной струны длиной L гармоники будут отличаться количеством полуволн, которые возможно уложить по всей длине струны. Если скорость распространения волн струны равна v, то спектр собственных частот определяется по формуле:
Рисунок 1. Формула 1. Автор24 — интернет-биржа студенческих работ
Наличие дисперсии волн искажает данное простое распределение частот, спектр которых определяется уже из дисперсионных уравнений.
Что касается реальных систем, то в них собственные колебания затухают из-за потерь энергии, поэтому их следует считать лишь приближенно гармоническими в интервале времени, меньшем $1/δ$. Затухающие колебания могут быть представлены в виде нескольких гармонических колебаний, непрерывно заполняющих определенный интервал частот, тем меньшим, чем меньше $δ$. В таком случае следует говорить о расширении спектральной линии, характеризуемой добротностью $Q$ и равной отношению запасенной энергии $W$ к потерям $P$. Отсюда следует, что отношение сгущение спектра из-за потерь энергии может повлечь за собой превращение дискретного спектра в сплошной при приближении ширины линий к интервалу между ними.
Колебания в нелинейных системах
Собственные колебания нелинейных систем не поддаются простой классификации. Нелинейность систем с дискретным спектром частот собственных колебаний приводят к переходу энергии по спектральным компонентам. При этом возникает явление конкуренции гармоник – выживание одних и подавление других.
Подобный процесс может стабилизировать дисперсия. Она может привести к появлению устойчивых пространственно-временных образований (например, солитоны).
Большое значение при возбуждении колебаний может иметь явление резонанса, которое заключается в резком увеличении амплитуды колебаний (отклика). Данное явление наблюдается при приближении частоты внешних воздействий на систему к некоторой резонансной частоте, которая характеризует настоящую систему.
Если система линейна и ее параметры находятся вне зависимости от времени, то резонансные частоты совпадают с частотой собственных ее колебаний. Отклик системы в данном случае будет усиливаться с увеличением добротности колебательной системы $Q$.
Раскачка будет происходить до тех пор, пока энергия, поступающая извне (например, полученная при отклонении маятника от положения равновесия) будет превышать потери за время осцилляции. Что касается линейных колебаний, то энергия, вносимая извне будет пропорциональна амплитуде, а потери будут расти пропорционально ее квадрату. Отсюда следует, что баланс энергии достижим во всех случаях.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме