Eigenvalues and eigenvectors
Syntax
Description
example
e = eig(A)
a column vector containing the eigenvalues of square matrix A.
example
[ returns diagonal matrix V,D] =
eig(A)D of
eigenvalues and matrix V whose columns are the
corresponding right eigenvectors, so that A*V = V*D.
example
[ also returns full matrix V,D,W]
= eig(A)W whose
columns are the corresponding left eigenvectors, so that W'*A.
= D*W'
The eigenvalue problem is to determine the solution to the equation Av = λv,
where A is an n-by-n matrix, v is
a column vector of length n, and λ is
a scalar. The values of λ that satisfy the
equation are the eigenvalues. The corresponding values of v that
satisfy the equation are the right eigenvectors. The left eigenvectors, w,
satisfy the equation w’A = λw’.
example
e = eig(A,B)
a column vector containing the generalized eigenvalues of square matrices A and B.
example
[ returnsV,D] =
eig(A,B)
diagonal matrix D of generalized eigenvalues and
full matrix V whose columns are the corresponding
right eigenvectors, so that A*V = B*V*D.
[ alsoV,D,W]
= eig(A,B)
returns full matrix W whose columns are the corresponding
left eigenvectors, so that W'*A = D*W'*B.
The generalized eigenvalue problem is to determine the solution
to the equation Av = λBv,
where A and B are n-by-n matrices, v is
a column vector of length n, and λ is
a scalar. The values of λ that satisfy the
equation are the generalized eigenvalues. The corresponding values
of v are the generalized right eigenvectors. The
left eigenvectors, w, satisfy the equation w’A = λw’B.
[___] = eig(,A,balanceOption)
where balanceOption is 'nobalance',
disables the preliminary balancing step in the algorithm. The default for
balanceOption is 'balance', which
enables balancing. The eig function can return any of the
output arguments in previous syntaxes.
example
[___] = eig(,A,B,algorithm)
where algorithm is 'chol', uses
the Cholesky factorization of B to compute the
generalized eigenvalues. The default for algorithm depends
on the properties of A and B,
but is generally 'qz', which uses the QZ algorithm.
If A is Hermitian and B is
Hermitian positive definite, then the default for algorithm is 'chol'.
example
[___] = eig(___,outputForm)
returns the eigenvalues in the form specified by outputForm
using any of the input or output arguments in previous syntaxes. Specify
outputForm as 'vector' to return the
eigenvalues in a column vector or as 'matrix' to return the
eigenvalues in a diagonal matrix.
Examples
collapse all
Eigenvalues of Matrix
Use gallery to create a symmetric positive definite matrix.
A = 4×4
1.0000 0.5000 0.3333 0.2500
0.5000 1.0000 0.6667 0.5000
0.3333 0.6667 1.0000 0.7500
0.2500 0.5000 0.7500 1.0000
Calculate the eigenvalues of A. The result is a column vector.
e = 4×1
0.2078
0.4078
0.8482
2.5362
Alternatively, use outputForm to return the eigenvalues in a diagonal matrix.
D = 4×4
0.2078 0 0 0
0 0.4078 0 0
0 0 0.8482 0
0 0 0 2.5362
Eigenvalues and Eigenvectors of Matrix
Use gallery to create a circulant matrix.
A = 3×3
1 2 3
3 1 2
2 3 1
Calculate the eigenvalues and right eigenvectors of A.
V = 3×3 complex
-0.5774 + 0.0000i 0.2887 - 0.5000i 0.2887 + 0.5000i
-0.5774 + 0.0000i -0.5774 + 0.0000i -0.5774 + 0.0000i
-0.5774 + 0.0000i 0.2887 + 0.5000i 0.2887 - 0.5000i
D = 3×3 complex
6.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i -1.5000 + 0.8660i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i -1.5000 - 0.8660i
Verify that the results satisfy A*V = V*D.
ans = 3×3 complex
10-14 ×
-0.2665 + 0.0000i -0.0444 + 0.0222i -0.0444 - 0.0222i
0.0888 + 0.0000i 0.0111 + 0.0777i 0.0111 - 0.0777i
-0.0444 + 0.0000i -0.0111 + 0.0833i -0.0111 - 0.0833i
Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then A*V can, at best, approach V*D. In other words, A*V - V*D is close to, but not exactly, 0.
Sorted Eigenvalues and Eigenvectors
By default eig does not always return the eigenvalues and eigenvectors in sorted order. Use the sort function to put the eigenvalues in ascending order and reorder the corresponding eigenvectors.
Calculate the eigenvalues and eigenvectors of a 5-by-5 magic square matrix.
A = 5×5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
V = 5×5
-0.4472 0.0976 -0.6330 0.6780 -0.2619
-0.4472 0.3525 0.5895 0.3223 -0.1732
-0.4472 0.5501 -0.3915 -0.5501 0.3915
-0.4472 -0.3223 0.1732 -0.3525 -0.5895
-0.4472 -0.6780 0.2619 -0.0976 0.6330
D = 5×5
65.0000 0 0 0 0
0 -21.2768 0 0 0
0 0 -13.1263 0 0
0 0 0 21.2768 0
0 0 0 0 13.1263
The eigenvalues of A are on the diagonal of D. However, the eigenvalues are unsorted.
Extract the eigenvalues from the diagonal of D using diag(D), then sort the resulting vector in ascending order. The second output from sort returns a permutation vector of indices.
d = 5×1
-21.2768
-13.1263
13.1263
21.2768
65.0000
Use ind to reorder the diagonal elements of D. Since the eigenvalues in D correspond to the eigenvectors in the columns of V, you must also reorder the columns of V using the same indices.
Ds = 5×5
-21.2768 0 0 0 0
0 -13.1263 0 0 0
0 0 13.1263 0 0
0 0 0 21.2768 0
0 0 0 0 65.0000
Vs = 5×5
0.0976 -0.6330 -0.2619 0.6780 -0.4472
0.3525 0.5895 -0.1732 0.3223 -0.4472
0.5501 -0.3915 0.3915 -0.5501 -0.4472
-0.3223 0.1732 -0.5895 -0.3525 -0.4472
-0.6780 0.2619 0.6330 -0.0976 -0.4472
Both (V,D) and (Vs,Ds) produce the eigenvalue decomposition of A. The results of A*V-V*D and A*Vs-Vs*Ds agree, up to round-off error.
e1 = norm(A*V-V*D); e2 = norm(A*Vs-Vs*Ds); e = abs(e1 - e2)
Left Eigenvectors
Create a 3-by-3 matrix.
A = [1 7 3; 2 9 12; 5 22 7];
Calculate the right eigenvectors, V, the eigenvalues, D, and the left eigenvectors, W.
V = 3×3
-0.2610 -0.9734 0.1891
-0.5870 0.2281 -0.5816
-0.7663 -0.0198 0.7912
D = 3×3
25.5548 0 0
0 -0.5789 0
0 0 -7.9759
W = 3×3
-0.1791 -0.9587 -0.1881
-0.8127 0.0649 -0.7477
-0.5545 0.2768 0.6368
Verify that the results satisfy W'*A = D*W'.
ans = 3×3
10-13 ×
-0.0444 -0.1066 -0.0888
-0.0011 0.0442 0.0333
0 0.0266 0.0178
Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then W'*A can, at best, approach D*W'. In other words, W'*A - D*W' is close to, but not exactly, 0.
Eigenvalues of Nondiagonalizable (Defective) Matrix
Create a 3-by-3 matrix.
A = [3 1 0; 0 3 1; 0 0 3];
Calculate the eigenvalues and right eigenvectors of A.
V = 3×3
1.0000 -1.0000 1.0000
0 0.0000 -0.0000
0 0 0.0000
D = 3×3
3 0 0
0 3 0
0 0 3
A has repeated eigenvalues and the eigenvectors are not independent. This means that A is not diagonalizable and is, therefore, defective.
Verify that V and D satisfy the equation, A*V = V*D, even though A is defective.
ans = 3×3
10-15 ×
0 0.8882 -0.8882
0 0 0.0000
0 0 0
Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then A*V can, at best, approach V*D. In other words, A*V - V*D is close to, but not exactly, 0.
Generalized Eigenvalues
Create two matrices, A and B, then solve the generalized eigenvalue problem for the eigenvalues and right eigenvectors of the pair (A,B).
A = [1/sqrt(2) 0; 0 1]; B = [0 1; -1/sqrt(2) 0]; [V,D]=eig(A,B)
V = 2×2 complex
1.0000 + 0.0000i 1.0000 + 0.0000i
0.0000 - 0.7071i 0.0000 + 0.7071i
D = 2×2 complex
0.0000 + 1.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 - 1.0000i
Verify that the results satisfy A*V = B*V*D.
The residual error A*V - B*V*D is exactly zero.
Generalized Eigenvalues Using QZ Algorithm for Badly Conditioned Matrices
Create a badly conditioned symmetric matrix containing values close to machine precision.
format long e A = diag([10^-16, 10^-15])
A = 2×2
1.000000000000000e-16 0
0 1.000000000000000e-15
Calculate the generalized eigenvalues and a set of right eigenvectors using the default algorithm. In this case, the default algorithm is 'chol'.
V1 = 2×2
1.000000000000000e+08 0
0 3.162277660168380e+07
D1 = 2×2
9.999999999999999e-01 0
0 1.000000000000000e+00
Now, calculate the generalized eigenvalues and a set of right eigenvectors using the 'qz' algorithm.
Check how well the 'chol' result satisfies A*V1 = A*V1*D1.
format short
A*V1 - A*V1*D1
ans = 2×2
10-23 ×
0.1654 0
0 -0.6617
Now, check how well the 'qz' result satisfies A*V2 = A*V2*D2.
When both matrices are symmetric, eig uses the 'chol' algorithm by default. In this case, the QZ algorithm returns more accurate results.
Generalized Eigenvalues Where One Matrix Is Singular
Create a 2-by-2 identity matrix, A, and a singular matrix, B.
A = eye(2); B = [3 6; 4 8];
If you attempt to calculate the generalized eigenvalues of the matrix B-1A with the command [V,D] = eig(BA), then MATLAB® returns an error because BA produces Inf values.
Instead, calculate the generalized eigenvalues and right eigenvectors by passing both matrices to the eig function.
V = 2×2
-0.7500 -1.0000
-1.0000 0.5000
It is better to pass both matrices separately, and let eig choose the best algorithm to solve the problem. In this case, eig(A,B) returns a set of eigenvectors and at least one real eigenvalue, even though B is not invertible.
Verify Av=λBv for the first eigenvalue and the first eigenvector.
eigval = D(1,1); eigvec = V(:,1); A*eigvec - eigval*B*eigvec
ans = 2×1
10-15 ×
0.1110
0.2220
Ideally, the eigenvalue decomposition satisfies the relationship. Since the decomposition is performed using floating-point computations, then A*eigvec can, at best, approach eigval*B*eigvec, as it does in this case.
Input Arguments
collapse all
A — Input matrix
square matrix
Input matrix, specified as a real or complex square matrix.
Data Types: double | single
Complex Number Support: Yes
B — Generalized eigenvalue problem input matrix
square matrix
Generalized eigenvalue problem input matrix, specified as a
square matrix of real or complex values. B must
be the same size as A.
Data Types: double | single
Complex Number Support: Yes
balanceOption — Balance option
'balance' (default) | 'nobalance'
Balance option, specified as: 'balance',
which enables a preliminary balancing step, or 'nobalance' which
disables it. In most cases, the balancing step improves the conditioning
of A to produce more accurate results. However,
there are cases in which balancing produces incorrect results. Specify 'nobalance' when A contains
values whose scale differs dramatically. For example, if A contains
nonzero integers, as well as very small (near zero) values, then the
balancing step might scale the small values to make them as significant
as the integers and produce inaccurate results.
'balance' is the default behavior. For more
information about balancing, see balance.
algorithm — Generalized eigenvalue algorithm
'chol' | 'qz'
Generalized eigenvalue algorithm, specified as 'chol' or 'qz',
which selects the algorithm to use for calculating the generalized
eigenvalues of a pair.
| algorithm | Description |
|---|---|
'chol' |
Computes the generalized eigenvalues of A and B usingthe Cholesky factorization of B. |
'qz' |
Uses the QZ algorithm, also known as the generalized Schur decomposition. This algorithm ignores the symmetry of A and B. |
In general, the two algorithms return the same result. The QZ
algorithm can be more stable for certain problems, such as those involving
badly conditioned matrices.
When you omit the algorithm argument, the eig function
selects an algorithm based on the properties of A and B.
It uses the 'chol' algorithm for symmetric (Hermitian) A and
symmetric (Hermitian) positive definite B. Otherwise,
it uses the 'qz' algorithm.
Regardless of the algorithm you specify, the eig function
always uses the QZ algorithm when A or B are
not symmetric.
outputForm — Output format of eigenvalues
'vector' | 'matrix'
Output format of eigenvalues, specified as 'vector' or
'matrix'. This option allows you to specify whether
the eigenvalues are returned in a column vector or a diagonal matrix. The
default behavior varies according to the number of outputs specified:
-
If you specify one output, such as
e = eig(A),
then the eigenvalues are returned as a column vector by
default. -
If you specify two or three outputs, such as
[V,D] =, then the eigenvalues are returned as a
eig(A)
diagonal matrix,D, by default.
Example: D = eig(A,'matrix') returns a diagonal matrix
of eigenvalues with the one output syntax.
Output Arguments
collapse all
e — Eigenvalues (returned as vector)
column vector
Eigenvalues, returned as a column vector containing the eigenvalues (or generalized
eigenvalues of a pair) with multiplicity. Each eigenvalue
e(k) corresponds with the right eigenvector
V(:,k) and the left eigenvector
W(:,k).
-
When
Ais real symmetric or
complex Hermitian, the
values ofethat satisfy
Av =
λv are real. -
When
Ais real skew-symmetric or complex skew-Hermitian, the values ofethat
satisfy Av =
λv are imaginary.
V — Right eigenvectors
square matrix
Right eigenvectors, returned as a square matrix whose columns
are the right eigenvectors of A or generalized
right eigenvectors of the pair, (A,B). The form
and normalization of V depends on the combination
of input arguments:
-
[V,D] = eig(A)returns matrixV,
whose columns are the right eigenvectors ofAsuch
thatA*V = V*D. The eigenvectors inVare
normalized so that the 2-norm of each is 1.If
Ais real symmetric, Hermitian,
or skew-Hermitian, then the right eigenvectors
Vare orthonormal. -
[V,D] = eig(A,'nobalance')also
returns matrixV. However, the 2-norm of each eigenvector
is not necessarily 1. -
[V,D] = eig(A,B)and[V,D] =return
eig(A,B,algorithm)Vas
a matrix whose columns are the generalized right eigenvectors
that satisfyA*V = B*V*D. The 2-norm of each
eigenvector is not necessarily 1. In this case,
Dcontains the generalized eigenvalues of
the pair,(A,B), along the main
diagonal.When
eiguses the
'chol'algorithm with symmetric
(Hermitian)Aand symmetric (Hermitian)
positive definiteB, it normalizes the
eigenvectors inVso that the
B-norm of each is 1.
Different machines and releases of MATLAB® can produce different eigenvectors that are still numerically accurate:
-
For real eigenvectors, the sign of the eigenvectors can change.
-
For complex eigenvectors, the eigenvectors can be multiplied by any complex number
of magnitude 1. -
For a multiple eigenvalue, its eigenvectors can be recombined through linear
combinations. For example, if Ax =
λx and Ay =
λy, then A(x+y) =
λ(x+y), so x+y also is an eigenvector of A.
D — Eigenvalues (returned as matrix)
diagonal matrix
Eigenvalues, returned as a diagonal matrix with the eigenvalues of A on the
main diagonal or the eigenvalues of the pair, (A,B), with
multiplicity, on the main diagonal. Each eigenvalue
D(k,k) corresponds with the right eigenvector
V(:,k) and the left eigenvector
W(:,k).
-
When
Ais real symmetric or
complex Hermitian, the
values ofDthat satisfy
Av =
λv are real. -
When
Ais real skew-symmetric or complex skew-Hermitian, the values ofDthat
satisfy Av =
λv are imaginary.
W — Left eigenvectors
square matrix
Left eigenvectors, returned as a square matrix whose columns
are the left eigenvectors of A or generalized left
eigenvectors of the pair, (A,B). The form and normalization
of W depends on the combination of input arguments:
-
[V,D,W] = eig(A)returns matrix
W, whose columns are the left eigenvectors of
Asuch thatW'*A = D*W'.
The eigenvectors inWare normalized so that the
2-norm of each is 1. IfAis symmetric,
thenWis the same as
V. -
[V,D,W] = eig(A,'nobalance')also
returns matrixW. However, the 2-norm of each eigenvector
is not necessarily 1. -
[V,D,W] = eig(A,B)and[V,D,W]returns
= eig(A,B,algorithm)Was a matrix
whose columns are the generalized left eigenvectors that satisfyW'*A. The 2-norm of each eigenvector is not necessarily
= D*W'*B
1. In this case,Dcontains the generalized eigenvalues
of the pair,(A,B), along the main diagonal.If
AandBare symmetric,
thenWis the same as
V.
Different machines and releases of MATLAB can produce different eigenvectors that are still numerically accurate:
-
For real eigenvectors, the sign of the eigenvectors can change.
-
For complex eigenvectors, the eigenvectors can be multiplied by any complex number
of magnitude 1. -
For a multiple eigenvalue, its eigenvectors can be recombined through linear
combinations. For example, if Ax =
λx and Ay =
λy, then A(x+y) =
λ(x+y), so x+y also is an eigenvector of A.
More About
collapse all
Symmetric Matrix
-
A square matrix,
A, is symmetric if it is equal to its nonconjugate transpose,A = A.'.In terms of the matrix elements, this means that
-
Since real matrices are unaffected by complex conjugation, a real matrix that is symmetric is also Hermitian. For example, the matrix
is both symmetric and Hermitian.
Skew-Symmetric Matrix
-
A square matrix,
A, is skew-symmetric if it is equal to the negation of its nonconjugate transpose,A = -A.'.In terms of the matrix elements, this means that
-
Since real matrices are unaffected by complex conjugation, a real matrix that is skew-symmetric is also skew-Hermitian. For example, the matrix
is both skew-symmetric and skew-Hermitian.
Hermitian Matrix
-
A square matrix,
A, is Hermitian if it is equal to its complex conjugate transpose,A = A'.In terms of the matrix elements, this means that
-
The entries on the diagonal of a Hermitian matrix are always real. Since real matrices are unaffected by complex conjugation, a real matrix that is symmetric is also Hermitian. For example, the matrix
is both symmetric and Hermitian.
-
The eigenvalues of a Hermitian matrix are real.
Skew-Hermitian Matrix
-
A square matrix,
A, is skew-Hermitian if it is equal to the negation of its complex conjugate transpose,A = -A'.In terms of the matrix elements, this means that
-
The entries on the diagonal of a skew-Hermitian matrix are always pure imaginary or zero. Since real matrices are unaffected by complex conjugation, a real matrix that is skew-symmetric is also skew-Hermitian. For example, the matrix
is both skew-Hermitian and skew-symmetric.
-
The eigenvalues of a skew-Hermitian matrix are purely imaginary or zero.
Tips
-
The
eigfunction can calculate
the eigenvalues of sparse matrices that are real and symmetric. To
calculate the eigenvectors of a sparse matrix, or to calculate the
eigenvalues of a sparse matrix that is not real and symmetric, use
theeigsfunction.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
-
Vmight represent a different basis of eigenvectors. This representation
means that the eigenvector calculated by the generated code might be
different in C and C++ code than in MATLAB. The eigenvalues inDmight not be in the
same order as in MATLAB. You can verify theVand
Dvalues by using the eigenvalue problem equation
A*V = V*D. -
If you specify the LAPACK library callback class, then the code generator supports these options:
-
The computation of left eigenvectors.
-
-
Outputs are complex.
-
Code generation does not support sparse matrix inputs for this
function.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
The eig function
partially supports GPU arrays. Some syntaxes of the function run on a GPU when you specify the
input data as a gpuArray (Parallel Computing Toolbox). Usage notes and limitations:
-
For the generalized case,
eig(A,B),
AandBmust be real symmetric or
complex Hermitian. Additionally,Bmust be positive
definite. -
The QZ algorithm,
eig(A,B,'qz'), is not
supported.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
-
For the generalized case,
eig(A,B),
AandBmust be real symmetric or
complex Hermitian. Additionally,Bmust be positive
definite. -
These syntaxes are not supported for full distributed arrays:
[__] = eig(A,B,'qz')[V,D,W] = eig(A,B)
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
expand all
R2021b: eig returns NaN for nonfinite inputs
eig returns NaN values when the input
contains nonfinite values (Inf or NaN).
Previously, eig threw an error when the input contained
nonfinite values.
R2021a: Improved algorithm for skew-Hermitian matrices
The algorithm for input matrices that are skew-Hermitian was improved. With the
function call [V,D] = eig(A), where A is
skew-Hermitian, eig now guarantees that the matrix of
eigenvectors V is unitary and the diagonal matrix of eigenvalues
D is purely imaginary.
Собственные значения и собственные вектора
Синтаксис
e = eig(A)
[V,D] =
eig(A)
[V,D,W]
= eig(A)
e = eig(A,B)
[V,D] =
eig(A,B)
[V,D,W]
= eig(A,B)
[___] = eig(A,balanceOption)
[___] = eig(A,B,algorithm)
[___] = eig(___,eigvalOption)
Описание
пример
e = eig(A)A.
пример
[ V,D] =
eig(A)возвращает диагональную матрицу D собственных значений и матрицы V, столбцы которой являются соответствующими правыми собственными векторами, так что A * V = V * D.
пример
[ также возвращает полный матричный V,D,W]
= eig(A)W, столбцы которого являются соответствующими левыми собственными векторами, так, чтобы W'*A = D*W'.
Задача о собственных значениях должна определить решение уравнения A v = λ v, где A является n-by-n матрица, v является вектор-столбцом длины n, и λ является скаляром. Значения λ, которые удовлетворяют уравнению, являются собственными значениями. Соответствующие значения v, которые удовлетворяют уравнению, являются правыми собственными векторами. Левые собственные вектора, w, удовлетворяют уравнению w ’A = λ w’.
пример
e = eig(A,B)A и B.
пример
[ возвращает диагональный матричный V,D] =
eig(A,B)D обобщенных собственных значений и полный матричный V, столбцы которого являются соответствующими правыми собственными векторами, так, чтобы A*V = B*V*D.
[ также возвращает полный матричный V,D,W]
= eig(A,B)W, столбцы которого являются соответствующими левыми собственными векторами, так, чтобы W'*A = D*W'*B.
Обобщенная задача о собственных значениях должна определить решение уравнения A v = λ B v, где A и B является n-by-n матрицы, v является вектор-столбцом длины n, и λ является скаляром. Значения λ, которые удовлетворяют уравнению, являются обобщенными собственными значениями. Соответствующие значения v являются обобщенными правыми собственными векторами. Левые собственные вектора, w, удовлетворяют уравнению w ’A = λ w ’B.
[___] = eig(, то, где A,balanceOption)balanceOption является 'nobalance', отключает предварительный шаг балансировки в алгоритме. Значением по умолчанию для balanceOption является 'balance', который позволяет балансироваться. Функция eig может возвратить любой из выходных аргументов в предыдущих синтаксисах.
пример
[___] = eig(, то, где A,B,algorithm)algorithm является 'chol', использует факторизацию Холесского B, чтобы вычислить обобщенные собственные значения. Значение по умолчанию для algorithm зависит от свойств A и B, но обычно является 'qz', который использует алгоритм QZ.
Если A является Эрмитовым, и B Эрмитов положительный определенный, то значением по умолчанию для algorithm является 'chol'.
пример
[___] = eig(___, возвращает собственные значения в форме, заданной eigvalOption)eigvalOption с помощью любого из аргументов ввода или вывода в предыдущих синтаксисах. Задайте eigvalOption как 'vector', чтобы возвратить собственные значения в вектор-столбце или как 'matrix', чтобы возвратить собственные значения в диагональной матрице.
Примеры
свернуть все
Собственные значения матрицы
Используйте gallery, чтобы создать симметричную положительную определенную матрицу.
A = 4×4
1.0000 0.5000 0.3333 0.2500
0.5000 1.0000 0.6667 0.5000
0.3333 0.6667 1.0000 0.7500
0.2500 0.5000 0.7500 1.0000
Вычислите собственные значения A. Результатом является вектор-столбец.
e = 4×1
0.2078
0.4078
0.8482
2.5362
Также используйте eigvalOption, чтобы возвратить собственные значения в диагональной матрице.
D = 4×4
0.2078 0 0 0
0 0.4078 0 0
0 0 0.8482 0
0 0 0 2.5362
Собственные значения и собственные вектора матрицы
Используйте gallery, чтобы создать циркулянтную матрицу.
A = 3×3
1 2 3
3 1 2
2 3 1
Вычислите собственные значения и правые собственные вектора A.
V = 3×3 complex
-0.5774 + 0.0000i 0.2887 - 0.5000i 0.2887 + 0.5000i
-0.5774 + 0.0000i -0.5774 + 0.0000i -0.5774 + 0.0000i
-0.5774 + 0.0000i 0.2887 + 0.5000i 0.2887 - 0.5000i
D = 3×3 complex
6.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i -1.5000 + 0.8660i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i -1.5000 - 0.8660i
Проверьте, что результаты удовлетворяют A*V = V*D.
ans = 3×3 complex
10-14 ×
-0.2665 + 0.0000i -0.0333 + 0.1110i -0.0333 - 0.1110i
0.0888 + 0.0000i 0.0000 + 0.1221i 0.0000 - 0.1221i
-0.0444 + 0.0000i -0.0111 + 0.1221i -0.0111 - 0.1221i
Идеально, разложение собственного значения удовлетворяет отношение. Поскольку eig выполняет разложение с помощью вычислений с плавающей точкой, затем A*V может, в лучшем случае приблизиться к V*D. Другими словами, A*V - V*D близко к, но не точно, 0.
Отсортированные собственные значения и собственные вектора
eig по умолчанию не всегда возвращает собственные значения и собственные вектора в отсортированном порядке. Используйте функцию sort, чтобы поместить собственные значения в порядке возрастания и переупорядочить соответствующие собственные вектора.
Вычислите собственные значения и собственные вектора матрицы магического квадрата 5 на 5.
A = 5×5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
V = 5×5
-0.4472 0.0976 -0.6330 0.6780 -0.2619
-0.4472 0.3525 0.5895 0.3223 -0.1732
-0.4472 0.5501 -0.3915 -0.5501 0.3915
-0.4472 -0.3223 0.1732 -0.3525 -0.5895
-0.4472 -0.6780 0.2619 -0.0976 0.6330
D = 5×5
65.0000 0 0 0 0
0 -21.2768 0 0 0
0 0 -13.1263 0 0
0 0 0 21.2768 0
0 0 0 0 13.1263
Собственные значения A находятся на диагонали D. Однако собственные значения не отсортированы.
Извлеките собственные значения от диагонали D с помощью diag(D), затем отсортируйте итоговый вектор в порядке возрастания. Второй вывод от sort возвращает вектор перестановки индексов.
d = 5×1
-21.2768
-13.1263
13.1263
21.2768
65.0000
Используйте ind, чтобы переупорядочить диагональные элементы D. Поскольку собственные значения в D соответствуют собственным векторам в столбцах V, необходимо также переупорядочить столбцы V с помощью тех же индексов.
Ds = 5×5
-21.2768 0 0 0 0
0 -13.1263 0 0 0
0 0 13.1263 0 0
0 0 0 21.2768 0
0 0 0 0 65.0000
Vs = 5×5
0.0976 -0.6330 -0.2619 0.6780 -0.4472
0.3525 0.5895 -0.1732 0.3223 -0.4472
0.5501 -0.3915 0.3915 -0.5501 -0.4472
-0.3223 0.1732 -0.5895 -0.3525 -0.4472
-0.6780 0.2619 0.6330 -0.0976 -0.4472
И (V,D) и (Vs,Ds) производят разложение собственного значения A. Результаты A*V-V*D и A*Vs-Vs*Ds соглашаются до ошибки округления.
e1 = norm(A*V-V*D); e2 = norm(A*Vs-Vs*Ds); e = abs(e1 - e2)
Левые собственные вектора
Создайте 3х3 матрицу.
A = [1 7 3; 2 9 12; 5 22 7];
Вычислите правые собственные вектора, V, собственные значения, D, и левые собственные вектора, W.
V = 3×3
-0.2610 -0.9734 0.1891
-0.5870 0.2281 -0.5816
-0.7663 -0.0198 0.7912
D = 3×3
25.5548 0 0
0 -0.5789 0
0 0 -7.9759
W = 3×3
-0.1791 -0.9587 -0.1881
-0.8127 0.0649 -0.7477
-0.5545 0.2768 0.6368
Проверьте, что результаты удовлетворяют W'*A = D*W'.
ans = 3×3
10-13 ×
0.1155 -0.0711 -0.0711
-0.0033 -0.0215 -0.0408
0.0022 0.0266 0.0178
Идеально, разложение собственного значения удовлетворяет отношение. Поскольку eig выполняет разложение с помощью вычислений с плавающей точкой, затем W'*A может, в лучшем случае приблизиться к D*W'. Другими словами, W'*A - D*W' близко к, но не точно, 0.
Собственные значения недиагонализируемой (дефектной) матрицы
Создайте 3х3 матрицу.
A = [3 1 0; 0 3 1; 0 0 3];
Вычислите собственные значения и правые собственные вектора A.
V = 3×3
1.0000 -1.0000 1.0000
0 0.0000 -0.0000
0 0 0.0000
D = 3×3
3 0 0
0 3 0
0 0 3
A повторил собственные значения, и собственные вектора весьма зависимы. Это означает, что A не является диагонализируемым и является, поэтому, дефектным.
Проверьте, что V и D удовлетворяют уравнению, A*V = V*D, даже при том, что A является дефектным.
ans = 3×3
10-15 ×
0 0.8882 -0.8882
0 0 0.0000
0 0 0
Идеально, разложение собственного значения удовлетворяет отношение. Поскольку eig выполняет разложение с помощью вычислений с плавающей точкой, затем A*V может, в лучшем случае приблизиться к V*D. Другими словами, A*V - V*D близко к, но не точно, 0.
Обобщенные собственные значения
Создайте две матрицы, A и B, затем решите обобщенную задачу о собственных значениях для собственных значений и правых собственных векторов парного (A,B).
A = [1/sqrt(2) 0; 0 1]; B = [0 1; -1/sqrt(2) 0]; [V,D]=eig(A,B)
V = 2×2 complex
1.0000 + 0.0000i 1.0000 + 0.0000i
0.0000 - 0.7071i 0.0000 + 0.7071i
D = 2×2 complex
0.0000 + 1.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 - 1.0000i
Проверьте, что результаты удовлетворяют A*V = B*V*D.
Остаточная ошибка A*V - B*V*D является точно нулевой.
Обобщенные собственные значения Используя алгоритм QZ для плохо обусловленных матриц
Создайте плохо обусловленную симметрическую матрицу, содержащую значения близко к точности машины.
format long e A = diag([10^-16, 10^-15])
A = 2×2
1.000000000000000e-16 0
0 1.000000000000000e-15
Вычислите обобщенные собственные значения и набор правых собственных векторов с помощью алгоритма по умолчанию. В этом случае алгоритмом по умолчанию является 'chol'.
V1 = 2×2
1.000000000000000e+08 0
0 3.162277660168380e+07
D1 = 2×2
9.999999999999999e-01 0
0 1.000000000000000e+00
Теперь, вычислите обобщенные собственные значения и набор правых собственных векторов с помощью алгоритма 'qz'.
Проверяйте, как хорошо результат 'chol' удовлетворяет A*V1 = A*V1*D1.
format short
A*V1 - A*V1*D1
ans = 2×2
10-23 ×
0.1654 0
0 -0.6617
Теперь, проверяйте, как хорошо результат 'qz' удовлетворяет A*V2 = A*V2*D2.
Когда обе матрицы симметричны, eig использует алгоритм 'chol' по умолчанию. В этом случае алгоритм QZ возвращает более точные результаты.
Обобщенные Собственные значения, Где Одна Матрица Сингулярна
Создайте единичную матрицу 2 на 2, A, и сингулярную матрицу, B.
A = eye(2); B = [3 6; 4 8];
При попытке вычислить обобщенные собственные значения матрицы B-1A с командой [V,D] = eig(BA) затем MATLAB® возвращает ошибку, потому что BA производит значения Inf.
Вместо этого вычислите обобщенные собственные значения и правые собственные вектора путем передачи обеих матриц функции eig.
V = 2×2
-0.7500 -1.0000
-1.0000 0.5000
Лучше передать обе матрицы отдельно и позволить eig выбрать лучший алгоритм, чтобы решить проблему. В этом случае eig(A,B) возвращает набор собственных векторов и по крайней мере одного действительного собственного значения, даже при том, что B не является обратимым.
Проверить Av=λBv для первого собственного значения и первого собственного вектора.
eigval = D(1,1); eigvec = V(:,1); A*eigvec - eigval*B*eigvec
ans = 2×1
10-15 ×
0.1110
0.2220
Идеально, разложение собственного значения удовлетворяет отношение. Поскольку разложение выполняется с помощью вычислений с плавающей точкой, затем A*eigvec может, в лучшем случае приблизиться к eigval*B*eigvec, как это делает в этом случае.
Входные параметры
свернуть все
A Введите матрицу
квадратная матрица
Введите матрицу, заданную как действительная или комплексная квадратная матрица.
Типы данных: double | single
Поддержка комплексного числа: Да
B Обобщенная входная матрица задачи о собственных значениях
квадратная матрица
Обобщенная входная матрица задачи о собственных значениях, заданная как квадратная матрица действительных или комплексных чисел. B должен быть одного размера как A.
Типы данных: double | single
Поддержка комплексного числа: Да
balanceOption BalanceOption
'balance' (значение по умолчанию) | 'nobalance'
Сбалансируйте опцию, заданную как: 'balance', который включает предварительный шаг балансировки или 'nobalance', который отключает его. В большинстве случаев балансирующийся шаг улучшает создание условий A, чтобы привести к более точным результатам. Однако существуют случаи, в которых балансировка приводит к неправильным результатам. Задайте 'nobalance', когда A содержит значения, шкала которых отличается существенно. Например, если A содержит ненулевые целые числа, а также очень маленький (около нуля) значения, то балансирующийся шаг может масштабировать маленькие значения, чтобы сделать их столь же значительными как целые числа и привести к неточным результатам.
'balance' является поведением по умолчанию. Для получения дополнительной информации о балансировке, смотрите balance.
algorithm — Обобщенный алгоритм собственного значения
'chol' | 'qz'
Обобщенный алгоритм собственного значения, заданный как 'chol' или 'qz', который выбирает алгоритм, чтобы использовать для вычисления обобщенных собственных значений пары.
| алгоритм | Описание |
|---|---|
'chol' |
Вычисляет обобщенные собственные значения A и B с помощью факторизации Холесского B. |
'qz' |
Использует алгоритм QZ, также известный как обобщенное разложение Шура. Этот алгоритм игнорирует симметрию A и B. |
В целом эти два алгоритма возвращают тот же результат. Алгоритм QZ может быть более стабильным для определенных проблем, таким как те, которые включают плохо обусловленные матрицы.
Когда вы не используете аргумент algorithm, функция eig выбирает алгоритм на основе свойств A и B. Это использует алгоритм 'chol' для симметричного (Эрмитового) A и симметричного (Эрмитового) положительного определенного B. В противном случае это использует алгоритм 'qz'.
Независимо от алгоритма вы задаете, функция eig всегда использует алгоритм QZ, когда A или B не симметричны.
eigvalOption Опция собственного значения
'vector' | 'matrix'
Опция собственного значения, заданная как 'vector' или 'matrix'. Эта опция позволяет вам задавать, возвращены ли собственные значения в вектор-столбце или диагональной матрице. Поведение по умолчанию отличается согласно количеству заданных выходных параметров:
-
Если вы задаете тот вывод, такой как
e = eig(A), то собственные значения возвращены как вектор-столбец по умолчанию. -
Если вы задаете два или три выходных параметров, такие как
[V,D] = eig(A), то собственные значения возвращены как диагональная матрица,D, по умолчанию.
Пример: D = eig (A, ‘matrix’) возвращает диагональную матрицу собственных значений с одним выходом.
Выходные аргументы
свернуть все
e Собственные значения (возвратился как вектор),
вектор-столбец
Собственные значения, возвращенные как вектор-столбец, содержащий собственные значения (или обобщенные собственные значения пары) с кратностью.
Когда A действителен и симметричен или комплексный Эрмитов, значения e, которые удовлетворяют A v =, λ v действителен.
V Правые собственные вектора
квадратная матрица
Правые собственные вектора, возвращенные как квадратная матрица, столбцы которой являются правыми собственными векторами A или обобщенными правыми собственными векторами пары, (A,B). Форма и нормализация V зависят от комбинации входных параметров:
-
[V,D] = eig(A)возвращает матричныйV, столбцы которого являются правыми собственными векторамиA, таким образом чтоA*V = V*D. Собственные вектора вVнормированы так, чтобы 2-норма каждого равнялась 1.Если
Aдействителен симметричный, то правые собственные вектора,V, ортонормированы. -
[V,D] = eig(A,'nobalance')также возвращает матричныйV. Однако 2-норма каждого собственного вектора не обязательно 1. -
[V,D] = eig(A,B)и[V,D] = eig(A,B,algorithm)возвращаютVкак матрицу, столбцы которой являются обобщенными правыми собственными векторами, которые удовлетворяютA*V = B*V*D. 2-норма каждого собственного вектора не обязательно 1. В этом случаеDсодержит обобщенные собственные значения пары,(A,B), по основной диагонали.Когда
eigиспользует алгоритм'chol'с симметричным (Эрмитовым)Aи симметричным (Эрмитовым) положительным определеннымB, это нормирует собственные вектора вVтак, чтобыB– норма каждого равнялась 1.
Различные машины и релизы MATLAB® могут произвести различные собственные вектора, которые все еще численно точны:
-
Для действительных собственных векторов может измениться знак собственных векторов.
-
Для комплексных собственных векторов собственные вектора могут быть умножены на любое комплексное число значения 1.
-
Для собственного значения кратного его собственные вектора могут быть повторно объединены через линейные комбинации. Например, если A x = λ x и A y = λ y, то A (x +y) = λ (x +y), таким образом, x +y также является собственным вектором A.
D Собственные значения (возвратился как матрица),
диагональная матрица
Собственные значения, возвращенные как диагональная матрица с собственными значениями A на основной диагонали или собственными значениями пары, (A,B), с кратностью, на основной диагонали.
Когда A действителен и симметричен или комплексный Эрмитов, значения D, которые удовлетворяют A v =, λ v действителен.
W Левые собственные вектора
квадратная матрица
Левые собственные вектора, возвращенные как квадратная матрица, столбцы которой являются левыми собственными векторами A или обобщенными левыми собственными векторами пары, (A,B). Форма и нормализация W зависят от комбинации входных параметров:
-
[V,D,W] = eig(A)возвращает матричныйW, столбцы которого являются левыми собственными векторамиA, таким образом чтоW'*A = D*W'. Собственные вектора вWнормированы так, чтобы 2-норма каждого равнялась 1. ЕслиAсимметричен, тоWсовпадает сV. -
[V,D,W] = eig(A,'nobalance')также возвращает матричныйW. Однако 2-норма каждого собственного вектора не обязательно 1. -
[V,D,W] = eig(A,B)и[V,D,W] = eig(A,B,algorithm)возвращаютWкак матрицу, столбцы которой являются обобщенными левыми собственными векторами, которые удовлетворяютW'*A = D*W'*B. 2-норма каждого собственного вектора не обязательно 1. В этом случаеDсодержит обобщенные собственные значения пары,(A,B), по основной диагонали.Если
AиBсимметричны, тоWсовпадает сV.
Различные машины и релизы MATLAB могут произвести различные собственные вектора, которые все еще численно точны:
-
Для действительных собственных векторов может измениться знак собственных векторов.
-
Для комплексных собственных векторов собственные вектора могут быть умножены на любое комплексное число значения 1.
-
Для собственного значения кратного его собственные вектора могут быть повторно объединены через линейные комбинации. Например, если A x = λ x и A y = λ y, то A (x +y) = λ (x +y), таким образом, x +y также является собственным вектором A.
Советы
-
Функция
eigможет вычислить собственные значения разреженных матриц, которые действительны и симметричны. Чтобы вычислить собственные вектора разреженной матрицы или вычислить собственные значения разреженной матрицы, которая не действительна и симметрична, используют функциюeigs.
Расширенные возможности
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Указания и ограничения по применению:
-
Vможет представлять различное основание собственных векторов. Собственные значения вDне могут быть в том же порядке как в MATLAB.-
Для обобщенной задачи о собственных значениях,
[V,D] = eig(A,B), генерация кода всегда использует опцию'qz'. -
Для стандартной задачи о собственных значениях
[V,D] = eig(A), когдаAявляется Эрмитовым, генерация кода, используетschur, чтобы вычислитьVиD. В противном случае результаты[V,D] = eig(A)подобны результатам, полученным при помощи[V,D] = eig(A,eye(size(A)),'qz')в MATLAB, за исключением того, что столбцыVнормированы.
-
-
'balance'и опции'nobalance'не поддержаны для стандартной задачи о собственных значениях. -
Опция
'chol'не поддержана для симметричной обобщенной задачи о собственных значениях. -
Опция, чтобы вычислить левые собственные вектора не поддержана.
-
Выходные параметры являются комплексными.
-
Когда входная матрица содержит неличное значение, сгенерированный код не выдает ошибку. Вместо этого вывод содержит значения
NaN. -
Генерация кода не поддерживает входные параметры разреженной матрицы для этой функции.
Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
-
Только эти синтаксисы входного параметра поддерживаются:
e = eig(A)[V,D] = eig(A)
Для получения дополнительной информации смотрите функции MATLAB Выполнения на графическом процессоре (Parallel Computing Toolbox).
Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
-
Для обобщенного случая
eig(A,B),AиBдолжны быть действительны симметричный или комплексный Эрмитов. Кроме того,Bдолжен быть положителен определенный. -
Эти синтаксисы не поддержаны для полных распределенных массивов:
[__] = eig(A,'balance')[__] = eig(A,B,'qz')[V,D,W] = eig(A,B)
Для получения дополнительной информации смотрите функции MATLAB Выполнения с Распределенными Массивами (Parallel Computing Toolbox).
Представлено до R2006a
eigs
Subset of eigenvalues and eigenvectors
Syntax
Description
example
d = eigs(A)
the six largest magnitude eigenvalues of matrix A. This is
most useful when computing all of the eigenvalues with eig
is computationally expensive, such as with large sparse matrices.
example
d = eigs(A,k)
the k largest magnitude eigenvalues.
example
d = eigs(A,k,sigma)
returns k eigenvalues based on the value of
sigma. For example,
eigs(A,k,'smallestabs') returns the k
smallest magnitude eigenvalues.
d = eigs(A,k,sigma,Name,Value)
specifies additional options with one or more name-value pair arguments. For
example, eigs(A,k,sigma,'Tolerance',1e-3) adjusts the
convergence tolerance for the algorithm.
example
d = eigs(A,k,sigma,opts)
specifies options using a structure.
example
d = eigs(A,B,___)
solves the generalized eigenvalue problem A*V = B*V*D. You
can optionally specify k, sigma,
opts, or name-value pairs as additional input
arguments.
d = eigs(Afun,n,___)
specifies a function handle Afun instead of a matrix. The
second input n gives the size of matrix A
used in Afun. You can optionally specify
B, k, sigma,
opts, or name-value pairs as additional input
arguments.
example
[ returns diagonal matrix V,D] =
eigs(___)D containing
the eigenvalues on the main diagonal, and matrix V whose
columns are the corresponding eigenvectors. You can use any of the
input argument combinations in previous syntaxes.
example
[ also returns a convergence flag.V,D,flag]
= eigs(___)
If flag is 0, then all the eigenvalues
converged.
Examples
collapse all
Largest Eigenvalues of Sparse Matrix
The matrix A = delsq(numgrid('C',15)) is a symmetric positive definite matrix with eigenvalues reasonably well-distributed in the interval (0 8). Compute the six largest magnitude eigenvalues.
A = delsq(numgrid('C',15));
d = eigs(A)
d = 6×1
7.8666
7.7324
7.6531
7.5213
7.4480
7.3517
Specify a second input to compute a specific number of the largest eigenvalues.
d = 3×1
7.8666
7.7324
7.6531
Smallest Eigenvalues of Sparse Matrix
The matrix A = delsq(numgrid('C',15)) is a symmetric positive definite matrix with eigenvalues reasonably well-distributed in the interval (0 8). Compute the five smallest eigenvalues.
A = delsq(numgrid('C',15)); d = eigs(A,5,'smallestabs')
d = 5×1
0.1334
0.2676
0.3469
0.4787
0.5520
Eigenvalues Using Function Handle
Create a 1500-by-1500 random sparse matrix with a 25% approximate density of nonzero elements.
n = 1500; A = sprand(n,n,0.25);
Find the LU factorization of the matrix, returning a permutation vector p that satisfies A(p,:) = L*U.
[L,U,p] = lu(A,'vector');
Create a function handle Afun that accepts a vector input x and uses the results of the LU decomposition to, in effect, return Ax.
Afun = @(x) U(L(x(p)));
Calculate the six smallest magnitude eigenvalues using eigs with the function handle Afun. The second input is the size of A.
d = eigs(Afun,1500,6,'smallestabs')
d = 6×1 complex
0.1423 + 0.0000i
0.4859 + 0.0000i
-0.3323 - 0.3881i
-0.3323 + 0.3881i
0.1019 - 0.5381i
0.1019 + 0.5381i
Types of Eigenvalues
west0479 is a real-valued 479-by-479 sparse matrix with both real and complex pairs of conjugate eigenvalues.
Load the west0479 matrix, then compute and plot all of the eigenvalues using eig. Since the eigenvalues are complex, plot automatically uses the real parts as the x-coordinates and the imaginary parts as the y-coordinates.
load west0479 A = west0479; d = eig(full(A)); plot(d,'+')
The eigenvalues are clustered along the real line (x-axis), particularly near the origin.
eigs has several options for sigma that can pick out the largest or smallest eigenvalues of varying types. Compute and plot some eigenvalues for each of the available options for sigma.
figure plot(d, '+') hold on la = eigs(A,6,'largestabs'); plot(la,'ro') sa = eigs(A,6,'smallestabs'); plot(sa,'go') hold off legend('All eigenvalues','Largest magnitude','Smallest magnitude') xlabel('Real axis') ylabel('Imaginary axis')
figure plot(d, '+') hold on ber = eigs(A,4,'bothendsreal'); plot(ber,'r^') bei = eigs(A,4,'bothendsimag'); plot(bei,'g^') hold off legend('All eigenvalues','Both ends real','Both ends imaginary') xlabel('Real axis') ylabel('Imaginary axis')
figure plot(d, '+') hold on lr = eigs(A,3,'largestreal'); plot(lr,'ro') sr = eigs(A,3,'smallestreal'); plot(sr,'go') li = eigs(A,3,'largestimag','SubspaceDimension',45); plot(li,'m^') si = eigs(A,3,'smallestimag','SubspaceDimension',45); plot(si,'c^') hold off legend('All eigenvalues','Largest real','Smallest real','Largest imaginary','Smallest imaginary') xlabel('Real axis') ylabel('Imaginary axis')
Difference Between 'smallestabs' and 'smallestreal' Eigenvalues
Create a symmetric positive definite sparse matrix.
A = delsq(numgrid('C', 150));
Compute the six smallest real eigenvalues using 'smallestreal', which employs a Krylov method using A.
tic
d = eigs(A, 6, 'smallestreal')
d = 6×1
0.0013
0.0025
0.0033
0.0045
0.0052
0.0063
Elapsed time is 3.153523 seconds.
Compute the same eigenvalues using 'smallestabs', which employs a Krylov method using the inverse of A.
tic
dsm = eigs(A, 6, 'smallestabs')
dsm = 6×1
0.0013
0.0025
0.0033
0.0045
0.0052
0.0063
Elapsed time is 0.503009 seconds.
The eigenvalues are clustered near zero. The 'smallestreal' computation struggles to converge using A since the gap between the eigenvalues is so small. Conversely, the 'smallestabs' option uses the inverse of A, and therefore the inverse of the eigenvalues of A, which have a much larger gap and are therefore easier to compute. This improved performance comes at the cost of factorizing A, which is not necessary with 'smallestreal'.
Sigma Value Near Eigenvalue
Compute eigenvalues near a numeric sigma value that is nearly equal to an eigenvalue.
The matrix A = delsq(numgrid('C',30)) is a symmetric positive definite matrix of size 632 with eigenvalues reasonably well-distributed in the interval (0 8), but with 18 eigenvalues repeated at 4.0. To calculate some eigenvalues near 4.0, it is reasonable to try the function call eigs(A,20,4.0). However, this call computes the largest eigenvalues of the inverse of A - 4.0*I, where I is an identity matrix. Because 4.0 is an eigenvalue of A, this matrix is singular and therefore does not have an inverse. eigs fails and produces an error message. The numeric value of sigma cannot be exactly equal to an eigenvalue. Instead, you must use a value of sigma that is near but not equal to 4.0 to find those eigenvalues.
Compute all of the eigenvalues using eig, and the 20 eigenvalues closest to 4 – 1e-6 using eigs to compare results. Plot the eigenvalues calculated with each method.
A = delsq(numgrid('C',30));
sigma = 4 - 1e-6;
d = eig(A);
D = sort(eigs(A,20,sigma));
plot(d(307:326),'ks') hold on plot(D,'k+') hold off legend('eig(A)','eigs(A,20,sigma)') title('18 Repeated Eigenvalues of A')
Eigenvalues of Permuted Cholesky Factor
Create sparse random matrices A and B that both have low densities of nonzero elements.
B = sprandn(1e3,1e3,0.001) + speye(1e3); B = B'*B; A = sprandn(1e3,1e3,0.005); A = A+A';
Find the Cholesky decomposition of matrix B, using three outputs to return the permutation vector s and test value p.
[R,p,s] = chol(B,'vector');
p
Since p is zero, B is a symmetric positive definite matrix that satisfies B(s,s) = R'*R.
Calculate the six largest magnitude eigenvalues and eigenvectors of the generalized eigenvalue problem involving A and R. Since R is the Cholesky factor of B, specify 'IsCholesky' as true. Furthermore, since B(s,s) = R'*R and thus R = chol(B(s,s)), use the permutation vector s as the value of 'CholeskyPermutation'.
[V,D,flag] = eigs(A,R,6,'largestabs','IsCholesky',true,'CholeskyPermutation',s); flag
Since flag is zero, all of the eigenvalues converged.
Input Arguments
collapse all
A — Input matrix
matrix
Input matrix, specified as a square matrix. A is
typically, but not always, a large and sparse matrix.
If A is symmetric, then eigs uses a specialized
algorithm for that case. If A is
nearly symmetric, then consider using A = to make
(A+A')/2A symmetric before calling
eigs. This ensures that eigs
calculates real eigenvalues instead of complex ones.
Data Types: double
Complex Number Support: Yes
B — Input matrix
matrix
Input matrix, specified as a square matrix of the same size as A. When
B is specified, eigs solves the
generalized eigenvalue problem A*V = B*V*D.
If B is symmetric positive definite, then eigs uses a
specialized algorithm for that case. If B is
nearly symmetric positive definite, then consider
using B = (B+B')/2 to make B symmetric
before calling eigs.
When A is scalar, you can specify B
as an empty matrix eigs(A,[],k) to solve the standard
eigenvalue problem and disambiguate between B and
k.
Data Types: double
Complex Number Support: Yes
k — Number of eigenvalues to compute
scalar
Number of eigenvalues to compute, specified as a positive scalar integer. If
k is larger than size(A,2), then
eigs uses the maximum valid value k = instead.
size(A,2)
Example: eigs(A,2) returns the two largest
eigenvalues of A.
sigma — Type of eigenvalues
'largestabs' (default) | 'smallestabs' | 'largestreal' | 'smallestreal' | 'bothendsreal' | 'largestimag' | 'smallestimag' | 'bothendsimag' | scalar
Type of eigenvalues, specified as one of the values in the table.
|
sigma |
Description |
sigma (R2017a and earlier) |
|---|---|---|
|
scalar (real or complex, including 0) |
The eigenvalues closest to the number |
No change |
|
|
Largest magnitude. |
'lm'
|
|
|
Smallest magnitude. Same as |
'sm'
|
|
|
Largest real. |
'lr', 'la' |
|
|
Smallest real. |
'sr', 'sa' |
|
|
Both ends, with |
'be' |
For nonsymmetric problems,
sigma also can be:
|
sigma |
Description |
sigma (R2017a and earlier) |
|---|---|---|
|
|
Largest imaginary part. |
'li' if A iscomplex. |
|
|
Smallest imaginary part. |
'si' if A iscomplex. |
|
|
Both ends, with |
'li' if A isreal. |
Example: eigs(A,k,1) returns the k eigenvalues
closest to 1.
Example: eigs(A,k,'smallestabs') returns the k smallest
magnitude eigenvalues.
Data Types: double | char | string
opts — Options structure
structure
Options structure, specified as a structure containing one or more of the fields in this
table.
Note
Use of the options structure to specify options is not recommended.
Use name-value pairs instead.
| Option Field | Description | Name-Value Pair |
|---|---|---|
issym |
Symmetry of |
'IsFunctionSymmetric' |
tol |
Convergence tolerance. |
'Tolerance' |
maxit |
Maximum number of iterations. |
'MaxIterations' |
p |
Number of Lanczos basis vectors. |
'SubspaceDimension' |
v0 |
Starting vector. |
'StartVector' |
disp |
Diagnostic information display level. |
'Display' |
fail |
Treatment of nonconverged eigenvalues in the output. |
'FailureTreatment' |
spdB |
Is B symmetric positivedefinite? |
'IsSymmetricDefinite' |
cholB |
Is |
'IsCholesky' |
permB |
Specify the permutation vector |
'CholeskyPermutation' |
Example: opts.issym = 1, opts.tol = 1e-10 creates
a structure with values set for the fields issym and tol.
Data Types: struct
Afun — Matrix function
function handle
Matrix function, specified as a function handle. The function y = Afun(x)
must return the proper value depending on the sigma input:
-
A*x— Ifsigmais
unspecified or any text option other than
'smallestabs'. -
Ax— Ifsigmais
0or
'smallestabs'. -
(A-sigma*I)x— If
sigmais a nonzero scalar (for standard
eigenvalue problem). -
(A-sigma*B)x— If
sigmais a nonzero scalar (for
generalized eigenvalue problem).
For example, the following Afun works when calling eigs
with sigma = 'smallestabs':
[L,U,p] = lu(A,'vector'); Afun = @(x) U(L(x(p))); d = eigs(Afun,100,6,'smallestabs')
For a generalized eigenvalue problem, add matrix B as
follows (B cannot be represented by a function
handle):
d = eigs(Afun,100,B,6,'smallestabs')
A is assumed to be nonsymmetric unless
'IsFunctionSymmetric' (or
opts.issym) specifies otherwise. Setting
'IsFunctionSymmetric' to true
ensures that eigs calculates real eigenvalues instead
of complex ones.
For information on how to provide additional parameters to the
Afun function, see Parameterizing Functions.
Tip
Call eigs with the 'Display'
option turned on to see what output is expected from
Afun.
n — Size of square matrix represented by Afun
scalar
Size of square matrix A that is represented by
Afun, specified as a positive scalar integer.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: d = loosens the
eigs(A,k,sigma,'Tolerance',1e-10,'MaxIterations',100)
convergence tolerance and uses fewer iterations.
General Options
collapse all
Tolerance — Convergence tolerance
1e-14 (default) | positive real scalar
Convergence tolerance, specified as the comma-separated pair
consisting of 'Tolerance' and a positive real numeric
scalar.
Example: s =
eigs(A,k,sigma,'Tolerance',1e-3)
MaxIterations — Maximum number of algorithm iterations
300 (default) | positive integer
Maximum number of algorithm iterations, specified as the
comma-separated pair consisting of 'MaxIterations'
and a positive integer.
Example: d =
eigs(A,k,sigma,'MaxIterations',350)
SubspaceDimension — Maximum size of Krylov subspace
max(2*k,20) (default) | nonnegative integer
Maximum size of Krylov subspace, specified as the comma-separated pair
consisting of 'SubspaceDimension' and a nonnegative
integer. The 'SubspaceDimension' value must be
greater than or equal to k + 1 for real symmetric
problems, and k + 2 otherwise, where
k is the number of eigenvalues.
The recommended value is p >= 2*k, or for real
nonsymmetric problems, p >= 2*k+1. If you do not
specify a 'SubspaceDimension' value, then the default
algorithm uses at least 20 Lanczos vectors.
For problems where eigs fails to converge,
increasing the value of 'SubspaceDimension' can
improve the convergence behavior. However, increasing the value too much
can cause memory issues.
Example: d =
eigs(A,k,sigma,'SubspaceDimension',25)
StartVector — Initial starting vector
random vector (default) | vector
Initial starting vector, specified as the comma-separated pair
consisting of 'StartVector' and a numeric
vector.
The primary reason to specify a different random starting vector is
when you want to control the random number stream used to generate the
vector.
Note
eigs selects the starting vectors in a
reproducible manner using a private random number stream. Changing
the random number seed does not affect the
starting vector.
Example: d = uses a random
eigs(A,k,sigma,'StartVector',randn(m,1))
starting vector that draws values from the global random number
stream.
Data Types: double
FailureTreatment — Treatment of nonconverged eigenvalues
'replacenan' (default) | 'keep' | 'drop'
Treatment of nonconverged eigenvalues, specified as the
comma-separated pair consisting of 'FailureTreatment'
and one of the options: 'replacenan',
'keep', or 'drop'.
The value of 'FailureTreatment' determines how
eigs displays nonconverged eigenvalues in the
output.
|
Option |
Affect on output |
|---|---|
|
|
Replace nonconverged eigenvalues with |
|
|
Include nonconverged eigenvalues in the |
|
|
Remove nonconverged eigenvalues from the output. |
Example: d = removes
eigs(A,k,sigma,'FailureTreatment','drop')
nonconverged eigenvalues from the output.
Data Types: char | string
Display — Toggle for diagnostic information display
false or
0 (default) | true or 1
Toggle for diagnostic information display, specified as the
comma-separated pair consisting of 'Display' and a
numeric or logical 1 (true) or
0 (false). Specify a value of
true or 1 to turn on the
display of diagnostic information during the calculation.
Options for Afun
collapse all
IsFunctionSymmetric — Symmetry of Afun matrix
true or 1 | false or 0
Symmetry of Afun matrix, specified as the
comma-separated pair consisting of
'IsFunctionSymmetric' and a numeric or logical
1 (true) or
0 (false).
This option specifies whether the matrix that Afun
applies to its input vector is symmetric. Specify a value of
true or 1 to indicate that
eigs should use a specialized algorithm for the
symmetric matrix and return real eigenvalues.
Options for generalized eigenvalue problem A*V =
B*V*D
collapse all
IsCholesky — Cholesky decomposition toggle for B
true or 1 | false or 0
Cholesky decomposition toggle for B, specified as
the comma-separated pair consisting of 'IsCholesky'
and a numeric or logical 1 (true)
or 0 (false).
This option specifies whether the input for matrix
B in the call eigs(A,B,___) is
actually the Cholesky factor R produced by R.
= chol(B)
Note
Do not use this option if sigma is
'smallestabs' or a numeric scalar.
CholeskyPermutation — Cholesky permutation vector
1:n (default) | vector
Cholesky permutation vector, specified as the comma-separated pair
consisting of 'CholeskyPermutation' and a numeric
vector. Specify the permutation vector permB if
sparse matrix B is reordered before factorization
according to chol(B(permB,permB)).
You also can use the three-output syntax of chol
for sparse matrices to directly obtain permB with
[R,p,permB] = chol(B,'vector').
Note
Do not use this option if sigma is
'smallestabs' or a numeric scalar.
IsSymmetricDefinite — Symmetric-positive-definiteness toggle for B
true or 1 | false or 0
Symmetric-positive-definiteness toggle for B,
specified as the comma-separated pair consisting of
'IsSymmetricDefinite' and a numeric or logical
1 (true) or
0 (false). Specify
true or 1 when you know that
B is symmetric positive definite, that is, it is
a symmetric matrix with strictly positive eigenvalues.
If B is symmetric positive semi-definite (some
eigenvalues are zero), then specifying
'IsSymmetricDefinite' as true
or 1 forces eigs to use the same
specialized algorithm that it uses when B is
symmetric positive definite.
Note
To use this option, the value of sigma must be
numeric or 'smallestabs'.
Output Arguments
collapse all
d — Eigenvalues
column vector
Eigenvalues, returned as a column vector. d is sorted differently depending
on the value of sigma.
|
Value of |
Output sorting |
|---|---|
|
|
Descending order by magnitude |
|
|
Descending order by real part |
|
|
Descending order by imaginary part |
|
|
Ascending order by magnitude |
|
|
Ascending order by real part |
|
|
Ascending order by imaginary part |
|
|
Descending order by absolute value of imaginary |
V — Eigenvectors
matrix
Eigenvectors, returned as a matrix. The columns in V correspond to the
eigenvalues along the diagonal of D. The form and
normalization of V depends on the combination of input
arguments:
-
[V,D] = eigs(A)returns matrix
V, whose columns are the right eigenvectors
ofAsuch thatA*V = V*D. The
eigenvectors inVare normalized so that the
2-norm of each is 1.If
Ais symmetric, then the eigenvectors,
V, are orthonormal. -
[V,D] = eigs(A,B)returnsV
as a matrix whose columns are the generalized right eigenvectors
that satisfyA*V = B*V*D. The 2-norm of each
eigenvector is not necessarily 1.If
Bis symmetric positive definite, then the
eigenvectors inVare normalized so that the
B-norm of each is 1. IfA
is also symmetric, then the eigenvectors are
B-orthonormal.
Different machines, releases of MATLAB®, or parameters (such as the starting vector and subspace
dimension) can produce different eigenvectors that are still numerically accurate:
-
For real eigenvectors, the sign of the eigenvectors can
change. -
For complex eigenvectors, the eigenvectors can be multiplied
by any complex number of magnitude 1. -
For a multiple eigenvalue, its eigenvectors can be recombined
through linear combinations. For example, if Ax =
λx and Ay =
λy, then A(x+y)
=
λ(x+y), so x+y also is an eigenvector of
A.
D — Eigenvalue matrix
matrix
Eigenvalue matrix, returned as a diagonal matrix with the eigenvalues
on the main diagonal.
flag — Convergence flag
0 | 1
Convergence flag, returned as 0 or 1. A value of
0 indicates that all the eigenvalues converged.
Otherwise, not all of the eigenvalues converged.
Use of this convergence flag output suppresses warnings about failed
convergence.
Tips
-
eigsgenerates the default starting vector using a private random number
stream to ensure reproducibility across runs. Setting the random number
generator state usingrngbefore calling
eigsdoes not affect the output. -
Using
eigsis not the most efficient way to find a few eigenvalues of
small, dense matrices. For such problems, it might be quicker to use
eig(full(A)). For example, finding three eigenvalues in a
500-by-500 matrix is a relatively small problem that is easily handled with
eig. -
If
eigsfails to converge for a given matrix, increase the number of
Lanczos basis vectors by increasing the value of
'SubspaceDimension'. As secondary options, adjusting the
maximum number of iterations,'MaxIterations', and the
convergence tolerance,'Tolerance', also can help with
convergence behavior.
References
[1] Stewart, G.W. “A Krylov-Schur
Algorithm for Large Eigenproblems.” SIAM Journal of Matrix Analysis and
Applications. Vol. 23, Issue 3, 2001, pp. 601–614.
[2] Lehoucq, R.B., D.C. Sorenson, and C. Yang. ARPACK Users’
Guide. Philadelphia, PA: SIAM, 1998.
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
expand all
R2017b: Behavior and algorithm change
-
Changes to sorting order of output
eigsnow sorts the output according to the value of
sigma. For example, the command
eigs(A,k,'largestabs')producesk
eigenvalues sorted in descending order by magnitude.Previously, the sorting order of the output produced by
eigswas not guaranteed. -
Reproducibility
Calling
eigsmultiple times in succession now
produces the same result. Set'StartVector'to a random
vector to change this behavior. -
Display
A display value of
2no longer returns timing
information. Instead,eigstreats a value of
2the same as a value of1. Also,
the messages shown by the'Display'option have changed.
The new messages show the residual in each iteration, instead of the Ritz
values.
|
Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
|
|
1 |
|
Как найти собственные значения и собственные векторы матрицы?17.12.2014, 08:28. Показов 39007. Ответов 9
Дано матрица вида Найти собственные значения и собственные векторы матрицы Отсюда при Отсюда при собственные значения Теперь, вопрос как найти собственные значения и собственные векторы матрицы на MatLab тут сказано что, функция eig поможет, но я не знаю как, помогите пожалуйста
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||
|
17.12.2014, 09:13 |
2 |
|||
|
Всё очень просто…Да, можно использовать функцию eig. Всё в Хэлпе написано.
Где V – правые собственные вектора; D – собственные значения; W – левые собственные вектора.
0 |
|
Maikl2020 Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
||||
|
17.12.2014, 11:18 [ТС] |
3 |
|||
|
illi2, Ну не знаю тут функции poly, roots что обозначат, но кажется собственные значения матрица найдено правильно!
Добавлено через 1 минуту
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||
|
17.12.2014, 11:47 |
4 |
|||
|
Не понял Вас вообще. Чем не устраивает функция eig()?
V содержит два искомых собственных вектора. Для собственного значения 1 (матрица D – диагональная,содержит все собственные значения расположенные по нарастанию собственного значения) – это первый столбец матрицы V(:,1):
0 |
|
Maikl2020 Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
||||
|
17.12.2014, 12:03 [ТС] |
5 |
|||
|
illi2, Как найти собственный вектор матрицы, без нормированный вектор. т.е. программа вывел X(-1;1). Добавлено через 1 минуту
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||||||||||
|
17.12.2014, 13:41 |
6 |
|||||||||||
|
Решение У Вас просто более старая версия Матлаба (я запускал в R2014а).
Не нормированный вектор Матлаб скорее всего не выведет (так как это целое множество подобных векторов)… Можно самому просто переправить как-нить так выходные векторы матрицы V:
Добавлено через 11 минут
1 |
|
Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
|
|
17.12.2014, 14:01 [ТС] |
7 |
|
illi2, Спасибо, Извините еще два вопроса у меня пожалуйста.
i=1:size(V,2) 2) Где можно скачать R2014а ? Добавлено через 9 минут
V= собственные векторы матрицы X=(1, -1) какой из них?
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||
|
17.12.2014, 14:28 |
8 |
|||
|
Решение
1) Объясните, пожалуйста Нормируем по столбцам.
– цикл по всем столбцам. size(V,2) – число столбцов матрицы V. В матрице V собственные вектора расположены в столбцах этой матрицы. V(:,i) – i-ый столбец матрицы V. Знак ( : ) – обозначает “все элементы”, ( : , i ) – все элементы столбца i. V(:,i) = V(:,i)/min(abs(V(:,i))); – нормируем каждый столбец по отдельности (равносильно “каждый вектор”) на min(abs(V(:,i))) – минимальный по абсолютному значению элемент данного столбца. Это чтобы в каждом столбце минимальное число получилось равно “1” (или “-1”).
собственные векторы матрицы X=(1, -1) какой из них? Для собственного значения 1 – это вектор (1,-1) – первый столбец в V. Для собственного значения 4 – это вектор (1,2) – 2-ой столбец. R2014a можно скачать на http://www.mathworks.com/
1 |
|
Maikl2020 Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
||||||||
|
20.12.2014, 20:09 [ТС] |
9 |
|||||||
|
illi2, Здравствуйте, почему MatLab выводит комплексные числи
Добавлено через 2 часа 36 минут
Добавлено через 18 минут
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||
|
22.12.2014, 14:09 |
10 |
|||
|
Решение Доброго времени суток. Другой вопрос: при решении системы линейных уравнений (на собственные числа или вектора) можно получить такие случаи, когда будет 0=0. То есть удовлетворяет любое значение. Матлаб в этом случае выдаст ответ (1 0 0) или что-то подобное, то есть единичный вектор или базис из единичных векторов.
V(:,i) = V(:,i)/min(abs(V(:,i))); % перенормировываем – Эта строка не работает, когда вектор имеет нулевые элементы, ибо min(abs(V(:,i))) = 0 и получаем деление на 0. Нужно что-то вроде такого:
1 |
Найти собственные числа и собственные векторы матрицы в матлабе
4 -е занятие по MATLAB
ЛАБОРАТОРНАЯ РАБОТА №4
I. Базовые операции символьной математики
системы MATLAB — SIMBOLIC MATHEMATICS TOOLBOX
1. Создание символьных переменных и массивов (x, y, z, a, b, c и т.д.).
Первый способ c помощью команды sym: x = sym(‘x’); y = sym(‘y’); z = sym(‘z’);
Второй способ с помощью команды syms: syms a b c;
1.1. Создание символьных матриц А1 (А2) или массивов:
1-й способ : A1 = sym(‘[a1 b1 c1;d1 e1 f1;g1 h1 k1]’); % матрица А1 размера 3 ´ 3
% Вывод матрицы А1 в командной строке
» A1 % После набора А1 нажать клавишу Enter
2- й способ : syms a b c d e f g h k
A2 = [a2 b2 c2;d2 e2 f2;g2 h2 k2]; % Матрица А2 размера 3 ´ 3
% Вывод матрицы А2 в командной строке
1.2. Проверить рабочую область c помощью команды whos.
1.3. Символьные числовые матрицы и элементы:
Ac1=sym([1 3 7;2 4 6;1 7 5]); % Без апострофа
Ас2 = sym(‘7’); % С апострофом
1.4. Детерминант символьной матрицы — det :
» det(A1) % Без присвоения результата
» D 2= det ( A 2) % С присвоением результата ячейке под именем D 2
» det ( Ac 1) % Детерминант символьной числовой матрицы
% Детерминант матрицы 2-го порядка A 3= sym (‘[ a 1 b 1; c 1 d 1]’)
1 .5. Выделение диагонали заданной символьной матрицы:
1.6. Выделение диагонали символьной числовой матрицы
1.7. Создание символьной диагональной матрицы по заданной:
1.8. Создание числовой символьной диагональной матрицы по заданной
1.9. Вычисление собственных значений и собственных векторов символьно-числовой матрицы.
Собственные векторы — это такие векторы v , которые преобразуются матрицей А в векторы, отличающиеся от исходных лишь скалярным множителем s :
.
» A=sym([-1 0 0;2 -2 0;0 4 -2.5])
% Вычисление собственных векторов и собственных значений квадратной матрицы А — eig
v = % Матрица правых собственных векторов матрицы А
s = % Диагональная матрица собственных значений матрицы А
% Справедливо следующее спектральное разложение: ,
% Спектральное разложение может быть осуществлено по вектору столбцу, например
» A*v(:,2) % По второму столбцу
» v(:,2)*s(2,2) % По второму столбцу
% Первый собственный вектор v1 — это первый столбец матрицы v: v1=(0, 1, 8)
% Второй собственный вектор v2 — это второй столбец матрицы v: v2=(1, 2 ,16/3)
% Третий собственный вектор v3 — это третий столбец матрицы v: v3=(0, 0 ,1)
% Собственные числа матрицы А: s1=-2, s2=-1, s3=-5/2=-2.5
% Справедливы следующие соотношения:
Задание: Найти собственные векторы и собственные значения матрицы [7,-2,0;-2,6,-2;0,-2,5] , проверить результат.
2. Графические построения символьных функций — ezplot .
2.1. 1-й способ. Область определения по умолчанию от -2* pi до 2* pi
» syms t % Определение символьной переменной
2.2. 2-й способ обращения к функции ezplot . Задаваемая область определения
2 .3. 3-й способ обращения к функции ezplot . Определение функции под знаком ezplot
2 .4. 4-й способ обращения к функции ezplot .
» ezplot exp(-0.5*t)*cos(5*t) [0 9],grid
» ezplot sin(t)/t [ -12 12 ],grid
3. Свойства собственнх значений матрицы:
где — след матрицы А, т.е. сумма элементов главной диагонали, — собственные значения матрицы А, , — размерность матрицы А.
% В системе MATLAB
» trace(A) % След матрицы А
» sum(eig(A)) % Сумма собственных значений матрицы А
» det(A) % Определитель матрицы А
» prod(eig(A)) % Произведение собственных значений матрицы А
4. Создание полиномов и характеристических полиномов.
4.1. Создание полинома по вектору заданных коэффициентов — poly2sym .
» poly2sym(c) % Вектор коэффициентов может быть непосредственно введен в poly2sym
% Переменная х устанавливается по умолчанию. Другие переменные следует определять
» c=[2 3 5 7 8]; % Можно определить и как вектор столбец
4.2. Характеристический полином заданной символьно-числовой матрицы
Характеристический полином определяется из следующего характеристического уравнения для заданной матрицы А:
где — единичная матрица
Каждое собственное число матрицы А удовлетворяет ее характеристическому уравнению
» syms s % Задали символьную переменную s
% Для чисто числовой матрицы функция poly определяет только строку коэффициентов
Задание. Вычислить собственные значения матрицы А с присвоением результата и подставить каждое из собственных значений в полученный характеристический полином. Результат должен быть равен нулю. Использовать функцию упрощения результата вычислений simplify.
4.3. Выделение коэффициентов из заданного полинома — sym2poly.
» p=poly2sym([1 3 4 6],s) % Формирование полинома с заданными коэффициентами
» sym2poly(p) % Выделение вектор-строки коэффициентов из заданного полинома
% Полученную вектор-строку можно переопределить с присвоением
Задание. Сформировать характеристический полином по полученному вектору-строки с использованием функции poly2sym по переменной z.
5. Решение символьных конечных уравнений — solve .
5.1. Решение квадратного уравнения
—
» syms x % Задание символьной переменной х
» solve(‘x^2+2*x-8=0’) % Формат записи решателя solve
—
[ -1-i*7^(1/2)] % Комплексное решение, i — мнимая единица
5.2. Решение нелинейных уравнений.
5.3. Решение систем нелинейных уравнений.
—
» simplify([X2,X1]) % Для упрощения результата
5.4. Решение систем трансцендентных уравнений.
Пример. Решить следующую систему трансцендентных уравнений:
где t1, t2, t3 — искомые переменные.
% Функция vpa используется д ля задания количества значащих цифр
O4=(1-0.5)*exp(T3(4))-2*exp(T2(4))+2*exp(T1(4))-1 % Для проверки
% Каждое из 6 решений должно удовлетворять любому из 3-х уравнений
II. Вычисление символьных выражений
с различным представлением результатов.
Вычисление пределов в MATLAB. Вычисление сумм, произведений.
в пакете SIMBOLIC MATHEMATICS TOOLBOX.
1. Представление результата в виде рационального числа — ‘r’ .
1.1. Вычисление дроби 1/3:
» r1=sym(1/3,’r’) % С присвоением результата
1.2. Вычисление натурального логарифма от 3 — :
1.3. Вычисление десятичного логарифма от 3 — :
1.4. Вычисление логарифма по основанию два от 3 — :
Замечание: Представление в виде рационального числа имеет формат либо p/q либо p*2^q, где p, q — целые числа.
2. Представление результата в виде числа с плавающей точкой — ‘f’ .
Все величины представляются в форме ‘1.F’*2^(e) или ‘-1.F’*2^(e), где F — это ряд из 13 шестнадцатиричных цифр, а e — целое число. В случае, когда результат вычисления не может быть представлен точно в форме с плавающей точкой, то выводятся буквы, имеющие то или иное назначение в интерпретации результата.
2.1. Вычисление дроби 1/2:
» f1=sym(1/2,’f’) % Формат записи
% Результат записан в виде точного представления в арифметике с плавающей точкой
2.2. Вычисление дроби 1/5:
% Результат записан в виде приближенного (буква а — approximately) представления в арифметике с плавающей точкой.
3. Рациональное число с оценкой погрешности полученного представления —‘e’.
Рациональное представление добавляется переменной ‘eps’, которая оценивает разницу между теоретическим рациональным выражением (результатом) и его действительной величиной с плавающей точкой.
3.1. Вычислить дробь 1/2:
1/2 % Результат как и в случае рационального представления
3.2. Вычислить дробь 1/3:
3.3. Вычислить выражение :
3.4. Вычислить дробь 3/33
4. Формат десятичного числа — ‘d’ .
4.1. Вычислить дробь 1/3:
.33333333333333331482961625624739 % По умолчанию поддерживаются 16 цифр %мантиссы полученного числа
4.2. вычислить выражение :
4.3. Вычислить дробь 1/3 с 23 знаками в мантиссе с использованием функции vpa :
4.4. Вычислить дробь 1/3 с 23 знаками в мантиссе с использованием vpa и digits
% Использование только digits приводит к выводу результата с заданным количеством цифр, но %с ограниченной точностью (в формате ‘d’):
5. Вычисление пределов — limit.
Вычисление пределов от символьных выражений производится с помощью встроенной функции limit . Соответствие между традиционным математическим описанием и символьным системы MATLAB приводится в таблице 1.
Таблица 1
Традиционное математическое действие
Команда MATLAB
% предел слева
% предел справа
Примечание: символ бесконечность ( ) в MATLAB записывается как inf . Неопределенное значение в MATLAB записывается как NaN .
5.1. Вычислить предел выражения :
1 % Предел отношения равен единицы
5.2. Вычислить предел выражения :
exp(1) % Ответ: число е в первой степени
5.3. Вычислить предел выражения при стремлении х к нулю слева:
-inf % Ответ: минус бесконечность
5.4. Вычислить предел выражения при стремлении х к нулю справа:
inf % Ответ: бесконечность (т.е. плюс бесконечность)
limit((sin(x+h)-sin(x))/h,h,0) returns cos(x)
5.5. Вычислить предел выражения :
» limit(y5,h,0) % Вычисление предела по одной из переменных — по h
6 . Дифференцирование функций одной переменной — diff .
6.1. Найти производную функции по переменной х:
6.2. Найти производную функции по переменной х:
» diff(sin(x+h)/x) % Формат записи без предварительного присвоения
6.3. Найти производную функции по переменной h :
» diff(sin(x+h)/x,h) % В записи указывается имя символьной переменной, по которой
6.4. Найти вторую производную от функции по переменной h :
6.5. Найти вторую производную от функции по переменной х:
» diff(sin(x+h)/x,2) % Цифра два указывает на порядок производной
6.6. Найти третью производную от функции по переменной h :
7. Интегрирование функции одной переменной — int .
7.1. Вычисление неопределенного интеграла:
% Вычислить интеграл :
% Вычислить интеграл :
» int((x+h)^2) % По умолчанию интегрирование ведется по переменной х
% Вычислить неопределенный интеграл от функции по переменной h :
% Вычислить неопределенный интеграл от функции по переменной x :
1/2*x^2+2*h*x+h^2*log(x) % В ответе имеется в виду натуральный логарифм
7.2. Вычисление определенного интеграла.
% Вычислить определенный интеграл :
% Вычислить определенный интеграл по переменной h :
8. Решение обыкновенных дифференциальных уравнений в символьном виде — dsolve .
Решатель дифференциальных уравнений может быть использован, если решение существует в аналитическом виде. Практически это означает, что решателем dsolve можно пользоваться только при поиске решения линейного дифференциального уравнения (или системы линейных уравнений).
8 .1. Решить дифференциальное уравнение с начальным условием Построить график решения в интервале [-0.5, 7].
% Создадим следующий сценарий под именем sdif1 :
% Решение диф.уравнения в символьном виде
% Область построения графика решения можно задавать без квадратных скобок
8 .2. Решить систему однородных дифференциальных уравнений с начальными условиями Построить график решения в интервале [-0.5, 13].
% Создадим следующий сценарий под именем sdif2 :
ezplot(x1,0,13),grid,hold on,ezplot(x2,[0,13]),title (‘Однородная система 2-х уравнений’)
8.3. Решить систему неоднородных дифференциальных уравнений
с нулевыми начальными условиями и построить график решения в интервале [0, 5] для первой координаты и в интервале [0, 9] для второй координаты .
% Создадим следующий сценарий под именем sdif3 :
ezplot(x1,[0,5]),grid,hold on,ezplot(x2,[0,9]),title( ‘ Неоднородная система 2-х уравнений ‘)
8.4. Решить дифференциальное уравнение 2-го порядка с нулевыми начальными условиями и построить график решения в интервале [-0.2, 9] .
% Создадим следующий сценарий под именем sdif4 :
ezplot(x,[-0.2 9]),grid,title (‘Д иф.уравнение 2-го порядка ‘)
8.5. Решить дифференциальное уравнение 3-го порядка с нулевыми начальными условиями и построить график решения в интервале [-0.2, 21] .
% Создадим следующий сценарий под именем sdif5 :
ezplot(x,[-0.2 21]),grid,title (‘Диф.уравнение 3-го порядка’)
8.6. Решить неоднородную систему дифференциальных уравнений 3-го порядка
с нулевыми начальными условиями и построить график решения по каждой координате в одной системе координат в интервале [-1, 19] с различными цветами по , , .
% Создадим следующий сценарий под именем sdif6 :
ezplot(x1,[-1,19]),grid, hold on,ezplot(x2,[-1,19],
title (‘Н еоднородная система 3-го порядка ‘),
% Функция ezplot не позволяет строить графики с заданными цветами. Применим fplot . Для этого в функцию fplot следует вставить решения из командного окна MATLAB. Например, решение по первой координате имеет вид
% Тогда формат записи fplot для графика по х1 будет следующий (с красным цветом):
% Через hold on можно добавить еще fplot по второй координате х2 и по третьей х3.
¾ Для объекта с передаточной функцией решить соответствующее дифференциальное уравнение при нулевых начальных условиях и построить график решения (переходный процесс).
¾ Для того же объекта с передаточной функцией W(s) записать систему дифференциальных уравнений первого порядка, решить ее и сравнить с решением соответствующего дифференциального уравнения 3-го порядка.
¾ Исследовать переходной процесс по выходным координатам двух колебательных звеньев, соединенных последовательно. Передаточные функции звеньев принять в виде:
¾ Решение в символьном виде систем дифференциальных уравнений сравнить с решением численного метода с помощью решателя ode45.
Найти собственные числа и собственные векторы матрицы в матлабе
Матричные операции линейной алгебры
Вычисление нормы и чисел обусловленности матрицы
Определитель и ранг матрицы
Определение нормы вектора
Определение ортонормированного базиса матрицы
Приведение матрицы к треугольной форме
Определение угла между двумя подпространствами
Вычисление следа матрицы
LU- и QR-разложения
Вычисление собственных значений и сингулярных чисел
Приведение матриц к формам Шура и Хессенберга
Линейная алгебра — область, в которой наиболее часто используются векторы и матрицы. Наряду с операциями общего характера, рассмотренными выше, применятся функции, решающие наиболее характерные задачи линейной алгебры. Они и рассмотрены в данном уроке.
Вычисление нормы и чисел обусловленности матрицы
Для понимания всего нижеизложенного материала необходимо учесть, что нормы матриц в MATLAB отличаются от норм векторов.
Пусть А —матрица. Тогда n=norm(A) эквивалентно п=погп(А,2) и возвращает вторую норму, т. е. самое большое сингулярное число А. Функция n=norm(A, 1) возвращает первую норму, т. е. самую большую из сумм абсолютных значений элементов матрицы по столбцам. Норма неопределенности n=norm(A, inf) возвращает самую большую из сумм абсолютных значений элементов матрицы по рядам. Норма Фробениуса (Frobenius) norm(A, ‘fro’) = sqrt(sum(diag(A’A))).
Числа обусловленности матрицы определяют чувствительность решения системы линейных уравнений к погрешностям исходных данных. Следующие функции позволяют найти числа обусловленности матриц.
cond(X) — возвращает число обусловленности, основанное на второй норме, то есть отношение самого большого сингулярного числа X к самому малому. Значение cond(X), близкое к 1, указывает на хорошо обусловленную матрицу;
с = cond(X.p) — возвращает число обусловленности матрицы, основанное на р -норме: norm(X.p)*norm(inv(X),p), где р определяет способ расчета:
р=1 — число обусловленности матрицы, основанное на первой норме;
р=2 — число обусловленности матрицы, основанное на второй норме;
p= ‘fro’ — число обусловленности матрицы, основанное на норме Фробе-ниуса (Frobenius);
р=’inf’ — число обусловленности матрицы, основанное на норме неопределенности.
с = cond(X) — возвращает число обусловленности матрицы, основанное на второй норме.
condeig(A) — возвращает вектор чисел обусловленности для собственных значений А. Эти числа обусловленности — обратные величины косинусов углов между левыми и правыми собственными векторами;
[V.D.s] = condeig(A) — эквивалентно [V,D] = eig(A): s = condeig(A);.
Большие числа обусловленности означают, что матрица А близка к матрице с кратными собственными значениями.
rcond(A) — возвращает обратную величину обусловленности матрицы А по первой норме, используя оценивающий обусловленность метод LAPACK. Если А — хорошо обусловленная матрица, то rcond(A) около 1.00, если плохо обусловленная, то около 0.00. По сравнению с cond функция rcond реализует более эффективный в плане затрат машинного времени, но менее достоверный метод оценки обусловленности матрицы.
Определитель и ранг матрицы
Для нахождения определителя (детерминанта) и ранга матриц в MATLAB имеются следующие функции:
det(X) — возвращает определитель квадратной матрицы X. Если X содержит только целые элементы, то результат — тоже целое число. Использование det(X)=0 как теста на вырожденность матрицы действительно только для матрицы малого порядка с целыми элементами.
-29
Детерминант матрицы вычисляется на основе треугольного разложения методом исключения Гаусса:
[L.U>lu(A): s=det(L): d=s*prod(diag(U)).
Ранг матрицы определяется количеством сингулярных чисел, превышающих порог
При этом используется следующий алгоритм:
Для вычисления ранга используется функция rank:
rank (А) — возвращает количество сингулярных чисел, которые являются большими, чем заданный по умолчанию допуск;
rank(A.tol) — возвращает количество сингулярных чисел, которые превышают tol. Пример:
Определение нормы вектора
Норма вектора — скаляр, дающий представление о величине элементов вектора. Нужно различать норму матрицы и норму вектора. Функция norm определяет, является ли ее аргументом (входным аргументом в терминологии MATLAB) вектор или матрица, и измеряет несколько различных типов норм векторов:
norm(X)=norm(X,2) — вторая норма возвращает наибольшее сингулярное число X, max(svd(X));
norm(X.p) , где р — целое положительное число, — возвращает корень степени р из суммы абсолютных значений элементов вектора, возведенных в степень р. При р = 1 это может совпадать либо с первой нормой, либо с нормой неопределенности матриц;
norm(X, ‘inf’) возвращает максимальное из абсолютных значений элементов вектора; О norm(X, ‘-Inf’) возвращает минимальное из абсолютных значений элементов вектора.
Определение ортонормированного базиса матрицы
Вычисление ортонормированного базиса матрицы обеспечивают нижеприведенные функции:
В = orth(A) — возвращает ортонормированный базис матрицы А. Столбцы В определяют то же пространство, что и столбцы матрицы А, но столбцы В ортогональны, то есть B*B=eye(rank(A)). Количество столбцов матрицы В равно рангу матрицы А.
» А=[2 4 6:9 8 2:12 23 43]
0.9776 0.1597 0.1371
null (А) — возвращает ортонормированный базис для нулевого (пустого) пространства А.
Функции приведения матрицы к треугольной форме
Треугольной называется квадратная матрица А, если при l>k (верхняя треугольная матрица) или при к>1(нижняя треугольная матрица) элементы матрицы A(l,k) равны нулю. В строго треугольной матрице нули находятся и на главной диагонали. В линейной алгебре часто используется приведение матриц к той или иной треугольной форме. Оно реализуется следующими функциями:
rref (A) — возвращает приведенную к треугольной форме матрицу, используя метод исключения Гаусса с частичным выбором ведущего элемента. По умолчанию принимается значение порога допустимости для незначительного элемента столбца, равное (max(s1ze(A))*eps*norm(A,inf));
[R, jb] = rref (A) — также возвращает вектор jb, так что:
r = length (jb) может служить оценкой ранга матрицы А;
х( jb) — связанные переменные в системе линейных уравнений вида Ах=b;
А(:, jb) — базис матрицы А;
R(l:r.jb) — единичная матрица размера rхr;
[R. jb] = rref (A,to!) — осуществляет приведение матрицы к треугольной форме, используя метод исключения Гаусса с частичным выбором ведущего элемента для заданного значения порога допустимости tol;
rrefmovie(A) — показывает пошаговое исполнение процедуры приведения матрицы к треугольной.
Определение угла между двумя подпространствами
Угол между двумя подпространствами вычисляет функция subsрасе:
theta = subspace(A.B) — возвращает угол между двумя подпространствами, натянутыми на столбцы матриц А и В. Если А и В — векторы-столбцы единичной длины, то угол вычисляется по формуле acos(A’*B). Если некоторый физический эксперимент описывается массивом А, а вторая реализация этого эксперимента — массивом В, то subspace(A.B) измеряет количество новой информации, полученной из второго эксперимента и не связанной со случайными ошибками и флуктуациями.
» Н = hadamard(20);A = Н(:.2:4);В = Н(:.5:8):
Вычисление следа матрицы
След матрицы А — это сумма ее диагональных элементов. Он вычисляется функцией trace:
trace(A) — возвращает след матрицы. Пример:
Разложение Холецкого — известный прием матричных вычислений. Функция chol находит это разложение для действительных и комплексных эрмитовых матриц.
R = chol(X) — для квадратной матрицы [Положительно определенной называется действительная симметрическая матрица, все собственные значения которой положительны. Поскольку используется только верхний треугольник матрицы X, матрица X не обязательно должна быть симметрической. — Примеч. ред.]. X возвращает верхнюю треугольную матрицу R, так что R’*R=X new . Если симметрическая матрица X new , заданная верхней треугольной частью и диагональю матрицы X, не является положительно определенной матрицей, выдает сообщение об ошибке. Разложение Холецкого возможно для действительных и комплексных эрмитовых матриц [Квадратная матрица с комплексными элементами, комплексно сопряженная матрица которой может быть получена транспонированием, т. е. равна транспонированной матрице (А*=А). — Примеч. ред.];
[R.p] = chol (X) с двумя выходными аргументами никогда не генерирует сообщение об ошибке в ходе выполнения разложения Холецкого квадратной матрицы X. Если верхняя треугольная часть и диагональ X задают положительно определенную матрицу, то р=0, a R совпадает с вышеописанным случаем, иначе р. — положительное целое число, a R — верхняя треугольная матрица порядка q=p-l, такая что R’*R=X(l:q,l:q).
Обращение матриц — функции inv, pinv
Обращение матриц — одна из наиболее распространенных операций матричного анализа. Обратной называют матрицу, получаемую в результате деления единичной матрицы Е на исходную матрицу X. Таким образом, Х^-1=Е/Х. Следующие функции обеспечивают реализацию данной операции:
inv(X) — возвращает матрицу, обратную квадратной матрице X. Предупреждающее сообщение выдается, если X плохо масштабирована или близка к вырожденной.
-0.76201.2122 1.7041 -1.2146
-2.04081.4228 1.5538 1.3730
На практике вычисление явной обратной матрицы не так уж необходимо. Чаще операцию обращения применяют при решении системы линейных уравнений вида Ах=b. Один из путей решения этой системы — вычисление x=inv(A)*b. Но лучшим с точки зрения минимизации времени расчета и повышения точности вычислений является использование оператора матричного деления х=Аb. Эта операция использует метод исключения Гаусса без явного формирования обратной матрицы.
В = pinv(A) — возвращает матрицу, псевдообратную матрице А (псевдообращение матрицы по Муру-Пенроузу). Результатом псевдообращения матрицы по Муру-Пенроузу является матрица В того же размера, что и А’, и удовлетворяющая условиям А*В*А=А и В*А*В=В. Вычисление основано на использовании функции svd(A) и приравнивании к нулю всех сингулярных чисел, меньших величины tol;
В = pinv (A. tol) — возвращает псевдообратную матрицу и отменяет заданный по умолчанию порог, равный max(size(A))*norm(A)*eps.
-0.87751.1636 0.6605 -0.0034
LU- и QR-разложения
Так называемые LU- и QR-разложения реализуются следующими матричными функциями:
Функция 1и выражает любую квадратную матрицу X как произведение двух треугольных матриц, одна из которых (возможно, с перестановками) — нижняя тре угольная матрица, а другая — верхняя треугольная матрица[ В MATLAB 6 аргументом (входным аргументом) функции lu может быть и полная прямоугольная матрица. — Примеч. ред.]. Иногда эту операцию называют LR-разложением. Для выполнения этой операции служит следующая функция:
[L,U] = lu(X) — возвращает верхнюю треугольную матрицу U и психологическую нижнюю матрицу L (т. е. произведение нижней треугольной матрицы и матрицы перестановок), так что X=L*U;
[L,U,P.] = lu(X) — возвращает верхнюю треугольную матрицу U, нижнюю треугольную матрицу L и сопряженную (эрмитову) матрицу матрицы перестановок Р, так что L*U =Р*Х;
lu(Х) — вызванная с одним выходным параметром функция возвращает результат из подпрограмм DGETRF (для действительных матриц) или ZGETRF (для комплексных) известного пакета программ линейной алгебры LAPACK.
lu(X, thresh) — где thresh в диапазоне [0. 1] управляет центрированием в разреженных матрицах (см. урок 12). Отдельная форма предыдущего случая. Центрирование происходит, если элемент столбца на диагонали меньше, чем произведение thresh и любого поддиагонального элемента. Thresh=l — значение по умолчанию. Thresh=0 задает центрирование по диагонали. Если матрица полная (не разреженная), выводится сообщение об ошибке.
Функция qr выполняет QR-разложепие матрицы. Эта операция полезна для квадратных и треугольных матриц. Она выполняет QR-разложение, вычисляя произведение унитарной [Квадратная матрица с комплексными элементами, обладающая тем свойством, что обратная матрица ее комплексно сопряженной матрицы равна транспонированной, т. е. (А*)”-А’. — Примеч. ред.] матрицы и верхней треугольной матрицы. Функция используется в следующих формах: [ Квадратная матрица с комплексными элементами, обладающая тем свойством, что обратная матрица ее комплексно сопряженной матрицы равна транспонированной, т. е. (А*)”-А’. — Примеч. ред.]
[Q.R] = qr(X) — вычисляет верхнюю треугольную матрицу R того же размера, как и у X, и унитарную матрицу Q, так что X=Q*R;
[Q.R.E] = qr(X) — вычисляет матрицу перестановок Е, верхнюю треугольную матрицу R с убывающими по модулю диагональными элементами и унитарную матрицу Q, так что X*E=Q*R. Матрица перестановок Е выбрана так, что abs(diag(R)) уменьшается;
[Q.R] = qr(X.O) и [Q.R.E] = qr(X,0) — вычисляют экономное разложение, в котором Е — вектор перестановок, так что Q*R=X(: ,Е). Матрица Е выбрана так, что abs(diag(R)) уменьшается;
А = qr(X) — возвращает результат из LAPACK. Пример:
0.8381 0.5028 0.1934 0.6979
0.0196 0.7095 0.6822 0.3784
0.6813 0.4289 0.3028 0.8600
0.3795 0.3046 0.5417 0.8537
0.8318 0.1897 0.1509 0.5936
-0.5922-0.11140.5197 0.0743 -0.6011
-0.0139-0.9278 -0.0011 -0.34480.1420
-0.4814-0.11730.0699 0.5940 0.6299
-1.4152 -0.7072 -0.5037 -1.4103
0 -0.7541 -0.7274 -0.4819
0 0 -0.3577 -0.4043
[Q,R] = qrdelete(Q,R, j) — изменяет Q и RTaKHM образом, чтобы пересчитать QR-разложение матрицы А для случая, когда в ней удален j-й столбец (А(:, j )=[ ]). Входные значения Q и R представляют QR-разложение матрицы А как результат действия [Q. R]=qr(A)..Аргумент j определяет столбец, который должен быть удален из матрицы А.
0.0164 0.0576 0.7176
0.1901 0.3676 0.6927
0.5869 0.6315 0.0841
[Q.R] = qrinsert(Q,R,j,x) — изменяет Q и R таким образом, чтобы пересчитать разложение матрицы А для случая, когда в матрице А перед j-м столбцом вставлен столбец х. Входные значения Q и R представляют QR-разложение матрицы А как результат действия [Q,R]=qr(A). Аргумент х — вектор-столбец, который нужно вставить в матрицу А. Аргумент j определяет столбец, перед которым будет вставлен вектор х.
0.1210 0.8928 0.8656
0.4508 0.2731 0.2324
0.7159 0.2548 0.8049
0 0.6112 0.6163 0.7369
Вычисление собственных значений и сингулярных чисел
Во многих областях математики и прикладных наук большое значение имеют средства для вычисления собственных значений (собственных чисел, характеристических чисел, решений векового уравнения) матриц, принадлежащих им векторов и сингулярных чисел. В новой версии MATLAB собственные вектора нормализуются, иначе, чем в предыдущих. Основной критерий: либо V’V=I, либо V’BV=I, где V — собственный вектор, I — единичная матрица. Поэтому результаты вычислений в новой версии, как правило, отличаются. Ниже дан список средств решения векового уравнения, реализованных в системе MATLAB.
Несимметрические матрицы могут быть плохо обусловлены при вычислении их собственных значений. Малые изменения элементов матрицы, такие как ошибки округления, могут вызвать большие изменения в собственных значениях. Масштабирование — это попытка перевести каждую плохую обусловленность собственных векторов матрицы в диагональное масштабирование. Однако масштабирование обычно не может преобразовать несимметрическую матрицу в симметрическую, а только пытается сделать (векторную) норму каждой строки равной норме соответствующего столбца. Масштабирование значительно повышает стабильность собственных значений.
[D.B] = balance(A) — возвращает диагональную матрицу D, элементы которой являются степенями основания 2, и масштабированную матрицу В, такую, что B=DA*D, а норма каждого ряда масштабированной матрицы приближается к норме столбца с тем же номером;
В = balance(A) — возвращает масштабированную матрицу В. Пример использования функции balance:
» А=[1 1000 10000:0.0001 1 1000:0.000001 0.0001 1]
0.0001 0.1000 1.0000
0.0000 0.0001 0.1000
0.0000 0.0000 0.0001
1.0000 0.9766 0.0095
0.1024 1.0000 0.9766
1.0486 0.1024 1.0000
Величина, связывающая погрешность вычисления собственных значений с погрешностью исходных данных, называется числом обусловленности (собственных значений) матрицы и вычисляется следующим образом:
cond(V) = norm(V)*norm(inv(V)) где [V.D]=eig(A).[ B=DA*D, а норма каждого ряда масштабированной матрицы приближается к норме столбца с тем же номером; ]
eig(A) — возвращает вектор собственных значений квадратной полной или симметрической разреженной матрицы А обычно после автоматического масштабирования, но для больших разреженных матриц (в терминологии MATLAB —
это просто полные матрицы со сравнительно большим [Но небольшим по сравнению с числом нулей разреженной матрицы. Эталонное число нулей разреженной матрицы данного размера можно вычислить, применив к полной матрице этого же размера функцию sparse. — Примеч. ред.] числом нулей), а также во всех случаях, где помимо собственных значений необходимо получать и собственные вектора разреженной матрицы, вместо нее рекомендовано использовать eigs(A);
eig(A.B) – возвращает вектор обобщенных собственных значений квадратных матриц А и В;
[V.D] = eig(A.B) — вычисляет диагональную матрицу обобщенных собственных значений D и матрицу V, столбцы которой являются соответствующими собственными векторами (правыми собственными векторами), таким образом что А V = В V D;
[V.D] = eig(A) — вычисляет диагональную матрицу собственных значений О матрицы А и матрицу V, столбцы которой являются соответствующими собственными векторами (правыми собственными векторами), таким образом что А V = V D.
Нужно использовать [W,D]=e1g(A’); W=W, чтобы вычислить левые собственные вектора, которые соответствуют уравнению W*A=D*W.
[V.D] = eig(A,’nobalance’) — находит собственные векторы и собственные значения без предварительного масштабирования. Иногда это улучшает обусловленность входной матрицы, обеспечивая большую точность вычисления собственных векторов для необычно масштабированных матриц;
eig(A.B. ‘chol’) — возвращает вектор, содержащий обобщенные собственные значения, используя разложение матрицы В по методу Холецкого; если А – симметрическая квадратная матрица и В — симметрическая положительно определенная квадратная матрица, то eig(A.B) по умолчанию работает точно так же;
eig(A,B, ‘qz’) — не требует, чтобы матрицы были симметрическими и возвращает вектор, содержащий обобщенные собственные значения, используя QZ-алгоритм; при явном указании этого флага QZ-алгоритм используется вместо алгоритма Холецкого даже для симметрической матрицы и симметрической положительно определенной матрицы В, так как может давать более стабильные значения, чем предыдущий метод. Для несимметрических матриц в MATLAB 6 всегда используется QZ-алгоритм и параметр ‘chol’ или ‘qz’ игнорируется;
[V.D] = eig(A.B) — возвращает диагональную матрицу обобщенных собственных значений D и матрицу V, чьи столбцы являются соответствующими собственными векторами, так чтобы A*V=B*V*D. Пример:
» В = [3 -12 -.6 2*eps:-2 48 -1 -eps;-eps/8 eps/2 -1 10;-.5 -.5 .3 1]
3.0000 -12.0000 -0.60000.0000
-0.0000 0.0000 -1.0000 10.0000
-0.5000 -0.5000 0.3000 1.0000
-0.2548 0.7420 -0.4842 0.1956
0.9670 0.0193 -0.0388 0.0276
-0.0015 -0.6181 -0.8575 0.9780
-0.0075 -0.2588 -0.1694 -0.0676
svd(X) — возвращает вектор сингулярных чисел. Команда svd выполняет сингулярное разложение матрицы X;
Вычисление собственных значений и собственных векторов симметричной матрицы
Вычислить собственные значения и собственные векторы симметричной матрицы А на ЭВМ (требуется составить программу в системе MATLAB (на М-языке)) и определить максимальное по модулю собственное число и соответствующий собственный вектор степенным методом (ручной счет). Варианты задания.
где p = 2(G + S); m = —p + S‘, К – номер факультета (института); G – номер группы; S – номер студента по журналу.
Пример выполнения лабораторной работы.
Пусть задана матрица
Ручной счет.
Задаем начальное приближение Выполняем нулевой шаг:
Выполняем второй шаг:
Выполняем третий шаг: Оцениваем погрешность:
Таким образом, можем записать ответ в виде
Выполнение работы на ЭВМ.
Для выполнения создается М-файл. Ниже приведен текст М-файла.
A=input(‘Введите матрицу А=’);
fprintf(‘п Исходная матрица (Матрица А) п’); for i=l:n
fprintf(‘ Вектор собственных чисел ‘) fprintf(‘%6.2f ‘,x);
fprintf(‘ Матрица собственных векторов ‘); for i=l:n
Результаты расчета в командном окне:
Исходная матрица (Матрица А) 5.00-3.00 4.00
Вектор собственных чисел
Матрица собственных векторов
- 0.7071 0.5774 0.4082
- 0 0.5774 -0.8165
- -0.7071 0.5774 0.4082
Ниже приведены пояснения к приведенному тексту программы.
- 1. Заметим, что в представленной программе (а также в последующих программах, относящихся к данной лабораторной работе), при задании значений элементов матрицы А множитель 1/6 учитывать не надо – деление на 6 уже предусмотрено в тексте программы. Это сделано для упрощения ввода исходных данных и исключения соответствующих погрешностей. После запуска программы в ответ на запрос о вводе матрицы А следует задать: [30 -18 24; -18 72 -18; 24 -18 30].
- 2. Функция [v,D]=eig(A) в системе MATLAB возвращает матрицу собственных векторов V (собственные векторы расположены по столбцам) и диагональную матрицу D собственных значений (матрица Жордана (элементы, расположенные на ее главной диагонали есть собственные значения матрицы а); каноническая форма матрицы а), т.е., по сути, определяется разложение Жордана (но при условия отсутствия в матрице Жордана жор- дановых клеток порядка, большего единицы) и справедливо равенство a*v=v*d. В частном случае, при обращении типа d=eig(A) возвращается вектор d, координаты (элементы) которого есть собственные значения (собственные числа) матрицы А.
Методы вычисления собственных значений и собственных векторов матриц
Собственные векторы и собственные значения неотрицательных матриц
Собственные значения и собственные векторы матрицы
СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦ
Собственные значения и собственные векторы матрицы.
Обращение матриц и нахождение их собственных значений и собственных векторов в MathCAD.
Анализ существующих методов нахождения собственных ЧИСЕЛ И СОБСТВЕННЫХ ВЕКТОРОВ
Собственные значения обратной матрицы.
‘, а // = 1/Л – собственное значение матрицы А
[spoiler title=”источники:”]
http://phys.nsu.ru/cherk/matlab6/Chapter%2011/1.htm
http://bstudy.net/712016/informatika/vychislenie_sobstvennyh_znacheniy_sobstvennyh_vektorov_simmetrichnoy_matritsy
[/spoiler]
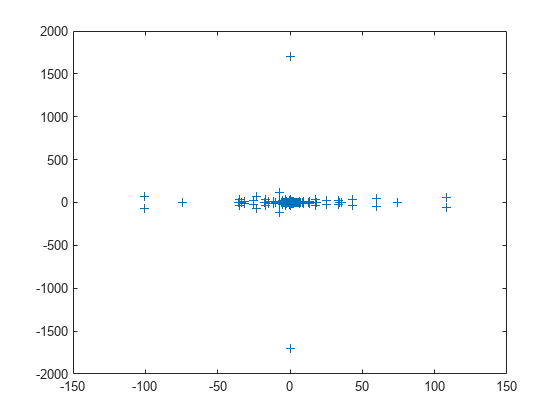
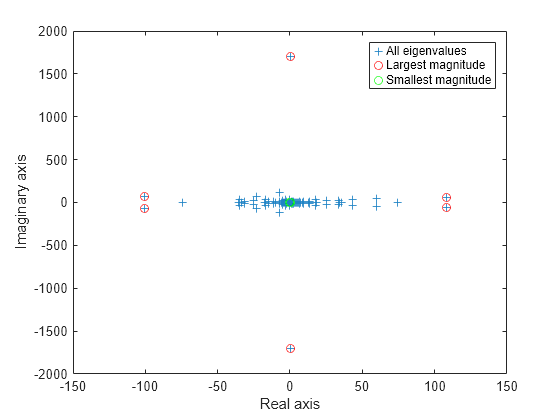
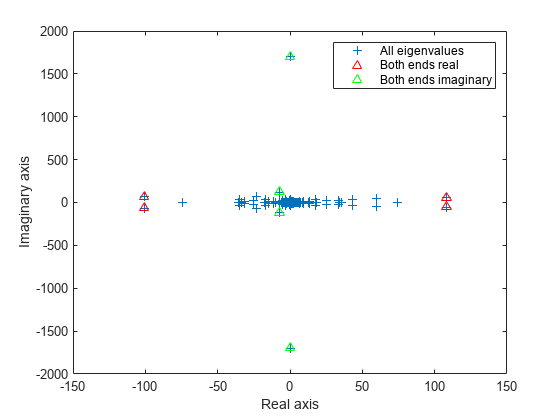
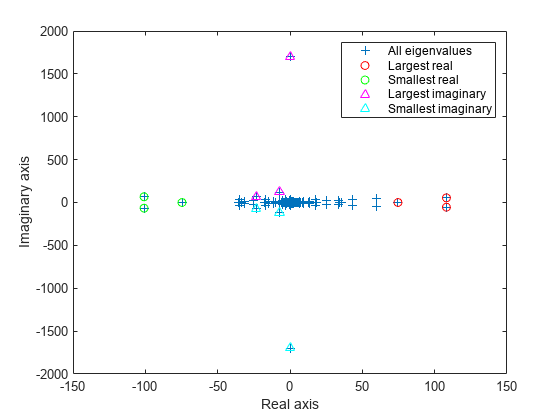
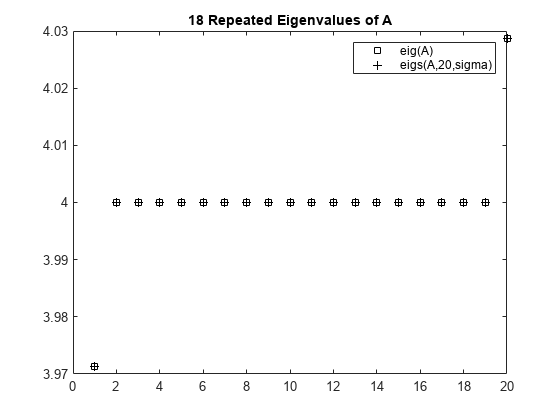

 Сообщение было отмечено Maikl2020 как решение
Сообщение было отмечено Maikl2020 как решение

