Собственные числа и собственные векторы линейного оператора
Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x 1, x 2, . x m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x 1, x 2, . x m оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x 1, x 2, . x n, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 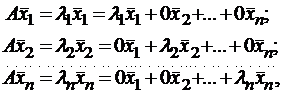 тогда
тогда  .
.
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе < ε i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса – собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
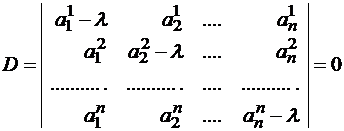
Пример №1 . Линейный оператор A действует в R3 по закону A· x =(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, . xn – координаты вектора x в базисе e 1=(1,0,0), e 2=(0,1,0), e 3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e 1=(1,4,6)
A· e 2=(-3,-7,-7)
A· e 3=(4,8,7) 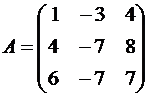 .
.
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
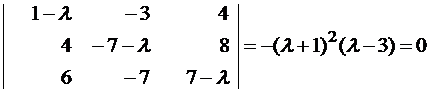
Пример №2 . Дана матрица  .
.
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x – собственный вектор



Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой ai k =ak i .
Замечания .
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Найти базис собственных векторов
Собственные числа и собственные векторы линейного оператора
Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x 1, x 2, . x m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x 1, x 2, . x m оператора A с попарно различными собственными числами λ1, λ2, …, λm линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x 1, x 2, . x n, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 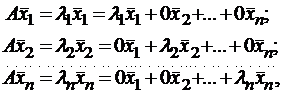 тогда
тогда  .
.
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
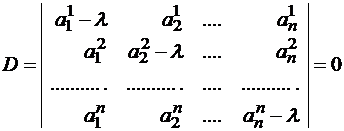
Пример №1 . Линейный оператор A действует в R3 по закону A· x =(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, . xn — координаты вектора x в базисе e 1=(1,0,0), e 2=(0,1,0), e 3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e 1=(1,4,6)
A· e 2=(-3,-7,-7)
A· e 3=(4,8,7) 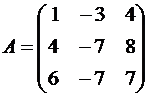 .
.
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
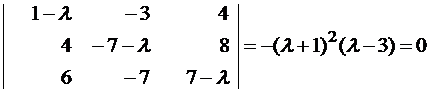
Пример №2 . Дана матрица  .
.
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор



Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой ai k =ak i .
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Найти базис собственных векторов
Найдем такие вектора (называются собственными векторами) v
и такие числа — значения (называются собственными значениями) l
матрицы A, для v, l и A выполняется:
A*v = l*v.
Также вычисляется кратность собственных значений и находит характеристическое уравнение матрицы.
© Контрольная работа РУ — калькуляторы онлайн
Где учитесь?
Для правильного составления решения, укажите:
Алгоритм нахождения векторов жорданова базиса
Собственные векторы и собственные значения
Пусть A – матрица некоторого линейного преобразования порядка n.
Определение. Многочлен n-ой степени
P(l)=det(A-lЕ) (1.1)
называется характеристическим многочленом матрицы А, а его корни, которые могут быть как действительными, так и комплексными, называются характеристическими корнями этой матрицы.
Определение. Ненулевой вектор x линейного пространства V, удовлетворяющий условию
А(х)=lх, (1.2)
называется собственным вектором преобразования A. Число l называется собственным значением.
Замечание. Если в пространстве V задан базис, то это условие можно переписать следующим образом:
Ах=lх, (1.3)
где A – матрица преобразования, x – координатный столбец.
Определение. Алгебраической кратностью собственного значения lj называется кратность корня lj характеристического многочлена.
Определение. Совокупность всех собственных значений называется спектром матрицы.
Алгоритм нахождения собственных значений и собственных векторов
1. Найти собственные значения матрицы:
· записать характеристическое уравнение:
det(A-lЕ)=0; (1.4)
· найти его корни l j, j=1. n и их кратности.
2. Найти собственные векторы матрицы:
· для каждого l j решить уравнение
· найденный вектор х и будет собственным вектором, отвечающим собственному значению l j.
Пример1
Найдем собственные значения и собственные векторы, если известна матрица преобразования:
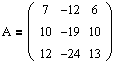
Записываем характеристический многочлен (1.1) и решаем характеристическое уравнение (1.4):
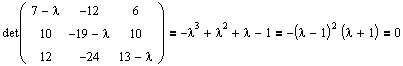
Получаем два собственных значения: l1=1 кратности m1=2 и l2=-1 кратности m2=1.
Далее с помощью соотношения (1.5) находим собственные векторы. Сначала ищем ФСР для l1=1:
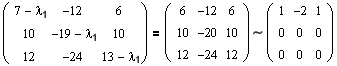
Очевидно, что rang=1, следовательно, число собственных векторов для l1=1 равно n-rang=2. Найдем их:
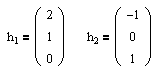
Аналогичным образом находим собственные векторы для l2=-1. В данном случае будет один вектор:
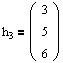
Понятие жордановой клетки и жордановой матрицы
Определение. Жордановой клеткой порядка m, отвечающей собственному значению l, называется матрица вида:
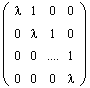 (2.1)
(2.1)
Иными словами, на главной диагонали такой матрицы располагается собственное значение l, диагональ, ближайшая к главной, сплошь занята единицами, а все остальные элементы матрицы равны нулю. Ниже даны примеры жордановых клеток соответственно первого, второго и третьего порядков:
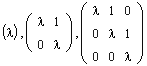
Определение. Блочно-диагональная матрица, на диагонали которой стоят жордановы клетки, называется жордановой матрицей:
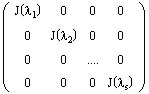 (2.2)
(2.2)
Пример
Ниже представлена жорданова матрица, состоящая из трех жордановых клеток:
— размера 1, отвечающая собственному значению l1=3;
— размера 2, отвечающая собственному значению l2=4;
— размера 3, отвечающая собственному значению l3=5.
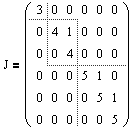
Количество и размер жордановых клеток
Пусть А — матрица, которую нужно привести к жордановой форме, lj (k=1. mj) — собственные значения этой матрицы.
Количество жордановых клеток размера k, отвечающих собственному значению lj, определяется следующим образом:
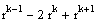 (3.1)
(3.1) 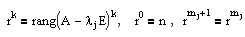 (3.2)
(3.2)
Пример
Пусть дана матрица преобразования:
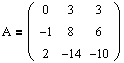
Найдем количество и размер жордановых клеток, соответствующих каждому собственному значению этого преобразования.
Как искать собственные значения, было подробно рассказано в первом параграфе учебника. Поэтому опустим все расчеты, а сразу укажем собственные числа матрицы А: l1=0 кратности m1=1 и l2=-1 кратности m2=2.
Используя соотношения (3.1) и (3.2), найдем количество и размер жордановых клеток, соответствующих l1=0, m1=1.
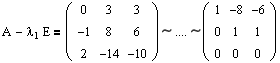
Очевидно, что rang(A-l1E)=2 и, соответственно, r 1 =r 2 =rang(A-l1E) 1 =2, r 0 =n=3.
Количество жордановых клеток размера 1 будет равно: r 0 -2r 1 +r 2 =3-2*2+2=1.
Ясно, что других клеток для этого собственного значения нет. Т.о., для l1=0, m1=1 мы имеем единственную жорданову клетку вида J1(0)=(0).
Далее аналогичным образом определяем клетки для второго собственного значения l2=-1 кратности m2=2.
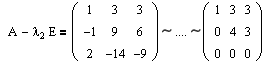
Очевидно, что rang(A-l2E)=2 и, соответственно, r 1 =r 2 =rang(A-l2E) 1 =2.
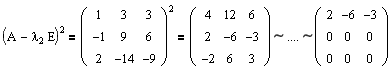
Т.е. rang(A-l1E) 2 =1 и, соответственно, r 1 =r 2 =rang(A-l1E) 2 =1.
Теперь можно определить количество и размер жордановых клеток для второго собственного значения:
— размера 1: r 0 -2r 1 +r 2 =3-2*2+1=0;
— размера 2: r 1 -2r 2 +r 3 =2-2*1+1=1.
Таким образом, для l2=-1 мы получили одну клетку размера 2:
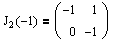
Соответственно, жорданова форма для исходной матрицы А будет иметь вид:
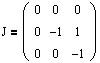
Жорданов базис
Пусть матрица А приведена к жордановой форме J. Рассмотрим систему HJ=AH, где
— матрица перехода от исходного базиса (e) к жорданову базису (h). Это система матричных n 2 уравнений с n 2 неизвестными.
Определение. Пусть e – собственный вектор преобразования А, т.е. имеет место равенство А(e) = le. Вектор e1, удовлетворяющий равенству
называется присоединенным вектором первого порядка;
вектор e2, удовлетворяющий равенству
— присоединенным вектором второго порядка;
вектор en, удовлетворяющий равенству
— присоединенным вектором n-ого порядка.
Заметим также, что
(А-lе) k ek=e. (4.5)
Алгоритм нахождения векторов жорданова базиса
Чтобы найти жорданов базис, необходимо проделать следующие действия для каждой жордановой клетки.
Рассмотрим жорданову клетку порядка k, отвечающую собственному значению l. Для нее ищутся вектора жорданова базиса:
h, h 1 , h 2 , . h k-1 , где:
h — собственный вектор, отвечающий собственному значению l;
h 1 — присоединенный вектор 1-ого порядка;
h 2 — присоединенный вектор 2-ого порядка;
h k-1 — присоединенный вектор (k-1)-ого порядка;
Эта совокупность векторов ищется, используя следующую систему:
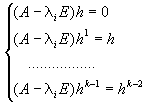 (4.6)
(4.6)
В результате применения этих операций ко всем жордановым клеткам, получим векторы, составляющие жорданов базис:
h, h 1 , h 2 , . h k-1 , f, f 1 , f 2 , . f p-1 .
Векторам h соответствует жорданова клетка размера k, векторам f – размера p и т.д.
ex3
Пример
Вернемся к примеру, рассмотренному в прошлом разделе. Там нами были получены две жордановы клетки:
J1(0)=(0) и 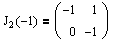
Рассмотрим первую, J1(0).
С помощью соотношения (1.5) из первого параграфа найдем собственный вектор, отвечающий собственному значению l1=0:
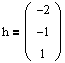
Присоединенных векторов для данной жордановой клетки, очевидно, нет.
Теперь рассмотрим вторую жорданову клетку, J2(-1). Очевидно, что для нее надо найти один собственный вектор и один присоединенный.
Используя систему (4.6), получим эти векторы:
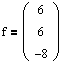 — собственный вектор, отвечающий l2=-1;
— собственный вектор, отвечающий l2=-1;
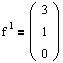 — присоединенный вектор.
— присоединенный вектор.
Мы получили все векторы, составляющие матрицу Н. Таким образом, матрица перехода к жорданову базису будет иметь следующий вид:
Как найти собственные вектора в заданном базисе
Найдем такие вектора (называются собственными векторами) v
и такие числа – значения (называются собственными значениями) l
матрицы A, для v, l и A выполняется:
A*v = l*v.
Также вычисляется кратность собственных значений и находит характеристическое уравнение матрицы.
© Контрольная работа РУ – калькуляторы онлайн
Где учитесь?
Для правильного составления решения, укажите:
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/nayti-bazis-sobstvennyh-vektorov
http://www.kontrolnaya-rabota.ru/s/matrix/sobstvennyie/
[/spoiler]
Собственные
векторы и собственные
значения
линейного оператора
Определение 1.
Собственным
вектором оператора
![]()
называют
ненулевой вектор
![]() ,
,
удовлетворяющий равенству:
![]() =
=![]() .
.
Определение 2.
Собственным
значением оператора
![]()
называют
число
![]() ,
,
для которого выполняется равенство:
![]() =
=![]() ,
,
где
![]()
– ненулевой вектор.
|
|
(1) |
|
|
(2) |
Решив последнее
уравнение относительно
![]() ,
,
найдем собственные значения матрицы.
Уравнение (5.8) называют характеристическим
уравнением матрицы
![]() .
.
Найдя корни характеристического
уравнения, последовательно подставляя
их в систему (1) и решая получаемые
системы, найдем собственные векторы
матрицы
![]() ,
,
каждый из которых соответствует
определенному собственному значению.
Рассмотрим несколько
примеров, в каждом из которых будем
выполнять последовательность действий
решения задачи об отыскании собственных
значений и собственных векторов матрицы.
Пример 1.
Найти собственные
значения и собственные векторы матрицы
![]() .
.
Дать геометрическую интерпретацию
полученного решения.
Решение
-
Матрица имеет
размерность 2 2,
2,
то есть является представлением
линейного оператора в пространстве
 .
.
Собственный вектор матрицы будем искать
в виде:
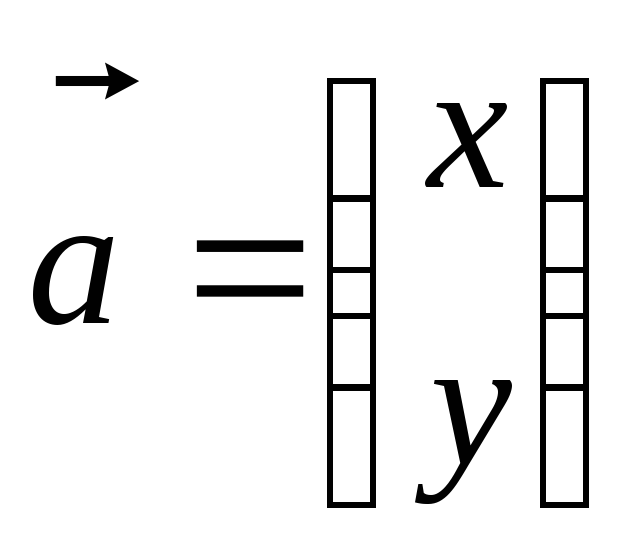 .
. -
Составим уравнение
для отыскания собственных векторов в
матричном виде:
![]()
![]()
![]()
![]()
![]()
3. Перепишем
матричное уравнение в виде системы
уравнений:
![]()
-
Однородная система
имеет ненулевые решения тогда и только
тогда, когда определитель ее главной
матрицы равен 0. Получаем характеристическое
уравнение системы и решаем его:
![]()
![]()
![]()
![]() .
.
Собственные
значения матрицы
![]() :
:
![]() ,
,
![]() .
.
-
Найдем собственные
векторы для каждого собственного
значения:
|
Пусть
|
Пусть
|
П ример
ример
2. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=![]() .
.
-
Составим и решим
характеристическое уравнение
 .
.
В нашей задаче
![]() .
.
Тогда характеристическое
уравнение принимает вид:
![]() ,
,
или
![]() ,
,
![]() ,
,
![]() ,
,
![]()
– собственные
значения линейного оператора.
-
Найдем собственные
векторы, соответствующие собственному
значению
 ,
,
решая матричное уравнение:
![]() х=0
х=0
или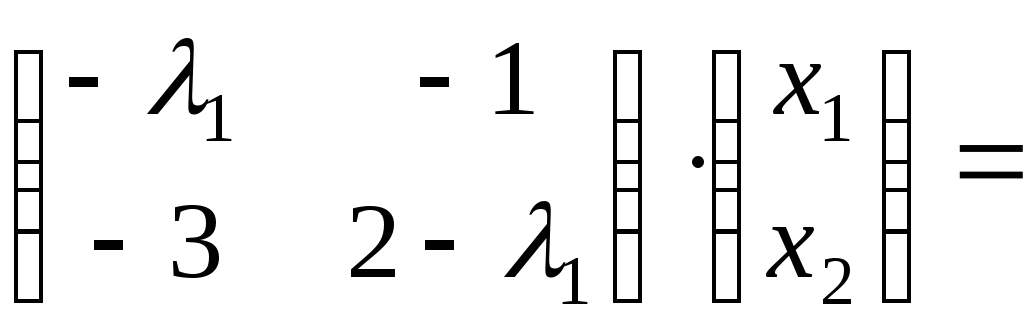
 ,
,
т.е.

![]()
![]() .
.
Полагая в последнем
равенстве
![]() ,
,
получим
![]() .
.
Откуда собственные
векторы, соответствующие собственному
значению
![]() ,
,
имеют вид х1=![]() .
.
-
Найдем собственные
векторы, соответствующие собственному
значению
 ,
,
решая матричное уравнение:
![]() х=0
х=0
или
 ,
,
т.е.

![]()
.
Полагая в последнем
равенстве
![]() ,
,
получим
![]() .
.
Откуда собственные
векторы, соответствующие собственному
значению
![]() ,
,
имеют вид х2=![]() .
.
Ответ. Собственному
значению![]()
соответствуют собственные векторы
х1=![]() ,
,
а собственному значению![]()
собственные векторы
х 2=
2=![]() .
.
П ример
ример
3. Найти собственные значения и
собственные векторы линейного оператора
, заданного в некотором базисе матрицей
А=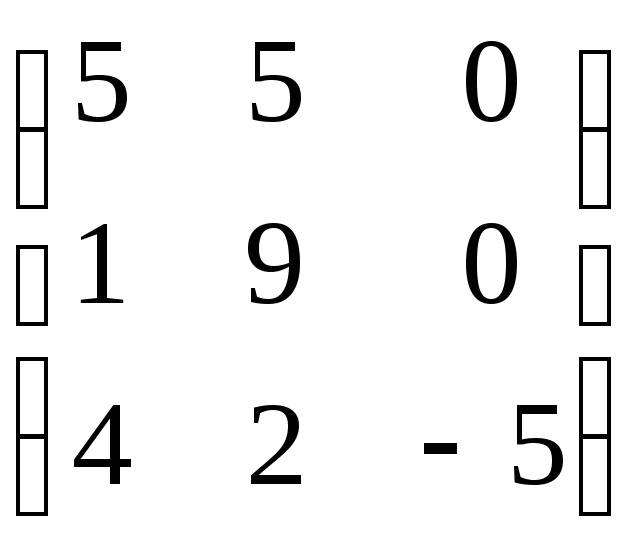 .
.
-
Найдем собственные
значения линейного оператора. Для этого
составим характеристическое уравнение
и найдем его корни:
 .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
– собственные значения линейного
оператора.
-
Найдем собственные
векторы, соответствующие собственному
значению
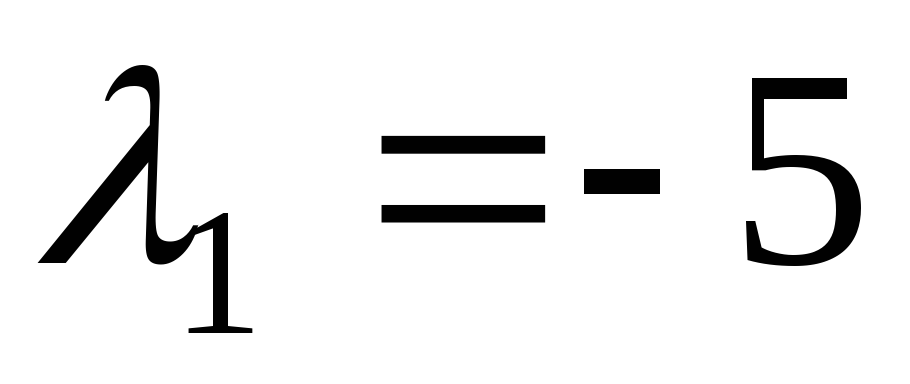 .
.
Исходя из соотношения
 х=0
х=0
или в нашем случае
 ,
,
запишем систему:
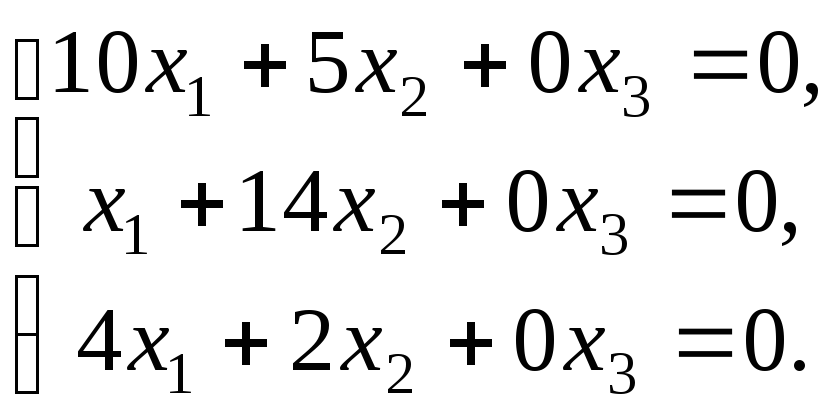
Решая методом
Гаусса, получаем

Поскольку ранг
матрицы системы (r=2)
меньше количества неизвестных, то
система имеет бесконечное множество
решений. Записывая преобразованную
систему и решая ее, получим
![]() ,
,
![]() .
.
Таким образом,
собственные векторы, соответствующие
собственному значению
![]() ,
,
имеют вид: Х1=![]() .
.
-
Найдем собственные
векторы, соответствующие собственному
значению
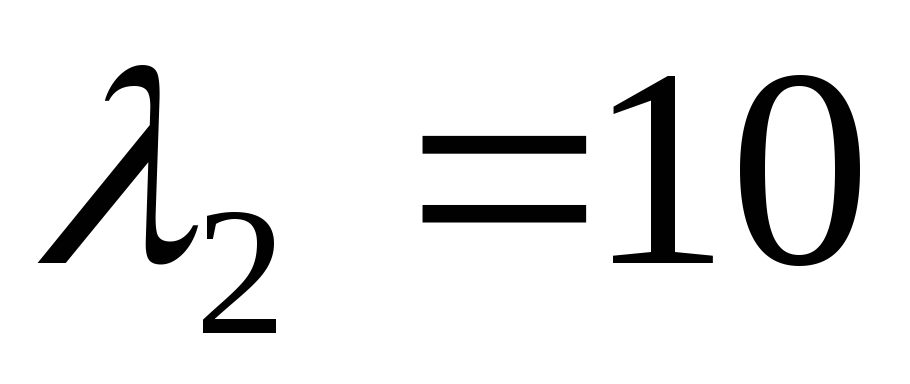 .
.
Исходя из соотношения
 х=0
х=0
или в нашем случае
 ,
,
т.е.

Решая методом
Гаусса, получаем

откуда, система
принимает вид

Полагая
![]() ,
,
получим
![]() .
.
Таким образом,
собственные векторы, соответствующие
собственному значению
![]() ,
,
имеют вид: Х2= .
.
-
Найдем собственные
векторы, соответствующие собственному
значению
 .
.
Исходя из соотношения
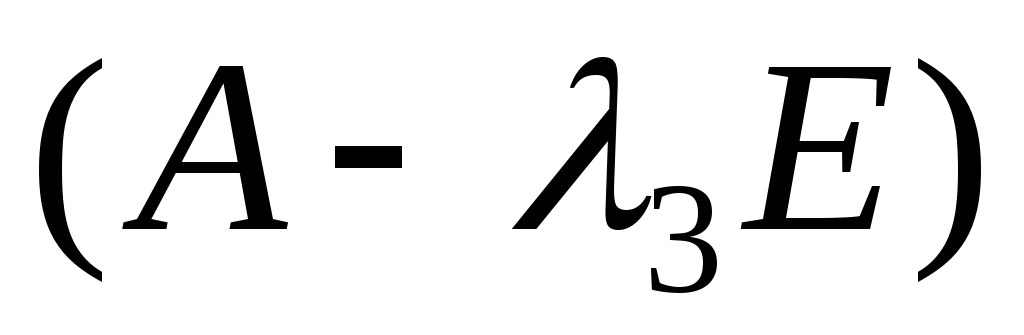 х=0
х=0
или в нашем случае
 ,
,
т.е.

Решая методом
Гаусса, получаем
 ,
,
откуда, система
принимает вид

Полагая
![]() ,
,
получим
![]() .
.
Т аким
аким
образом, собственные векторы,
соответствующие собственному значению
![]() ,
,
имеют вид: Х3= .
.
Соседние файлы в папке Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
Собственные числа и собственные векторы линейного оператора
Наиболее просто устроены матрицы диагонального вида  . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.
. Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.
Пусть дано линейное пространство Rn и действующий в нем линейный оператор A; в этом случае оператор A переводит Rn в себя, то есть A:Rn
→ Rn.
Определение. Ненулевой вектор x называется собственным вектором оператора A, если оператор A переводит x в коллинеарный ему вектор, то есть A·x = λ·x. Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x.
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x1, x2, …, xm оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x1, x2, …, xm оператора A с попарно различными собственными числами λ1, λ2, …, λm
линейно независимы.
3. Если собственные числа λ1=λ2= λm= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.
Итак, если имеется n линейно независимых собственных векторов x1, x2, …, xn, соответствующих различным собственным числам λ1, λ2, …, λn, то они линейно независимы, следовательно, их можно принять за базис пространства Rn. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 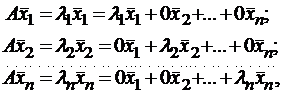 тогда
тогда  .
.
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.
Теорема. Матрица линейного оператора A в базисе {εi} (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса – собственные векторы оператора A.
Правило отыскания собственных чисел и собственных векторов
Пусть дан вектор x=(x1, x2, …, xn), где x1, x2, …, xn – координаты вектора x относительно базиса {ε1, ε2, …, εn} и x – собственный вектор линейного оператора A, соответствующий собственному числу λ, то есть A·x=λ·x. Это соотношение можно записать в матричной форме
x·(A-λ·E). (*)
Уравнение (*) можно рассматривать как уравнение для отыскания x, причем x ≠ 0, то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A – λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A – λE) = 0.
Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:
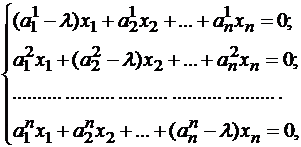 (1)
(1)
где  – матрица линейного оператора.
– матрица линейного оператора.
Система (1) имеет ненулевое решение, если ее определитель D равен нулю
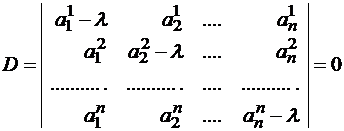
Получили уравнение для нахождения собственных чисел.
Это уравнение называется характеристическим уравнением, а его левая часть – характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду.
Пусть λ1, λ2, …, λn – вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.
Пример №1. Линейный оператор A действует в R3 по закону A·x=(x1-3x2+4x3, 4x1-7x2+8x3, 6x1-7x2+7x3), где x1, x2, .., xn – координаты вектора x в базисе e1=(1,0,0), e2=(0,1,0), e3=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A·e1=(1,4,6)
A·e2=(-3,-7,-7)
A·e3=(4,8,7)
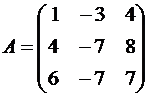 .
.
Составляем систему для определения координат собственных векторов:
(1-λ)x1-3x2+4x3=0
x1-(7+λ)x2+8x3=0
x1-7x2+(7-λ)x3=0
Составляем характеристическое уравнение и решаем его:
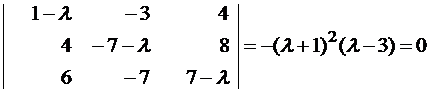
λ1,2 = -1, λ3 = 3.
Подставляя λ = -1 в систему, имеем:
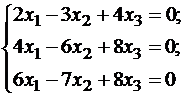 или
или 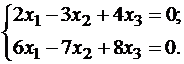
Так как 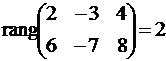 , то зависимых переменных два, а свободное одно.
, то зависимых переменных два, а свободное одно.
Пусть x1 – свободное неизвестное, тогда 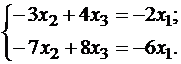 Решаем эту систему любым способом и находим общее решение этой системы:
Решаем эту систему любым способом и находим общее решение этой системы:  Фундаментальная система решений состоит из одного решения, так как n – r = 3 – 2 = 1.
Фундаментальная система решений состоит из одного решения, так как n – r = 3 – 2 = 1.
Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: (x1, 2x1, x1)=x1(1,2,1), где x1 – любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x1 = 1: x1=(1,2,1).
Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: x2=(1,2,2).
В пространстве R3 базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R3 составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем.
Пример №2. Дана матрица  .
.
1. Доказать, что вектор x=(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение находим с помощью калькулятора.
1. Если A·x=λ·x, то x – собственный вектор

Вектор (1, 8, -1) – собственный вектор. Собственное число λ = -1.
Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.
Собственные векторы ищем из системы:
(2-λ)x1+3x3=0;
10x1-(3+λ)x2-6x3=0;
-x1-(2+λ)x3=0;
Характеристическое уравнение:  ;
;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2 – 1) = 0
λ1 = -3, λ2 = 1, λ3 = -1.
Найдем собственный вектор, отвечающий собственному числу λ = -3:
5x1+3x3=0;
10x1-6x3=0;
-x1+x3=0;
Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x1 = x3 = 0. x2 здесь может быть любым, отличным от нуля, например, x2 = 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим:

Если λ = 1, то получаем систему 
Ранг матрицы равен двум. Последнее уравнение вычеркиваем.
Пусть x3 – свободное неизвестное. Тогда x1 = -3x3, 4x2 = 10x1 – 6x3 = -30x3 – 6x3, x2 = -9x3.
Полагая x3 = 1, имеем (-3,-9,1) – собственный вектор, отвечающий собственному числу λ = 1. Проверка:

Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R3. Таким образом, в базисе f1=(1,8,-1), f2=(0,1,0), f3=(-3,-9,1) матрица A имеет вид:
 .
.
Не всякую матрицу линейного оператора A:Rn→ Rn можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов.
Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой aik=aki.
Замечания.
- Все собственные числа симметрической матрицы вещественны.
- Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.
Перейти к онлайн решению своей задачи
Задание 1. Линейный оператор ![]() преобразует векторы
преобразует векторы ![]() ,
, ![]() ,
, ![]() в векторы
в векторы ![]() ,
, ![]() ,
, ![]() . Найти матрицу
. Найти матрицу ![]() линейного оператора.
линейного оператора.
Решение. Матрицы
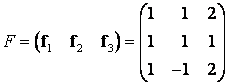 ,
, 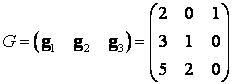 и
и ![]()
Связаны между собой соотношением ![]() , откуда
, откуда ![]() .
.
Так как ![]() , то
, то 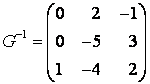 , а искомая матрица линейного оператора
, а искомая матрица линейного оператора 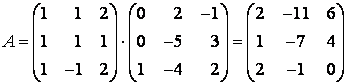 .
.
Ответ: .
Задание 2. Пусть линейный оператор ![]() в базисе
в базисе ![]() задан матрицей
задан матрицей 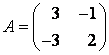 . Найти матрицу
. Найти матрицу ![]() этого линейного оператора в базисе
этого линейного оператора в базисе ![]() , если матрица
, если матрица 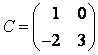 является матрицей перехода от базиса
является матрицей перехода от базиса ![]() к базису
к базису ![]() .
.
Решение. Матрицы ![]() и
и ![]() линейного оператора
линейного оператора ![]() , заданного в разных базисах, связаны между собой соотношением
, заданного в разных базисах, связаны между собой соотношением ![]() . Так как
. Так как 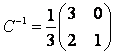 , то
, то
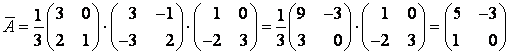 .
.
Ответ: 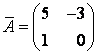 .
.
Задание 3. Линейный оператор ![]() в базисе
в базисе ![]() задан матрицей
задан матрицей 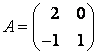 . Найти матрицу
. Найти матрицу ![]() этого линейного оператора в базисе
этого линейного оператора в базисе ![]() , если
, если ![]() ,
, ![]() .
.
Решение. Связь между матрицами ![]() и
и ![]() линейного оператора в разных базисах определяется формулой
линейного оператора в разных базисах определяется формулой ![]() , где
, где ![]() – матрица перехода от базиса
– матрица перехода от базиса ![]() к базису
к базису ![]() .
.
Составим матрицу ![]() :
: 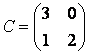 , тогда
, тогда 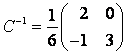 и, следовательно,
и, следовательно,
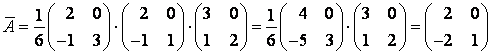 .
.
Ответ: 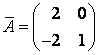 .
.
Задание 4. Линейный оператор ![]() в базисе
в базисе ![]() задан матрицей
задан матрицей  . Найти матрицу
. Найти матрицу ![]() этого линейного оператора в базисе
этого линейного оператора в базисе ![]() , если
, если ![]()
![]() ,
, ![]() .
.
Решение. Матрицы ![]() и
и ![]() связаны между собой соотношением
связаны между собой соотношением ![]() , где
, где ![]() – матрица перехода от базиса
– матрица перехода от базиса ![]() к базису
к базису ![]() .
.
Составим матрицу ![]() :
:  , тогда
, тогда  и, следовательно,
и, следовательно,


Ответ:  .
.
Задание 5. Найти собственные значения и собственные векторы линейного оператора ![]() , заданного в некотором базисе матрицей
, заданного в некотором базисе матрицей 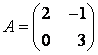 .
.
Решение. Для нахождения собственных значений линейного оператора составим характеристическое уравнение ![]() , т. е.
, т. е. 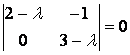 . Раскрывая определитель, получим
. Раскрывая определитель, получим ![]() , т. е.
, т. е. ![]() ,
, ![]() .
.
По определению ![]() называется собственным вектором линейного оператора
называется собственным вектором линейного оператора ![]() , соответствующим собственному значению
, соответствующим собственному значению ![]() , если
, если ![]() .
.
Найдём собственные векторы ![]() и
и ![]() , соответствующие собственным значениям
, соответствующие собственным значениям ![]() и
и ![]() .
.
При ![]() получим:
получим: 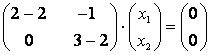 , что равносильно такой однородной системе уравнений:
, что равносильно такой однородной системе уравнений: 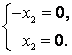
Если ![]() – базисная переменная, а
– базисная переменная, а ![]() – свободная, то
– свободная, то 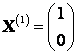 .
.
При ![]() :
: 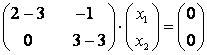 , что равносильно однородной системе уравнений
, что равносильно однородной системе уравнений 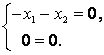
Пусть ![]() – базисная переменная,
– базисная переменная, ![]() – свободная. Примем
– свободная. Примем ![]() , тогда
, тогда ![]() , а следовательно,
, а следовательно,  .
.
Так как собственные векторы соответствуют различным собственным значениям, то они должны быть линейно независимы. Проверим линейную независимость полученных собственных векторов 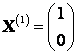 и
и  .
.
Составим матрицу  . Так как
. Так как ![]() , то собственные векторы
, то собственные векторы ![]() и
и ![]() линейно независимы.
линейно независимы.
Ответ: собственные числа ![]() ,
, ![]() ; собственные векторы
; собственные векторы 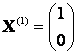 ,
,  .
.
Задание 6. Привести матрицу 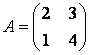 линейного оператора
линейного оператора ![]() к диагональному виду.
к диагональному виду.
Решение. Матрица линейного оператора будет диагональной в базисе из собственных векторов, если такой базис существует. Найдём собственные значения и собственные векторы линейного оператора.
Запишем характеристическое уравнение: 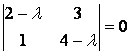 , т. е.
, т. е. ![]() или
или ![]() , откуда получаем
, откуда получаем ![]() ,
, ![]() .
.
Найдём собственные векторы ![]() И
И ![]() .
.
При ![]() получим:
получим:  , что соответствует следующей однородной системе уравнений:
, что соответствует следующей однородной системе уравнений: 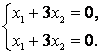
Пусть ![]() – базисная переменная,
– базисная переменная, ![]() – свободная. Полагая
– свободная. Полагая ![]() , получим
, получим 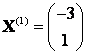 .
.
При ![]() :
: 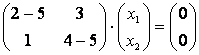 . Соответствующая однородная система уравнений имеет вид:
. Соответствующая однородная система уравнений имеет вид:
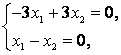
Откуда ![]() . Пусть
. Пусть ![]() – базисная переменная,
– базисная переменная, ![]() – свободная, примем
– свободная, примем ![]() тогда
тогда ![]() , а, следовательно,
, а, следовательно,  .
.
Собственные векторы ![]() и
и ![]() отвечают различным собственным значениям, поэтому они линейно независимы, т. е. могут составить базис. Матрица
отвечают различным собственным значениям, поэтому они линейно независимы, т. е. могут составить базис. Матрица ![]() линейного оператора в базисе из собственных векторов
линейного оператора в базисе из собственных векторов ![]() и
и ![]() имеет диагональный вид:
имеет диагональный вид: 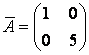 .
.
Можно проверить полученный результат. Так как ![]() , где матрица
, где матрица ![]() в случае перехода к базису из собственных векторов
в случае перехода к базису из собственных векторов 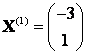 и
и  имеет вид
имеет вид  , следовательно,
, следовательно,
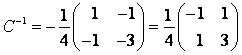 ,
,
Тогда
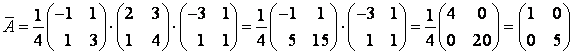 .
.
Ответ: 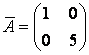 .
.
Задание 7. Найти собственные значения и собственные векторы линейного оператора ![]() , заданного в некотором базисе матрицей
, заданного в некотором базисе матрицей 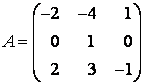 . Построить, если это возможно, базис из собственных векторов и найти матрицу
. Построить, если это возможно, базис из собственных векторов и найти матрицу ![]() этого линейного оператора в базисе из собственных векторов.
этого линейного оператора в базисе из собственных векторов.
Решение. Запишем характеристическое уравнение:
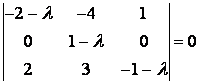 ,
,
Т. е. ![]() ,
, ![]()
![]() , откуда получаем
, откуда получаем ![]() ,
, ![]() ,
, ![]() .
.
Найдём собственные векторы линейного оператора.
При ![]() :
:  , тогда соответствующая однородная система уравнений примет вид:
, тогда соответствующая однородная система уравнений примет вид:
 или
или 
Что равносильно такой системе: 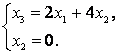
Пусть ![]() и
и ![]() – базисные переменные,
– базисные переменные, ![]() – свободная. Полагая
– свободная. Полагая ![]() , получим
, получим 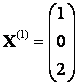 .
.
При ![]() :
: 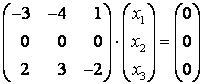 , или, переходя к однородной системе уравнений, получим
, или, переходя к однородной системе уравнений, получим
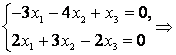
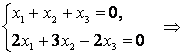
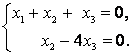
Пусть ![]() и
и ![]() – базисные переменные,
– базисные переменные, ![]() – свободная. Если
– свободная. Если ![]() , то
, то 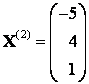 .
.
При ![]() получим:
получим: 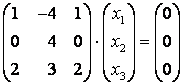 , и однородная система уравнений примет вид:
, и однородная система уравнений примет вид:


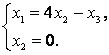
Пусть ![]() и
и ![]() – базисные переменные,
– базисные переменные, ![]() – свободная. Тогда если
– свободная. Тогда если ![]() , то
, то  . Найденные собственные векторы соответствуют различным собственным значениям, поэтому они линейно независимы, значит, существует базис из собственных векторов. Матрица перехода к такому базису
. Найденные собственные векторы соответствуют различным собственным значениям, поэтому они линейно независимы, значит, существует базис из собственных векторов. Матрица перехода к такому базису 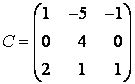 , тогда
, тогда
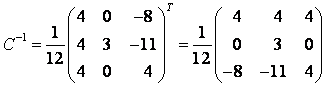 .
.
Матрица ![]() линейного оператора
линейного оператора ![]() в базисе из собственных векторов имеет вид:
в базисе из собственных векторов имеет вид:  .
.
Можно сделать проверку полученных результатов:
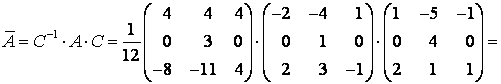

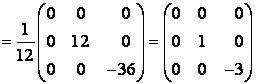 .
.
Ответ: ![]() ,
, ![]() ,
, ![]() ;
; 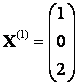 ,
, 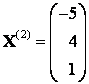 ,
,  ; матрица линейного оператора в базисе из собственных векторов
; матрица линейного оператора в базисе из собственных векторов  .
.
| < Предыдущая | Следующая > |
|---|
Линейные операторы
Собственные вектора и собственные значения линейного оператора
Определение
Самый простой линейный оператор – умножение вектора на число (lambda ). Этот оператор просто растягивает все вектора в (lambda ) раз. Его матричная форма в любом базисе – (diag(lambda ,lambda ,…,lambda )). Фиксируем для определенности базис ({e}) в векторном пространстве (mathit{L}) и рассмотрим линейный оператор с диагональной матричной формой в этом базисе, (alpha = diag(lambda _1,lambda _2,…,lambda _n)). Этот оператор, согласно определению матричной формы, растягивает (e_k) в (lambda _k) раз, т.е. (Ae_k=lambda _ke_k) для всех (k=1,2,…,n). С диагональными матрицами удобно работать, для них просто строится функциональное исчисление: для любой функции (f(x)) можно положить (f(diag(lambda _1,lambda _2,…,lambda _n))=diag(f(lambda _1),f(lambda _2),…,f(lambda _n))). Таким образом возникает естественный вопрос: пусть имеется линейный оператор (A), можно ли выбрать такой базис в векторном пространстве, чтобы матричная форма оператора (A) была диагональной в этом базисе? Этот вопрос приводит к определению собственных чисел и собственных векторов.
Определение.
Пусть для линейного оператора (A) существует ненулевой вектор (u) и число (lambda ) такие, что
[
Au=lambda cdot u. quad quad(59)
]
Тогда вектор (u) называют собственным вектором оператора (A), а число (lambda ) – соответствующим собственным числом оператора (A). Совокупность всех собственных чисел называют спектром линейного оператора (A).
Возникает естественная задача: найти для заданного линейного оператора его собственные числа и соответствующие собственные вектора. Эту задачу называют задачей о спектре линейного оператора.
Уравнение для собственных значений
Фиксируем для определенности базис в векторном пространстве, т.е. будем считать, что он раз и навсегда задан. Тогда, как обсуждалось выше, рассмотрение линейных операторов можно свести к рассмотрению матриц – матричных форм линейных операторов. Уравнение (59) перепишем в виде
[
(alpha -lambda E)u=0.
]
Здесь (E) – единичная матрица, а (alpha) – матричная форма нашего линейного оператора (A). Это соотношение можно трактовать как систему (n) линейных уравнений для (n) неизвестных – координат вектора (u). Причем это однородная система уравнений, и нам следует найти ее нетривиальное решение. Ранее было приведено условие существования такого решения – для этого необходимо и достаточно, чтобы ранг системы был меньше числа неизвестных. Отсюда следует уравнение для собственных чисел:
[
det(alpha -lambda E)=0. quad quad(60)
]
Определение. Уравнение (60) называется характеристическим уравнением для линейного оператора (A).
Опишем свойства этого уравнения и его решений. Если его выписывать в явном виде, получим уравнение вида
[
(-1)^nlambda ^n+…+det(A)=0. quad quad(61)
]
В левой части стоит полином по переменной (lambda ). Такие уравнения называются алгебраическими степени (n). Приведем необходимые сведения об этих уравнениях.
Справка об алгебраических уравнениях.
Основная теорема алгебры.
Уравнение (61) имеет решение на комплексной плоскости (mathbb{C}).
Следствие.
Уравнение (61) имеет на комплексной плоскости столько решений, какова его степень (решения учитываются с учетом кратности).
Пример.
Рассмотрим уравнение
[
lambda (lambda-1)^2(lambda+1)^3=0.
]
Это уравнение 6 степени. Оно имеет следующие решения: ( lambda =0), ( lambda =1), ( lambda =-1), причем кратность первого решения равна 1 (такие решения называют простыми корнями), кратность второго решения равна 2, кратность третьего решения равна 3. Решения, кратность которых выше 1, называют кратными . В нашем случае 1+2+3=6. Уравнения степени (n geq 5) невозможно решить с помощью радикалов (теорема Абеля-Руффини). Для уравнений степени (n=2,3,4) такие явные формулы существуют. Однако на практике уравнения высокой степени можно успешно решать с помощью компьютеров. Таким образом, в дальнейшем будем считать, что мы тем или иным способом построили решения уравнения (61).
Собственные вектора
Рассмотрим вопрос о построении собственного вектора, соответствующего известному собственному числу (lambda _k). Для этого обратимся к уравнению
[
(alpha -lambda_k E)u=0.
]
Это уравнение можно понимать как систему линейных уравнений для координат вектора (u) – собственного вектора, соответствующего собственному числу (lambda _k). При этом данная система имеет нетривиальное решение, так как ранг этой системы меньше числа неизвестных. Решая эту систему методом Гаусса, можно определить координаты вектора (u). Перебирая все значения (lambda _k), (k=1,2,…,n), находим соответствующие собственные вектора (u_k).
Пример. Найдем собственные значения и собственные вектора линейного преобразования, заданного в некотором базисе следующей матрицей:
[
A=left ( begin{array}{ccc}5 & -7 & 0 \-3 & 1 & 0 \12 & 6 & -3 end{array} right ).
]
Матрица (A-lambda E) имеет в данном случае вид:
[
A- lambda E=left ( begin{array}{ccc}5 -lambda & -7 & 0 \-3 & 1-lambda & 0 \12 & 6 & -3 -lambdaend{array} right ).
]
Вычисляем определитель (det(A-lambda E)) и выписываем уравнение на собственные значения:
[
det(A-lambda E)=-(lambda +3)(lambda ^2-6lambda -16)=0.
]
Отсюда находим 3 собственных значения: (lambda _1=-3, lambda _2=8, lambda _3=-2). Мы получили 3 собсвенных значения, все они имеют кратность 1, т.е. это
простые собственные числа. Вычислим соответствующие собственные вектора.
1. Рассмотрим (lambda _1=-3). Соответствующее уравнение для собственного вектора (u=(u_1,u_2,u_3)^T) имеет вид:
[
left( begin{array}{ccc}8 & -7 & 0 \-3 & 4 & 0 \12 & 6 & 0end{array} right) left( begin{array}{c}u_1 \ u_2 \ u_3 end{array} right)=0,
]
где справа стоит нулевой 3-вектор. Эта система уравнений для 3 неизвестных имеет следующее решение: (u=(0,0,1)^T).
2. Рассмотрим (lambda _2=8). Соответствующее уравнение для собственного вектора (u=(u_1,u_2,u_3)^T) имеет вид:
[
left ( begin{array}{ccc}-3 & -7 & 0 \-3 & -7 & 0 \12 & 6 & 5 end{array} right ) left( begin{array}{c}u_1 \ u_2 \ u_3 end{array} right)=0,
]
где справа стоит нулевой 3-вектор. Эта однородная система уравнений для неизвестных (u_1,u_2,u_3) имеет решение: (u=(7, -3, 0)^T).
3. Рассмотрим (lambda _3=-2). Соответствующее уравнение для собственного вектора (u=(u_1,u_2,u_3)^T) имеет вид:
[
left ( begin{array}{ccc}7 & -7 & 0 \-3 & 3 & 0 \12 & 6 & -1 end{array} right ) left( begin{array}{c}u_1 \ u_2 \ u_3 end{array} right)=0,
]
где справа стоит нулевой 3-вектор. Эта однородная система уравнений для неизвестных (u_1,u_2,u_3) имеет решение: (u=(1,1,0)^T).
Теорема.
Пусть все собственные числа линейного оператора (A) – простые. Тогда набор собственных векторов, соответствующих этим собственным числам, образует базис векторного пространства.
Из условий теоремы следует, что все собственные числа оператора (A) различны. Предположим, что набор собственных векторов линейно зависим, так что существуют константы (c_1,c_2,…,c_n), не все из которых нули, удовлетворяющие условию:
[
sum_{k=1}^nc_ku_k=0. quad quad(62)
]
Рассмотрим среди таких формул такую, которая включает минимальное число слагаемых, и подействуем на нее оператором (A). В силу его линейности получаем:
[
Aleft (sum_{k=1}^nc_ku_k right )=sum_{k=1}^nc_kAu_k=sum_{k=1}^nc_klambda _ku_k=0. quad quad(63)
]
Пусть, для определенности, (c_1 neq 0). Умножая (62) на (lambda _1) и вычитая из (63), получим соотношение вида (62), но содержащее на одно слагаемое меньше. Противоречие доказывает теорему.
Итак, в условиях теоремы появляется базис, связанный с данным линейным оператором – базис его собственных векторов. Рассмотрим матричную форму оператора в таком базисе. Как упоминалось выше, (k)-ый столбец этой матрицы – это разложение вектора (Au_k) по базису. Однако по определению (Au_k=lambda _ku_k), так что это разложение (то, что выписано в правой части) содержит только одно слагаемое и построенная матрица оказывается диагональной. В итоге получаем, что в условиях теоремы матричная форма оператора в базисе его собственных векторов равна (diag(lambda _1,lambda _2,…,lambda _n)). Поэтому если необходимо развивать функциональное исчисление для линейного оператора разумно работать в базисе его собственных векторов.
Если же среди собственных чисел линейного оператора есть кратные, описание ситуации становится сложнее и может включать так называемые жордановы клетки. Мы отошлем читателя к более продвинутым руководствам для изучения соответствующих ситуаций.
Найти собственные числа и собственные вектора линейного оператора, заданного в некотором базисе матрицей (A).
1.
[
A=left ( begin{array}{ccc}0 & 1 & 0 \-3 & 4 & 0 \-2 & 1 & 4 end{array} right ).
]
2.
[
A=left ( begin{array}{ccc}-3 & 2 & 0 \-2 & 1 & 0 \15 & -7 & 4 end{array} right ).
]
3.
[
A=left ( begin{array}{ccc}4 & 0 & 5 \ 7 & -2 & 9 \3 & 0 & 6 end{array} right ).
]
4.
[
A=left ( begin{array}{ccc}-1 & -2 & 12 \0 & 4 & 3 \0 & 5 & 6 end{array} right ).
]
|
|
Предыдущий раздел |
|
Назад | Следующий раздел |
|

