Собственные векторы и собственные значения матрицы
Пусть — числовая квадратная матрица n-го порядка. Матрица
называется характеристической для
, а ее определитель
характеристическим многочленом матрицы
(7.12)
Характеристическая матрица — это λ-матрица. Ее можно представить в виде регулярного многочлена первой степени с матричными коэффициентами. Нетрудно заметить, что степень характеристического многочлена равна порядку характеристической матрицы.
Пусть — числовая квадратная матрица n-го порядка. Ненулевой столбец
, удовлетворяющий условию
(7.13)
называется собственным вектором матрицы . Число
в равенстве (7.13) называется собственным значением матрицы
. Говорят, что собственный вектор
соответствует {принадлежит) собственному значению
.
Поставим задачу нахождения собственных значений и собственных векторов матрицы. Определение (7.13) можно записать в виде , где
— единичная матрица n-го порядка. Таким образом, условие (7.13) представляет собой однородную систему
линейных алгебраических уравнений с
неизвестными
(7.14)
Поскольку нас интересуют только нетривиальные решения однородной системы, то определитель матрицы системы должен быть равен нулю:
(7.15)
В противном случае по теореме 5.1 система имеет единственное тривиальное решение. Таким образом, задача нахождения собственных значений матрицы свелась к решению уравнения (7.15), т.е. к отысканию корней характеристического многочлена матрицы
. Уравнение
называется характеристическим уравнением матрицы
. Так как характеристический многочлен имеет n-ю степень, то характеристическое уравнение — это алгебраическое уравнение n-го порядка. Согласно следствию 1 основной теоремы алгебры, характеристический многочлен можно представить в виде
где — корни многочлена кратности
соответственно, причем
. Другими словами, характеристический многочлен имеет п корней, если каждый корень считать столько раз, какова его кратность.
Теорема 7.4 о собственных значениях матрицы. Все корни характеристического многочлена (характеристического уравнения (7-15)) и только они являются собственными значениями матрицы.
Действительно, если число — собственное значение матрицы
, которому соответствует собственный вектор
, то однородная система (7.14) имеет нетривиальное решение, следовательно, матрица системы вырожденная, т.е. число
удовлетворяет характеристическому уравнению (7.15). Наоборот, если
— корень характеристического многочлена, то определитель (7.15) матрицы однородной системы (7.14) равен нулю, т.е.
.В этом случае система имеет бесконечное множество решений, включая ненулевые решения. Поэтому найдется столбец
, удовлетворяющий условию (7.14). Значит,
— собственное значение матрицы
.
Свойства собственных векторов
Пусть — квадратная матрица n-го порядка.
1. Собственные векторы, соответствующие различным собственным значениям, линейно независимы.
В самом деле, пусть и
— собственные векторы, соответствующие собственным значениям
и
, причем
. Составим произвольную линейную комбинацию этих векторов и приравняем ее нулевому столбцу:
(7.16)
Надо показать, что это равенство возможно только в тривиальном случае, когда . Действительно, умножая обе части на матрицу
и подставляя
и
имеем
Прибавляя к последнему равенству равенство (7.16), умноженное на , получаем
Так как и
, делаем вывод, что
. Тогда из (7.16) следует, что и
(поскольку
). Таким образом, собственные векторы
и
линейно независимы. Доказательство для любого конечного числа собственных векторов проводится по индукции.
2. Ненулевая линейная комбинация собственных векторов, соответствующих одному собственному значению, является собственным вектором, соответствующим тому же собственному значению.
Действительно, если собственному значению соответствуют собственные векторы
, то из равенств
, следует, что вектор
также собственный, поскольку:
3. Пусть — присоединенная матрица для характеристической матрицы
. Если
— собственное значение матрицы
, то любой ненулевой столбец матрицы
является собственным вектором, соответствующим собственному значению
.
В самом деле, применяя формулу (7.7) имеем . Подставляя корень
, получаем
. Если
— ненулевой столбец матрицы
, то
. Значит,
— собственный вектор матрицы
.
Замечания 7.5
1. По основной теореме алгебры характеристическое уравнение имеет п в общем случае комплексных корней (с учетом их кратностей). Поэтому собственные значения и собственные векторы имеются у любой квадратной матрицы. Причем собственные значения матрицы определяются однозначно (с учетом их кратности), а собственные векторы — неоднозначно.
2. Чтобы из множества собственных векторов выделить максимальную линейно независимую систему собственных векторов, нужно для всех раз личных собственных значений записать одну за другой системы линейно независимых собственных векторов, в частности, одну за другой фундаментальные системы решений однородных систем
Полученная система собственных векторов будет линейно независимой в силу свойства 1 собственных векторов.
3. Совокупность всех собственных значений матрицы (с учетом их кратностей) называют ее спектром.
4. Спектр матрицы называется простым, если собственные значения матрицы попарно различные (все корни характеристического уравнения простые).
5. Для простого корня характеристического уравнения соответствующий собственный вектор можно найти, раскладывая определитель матрицы
по одной из строк. Тогда ненулевой вектор, компоненты которого равны алгебраическим дополнениям элементов одной из строк матрицы
, является собственным вектором.
Нахождение собственных векторов и собственных значений матрицы
Для нахождения собственных векторов и собственных значений квадратной матрицы n-го порядка надо выполнить следующие действия.
1. Составить характеристический многочлен матрицы .
2. Найти все различные корни характеристического уравнения
(кратности
корней определять не нужно).
3. Для корня найти фундаментальную систему
решений однородной системы уравнений
, где
Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы (см. пункт 3 замечаний 5.3, пункт 1 замечаний 5.5).
4. Записать линейно независимые собственные векторы матрицы , отвечающие собственному значению
(7.17)
где — отличные от нуля произвольные постоянные. Совокупность всех собственных векторов, отвечающих собственному значению
, образуют ненулевые столбцы вида
. Здесь и далее собственные векторы матрицы будем обозначать буквой
.
Повторить пункты 3,4 для остальных собственных значений .
Пример 7.8. Найти собственные значения и собственные векторы матриц:
Решение. Матрица . 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(1). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов второй строки матрицы , то есть
. Умножив этот столбец на (-1), получим
.
3(2). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(2). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , т.е.
. Поделив его на (- 3), получим
.
Матрица . 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(1). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , то есть
. Умножив этот столбец на (-1), получим
.
3(2). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(2). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , т.е.
. Умножив его на (-1), получим
.
Матрица 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду (ведущие элементы выделены полужирным курсивом):
Ранг матрицы системы равен 2 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисные переменные
через свободную
и, полагая
, получаем решение
.
4(1). Все собственные векторы, соответствующие собственному значению , вычисляются по формуле
, где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , то есть
, так как
Разделив его на 3, получим .
3(2). Для собственного значения имеем однородную систему
. Решаем ее методом Гаусса:
Ранг матрицы системы равен единице , следовательно, фундаментальная система решений состоит из двух решений
. Базисную переменную
, выражаем через свободные:
. Задавая стандартные наборы свободных переменных
и
, получаем два решения
4(2). Записываем множество собственных векторов, соответствующих собственному значению , где
— произвольные постоянные, не равные нулю одновременно. В частности, при
получаем
; при
. Присоединяя к этим собственным векторам собственный вектор
, соответствующий собственному значению
(см. пункт 4(1) при
), находим три линейно независимых собственных вектора матрицы
Заметим, что для корня собственный вектор нельзя найти, применяя пункт 5 замечаний 7.5, так как алгебраическое дополнение каждого элемента матрицы
равно нулю.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Нахождение собственных чисел и собственных
векторов матриц
Теорема
19.1 Собственными
числами матрицы
![]() являются
являются
корни уравнения
![]()
и только они.
Доказательство.
Пусть столбец
![]() —
—
собственный вектор матрицы
![]() с
с
собственным числом
![]() .
.
Тогда, по определению,
![]() .
.
Это равенство можно переписать в виде
![]() .
.
Так как для единичной матрицы
![]() выполнено
выполнено
![]() ,
,
то
![]() .
.
По свойству матричного умножения
![]() и
и
предыдущее равенство принимает вид
|
|
(19.4) |
Допустим, что определитель матрицы
![]() отличен
отличен
от нуля,
![]() .
.
Тогда у этой матрицы существует обратная
![]() .
.
Из равенства (19.4)
получим, что
![]() ,
,
что противоречит определению собственного
вектора. Значит, предположение, что
![]() ,
,
неверно, то есть все собственные числа
должны являться корнями уравнения
![]() .
.
Пусть
![]() —
—
корень уравнения
![]() .
.
Тогда базисный минор матрицы
![]() не
не
может совпадать с определителем матрицы
и поэтому
![]() ,
,
![]() —
—
порядок матрицы
![]() .
.
Уравнение (19.4)
является матричной записью однородной
системы линейных уравнений с неизвестными
![]() ,
,
являющимися элементами матрицы-столбца
![]() .
.
По теореме
15.3 число решений в фундаментальной
системе решений равно
![]() ,
,
что больше нуля. Таким образом,
система (19.4)
имеет хотя бы одно ненулевое решение,
то есть числу
![]() соответствует
соответствует
хотя бы один собственный вектор матрицы
![]() .
.
Определитель
![]() является
является
многочленом степени
![]() от
от
переменного
![]() ,
,
так как при вычислении определителя
никаких арифметических действий кроме
сложения, вычитания и умножения выполнять
не приходится.
Определение
19.5 Матрица
![]() называется
называется
характеристической матрицей матрицы
![]() ,
,
многочлен
![]() называется
называется
характеристическим многочленом матрицы
![]() ,
,
уравнение
![]() называется
называется
характеристическим уравнением матрицы
![]() .
.
Пример 19.10
Найдите собственные числа и
собственные векторы матрицы

Решение. Составляем характеристическую
матрицу
![]() :
:

Находим характеристический многочлен

Решим характеристическое уравнение
![]()
Подбором находим, что один корень
уравнения равен
![]() .
.
Есть теорема, которая говорит, что если
число
![]() является
является
корнем многочлена
![]() ,
,
то многочлен
![]() делится
делится
на разность
![]() ,
,
то есть
![]() ,
,
где
![]() —
—
многочлен. В соответствии с этой теоремой
многочлен
![]() должен
должен
делиться на
![]() .
.
Выделим в характеристическом многочлене
этот множитель
![]() :
:

Находим корни трехчлена
![]() .
.
Они равны
![]() и
и
3. Таким образом,
![]()
![]() —
—
корень кратности 2 17.7 b,
![]() —
—
простой корень. Итак, собственные числа
матрицы
![]() равны
равны
![]() ,
,
![]() .
.
Найдем соответствующие им собственные
векторы.
Пусть
![]() ,
,
тогда для собственного вектора
![]() получаем
получаем
матричное уравнение

что соответствует системе уравнений

Решаем ее методом Гаусса (раздел “Алгоритм
нахождения решений произвольной системы
линейных уравнений (метод Гаусса)”).
Выписываем расширенную матрицу системы

Первую строку, умноженную на числа
![]() и
и
![]() прибавляем
прибавляем
соответственно ко второй и третьей
строкам

Меняем местами вторую и третью строки

Возвращаемся к системе уравнений

Базисный минор матрицы
![]() находится
находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальня
система содержит только одно решение.
Переменные
![]() и
и
![]() оставляем
оставляем
в левой части, а переменное
![]() переносим
переносим
в правую часть

Полагаем
![]() ,
,
находим
![]() ,
,
![]() .
.
Итак, собственному числу
![]() соответствует
соответствует
собственный вектор
 .
.
Пусть
![]() ,
,
тогда для собственного вектора
![]() получаем
получаем
матричное уравнение

что соответствует системе уравнений

Решаем ее методом Гаусса. Выписываем
расширенную матрицу

Первую строку умножаем на числа 2 и 3 и
прибавляем соответственно ко второй и
третьей строкам

Вторую строку умножаем на
![]() и
и
прибавляем к третьей

Возвращаемся к системе уравнений

Базисный минор матрицы
![]() находится
находится
в первых двух столбцах и первых двух
строках, ранг равен 2. Поэтому фундаментальная
система содержит только одно решение.
Переменные
![]() и
и
![]() оставляем
оставляем
в левой части, а переменное
![]() переносим
переносим
в правую часть

Полагаем
![]() ,
,
находим
![]() ,
,
![]() .
.
Итак, собственному числу
![]() соответствует
соответствует
собственный вектор
 .
.
Чтобы избавиться от дроби, умножим
собственный вектор на 2, получим
собственный вектор с тем же самым
собственным числом. В итоге собственному
числу
![]() соответствует
соответствует
собственный вектор
 .
.
Ответ: Собственные числа:
![]() ,
,
![]() ,
,
соответствующие собственные векторы:
 ,
,
 .
.
Соседние файлы в папке Анал_Геом
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как найти вектор матрицы
Найдем такие вектора (называются собственными векторами) v
и такие числа – значения (называются собственными значениями) l
матрицы A, для v, l и A выполняется:
A*v = l*v.
Также вычисляется кратность собственных значений и находит характеристическое уравнение матрицы.
© Контрольная работа РУ – калькуляторы онлайн
Где учитесь?
Для правильного составления решения, укажите:
Собственные векторы матрицы
Онлайн калькулятор нахождение собственных чисел и собственных векторов – Собственный вектор — понятие в линейной алгебре, определяемое для квадратной матрицы или произвольного линейного преобразования как вектор, умножение матрицы на который или применение к которому преобразования даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение, называемое собственным числом матрицы или линейного преобразования.
Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.
Содержание
В этом документе собраны основные сведения из алгебры матриц и векторов, которые используются в хемометрике. Приведенный текст не может служить учебником по матричной алгебре — он скорее является конспектом, справочником в этой области. Более глубокое и систематическое изложение может быть найдено в литературе.
Текст разбит на две части названные — “Базовые сведения” и “Дополнительная информация”. В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части — факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls, которая сопровождает этот документ.
Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.
Большинство измерений, проводимых в аналитической химии, являются не прямыми, а косвенными . Это означает, что в эксперименте вместо значения искомого аналита C (концентрации) получается другая величина x (сигнал), связанная, но не равная C, т.е. x (C) ≠ С. Как правило, вид зависимости x (C) не известен, однако, к счастью, в аналитической химии большинство измерений пропорциональны. Это означает, что при увеличении концентрации С в a раз, сигнал X увеличится на столько же., т.е. x ( a C) = a x (C). Кроме того, сигналы еще и аддитивны, так что сигнал от пробы, в которой присутствуют два вещества с концентрациями C 1 и C 2 , будет равен сумме сигналов от каждого компонента, т.е. x (C 1 + C 2 ) = x (C 1 )+ x (C 2 ). Пропорциональность и аддитивность вместе дают линейность . Можно привести много примеров, иллюстрирующих принцип линейности, но достаточно упомянуть два самых ярких примера — хроматографию и спектроскопию. Вторая особенность, присущая эксперименту в аналитической химии — это многоканальность . Современное аналитическое оборудование одновременно измеряет сигналы для многих каналов. Например, измеряется интенсивность пропускания света сразу для нескольких длин волн, т.е. спектр. Поэтому в эксперименте мы имеем дело со множеством сигналов x 1 , x 2 . x n , характеризующих набор концентраций C 1 ,C 2 , . C m веществ, присутствующих в изучаемой системе.
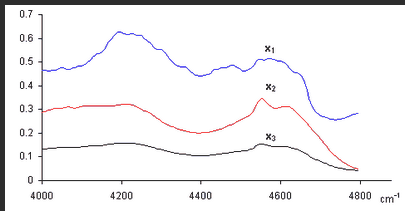
Итак, аналитический эксперимент характеризуется линейностью и многомерностью. Поэтому удобно рассматривать экспериментальные данные как векторы и матрицы и манипулировать с ними, используя аппарат матричной алгебры. Плодотворность такого подхода иллюстрирует пример, показанный на Рис. 1, где представлены три спектра, снятые для 200 длин волн от 4000 до 4796 cm −1 . Первый ( x 1 ) и второй ( x 2 ) спектры получены для стандартных образцов, в которых концентрация двух веществ A и B, известны: в первом образце [A] = 0.5, [B] = 0.1, а во втором образце [A] = 0.2, [B] = 0.6. Что можно сказать о новом, неизвестном образце, спектр которого обозначен x 3 ?
Рассмотрим три экспериментальных спектра x 1 , x 2 и x 3 как три вектора размерности 200. Средствами линейной алгебры можно легко показать, что x 3 = 0.1 x 1 +0.3 x 2 , поэтому в третьем образце очевидно присутствуют только вещества A и B в концентрациях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 и [B] = 0.1×0.1 + 0.6×0.3 = 0.19.
1. Базовые сведения
1.1 Матрицы
Матрицей называется прямоугольная таблица чисел, например
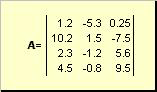
Матрицы обозначаются заглавными полужирными буквами ( A ), а их элементы — соответствующими строчными буквами с индексами, т.е. a ij . Первый индекс нумерует строки, а второй — столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как < a ij , i = 1. I ; j = 1. J >. Для приведенной в примере матрицы I = 4, J = 3 и a 23 = −7.5.
Пара чисел I и J называется размерностью матрицы и обознается как I × J . Примером матрицы в хемометрике может служить набор спектров, полученный для I образцов на J длинах волн.
1.2. Простейшие операции с матрицами
Матрицы можно умножать на числа. При этом каждый элемент умножается на это число. Например —

Рис. 3 Умножение матрицы на число
Две матрицы одинаковой размерности можно поэлементно складывать и вычитать. Например,
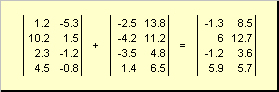
Рис. 4 Сложение матриц
В результате умножения на число и сложения получается матрица той же размерности.
Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O . Очевидно, что A + O = A , A − A = O и 0 A = O .
Матрицу можно транспонировать . При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A ‘ или индексом A t . Таким образом, если A = < a ij , i = 1. I ; j = 1. J >, то A t = < a ji , j = 1. J ; i = 1. I >. Например

Рис. 5 Транспонирование матрицы
Очевидно, что ( A t ) t = A , ( A + B ) t = A t + B t .
1.3. Умножение матриц
Матрицы можно перемножать, но только в том случае, когда они имеют соответствующие размерности. Почему это так, будет ясно из определения. Произведением матрицы A , размерностью I × K , и матрицы B , размерностью K × J , называется матрица C , размерностью I × J , элементами которой являются числа
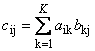
Таким образом для произведения AB необходимо, чтобы число столбцов в левой матрице A было равно числу строк в правой матрице B . Пример произведения матриц —
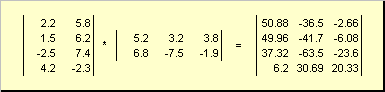
Рис.6 Произведение матриц
Правило перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C , стоящий на пересечении i -ой строки и j -ого столбца ( c ij ) надо поэлементно перемножить i -ую строку первой матрицы A на j -ый столбец второй матрицы B и сложить все результаты. Так в показанном примере, элемент из третьей строки и второго столбца, получается как сумма поэлементных произведений третьей строки A и второго столбца B
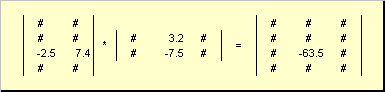
Рис.7 Элемент произведения матриц
Произведение матриц зависит от порядка, т.е. AB ≠ BA , хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = ( AB ) C = A ( BC ). Кроме того, оно еще и дистрибутивно, т.е. A ( B + C ) = AB + AC . Очевидно, что AO = O .
1.4. Квадратные матрицы
Если число столбцов матрицы равно числу ее строк ( I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.
Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.
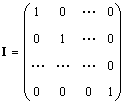
Очевидно AI = IA = A .
Матрица называется диагональной , если все ее элементы, кроме диагональных ( a ii ) равны нулю. Например
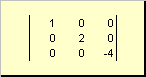
Рис. 8 Диагональная матрица
Матрица A называется верхней треугольной , если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a ij = 0, при i > j . Например

Рис. 9 Верхняя треугольная матрица
Аналогично определяется и нижняя треугольная матрица.
Матрица A называется симметричной , если A t = A . Иными словами a ij = a ji . Например

Рис. 10 Симметричная матрица
Матрица A называется ортогональной , если
Матрица называется нормальной если
1.5. След и определитель
Следом квадратной матрицы A (обозначается Tr( A ) или Sp( A )) называется сумма ее диагональных элементов,
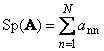

Рис. 11 След матрицы
Sp(α A ) = α Sp( A ) и
Sp( A + B ) = Sp( A )+ Sp( B ).
Можно показать, что
Sp( A ) = Sp( A t ), Sp( I ) = N ,
Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det( A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда
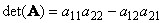
Для матрицы (3×3) определитель будет равен
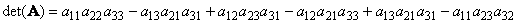
В случае матрицы ( N × N ) определитель вычисляется как сумма 1·2·3· . · N = N ! слагаемых, каждый из которых равен
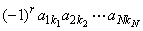
Индексы k 1 , k 2 . k N определяются как всевозможные упорядоченные перестановки r чисел в наборе (1, 2, . , N ). Вычисление определителя матрицы — это сложная процедура, которую на практике осуществляется с помощью специальных программ. Например,

Рис. 12 Определитель матрицы
Отметим только очевидные свойства:
det( I ) = 1, det( A ) = det( A t ),
det( AB ) = det( A )det( B ).
1.6. Векторы
Если матрица состоит только из одного столбца ( J = 1), то такой объект называется вектором . Точнее говоря, вектором-столбцом. Например
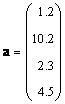
Можно рассматривать и матрицы, состоящие из одной строки, например
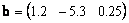
Этот объект также является вектором, но вектором-строкой . При анализе данных важно понимать, с какими векторами мы имеем дело — со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.
Размерностью вектора называется число его элементов.
Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.
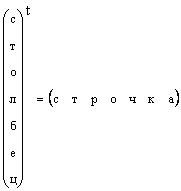
В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0 .
1.7. Простейшие операции с векторами
Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,

Рис. 13 Операции с векторами
Два вектора x и y называются колинеарными , если существует такое число α, что
1.8. Произведения векторов
Два вектора одинаковой размерности N можно перемножить. Пусть имеются два вектора x = ( x 1 , x 2 . x N ) t и y = ( y 1 , y 2 . y N ) t . Руководствуясь правилом перемножения “строка на столбец”, мы можем составить из них два произведения: x t y и xy t . Первое произведение
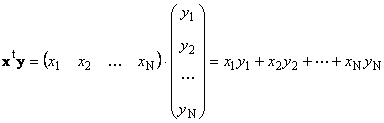
называется скалярным или внутренним . Его результат — это число. Для него также используется обозначение ( x , y ) = x t y . Например,
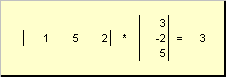
Рис. 14 Внутреннее (скалярное) произведение
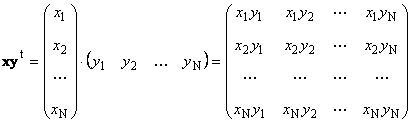
называется внешним . Его результат — это матрица размерности ( N × N ). Например,
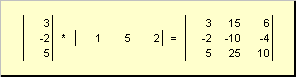
Рис. 15 Внешнее произведение
Векторы, скалярное произведение которых равно нулю, называются ортогональными .
1.9. Норма вектора
Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина
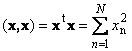
определяет квадрат длины вектора x . Для обозначения длины (называемой также нормой вектора) используется обозначение
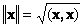
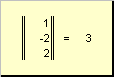
Рис. 16 Норма вектора
Вектор единичной длины (|| x || = 1) называется нормированным. Ненулевой вектор ( x ≠ 0 ) можно нормировать, разделив его на длину, т.е. x = || x || ( x/ || x ||) = || x || e . Здесь e = x/ || x || — нормированный вектор.
Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.
1.10. Угол между векторами
Скалярное произведение определяет и угол φ между двумя векторами x и y
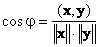
Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.
1.11. Векторное представление матрицы
Каждую матрицу A размера I × J можно представить как набор векторов
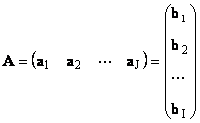
Здесь каждый вектор a j является j -ым столбцом, а вектор-строка b i является i -ой строкой матрицы A
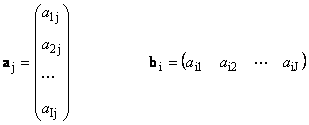
1.12. Линейно зависимые векторы
Векторы одинаковой размерности ( N ) можно складывать и умножать на число, также как матрицы. В результате получится вектор той же размерности. Пусть имеется несколько векторов одной размерности x 1 , x 2 . x K и столько же чисел α α 1 , α 2 . α K . Вектор
y = α 1 x 1 + α 2 x 2 +. + α K x K
называется линейной комбинацией векторов x k .
Если существуют такие ненулевые числа α k ≠ 0, k = 1. K , что y = 0 , то такой набор векторов x k называется линейно зависимым . В противном случае векторы называются линейно независимыми. Например, векторы x 1 = (2, 2) t и x 2 = (−1, −1) t линейно зависимы, т.к. x 1 +2 x 2 = 0
1.13. Ранг матрицы
Рассмотрим набор из K векторов x 1 , x 2 . x K размерности N . Рангом этой системы векторов называется максимальное число линейно-независимых векторов. Например в наборе
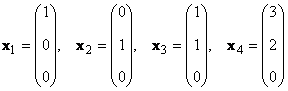
имеются только два линейно независимых вектора, например x 1 и x 2 , поэтому ее ранг равен 2.
Очевидно, что если векторов в наборе больше, чем их размерность ( K > N ), то они обязательно линейно зависимы.
Рангом матрицы (обозначается rank( A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.
rank( A ) = rank( A t ).
1.14. Обратная матрица
Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1 , определяемую условиями
Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является
det( A ) ≠ 0 или rank( A ) = N .
Обращение матрицы — это сложная процедура, для выполнения которой существуют специальные программы. Например,

Рис. 17 Обращение матрицы
Приведем формулы для простейшего случая — матрицы 2×2
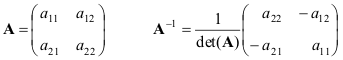
Если матрицы A и B невырождены, то
1.15. Псевдообратная матрица
Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A + , что
Псевдобратная матрица — не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза.
Если число столбцов меньше числа строк, то
A + =(A t A) −1 A t

Рис. 1 7a Псевдообращение матрицы
Если же число столбцов больше числа строк, то
A + =A t (AA t ) −1
1.16. Умножение вектора на матрицу
Вектор x можно умножать на матрицу A подходящей размерности. При этом вектор-столбец умножается справа Ax , а вектор строка — слева x t A . Если размерность вектора J , а размерность матрицы I × J то в результате получится вектор размерности I . Например,

Рис. 18 Умножение вектора на матрицу
Если матрица A — квадратная ( I × I ), то вектор y = Ax имеет ту же размерность, что и x . Очевидно, что
A (α 1 x 1 + α 2 x 2 ) = α 1 Ax 1 + α 2 Ax 2 .
Поэтому матрицы можно рассматривать как линейные преобразования векторов. В частности Ix = x , Ox = 0 .
2. Дополнительная информация
2.1. Системы линейных уравнений
Пусть A — матрица размером I × J , а b — вектор размерности J . Рассмотрим уравнение
относительно вектора x , размерности I . По сути — это система из I линейных уравнений с J неизвестными x 1 . x J . Решение существует в том, и только в том случае, когда
rank( A ) = rank( B ) = R ,
где B — это расширенная матрица размерности I ×( J+1 ), состоящая из матрицы A , дополненной столбцом b , B = ( A b ). В противном случае уравнения несовместны.
Если R = I = J , то решение единственно
Если R I , то существует множество различных решений, которые можно выразить через линейную комбинацию J − R векторов. Система однородных уравнений Ax = 0 с квадратной матрицей A ( N × N ) имеет нетривиальное решение ( x ≠ 0 ) тогда и только тогда, когда det( A ) = 0. Если R = rank( A ) N , то существуют N − R линейно независимых решений.
2.2. Билинейные и квадратичные формы
Если A — это квадратная матрица , а x и y — вектора соответствующей размерности, то скалярное произведение вида x t Ay называется билинейной формой , определяемой матрицей A . При x = y выражение x t Ax называется квадратичной формой.
2.3. Положительно определенные матрицы
Квадратная матрица A называется положительно определенной, если для любого ненулевого вектора x ≠ 0 ,
Аналогично определяются отрицательно ( x t Ax x t Ax ≥ 0) и неположительно ( x t Ax ≤ 0) определенные матрицы.
2.4. Разложение Холецкого
Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой

Рис. 19 Разложение Холецкого
2.5. Полярное разложение
Пусть A — это невырожденная квадратная матрица размерности N × N . Тогда существует однозначное полярное представление
где S — это неотрицательная симметричная матрица, а R — это ортогональная матрица. Матрицы S и R могут быть определены явно:
S 2 = AA t или S = ( AA t ) ½ и R = S −1 A = ( AA t ) −½ A .
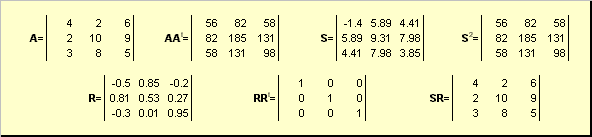
Рис. 20 Полярное разложение
Если матрица A вырождена, то разложение не единственно — а именно: S по-прежнему одна, а вот R может быть много. Полярное разложение представляет матрицу A как комбинацию сжатия/растяжения S и поворота R .
2.6. Собственные векторы и собственные значения
Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A , если
где число λ называется собственным значением матрицы A . Таким образом преобразование, которое выполняет матрица A над вектором v , сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и α v — тоже собственный вектор.
2.7. Собственные значения
У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению
являющемуся алгебраическим уравнением N -го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид
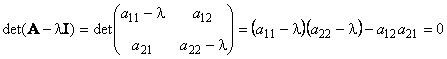

Рис. 21 Собственные значения
Набор собственных значений λ 1 . λ N матрицы A называется спектром A .
Спектр обладает разнообразными свойствами. В частности
det( A ) = λ 1 ×. ×λ N , Sp( A ) = λ 1 +. +λ N .
Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная ( A t = A ), то ее собственные значения вещественны.
2.8. Собственные векторы
У матрицы A , размерностью ( N × N ) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v n нужно решить систему однородных уравнений
Она имеет нетривиальное решение, поскольку det( A − λ n I ) = 0.

Рис. 22 Собственные вектора
Собственные вектора симметричной матрицы ортогональны.
2.9. Эквивалентные и подобные матрицы
Две прямоугольные матрицы A и B одной размерности I × J эквивалентны , если существуют такие квадратные матрицы S , размерности I × I , и T , размерности J × J , что
Эквивалентные матрицы имею один и тот же ранг.
Две прямоугольные матрицы A и B одной размерности N × N подобны , если существует такая невырожденная матрица T , что
Матрица T называется преобразованием подобия.
Подобные матрицы имеют один и тот же ранг, след, определитель и спектр.
2.10. Приведение матрицы к диагональному виду
Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия —
Здесь Λ = diag(λ 1 . λ N ) — это диагональная матрица, элементами которой являются собственные значения матрицы A , а T — это матрица, составленная из соответствующих собственных векторов матрицы A , т.е. T = ( v 1 . v N ).
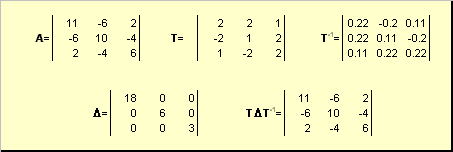
Рис. 23 Приведение к диагональному виду
2.11. Разложение по сингулярным значениям (SVD)
Пусть имеется прямоугольная матрица A размерностью I × J ранга R ( I ≤ J ≤ R ). Ее можно разложить в произведение трех матриц P R ( I × R ), D R ( R × R ) и Q R ( J × R ) —
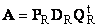
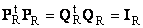 .
.
Здесь P R — матрица, образованная R ортонормированными собственными векторами p r матрицы AA t , соответствующим R наибольшим собственным значениям λ r ;
AA t p r = λ r p r ;
Q R — матрица, образованная R ортонормированными собственными векторами q r матрицы A t A ;
A t Aq r = λ r q r .
D R = diag (σ 1 . σ R ) — положительно определенная диагональная матрица , элементами которой являются σ 1 ≥. ≥σ R ≥0 — сингулярные значения матрицы A , равные квадратным корням из собственных значений матрицы A t A —
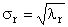
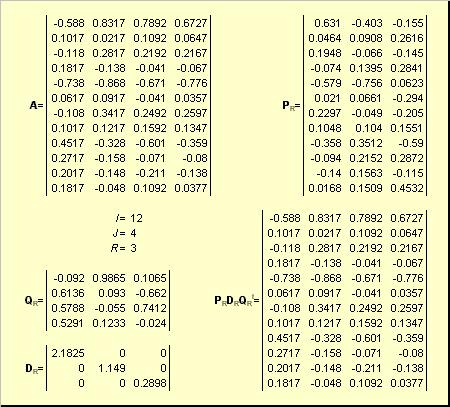
Рис. 24 SVD разложение
Дополняя матрицы P R и Q R ортонормированными столбцами, а матрицу D R нулевыми значениями, можно сконструировать матрицы P ( I × J ), D ( J × J ) и Q ( J × J ) такие, что
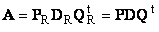
2.12. Линейное пространство
Рассмотрим все возможные векторы размерности N . Это множество называется линейным пространством размерности N и обозначается R N . Так как в R N включены все возможные векторы, то любая линейная комбинация векторов из R N будет также принадлежать этому пространству.
2.13. Базис линейного пространства
Любой набор из N линейно независимых векторов называется базисом в пространстве R N . Простейший пример базиса — это набор векторов
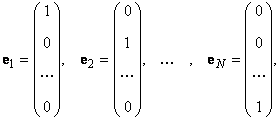
в каждом из которых только один элемент равен 1, а остальные равны нулю. Тогда любой вектор x = ( x 1 , x 2 . x N ) t может быть представлен как линейная комбинация x = x 1 e 1 + x 2 e 2+ . + x N e N базисных векторов.
Базис, составленный из попарно ортогональных векторов, называется ортогональным , а если базисные вектора еще и нормированы, то этот базис называется ортонормированным .
2.14. Геометрическая интерпретация
Линейному пространству можно дать удобную геометрическую интерпретацию. Представим себе N -мерное пространство, в котором базисные вектора задают направления осей координат. Тогда произвольный вектор x = ( x 1 , x 2 . x N ) t можно изобразить точкой в этом пространстве с координатами ( x 1 , x 2 . x N ).
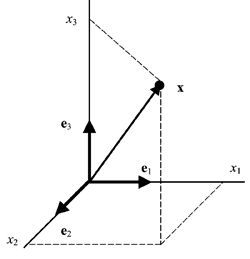
Рис. 25 Координатное пространство
2.15. Множественность базисов
В линейном пространстве могут быть неограниченное число базисов. Так, в пространстве R 3 помимо обычного ортонормированного базиса
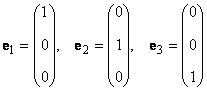
можно установить и другой ортонормированный базис, например
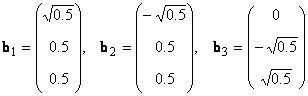
Каждый базис можно представить матрицей B = ( b 1 . b N ), составленной из базисных векторов. Переход от одного базиса к другому осуществляется с помощью невырожденной квадратной матрицы T , т.е. B 2 = TB 1 .
2.16. Подпространство
Пусть имеется набор из K линейно независимых векторов x 1 , x 2 . x K в пространстве R N . Рассмотрим все возможные линейные комбинации этих векторов
x = α 1 x 1 + α 2 x 2 +. + α K x K
О получившимся множестве Q говорят, что оно является линейной оболочкой или что оно натянуто на векторы x 1 , x 2 . x K . По определению линейного пространства это множество Q само является линейным пространством размерности K . При этом оно принадлежит пространству R N , поэтому Q называется линейным подпространством R K в пространстве R N .
2.17. Проекция на подпространство
Рассмотрим подпространство R K , натянутое на векторы X = ( x 1 , x 2 . x K ) в пространстве R N . Матрица базиса X имеет размерность ( N × K ). Любой вектор y из R N может быть спроецирован на подпространство R K , т.е. представлен в виде
где вектор y || принадлежит R K , а вектор y ⊥ ортогонален y || .
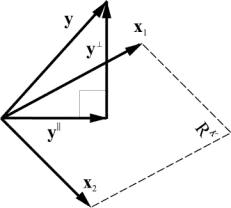
Рис. 26 Проекция на подпространство
Проекцию y || можно представить как результат действия проекционной матрицы P
Проекционная матрица определяется как
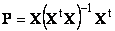
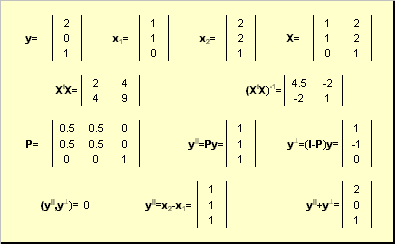
Рис. 27 Проекционное разложение
Заключение
Матричные методы активно используются при анализе данных, в том числе и хемометрическими методами.
[spoiler title=”источники:”]
http://allcalc.ru/node/648
http://rcs.chemometrics.ru/old/Tutorials/matrix.htm
[/spoiler]
Download Article
Download Article
The matrix equation 


Eigenvalues and eigenvectors have immense applications in the physical sciences, especially quantum mechanics, among other fields.
Steps
-

1
Understand determinants. The determinant of a matrix
when
is non-invertible. When this occurs, the null space of
becomes non-trivial – in other words, there are non-zero vectors that satisfy the homogeneous equation
[1]
-

2
Advertisement
-

3
-

4
-

5
Solve the characteristic polynomial for the eigenvalues. This is, in general, a difficult step for finding eigenvalues, as there exists no general solution for quintic functions or higher polynomials. However, we are dealing with a matrix of dimension 2, so the quadratic is easily solved.
-

6
Substitute the eigenvalues into the eigenvalue equation, one by one. Let’s substitute
first.[3]
- The resulting matrix is obviously linearly dependent. We are on the right track here.
-

7
Row-reduce the resulting matrix. With larger matrices, it may not be so obvious that the matrix is linearly dependent, and so we must row-reduce. Here, however, we can immediately perform the row operation
to obtain a row of 0’s.[4]
-

8
Advertisement
Add New Question
-
Question
Why do we replace y with 1 and not any other number while finding eigenvectors?

For simplicity. Eigenvectors are only defined up to a multiplicative constant, so the choice to set the constant equal to 1 is often the simplest.
-
Question
How do you find the eigenvectors of a 3×3 matrix?

Alphabet
Community Answer
First, find the solutions x for det(A – xI) = 0, where I is the identity matrix and x is a variable. The solutions x are your eigenvalues. Let’s say that a, b, c are your eignevalues. Now solve the systems [A – aI | 0], [A – bI | 0], [A – cI | 0]. The basis of the solution sets of these systems are the eigenvectors.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
The determinant of a triangular matrix is easy to find – it is simply the product of the diagonal elements. The eigenvalues are immediately found, and finding eigenvectors for these matrices then becomes much easier.[5]
- Beware, however, that row-reducing to row-echelon form and obtaining a triangular matrix does not give you the eigenvalues, as row-reduction changes the eigenvalues of the matrix in general.
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Thanks to all authors for creating a page that has been read 108,884 times.


