Eigenvalues and eigenvectors
Syntax
Description
example
e = eig(A)
a column vector containing the eigenvalues of square matrix A.
example
[ returns diagonal matrix V,D] =
eig(A)D of
eigenvalues and matrix V whose columns are the
corresponding right eigenvectors, so that A*V = V*D.
example
[ also returns full matrix V,D,W]
= eig(A)W whose
columns are the corresponding left eigenvectors, so that W'*A.
= D*W'
The eigenvalue problem is to determine the solution to the equation Av = λv,
where A is an n-by-n matrix, v is
a column vector of length n, and λ is
a scalar. The values of λ that satisfy the
equation are the eigenvalues. The corresponding values of v that
satisfy the equation are the right eigenvectors. The left eigenvectors, w,
satisfy the equation w’A = λw’.
example
e = eig(A,B)
a column vector containing the generalized eigenvalues of square matrices A and B.
example
[ returnsV,D] =
eig(A,B)
diagonal matrix D of generalized eigenvalues and
full matrix V whose columns are the corresponding
right eigenvectors, so that A*V = B*V*D.
[ alsoV,D,W]
= eig(A,B)
returns full matrix W whose columns are the corresponding
left eigenvectors, so that W'*A = D*W'*B.
The generalized eigenvalue problem is to determine the solution
to the equation Av = λBv,
where A and B are n-by-n matrices, v is
a column vector of length n, and λ is
a scalar. The values of λ that satisfy the
equation are the generalized eigenvalues. The corresponding values
of v are the generalized right eigenvectors. The
left eigenvectors, w, satisfy the equation w’A = λw’B.
[___] = eig(,A,balanceOption)
where balanceOption is 'nobalance',
disables the preliminary balancing step in the algorithm. The default for
balanceOption is 'balance', which
enables balancing. The eig function can return any of the
output arguments in previous syntaxes.
example
[___] = eig(,A,B,algorithm)
where algorithm is 'chol', uses
the Cholesky factorization of B to compute the
generalized eigenvalues. The default for algorithm depends
on the properties of A and B,
but is generally 'qz', which uses the QZ algorithm.
If A is Hermitian and B is
Hermitian positive definite, then the default for algorithm is 'chol'.
example
[___] = eig(___,outputForm)
returns the eigenvalues in the form specified by outputForm
using any of the input or output arguments in previous syntaxes. Specify
outputForm as 'vector' to return the
eigenvalues in a column vector or as 'matrix' to return the
eigenvalues in a diagonal matrix.
Examples
collapse all
Eigenvalues of Matrix
Use gallery to create a symmetric positive definite matrix.
A = 4×4
1.0000 0.5000 0.3333 0.2500
0.5000 1.0000 0.6667 0.5000
0.3333 0.6667 1.0000 0.7500
0.2500 0.5000 0.7500 1.0000
Calculate the eigenvalues of A. The result is a column vector.
e = 4×1
0.2078
0.4078
0.8482
2.5362
Alternatively, use outputForm to return the eigenvalues in a diagonal matrix.
D = 4×4
0.2078 0 0 0
0 0.4078 0 0
0 0 0.8482 0
0 0 0 2.5362
Eigenvalues and Eigenvectors of Matrix
Use gallery to create a circulant matrix.
A = 3×3
1 2 3
3 1 2
2 3 1
Calculate the eigenvalues and right eigenvectors of A.
V = 3×3 complex
-0.5774 + 0.0000i 0.2887 - 0.5000i 0.2887 + 0.5000i
-0.5774 + 0.0000i -0.5774 + 0.0000i -0.5774 + 0.0000i
-0.5774 + 0.0000i 0.2887 + 0.5000i 0.2887 - 0.5000i
D = 3×3 complex
6.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i -1.5000 + 0.8660i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i -1.5000 - 0.8660i
Verify that the results satisfy A*V = V*D.
ans = 3×3 complex
10-14 ×
-0.2665 + 0.0000i -0.0444 + 0.0222i -0.0444 - 0.0222i
0.0888 + 0.0000i 0.0111 + 0.0777i 0.0111 - 0.0777i
-0.0444 + 0.0000i -0.0111 + 0.0833i -0.0111 - 0.0833i
Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then A*V can, at best, approach V*D. In other words, A*V - V*D is close to, but not exactly, 0.
Sorted Eigenvalues and Eigenvectors
By default eig does not always return the eigenvalues and eigenvectors in sorted order. Use the sort function to put the eigenvalues in ascending order and reorder the corresponding eigenvectors.
Calculate the eigenvalues and eigenvectors of a 5-by-5 magic square matrix.
A = 5×5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
V = 5×5
-0.4472 0.0976 -0.6330 0.6780 -0.2619
-0.4472 0.3525 0.5895 0.3223 -0.1732
-0.4472 0.5501 -0.3915 -0.5501 0.3915
-0.4472 -0.3223 0.1732 -0.3525 -0.5895
-0.4472 -0.6780 0.2619 -0.0976 0.6330
D = 5×5
65.0000 0 0 0 0
0 -21.2768 0 0 0
0 0 -13.1263 0 0
0 0 0 21.2768 0
0 0 0 0 13.1263
The eigenvalues of A are on the diagonal of D. However, the eigenvalues are unsorted.
Extract the eigenvalues from the diagonal of D using diag(D), then sort the resulting vector in ascending order. The second output from sort returns a permutation vector of indices.
d = 5×1
-21.2768
-13.1263
13.1263
21.2768
65.0000
Use ind to reorder the diagonal elements of D. Since the eigenvalues in D correspond to the eigenvectors in the columns of V, you must also reorder the columns of V using the same indices.
Ds = 5×5
-21.2768 0 0 0 0
0 -13.1263 0 0 0
0 0 13.1263 0 0
0 0 0 21.2768 0
0 0 0 0 65.0000
Vs = 5×5
0.0976 -0.6330 -0.2619 0.6780 -0.4472
0.3525 0.5895 -0.1732 0.3223 -0.4472
0.5501 -0.3915 0.3915 -0.5501 -0.4472
-0.3223 0.1732 -0.5895 -0.3525 -0.4472
-0.6780 0.2619 0.6330 -0.0976 -0.4472
Both (V,D) and (Vs,Ds) produce the eigenvalue decomposition of A. The results of A*V-V*D and A*Vs-Vs*Ds agree, up to round-off error.
e1 = norm(A*V-V*D); e2 = norm(A*Vs-Vs*Ds); e = abs(e1 - e2)
Left Eigenvectors
Create a 3-by-3 matrix.
A = [1 7 3; 2 9 12; 5 22 7];
Calculate the right eigenvectors, V, the eigenvalues, D, and the left eigenvectors, W.
V = 3×3
-0.2610 -0.9734 0.1891
-0.5870 0.2281 -0.5816
-0.7663 -0.0198 0.7912
D = 3×3
25.5548 0 0
0 -0.5789 0
0 0 -7.9759
W = 3×3
-0.1791 -0.9587 -0.1881
-0.8127 0.0649 -0.7477
-0.5545 0.2768 0.6368
Verify that the results satisfy W'*A = D*W'.
ans = 3×3
10-13 ×
-0.0444 -0.1066 -0.0888
-0.0011 0.0442 0.0333
0 0.0266 0.0178
Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then W'*A can, at best, approach D*W'. In other words, W'*A - D*W' is close to, but not exactly, 0.
Eigenvalues of Nondiagonalizable (Defective) Matrix
Create a 3-by-3 matrix.
A = [3 1 0; 0 3 1; 0 0 3];
Calculate the eigenvalues and right eigenvectors of A.
V = 3×3
1.0000 -1.0000 1.0000
0 0.0000 -0.0000
0 0 0.0000
D = 3×3
3 0 0
0 3 0
0 0 3
A has repeated eigenvalues and the eigenvectors are not independent. This means that A is not diagonalizable and is, therefore, defective.
Verify that V and D satisfy the equation, A*V = V*D, even though A is defective.
ans = 3×3
10-15 ×
0 0.8882 -0.8882
0 0 0.0000
0 0 0
Ideally, the eigenvalue decomposition satisfies the relationship. Since eig performs the decomposition using floating-point computations, then A*V can, at best, approach V*D. In other words, A*V - V*D is close to, but not exactly, 0.
Generalized Eigenvalues
Create two matrices, A and B, then solve the generalized eigenvalue problem for the eigenvalues and right eigenvectors of the pair (A,B).
A = [1/sqrt(2) 0; 0 1]; B = [0 1; -1/sqrt(2) 0]; [V,D]=eig(A,B)
V = 2×2 complex
1.0000 + 0.0000i 1.0000 + 0.0000i
0.0000 - 0.7071i 0.0000 + 0.7071i
D = 2×2 complex
0.0000 + 1.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 - 1.0000i
Verify that the results satisfy A*V = B*V*D.
The residual error A*V - B*V*D is exactly zero.
Generalized Eigenvalues Using QZ Algorithm for Badly Conditioned Matrices
Create a badly conditioned symmetric matrix containing values close to machine precision.
format long e A = diag([10^-16, 10^-15])
A = 2×2
1.000000000000000e-16 0
0 1.000000000000000e-15
Calculate the generalized eigenvalues and a set of right eigenvectors using the default algorithm. In this case, the default algorithm is 'chol'.
V1 = 2×2
1.000000000000000e+08 0
0 3.162277660168380e+07
D1 = 2×2
9.999999999999999e-01 0
0 1.000000000000000e+00
Now, calculate the generalized eigenvalues and a set of right eigenvectors using the 'qz' algorithm.
Check how well the 'chol' result satisfies A*V1 = A*V1*D1.
format short
A*V1 - A*V1*D1
ans = 2×2
10-23 ×
0.1654 0
0 -0.6617
Now, check how well the 'qz' result satisfies A*V2 = A*V2*D2.
When both matrices are symmetric, eig uses the 'chol' algorithm by default. In this case, the QZ algorithm returns more accurate results.
Generalized Eigenvalues Where One Matrix Is Singular
Create a 2-by-2 identity matrix, A, and a singular matrix, B.
A = eye(2); B = [3 6; 4 8];
If you attempt to calculate the generalized eigenvalues of the matrix B-1A with the command [V,D] = eig(BA), then MATLAB® returns an error because BA produces Inf values.
Instead, calculate the generalized eigenvalues and right eigenvectors by passing both matrices to the eig function.
V = 2×2
-0.7500 -1.0000
-1.0000 0.5000
It is better to pass both matrices separately, and let eig choose the best algorithm to solve the problem. In this case, eig(A,B) returns a set of eigenvectors and at least one real eigenvalue, even though B is not invertible.
Verify Av=λBv for the first eigenvalue and the first eigenvector.
eigval = D(1,1); eigvec = V(:,1); A*eigvec - eigval*B*eigvec
ans = 2×1
10-15 ×
0.1110
0.2220
Ideally, the eigenvalue decomposition satisfies the relationship. Since the decomposition is performed using floating-point computations, then A*eigvec can, at best, approach eigval*B*eigvec, as it does in this case.
Input Arguments
collapse all
A — Input matrix
square matrix
Input matrix, specified as a real or complex square matrix.
Data Types: double | single
Complex Number Support: Yes
B — Generalized eigenvalue problem input matrix
square matrix
Generalized eigenvalue problem input matrix, specified as a
square matrix of real or complex values. B must
be the same size as A.
Data Types: double | single
Complex Number Support: Yes
balanceOption — Balance option
'balance' (default) | 'nobalance'
Balance option, specified as: 'balance',
which enables a preliminary balancing step, or 'nobalance' which
disables it. In most cases, the balancing step improves the conditioning
of A to produce more accurate results. However,
there are cases in which balancing produces incorrect results. Specify 'nobalance' when A contains
values whose scale differs dramatically. For example, if A contains
nonzero integers, as well as very small (near zero) values, then the
balancing step might scale the small values to make them as significant
as the integers and produce inaccurate results.
'balance' is the default behavior. For more
information about balancing, see balance.
algorithm — Generalized eigenvalue algorithm
'chol' | 'qz'
Generalized eigenvalue algorithm, specified as 'chol' or 'qz',
which selects the algorithm to use for calculating the generalized
eigenvalues of a pair.
| algorithm | Description |
|---|---|
'chol' |
Computes the generalized eigenvalues of A and B usingthe Cholesky factorization of B. |
'qz' |
Uses the QZ algorithm, also known as the generalized Schur decomposition. This algorithm ignores the symmetry of A and B. |
In general, the two algorithms return the same result. The QZ
algorithm can be more stable for certain problems, such as those involving
badly conditioned matrices.
When you omit the algorithm argument, the eig function
selects an algorithm based on the properties of A and B.
It uses the 'chol' algorithm for symmetric (Hermitian) A and
symmetric (Hermitian) positive definite B. Otherwise,
it uses the 'qz' algorithm.
Regardless of the algorithm you specify, the eig function
always uses the QZ algorithm when A or B are
not symmetric.
outputForm — Output format of eigenvalues
'vector' | 'matrix'
Output format of eigenvalues, specified as 'vector' or
'matrix'. This option allows you to specify whether
the eigenvalues are returned in a column vector or a diagonal matrix. The
default behavior varies according to the number of outputs specified:
-
If you specify one output, such as
e = eig(A),
then the eigenvalues are returned as a column vector by
default. -
If you specify two or three outputs, such as
[V,D] =, then the eigenvalues are returned as a
eig(A)
diagonal matrix,D, by default.
Example: D = eig(A,'matrix') returns a diagonal matrix
of eigenvalues with the one output syntax.
Output Arguments
collapse all
e — Eigenvalues (returned as vector)
column vector
Eigenvalues, returned as a column vector containing the eigenvalues (or generalized
eigenvalues of a pair) with multiplicity. Each eigenvalue
e(k) corresponds with the right eigenvector
V(:,k) and the left eigenvector
W(:,k).
-
When
Ais real symmetric or
complex Hermitian, the
values ofethat satisfy
Av =
λv are real. -
When
Ais real skew-symmetric or complex skew-Hermitian, the values ofethat
satisfy Av =
λv are imaginary.
V — Right eigenvectors
square matrix
Right eigenvectors, returned as a square matrix whose columns
are the right eigenvectors of A or generalized
right eigenvectors of the pair, (A,B). The form
and normalization of V depends on the combination
of input arguments:
-
[V,D] = eig(A)returns matrixV,
whose columns are the right eigenvectors ofAsuch
thatA*V = V*D. The eigenvectors inVare
normalized so that the 2-norm of each is 1.If
Ais real symmetric, Hermitian,
or skew-Hermitian, then the right eigenvectors
Vare orthonormal. -
[V,D] = eig(A,'nobalance')also
returns matrixV. However, the 2-norm of each eigenvector
is not necessarily 1. -
[V,D] = eig(A,B)and[V,D] =return
eig(A,B,algorithm)Vas
a matrix whose columns are the generalized right eigenvectors
that satisfyA*V = B*V*D. The 2-norm of each
eigenvector is not necessarily 1. In this case,
Dcontains the generalized eigenvalues of
the pair,(A,B), along the main
diagonal.When
eiguses the
'chol'algorithm with symmetric
(Hermitian)Aand symmetric (Hermitian)
positive definiteB, it normalizes the
eigenvectors inVso that the
B-norm of each is 1.
Different machines and releases of MATLAB® can produce different eigenvectors that are still numerically accurate:
-
For real eigenvectors, the sign of the eigenvectors can change.
-
For complex eigenvectors, the eigenvectors can be multiplied by any complex number
of magnitude 1. -
For a multiple eigenvalue, its eigenvectors can be recombined through linear
combinations. For example, if Ax =
λx and Ay =
λy, then A(x+y) =
λ(x+y), so x+y also is an eigenvector of A.
D — Eigenvalues (returned as matrix)
diagonal matrix
Eigenvalues, returned as a diagonal matrix with the eigenvalues of A on the
main diagonal or the eigenvalues of the pair, (A,B), with
multiplicity, on the main diagonal. Each eigenvalue
D(k,k) corresponds with the right eigenvector
V(:,k) and the left eigenvector
W(:,k).
-
When
Ais real symmetric or
complex Hermitian, the
values ofDthat satisfy
Av =
λv are real. -
When
Ais real skew-symmetric or complex skew-Hermitian, the values ofDthat
satisfy Av =
λv are imaginary.
W — Left eigenvectors
square matrix
Left eigenvectors, returned as a square matrix whose columns
are the left eigenvectors of A or generalized left
eigenvectors of the pair, (A,B). The form and normalization
of W depends on the combination of input arguments:
-
[V,D,W] = eig(A)returns matrix
W, whose columns are the left eigenvectors of
Asuch thatW'*A = D*W'.
The eigenvectors inWare normalized so that the
2-norm of each is 1. IfAis symmetric,
thenWis the same as
V. -
[V,D,W] = eig(A,'nobalance')also
returns matrixW. However, the 2-norm of each eigenvector
is not necessarily 1. -
[V,D,W] = eig(A,B)and[V,D,W]returns
= eig(A,B,algorithm)Was a matrix
whose columns are the generalized left eigenvectors that satisfyW'*A. The 2-norm of each eigenvector is not necessarily
= D*W'*B
1. In this case,Dcontains the generalized eigenvalues
of the pair,(A,B), along the main diagonal.If
AandBare symmetric,
thenWis the same as
V.
Different machines and releases of MATLAB can produce different eigenvectors that are still numerically accurate:
-
For real eigenvectors, the sign of the eigenvectors can change.
-
For complex eigenvectors, the eigenvectors can be multiplied by any complex number
of magnitude 1. -
For a multiple eigenvalue, its eigenvectors can be recombined through linear
combinations. For example, if Ax =
λx and Ay =
λy, then A(x+y) =
λ(x+y), so x+y also is an eigenvector of A.
More About
collapse all
Symmetric Matrix
-
A square matrix,
A, is symmetric if it is equal to its nonconjugate transpose,A = A.'.In terms of the matrix elements, this means that
-
Since real matrices are unaffected by complex conjugation, a real matrix that is symmetric is also Hermitian. For example, the matrix
is both symmetric and Hermitian.
Skew-Symmetric Matrix
-
A square matrix,
A, is skew-symmetric if it is equal to the negation of its nonconjugate transpose,A = -A.'.In terms of the matrix elements, this means that
-
Since real matrices are unaffected by complex conjugation, a real matrix that is skew-symmetric is also skew-Hermitian. For example, the matrix
is both skew-symmetric and skew-Hermitian.
Hermitian Matrix
-
A square matrix,
A, is Hermitian if it is equal to its complex conjugate transpose,A = A'.In terms of the matrix elements, this means that
-
The entries on the diagonal of a Hermitian matrix are always real. Since real matrices are unaffected by complex conjugation, a real matrix that is symmetric is also Hermitian. For example, the matrix
is both symmetric and Hermitian.
-
The eigenvalues of a Hermitian matrix are real.
Skew-Hermitian Matrix
-
A square matrix,
A, is skew-Hermitian if it is equal to the negation of its complex conjugate transpose,A = -A'.In terms of the matrix elements, this means that
-
The entries on the diagonal of a skew-Hermitian matrix are always pure imaginary or zero. Since real matrices are unaffected by complex conjugation, a real matrix that is skew-symmetric is also skew-Hermitian. For example, the matrix
is both skew-Hermitian and skew-symmetric.
-
The eigenvalues of a skew-Hermitian matrix are purely imaginary or zero.
Tips
-
The
eigfunction can calculate
the eigenvalues of sparse matrices that are real and symmetric. To
calculate the eigenvectors of a sparse matrix, or to calculate the
eigenvalues of a sparse matrix that is not real and symmetric, use
theeigsfunction.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
-
Vmight represent a different basis of eigenvectors. This representation
means that the eigenvector calculated by the generated code might be
different in C and C++ code than in MATLAB. The eigenvalues inDmight not be in the
same order as in MATLAB. You can verify theVand
Dvalues by using the eigenvalue problem equation
A*V = V*D. -
If you specify the LAPACK library callback class, then the code generator supports these options:
-
The computation of left eigenvectors.
-
-
Outputs are complex.
-
Code generation does not support sparse matrix inputs for this
function.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
The eig function
partially supports GPU arrays. Some syntaxes of the function run on a GPU when you specify the
input data as a gpuArray (Parallel Computing Toolbox). Usage notes and limitations:
-
For the generalized case,
eig(A,B),
AandBmust be real symmetric or
complex Hermitian. Additionally,Bmust be positive
definite. -
The QZ algorithm,
eig(A,B,'qz'), is not
supported.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
Usage notes and limitations:
-
For the generalized case,
eig(A,B),
AandBmust be real symmetric or
complex Hermitian. Additionally,Bmust be positive
definite. -
These syntaxes are not supported for full distributed arrays:
[__] = eig(A,B,'qz')[V,D,W] = eig(A,B)
For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
expand all
R2021b: eig returns NaN for nonfinite inputs
eig returns NaN values when the input
contains nonfinite values (Inf or NaN).
Previously, eig threw an error when the input contained
nonfinite values.
R2021a: Improved algorithm for skew-Hermitian matrices
The algorithm for input matrices that are skew-Hermitian was improved. With the
function call [V,D] = eig(A), where A is
skew-Hermitian, eig now guarantees that the matrix of
eigenvectors V is unitary and the diagonal matrix of eigenvalues
D is purely imaginary.
Собственные значения и собственные вектора
Синтаксис
Описание
пример
e = eig(A)A.
пример
[ возвращает диагональный матричный V,D] =
eig(A)D из собственных значений и матричного V чьи столбцы являются соответствующими правыми собственными векторами, так, чтобы A*V = V*D.
пример
[ также возвращает полный матричный V,D,W]
= eig(A)W чьи столбцы являются соответствующими левыми собственными векторами, так, чтобы W'*A = D*W'.
Задача о собственных значениях должна определить решение уравнения A v = λ v, где A является n– n матрица, v является вектор-столбцом длины n, и λ является скаляром. Значения λ, которые удовлетворяют уравнению, являются собственными значениями. Соответствующие значения v, которые удовлетворяют уравнению, являются правыми собственными векторами. Левые собственные вектора, w, удовлетворяют уравнению w ’A = λ w’.
пример
e = eig(A,B)A и B.
пример
[ возвращает диагональный матричный V,D] =
eig(A,B)D из обобщенных собственных значений и полного матричного V чьи столбцы являются соответствующими правыми собственными векторами, так, чтобы A*V = B*V*D.
[ также возвращает полный матричный V,D,W]
= eig(A,B)W чьи столбцы являются соответствующими левыми собственными векторами, так, чтобы W'*A = D*W'*B.
Обобщенная задача о собственных значениях должна определить решение уравнения A v = λ B v, где A и B является n– n матрицы, v является вектор-столбцом длины n, и λ является скаляром. Значения λ, которые удовлетворяют уравнению, являются обобщенными собственными значениями. Соответствующие значения v являются обобщенными правыми собственными векторами. Левые собственные вектора, w, удовлетворяют уравнению w ’A = λ w ’B.
[___] = eig(, где A,balanceOption)balanceOption 'nobalance', отключает предварительный шаг балансировки в алгоритме. Значение по умолчанию для balanceOption 'balance', который позволяет балансироваться. eig функция может возвратить любой из выходных аргументов в предыдущих синтаксисах.
пример
[___] = eig(, где A,B,algorithm)algorithm 'chol', использует факторизацию Холесского B вычислить обобщенные собственные значения. Значение по умолчанию для algorithm зависит от свойств A и B, но обычно 'qz', который использует алгоритм QZ.
Если A является Эрмитовым и B Эрмитов положительный определенный, затем значение по умолчанию для algorithm 'chol'.
пример
[___] = eig(___, возвращает собственные значения в форме, заданной outputForm)outputForm использование любого из аргументов ввода или вывода в предыдущих синтаксисах. Задайте outputForm как 'vector' возвратить собственные значения в вектор-столбце или как 'matrix' возвратить собственные значения в диагональной матрице.
Примеры
свернуть все
Собственные значения матрицы
Используйте gallery создать симметричную положительную определенную матрицу.
A = 4×4
1.0000 0.5000 0.3333 0.2500
0.5000 1.0000 0.6667 0.5000
0.3333 0.6667 1.0000 0.7500
0.2500 0.5000 0.7500 1.0000
Вычислите собственные значения A. Результатом является вектор-столбец.
e = 4×1
0.2078
0.4078
0.8482
2.5362
В качестве альтернативы используйте outputForm возвратить собственные значения в диагональной матрице.
D = 4×4
0.2078 0 0 0
0 0.4078 0 0
0 0 0.8482 0
0 0 0 2.5362
Собственные значения и собственные вектора матрицы
Используйте gallery создать циркулянтную матрицу.
A = 3×3
1 2 3
3 1 2
2 3 1
Вычислите собственные значения и правые собственные вектора A.
V = 3×3 complex
-0.5774 + 0.0000i 0.2887 - 0.5000i 0.2887 + 0.5000i
-0.5774 + 0.0000i -0.5774 + 0.0000i -0.5774 + 0.0000i
-0.5774 + 0.0000i 0.2887 + 0.5000i 0.2887 - 0.5000i
D = 3×3 complex
6.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i -1.5000 + 0.8660i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 + 0.0000i -1.5000 - 0.8660i
Проверьте, что результаты удовлетворяют A*V = V*D.
ans = 3×3 complex
10-14 ×
-0.2665 + 0.0000i -0.0333 + 0.1110i -0.0333 - 0.1110i
0.0888 + 0.0000i 0.0000 + 0.1221i 0.0000 - 0.1221i
-0.0444 + 0.0000i -0.0111 + 0.1221i -0.0111 - 0.1221i
Идеально, разложение собственного значения удовлетворяет отношению. Начиная с eig выполняет разложение с помощью расчетов с плавающей точкой, затем A*V может, в лучшем случае приблизиться к V*D. Другими словами, A*V - V*D близко к, но не точно, 0.
Отсортированные собственные значения и собственные вектора
eig по умолчанию не всегда возвращает собственные значения и собственные вектора в отсортированном порядке. Используйте sort функционируйте, чтобы поместить собственные значения в порядке возрастания и переупорядочить соответствующие собственные вектора.
Вычислите собственные значения и собственные вектора матрицы магического квадрата 5 на 5.
A = 5×5
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
V = 5×5
-0.4472 0.0976 -0.6330 0.6780 -0.2619
-0.4472 0.3525 0.5895 0.3223 -0.1732
-0.4472 0.5501 -0.3915 -0.5501 0.3915
-0.4472 -0.3223 0.1732 -0.3525 -0.5895
-0.4472 -0.6780 0.2619 -0.0976 0.6330
D = 5×5
65.0000 0 0 0 0
0 -21.2768 0 0 0
0 0 -13.1263 0 0
0 0 0 21.2768 0
0 0 0 0 13.1263
Собственные значения A находятся на диагонали D. Однако собственные значения не отсортированы.
Извлеките собственные значения из диагонали D использование diag(D), затем отсортируйте итоговый вектор в порядке возрастания. Второй выход от sort возвращает вектор сочетания из индексов.
d = 5×1
-21.2768
-13.1263
13.1263
21.2768
65.0000
Используйте ind переупорядочить диагональные элементы D. Начиная с собственных значений в D соответствуйте собственным векторам в столбцах V, необходимо также переупорядочить столбцы V использование тех же индексов.
Ds = 5×5
-21.2768 0 0 0 0
0 -13.1263 0 0 0
0 0 13.1263 0 0
0 0 0 21.2768 0
0 0 0 0 65.0000
Vs = 5×5
0.0976 -0.6330 -0.2619 0.6780 -0.4472
0.3525 0.5895 -0.1732 0.3223 -0.4472
0.5501 -0.3915 0.3915 -0.5501 -0.4472
-0.3223 0.1732 -0.5895 -0.3525 -0.4472
-0.6780 0.2619 0.6330 -0.0976 -0.4472
Оба (V,D) и (Vs,Ds) произведите разложение собственного значения A. Результаты A*V-V*D и A*Vs-Vs*Ds согласитесь до ошибки округления.
e1 = norm(A*V-V*D); e2 = norm(A*Vs-Vs*Ds); e = abs(e1 - e2)
Левые собственные вектора
Создайте 3х3 матрицу.
A = [1 7 3; 2 9 12; 5 22 7];
Вычислите правые собственные вектора, V, собственные значения, D, и левые собственные вектора, W.
V = 3×3
-0.2610 -0.9734 0.1891
-0.5870 0.2281 -0.5816
-0.7663 -0.0198 0.7912
D = 3×3
25.5548 0 0
0 -0.5789 0
0 0 -7.9759
W = 3×3
-0.1791 -0.9587 -0.1881
-0.8127 0.0649 -0.7477
-0.5545 0.2768 0.6368
Проверьте, что результаты удовлетворяют W'*A = D*W'.
ans = 3×3
10-13 ×
0.1155 -0.0711 -0.0711
-0.0033 -0.0215 -0.0408
0.0022 0.0266 0.0178
Идеально, разложение собственного значения удовлетворяет отношению. Начиная с eig выполняет разложение с помощью расчетов с плавающей точкой, затем W'*A может, в лучшем случае приблизиться к D*W'. Другими словами, W'*A - D*W' близко к, но не точно, 0.
Собственные значения недиагонализируемой (дефектной) матрицы
Создайте 3х3 матрицу.
A = [3 1 0; 0 3 1; 0 0 3];
Вычислите собственные значения и правые собственные вектора A.
V = 3×3
1.0000 -1.0000 1.0000
0 0.0000 -0.0000
0 0 0.0000
D = 3×3
3 0 0
0 3 0
0 0 3
A повторил собственные значения, и собственные вектора весьма зависимы. Это означает тот A не является диагонализируемым и является, поэтому, дефектным.
Проверьте тот V и D удовлетворите уравнению, A*V = V*D, даже при том, что A является дефектным.
ans = 3×3
10-15 ×
0 0.8882 -0.8882
0 0 0.0000
0 0 0
Идеально, разложение собственного значения удовлетворяет отношению. Начиная с eig выполняет разложение с помощью расчетов с плавающей точкой, затем A*V может, в лучшем случае приблизиться к V*D. Другими словами, A*V - V*D близко к, но не точно, 0.
Обобщенные собственные значения
Создайте две матрицы, A и B, затем решите обобщенную задачу о собственных значениях для собственных значений и правых собственных векторов парного (A,B).
A = [1/sqrt(2) 0; 0 1]; B = [0 1; -1/sqrt(2) 0]; [V,D]=eig(A,B)
V = 2×2 complex
1.0000 + 0.0000i 1.0000 + 0.0000i
0.0000 - 0.7071i 0.0000 + 0.7071i
D = 2×2 complex
0.0000 + 1.0000i 0.0000 + 0.0000i
0.0000 + 0.0000i 0.0000 - 1.0000i
Проверьте, что результаты удовлетворяют A*V = B*V*D.
Остаточная ошибка A*V - B*V*D ниже нуля.
Обобщенные собственные значения Используя алгоритм QZ для плохо обусловленных матриц
Создайте плохо обусловленную симметрическую матрицу, содержащую значения близко к точности машины.
format long e A = diag([10^-16, 10^-15])
A = 2×2
0.1000 0
0 1.0000
Вычислите обобщенные собственные значения и набор правых собственных векторов с помощью алгоритма по умолчанию. В этом случае алгоритмом по умолчанию является 'chol'.
V1 = 2×2
1.0000 0
0 0.3162
D1 = 2×2
1.0000 0
0 1.0000
Теперь вычислите обобщенные собственные значения и набор правых собственных векторов с помощью 'qz' алгоритм.
Проверяйте как хорошо 'chol' результат удовлетворяет A*V1 = A*V1*D1.
format short
A*V1 - A*V1*D1
ans = 2×2
10-23 ×
0.1654 0
0 -0.6617
Теперь проверяйте как хорошо 'qz' результат удовлетворяет A*V2 = A*V2*D2.
Когда обе матрицы симметричны, eig использует 'chol' алгоритм по умолчанию. В этом случае алгоритм QZ возвращает более точные результаты.
Обобщенные Собственные значения, Где Одна Матрица Сингулярна
Создайте единичную матрицу 2 на 2, A, и сингулярная матрица, B.
A = eye(2); B = [3 6; 4 8];
При попытке вычислить обобщенные собственные значения матрицы B-1A с командой [V,D] = eig(BA), затем MATLAB® возвращает ошибку потому что BA производит Inf значения.
Вместо этого вычислите обобщенные собственные значения и правые собственные вектора путем передачи обеих матриц eig функция.
V = 2×2
-0.7500 -1.0000
-1.0000 0.5000
Лучше передать обе матрицы отдельно и позволить eig выберите лучший алгоритм, чтобы решить задачу. В этом случае, eig(A,B) возвращает набор собственных векторов и по крайней мере одного действительного собственного значения, даже при том, что B не является обратимым.
Проверить Av=λBv для первого собственного значения и первого собственного вектора.
eigval = D(1,1); eigvec = V(:,1); A*eigvec - eigval*B*eigvec
ans = 2×1
10-15 ×
0.1110
0.2220
Идеально, разложение собственного значения удовлетворяет отношению. Поскольку разложение выполняется с помощью расчетов с плавающей точкой, затем A*eigvec может, в лучшем случае приблизиться к eigval*B*eigvec, когда это делает в этом случае.
Входные параметры
свернуть все
A — Введите матрицу
квадратная матрица
Введите матрицу в виде действительной или комплексной квадратной матрицы.
Типы данных: double | single
Поддержка комплексного числа: Да
B — Обобщенная входная матрица задачи о собственных значениях
квадратная матрица
Обобщенная входная матрица задачи о собственных значениях в виде квадратной матрицы действительных или комплексных чисел. B должен быть одного размера с A.
Типы данных: double | single
Поддержка комплексного числа: Да
balanceOption balanceOption
'balance' (значение по умолчанию) | 'nobalance'
Сбалансируйте опцию в виде: 'balance', который включает предварительный шаг балансировки или 'nobalance' который отключает его. В большинстве случаев балансирующийся шаг улучшает создание условий A приводить к более точным результатам. Однако существуют случаи, в которых балансировка приводит к неправильным результатам. Задайте 'nobalance' когда A содержит значения, шкала которых отличается существенно. Например, если A содержит ненулевые целые числа, а также очень маленький (около нуля) значения, затем балансирующийся шаг может масштабировать маленькие значения, чтобы сделать их столь же значительными как целые числа и привести к неточным результатам.
'balance' поведение по умолчанию. Для получения дополнительной информации о балансировке, смотрите balance.
algorithm — Обобщенный алгоритм собственного значения
'chol' | 'qz'
Обобщенный алгоритм собственного значения в виде 'chol' или 'qz', который выбирает алгоритм, чтобы использовать для вычисления обобщенных собственных значений пары.
| алгоритм | Описание |
|---|---|
'chol' |
Вычисляет обобщенные собственные значения A и B использование факторизации Холесского B. |
'qz' |
Использует алгоритм QZ, также известный как обобщенное разложение Шура. Этот алгоритм игнорирует симметрию A и B. |
В общем случае эти два алгоритма возвращают тот же результат. Алгоритм QZ может быть более устойчивым для определенных проблем, таким как те, которые включают плохо обусловленные матрицы.
Когда вы не используете algorithm аргумент, eig функция выбирает алгоритм на основе свойств A и B. Это использует 'chol' алгоритм для симметричного (Эрмитового) A и симметричный (Эрмитов) положительный определенный B. В противном случае это использует 'qz' алгоритм.
Независимо от алгоритма вы задаете, eig функционируйте всегда использует алгоритм QZ когда A или B не симметричны.
outputForm — Выходной формат собственных значений
'vector' | 'matrix'
Выходной формат собственных значений в виде 'vector' или 'matrix'. Эта опция позволяет вам задавать, возвращены ли собственные значения в вектор-столбце или диагональной матрице. Поведение по умолчанию варьируется согласно количеству заданных выходных параметров:
-
Если вы задаете тот выход, такой как
e = eig(A), затем собственные значения возвращены как вектор-столбец по умолчанию. -
Если вы задаете два или три выходных параметров, такие как
[V,D] = eig(A), затем собственные значения возвращены как диагональная матрица,D, по умолчанию.
Пример: D = eig(A,'matrix') возвращает диагональную матрицу собственных значений с одним выходом.
Выходные аргументы
свернуть все
e — Собственные значения (возвратился как вектор),
вектор-столбец
Собственные значения, возвращенные как вектор-столбец, содержащий собственные значения (или обобщенные собственные значения пары) с кратностью. Каждое собственное значение e(k) соответствует правому собственному вектору V(:,k) и левый собственный вектор W(:,k).
-
Когда
Aдействителен симметричный или комплексный Эрмитов, значенияeэто удовлетворяет A v =, λ v действителен. -
Когда
Aдействителен скошено-симметричный или комплексный скошено-эрмитов, значенияeэто удовлетворяет A v =, λ v является мнимым.
V — Правые собственные вектора
квадратная матрица
Правые собственные вектора, возвращенные как квадратная матрица, столбцы которой являются правыми собственными векторами A или обобщенные правые собственные вектора пары, (A,B). Форма и нормализация V зависит от комбинации входных параметров:
-
[V,D] = eig(A)возвращает матричныйV, чьи столбцы являются правыми собственными векторамиAтаким образом, чтоA*V = V*D. Собственные вектора вVнормированы так, чтобы 2-норма каждого равнялась 1.Если
Aдействителен симметричный, Эрмитов, или скошено-эрмитов, затем правые собственные вектораVортонормированы. -
[V,D] = eig(A,'nobalance')также возвращает матричныйV. Однако 2-норма каждого собственного вектора не обязательно 1. -
[V,D] = eig(A,B)и[V,D] = eig(A,B,algorithm)возвратитеVкак матрица, столбцы которой являются обобщенными правыми собственными векторами, которые удовлетворяютA*V = B*V*D. 2-норма каждого собственного вектора не обязательно 1. В этом случае,Dсодержит обобщенные собственные значения пары,(A,B), по основной диагонали.Когда
eigиспользует'chol'алгоритм с симметричным (Эрмитовым)Aи симметричный (Эрмитов) положительный определенныйB, это нормирует собственные вектора вVтак, чтобыB– норма каждого равняется 1.
Различные машины и релизы MATLAB® может произвести различные собственные вектора, которые все еще численно точны:
-
Для действительных собственных векторов может измениться знак собственных векторов.
-
Для комплексных собственных векторов собственные вектора могут быть умножены на любое комплексное число величины 1.
-
Для собственного значения кратного его собственные вектора могут быть повторно объединены через линейные комбинации. Например, если A x = λ x и A y = λ y, то A (x +y) = λ (x +y), таким образом, x +y также является собственным вектором A.
D — Собственные значения (возвратился как матрица),
диагональная матрица
Собственные значения, возвращенные как диагональная матрица с собственными значениями A на основной диагонали или собственных значениях пары, (A,B), с кратностью, на основной диагонали. Каждое собственное значение D(k,k) соответствует правому собственному вектору V(:,k) и левый собственный вектор W(:,k).
-
Когда
Aдействителен симметричный или комплексный Эрмитов, значенияDэто удовлетворяет A v =, λ v действителен. -
Когда
Aдействителен скошено-симметричный или комплексный скошено-эрмитов, значенияDэто удовлетворяет A v =, λ v является мнимым.
W Левые собственные вектора
квадратная матрица
Левые собственные вектора, возвращенные как квадратная матрица, столбцы которой являются левыми собственными векторами A или обобщенные левые собственные вектора пары, (A,B). Форма и нормализация W зависит от комбинации входных параметров:
-
[V,D,W] = eig(A)возвращает матричныйW, чьи столбцы являются левыми собственными векторамиAтаким образом, чтоW'*A = D*W'. Собственные вектора вWнормированы так, чтобы 2-норма каждого равнялась 1. ЕслиAсимметрично, затемWсовпадает сV. -
[V,D,W] = eig(A,'nobalance')также возвращает матричныйW. Однако 2-норма каждого собственного вектора не обязательно 1. -
[V,D,W] = eig(A,B)и[V,D,W] = eig(A,B,algorithm)возвращаетWкак матрица, столбцы которой являются обобщенными левыми собственными векторами, которые удовлетворяютW'*A = D*W'*B. 2-норма каждого собственного вектора не обязательно 1. В этом случае,Dсодержит обобщенные собственные значения пары,(A,B), по основной диагонали.Если
AиBсимметричны, затемWсовпадает сV.
Различные машины и релизы MATLAB могут произвести различные собственные вектора, которые все еще численно точны:
-
Для действительных собственных векторов может измениться знак собственных векторов.
-
Для комплексных собственных векторов собственные вектора могут быть умножены на любое комплексное число величины 1.
-
Для собственного значения кратного его собственные вектора могут быть повторно объединены через линейные комбинации. Например, если A x = λ x и A y = λ y, то A (x +y) = λ (x +y), таким образом, x +y также является собственным вектором A.
Больше о
свернуть все
Симметрическая матрица
-
Квадратная матрица,
A, симметрично, если это равно своему несопряженному, транспонируют,A = A.'.В терминах элементов матрицы это означает это
-
Поскольку действительные матрицы незатронуты комплексным спряжением, действительная матрица, которая симметрична, является также Эрмитовой. Например, матрица
является и симметричным и Эрмитовым.
Кососимметрическая матрица
-
Квадратная матрица,
A, скошено-симметрично, если это равно отрицанию своего несопряженного, транспонируют,A = -A.'.В терминах элементов матрицы это означает это
-
Поскольку действительные матрицы незатронуты комплексным спряжением, действительная матрица, которая скошено-симметрична, является также скошено-эрмитовой. Например, матрица
является и скошено-симметричным и скошено-эрмитовым.
Эрмитова матрица
-
Квадратная матрица,
A, является Эрмитовым, если это равно своему комплексному сопряженному транспонированию,A = A'.В терминах элементов матрицы это означает это
-
Записи на диагонали Эрмитовой матрицы всегда действительны. Поскольку действительные матрицы незатронуты комплексным спряжением, действительная матрица, которая симметрична, является также Эрмитовой. Например, матрица
является и симметричным и Эрмитовым.
-
Собственные значения Эрмитовой матрицы действительны.
Скошенная эрмитова матрица
-
Квадратная матрица,
A, является скошено-эрмитовым, если это равно отрицанию своего комплексного сопряженного транспонирования,A = -A'.В терминах элементов матрицы это означает это
-
Записи на диагонали скошенной Эрмитовой матрицы всегда чисты мнимый или нуль. Поскольку действительные матрицы незатронуты комплексным спряжением, действительная матрица, которая скошено-симметрична, является также скошено-эрмитовой. Например, матрица
является и скошено-эрмитовым и скошено-симметричным.
-
Собственные значения скошенной Эрмитовой матрицы являются чисто мнимыми или нуль.
Советы
-
eigфункция может вычислить собственные значения разреженных матриц, которые действительны и симметричны. Вычислить собственные вектора разреженной матрицы или вычислить собственные значения разреженной матрицы, которая не действительна и симметрична, использованиеeigsфункция.
Вопросы совместимости
развернуть все
eig возвращает NaN для неличных входных параметров
Поведение изменяется в R2021b
eig возвращает NaN значения, когда вход содержит неличные значения (Inf или NaN). Ранее eig выдал ошибку, когда вход содержал неличные значения.
Расширенные возможности
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Указания и ограничения по применению:
-
Vможет представлять различный базис собственных векторов. Это представление означает, что собственный вектор, вычисленный сгенерированным кодом, может отличаться в C и Коде С++, чем в MATLAB. Собственные значения вDне может быть в том же порядке как в MATLAB. Можно проверитьVиDзначения при помощи уравненияA*V = V*Dзадачи о собственных значениях.-
Для стандартной задачи о собственных значениях,
[V,D] = eig(A), когдаAявляется Эрмитовым или скошено-эрмитовым, использование генерации кодаschurвычислитьVиD. В противном случае, результаты[V,D] = eig(A)похожи на результаты, полученные при помощи[V,D] = eig(A,eye(size(A)),'qz')в MATLAB, за исключением того, что столбцыVнормированы.
-
-
Если вы задаете класс коллбэка библиотеки LAPACK, то генератор кода поддерживает эти опции:
-
'balance'и'nobalance'опции для стандартной задачи о собственных значениях. -
Расчет левых собственных векторов.
-
-
Выходные параметры являются комплексными.
-
Когда входная матрица содержит неличное значение, сгенерированный код не выдает ошибку. Вместо этого выход содержит
NaNзначения. -
Генерация кода не поддерживает входные параметры разреженной матрицы для этой функции.
Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.
Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.
Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
-
Только эти синтаксисы одно входного параметра поддерживаются:
-
e = eig(A) -
[V,D] = eig(A)
-
-
Если входная матрица
AсодержитNaNилиInf, затем функция возвращает ошибку.
Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).
Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
-
Для несимметричного полного матричного
A, необходимо использоватьeig(A,'nobalance')синтаксис. -
Для обобщенного случая,
eig(A,B)AиBдолжен быть действителен симметричный или комплексный Эрмитов. Кроме того,Bдолжен быть положителен определенный. -
Эти синтаксисы не поддерживаются для полных распределенных массивов:
[__] = eig(A,'balance')для несимметричногоA.[__] = eig(A,B,'qz')[V,D,W] = eig(A,B)
Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).
Представлено до R2006a
Важной задачей
линейной алгебры является задача на
собственные значения.
Собственные
числа
(значения)
λi
и собственные
векторы
(ui
≠
0)
квадратной матрицы А
удовлетворяют равенствам
Aui
= λiui.
Собственные
значения λ
квадратной матрицы А
являются корнями ее характеристического
уравнения│A
– λE│
=
0,
где E
– единичная матрица того же порядка n,
что и А.
Многочлен │A
– λE│называется
характеристическим полиномом матрицы
А.
В общем случае имеется n
различных комплексных или вещественных
корней характеристического уравнения.
Их количество будет меньше в случае
кратных корней.
Пример:
Дана квадратная
матрица второго порядка
A
=
Решить
задачу на собственные значения вручную
и средствами MATLAB.
Решение:
Находим
характеристический полином матрицы A.
E
= ,
│A
– λE│
= = (3
– λ)(2
– λ)
– 20 = λ2
– 5λ
– 14.
В
MATLAB
массив коэффициентов характеристического
полинома матрицы А
возвращает команда poly:
>>
poly(A)
ans
=
1
-5 -14
Характеристическим
уравненим является квадратное уравнение
λ2
– 5λ
– 14 = 0.
Вычисляем корни
этого уравнения.
λ1,2
= = = = = .
Корни
уравнения λ1
= -2
и λ2
= 7
являются собственными значениями
матрицы А.
Найдем теперь
собственные векторы, соответствующие
этим собственным значениям. Собственный
вектор
U
= ,
соответствующий
собственному значению λ1
= -2,
определяется уравнениями
т.
е. 5u1
+
4u2
= 0.
Из этого равенства следует, что собственный
вектор U
определяется с точностью до числового
множителя, поэтому одну из координат
собственного вектора можно зафиксировать.
Полагая u1
= -4,
найдем u2
= 5
и получим
U
= .
Аналогично,
собственный вектор
V
= ,
соответствующий
собственному значению λ2
= 7,
определяется уравнениями
т.
е. v1
– v2
= 0.
Полагая v1
= 1,
найдем v2
= 1
и получим
V
= .
Следовательно,
собственным значениям λ1
= -2 и
λ2
= 7
соответствуют собственные векторы
U
= и V
= .
На рассмотренном
примере мы убедились, что задача на
собственные значения оказалась достаточно
сложной и трудоемкой даже для матрицы
минимального (второго) порядка.
В
MATLAB
собственные значения матрицы A
вычисляет
команда eig(A):
>>
A=[3 4;5 2];
>>
Lambda=eig(A)
Lambda
=
7
-2
Команда
[R,Lam]=eig(A)
вычисляет как собственные значения,
так и собственные векторы:
>> [R,Lam]=eig(A)
R
=
0.7071 -0.6247
0.7071 0.7809
Lam
=
7
0
0 -2
Собственные
значения являются диагональными
элементами диагональной матрицы Lam,
а столбцы матрицы R
являются собственными векторами. Итак,
собственным значениям λ1
= -2 и
λ2
= 7
соответствуют собственные векторы
R1
= и R2
= .
Как
указывалось выше, собственные векторы
определяются с точностью до числового
множителя. Команда eig
вычисляет единичные
или нормированными
по евклидовой норме
собственные векторы.
Существуют
различные типы векторных норм. Норма
||R||p
вектора R
длины
n
определяется следующим образом:
||R||p
= (p = 1, 2, …).
Если
p=2
– норма называется евклидовой.
В
MATLAB
норму ||R||p
вектора R
вычисляет команда norm(R,p).
Команда norm(R)
вычисляет евклидову норму вектора R
по умолчанию. Если norm(R)
= 1,
вектор R
называется единичным
или нормированным.
Вектор
R
нормируется следующим образом:
Rnorm
= .
Пронормируем
найденные вручную собственные векторы
U
= и
V
= :
>> U=[-4;5];V=[1;1];
>> disp(U/norm(U))
-0.6247
0.7809
>> disp(V/norm(V))
0.7071
0.7071
Результы
совпали с собственными векторами R1
и R2,
вычисленными командой eig.
Для получения
вычисленных в символьной форме пар
собственных значений и собственных
векторов, введем следующую команду:
>>
[R,Lam]=eig(sym(A))
R
=
[ 1, 1]
[ 1, -5/4]
Lam
=
[ 7, 0]
[ 0, -2]
Некоторые
команды линейной алгебры MATLAB
мы рассматривали ранее. К ним относятся,
в частности, команды вычисления
определителя и обратной матрицы det
и inv.(см.
разд. 1.10).
В
MATLAB
cуществует
и другие команды решения типовых задач
линейной алгебры.
Так,
команда norm
вычисляет различные виды норм векторов
и матриц. Справку по этой команде можно
получить, набрав в командной строке doc
norm.
Команда rank(B)возвращает ранг прямоугольной матрицыB.
Ранг
матрицы
B
есть такое число r
= rB,
что по крайней мере один из определителей
r
– го порядка, получаемый из этой матрицы
при удалении строк и/или столбцов,
отличен от нуля, а все определители
(r+1)
– го порядка равны нулю. Ранг матрицы
равен наибольшему числу линейно
независимых строк (или столбцов).
Квадратная
матрица B порядка n
является невырожденной в том и только
в тот случае, когда ее ранг
rB
=
n,
т. е. det(B)
≠ 0.
Найдем ранг
рассмотренной выше матрицы
A
= :
>>
disp(rank(A))
2
Поскольку
ранг и порядок квадратной матрицы А
совпадают, ее определитель должен быть
ненулевым. Проверка:
>>
det(A)
ans
=
-14
Перечислим некоторые
из команд линейной алгебры:
cond
– число обусловленности матрицы;
lu
– разложение
на треугольные матрицы;
svd
– сингулярное разложение матрицы и т.
д.
Справочная информация
по командам линейной алгебры находится
в разделе matfunсправочной системы
MATLAB.
Соседние файлы в папке Методички
- #
- #
- #
- #
|
Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
|
|
1 |
|
Как найти собственные значения и собственные векторы матрицы?17.12.2014, 08:28. Показов 38920. Ответов 9
Дано матрица вида Найти собственные значения и собственные векторы матрицы Отсюда при Отсюда при собственные значения Теперь, вопрос как найти собственные значения и собственные векторы матрицы на MatLab тут сказано что, функция eig поможет, но я не знаю как, помогите пожалуйста
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||
|
17.12.2014, 09:13 |
2 |
|||
|
Всё очень просто…Да, можно использовать функцию eig. Всё в Хэлпе написано.
Где V – правые собственные вектора; D – собственные значения; W – левые собственные вектора.
0 |
|
Maikl2020 Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
||||
|
17.12.2014, 11:18 [ТС] |
3 |
|||
|
illi2, Ну не знаю тут функции poly, roots что обозначат, но кажется собственные значения матрица найдено правильно!
Добавлено через 1 минуту
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||
|
17.12.2014, 11:47 |
4 |
|||
|
Не понял Вас вообще. Чем не устраивает функция eig()?
V содержит два искомых собственных вектора. Для собственного значения 1 (матрица D – диагональная,содержит все собственные значения расположенные по нарастанию собственного значения) – это первый столбец матрицы V(:,1):
0 |
|
Maikl2020 Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
||||
|
17.12.2014, 12:03 [ТС] |
5 |
|||
|
illi2, Как найти собственный вектор матрицы, без нормированный вектор. т.е. программа вывел X(-1;1). Добавлено через 1 минуту
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||||||||||
|
17.12.2014, 13:41 |
6 |
|||||||||||
|
Решение У Вас просто более старая версия Матлаба (я запускал в R2014а).
Не нормированный вектор Матлаб скорее всего не выведет (так как это целое множество подобных векторов)… Можно самому просто переправить как-нить так выходные векторы матрицы V:
Добавлено через 11 минут
1 |
|
Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
|
|
17.12.2014, 14:01 [ТС] |
7 |
|
illi2, Спасибо, Извините еще два вопроса у меня пожалуйста.
i=1:size(V,2) 2) Где можно скачать R2014а ? Добавлено через 9 минут
V= собственные векторы матрицы X=(1, -1) какой из них?
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||
|
17.12.2014, 14:28 |
8 |
|||
|
Решение
1) Объясните, пожалуйста Нормируем по столбцам.
– цикл по всем столбцам. size(V,2) – число столбцов матрицы V. В матрице V собственные вектора расположены в столбцах этой матрицы. V(:,i) – i-ый столбец матрицы V. Знак ( : ) – обозначает “все элементы”, ( : , i ) – все элементы столбца i. V(:,i) = V(:,i)/min(abs(V(:,i))); – нормируем каждый столбец по отдельности (равносильно “каждый вектор”) на min(abs(V(:,i))) – минимальный по абсолютному значению элемент данного столбца. Это чтобы в каждом столбце минимальное число получилось равно “1” (или “-1”).
собственные векторы матрицы X=(1, -1) какой из них? Для собственного значения 1 – это вектор (1,-1) – первый столбец в V. Для собственного значения 4 – это вектор (1,2) – 2-ой столбец. R2014a можно скачать на http://www.mathworks.com/
1 |
|
Maikl2020 Всегда онлайн 49 / 49 / 10 Регистрация: 13.04.2014 Сообщений: 1,407 |
||||||||
|
20.12.2014, 20:09 [ТС] |
9 |
|||||||
|
illi2, Здравствуйте, почему MatLab выводит комплексные числи
Добавлено через 2 часа 36 минут
Добавлено через 18 минут
0 |
|
illi2 19 / 19 / 9 Регистрация: 26.07.2013 Сообщений: 51 |
||||
|
22.12.2014, 14:09 |
10 |
|||
|
Решение Доброго времени суток. Другой вопрос: при решении системы линейных уравнений (на собственные числа или вектора) можно получить такие случаи, когда будет 0=0. То есть удовлетворяет любое значение. Матлаб в этом случае выдаст ответ (1 0 0) или что-то подобное, то есть единичный вектор или базис из единичных векторов.
V(:,i) = V(:,i)/min(abs(V(:,i))); % перенормировываем – Эта строка не работает, когда вектор имеет нулевые элементы, ибо min(abs(V(:,i))) = 0 и получаем деление на 0. Нужно что-то вроде такого:
1 |

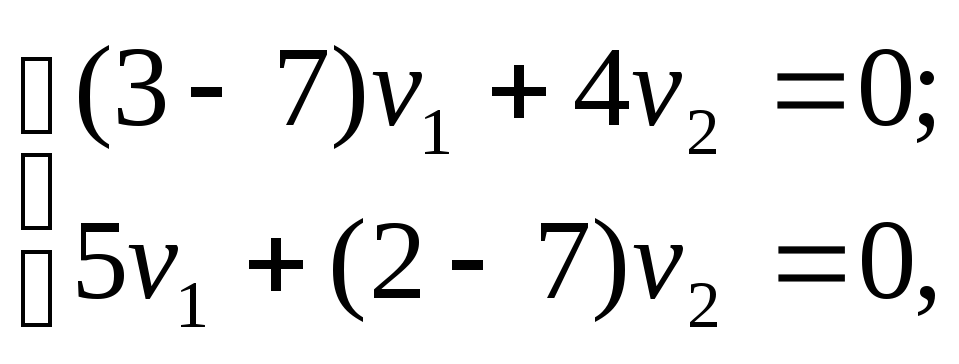

 Сообщение было отмечено Maikl2020 как решение
Сообщение было отмечено Maikl2020 как решение

