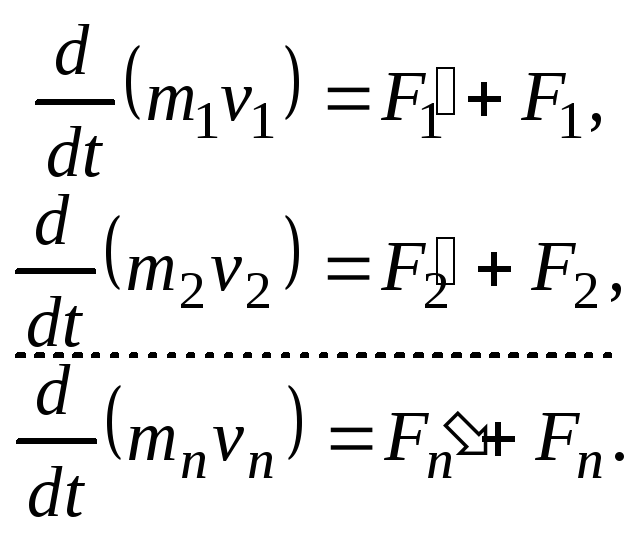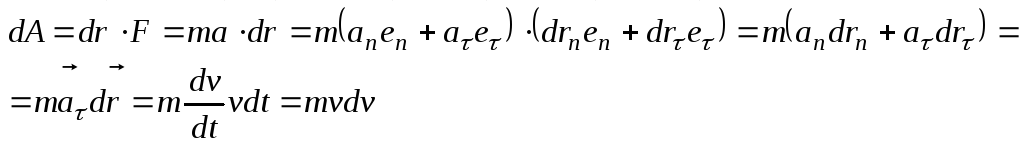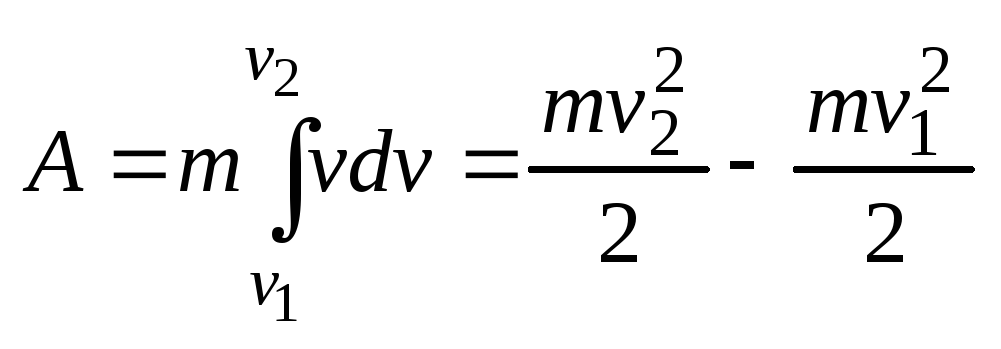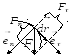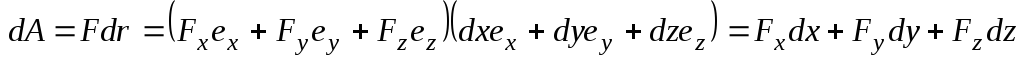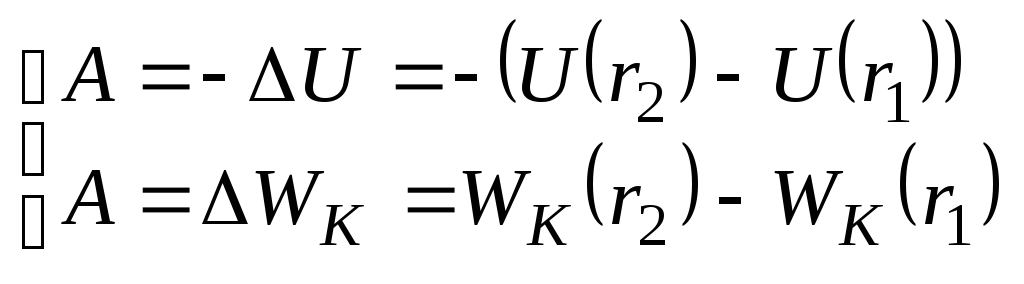Как найти собственный момент инерции

9. Закон сохранения
импульса.

Механическая
система –
совокупность материальных точек
(тел), рассматриваемых как единое
целое.

Силы взаимодействия
между материальными точками механической
системы называются внутренними.

Силы, с которыми
на материальные точки системы действуют
внешние тела, называются внешними.

Механическая
система тел, на которую не действуют
внешние силы, называется замкнутой
(изолированной).

Импульс –
обобщенная мера конкретного движения
объекта.

,
где

– индивидуальная особенность объекта.

– Второй закон
Ньютона.

,

Импульс остается
неизменным как по величине, так и по
направлению.

Механическая
система.

– совокупность
из

штук объектов.

Рассмотрим
механическую систему, состоящую из n
тел, масса и скорость которых
соответственно равны m₁,
m₂,
…, m_n
и v₁,
v₂,
…, v_n.
Пусть F₁,
F₂,
…, F_n
– равнодействующие внешних сил, а

– равнодействующие внутренних сил,
действующих на каждое из этих тел.
Запишем второй закон Ньютона для
каждого из n
тел механической системы:

Складывая
почленно эти уравнения, получаем:

Но так как
геометрическая сумма внутренних сил
механической системы по третьему
закону Ньютона равна нулю, то

или

Производная по времени от импульса
механической системы равна геометрической
сумме внешних сил, действующих на
систему.

В
случае отсутствия внешних сил (замкнутая
система).

10. Уравнение
динамики вращательного движения
материальной точки.

Причина –
воздействие.

Следствие –
изменение характера вращательного
движения.

Предположим, что
на этот объект действует сила
.

– мера воздействия
на данный объект со стороны другого
объекта.

– 2 закон Ньютона.

Радиус-вектор,
задающий положение движущейся точки
в пространстве, мы векторно умножим
на правую часть 2 закона Ньютона.
Равенство не нарушится.

– момент силы.

Вектор

перпендикулярен плоскости, которой
принадлежат вектора сомножители.

– момент импульса.

Угол
между

и

не меняется с течением времени, это
значит, что можно

внести под знак дифференциала.

2 закон Ньютона:

– для вращательного
движения;

– для поступательного
движения.

11. Момент инерции
твердого тела. Собственные моменты
инерции тел.

Линия

– ось вращения.

– масса на квадрат
радиуса окружности, по которой движется
материальная точка.

Твердое тело
– материальный объект, объем и форма
которого не меняется при слабом
механическом воздействии.

Все
тело мысленно разбиваем на маленькие
объемы. Масса этого кусочка
.

Твердое тело
представляется как совокупность
системы точечных масс.

– расстояние, на
котором находится точка от оси вращения.

– общий алгоритм
определения собственного момента
инерции твердого тела, относительно
оси проходящей через центр инерции
данного тела.

Собственные
моменты инерции тел простейших форм:

1. Тонкое кольцо.

Разобьем
кольцо на маленькие кусочки по радиусу.

– длина дуги;

– центральный
угол.

2. Тонкий диск.

Ось перпендикулярна
плоскости диска.

Мысленно разобьем
диск на совокупность колец.

– радиус одного
из колец;

– масса выделенного
кольца

12. Момент инерции
твердого тела относительно произвольной
оси. Теорема Штейнера.

Для того, чтобы
рассчитать

для произвольной оси, не проходящей
через центр инерции используют теорему
Штейнера.

– теорема Штейнера.

– момент инерции;

– собственный
момент инерции данного тела;

– масса;

– расстояние между
осями.

Теорема
Штейнера:
момент инерции относительно произвольной
оси равен моменту инерции относительно
параллельной оси, проходящей через
цент масс тела, сложенному с произведением
массы тела на квадрат расстояния между
осями.

П

о теореме Штейнера найдем момент
инерции однородного тонкого
цилиндрического стержня длинной

и массой
,
относительно оси
,
проходящей через конец стержня,
перпендикулярно стержню.

Значения моментов
инерции для некоторых тел.

Тело	Положение оси	Момент инерции
Полый тонкостенный цилиндр радиусом Сплошной цилиндр или диск радиусом Прямой тонкий стержень длиной Прямой тонкий стержень длиной Шар радиусом	Ось симметрии То же Ось, перпендикулярна стержню и проходит через его середину Ось, перпендикулярна стержню и проходит через его конец Ось проходит через центр шара

– момент инерции
материальной точки.

– уравнение
динамики вращательного движения.

Особенность движения	Поступательное движение	Вращательное движение
1. Инертность объекта
2. Быстрота изменения положения
3. Обобщенная мера движения
4. Уравнение движения

Момент инерции
характеризует инерционность объекта
в отношении вращательного движения.
Это аналог массы.

,
т. е.

– закон сохранения импульса.

Закон сохранения
импульса:

Импульс замкнутой
системы сохраняется, т. е. не изменяется
с течением времени.

Импульс сохраняется
и для незамкнутой системы, если
геометрическая сумма всех внешних
сил равна нулю.

,

– результирующая всех сил, действующих
из вне на тела системы.

– суммарный
импульс системы –
векторная сумма импульсов всех сил,
входящих в состав системы.

,
где

и

– любые моменты времени.

Каждое слагаемое
суммы меняется, но сама сумма остается
неизменной.

3. Толстого кольца.

Толстое
кольцо представляем в виде суммы
тонких колец.

4.
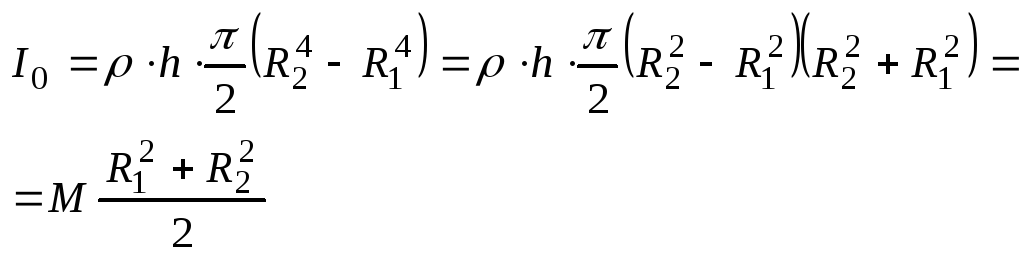
Стержень круглого сечения.

Мысленно распиливаем
цилиндр на кусочки.

5.
Шар.

– масса

– радиус

6.
Конус.

– масса

– радиус

13. Уравнение
динамики вращательного движения
механической системы. Закон сохранения
момента импульса.

Момент импульса
:
.

Момент сил:

Момент импульса
меняется под действием момента силы.

III
закон Ньютона для вращательного
движения:

При взаимодействии
двух вращающихся тел, момент силы, с
которой первое тело действует на
второе, равен моменту силы, с которым
второе тело действует на первое и они
направлены в противоположные стороны.

Тогда на основании
уравнения закона динамики для
вращательного движения
,
можно записать следующее:

– моменты инерции
первого и второго тела.

– соответствующие угловые скорости
до взаимодействия.

– после взаимодействия.

моменты инерции
первого и второго тела после
взаимодействия не меняются.

Сумма моментов
импульсов тел замкнутой системы в
результате их взаимодействия осталась
постоянной.

При этом следует
считать, что внешние силы отсутствуют
или таковы, что их векторная сумма
равна 0.

Закон сохранения
момента импульса:

Если суммарный
момент всех внешних сил действующих
на систему тел относительно произвольной
неподвижной оси равен 0, то векторная
сумма моментов импульсов тел системы
не изменяется с течением времени

Каждое из слагаемых
в этой сумме с течением времени может
меняться, однако сумма остается
постоянной.

14. Кинетическая
энергия поступательного движения
материальной точки.

Кинетическая
энергия механической системы
– это энергия механического движения
этой системы.

Сила
,
действуя на покоящееся тело и вызывая
его движение, совершает работу, а
энергия движущегося тела возрастает
на величину затраченной работы. Таким
образом, работа

силы

на пути, который тело прошло за время
возрастания скорости от

до
,
идет на увеличение кинетической
энергии

тела, т. е.
.

– перемещение
материальной точки в течение интервала
времени
.

Используя

– Второй закон Ньютона и умножая на
,
получаем:

– работа силы,

– обобщенная мера воздействия и
движения;

– мера воздействия;

– изменение, в результате воздействия.

– проекция вектора
перемещения на нормальную ось, т. к.
,
то
.

– информация о
воздействии на объект. Это обобщенная
характеристика воздействия и движения.

Все зависит от
того, какой угол.

– мера изменения
кинетической энергии движения тела.

При поступательном
движении тело массой
,
движущееся со скоростью
,
обладает кинетической энергией

15. Кинетическая
энергия вращательного движения
материальной точки.

Кинетическая
энергия механической системы
– это энергия механического движения
этой системы.

– проекция силы
на тангенциальную ось.

– момент силы.

При вращении
твердого тела относительно неподвижной
оси отдельные его элементарные объемы
массами

опишут окружности различных радиусов

и имеют различные линейные скорости
.
Угловая скорость вращения этих объемов
одинакова (абсолютно твердое тело):
.

Кинетическую
энергию вращающегося тела найдем как
сумму кинетических энергий его
элементарных объемов:

или

Таким образом,
кинетическая энергия вращающегося
тела:

.
Формула справедлива для тела,
вращающегося вокруг неподвижной оси.

Момент инерции

– мера инертности тела при вращательном
движении.

В случае плоского
движения тела, например цилиндра,
скатывающегося с наклонной плоскости
без скольжения, энергия движения
складывается из энергии поступательного
движения и энергии вращения:

,
где

– масса катящегося тела;

– скорость центра масс тела;

– момент инерции тела относительно
оси, проходящей через его центр масс;

– угловая скорость тела.

16. Силовое поле.
Классификация силовых полей.

Силовое поле –
это физическая млдель реального
пространства. Поле – пространство
(синонимы).

–
результирующая.

Силовое поле
считается заданным, если величина
силы, действующей на объект, определена
во всех точках.

Классификация
силовых полей:

1. Потенциальные;

2. Вихревые.

Признак
классификации:

– работа
по перемещению тела силами поля вдаль
замкнутой траектории.

1. Потенц.
   –
   Все силы, кроме сил сопротивления

2. Если
   – вихревое силовое поле, все силы
   сопротивления.

Потенциальная
энергия вводится только для потенциальных
силовых полей. т.е.

есть мера убыли некой величины, которая
получила название потенциальнея
энергия взаимодейстя (U).

Потенциальная-возможная.

(Информация
только о движении объекта)

(Информация
только о взаимодействии)

Взаимодействие:
1) 1-ая мера – это
сила;

2)
2-ая мера взаимодействия – это
(потенциальная
энергия)

Работа
по перемещению объекта силой есть
мера убыли потенциальной энергии
перемещаемого тела.

–
проекции вектора силы на координатные
оси.

.

– инерционность
объекта в отношении поступательного
движения.

Кинетическая
энергия зависит только от массы и
скорости тела, т. е. кинетическая
энергия системы есть функция состояния
ее движения.

Кинетическая
энергия зависит от выбора системы
отсчета.

– орты
осей единичные векторы, показывающие
направление осей.

–
проекции вектора перемещения на оси
.

(Полный дифференциал
функции 3х координат)

–
Частное поизводное, показывает как
быстро изменяется ф-я при изменении
только одного аргумента, ост.считаются
const.

(-
градиент U)

Символика
обозначения математического оператора.

Математический
оператор – это математическое
преобразование физической величины.

17. Потенциальная
энергия.

Физическая
величина, характеризующая способность
совершать работу называется энергией
тела.

Энергия
– общая мера различных процессов и
видов взаимодействия. Все формы
движения материи при соответствующих
условиях могут превращаться друг в
друга в строго определенных количественных
отношениях.

Потенциальная
энергия –
энергия, обусловленная взаимным
расположением тел или частей тела,
характеризуется их взаимодействием.
При соответствующих условиях возможно
изменение потенциальной энергии,
засчет чего совершается работа.

Пусть взаимодействие
тел осуществляется посредством силовых
полей (например, поля упругих сил, поля
гравитационных сил), характеризующихся
тем, что работа, совершаемая действующими
силами при перемещении тела из одного
положения в другое, не зависит от того,
по какой траектории это перемещение
произошло, а зависит только от начального
и конечного положений. Такие поля
называются потенциальными, а силы,
действующие в них, – консервативными.
Если же работа, совершаемая силой,
зависит от траектории перемещения
тела из одной точки в другую, то такая
сила называется диссипативной; ее
примером является сила трения.

– мера убыли
некоторой величины и это потенциальная
энергия взаимодействия.

Сила есть мера
убыли потенциальной энергии перемещения
тела.

– проекции силы
на оси
.

– орты этих осей.

– проекции вектора
перемещения на оси
.

– частная
производная.

(градиент)

Математический
оператор
– это математический преобразователь
физических величин.

Потенциальная
энергия находится в поле силы тяжести.

Работа пойдет
на увеличение энергии замкнутой
системы.

18. Закон
сохранения полной механической
энергии.

Рассматриваем
процесс падения тела и соответствующие
изменения его состояния при поднятии
и падении.

Кинетическая
энергия упавшего с высоты тела оказалась
равной его потенциальной энергии,
которую тело имело до начала падения.

На поверхности
земли
:

.

:

– сумма энергий
во всех точках остается постоянной,
если не рассеяна.

Если не происходит
превращение механической энергии в
другие виды, то

Закон сохранения
полной механической энергии:

Полная механическая
энергия замкнутой системы тел, между
которыми действуют только консервативные
силы, остается постоянной при всех
происходящих в ней процессах и
превращениях.

Потенциальная
энергия –
энергия, обусловленная взаимным
расположением тел или частей тела,
характеризуется их взаимодействием.

Кинетическая
энергия –
энергия движущегося тела.

Физическая
величина, характеризующая способность
совершать работу называется энергией
тела.

19. Движение тела
в диссипативной среде.

Диссипация (лат.)
– поглощение.

В
диссипативной среде (воздух, вода)
происходит преобразование кинетической
энергии тела в тепловую энергию.

æ.

æ
– коэффициент
пропорциональности.

пропорциональна
скорости.

Это результат
столкновения множества молекул этой
среды газа или жидкости у поверхности
тела.

– результирующая
сила, действующая на объект.

æ

æ
(æ=ae)

Быстрота изменения
скорости.

– производная
скорости от времени.

– уравнение
движения тела в диссипативной среде
(неоднородное дифференциальное
уравнение 1^го
порядка).

Решение
дифференциального уравнения –
нахождение функции, при подстановке
которой в уравнение получается
тождество.

– однородное
дифференциальное уравнение.

– частное решение.

– общее решение.

при

20. Гармонический
осциллятор.

Гармонический
(лат.) – протекающий согласованно.

Осциллятор (лат.)
– колебания.

Обобщенной моделью
колебательного движения является
гармонический осциллятор.

Основные свойства
гармонического осциллятора:

1. частота колебаний
   не зависит от амплитуды;

2. принцип
   суперпозиции:

Если на систему
действует несколько колебательных
сил, то эффект суммарного воздействия
может быть получен сложением эффектов
от каждой из сил в отдельности.

Колебательным
называют процесс, при котором
.

– фаза колебания
(рад).

– начальная фаза
колебаний (рад).

– частота колебаний
(рад/с).

– амплитудное
значение данной физической величины.

Примерами
гармонического осциллятора являются:

1. Пружинный
маятник.

Осциллятор –
совокупность нескольких тел, одно из
которых может колебаться.

2. Крутильный
маятник.

3.
Любые механические часы.

Этот осциллятор
задает нужный интервал времени.

– полная механическая
энергия.

Считая, что в
состоянии, когда тело находится на
поверхности земли

Потенциальная
энергия тела, находящегося в состоянии
упругой деформации.

x
– координата конца пружины.

4. Физический
маятник. 5. Твердое
тело (кристалл).

– радиус-вектор,
характеризующий отдельное положение
атома, меняется.

–
работа – мера изменения кинетической
энергии.

– мощность –
количественная мера преобразования
энергии из одного вида в другой.

– количество
энергии, которое преобразовалось в
течение интервала времени
,
из кинетической в тепловую.

Мощность зависит
от времени.

Обратите внимание, на этом сайте есть онлайн-сервис для вычисления центра тяжести и моментов инерции составных сечений, которые состоят из прокатных профилей (двутавр, уголок и т.д.) и из простых фигур.

Часто при расчете элементов строительных конструкций приходится определять геометрические характеристики профилей, составленных из элементарных геометрических фигур (прямоугольник, круг и т.п.) и прокатных профилей. Рассмотрим подробно пример расчета.

Необходимо определить геометрические характеристики составного сечения (рис.), который состоит из уголка 20/12,5/1,2, уголка 14/1 и прямоугольника 20х2см.

Определение собственных характеристик отдельных профилей – составляющих сечения

Собственные характеристики прокатных профилей определяются из сортамента.

Для неравнополочного уголка 20/12,5/1,2:

– высота и ширина уголка h = 20 см, b = 12,5 см;

– площадь $A$= 37,9 см2;

– собственные осевые моменты инерции ${I_x}$=1570 см4, ${I_y}$= 482 см4;

– собственный центробежный момент инерции ${I_{xy}}$=505 см4;

– координаты центра тяжести ${x_c}$= 2,83 см, ${y_c}$= 6,51 см.

Для равнополочного уголка 14/1:

– высота и ширина уголка h = b = 14 см;

– площадь $A$= 27,3 см2;

– собственные осевые моменты инерции ${I_x}$= ${I_y}$= 512 см4;

– собственный центробежный момент инерции ${I_{xy}}$=301 см4;

– координаты центра тяжести ${x_c}$= ${y_c}$= 3,82 см.

Для прямоугольника 20х2см:

– высота и ширина прямоугольника h = 20 см, b = 2 см;

– площадь $A$= 20∙2 = 40 см²;

– собственные осевые моменты инерции ${I_x} = frac{{2 cdot {{20}^3}}}{{12}} = 1330$ см⁴, ${I_y} = frac{{20 cdot {2^3}}}{{12}} = 13,3$см⁴;

– собственный центробежный момент инерции ${I_{xy}}$= 0, так как профиль имеет ось симметрии.

Определение центра тяжести сечения

Общая площадь всего сечения    A = 37,9+27,3+40 = 105см2.

Проводим вспомогательные оси $X$ и $Y$ и определяем относительно них центр тяжести сечения:

${X_c} = frac{{sum {{X_i} cdot {A_i}} }}{A} = frac{{{text{37}}{text{,9}} cdot {text{( – 13}}{text{,5) + 27}}{text{,3}} cdot {text{( – 3}}{text{,82) + 40}} cdot {text{1}}}}{{{text{105}}}}{text{ =  – 5}}{text{,49}}$см;

${Y_c} = frac{{sum {{Y_i} cdot {A_i}} }}{A} = frac{{{text{37}}{text{,9}} cdot {text{( – 2}}{text{,83) + 27}}{text{,3}} cdot {text{10}}{text{,2 + 40}} cdot {text{10}}}}{{105}} = 5,44$.

При этом в координатах центров тяжести составных обязанности’обязательно учитываем знак. Откладываем оси, которые проходят через центр тяжести –центральные оси $Xc$ и ${Y_c}$.

Определение центральных моментов инерции

Осевые и центробежный моменты инерции сечения определяем по формулам перехода между параллельными осями. Для этого находим и показываем на чертеже расстояния между центральными осями всего сечения и собственными осями каждой из фигур.

$Ix = sum {left( {I{x_i} + A cdot {b^2}} right) = {text{482 + 8}}{text{,2}}{{text{7}}^{text{2}}} cdot {text{37}}{text{,9 + 512 + 4}}{text{,7}}{{text{6}}^{text{2}}} cdot {text{27}}{text{,3 + 1330 + 4}}{text{,5}}{{text{6}}^{text{2}}} cdot {text{40  =  6360}}} $см4;

$Iy = sum {left( {I{y_i} + A cdot {a^2}} right)}  = {text{1570 + 8}}{text{,0}}{{text{1}}^{text{2}}} cdot {text{37}}{text{,9 + 512 + 1}}{text{,6}}{{text{7}}^{text{2}}} cdot {text{27}}{text{,3 + 13}}{text{,3 + 6}}{text{,4}}{{text{9}}^{text{2}}} cdot {text{40  =  6280}}$см4;

${I_{xy}} = sum {left( {{I_{xy}}_i + A cdot a cdot b} right)}  = $

$ = 505 + ( – 8,01) cdot ( – 8,27) cdot 37,9 – 301 + 1,67 cdot 4,76 cdot 27,3 + 0 + 6,49 cdot 4,56 cdot 40 = 4120$см4.

При этом обязанности’обязательно учитываем размещения фигур относительно рассматриваемых осей. Так, при определении момента инерции ${I_x}$ в формулу подставляем собственный момент инерции неравнополочного уголка относительно оси, которая параллельна оси ${X_c}$, в сортаменте это ось $Y$, и наоборот.

Определение положения главных осей и главных моментов инерции

Угол поворота главных осей относительно осей, для которых известны моменты инерции, определяется по формуле

[tg,2alpha  = frac{{2 cdot {I_{xy}}}}{{{I_y} – {I_x}}} = frac{{2 cdot 4120}}{{6280 – 6360}} =  – 97]                  $alpha  = frac{{arctg( – 97)}}{2} =  – 44,7^circ $.

Если $alpha  > 0$, главные оси откладываются против часовой стрелки, и наоборот.

Главные моменты инерции определяются так

${I_{x0}} = {I_x} cdot {cos ^2}alpha  + {I_y} cdot {sin ^2}alpha  – {I_{xy}} cdot sin 2alpha  = $

$ = 6360 cdot {cos ^2}( – 44,7^circ ) + 6280 cdot {sin ^2}( – 44,7^circ ) – 4120 cdot sin ( – 2 cdot 44,7^circ ) = 10430$см4.

${I_{y0}} = {I_y} cdot {cos ^2}alpha  + {I_x} cdot {sin ^2}alpha  + {I_{xy}} cdot sin 2alpha  = $

$ = 6280 cdot {cos ^2}( – 44,7^circ ) + 6360 cdot {sin ^2}( – 44,7^circ ) + 4120 cdot sin ( – 2 cdot 44,7^circ ) = 2210$см4.

Центробежный момент инерции относительно главных осей равен нулю.

Радиусы инерции. Моменты сопротивления

Радиусы инерции сечения

${i_x} = sqrt[{}]{{frac{{{I_x}}}{A}}} = sqrt[{}]{{frac{{10430}}{{105}}}} = 9,96$см,                 ${i_y} = sqrt[{}]{{frac{{{I_y}}}{A}}} = sqrt[{}]{{frac{{2210}}{{105}}}} = 4,58$см.

Моменты сопротивления сечения определяем относительно центральных осей. Для этого необходимо определить расстояния ${x_{max }}$ и ${y_{max }}$ до максимально удаленных точек от главных осей. Сначала необходимо по чертежам определить, какие точки являются наиболее удаленными. В нашем случае это точки $A$ и $B$ (рис.). Искомые расстояния можно определить, имея координаты этих точек в центральных (не возвращенных осям).

${x_{max }} = {x_A} cdot cos left( alpha  right) + {y_A} cdot sin left( alpha  right)$

${y_{max }} = {y_B} cdot cos left( alpha  right) – {x_B} cdot sin left( alpha  right)$

XА= –8,53см       YA=8,57см

XB= –14,5см      YB= –18см

xmax = –12,1см   ymax = –23см

Моменты сопротивления

${W_x} = frac{{{I_x}}}{{{y_{max }}}} = frac{{10430}}{{23}} = 454$см3;                ${W_y} = frac{{{I_y}}}{{{x_{max }}}} = frac{{2210}}{{12.1}} = 183$см3.

МОМЕНТЫ ИНЕРЦИИ ТЕЛ, РАЗЛИЧНОЙ ФОРМЫ
В прошлый раз мы разбирали основные законы, описывающие вращательное движение твердых тел. Напомню их еще раз:
Первый закон Ньютона (закон инерции). При отсутствии действующих моментов сил или, если все действующие на тело
с закрепленной осью вращения моменты сил скомпенсированы, то тело будет равномерно вращаться сколь угодно
долго. Закон говорит о том, как тело себя ведет, когда нет никакого действия. Если нет действия, то нет изменения движения
тела.
Второй закон Ньютона (закон действия). Угловое ускорение, сообщаемое телу с закрепленной осью вращения, прямо
пропорционально действующему на него моменту силы и обратно пропорционально моменту инерции тела. Закон
говорит о результате действия и определяет само действие – момент силы, вызывающее изменение вращательного движения
тела. Момент инерции тела – это мера инертности тела при вращательном движении.
Третий закон Ньютона (закон взаимодействия). При взаимодействии двух тел момент силы, с которым первое тело
действует на второе, равен по величине и противоположен по направлению моменту силы, с которым второе тело
действует на первое. Закон говорит о том, что действия самого по себе не бывает. Любое действие есть результат
взаимодействия тел. Любые взаимодействия можно представить в виде суммы взаимодействий двух тел.
Мы определили момент инерции тела, как сумму произведений массы всех
элементов тела на квадрат расстояния от оси вращения до элемента массы:
. В общем виде момент инерции тела
, где M – масса тела, a –
его характерный размер и k – коэффициент пропорциональности, зависящий от
формы тела (распределения массы по объему) и от положения оси вращения.
ТЕОРЕМА ШТЕЙНЕРА
Пусть тело вращается вокруг некоторой оси, перпендикулярной плоскости
рисунка. Момент инерции тела при вращении вокруг этой оси – J. Расстояние от
оси до центра массы тела – rc. Делая оборот вокруг этой оси, тело совершает один
оборот вокруг оси, ей параллельной и проходящей через центр массы тела.
Исходное движение можно разбить на две компоненты. Первое – вращательное
движение материальной точки, в которой сконцентрирована вся масса тела, и
второе – вращение тела вокруг собственной оси. Первому соответствует момент
инерции равный mrc2, второму – J0. Поэтому
(теорема Штейнера).
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТЕЛ
Используя теорему Штейнера, можно вычислять моменты инерции тел, которые могут быть разделены на себе подобные.
Например, тонкий стержень может быть разделен пополам на два стержня. Пусть собственный момент инерции стержня
, где M – масса стержня и a – его длина. Момент инерции целого стержня равен сумме моментов инерции его
половинок
. Собственный момент инерции половинки, имеющей массу M/2 и длину a/2, –
. При
вращении стержня вокруг собственной оси расстояние от центра массы стержня до центра массы половинки – a/4. Поэтому по
теореме Штейнера
. Тогда
, и
. Таким образом, момент инерции
тонкого стержня при вращении вокруг перпендикулярной ему оси, проходящей через его середину равен
. По
теореме Штейнера не сложно посчитать, что при вращении вокруг конца момент инерции стержня
.
Вычисление моментов инерции тел можно производить и по исходной формуле
. Для этого удобно делить тело на элементы такой формы, для которой
момент инерции уже вычислен. При вращении вокруг оси x, расположенной в
плоскости, плоские фигуры (пластины) удобно делить на элементы массы в форме
стержня, перпендикулярного оси вращения. Если y(x) – функция, ограничивающая
часть пластины, отрезанную осью, то для этой части пластины
,
где ρ – масса единицы площади пластины. Например, для тонкого диска с массой M
и радиусом r при вращении вокруг диаметра ρ
,
, тогда
. Делая замену переменных
,
,
–
. Используя формулы для синуса и косинуса двойного угла,
несложно получить, что
. Тогда
.
МОМЕНТ ИНЕРЦИИ ТЕЛ ВРАЩЕНИЯ
Для вычисления моментов инерции тел вращения исходной является формула для
момента инерции тонкого кольца с массой m и радиусом r –
. Тогда тонкий
диск можно разделить на тонкие кольца. Соответственно для диска с массой M и
радиусом R масса единицы площади ρ
,
ρ
и
. Для цилиндра, как не трудно догадаться, момент инерции
вычисляется по точно такой же формуле.
Подобно тому, как пластины удобно делить на элементы массы в форме стержня, тела вращения удобно делить на элементы
массы в форме диска. Тело вращения – это фигура, ограниченная поверхностью, получаемой при вращении непрерывной
линии, начинающейся и заканчивающейся на оси вращения. Если эти две точки имеют координаты h1 и h2, а r(h) – функция,
определяющая зависимость расстояния от линии до оси вращения от координаты, то
ρ
, где ρ – масса единицы
объема тела. Тогда
иρ
. Например, для шара с массой M и радиусом R:
, тогда
,
,а
.
Таким образом, мы с вами рассмотрели, что такое момент инерции тела и какие существуют методы расчета моментов
инерции тел. Используя теорему Штейнера удобно находить моменты инерции тел, которые могут быть разделены на
себе подобные. Непосредственным интегрированием (по определению момента инерции тела) удобно пользоваться,
когда тела легко разделить на элементы массы, для которых моменты инерции уже известны. Пластины удобно
делить на элементы массы в форме стержня, тела вращения удобно делить на элементы массы в форме диска.

В этом уроке посмотрим, как определяются осевые моменты инерции для сложного сечения (состоящего из простых фигур).

Условие задачи

В качестве примера возьмём симметричное сечение, имеющее две оси симметрии:

Определение положения центра тяжести

Первым делом, необходимо определить положение центра тяжести сечения. Как это делается, можешь посмотреть в отдельном уроке, перейдя по указанной ссылке. Здесь же, я приведу только расчёт.

Подготовим сечение к расчёту:

• разобьём сечение на простейшие фигуры;
• обозначим центры тяжести отдельных фигур;
• введём вспомогательные координатные оси (y₀, x₀).

Площадь сечения

Используя эту страничку, найдём площади отдельных фигур:

Расстояния от центров тяжести отдельных фигур до вспомогательных осей

Статические моменты

Координаты центра тяжести

Покажем центр тяжести всего сечения:

Как видишь, центр тяжести находится ровно посередине сечения. Это свойство симметричного сечения. У такого сечения, которое имеет две оси симметрии, центр тяжести находится на пересечении этих осей. Поэтому для симметричного сечения можно и НЕ рассчитывать положение центра тяжести.

Расчёт осевых моментов инерции

Для выполнения дальнейшего расчёта следует обозначить центральные оси для всего сечения (x, y), а также собственные оси для каждой отдельной фигуры, которые формируют сечение:

Как определить моменты инерции относительно центральных осей?

Осевые моменты инерции (I_x, I_y) относительно центральных осей (x, y) можно определить по следующим формулам:

где I_xi, I_yi – моменты инерции отдельных фигур относительно собственных осей;

A_i – площади отдельных фигур;

y_ci, x_ci – расстояния от центров тяжести отдельных фигур до соответствующей центральной оси.

Определение моментов инерции для каждой фигуры

Определим осевые моменты инерции каждой отдельной фигуры, пользуясь справочной информацией:

Определение расстояний от центров тяжести каждой фигуры до центральных осей

Определение моментов инерции относительно центральных осей

Другие уроки, на проекте – ssopromat.ru, по расчёту геометрических характеристик можно найти здесь.