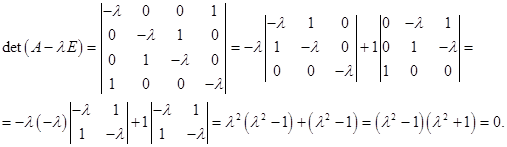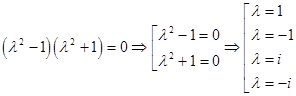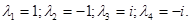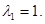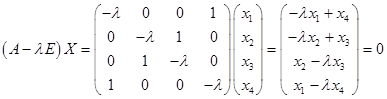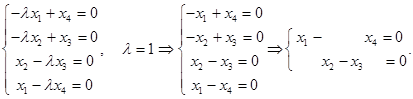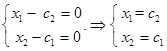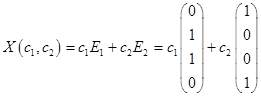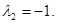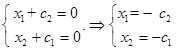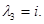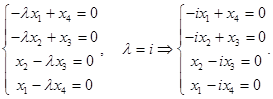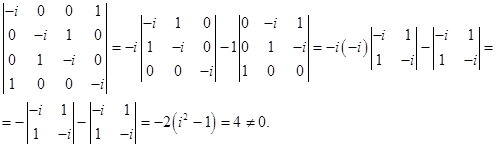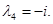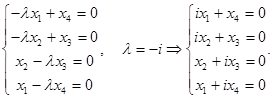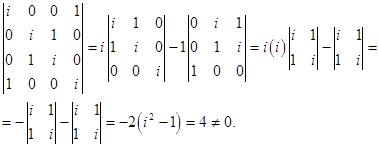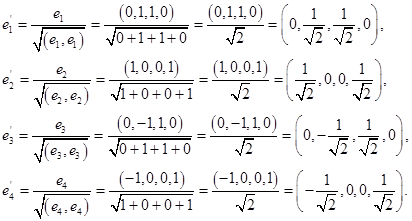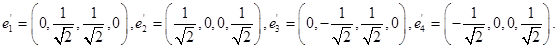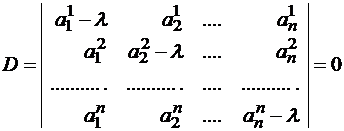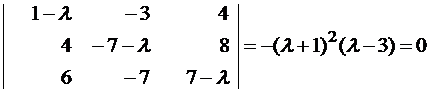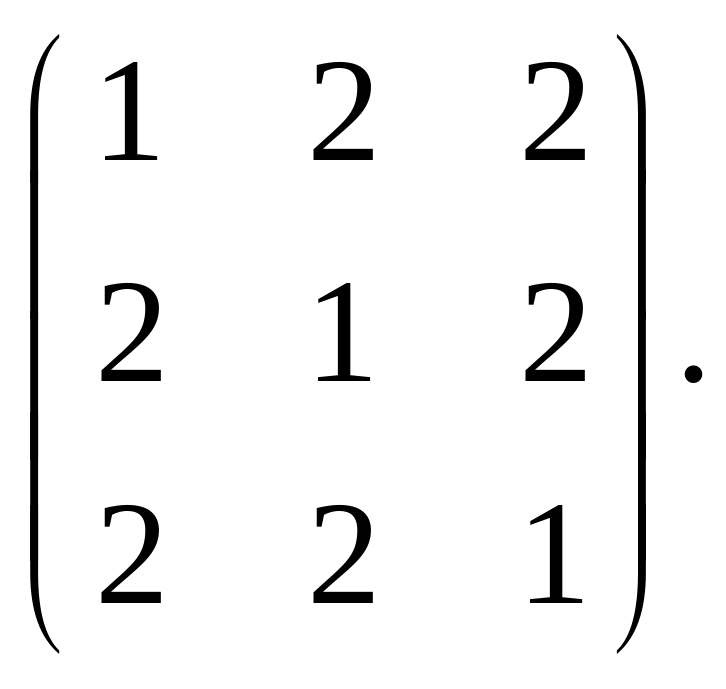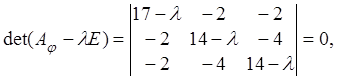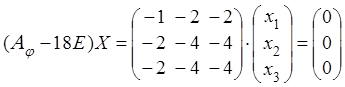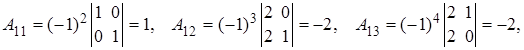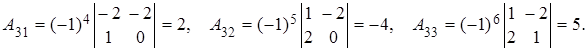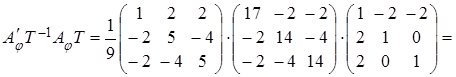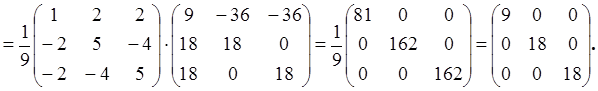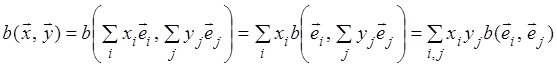Как найти собственный ортонормированный базис матрицы - Сайт, где вы сможете решить свои вопросы

Решение.

Найдем собственные вектора заданного линейного оператора.

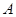
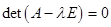
Число есть собственное число оператора в том и только том случае, когда . Запишем характеристическое уравнение:

Решая его, имеем

Таким образом, получаем собственные числа оператора:

Для каждого из полученных собственных значений найдем собственные векторы.

Их можно найти их системы .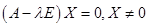

А)

Решим однородную систему уравнений.

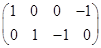
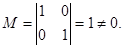
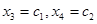
Матрица коэффициентов имеет ранг 2. Выберем в качестве базисного минора Тогда, полагая , имеем

Таким образом, общее решение системы

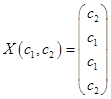
Из общего решения находим фундаментальную систему решений:

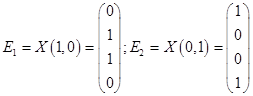
С использованием фундаментальной системы решений, общее решение может быть записано в виде .

Б)

Решим однородную систему уравнений

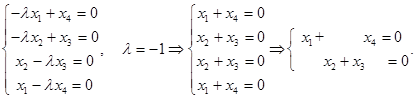
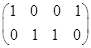
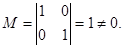
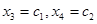
Матрица коэффициентов имеет ранг 2. Выберем в качестве базисного минора Тогда, полагая , имеем

Таким образом, общее решение системы .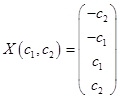

Из общего решения находим фундаментальную систему решений:

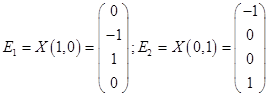
С использованием фундаментальной системы решений, общее решение может быть записано в виде

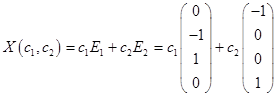
В)

Решим однородную систему уравнений.

Матрица коэффициентов 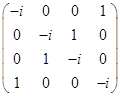имеет ранг 4, поскольку

Так как ранг равен количеству неизвестных, то система имеет только тривиальное решение.

Г)

Решим однородную систему уравнений.

Матрица коэффициентов 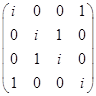имеет ранг 4, поскольку

Так как ранг равен количеству неизвестных, то система имеет только тривиальное решение.

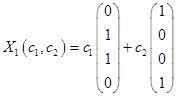
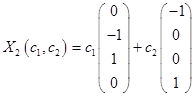
Таким образом, имеем собственные вектора и .

Выберем в качестве ортогонального базиса вектора , , , .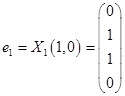

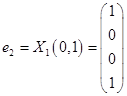
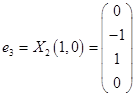
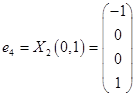
Нормируем найденный ортогональный базис:

Ответ:

Источник

104. Построение ортонормированного базиса из собственных векторов самосопряженного оператора

1) Составить характеристическое уравнение линейного оператора |A – l.E| = 0.

2) Найдем все корни характеристического уравнения.

3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A – l.E)X=0.

4) Ортонормируем, полученный базис.

Пример. Линейный оператор A, действующий в евклидовом пространстве Е3, имеет в ортонормированном базисе E1, E2, E3 матрицу

Найти в Е3 ортонормированный базис из собственных векторов оператора A и составить матрицу оператора A в этом базисе.

Решение. 1) Составить характеристическое уравнение линейного оператора |A – l.E| = 0.

2) Найдем все корни характеристического уравнения: l1=-1, l2 = l3 = 1. Тогда матрица линейного оператора в ортонормированном базисе, составленном из собственных векторов имеет вид

3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A – l.E)X=0.

Пусть l1=-1. Матричное уравнение (A – l1E)X=0 принимает вид:

Пусть l2 = l3 = 1. Матричное уравнение (A – l1E)X=0 принимает вид:

4) Ортонормируем, полученный базис.

B1 = (1,-2,1), B2 = (2,1,0), B3 = A3 + k b2, , b3 =(-1/5, 2/5, 1/5).

Собственные числа и собственные векторы линейного оператора

Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x ₁, x ₂, . x _m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x ₁, x ₂, . x _m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.
3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x ₁, x ₂, . x _n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 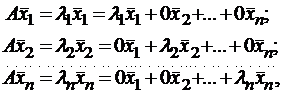тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе < ε _i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса – собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n – координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)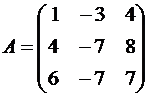
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x – собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

Замечания .

Все собственные числа симметрической матрицы вещественны.
Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Ортогональный и ортонормированный базисы евклидова пространства

Так как евклидово пространство является линейным, на него переносятся все понятия и свойства, относящиеся к линейному пространству, в частности, понятия базиса и размерности.

Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортогональным , если все образующие его векторы попарно ортогональны, т.е.

Базис [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] евклидова пространства называется ортонормированным , если его векторы попарно ортогональны и длина каждого из них равна единице:

Теорема 8.5. В конечномерном евклидовом пространстве любую систему ортогональных (ортонормированных) векторов можно дополнить до ортогонального (ортонормированного) базиса.

В самом деле, по теореме 8.2 любую систему линейно независимых векторов, в частности, ортогональную (ортонормированную), можно дополнить до базиса. Применяя к этому базису процесс ортогонализации, получаем ортогональный базис. Нормируя векторы этого базиса (см. пункт 4 замечаний 8.11), получаем ортонормированный базис.

Выражение скалярного произведения через координаты сомножителей

Пусть [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] — базис евклидова пространства, в котором векторы [math]mathbf[/math] и [math]mathbf[/math] имеют координаты [math]x_1,x_2,ldots,x_n[/math] и [math]y_1,y_2,ldots,y_n[/math] соответственно, т.е.

Выразим скалярное произведение, используя следствие 3 из аксиом скалярного произведения:

Преобразуем это выражение, используя операции с матрицами:

y=begin y_1&cdots& y_n end^T[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] , a [math]G(mathbf_1,mathbf_2,ldots, mathbf_n)[/math] — квадратная симметрическая матрица, составленная из скалярных произведений

которая называется матрицей Грама системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] .

Преимущества ортонормированного базиса

Для ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] формула (8.32) упрощается, так как из условия (8.31) следует, что матрица Грама [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)[/math] ортонормированной системы [math]mathbf_1, mathbf_2,ldots, mathbf_n[/math] равна единичной матрице: [math]G(mathbf_1, mathbf_2,ldots,mathbf_n)=E[/math] .

1. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] находится по формуле: [math]langle mathbf,mathbfrangle= x_1y_1+x_2y_2+ldots+x_ny_n[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] , а [math]y_1,ldots,y_n[/math] — координаты вектора [math]mathbf[/math] .

2. В ортонормированном базисе [math]mathbf_1,mathbf_2,ldots, mathbf_n[/math] длина вектора [math]mathbf[/math] вычисляется по формуле [math]|mathbf|= sqrt[/math] , где [math]x_1,ldots,x_n[/math] — координаты вектора [math]mathbf[/math] .

3. Координаты [math]x_1,ldots,x_n[/math] вектора [math]mathbf[/math] относительно ортонормированного базиса [math]mathbf_1,mathbf_2,ldots,mathbf_n[/math] находятся при помощи скалярного произведения по формулам: [math]x_1=langle mathbf,mathbf_1rangle,ldots, x_n=langle mathbf,mathbf_nrangle[/math] .

В самом деле, умножая обе части равенства [math]mathbf= x_1 mathbf_1+ldots+x_n mathbf_n[/math] на [math]mathbf_1[/math] , получаем

Аналогично доказываются остальные формулы.

Изменение матрицы Грама при переходе от одного базиса к другому

Пусть [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] и [math](mathbf)= (mathbf_1,ldots,mathbf_n)[/math] — два базиса евклидова пространства [math]mathbb[/math] , a [math]S[/math] — матрица перехода от базиса [math](mathbf)[/math] к базису [math](mathbf)colon, (mathbf)=(mathbf)S[/math] . Требуется найти связь матриц Грама систем векторов [math](mathbf)[/math] и [math](mathbf)[/math]

По формуле (8.32) вычислим скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] в разных базисах:

где [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] и [math]mathoplimits_<(mathbf)>,, mathoplimits_<(mathbf)>[/math] — координатные столбцы векторов [math]mathbf[/math] и [math]mathbf[/math] в соответствующих базисах. Подставляя в последнее равенство связи [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>,[/math] [math]mathoplimits_<(mathbf)>= S mathoplimits_<(mathbf)>[/math] , получаем тождество

Отсюда следует формула изменения матрицы Грама при переходе от одного базиса к другому :

Записав это равенство для ортонормированных базисов [math](mathbf)[/math] и [math](mathbf)[/math] , получаем [math]E=S^TES[/math] , так как матрицы Грама ортонормированных базисов единичные: [math]G(mathbf_1,ldots,mathbf_n)= G(mathbf_1,ldots,mathbf_n)=E[/math] . Поэтому матрица [math]S[/math] перехода от одного ортонормированного базиса к другому является ортогональной: [math]S^<-1>=S^T[/math] .

Свойства определителя Грама

Определитель матрицы (8.33) называется определителем Грама. Рассмотрим свойства этого определителя.

1. Критерий Грама линейной зависимости векторов: система векторов [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима тогда и только тогда, когда определитель Грама этой системы равен нулю.

Действительно, если система [math]mathbf_1, mathbf_2, ldots,mathbf_k[/math] линейно зависима, то существуют такие числа [math]x_1,x_2,ldots,x_k[/math] , не равные нулю одновременно, что

Умножая это равенство скалярно на [math]mathbf_1[/math] , затем на [math]mathbf_2[/math] и т.д. на [math]mathbf_k[/math] , получаем однородную систему уравнений [math]G(mathbf_1,mathbf_2,ldots,mathbf_k)x=o[/math] , которая имеет нетривиальное решение [math]x=beginx_1&cdots&x_k end^T[/math] . Следовательно, ее определитель равен нулю. Необходимость доказана. Достаточность доказывается, проводя рассуждения в обратном порядке.

Следствие. Если какой-либо главный минор матрицы Грама равен нулю, то и определитель Грама равен нулю.

Главный минор матрицы Грама системы [math]mathbf_1, mathbf_2,ldots,mathbf_k[/math] представляет собой определитель Грама подсистемы векторов. Если подсистема линейно зависима, то и вся система линейно зависима.

2. Определитель Грама [math]det_1,mathbf_2, ldots, mathbf_k)>[/math] не изменяется в процессе ортогонализации системы векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] . Другими словами, если в процессе ортогонализации векторов [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] получены векторы [math]mathbf_1,mathbf_2,ldots,mathbf_k[/math] , то

Действительно, в процессе ортогонализации по векторам [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] последовательно строятся векторы

После первого шага определитель Грама не изменяется

Выполним с определителем [math]det G(mathbf_1, mathbf_2, ldots,mathbf_k)[/math] следующие преобразования. Прибавим ко второй строке первую, умноженную на число [math](-alpha_<21>)[/math] , а затем ко второму столбцу прибавим первый, умноженный на [math](-alpha_<21>)[/math] . Получим определитель

Так как при этих преобразованиях определитель не изменяется, то

Значит, после второго шага в процессе ортогонализации определитель не изменяется. Продолжая аналогично, получаем после [math]k[/math] шагов:

Вычислим правую часть этого равенства. Матрица [math]G(mathbf_1,mathbf_2,ldots, mathbf_k)[/math] Грама ортогональной системы [math]mathbf_1,mathbf_2, ldots,mathbf_k[/math] векторов является диагональной, так как [math]langle mathbf_i,mathbf_jrangle=0[/math] при [math]ine j[/math] . Поэтому ее определитель равен произведению элементов, стоящих на главной диагонали:

3. Определитель Грама любой системы [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] векторов удовлетворяет двойному неравенству

Докажем неотрицательность определителя Грама. Если система [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] линейно зависима, то определитель равен нулю (по свойству 1). Если же система [math]mathbf_1,mathbf_2,ldots, mathbf_k[/math] линейно независима, то, выполнив процесс ортогонализации, получим ненулевые векторы [math]mathbf_1,mathbf_2, ldots, mathbf_k[/math] , для которых по свойству 2:

Оценим теперь скалярный квадрат [math]langle mathbf_j,mathbf_jrangle[/math] . Выполняя процесс ортого-1нализации, имеем [math]mathbf_j= mathbf_j+ alpha_mathbf_1+ ldots+ alpha_mathbf_[/math] . Отсюда

Следовательно, по свойству 2 имеем

1. Матрица Грама любой системы векторов является неотрицательно определенной, так как все ее главные миноры также являются определителями Грама соответствующих подсистем векторов и неотрицательны в силу свойства 3.

2. Матрица Грама любой линейно независимой системы векторов является положительно определенной, так как все ее угловые миноры положительны (в силу свойств 1,3), поскольку являются определителями Грама линейно независимых подсистем векторов.

3. Определитель квадратной матрицы [math]A[/math] (n-го порядка) удовлетворяет неравенству Адамара :

Действительно, обозначив [math]a_1,a_2,ldots,a_n[/math] столбцы матрицы [math]A[/math] , элементы матрицы [math]A^TA[/math] можно представить как скалярные произведения (8.27): [math]langle a_i,a_jrangle= (a_i)^Ta_j[/math] . Тогда [math]A^TA=G(a_1,a_2,ldots,a_n)[/math] — матрица Грама системы [math]a_1,a_2,ldots,a_n[/math] векторов пространства [math]mathbb^n[/math] . По свойству 3, теореме 2.2 и свойству 1 определителя получаем доказываемое неравенство:

4. Если [math]A[/math] — невырожденная квадратная матрица, то любой главный минор матрицы [math]A^TA[/math] положителен. Это следует из пункта 2, учитывая представление произведения [math]A^TA=G(a_1,ldots,a_n)[/math] как матрицы Грама системы линейно независимых векторов [math]a_1,ldots,a_n[/math] — столбцов матрицы [math]A[/math] (см. пункт 3).

Изоморфизм евклидовых пространств

Два евклидовых пространства [math]mathbb[/math] и [math]mathbb'[/math] называются изоморфными [math](mathbbleftrightarrow mathbb’)[/math] , если они изоморфны как линейные пространства и скалярные произведения соответствующих векторов равны:

где [math](cdot,cdot)[/math] и [math](cdot,cdot)'[/math] — скалярные произведения в пространствах [math]mathbb[/math] и [math]mathbb'[/math] соответственно.

Напомним, что для изоморфизма конечномерных линейных пространств необходимо и достаточно, чтобы их размерности совпадали (см. теорему 8.3). Покажем, что это условие достаточно для изоморфизма евклидовых пространств (необходимость следует из определения). Как и при доказательстве теоремы 8.3, установим изоморфизм n-мерного евклидова пространства [math]mathbb[/math] с вещественным арифметическим пространством [math]mathbb^n[/math] со скалярным произведением (8.27). В самом деле, взяв в пространстве [math]mathbb[/math] какой-нибудь ортонормированный базис [math](mathbf)=(mathbf_1,ldots,mathbf_n)[/math] , поставим в соответствие каждому вектору [math]mathbfin mathbb[/math] его координатный столбец [math]xin mathbb^n

(mathbfleftrightarrow x)[/math] . Это взаимно однозначное соответствие устанавливает изоморфизм линейных пространств: [math]mathbbleftrightarrow mathbb^n[/math] . В ортонормированном базисе скалярное произведение векторов [math]mathbf[/math] и [math]mathbf[/math] пространства [math]mathbb[/math] находится по формуле

(см. пункт 1 преимуществ ортонормированного базиса). Такое же выражение дает скалярное произведение (8.27) координатных столбцов [math]x[/math] и [math]y[/math] , т.е. скалярные произведения соответствующих элементов равны

Следовательно, евклидовы пространства [math]mathbb[/math] и [math]mathbb^n[/math] изоморфны.

Таким образом, изучение конечномерных евклидовых пространств может быть сведено к исследованию вещественного арифметического пространства [math]mathbb^n[/math] со стандартным скалярным произведением (8.27).

[spoiler title=”источники:”]

http://math.semestr.ru/math/vector.php

http://mathhelpplanet.com/static.php?p=ortogonalnyi-i-ortonormirovannyi-bazisy-evklidova-prostranstva

[/spoiler]

Источник

Собственные векторы симметрической матрицы

Ниже будет доказано,
что в пространстве

имеется ортонормированный базис,
состоящий из собственных векторов
симметрического преобразования. Сначала
докажем следующие леммы.

Лемма 1.
Даны две
матрицы

порядка n

где

и
–
матрицы порядка

.
Тогда
справедливы следующие утверждения:

2 . Если матрица

обратима и

,
то матрица

обратима и

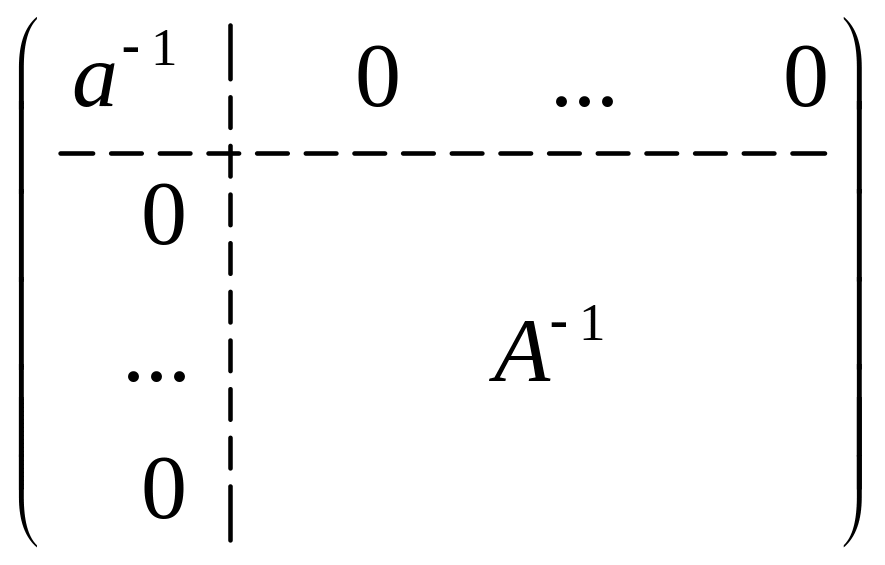
Доказательство

Найдем первую
строку и первый столбец матрицы

Теперь найдем
элемент матрицы

,
расположенный в

-й
строке и

-м
столбце,

,

2. Используя
доказанное выше первое утверждение
леммы, имеем

.
■

□ Лемма 2.
Если

– ортогональная матрица порядка

,
то

− ортогональная
матрица порядка
n.

Доказательство.
Из ортогональности матрицы

следует, что

(теорема 1.16). Ортогональность матрицы

будет вытекать из равенства

,
которое установим, используя лемму 1

■

Построение
ортонормированного базиса

,
состоящего из собственных векторов
симметрической матрицы, будет основываться
на следующей теореме.

□ Теорема 3.21.
Каждую
симметрическую матрицу

можно при помощи ортогональной матрицы

привести к диагональному виду

Доказательство
проведем
методом математической индукции по
порядку матрицы

.
Если матрица

имеет порядок, равный единице, т. е.

,
то она уже является диагональной. Далее,
единичная матрица

первого порядка, т. е.

,
обратима и обратная матрица имеет вид

.
Обе эти матрицы являются ортогональными.
Наконец, из матричного равенства

следует, что

.

Пусть теперь
утверждение теоремы справедливо для
всех симметрических матриц, порядок
которых равен

.
Докажем теорему для симметрической
матрицы

порядка

.
Из теоремы 3.20 следует, что матрица

имеет собственное значение

.
Возьмем в подпространстве

ненулевой вектор и нормируем его.
Полученный вектор обозначим символом

.
Так как

,
то

.
Дополним нормированный вектор

до ортонормированного базиса

пространства

и рассмотрим ортогональную матрицу

,
столбцами которой являются координаты
векторов этого ортонормированного
базиса. Теперь для первого столбца
матрицы

получим следующее выражение:

Отсюда следует,
что матрица

может быть записана в виде

Так как матрица

симметрическая (теорема 3.19), то все
элементы этой матрицы, расположенные
в первой строке, за исключением быть
может

,
равны нулю. Итак

Из леммы 1 вытекает,
что

Из симметричности
матрицы

вытекает равенство

.
Отсюда следует, что

и, значит,

симметрическая
матрица.

Симметрическая
матрица

имеет порядок

и, по предположению индукции, найдется
такая ортогональная матрица

,
что

Из леммы 2 следует
ортогональность матрицы

а из леммы 1 вытекает,
что матрица

обратима и

Теперь обозначим
произведение ортогональных матриц

символом

,
т. е.

.
Из теоремы 3.17 следует, что

– ортогональная матрица. Используя
лемму 1, получим следующую цепочку
равенств:

т. е. ортогональная
матрица

приводит матрицу

к диагональному виду. ■

Теперь доказанная
теорема 3.21 позволяет построить в
пространстве Rⁿ
ортонормированный базис, состоящий из
собственных векторов симметрического
преобразования

□ Теорема 3.22.
Пусть

все различные собственные значения
симметрической матрицы
_.
Тогда объединение ортонормированных
базисов подпространств

является ортонормированным базисом
пространства

Доказательство.
В каждом подпространстве

выберем ортонормированный базис. Из
теорем 3.21 и 3.11 следует, что объединенная
система этих базисов

является базисом Rⁿ.
В силу построения векторы

нормированы. Докажем ортогональность
этой системы векторов.

Пусть

– произвольные различные векторы
системы

.
Если они лежат в одном подпространстве

то они принадлежат ортонормированному
базису этого подпространства и, значит,
ортогональны. Пусть теперь

и

.
Тогда

Отсюда следует

,

Из симметричности
матрицы

вытекает равенство левых частей этих
равенств и, значит, равны их правые части

Так как собственные
значения

различны, то

и, значит,

■

Алгоритм построения
ортонормированного базиса пространства
,
состоящего из собственных векторов
симметрической матрицы

1. Найти собственные
значения матрицы

2. Для каждого
собственного значения

найти фундаментальный набор решений
системы уравнений

,
т. е. найти базис подпространства

3. Ортогонализировать
и нормировать найденные базисы
под-пространств.

4. Объединить
ортонормированные базисы подпространств

Пример

Найти ортонормированный
базис пространства

состоящий из собственных векторов
матрицы

Решение.
Сначала
найдем характеристический многочлен
матрицы

Собственные
значения матрицы

равны

2,
2 и 4.

Теперь надо найти
базисы подпространств

,

и

,
т. е. найти фундаментальные наборы
решений систем уравнений:

,

Базис подпространства

состоит из одного вектора

,
базис A(2)
образуют векторы

,

и базис подпространства

состоит из одного вектора

.

Базис подпространства

не является ортогональным. После его
ортогонализации и объединения базисов
всех подпространств получим
ортонормированный базис пространства

,
состоящий из собственных векторов
матрицы

:

.

Задачи

1. Доказать, что
для любой матрицы

матрица

– симметрическая матрица.

2. Доказать, что
для любой обратимой матрицы

матрица

будет симметрической тогда и только
тогда, когда симметрической будет
матрица

3. Доказать, что
если

− симметрические матрицы, то матрицы

также симметрические.

4. Доказать, что
симметрические матрицы

перестановочны тогда и только тогда,
когда

симметрическая матрица.

5. Доказать, что
матрица

cимметрическая,
если матрица

ортогональная и

=
Е.

6. Доказать, что
матрица

симметрическая, если в пространстве

имеется ортонормированный базис,
состоящий из собственных векторов
матрицы

Найти ортонормированный
базис пространства R
,
состоящий из собственных векторов
симметрической матрицы.

Найти ортогональную
матрицу, которая приводит симметрическую
матрицу к диагональному виду, написать
этот диагональный вид.

10.

11.

12.

13. Найти все
диагональные матрицы, к которым приводится
при помощи ортогональной матрицы
симметрическая матрица

106

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

1) Составить характеристическое уравнение линейного оператора |A – l.E| = 0.

2) Найдем все корни характеристического уравнения.

3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A – l.E)X=0.

4) Ортонормируем, полученный базис.

Решение. 1) Составить характеристическое уравнение линейного оператора |A – l.E| = 0.

3) Вычислим собственные векторы линейного оператора A, решая матричное уравнение (A – l.E)X=0.

Пусть l1=-1. Матричное уравнение (A – l1E)X=0 принимает вид:

Решая систему, находим решение X = C(1,-2,1), C€R.

Пусть l2 = l3 = 1. Матричное уравнение (A – l1E)X=0 принимает вид:

Решая систему, находим решение X = C1(2,1,0) + C2(-1,0,1), C€R.

4) Ортонормируем, полученный базис.

A1 = (1,-2,1), A2 = (2,1,0), A3 =(-1,0,1).

B1 = (1,-2,1), B2 = (2,1,0), B3 = A3 + k b2, , b3 =(-1/5, 2/5, 1/5).

< Предыдущая		Следующая >

Источник

, , следовательно, , так как –
произвольные векторы, то , следовательно, по
определению – ортогональная матрица и .

Пример 6.1. Пусть
линейный оператор , действующий в
евклидовом пространстве,
имеет в ортонормированном базисе матрицу . Построить в этом пространстве
базис из собственных векторов оператора и найти матрицу оператора в этом базисе.

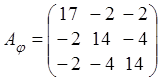
Решение.
1) Найдем собственные числа оператора , для
чего составим и решим характеристическое уравнение (4.3):

Приравняв
к нулю, находим:

2)
Находим собственные векторы, соответствующие найденным собственным значениям,
для чего при каждом составляем и решаем систему
(4.2): а)
при , получаем

что равносильно системе (здесь )

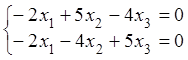
, полагая в которой, например, , находим , таким образом, собственный вектор,
соответствующий собственному значению 9, есть

б)
при , получаем

что равносильно
уравнению (здесь )

, полагая в котором
сначала , а затем ,
получаем еще два линейно независимых собственных вектора:

3)
Находим матрицу перехода к базису из собственных векторов и обратную к ней
(столбцами матрицы перехода являются координатные столбцы векторов (см.
раздел 1)):

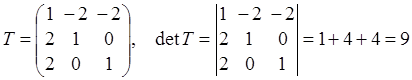
4)
Теперь по формуле (4.1) находим – матрицу
линейного оператора в базисе из собственных векторов

Таким
образом, матрица линейного оператора в базисе из собственных векторов диагональная!

7. БИЛИНЕЙНЫЕ
И КВАДРАТИЧНЫЕ ФОРМЫ

7.1.
Билинейные формы

Определение.
Отображение называется числовой функцией, т.е.
числовая функция – закон или правило, по которому каждому вектору (каждой паре векторов ) ставится в соответствие число из R.

Определение.
Числовая функция называется линейной формой,если и справедливо:

Определение.
Числовая функция двух аргументов – закон или правило, по которому каждой паре
векторов ставится в
соответствие число из .

Определение.
Числовая функция , аргументами которой
являются всевозможные векторы , называется билинейной
формой, если и выполняются соотношения:

а)

б)

в)

г)

т.е. функция является линейной по каждому из аргументов, где условия а),
в) означают линейность по первому аргументу; условия б), г) – по
второму.

Выберем какой – либо базис в . Тогда

и значение билинейной формы может
быть вычислено следующим образом

или

(7.1)

где (i, j = l, 2, …, n)
– значения билинейной формы на всевозможных парах базисных векторов,
которые называются коэффициентами билинейной формы в базисе е.

Коэффициенты образуют квадратную матрицу порядка п

, которая называется матрицей
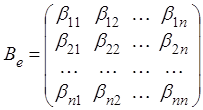
билинейной формы в данном базисе е. Как легко проверить, в матричном
виде равенство (7.1) имеет вид

(7.2)

Теорема
7.1. Любая квадратная матрица в некотором базисе
является матрицей билинейной формы.

Доказательство.
Определим с базисом с помощью матрицы числовую
функцию по правилу

Легко проверяются свойства
(7.1). Но тогда элементы равны , где , и
записанная формула есть определение билинейной формы (7.2).

Согласно
теореме 7.1., естественно называть представление (7.2.) общим видом билинейной
формы в n-мерном линейном Евклидовом пространстве .

Определение.
Билинейная форма называется симметричной
(кососимметричной), если выполняется равенство

Теорема
7.2. Билинейная форма является симметричной (кососимметричной) тогда и
только тогда, когда ее матрица симметрическая, т.е. или (кососимметрическая, т.е. или ).