Собственные векторы и собственные значения матрицы
Пусть — числовая квадратная матрица n-го порядка. Матрица
называется характеристической для
, а ее определитель
характеристическим многочленом матрицы
(7.12)
Характеристическая матрица — это λ-матрица. Ее можно представить в виде регулярного многочлена первой степени с матричными коэффициентами. Нетрудно заметить, что степень характеристического многочлена равна порядку характеристической матрицы.
Пусть — числовая квадратная матрица n-го порядка. Ненулевой столбец
, удовлетворяющий условию
(7.13)
называется собственным вектором матрицы . Число
в равенстве (7.13) называется собственным значением матрицы
. Говорят, что собственный вектор
соответствует {принадлежит) собственному значению
.
Поставим задачу нахождения собственных значений и собственных векторов матрицы. Определение (7.13) можно записать в виде , где
— единичная матрица n-го порядка. Таким образом, условие (7.13) представляет собой однородную систему
линейных алгебраических уравнений с
неизвестными
(7.14)
Поскольку нас интересуют только нетривиальные решения однородной системы, то определитель матрицы системы должен быть равен нулю:
(7.15)
В противном случае по теореме 5.1 система имеет единственное тривиальное решение. Таким образом, задача нахождения собственных значений матрицы свелась к решению уравнения (7.15), т.е. к отысканию корней характеристического многочлена матрицы
. Уравнение
называется характеристическим уравнением матрицы
. Так как характеристический многочлен имеет n-ю степень, то характеристическое уравнение — это алгебраическое уравнение n-го порядка. Согласно следствию 1 основной теоремы алгебры, характеристический многочлен можно представить в виде
где — корни многочлена кратности
соответственно, причем
. Другими словами, характеристический многочлен имеет п корней, если каждый корень считать столько раз, какова его кратность.
Теорема 7.4 о собственных значениях матрицы. Все корни характеристического многочлена (характеристического уравнения (7-15)) и только они являются собственными значениями матрицы.
Действительно, если число — собственное значение матрицы
, которому соответствует собственный вектор
, то однородная система (7.14) имеет нетривиальное решение, следовательно, матрица системы вырожденная, т.е. число
удовлетворяет характеристическому уравнению (7.15). Наоборот, если
— корень характеристического многочлена, то определитель (7.15) матрицы однородной системы (7.14) равен нулю, т.е.
.В этом случае система имеет бесконечное множество решений, включая ненулевые решения. Поэтому найдется столбец
, удовлетворяющий условию (7.14). Значит,
— собственное значение матрицы
.
Свойства собственных векторов
Пусть — квадратная матрица n-го порядка.
1. Собственные векторы, соответствующие различным собственным значениям, линейно независимы.
В самом деле, пусть и
— собственные векторы, соответствующие собственным значениям
и
, причем
. Составим произвольную линейную комбинацию этих векторов и приравняем ее нулевому столбцу:
(7.16)
Надо показать, что это равенство возможно только в тривиальном случае, когда . Действительно, умножая обе части на матрицу
и подставляя
и
имеем
Прибавляя к последнему равенству равенство (7.16), умноженное на , получаем
Так как и
, делаем вывод, что
. Тогда из (7.16) следует, что и
(поскольку
). Таким образом, собственные векторы
и
линейно независимы. Доказательство для любого конечного числа собственных векторов проводится по индукции.
2. Ненулевая линейная комбинация собственных векторов, соответствующих одному собственному значению, является собственным вектором, соответствующим тому же собственному значению.
Действительно, если собственному значению соответствуют собственные векторы
, то из равенств
, следует, что вектор
также собственный, поскольку:
3. Пусть — присоединенная матрица для характеристической матрицы
. Если
— собственное значение матрицы
, то любой ненулевой столбец матрицы
является собственным вектором, соответствующим собственному значению
.
В самом деле, применяя формулу (7.7) имеем . Подставляя корень
, получаем
. Если
— ненулевой столбец матрицы
, то
. Значит,
— собственный вектор матрицы
.
Замечания 7.5
1. По основной теореме алгебры характеристическое уравнение имеет п в общем случае комплексных корней (с учетом их кратностей). Поэтому собственные значения и собственные векторы имеются у любой квадратной матрицы. Причем собственные значения матрицы определяются однозначно (с учетом их кратности), а собственные векторы — неоднозначно.
2. Чтобы из множества собственных векторов выделить максимальную линейно независимую систему собственных векторов, нужно для всех раз личных собственных значений записать одну за другой системы линейно независимых собственных векторов, в частности, одну за другой фундаментальные системы решений однородных систем
Полученная система собственных векторов будет линейно независимой в силу свойства 1 собственных векторов.
3. Совокупность всех собственных значений матрицы (с учетом их кратностей) называют ее спектром.
4. Спектр матрицы называется простым, если собственные значения матрицы попарно различные (все корни характеристического уравнения простые).
5. Для простого корня характеристического уравнения соответствующий собственный вектор можно найти, раскладывая определитель матрицы
по одной из строк. Тогда ненулевой вектор, компоненты которого равны алгебраическим дополнениям элементов одной из строк матрицы
, является собственным вектором.
Нахождение собственных векторов и собственных значений матрицы
Для нахождения собственных векторов и собственных значений квадратной матрицы n-го порядка надо выполнить следующие действия.
1. Составить характеристический многочлен матрицы .
2. Найти все различные корни характеристического уравнения
(кратности
корней определять не нужно).
3. Для корня найти фундаментальную систему
решений однородной системы уравнений
, где
Для этого можно использовать либо алгоритм решения однородной системы, либо один из способов нахождения фундаментальной матрицы (см. пункт 3 замечаний 5.3, пункт 1 замечаний 5.5).
4. Записать линейно независимые собственные векторы матрицы , отвечающие собственному значению
(7.17)
где — отличные от нуля произвольные постоянные. Совокупность всех собственных векторов, отвечающих собственному значению
, образуют ненулевые столбцы вида
. Здесь и далее собственные векторы матрицы будем обозначать буквой
.
Повторить пункты 3,4 для остальных собственных значений .
Пример 7.8. Найти собственные значения и собственные векторы матриц:
Решение. Матрица . 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(1). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов второй строки матрицы , то есть
. Умножив этот столбец на (-1), получим
.
3(2). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(2). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , т.е.
. Поделив его на (- 3), получим
.
Матрица . 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(1). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , то есть
. Умножив этот столбец на (-1), получим
.
3(2). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду
Ранг матрицы системы равен 1 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисную переменную
через свободную:
. Полагая
, получаем решение
.
4(2). Записываем собственные векторы, соответствующие собственному значению , где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , т.е.
. Умножив его на (-1), получим
.
Матрица 1. Составляем характеристический многочлен матрицы
2. Решаем характеристическое уравнение: .
3(1). Для корня составляем однородную систему уравнений
Решаем эту систему методом Гаусса, приводя расширенную матрицу системы к упрощенному виду (ведущие элементы выделены полужирным курсивом):
Ранг матрицы системы равен 2 , число неизвестных
, следовательно, фундаментальная система решений состоит из
решения. Выражаем базисные переменные
через свободную
и, полагая
, получаем решение
.
4(1). Все собственные векторы, соответствующие собственному значению , вычисляются по формуле
, где
— отличная от нуля произвольная постоянная.
Заметим, что, согласно пункту 5 замечаний 7.5, в качестве собственного вектора можно выбрать вектор, составленный из алгебраических дополнений элементов первой строки матрицы , то есть
, так как
Разделив его на 3, получим .
3(2). Для собственного значения имеем однородную систему
. Решаем ее методом Гаусса:
Ранг матрицы системы равен единице , следовательно, фундаментальная система решений состоит из двух решений
. Базисную переменную
, выражаем через свободные:
. Задавая стандартные наборы свободных переменных
и
, получаем два решения
4(2). Записываем множество собственных векторов, соответствующих собственному значению , где
— произвольные постоянные, не равные нулю одновременно. В частности, при
получаем
; при
. Присоединяя к этим собственным векторам собственный вектор
, соответствующий собственному значению
(см. пункт 4(1) при
), находим три линейно независимых собственных вектора матрицы
Заметим, что для корня собственный вектор нельзя найти, применяя пункт 5 замечаний 7.5, так как алгебраическое дополнение каждого элемента матрицы
равно нулю.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Алгоритм вычисления собственных значений — алгоритм, позволяющий определить собственные значения и собственные векторы заданной матрицы. Создание эффективных и устойчивых алгоритмов для этой задачи является одной из ключевых задач вычислительной математики.
Собственные значения и собственные векторы[править | править код]
Если задана n × n квадратная матрица A над вещественными или комплексными числами, то собственное значение λ и соответствующий ему корневой вектор v — это пара, удовлетворяющая равенству[1]
где v ненулевой n × 1 вектор-столбец, E является n × n единичной матрицей, k — положительным целым, а λ и v могут быть комплексными, даже если A вещественна. Если k = 1, вектор просто называется собственным вектором. В этом случае Av = λv. Любое собственное значение λ матрицы A имеет простой[note 1] собственный вектор, соответствующий ему так, что если k — наименьшее целое, при котором (A – λE)k v = 0 для корневого вектора v, то (A – λE)k-1 v будет простым собственным вектором. Значение k всегда можно взять меньше либо равным n. В частности, (A – λE)n v = 0 для всех корневых векторов v, соответствующих λ.
Для любого собственного значения λ матрицы A ядро ker(A – λE) состоит из всех собственных векторов, соответствующих λ, (вместе с 0) и называется собственным подпространством числа λ, а векторное подпространство ker((A – λE)n) состоит из всех корневых векторов (дополненное нулевым вектором) и называется корневым подпространством. Геометрическая кратность значения λ является размерностью его собственного подпространства. Алгебраическая кратность значения λ является размерностью его корневого подпространства. Дальнейшие термины связаны с равенством
Здесь det — определитель, λi — все различные собственные значения матрицы A, а αi — соответствующие алгебраические кратности. Функция pA(z) — это характеристический многочлен матрицы A. Таким образом, алгебраическая кратность является кратностью собственных значений как корней характеристического многочлена. Поскольку любой собственный вектор является корневым вектором, геометрическая кратность меньше либо равна алгебраической кратности. Сумма алгебраических кратностей равна n степени характеристического многочлена. Уравнение pA(z) = 0 называется характеристическим уравнением, поскольку его корни являются в точности собственными значениями матрицы A. По теореме Гамильтона — Кэли сама матрица A удовлетворяет тому же самому уравнению: pA(A) = 0[note 2]. Как следствие, столбцы матрицы 

Любой набор корневых векторов различных собственных значений линейно независим, так что базис для всего C n можно выбрать из набора корневых векторов. Точнее этот базис {vi}n
i=1 можно выбрать и выстроить так, что
-
- если vi и vj имеют одно и то же собственное значение, то тоже будет верно для любого vk при k между i и j;
- если vi не является простым собственным вектором и если λi его собственное значение, то (A – λiE )vi = vi-1 (в частности v1 должен быть простым собственным вектором).
Если эти базисные вектора расположить как столбцы матрицы V = [ v1 v2 … vn ], то V можно использовать для преобразования матрицы A в её нормальную жорданову форму:
где λi — собственные значения, βi = 1 если (A – λi+1)vi+1 = vi и βi = 0 в других случаях.
Если W является обратимой матрицей и λ — собственное значение матрицы A с соответствующим корневым вектором v, то (W -1AW – λE )k W –kv = 0. Таким образом, λ является собственным значением матрицы W -1AW с соответствующим корневым вектором W –kv. Таким образом, подобные матрицы имеют те же самые собственные значения.
Нормальные, эрмитовы и вещественные симметричные матрицы[править | править код]
Эрмитово-сопряжённая матрица M* к комплексной матрице M — это траспонированная матрица с заменой всех элементов на сопряжённые значения: M * = M T. Квадратная матрица A называется нормальной, если она коммутирует с эрмитово-сопряжённой: A*A = AA*. Матрица называется эрмитовой, если она равна своей сопряжённой: A* = A. Все эрмитовы матрицы нормальны. Если A имеет только вещественные элементы, то сопряжённая к ней — это просто транспонированная матрица, и она будет эрмитовой в том и только в том случае, когда она симметрична. Если применить это к столбцам, сопряжённость можно использовать для определения канонического скалярного произведения в C n: w • v = w* v[note 3]. Нормальные, эрмитовы и вещественные симметричные матрицы имеют ряд полезных свойств:
-
- Каждый корневой собственный вектор нормальной матрицы является простым собственным вектором.
- Любая нормальная матрица подобна диагональной, поскольку её нормальная жорданова форма является диагональной матрицей.
- Собственные вектора, соответствующие различным собственным значениям нормальной матрицы, ортогональны.
- Для любой нормальной матрицы A C n имеет ортонормальный базис, состоящий из собственных векторов матрицы A. Соответствующая матрица собственных векторов является унитарной.
- Собственные значения эрмитовой матрицы являются вещественными числами, поскольку (λ – λ)v = (A* – A)v = (A – A)v = 0 для ненулевого собственного вектора v.
- Если матрица A вещественна, существует ортонормальный базис для R n, состоящий из собственных векторов матрицы A, в том и только в том случае, когда A симметрична.
Возможно как для вещественных, так и для комплексных матриц иметь все собственные значения вещественными, не будучи при этом эрмитовой матрицей. Например, вещественная треугольная матрица имеет все свои собственные значения на диагонали, но, в общем случае, не симметрична.
Число обусловленности[править | править код]
Любую задачу вычислительной математики можно рассматривать как вычисление некоторой функции ƒ от некоторого аргумента x. Число обусловленности κ(ƒ, x) задачи — это отношение относительной ошибки результата вычисления к относительной ошибке параметра функции и зависит как от функции, так и от параметра. Число обусловленности описывает насколько возрастает ошибка во время вычислений. Десятичный логарифм этого числа говорит о количестве знаков, которые мы теряем по отношению к исходным данным. Число обусловленности относится к наилучшему сценарию, отражая нестабильность самой задачи, независимо от способа решения. Никакой алгоритм не может дать результат лучше, чем определённый числом обусловленности, разве что случайно. Однако плохо разработанный алгоритм может дать существенно более плохие результаты. Например, как будет упомянуто ниже, задача нахождения собственных значений нормальной матрицы всегда хорошо обусловлена, однако задача нахождения корней многочлена может быть очень плохо обусловлена[en]. Такие алгоритмы вычисления собственных значений, которые работают путём нахождения корней характеристического многочлена, могут оказаться плохо обусловленными, даже если сама задача хорошо обусловлена.
Для задачи решения системы линейных уравнений Av = b, где A является обратимой, число обусловленности κ(A-1, b) определяется выражением ||A||op||A-1||op, где || ||op — операторная норма, подчинённая обычной евклидовой норме на C n. Поскольку это число не зависит от b и является тем же самым как для A, так и для A-1, оно обычно называется числом обусловленности κ(A) матрицы A. Это значение κ(A) является также абсолютным значением отношения наибольшего собственного значения матрицы A к её наименьшему собственному значению. Если A является унитарной, то ||A||op = ||A-1||op = 1, так что κ(A) = 1. В общем случае для матриц часто сложно вычислить операторную норму. По этой причине обычно используют другие нормы матрицы для оценки числа обусловленности.
Для задачи вычисления собственных значений Бауэр и Файк доказали[en], что если λ является собственным значением диагонализируемой n × n матрицы A с матрицей собственных векторов V, то абсолютная ошибка вычисления λ ограничена произведением κ(V) и абсолютной ошибкой в A:
[2]. Как следствие, число обусловленности для вычисления λ равно
κ(λ, A) = κ(V) = ||V ||op ||V -1||op. Если матрица A нормальна, то V является унитарной и κ(λ, A) = 1. Таким образом, задача вычисления собственных значений нормальных матриц хорошо обусловлена.
Было показано, что число обусловленности задачи вычисления собственного подпространства нормальной матрицы A, соответствующего собственному значению λ, обратно пропорционально минимальному расстоянию между λ и другими, отличными от λ, собственными значениями матрицы A[3]. В частности, задача определения собственного подпространства для нормальных матриц хорошо обусловлена для изолированных собственных значений. Если собственные значения не изолированы, лучшее, на что мы можем рассчитывать, это определение подпространства всех собственных векторов близлежащих собственных значений.
Алгоритмы[править | править код]
Любой нормированный многочлен является характеристическим многочленом сопровождающей матрицы, поэтому алгоритм для вычисления собственных значений можно использовать для нахождения корней многочленов. Теорема Абеля — Руффини показывает, что любой такой алгоритм для размерности большей 4 должен либо быть бесконечным, либо вовлекать функции более сложные, чем элементарные арифметические операции или дробные степени. По этой причине алгоритмы, вычисляющие точно собственные значения за конечное число шагов, существуют только для специальных классов матриц. В общем случае алгоритмы являются итеративными, дающими на каждой итерации очередное приближение к решению.
Некоторые алгоритмы дают все собственные значения, другие дают несколько значений или даже всего одно, однако и эти алгоритмы можно использовать для вычисления всех собственных значений. Как только собственное значение λ матрицы A определено, его можно использовать либо для приведения алгоритма к получению другого собственного значения, либо для сведения задачи к такой, которая не имеет λ в качестве решения.
Приведение обычно осуществляется сдвигом: A заменяется на A – μE для некоторой константы μ. Собственное значение, найденное для A – μE, должно быть добавлено к μ, чтобы получить собственное значение матрицы A. Например, в степенном методе μ = λ. Итерация степенного метода находит самое большое по абсолютной величине значение, так что даже если λ является приближением к собственному значению, итерация степенного метода вряд ли найдёт его во второй раз. И наоборот, методы, основанные на обратных итерациях находят наименьшее собственное значение, так что μ выбирается подальше от λ в надежде оказаться ближе к какому-нибудь другому собственному значению.
Приведение можно совершить путём сужения матрицы A к пространству столбцов матрицы A – λE. Поскольку A – λE вырождена, пространство столбцов имеет меньшую размерность. Алгоритм вычисления собственных значений можно тогда применить к этой суженой матрице. Процесс можно продолжать, пока не будут найдены все собственные значения.
Если алгоритм не даёт к собственные значения, общей практикой является применение алгоритма, основанного на обратной итерации, с приравниванием μ к ближайшей аппроксимации собственного значения. Это быстро приводит к собственному вектору ближайшего к μ собственного значения. Для небольших матриц альтернативой служит использование столбцового подпространства произведения A – λ́E для каждого из остальных собственных значений λ́.
Матрицы Хессенберга и трёхдиагональные матрицы[править | править код]
Поскольку собственными значениями треугольной матрицы являются диагональные элементы, в общем случае не существует конечного метода, подобного исключениям Гаусса, для приведения матрицы к треугольной форме, сохраняя при этом собственные значения, однако можно получить нечто близкое к треугольной матрице. Верхняя матрица Хессенберга — это квадратная матрица, у которой все элементы ниже первой поддиагонали равны нулю. Нижняя матрица Хессенберга — это квадратная матрица, у которой все члены выше первой наддиагонали равны нулю. Матрицы, которые являются как нижними, так и верхними матрицами Хессенберга — это трёхдиагональные матрицы. Матрицы Хессенберга и трёхдиагональные матрицы являются исходными точками многих алгоритмов вычисления собственных значений, поскольку нулевые значения уменьшают сложность задачи. Существует несколько методов сведения матриц к матрицам Хессенберга с теми же собственными значениями. Если исходная матрица симметрична или эрмитова, то результирующая матрица будет трёхдиагональной.
Если нужны только собственные значения, нет необходимости вычислять матрицу подобия, поскольку преобразованная матрица имеет те же собственные значения. Если также нужны и собственные векторы, матрица подобия необходима для преобразования собственных векторов матрицы Хессенберга к собственным векторам исходной матрицы.
| Метод | Применим к матрицам | Результат | Цена без матрицы подобия | Цена с матрицей подобия | Описание |
|---|---|---|---|---|---|
| Преобразования Хаусхолдера | общего вида | матрица Хессенберга | 2n3⁄3 + O(n2)[4] | 4n3⁄3 + O(n2)[4] | Отражение каждого столбца относительно подпространства для обнуления нижних элементов столбца. |
| Повороты Гивенса | общего вида | матрица Хессенберга | 4n3⁄3 + O(n2)[4] | Осуществляется плоское вращении для обнуления отдельных элементов. Вращения упорядочены так, что следующие вращения не затрагивают нулевые элементы. | |
| Итерации Арнольди | общего вида | матрица Хессенберга | Осуществляется ортогонализация Грама ― Шмидта на подпространствах Крылова. | ||
| Алгоритм Ланцоша[en][5] | эрмитова | трёхдиагональная матрица | Итерации Арнольди для эрмитовых матриц. |
Итеративные алгоритмы[править | править код]
Итеративные алгоритмы решают задачу вычисления собственных значений путём построения последовательностей, сходящихся к собственным значениям. Некоторые алгоритмы дают также последовательности векторов, сходящихся к собственным векторам. Чаще всего последовательности собственных значений выражаются через последовательности подобных матриц, которые сходятся к треугольной или диагональной форме, что позволяет затем просто получить собственные значения. Последовательности собственных векторов выражаются через соответствующие матрицы подобия.
| Метод | Применим к матрицам | Результат | Цена за один шаг | Сходимость | Описание |
|---|---|---|---|---|---|
| Степенной метод | общего вида | наибольшее собственное значение и соответствующий вектор | O(n2) | Линейная | Многократное умножение матрицы на произвольно выбранный начальный вектор с последующей нормализацией. |
| Обратный степенной метод | общего вида | ближайшее к μ собственное значение и соответствующий вектор | Линейная | Степенная итерация с матрицей (A – μE )-1 | |
| Метод итераций Рэлея | общего вида | ближайшее к μ собственное значение и соответствующий вектор | Кубическая | Степенная итерация с матрицей (A – μiE )-1, где μi является отношением Рэлея от предыдущей итерации. | |
| Предобусловленная обратная итерация[6] или LOBPCG[en] | положительно определённая вещественная симметричная | ближайшее к μ собственное значение и соответствующий вектор | Обратная итерация с предобуславливанием (приближённое обращение матрицы A). | ||
| Метод деления пополам[7] | вещественная симметричная трёхдиагональная | любое собственное значение | Линейная | Использует метод бисекции для поиска корней характеристического многочлена и свойства последовательности Штурма. | |
| Итерации Лагерра | вещественная симметричная трёхдиагональная | любое собственное значение | Кубическая[8] | Использует метод Лагерра[en] вычисления корней характеристического многочлена и свойства последовательности Штурма. | |
| QR-алгоритм[9] | хессенберга | все собственные значения | O(n2) | Кубическая | Разложение A = QR, где Q ортогональная, R ― треугольная, затем используется итерация к RQ. |
| все собственные значения | 6n3 + O(n2) | ||||
| Метод Якоби | вещественная симметричная | все собственные значения | O(n3) | квадратичная | Использует поворот Гивенса в попытке избавиться от недиагональных элементов. Попытка не удаётся, но усиливает диагональ. |
| Разделяй и властвуй[en] | эрмитова трёхдиагональная | все собственные значения | O(n2) | Матрица разбивается на подматрицы, которые диагонализируются, затем воссоединяются. | |
| все собственные значения | (4⁄3)n3 + O(n2) | ||||
| Метод гомотопии | вещественная симметричная трёхдиагональная | все собственные значения | O(n2)[10] | Строится вычисляемая гомотопия. | |
| Метод спектральной свёртки[en] | вещественная симметричная | ближайшее к μ собственное значение и соответствующий собственный вектор | Предобусловленная обратная итерация, применённая к (A – μE )2 | ||
| Алгоритм MRRR[11] | вещественная симметричная трёхдиагональная | некоторые или все собственные значения и соответствующие собственные вектора | O(n2) | «Multiple Relatively Robust Representations» — Осуществляется обратная итерация с разложением LDLT смещённой матрицы. |
Прямое вычисление[править | править код]
Не существует простых алгоритмов прямого вычисления собственных значений для матриц в общем случае, но для многих специальных классов матриц собственные значения можно вычислить прямо. Это:
Треугольные матрицы[править | править код]
Поскольку определитель треугольной матрицы является произведением её диагональных элементов, то для треугольной матрицы T 
Разложимые полиномиальные уравнения[править | править код]
Если p ― любой многочлен и p(A) = 0, то собственные значения матрицы A удовлетворяют тому же уравнению. Если удаётся разложить многочлен p на множители, то собственные значения A находятся среди его корней.
Например, проектор ― это квадратная матрица P, удовлетворяющая уравнению P2 = P. Корнями соответствующего скалярного полиномиального уравнения λ2 = λ будут 0 и 1. Таким образом, проектор имеет 0 и 1 в качестве собственных значений. Кратность собственного значения 0 ― это дефект P, в то время как кратность 1 ― это ранг P.
Другой пример ― матрица A, удовлетворяющая уравнению A2 = α2E для некоторого скаляра α. Собственные значения должны быть равны ±α. Операторы проектирования
удовлетворяют равенствам
и
Пространства столбцов матриц P+ и P– являются подпространствами собственных векторов матрицы A, соответствующими +α и -α, соответственно.
Матрицы 2×2[править | править код]
Для размерностей от 2 до 4 существуют использующие радикалы формулы, которые можно использовать для вычисления собственных значений. Для матриц 2×2 и 3×3 это обычная практика, но для матриц 4×4 растущая сложность формул корней[en] делает этот подход менее привлекательным.
Для матриц 2×2
характеристический многочлен равен
Собственные значения можно найти как корни квадратного уравнения:
Если определить 
с подобными формулами для c и d. Отсюда следует, что вычисление хорошо обусловлено, если собственные значения изолированы.
Собственные векторы можно получить, используя теорему Гамильтона — Кэли. Если λ1, λ2 — собственные значения, то (A – λ1E )(A – λ2E ) = (A – λ2E )(A – λ1E ) = 0, так что столбцы (A – λ2E ) обнуляются матрицей (A – λ1E ) и наоборот. Предполагая, что ни одна из матриц не равна нулю, столбцы каждой матрицы должны содержать собственные векторы для другого собственного значения (если же матрица нулевая, то A является произведением единичной матрицы на константу и любой ненулевой вектор является собственным).
Например, пусть
тогда tr(A) = 4 – 3 = 1 и det(A) = 4(-3) – 3(-2) = -6, так что характеристическое уравнение равно
а собственные значения равны 3 и −2. Теперь
,
В обеих матрицах столбцы отличаются скалярными коэффициентами, так что можно выбирать любой столбец. Так, (1, -2) можно использовать в качестве собственного вектора, соответствующего собственному значению −2, а (3, -1) в качестве собственного вектора для собственного числа 3, что легко можно проверить умножением на матрицу A.
Матрицы 3×3[править | править код]
Если A является матрицей 3×3, то характеристическим уравнением будет:
Это уравнение можно решить с помощью методов Кардано или Лагранжа, но аффинное преобразование матрицы A существенно упрощает выражение и ведёт прямо к тригонометрическому решению. Если A = pB + qE, то A и B имеют одни и те же собственные векторы и β является собственным значением матрицы B тогда и только тогда, когда α = pβ + q является собственным значением матрицы A. Если положить 

Подстановка β = 2cos θ и некоторое упрощение с использованием тождества cos 3θ = 4cos3 θ – 3cos θ сводит уравнение к cos 3θ = det(B) / 2. Таким образом,
Если det(B) является комплексным числом или больше 2 по абсолютной величине, арккосинус для всех трёх величин k следует брать из одной и той же ветви. Проблема не возникает, если A вещественна и симметрична, приводя к простому алгоритму:[12]
% Given a real symmetric 3x3 matrix A, compute the eigenvalues p1 = A(1,2)^2 + A(1,3)^2 + A(2,3)^2 if (p1 == 0) % A is diagonal. eig1 = A(1,1) eig2 = A(2,2) eig3 = A(3,3) else q = trace(A)/3 p2 = (A(1,1) - q)^2 + (A(2,2) - q)^2 + (A(3,3) - q)^2 + 2 * p1 p = sqrt(p2 / 6) B = (1 / p) * (A - q * E) % E is the identity matrix r = det(B) / 2 % In exact arithmetic for a symmetric matrix -1 <= r <= 1 % but computation error can leave it slightly outside this range. if (r <= -1) phi = pi / 3 elseif (r >= 1) phi = 0 else phi = acos(r) / 3 end % the eigenvalues satisfy eig3 <= eig2 <= eig1 eig1 = q + 2 * p * cos(phi) eig3 = q + 2 * p * cos(phi + (2*pi/3)) eig2 = 3 * q - eig1 - eig3 % since trace(A) = eig1 + eig2 + eig3 end
Снова, собственные векторы A можно получить путём использования теоремы Гамильтона — Кэли. Если α1, α2, α3 — различные собственные значения матрицы A, то (A – α1E)(A – α2E)(A – α3E) = 0. Тогда столбцы произведения любых двух из этих матриц содержат собственные векторы третьего собственного значения. Однако если a3 = a1, то (A – α1E)2(A – α2E) = 0 и (A – α2E)(A – α1E)2 = 0. Таким образом, корневое собственное подпространство α1 натянуто на столбцы A – α2E, в то время как обычное собственное подпространство натянуто на столбцы (A – α1E)(A – α2E). Обычное собственное подпространство α2 натянуто на столбцы (A – α1E)2.
Например, пусть
Характеристическое уравнение равно
с собственными значениями 1 (кратности 2) и −1. Вычисляем
,
а затем
.
Тогда (-4, -4, 4) является собственным вектором для −1, а (4, 2, -2) является собственным вектором для 1. Векторы (2, 3, -1) и (6, 5, -3) являются корневыми векторами, соответствующими значению 1, любой из которых можно скомбинировать с (-4, -4, 4) и (4, 2, -2), образуя базис корневых векторов матрицы A.
См. также[править | править код]
- Список алгоритмов вычисления собственных значений[en]
Комментарии[править | править код]
- ↑ Термин «простой» здесь употребляется лишь для подчёркивания различия между «собственным вектором» и «корневым вектором».
- ↑ где постоянный член умножается на единичную матрицу E.
- ↑ Такой порядок в скалярном произведении (с сопряжённым элементом слева) предпочитают физики. Алгебраисты часто предпочитают запись w • v = v* w.
Примечания[править | править код]
- ↑ Sheldon Axler. Down with Determinants! // American Mathematical Monthly. — 1995. — Вып. 102. — С. 139—154.
- ↑ F. L. Bauer, C. T. Fike. Norms and exclusion theorems // Numer. Math. — 1960. — Вып. 2. — С. 137—141.
- ↑ S. C. Eisenstat, I. C. F. Ipsen. Relative Perturbation Results for Eigenvalues and Eigenvectors of Diagonalisable Matrices // BIT. — 1998. — Т. 38, вып. 3. — С. 502—9. — doi:10.1007/bf02510256.
- ↑ 1 2 3 William H. Press, Saul A. Teukolsky, William T. Vetterling, Brian P. Flannery. Numerical Recipes in C. — 2nd. — Cambridge University Press, 1992. — ISBN 0-521-43108-5.
- ↑ Х. Д. Икрамов. Разреженные матрицы. — 1982. — Т. 20. — (Итоги науки и техники. Сер. Мат. анал).
- ↑ K. Neymeyr. A geometric theory for preconditioned inverse iteration IV: On the fastest convergence cases. // Linear Algebra Appl. — 2006. — Т. 415, вып. 1. — С. 114—139. — doi:10.1016/j.laa.2005.06.022.
- ↑ Уилкинсон, 1970, стр. 274, Метод деления пополам
- ↑ T. Y Li, Zhonggang Zeng. Laguerre’s Iteration In Solving The Symmetric Tridiagonal Eigenproblem – Revisited // SIAM Journal on Scientific Computing. — 1992.
- ↑ Парлетт, 1983, стр. 156, глава 8, Алгоритмы QR и QL
- ↑ Moody T. Chu. A Note on the Homotopy Method for Linear Algebraic Eigenvalue Problems // Linear Algebra Appl. — 1988. — Т. 105. — С. 225—236. — doi:10.1016/0024-3795(88)90015-8.
- ↑ Inderjit S. Dhillon, Beresford N. Parlett, Christof Vömel. The Design and Implementation of the MRRR Algorithm // ACM Transactions on Mathematical Software. — 2006. — Т. 32, вып. 4. — С. 533—560. — doi:10.1145/1186785.1186788.
- ↑ Oliver K. Smith. Eigenvalues of a symmetric 3 × 3 matrix // Communications of the ACM. — Т. 4, вып. 4. — С. 168. — doi:10.1145/355578.366316.
Литература[править | править код]
- Дж. Голуб, Ч. Ван Лоун. Матричные вычисления. — Москва: «Мир», 1999. — ISBN 5-03-002406-9.
- Б. Парлетт. Симметричная проблема собственных значений. — Москва: «Мир», 1983.
- Дж. Х. Уилкинсон. Алгебраическая проблема собственных значений. — Москва: «Наука» Главная редакция физико-математической литературы, 1970.
Дополнительная литература[править | править код]
- Adam W. Bojanczyk, Adam Lutoborski. Computation of the Euler angles of a symmetric 3X3 matrix // SIAM Journal on Matrix Analysis and Applications. — Jan 1991. — Т. 12, вып. 1. — С. 41—48. — doi:10.1137/0612005.
Собственные числа и собственные векторы матрицы.
Определение 9.3. Вектор х
называется собственным вектором
матрицы А, если найдется такое число
λ, что выполняется равенство: Ах
= λх, то есть результатом
применения к х линейного
преобразования, задаваемого матрицей
А, является умножение этого вектора
на число λ. Само число λ называется
собственным числом матрицы А.
Подставив в формулы (9.3) x`j
= λxj,
получим систему уравнений для определения
координат собственного вектора:
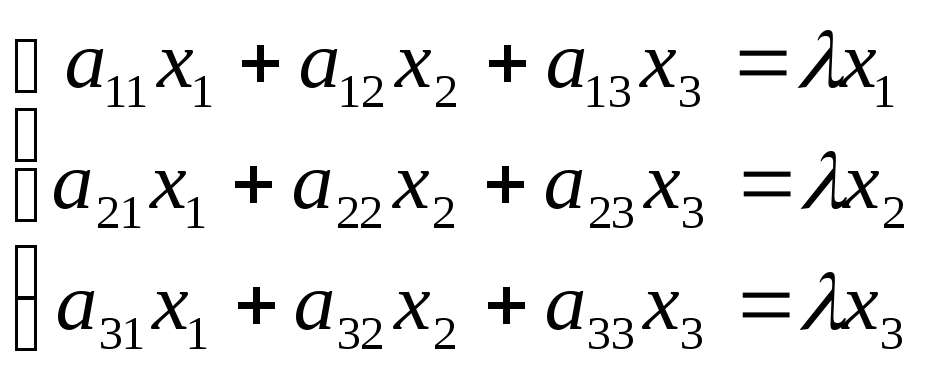
Отсюда

(9.5)
Эта линейная однородная система будет
иметь нетривиальное решение только в
случае, если ее главный определитель
равен 0 (правило Крамера). Записав это
условие в виде:
получим уравнение для определения
собственных чисел λ, называемое
характеристическим уравнением.
Кратко его можно представить так:
| A
– λE
| = 0,
(9.6)
поскольку в его левой части стоит
определитель матрицы А-λЕ. Многочлен
относительно λ | A
– λE| называется
характеристическим многочленом
матрицы А.
Свойства характеристического
многочлена:
-
Характеристический многочлен линейного
преобразования не зависит от выбора
базиса.
Доказательство.
(см.
(9.4)), но
следовательно,
.
Таким образом,
не зависит от выбора базиса. Значит, и
|A-λE|
не изменяется при переходе к новому
базису. -
Если матрица А линейного преобразования
является симметрической (т.е.
аij=aji),
то все корни характеристического
уравнения (9.6) – действительные числа.
Свойства собственных чисел и
собственных векторов:
-
Если выбрать базис из собственных
векторов х1,
х2, х3,
соответствующих собственным значениям
λ1, λ2, λ3
матрицы А, то в этом базисе линейное
преобразование А имеет матрицу
диагонального вида:
(9.7)
Доказательство
этого свойства следует из определения
собственных векторов.
-
Если собственные значения преобразования
А различны, то соответствующие им
собственные векторы линейно независимы. -
Если характеристический многочлен
матрицы А имеет три различных корня,
то в некотором базисе матрица А
имеет диагональный вид.
Пример.
Найдем собственные числа и собственные
векторы матрицы
Составим характеристическое уравнение:
(1- λ)(5 –
λ)(1 – λ) + 6 – 9(5 – λ) – (1 – λ) –
(1 – λ) = 0, λ³ – 7λ² + 36 = 0, λ1
= -2, λ2 = 3, λ3 = 6.
Найдем координаты собственных векторов,
соответствующих каждому найденному
значению λ. Из (9.5) следует, что если
х(1)={x1,x2,x3}
– собственный вектор, соответствующий
λ1=-2, то
– совместная, но неопределенная система.
Ее решение можно записать в виде
х(1)={a,0,-a},
где а – любое число. В частности, если
потребовать, чтобы |x(1)|=1,
х(1)=
Подставив в систему (9.5) λ2=3,
получим систему для определения координат
второго собственного вектора –
x(2)={y1,y2,y3}:

откуда х(2)={b,-b,b}
или, при условии |x(2)|=1,
x(2)=
Для λ3 = 6 найдем собственный
вектор x(3)={z1,
z2, z3}:

x(3)={c,2c,c}
или в нормированном варианте
х(3) =
Можно
заметить, что х(1)х(2)
= ab – ab
= 0, x(1)x(3)
= ac – ac
= 0, x(2)x(3)
= bc – 2bc
+ bc = 0. Таким
образом, собственные векторы этой
матрицы попарно ортогональны.
Лекция 10.
Квадратичные формы и их связь с
симметричными матрицами. Свойства
собственных векторов и собственных
чисел симметричной матрицы. Приведение
квадратичной формы к каноническому
виду.
Определение 10.1. Квадратичной
формой действительных переменных
х1, х2,…,хn
называется многочлен второй степени
относительно этих переменных, не
содержащий свободного члена и членов
первой степени.
Примеры квадратичных форм:
(n = 2),
(n = 3). (10.1)
Напомним данное в прошлой лекции
определение симметрической матрицы:
Определение 10.2. Квадратная матрица
называется симметрической, если
,
то есть если равны элементы матрицы,
симметричные относительно главной
диагонали.
Свойства собственных чисел и
собственных векторов симметрической
матрицы:
-
Все собственные числа симметрической
матрицы действительные.
Доказательство (для n
= 2).
Пусть матрица А имеет вид:

Составим характеристическое уравнение:
(10.2) Найдем дискриминант:
следовательно, уравнение имеет только
действительные корни.
-
Собственные векторы симметрической
матрицы ортогональны.
Доказательство (для n
= 2).
Координаты собственных векторов
и
должны удовлетворять уравнениям:
Следовательно, их можно задать так:
.
Скалярное произведение этих векторов
имеет вид:
По теореме Виета из уравнения (10.2)
получим, что
Подставим эти соотношения в предыдущее
равенство:
Значит,
.
Замечание. В примере, рассмотренном в
лекции 9, были найдены собственные
векторы симметрической матрицы и
обращено внимание на то, что они оказались
попарно ортогональными.
Определение 10.3. Матрицей квадратичной
формы (10.1) называется симметрическая
матрица

(10.3)
Таким образом, все собственные числа
матрицы квадратичной формы действительны,
а все собственные векторы ортогональны.
Если все собственные числа различны,
то из трех нормированных собственных
векторов матрицы (10.3) можно построить
базис в трехмерном пространстве. В этом
базисе квадратичная форма будет иметь
особый вид, не содержащий произведений
переменных.
Соседние файлы в папке лекции, 1 сем.
- #
- #
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by 
Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed.[1] Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated.
Formal definition[edit]
If T is a linear transformation from a vector space V over a field F into itself and v is a nonzero vector in V, then v is an eigenvector of T if T(v) is a scalar multiple of v.[2] This can be written as
where λ is a scalar in F, known as the eigenvalue, characteristic value, or characteristic root associated with v.
There is a direct correspondence between n-by-n square matrices and linear transformations from an n-dimensional vector space into itself, given any basis of the vector space. Hence, in a finite-dimensional vector space, it is equivalent to define eigenvalues and eigenvectors using either the language of matrices, or the language of linear transformations.[3][4]
If V is finite-dimensional, the above equation is equivalent to[5]
where A is the matrix representation of T and u is the coordinate vector of v.
Overview[edit]
Eigenvalues and eigenvectors feature prominently in the analysis of linear transformations. The prefix eigen- is adopted from the German word eigen (cognate with the English word own) for ‘proper’, ‘characteristic’, ‘own’.[6][7] Originally used to study principal axes of the rotational motion of rigid bodies, eigenvalues and eigenvectors have a wide range of applications, for example in stability analysis, vibration analysis, atomic orbitals, facial recognition, and matrix diagonalization.
In essence, an eigenvector v of a linear transformation T is a nonzero vector that, when T is applied to it, does not change direction. Applying T to the eigenvector only scales the eigenvector by the scalar value λ, called an eigenvalue. This condition can be written as the equation
referred to as the eigenvalue equation or eigenequation. In general, λ may be any scalar. For example, λ may be negative, in which case the eigenvector reverses direction as part of the scaling, or it may be zero or complex.
In this shear mapping the red arrow changes direction, but the blue arrow does not. The blue arrow is an eigenvector of this shear mapping because it does not change direction, and since its length is unchanged, its eigenvalue is 1.
A 2×2 real and symmetric matrix representing a stretching and shearing of the plane. The eigenvectors of the matrix (red lines) are the two special directions such that every point on them will just slide on them.
The Mona Lisa example pictured here provides a simple illustration. Each point on the painting can be represented as a vector pointing from the center of the painting to that point. The linear transformation in this example is called a shear mapping. Points in the top half are moved to the right, and points in the bottom half are moved to the left, proportional to how far they are from the horizontal axis that goes through the middle of the painting. The vectors pointing to each point in the original image are therefore tilted right or left, and made longer or shorter by the transformation. Points along the horizontal axis do not move at all when this transformation is applied. Therefore, any vector that points directly to the right or left with no vertical component is an eigenvector of this transformation, because the mapping does not change its direction. Moreover, these eigenvectors all have an eigenvalue equal to one, because the mapping does not change their length either.
Linear transformations can take many different forms, mapping vectors in a variety of vector spaces, so the eigenvectors can also take many forms. For example, the linear transformation could be a differential operator like 
Alternatively, the linear transformation could take the form of an n by n matrix, in which case the eigenvectors are n by 1 matrices. If the linear transformation is expressed in the form of an n by n matrix A, then the eigenvalue equation for a linear transformation above can be rewritten as the matrix multiplication
where the eigenvector v is an n by 1 matrix. For a matrix, eigenvalues and eigenvectors can be used to decompose the matrix—for example by diagonalizing it.
Eigenvalues and eigenvectors give rise to many closely related mathematical concepts, and the prefix eigen- is applied liberally when naming them:
- The set of all eigenvectors of a linear transformation, each paired with its corresponding eigenvalue, is called the eigensystem of that transformation.[8][9]
- The set of all eigenvectors of T corresponding to the same eigenvalue, together with the zero vector, is called an eigenspace, or the characteristic space of T associated with that eigenvalue.[10]
- If a set of eigenvectors of T forms a basis of the domain of T, then this basis is called an eigenbasis.
History[edit]
Eigenvalues are often introduced in the context of linear algebra or matrix theory. Historically, however, they arose in the study of quadratic forms and differential equations.
In the 18th century, Leonhard Euler studied the rotational motion of a rigid body, and discovered the importance of the principal axes.[a] Joseph-Louis Lagrange realized that the principal axes are the eigenvectors of the inertia matrix.[11]
In the early 19th century, Augustin-Louis Cauchy saw how their work could be used to classify the quadric surfaces, and generalized it to arbitrary dimensions.[12] Cauchy also coined the term racine caractéristique (characteristic root), for what is now called eigenvalue; his term survives in characteristic equation.[b]
Later, Joseph Fourier used the work of Lagrange and Pierre-Simon Laplace to solve the heat equation by separation of variables in his famous 1822 book Théorie analytique de la chaleur.[13] Charles-François Sturm developed Fourier’s ideas further, and brought them to the attention of Cauchy, who combined them with his own ideas and arrived at the fact that real symmetric matrices have real eigenvalues.[12] This was extended by Charles Hermite in 1855 to what are now called Hermitian matrices.[14]
Around the same time, Francesco Brioschi proved that the eigenvalues of orthogonal matrices lie on the unit circle,[12] and Alfred Clebsch found the corresponding result for skew-symmetric matrices.[14] Finally, Karl Weierstrass clarified an important aspect in the stability theory started by Laplace, by realizing that defective matrices can cause instability.[12]
In the meantime, Joseph Liouville studied eigenvalue problems similar to those of Sturm; the discipline that grew out of their work is now called Sturm–Liouville theory.[15] Schwarz studied the first eigenvalue of Laplace’s equation on general domains towards the end of the 19th century, while Poincaré studied Poisson’s equation a few years later.[16]
At the start of the 20th century, David Hilbert studied the eigenvalues of integral operators by viewing the operators as infinite matrices.[17] He was the first to use the German word eigen, which means “own”,[7] to denote eigenvalues and eigenvectors in 1904,[c] though he may have been following a related usage by Hermann von Helmholtz. For some time, the standard term in English was “proper value”, but the more distinctive term “eigenvalue” is the standard today.[18]
The first numerical algorithm for computing eigenvalues and eigenvectors appeared in 1929, when Richard von Mises published the power method. One of the most popular methods today, the QR algorithm, was proposed independently by John G. F. Francis[19] and Vera Kublanovskaya[20] in 1961.[21][22]
Eigenvalues and eigenvectors of matrices[edit]
Eigenvalues and eigenvectors are often introduced to students in the context of linear algebra courses focused on matrices.[23][24]
Furthermore, linear transformations over a finite-dimensional vector space can be represented using matrices,[3][4] which is especially common in numerical and computational applications.[25]
Matrix A acts by stretching the vector x, not changing its direction, so x is an eigenvector of A.
Consider n-dimensional vectors that are formed as a list of n scalars, such as the three-dimensional vectors
These vectors are said to be scalar multiples of each other, or parallel or collinear, if there is a scalar λ such that
In this case 
Now consider the linear transformation of n-dimensional vectors defined by an n by n matrix A,
or
where, for each row,
If it occurs that v and w are scalar multiples, that is if
-
(1)
then v is an eigenvector of the linear transformation A and the scale factor λ is the eigenvalue corresponding to that eigenvector. Equation (1) is the eigenvalue equation for the matrix A.
Equation (1) can be stated equivalently as
-
(2)
where I is the n by n identity matrix and 0 is the zero vector.
Eigenvalues and the characteristic polynomial[edit]
Equation (2) has a nonzero solution v if and only if the determinant of the matrix (A − λI) is zero. Therefore, the eigenvalues of A are values of λ that satisfy the equation
-
(3)
Using the Leibniz formula for determinants, the left-hand side of Equation (3) is a polynomial function of the variable λ and the degree of this polynomial is n, the order of the matrix A. Its coefficients depend on the entries of A, except that its term of degree n is always (−1)nλn. This polynomial is called the characteristic polynomial of A. Equation (3) is called the characteristic equation or the secular equation of A.
The fundamental theorem of algebra implies that the characteristic polynomial of an n-by-n matrix A, being a polynomial of degree n, can be factored into the product of n linear terms,
-
(4)
where each λi may be real but in general is a complex number. The numbers λ1, λ2, …, λn, which may not all have distinct values, are roots of the polynomial and are the eigenvalues of A.
As a brief example, which is described in more detail in the examples section later, consider the matrix
Taking the determinant of (A − λI), the characteristic polynomial of A is
Setting the characteristic polynomial equal to zero, it has roots at λ=1 and λ=3, which are the two eigenvalues of A. The eigenvectors corresponding to each eigenvalue can be found by solving for the components of v in the equation 
If the entries of the matrix A are all real numbers, then the coefficients of the characteristic polynomial will also be real numbers, but the eigenvalues may still have nonzero imaginary parts. The entries of the corresponding eigenvectors therefore may also have nonzero imaginary parts. Similarly, the eigenvalues may be irrational numbers even if all the entries of A are rational numbers or even if they are all integers. However, if the entries of A are all algebraic numbers, which include the rationals, the eigenvalues must also be algebraic numbers (that is, they cannot magically become transcendental numbers).
The non-real roots of a real polynomial with real coefficients can be grouped into pairs of complex conjugates, namely with the two members of each pair having imaginary parts that differ only in sign and the same real part. If the degree is odd, then by the intermediate value theorem at least one of the roots is real. Therefore, any real matrix with odd order has at least one real eigenvalue, whereas a real matrix with even order may not have any real eigenvalues. The eigenvectors associated with these complex eigenvalues are also complex and also appear in complex conjugate pairs.
Algebraic multiplicity[edit]
Let λi be an eigenvalue of an n by n matrix A. The algebraic multiplicity μA(λi) of the eigenvalue is its multiplicity as a root of the characteristic polynomial, that is, the largest integer k such that (λ − λi)k divides evenly that polynomial.[10][26][27]
Suppose a matrix A has dimension n and d ≤ n distinct eigenvalues. Whereas Equation (4) factors the characteristic polynomial of A into the product of n linear terms with some terms potentially repeating, the characteristic polynomial can instead be written as the product of d terms each corresponding to a distinct eigenvalue and raised to the power of the algebraic multiplicity,
If d = n then the right-hand side is the product of n linear terms and this is the same as Equation (4). The size of each eigenvalue’s algebraic multiplicity is related to the dimension n as
If μA(λi) = 1, then λi is said to be a simple eigenvalue.[27] If μA(λi) equals the geometric multiplicity of λi, γA(λi), defined in the next section, then λi is said to be a semisimple eigenvalue.
Eigenspaces, geometric multiplicity, and the eigenbasis for matrices[edit]
Given a particular eigenvalue λ of the n by n matrix A, define the set E to be all vectors v that satisfy Equation (2),
On one hand, this set is precisely the kernel or nullspace of the matrix (A − λI). On the other hand, by definition, any nonzero vector that satisfies this condition is an eigenvector of A associated with λ. So, the set E is the union of the zero vector with the set of all eigenvectors of A associated with λ, and E equals the nullspace of (A − λI). E is called the eigenspace or characteristic space of A associated with λ.[28][10] In general λ is a complex number and the eigenvectors are complex n by 1 matrices. A property of the nullspace is that it is a linear subspace, so E is a linear subspace of 
Because the eigenspace E is a linear subspace, it is closed under addition. That is, if two vectors u and v belong to the set E, written u, v ∈ E, then (u + v) ∈ E or equivalently A(u + v) = λ(u + v). This can be checked using the distributive property of matrix multiplication. Similarly, because E is a linear subspace, it is closed under scalar multiplication. That is, if v ∈ E and α is a complex number, (αv) ∈ E or equivalently A(αv) = λ(αv). This can be checked by noting that multiplication of complex matrices by complex numbers is commutative. As long as u + v and αv are not zero, they are also eigenvectors of A associated with λ.
The dimension of the eigenspace E associated with λ, or equivalently the maximum number of linearly independent eigenvectors associated with λ, is referred to as the eigenvalue’s geometric multiplicity γA(λ). Because E is also the nullspace of (A − λI), the geometric multiplicity of λ is the dimension of the nullspace of (A − λI), also called the nullity of (A − λI), which relates to the dimension and rank of (A − λI) as
Because of the definition of eigenvalues and eigenvectors, an eigenvalue’s geometric multiplicity must be at least one, that is, each eigenvalue has at least one associated eigenvector. Furthermore, an eigenvalue’s geometric multiplicity cannot exceed its algebraic multiplicity. Additionally, recall that an eigenvalue’s algebraic multiplicity cannot exceed n.
To prove the inequality 




















Suppose 





is the dimension of the sum of all the eigenspaces of 


Additional properties of eigenvalues[edit]
Let 




- The trace of
, defined as the sum of its diagonal elements, is also the sum of all eigenvalues,[29][30][31]
- The determinant of
is the product of all its eigenvalues,[29][32][33]
- The eigenvalues of the
th power of
; i.e., the eigenvalues of
, for any positive integer
, are
.
- The matrix
is invertible if and only if every eigenvalue is nonzero.
- If
is invertible, then the eigenvalues of
are
and each eigenvalue’s geometric multiplicity coincides. Moreover, since the characteristic polynomial of the inverse is the reciprocal polynomial of the original, the eigenvalues share the same algebraic multiplicity.
- If
is equal to its conjugate transpose
, or equivalently if
is Hermitian, then every eigenvalue is real. The same is true of any symmetric real matrix.
- If
is not only Hermitian but also positive-definite, positive-semidefinite, negative-definite, or negative-semidefinite, then every eigenvalue is positive, non-negative, negative, or non-positive, respectively.
- If
is unitary, every eigenvalue has absolute value
.
- if
is a
matrix and
are its eigenvalues, then the eigenvalues of matrix
(where
is the identity matrix) are
. Moreover, if
, the eigenvalues of
are
. More generally, for a polynomial
the eigenvalues of matrix
are
.
Left and right eigenvectors[edit]
Many disciplines traditionally represent vectors as matrices with a single column rather than as matrices with a single row. For that reason, the word “eigenvector” in the context of matrices almost always refers to a right eigenvector, namely a column vector that right multiplies the 

The eigenvalue and eigenvector problem can also be defined for row vectors that left multiply matrix 
where 





Comparing this equation to Equation (1), it follows immediately that a left eigenvector of 





Diagonalization and the eigendecomposition[edit]
Suppose the eigenvectors of A form a basis, or equivalently A has n linearly independent eigenvectors v1, v2, …, vn with associated eigenvalues λ1, λ2, …, λn. The eigenvalues need not be distinct. Define a square matrix Q whose columns are the n linearly independent eigenvectors of A,
Since each column of Q is an eigenvector of A, right multiplying A by Q scales each column of Q by its associated eigenvalue,
With this in mind, define a diagonal matrix Λ where each diagonal element Λii is the eigenvalue associated with the ith column of Q. Then
Because the columns of Q are linearly independent, Q is invertible. Right multiplying both sides of the equation by Q−1,
or by instead left multiplying both sides by Q−1,
A can therefore be decomposed into a matrix composed of its eigenvectors, a diagonal matrix with its eigenvalues along the diagonal, and the inverse of the matrix of eigenvectors. This is called the eigendecomposition and it is a similarity transformation. Such a matrix A is said to be similar to the diagonal matrix Λ or diagonalizable. The matrix Q is the change of basis matrix of the similarity transformation. Essentially, the matrices A and Λ represent the same linear transformation expressed in two different bases. The eigenvectors are used as the basis when representing the linear transformation as Λ.
Conversely, suppose a matrix A is diagonalizable. Let P be a non-singular square matrix such that P−1AP is some diagonal matrix D. Left multiplying both by P, AP = PD. Each column of P must therefore be an eigenvector of A whose eigenvalue is the corresponding diagonal element of D. Since the columns of P must be linearly independent for P to be invertible, there exist n linearly independent eigenvectors of A. It then follows that the eigenvectors of A form a basis if and only if A is diagonalizable.
A matrix that is not diagonalizable is said to be defective. For defective matrices, the notion of eigenvectors generalizes to generalized eigenvectors and the diagonal matrix of eigenvalues generalizes to the Jordan normal form. Over an algebraically closed field, any matrix A has a Jordan normal form and therefore admits a basis of generalized eigenvectors and a decomposition into generalized eigenspaces.
Variational characterization[edit]
In the Hermitian case, eigenvalues can be given a variational characterization. The largest eigenvalue of 


Matrix examples[edit]
Two-dimensional matrix example[edit]
The transformation matrix A = ![{displaystyle left[{begin{smallmatrix}2&1\1&2end{smallmatrix}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/838a30dc9d065ec434dff490bd84061ed569db3b)
Consider the matrix
The figure on the right shows the effect of this transformation on point coordinates in the plane. The eigenvectors v of this transformation satisfy Equation (1), and the values of λ for which the determinant of the matrix (A − λI) equals zero are the eigenvalues.
Taking the determinant to find characteristic polynomial of A,
Setting the characteristic polynomial equal to zero, it has roots at λ=1 and λ=3, which are the two eigenvalues of A.
For λ=1, Equation (2) becomes,
Any nonzero vector with v1 = −v2 solves this equation. Therefore,
is an eigenvector of A corresponding to λ = 1, as is any scalar multiple of this vector.
For λ=3, Equation (2) becomes
Any nonzero vector with v1 = v2 solves this equation. Therefore,
is an eigenvector of A corresponding to λ = 3, as is any scalar multiple of this vector.
Thus, the vectors vλ=1 and vλ=3 are eigenvectors of A associated with the eigenvalues λ=1 and λ=3, respectively.
Three-dimensional matrix example[edit]
Consider the matrix
The characteristic polynomial of A is
The roots of the characteristic polynomial are 2, 1, and 11, which are the only three eigenvalues of A. These eigenvalues correspond to the eigenvectors 


Three-dimensional matrix example with complex eigenvalues[edit]
Consider the cyclic permutation matrix
This matrix shifts the coordinates of the vector up by one position and moves the first coordinate to the bottom. Its characteristic polynomial is 1 − λ3, whose roots are
where 

For the real eigenvalue λ1 = 1, any vector with three equal nonzero entries is an eigenvector. For example,
For the complex conjugate pair of imaginary eigenvalues,
Then
and
Therefore, the other two eigenvectors of A are complex and are 

Diagonal matrix example[edit]
Matrices with entries only along the main diagonal are called diagonal matrices. The eigenvalues of a diagonal matrix are the diagonal elements themselves. Consider the matrix
The characteristic polynomial of A is
which has the roots λ1 = 1, λ2 = 2, and λ3 = 3. These roots are the diagonal elements as well as the eigenvalues of A.
Each diagonal element corresponds to an eigenvector whose only nonzero component is in the same row as that diagonal element. In the example, the eigenvalues correspond to the eigenvectors,
respectively, as well as scalar multiples of these vectors.
Triangular matrix example[edit]
A matrix whose elements above the main diagonal are all zero is called a lower triangular matrix, while a matrix whose elements below the main diagonal are all zero is called an upper triangular matrix. As with diagonal matrices, the eigenvalues of triangular matrices are the elements of the main diagonal.
Consider the lower triangular matrix,
The characteristic polynomial of A is
which has the roots λ1 = 1, λ2 = 2, and λ3 = 3. These roots are the diagonal elements as well as the eigenvalues of A.
These eigenvalues correspond to the eigenvectors,
respectively, as well as scalar multiples of these vectors.
Matrix with repeated eigenvalues example[edit]
As in the previous example, the lower triangular matrix
has a characteristic polynomial that is the product of its diagonal elements,
The roots of this polynomial, and hence the eigenvalues, are 2 and 3. The algebraic multiplicity of each eigenvalue is 2; in other words they are both double roots. The sum of the algebraic multiplicities of all distinct eigenvalues is μA = 4 = n, the order of the characteristic polynomial and the dimension of A.
On the other hand, the geometric multiplicity of the eigenvalue 2 is only 1, because its eigenspace is spanned by just one vector 

Eigenvector-eigenvalue identity[edit]
For a Hermitian matrix, the norm squared of the jth component of a normalized eigenvector can be calculated using only the matrix eigenvalues and the eigenvalues of the corresponding minor matrix,
where 
Eigenvalues and eigenfunctions of differential operators[edit]
The definitions of eigenvalue and eigenvectors of a linear transformation T remains valid even if the underlying vector space is an infinite-dimensional Hilbert or Banach space. A widely used class of linear transformations acting on infinite-dimensional spaces are the differential operators on function spaces. Let D be a linear differential operator on the space C∞ of infinitely differentiable real functions of a real argument t. The eigenvalue equation for D is the differential equation
The functions that satisfy this equation are eigenvectors of D and are commonly called eigenfunctions.
Derivative operator example[edit]
Consider the derivative operator 
This differential equation can be solved by multiplying both sides by dt/f(t) and integrating. Its solution, the exponential function
is the eigenfunction of the derivative operator. In this case the eigenfunction is itself a function of its associated eigenvalue. In particular, for λ = 0 the eigenfunction f(t) is a constant.
The main eigenfunction article gives other examples.
General definition[edit]
The concept of eigenvalues and eigenvectors extends naturally to arbitrary linear transformations on arbitrary vector spaces. Let V be any vector space over some field K of scalars, and let T be a linear transformation mapping V into V,
We say that a nonzero vector v ∈ V is an eigenvector of T if and only if there exists a scalar λ ∈ K such that
-
(5)
This equation is called the eigenvalue equation for T, and the scalar λ is the eigenvalue of T corresponding to the eigenvector v. T(v) is the result of applying the transformation T to the vector v, while λv is the product of the scalar λ with v.[37][38]
Eigenspaces, geometric multiplicity, and the eigenbasis[edit]
Given an eigenvalue λ, consider the set
which is the union of the zero vector with the set of all eigenvectors associated with λ. E is called the eigenspace or characteristic space of T associated with λ.[39]
By definition of a linear transformation,
for x, y ∈ V and α ∈ K. Therefore, if u and v are eigenvectors of T associated with eigenvalue λ, namely u, v ∈ E, then
So, both u + v and αv are either zero or eigenvectors of T associated with λ, namely u + v, αv ∈ E, and E is closed under addition and scalar multiplication. The eigenspace E associated with λ is therefore a linear subspace of V.[40]
If that subspace has dimension 1, it is sometimes called an eigenline.[41]
The geometric multiplicity γT(λ) of an eigenvalue λ is the dimension of the eigenspace associated with λ, i.e., the maximum number of linearly independent eigenvectors associated with that eigenvalue.[10][27][42] By the definition of eigenvalues and eigenvectors, γT(λ) ≥ 1 because every eigenvalue has at least one eigenvector.
The eigenspaces of T always form a direct sum. As a consequence, eigenvectors of different eigenvalues are always linearly independent. Therefore, the sum of the dimensions of the eigenspaces cannot exceed the dimension n of the vector space on which T operates, and there cannot be more than n distinct eigenvalues.[d]
Any subspace spanned by eigenvectors of T is an invariant subspace of T, and the restriction of T to such a subspace is diagonalizable. Moreover, if the entire vector space V can be spanned by the eigenvectors of T, or equivalently if the direct sum of the eigenspaces associated with all the eigenvalues of T is the entire vector space V, then a basis of V called an eigenbasis can be formed from linearly independent eigenvectors of T. When T admits an eigenbasis, T is diagonalizable.
Spectral theory[edit]
If λ is an eigenvalue of T, then the operator (T − λI) is not one-to-one, and therefore its inverse (T − λI)−1 does not exist. The converse is true for finite-dimensional vector spaces, but not for infinite-dimensional vector spaces. In general, the operator (T − λI) may not have an inverse even if λ is not an eigenvalue.
For this reason, in functional analysis eigenvalues can be generalized to the spectrum of a linear operator T as the set of all scalars λ for which the operator (T − λI) has no bounded inverse. The spectrum of an operator always contains all its eigenvalues but is not limited to them.
Associative algebras and representation theory[edit]
One can generalize the algebraic object that is acting on the vector space, replacing a single operator acting on a vector space with an algebra representation – an associative algebra acting on a module. The study of such actions is the field of representation theory.
The representation-theoretical concept of weight is an analog of eigenvalues, while weight vectors and weight spaces are the analogs of eigenvectors and eigenspaces, respectively.
Dynamic equations[edit]
The simplest difference equations have the form
The solution of this equation for x in terms of t is found by using its characteristic equation
which can be found by stacking into matrix form a set of equations consisting of the above difference equation and the k – 1 equations 


A similar procedure is used for solving a differential equation of the form
Calculation[edit]
The calculation of eigenvalues and eigenvectors is a topic where theory, as presented in elementary linear algebra textbooks, is often very far from practice.
Classical method[edit]
The classical method is to first find the eigenvalues, and then calculate the eigenvectors for each eigenvalue. It is in several ways poorly suited for non-exact arithmetics such as floating-point.
Eigenvalues[edit]
The eigenvalues of a matrix 

In theory, the coefficients of the characteristic polynomial can be computed exactly, since they are sums of products of matrix elements; and there are algorithms that can find all the roots of a polynomial of arbitrary degree to any required accuracy.[43] However, this approach is not viable in practice because the coefficients would be contaminated by unavoidable round-off errors, and the roots of a polynomial can be an extremely sensitive function of the coefficients (as exemplified by Wilkinson’s polynomial).[43] Even for matrices whose elements are integers the calculation becomes nontrivial, because the sums are very long; the constant term is the determinant, which for an 

Explicit algebraic formulas for the roots of a polynomial exist only if the degree 


Eigenvectors[edit]
Once the (exact) value of an eigenvalue is known, the corresponding eigenvectors can be found by finding nonzero solutions of the eigenvalue equation, that becomes a system of linear equations with known coefficients. For example, once it is known that 6 is an eigenvalue of the matrix
we can find its eigenvectors by solving the equation 
This matrix equation is equivalent to two linear equations
that is
Both equations reduce to the single linear equation 




The matrix 




Simple iterative methods[edit]
The converse approach, of first seeking the eigenvectors and then determining each eigenvalue from its eigenvector, turns out to be far more tractable for computers. The easiest algorithm here consists of picking an arbitrary starting vector and then repeatedly multiplying it with the matrix (optionally normalizing the vector to keep its elements of reasonable size); this makes the vector converge towards an eigenvector. A variation is to instead multiply the vector by 

If 

where 

Modern methods[edit]
Efficient, accurate methods to compute eigenvalues and eigenvectors of arbitrary matrices were not known until the QR algorithm was designed in 1961.[43] Combining the Householder transformation with the LU decomposition results in an algorithm with better convergence than the QR algorithm.[citation needed] For large Hermitian sparse matrices, the Lanczos algorithm is one example of an efficient iterative method to compute eigenvalues and eigenvectors, among several other possibilities.[43]
Most numeric methods that compute the eigenvalues of a matrix also determine a set of corresponding eigenvectors as a by-product of the computation, although sometimes implementors choose to discard the eigenvector information as soon as it is no longer needed.
Applications[edit]
Eigenvalues of geometric transformations[edit]
The following table presents some example transformations in the plane along with their 2×2 matrices, eigenvalues, and eigenvectors.
| Scaling | Unequal scaling | Rotation | Horizontal shear | Hyperbolic rotation | |
|---|---|---|---|---|---|
| Illustration | 
|
|
|
|

|
| Matrix | 
|

|

|

|

|
| Characteristic polynomial |

|

|

|

|

|
Eigenvalues, 
|

|

|

|

|

|
Algebraic mult.,
|

|

|

|

|

|
Geometric mult.,
|

|

|

|

|

|
| Eigenvectors | All nonzero vectors | 
|

|

|

|
The characteristic equation for a rotation is a quadratic equation with discriminant 

A linear transformation that takes a square to a rectangle of the same area (a squeeze mapping) has reciprocal eigenvalues.
Schrödinger equation[edit]
An example of an eigenvalue equation where the transformation 
where 


However, in the case where one is interested only in the bound state solutions of the Schrödinger equation, one looks for 


The bra–ket notation is often used in this context. A vector, which represents a state of the system, in the Hilbert space of square integrable functions is represented by 
where 






Wave transport[edit]
Light, acoustic waves, and microwaves are randomly scattered numerous times when traversing a static disordered system. Even though multiple scattering repeatedly randomizes the waves, ultimately coherent wave transport through the system is a deterministic process which can be described by a field transmission matrix 





Molecular orbitals[edit]
In quantum mechanics, and in particular in atomic and molecular physics, within the Hartree–Fock theory, the atomic and molecular orbitals can be defined by the eigenvectors of the Fock operator. The corresponding eigenvalues are interpreted as ionization potentials via Koopmans’ theorem. In this case, the term eigenvector is used in a somewhat more general meaning, since the Fock operator is explicitly dependent on the orbitals and their eigenvalues. Thus, if one wants to underline this aspect, one speaks of nonlinear eigenvalue problems. Such equations are usually solved by an iteration procedure, called in this case self-consistent field method. In quantum chemistry, one often represents the Hartree–Fock equation in a non-orthogonal basis set. This particular representation is a generalized eigenvalue problem called Roothaan equations.
Geology and glaciology[edit]
In geology, especially in the study of glacial till, eigenvectors and eigenvalues are used as a method by which a mass of information of a clast fabric’s constituents’ orientation and dip can be summarized in a 3-D space by six numbers. In the field, a geologist may collect such data for hundreds or thousands of clasts in a soil sample, which can only be compared graphically such as in a Tri-Plot (Sneed and Folk) diagram,[47][48] or as a Stereonet on a Wulff Net.[49]
The output for the orientation tensor is in the three orthogonal (perpendicular) axes of space. The three eigenvectors are ordered 










Principal component analysis[edit]
PCA of the multivariate Gaussian distribution centered at 

The eigendecomposition of a symmetric positive semidefinite (PSD) matrix yields an orthogonal basis of eigenvectors, each of which has a nonnegative eigenvalue. The orthogonal decomposition of a PSD matrix is used in multivariate analysis, where the sample covariance matrices are PSD. This orthogonal decomposition is called principal component analysis (PCA) in statistics. PCA studies linear relations among variables. PCA is performed on the covariance matrix or the correlation matrix (in which each variable is scaled to have its sample variance equal to one). For the covariance or correlation matrix, the eigenvectors correspond to principal components and the eigenvalues to the variance explained by the principal components. Principal component analysis of the correlation matrix provides an orthogonal basis for the space of the observed data: In this basis, the largest eigenvalues correspond to the principal components that are associated with most of the covariability among a number of observed data.
Principal component analysis is used as a means of dimensionality reduction in the study of large data sets, such as those encountered in bioinformatics. In Q methodology, the eigenvalues of the correlation matrix determine the Q-methodologist’s judgment of practical significance (which differs from the statistical significance of hypothesis testing; cf. criteria for determining the number of factors). More generally, principal component analysis can be used as a method of factor analysis in structural equation modeling.
Vibration analysis[edit]
Mode shape of a tuning fork at eigenfrequency 440.09 Hz
Eigenvalue problems occur naturally in the vibration analysis of mechanical structures with many degrees of freedom. The eigenvalues are the natural frequencies (or eigenfrequencies) of vibration, and the eigenvectors are the shapes of these vibrational modes. In particular, undamped vibration is governed by
or
that is, acceleration is proportional to position (i.e., we expect 
In 


where 


leads to a so-called quadratic eigenvalue problem,
This can be reduced to a generalized eigenvalue problem by algebraic manipulation at the cost of solving a larger system.
The orthogonality properties of the eigenvectors allows decoupling of the differential equations so that the system can be represented as linear summation of the eigenvectors. The eigenvalue problem of complex structures is often solved using finite element analysis, but neatly generalize the solution to scalar-valued vibration problems.
Eigenfaces[edit]
In image processing, processed images of faces can be seen as vectors whose components are the brightnesses of each pixel.[52] The dimension of this vector space is the number of pixels. The eigenvectors of the covariance matrix associated with a large set of normalized pictures of faces are called eigenfaces; this is an example of principal component analysis. They are very useful for expressing any face image as a linear combination of some of them. In the facial recognition branch of biometrics, eigenfaces provide a means of applying data compression to faces for identification purposes. Research related to eigen vision systems determining hand gestures has also been made.
Similar to this concept, eigenvoices represent the general direction of variability in human pronunciations of a particular utterance, such as a word in a language. Based on a linear combination of such eigenvoices, a new voice pronunciation of the word can be constructed. These concepts have been found useful in automatic speech recognition systems for speaker adaptation.
Tensor of moment of inertia[edit]
In mechanics, the eigenvectors of the moment of inertia tensor define the principal axes of a rigid body. The tensor of moment of inertia is a key quantity required to determine the rotation of a rigid body around its center of mass.
Stress tensor[edit]
In solid mechanics, the stress tensor is symmetric and so can be decomposed into a diagonal tensor with the eigenvalues on the diagonal and eigenvectors as a basis. Because it is diagonal, in this orientation, the stress tensor has no shear components; the components it does have are the principal components.
Graphs[edit]
In spectral graph theory, an eigenvalue of a graph is defined as an eigenvalue of the graph’s adjacency matrix 











The principal eigenvector is used to measure the centrality of its vertices. An example is Google’s PageRank algorithm. The principal eigenvector of a modified adjacency matrix of the World Wide Web graph gives the page ranks as its components. This vector corresponds to the stationary distribution of the Markov chain represented by the row-normalized adjacency matrix; however, the adjacency matrix must first be modified to ensure a stationary distribution exists. The second smallest eigenvector can be used to partition the graph into clusters, via spectral clustering. Other methods are also available for clustering.
Basic reproduction number[edit]
The basic reproduction number (




See also[edit]
- Antieigenvalue theory
- Eigenoperator
- Eigenplane
- Eigenmoments
- Eigenvalue algorithm
- Introduction to eigenstates
- Jordan normal form
- List of numerical-analysis software
- Nonlinear eigenproblem
- Normal eigenvalue
- Quadratic eigenvalue problem
- Singular value
- Spectrum of a matrix
Notes[edit]
- ^ Note:
- In 1751, Leonhard Euler proved that any body has a principal axis of rotation: Leonhard Euler (presented: October 1751; published: 1760) “Du mouvement d’un corps solide quelconque lorsqu’il tourne autour d’un axe mobile” (On the movement of any solid body while it rotates around a moving axis), Histoire de l’Académie royale des sciences et des belles lettres de Berlin, pp. 176–227. On p. 212, Euler proves that any body contains a principal axis of rotation: “Théorem. 44. De quelque figure que soit le corps, on y peut toujours assigner un tel axe, qui passe par son centre de gravité, autour duquel le corps peut tourner librement & d’un mouvement uniforme.” (Theorem. 44. Whatever be the shape of the body, one can always assign to it such an axis, which passes through its center of gravity, around which it can rotate freely and with a uniform motion.)
- In 1755, Johann Andreas Segner proved that any body has three principal axes of rotation: Johann Andreas Segner, Specimen theoriae turbinum [Essay on the theory of tops (i.e., rotating bodies)] ( Halle (“Halae”), (Germany): Gebauer, 1755). (https://books.google.com/books?id=29 p. xxviiii [29]), Segner derives a third-degree equation in t, which proves that a body has three principal axes of rotation. He then states (on the same page): “Non autem repugnat tres esse eiusmodi positiones plani HM, quia in aequatione cubica radices tres esse possunt, et tres tangentis t valores.” (However, it is not inconsistent [that there] be three such positions of the plane HM, because in cubic equations, [there] can be three roots, and three values of the tangent t.)
- The relevant passage of Segner’s work was discussed briefly by Arthur Cayley. See: A. Cayley (1862) “Report on the progress of the solution of certain special problems of dynamics,” Report of the Thirty-second meeting of the British Association for the Advancement of Science; held at Cambridge in October 1862, 32: 184–252; see especially pp. 225–226.
- ^ Kline 1972, pp. 807–808 Augustin Cauchy (1839) “Mémoire sur l’intégration des équations linéaires” (Memoir on the integration of linear equations), Comptes rendus, 8: 827–830, 845–865, 889–907, 931–937. From p. 827: “On sait d’ailleurs qu’en suivant la méthode de Lagrange, on obtient pour valeur générale de la variable prinicipale une fonction dans laquelle entrent avec la variable principale les racines d’une certaine équation que j’appellerai l’équation caractéristique, le degré de cette équation étant précisément l’order de l’équation différentielle qu’il s’agit d’intégrer.” (One knows, moreover, that by following Lagrange’s method, one obtains for the general value of the principal variable a function in which there appear, together with the principal variable, the roots of a certain equation that I will call the “characteristic equation”, the degree of this equation being precisely the order of the differential equation that must be integrated.)
- ^ See:
- David Hilbert (1904) “Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen. (Erste Mitteilung)” (Fundamentals of a general theory of linear integral equations. (First report)), Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (News of the Philosophical Society at Göttingen, mathematical-physical section), pp. 49–91. From p. 51: “Insbesondere in dieser ersten Mitteilung gelange ich zu Formeln, die die Entwickelung einer willkürlichen Funktion nach gewissen ausgezeichneten Funktionen, die ich ‘Eigenfunktionen’ nenne, liefern: …” (In particular, in this first report I arrive at formulas that provide the [series] development of an arbitrary function in terms of some distinctive functions, which I call eigenfunctions: … ) Later on the same page: “Dieser Erfolg ist wesentlich durch den Umstand bedingt, daß ich nicht, wie es bisher geschah, in erster Linie auf den Beweis für die Existenz der Eigenwerte ausgehe, … “ (This success is mainly attributable to the fact that I do not, as it has happened until now, first of all aim at a proof of the existence of eigenvalues, … )
- For the origin and evolution of the terms eigenvalue, characteristic value, etc., see: Earliest Known Uses of Some of the Words of Mathematics (E)
- ^ For a proof of this lemma, see Roman 2008, Theorem 8.2 on p. 186; Shilov 1977, p. 109; Hefferon 2001, p. 364; Beezer 2006, Theorem EDELI on p. 469; and Lemma for linear independence of eigenvectors
- ^ By doing Gaussian elimination over formal power series truncated to
terms it is possible to get away with
operations, but that does not take combinatorial explosion into account.
Citations[edit]
- ^ Burden & Faires 1993, p. 401.
- ^ Roman 2008, p. 185 §8
- ^ a b Herstein 1964, pp. 228, 229.
- ^ a b Nering 1970, p. 38.
- ^ Weisstein n.d.
- ^ Betteridge 1965.
- ^ a b “Eigenvector and Eigenvalue”. www.mathsisfun.com. Retrieved 19 August 2020.
- ^ Press et al. 2007, p. 536.
- ^ Wolfram.com: Eigenvector.
- ^ a b c d Nering 1970, p. 107.
- ^ Hawkins 1975, §2.
- ^ a b c d Hawkins 1975, §3.
- ^ Kline 1972, p. 673.
- ^ a b Kline 1972, pp. 807–808.
- ^ Kline 1972, pp. 715–716.
- ^ Kline 1972, pp. 706–707.
- ^ Kline 1972, p. 1063, p..
- ^ Aldrich 2006.
- ^ Francis 1961, pp. 265–271.
- ^ Kublanovskaya 1962.
- ^ Golub & Van Loan 1996, §7.3.
- ^ Meyer 2000, §7.3.
- ^ Cornell University Department of Mathematics (2016) Lower-Level Courses for Freshmen and Sophomores. Accessed on 2016-03-27.
- ^ University of Michigan Mathematics (2016) Math Course Catalogue Archived 2015-11-01 at the Wayback Machine. Accessed on 2016-03-27.
- ^ Press et al. 2007, p. 38.
- ^ Fraleigh 1976, p. 358.
- ^ a b c Golub & Van Loan 1996, p. 316.
- ^ Anton 1987, pp. 305, 307.
- ^ a b Beauregard & Fraleigh 1973, p. 307.
- ^ Herstein 1964, p. 272.
- ^ Nering 1970, pp. 115–116.
- ^ Herstein 1964, p. 290.
- ^ Nering 1970, p. 116.
- ^ Wolchover 2019.
- ^ a b Denton et al. 2022.
- ^ Van Mieghem 2014.
- ^ Korn & Korn 2000, Section 14.3.5a.
- ^ Friedberg, Insel & Spence 1989, p. 217.
- ^ Roman 2008, p. 186 §8
- ^ Nering 1970, p. 107; Shilov 1977, p. 109 Lemma for the eigenspace
- ^ Lipschutz & Lipson 2002, p. 111.
- ^ Roman 2008, p. 189 §8.
- ^ a b c d Trefethen & Bau 1997.
- ^ Vellekoop & Mosk 2007, pp. 2309–2311.
- ^ a b Rotter & Gigan 2017, p. 15005.
- ^ Bender et al. 2020, p. 165901.
- ^ Graham & Midgley 2000, pp. 1473–1477.
- ^ Sneed & Folk 1958, pp. 114–150.
- ^ Knox-Robinson & Gardoll 1998, p. 243.
- ^ Busche, Christian; Schiller, Beate. “Endogene Geologie – Ruhr-Universität Bochum”. www.ruhr-uni-bochum.de.
- ^ Benn & Evans 2004, pp. 103–107.
- ^ Xirouhakis, Votsis & Delopoulus 2004.
- ^ Diekmann, Heesterbeek & Metz 1990, pp. 365–382.
- ^ Heesterbeek & Diekmann 2000.
Sources[edit]
- Aldrich, John (2006), “Eigenvalue, eigenfunction, eigenvector, and related terms”, in Miller, Jeff (ed.), Earliest Known Uses of Some of the Words of Mathematics
- Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley, ISBN 0-471-84819-0
- Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Co., ISBN 0-395-14017-X
- Beezer, Robert A. (2006), A first course in linear algebra, Free online book under GNU licence, University of Puget Sound
- Bender, Nicholas; Yamilov, Alexey; Yilmaz, Hasan; Cao, Hui (14 October 2020). “Fluctuations and Correlations of Transmission Eigenchannels in Diffusive Media”. Physical Review Letters. 125 (16): 165901. arXiv:2004.12167. Bibcode:2020PhRvL.125p5901B. doi:10.1103/physrevlett.125.165901. ISSN 0031-9007. PMID 33124845. S2CID 216553547.
- Benn, D.; Evans, D. (2004), A Practical Guide to the study of Glacial Sediments, London: Arnold, pp. 103–107
- Betteridge, Harold T. (1965), The New Cassell’s German Dictionary, New York: Funk & Wagnall, LCCN 58-7924
- Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (5th ed.), Boston: Prindle, Weber and Schmidt, ISBN 0-534-93219-3
- Denton, Peter B.; Parke, Stephen J.; Tao, Terence; Zhang, Xining (January 2022). “Eigenvectors from Eigenvalues: A Survey of a Basic Identity in Linear Algebra” (PDF). Bulletin of the American Mathematical Society. 59 (1): 31–58. arXiv:1908.03795. doi:10.1090/bull/1722. S2CID 213918682. Archived (PDF) from the original on 19 January 2022.
- Diekmann, O; Heesterbeek, JA; Metz, JA (1990), “On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations”, Journal of Mathematical Biology, 28 (4): 365–382, doi:10.1007/BF00178324, hdl:1874/8051, PMID 2117040, S2CID 22275430
- Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd ed.), Reading: Addison-Wesley, ISBN 0-201-01984-1
- Francis, J. G. F. (1961), “The QR Transformation, I (part 1)”, The Computer Journal, 4 (3): 265–271, doi:10.1093/comjnl/4.3.265
- Francis, J. G. F. (1962), “The QR Transformation, II (part 2)”, The Computer Journal, 4 (4): 332–345, doi:10.1093/comjnl/4.4.332
- Friedberg, Stephen H.; Insel, Arnold J.; Spence, Lawrence E. (1989), Linear algebra (2nd ed.), Englewood Cliffs, NJ: Prentice Hall, ISBN 0-13-537102-3
- Golub, Gene H.; Van Loan, Charles F. (1996), Matrix computations (3rd ed.), Baltimore, MD: Johns Hopkins University Press, ISBN 978-0-8018-5414-9
- Graham, D.; Midgley, N. (2000), “Graphical representation of particle shape using triangular diagrams: an Excel spreadsheet method”, Earth Surface Processes and Landforms, 25 (13): 1473–1477, Bibcode:2000ESPL…25.1473G, doi:10.1002/1096-9837(200012)25:13<1473::AID-ESP158>3.0.CO;2-C, S2CID 128825838
- Hawkins, T. (1975), “Cauchy and the spectral theory of matrices”, Historia Mathematica, 2: 1–29, doi:10.1016/0315-0860(75)90032-4
- Heesterbeek, J. A. P.; Diekmann, Odo (2000), Mathematical epidemiology of infectious diseases, Wiley series in mathematical and computational biology, West Sussex, England: John Wiley & Sons
- Hefferon, Jim (2001), Linear Algebra, Colchester, VT: Online book, St Michael’s College
- Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
- Kline, Morris (1972), Mathematical thought from ancient to modern times, Oxford University Press, ISBN 0-19-501496-0
- Knox-Robinson, C.; Gardoll, Stephen J. (1998), “GIS-stereoplot: an interactive stereonet plotting module for ArcView 3.0 geographic information system”, Computers & Geosciences, 24 (3): 243, Bibcode:1998CG…..24..243K, doi:10.1016/S0098-3004(97)00122-2
- Korn, Granino A.; Korn, Theresa M. (2000), “Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review”, New York: McGraw-Hill (2nd Revised ed.), Bibcode:1968mhse.book…..K, ISBN 0-486-41147-8
- Kublanovskaya, Vera N. (1962), “On some algorithms for the solution of the complete eigenvalue problem”, USSR Computational Mathematics and Mathematical Physics, 1 (3): 637–657, doi:10.1016/0041-5553(63)90168-X
- Lipschutz, Seymour; Lipson, Marc (12 August 2002). Schaum’s Easy Outline of Linear Algebra. McGraw Hill Professional. p. 111. ISBN 978-007139880-0.
- Meyer, Carl D. (2000), Matrix analysis and applied linear algebra, Philadelphia: Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8
- Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
- Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), Numerical Recipes: The Art of Scientific Computing (3rd ed.), ISBN 978-0521880688
- Roman, Steven (2008), Advanced linear algebra (3rd ed.), New York: Springer Science + Business Media, ISBN 978-0-387-72828-5
- Rotter, Stefan; Gigan, Sylvain (2 March 2017). “Light fields in complex media: Mesoscopic scattering meets wave control”. Reviews of Modern Physics. 89 (1): 015005. arXiv:1702.05395. Bibcode:2017RvMP…89a5005R. doi:10.1103/RevModPhys.89.015005. S2CID 119330480.
- Shilov, Georgi E. (1977), Linear algebra, Translated and edited by Richard A. Silverman, New York: Dover Publications, ISBN 0-486-63518-X
- Sneed, E. D.; Folk, R. L. (1958), “Pebbles in the lower Colorado River, Texas, a study of particle morphogenesis”, Journal of Geology, 66 (2): 114–150, Bibcode:1958JG…..66..114S, doi:10.1086/626490, S2CID 129658242
- Trefethen, Lloyd N.; Bau, David (1997), Numerical Linear Algebra, SIAM
- Van Mieghem, Piet (18 January 2014). “Graph eigenvectors, fundamental weights and centrality metrics for nodes in networks”. arXiv:1401.4580 [math.SP].
- Vellekoop, I. M.; Mosk, A. P. (15 August 2007). “Focusing coherent light through opaque strongly scattering media”. Optics Letters. 32 (16): 2309–2311. Bibcode:2007OptL…32.2309V. doi:10.1364/OL.32.002309. ISSN 1539-4794. PMID 17700768. S2CID 45359403.
- Weisstein, Eric W. “Eigenvector”. mathworld.wolfram.com. Retrieved 4 August 2019.
- Weisstein, Eric W. (n.d.). “Eigenvalue”. mathworld.wolfram.com. Retrieved 19 August 2020.
- Wolchover, Natalie (13 November 2019). “Neutrinos Lead to Unexpected Discovery in Basic Math”. Quanta Magazine. Retrieved 27 November 2019.
- Xirouhakis, A.; Votsis, G.; Delopoulus, A. (2004), Estimation of 3D motion and structure of human faces (PDF), National Technical University of Athens
Further reading[edit]
- Golub, Gene F.; van der Vorst, Henk A. (2000), “Eigenvalue Computation in the 20th Century” (PDF), Journal of Computational and Applied Mathematics, 123 (1–2): 35–65, Bibcode:2000JCoAM.123…35G, doi:10.1016/S0377-0427(00)00413-1, hdl:1874/2663
- Hill, Roger (2009). “λ – Eigenvalues”. Sixty Symbols. Brady Haran for the University of Nottingham.
- Kuttler, Kenneth (2017), An introduction to linear algebra (PDF), Brigham Young University
- Strang, Gilbert (1993), Introduction to linear algebra, Wellesley, MA: Wellesley-Cambridge Press, ISBN 0-9614088-5-5
- Strang, Gilbert (2006), Linear algebra and its applications, Belmont, CA: Thomson, Brooks/Cole, ISBN 0-03-010567-6
External links[edit]
- What are Eigen Values? – non-technical introduction from PhysLink.com’s “Ask the Experts”
- Eigen Values and Eigen Vectors Numerical Examples – Tutorial and Interactive Program from Revoledu.
- Introduction to Eigen Vectors and Eigen Values – lecture from Khan Academy
- Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10 – A visual explanation with 3Blue1Brown
- Matrix Eigenvectors Calculator from Symbolab (Click on the bottom right button of the 2×12 grid to select a matrix size. Select an
size (for a square matrix), then fill out the entries numerically and click on the Go button. It can accept complex numbers as well.)
Theory[edit]
- Computation of Eigenvalues
- Numerical solution of eigenvalue problems Edited by Zhaojun Bai, James Demmel, Jack Dongarra, Axel Ruhe, and Henk van der Vorst
Нахождение собственных чисел и собственных векторов
Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.
Больше:
Выводить десятичную дробь
,
- Оставляйте лишние ячейки пустыми для ввода неквадратных матриц.
-
Элементы матриц – десятичные (конечные и периодические) дроби:
1/3,3,14,-1,3(56)или1,2e-4; либо арифметические выражения:2/3+3*(10-4),(1+x)/y^2,2^0,5 (=2),2^(1/3),2^n,sin(phi),cos(3,142rad),a_1или(root of x^5-x-1 near 1,2).-
decimal (finite and periodic) fractions:
1/3,3,14,-1,3(56)или1,2e-4 -
2/3+3*(10-4),(1+x)/y^2,2^0,5 (=2),2^(1/3),2^n,sin(phi),cos(3,142rad),a_1или(root of x^5-x-1 near 1,2) -
matrix literals:
{{1,3},{4,5}} -
operators:
+,-,*,/,,!,^,^{*},,,;,≠,=,⩾,⩽,>и< -
functions:
sqrt,cbrt,exp,log,abs,conjugate,min,max,gcd,rank,adjugate,inverse,determinant,transpose,pseudoinverse,cos,sin,tan,cot,cosh,sinh,tanh,coth,arccos,arcsin,arctan,arccot,arcosh,arsinh,artanhиarcoth -
units:
rad,deg -
special symbols:
pi,e,i— mathematical constantsk,n— integersIorE— identity matrixX,Y— matrix symbols
-
- Используйте ↵ Ввод, Пробел, ←↑↓→, ⌫ и Delete для перемещения по ячейкам, Ctrl⌘ Cmd+C/Ctrl⌘ Cmd+V – для копирования матриц.
- Перетаскивайте матрицы из результата (drag-and-drop), или даже из текстового редактора.
- За теорией о матрицах и операциях над ними обращайтесь к страничке на Википедии.
Примеры
- Найти собственные векторы
({{-26,-33,-25},{31,42,23},{-11,-15,-4}})























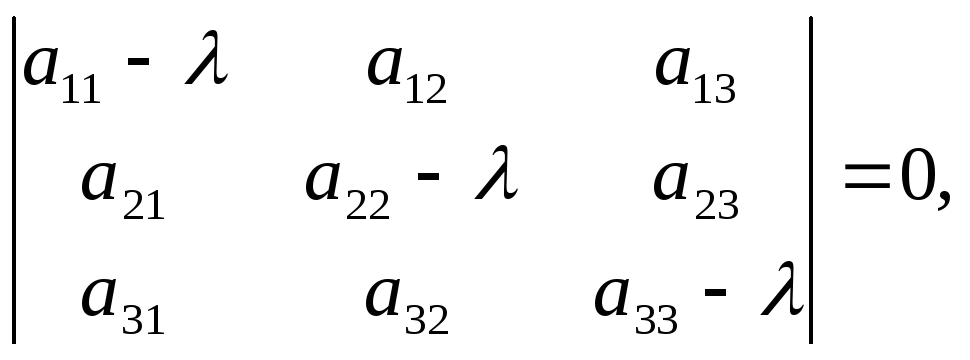























































![{displaystyle {begin{aligned}|A-lambda I|&=left|{begin{bmatrix}2&1\1&2end{bmatrix}}-lambda {begin{bmatrix}1&0\0&1end{bmatrix}}right|={begin{vmatrix}2-lambda &1\1&2-lambda end{vmatrix}}\[6pt]&=3-4lambda +lambda ^{2}\[6pt]&=(lambda -3)(lambda -1).end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0084c80ab8c7637830cdf01f1c754f92a6598ac0)






![{displaystyle {begin{aligned}|A-lambda I|&=left|{begin{bmatrix}2&0&0\0&3&4\0&4&9end{bmatrix}}-lambda {begin{bmatrix}1&0&0\0&1&0\0&0&1end{bmatrix}}right|={begin{vmatrix}2-lambda &0&0\0&3-lambda &4\0&4&9-lambda end{vmatrix}},\[6pt]&=(2-lambda ){bigl [}(3-lambda )(9-lambda )-16{bigr ]}=-lambda ^{3}+14lambda ^{2}-35lambda +22.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30165fb86a7e23644d2e3373a1c2c68af4756523)