Требуется собрать нагрузки на монолитную плиту перекрытия жилого дома. Толщина плиты 200 мм. Состав пола представлен на рис. 1.
Решение
Определим нормативные значения действующих нагрузок. Для удобства восприятия материала постоянные нагрузки будем обозначать индексом q, кратковременные — индексом ν, длительные — индексом p.
Жилые здания относятся ко II уровню ответственности, следовательно, коэффициент надежности по ответственности γн = 1,0. На этот коэффициент будем умножать значения всех нагрузок. (Для выбора коэффициента см. статью Коэффициент надежности по ответственности зданий и сооружений)
Сначала рассмотрим нагрузки от плиты перекрытия и конструкции пола. Эти нагрузки являются постоянными, т.к. действуют на всем протяжении эксплуатации здания.
1. Объемный вес железобетона равен 2500 кг/м3 (25 кН/м3). Толщина плиты δ1 = 200 мм = 0,2 м, тогда нормативное значение нагрузки от собственного веса плиты перекрытия составляет:
q1 = 25*δ1*γн = 25*0,2*1,0 = 5,0 кН/м2.
2. Нормативная нагрузка от звукоизоляционного слоя из экструдированного пенополистирола плотностью ρ2 = 35 кг/м3 (0,35 кН/м3) и толщиной δ2 = 30 мм = 0,03 м:
q2 = ρ2*δ2*γн = 0,35*0,03*1,0 = 0,01 кН/м2.
3. Нормативная нагрузка от цементно-песчаной стяжки плотностью ρ3 = 1800 кг/м3 (18 кН/м3) и толщиной δ3 = 40 мм = 0,04 м:
q3 = ρ3*δ3*γн = 18*0,04*1,0 = 0,72 кН/м2.
4. Нормативная нагрузка от плиты ДВП плотностью ρ4 = 800 кг/м3 (8 кН/м3) и толщиной δ4 = 5 мм = 0,005 м:
q4 = ρ4*δ4*γн = 8*0,005*1,0 = 0,04 кН/м2.
5. Нормативная нагрузка от паркетной доски плотностью ρ5 = 600 кг/м3 (6 кН/м3) и толщиной δ5 = 20 мм = 0,02 м:
q5 = ρ5*δ5*γн = 6*0,02*1,0 = 0,12 кН/м2.
Суммарная нормативная постоянная нагрузка составляет
q = q1 + q2 + q3 + q4 + q5 = 5 + 0,01 + 0,72 + 0,04 + 0,12 +5,89 кН/м2.
Расчетное значение нагрузки получаем путем умножения ее нормативного значения на коэффициент надежности по нагрузке γt.
Теперь определим временные (кратковременные и длительные) нагрузки. Полное (кратковременное) нормативное значение нагрузки от людей и мебели (так называемая полезная нагрузка) для квартир жилых зданий составляет 1,5 кПа (1,5 кН/м2). Учитывая коэффициент надежности по ответственности здания γн = 1,0, итоговая кратковременная нагрузка от людей составляет:
ν1p = ν1*γt = 1,5*1,3 = 1,95 кН/м2.
Длительную нагрузку от людей и мебели получаем путем умножения ее полного значения на коэффициент 0,35, указанный в табл. 6, т.е:
р1 = 0,35*ν1 = 0,35*1,5 = 0,53 кН/м2;
р1р = р1*γt =0,53*1,3 = 0,69 кН/м2.
Полученные данные запишем в таблицу 1.
Помимо нагрузки от людей необходимо учесть нагрузки от перегородок. Поскольку мы проектируем современное здание со свободной планировкой и заранее не знаем расположение перегородок (нам известно лишь то, что они будут кирпичными толщиной 120 мм при высоте этажа 3,3 м), принимаем эквивалентную равномерно распределенную нагрузку с нормативным значением 0,5 кН/м2. С учетом коэффициента γн = 1,0 окончательное значение составит:
р2 = 0,5*γн = 0,5*1,9 =0,5 кН/м2.
При соответствующем обосновании в случае необходимости нормативная нагрузка от перегородок может приниматься и большего значения.
Коэффициент надежности по нагрузке γt = 1,3, поскольку перегородки выполняются на строительной площадке. Тогда расчетное значение нагрузки от перегородок составит:
р2р = р2*γt = 0,5*1,3 = 0,65 кН/м2.
(Для выбора плотности основных строй материалов см. статьи:
- Классификация нагрузок по продолжительности действия.
- Плотность стройматериалов по данным СНиП II-3-79
Для удобства все найденные значения запишем в таблицу сбора нагрузок (табл.1).
Таблица 1
Сбор нагрузок на плиту перекрытия
Вид нагрузки |
Норм. кН/м2 |
Коэф. γt |
Расч. кН/м2 |
Постоянная нагрузка |
|||
1. Ж.б. плита |
5,0 |
1,1 |
5,5 |
2. Пенополистирол |
0,01 |
1,3 |
0,013 |
3. Цем — песч. стяжка |
0,72 |
1,3 |
0,94 |
4. Плита ДВП |
0,04 |
1,1 |
0,044 |
5. Паркетная доска |
0,12 |
1,1 |
0,132 |
Всего: |
5,89 |
|
6,63 |
Временная нагрузка |
|||
1. Полезная нагрузка |
|||
кратковременная ν1 |
1,5 |
1,3 |
1,95 |
длительная р1 |
0,53 |
1,3 |
0,69 |
2. Перегородки (длительная) р2 |
0,5 |
1,3 |
0,65 |
В нашем примере сейсмические, взрывные и т.п. воздействия (т.е. особые нагрузки) отсутствуют. Следовательно, будем рассматривать основные сочетания нагрузок.
I сочетание: постоянная нагрузка (собственный вес перекрытия и пола) + полезная (кратковременная).
При учете основных сочетаний, включающих постоянные нагрузки и одну временную нагрузку (длительную или кратковременную), коэффициенты Ψl, Ψt вводить не следует.
Тогда qI = q + ν1 = 5,89 + 1,5 = 7,39, кН/м2;
qIр = qp + ν1p = 6,63 + 1,95 = 8,58 кН/м2.
II вариант: постоянная нагрузка (собственный вес перекрытия и пола) + полезная (кратковременная) + нагрузка от перегородок (длительная).
Для основных сочетаний коэффициент сочетаний длительных нагрузок Ψl принимается: для первой (по степени влияния) длительной нагрузки — 1,0, для остальных — 0,95. Коэффициент Ψt для кратковременных нагрузок принимается: для первой (по степени влияния) кратковременной нагрузки — 1,0, для второй — 0,9, для остальных — 0,7.
Поскольку во II сочетании присутствует одна кратковременная и одна длительная нагрузка, то коэффициенты Ψl и Ψt = 1,0.
qII = q + ν1 + p2 = 5,89 + 1,5 + 0,5 =7,89 кН/м2;
qIIр = qр + ν1р + p2р = 6,63+ 1,95 + 0,65 =9,23 кН/м2.
Совершенно очевидно, что II основное сочетание дает наибольшие значения нормативной и расчетной нагрузки.
Смотрите также:
Понятие нормативных и расчетных нагрузок. Коэффициенты надежности.
Нормативные и расчетные значения нагрузок
Коэффициент надежности по ответственности зданий и сооружений
Справочные данные
Примеры:
-
Пример 1.2 Сбор нагрузок на плиту покрытия
-
Пример 1.3 Сбор нагрузок на балку перекрытия
-
Пример 1.4. Сбор нагрузок на колонну
-
Пример 2.1 Определение несущей способности буронабивной сваи длиной 2,2 м
-
Пример 2.2. Определение несущей способности забивной сваи по грунту
-
Пример 2.3. Определение несущей способности сваи по материалу
-
Пример 2.4. Определение нагрузок на сваи во внецентренно-нагруженном фундаменте
-
Пример 3.1. Расчет стыка балки с накладками
-
Пример 3.2. Расчет соединения столика с колонной
-
Пример 3.3. Расчет балки настила
-
Пример 3.4. Расчет заделки в кладку консольной балки и проверка кладки на местное смятие
-
Пример 3.5. Проверка сечения колонны из двутавра на сжатие
-
Пример 4.1. Проверка сечения центрально-сжатого элемента
-
Пример 5.1. Расчет ботового соединения двух листов с двумя накладками
-
Пример 6.1. Проверка устойчивости ленточного фундамента на действие сил морозного пучения
-
Пример 6.2. Расчет основания фундамента по несущей способности
-
Пример 6.3. Проверка фундамента на сдвиг
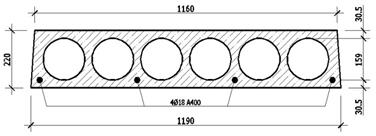
Поперечное сечение плиты по результатам выполненного инженерно-технического обследования.
Исходные данные для расчета: Плита шарнирно опирается на сборные железобетонные ригели, размер плиты в плане – 1200х6000мм, высота – 220 мм. Бетон В20: Rb=11,5МПа. Продольная рабочая арматура — 4Ø18 А400, Rs=355 МПа. Состав пола плиты: — цементно-песчаная стяжка толщиной t=50мм (ρ=1800кг/м3)$ — керамогранитная плитка. Планируемая нормативная полезная нагрузка – 1,2т/м2.
Сбор нагрузок и определение усилий в железобетонной плите перекрытия:
| Вид нагрузки | Нормативная нагрузка, т/м2 | Коэффициент надежности по нагрузке γf | Расчетная нагрузка, т/м2 |
| Постоянная: | |||
| Керамогранитная плитка | 0,01 | 1,2 | 0,012 |
| Цементно-песчаная стяжка (t=50мм, ρ=1800кг/м3) | 0,09 | 1,3 | 0,117 |
| Собственный вес ж/б плиты перекрытия (ρ=1800кг/м3) | 0,31 | 1,1 | 0,341 |
| Итого постоянная нагрузка | 0,41 | 0,47 | |
| Временная: | |||
| Полезная нагрузка на перекрытие | 1,2 | 1,2 | 1,44 |
| в т.ч. длительно действующая | 1,2х0,7=0,84 | 1,2 | 1,008 |
| Итого полная нагрузка: | 1,61 | 1,91 | |
| в т.ч. постоянная и длительно действующая | 1,25 | 1,478 |
Сбор нагрузок выполнен в соответствии с СП 20.13330.2011 Нагрузки и воздействия (Актуализированная редакция СНиП 2.01.07-85)
Полная расчетная нагрузка на плиту при ее ширине 1,2м составит:
q=1,91т/м2*1,2 м = 2,292 т/м.
Определяем расчетный изгибающий момент в середине пролета плиты:
М1= q•l02/2 l0=l-bриг/2,
где l =6,0 м – номинальный пролет плиты,
bриг – ширина сечения ригеля.
l0=6,0-0,3/2=5,85 м
М1=2,292•5,852/2=39,22 тм
Определение расчетной схемы и расчетного поперечного сечения плиты:
Определение геометрических размеров расчетного поперечного сечения плиты:
b=1160-6•159=206 мм;
a – расстояние до центра арматуры (толщина защитного слоя), определено по результатам вскрытия плиты;
h0=h-a=220-30,5=189,5 мм – рабочая высота сечения;
согласно п.3.26 Пособия по проектированию бетонных и железобетонных конструкций из тяжелого бетона без предварительного напряжения арматуры к СП 52-101-2003 – значение b’f, вводимое в расчет, принимают из условия, что ширина свеса полки в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:
а) при наличии поперечных ребер или при h’f ≥ 0,1h — 1/2 расстояния в свету между про-дольными ребрами;
б) при отсутствии поперечных ребер (или при расстояниях между ними больших, чем рас-стояния между продольными ребрами) и при h’f < 0,1h — 6h’f;
в) при консольных свесах полки:
— при h’f ≥ 0,1h — 6h’f ,
— при 0,05h ≤ h’f < 0,1h — 3h’f;
— при h’f < 0,05h — свесы не учитывают.
т.к h’f=30,5мм ≥ 0,1h=0,1•220=22 мм, то ширина свеса полки в каждую сторону от ребра составит 6h’f=6•30,5= 183 мм.
Тогда b’f будет равно:
b’f=206+2•183=572мм < 1/6•6000=1000 мм.
Окончательно принимаем b’f=572 мм.

Плиты укладываются в пролёте между вертикальными опорами – стенами, пилонами или колоннами.
Преимущественно работают на изгиб и выполняют роль жёсткого диска, объединяющего отдельные элементы каркаса сооружения в единую геометрически неизменяемую систему.
При расчёте плит перекрытий определяются такие важные параметры, как их толщина, армирование, прогиб и необходимость устройства дополнительных подпирающих элементов (балок или капителей).
Как провести расчет нагрузок на перекрытие, расскажем далее.
Содержание
- 1 Что это такое?
- 2 Виды нагрузок на плиты перекрытий по СНиП и СП
- 3 Расчёт пролетных конструкций
- 4 Как рассчитать значения?
- 4.1 Предельные
- 4.2 Точечные
- 4.3 Пересчёт на м2
- 4.3.1 Пример
- 4.4 Изгибающий момент
- 4.5 Как посчитать несущую способность?
- 4.6 Прочность ЖБ элемента
- 5 Возможные сложности и ошибки
- 6 Заключение
Что это такое?
Нагрузки, прикладываемые к перекрытию, представляют собой сочетание внешних сил, действующих на конструктивный элемент, вызывая в нём внутренние усилия. Несущая способность элемента определяется из условия равновесия, достигаемого при приложении нагрузок.
Виды нагрузок на плиты перекрытий по СНиП и СП
Нагрузки на пролётные конструкции определяются, исходя из требований нормативных документов – СНиП 2.01.07-85 и его обновлённой версии – СП 20.13330.2011 «Нагрузки и воздействия».
В соответствии с пунктами этих нормативов, нагрузки классифицируются на следующие виды:
-
Полезные – нагрузки, необходимые для обеспечения комфортной эксплуатации помещения, в соответствии с его функциональным назначением.
Например, в жилых квартирах или частных домах – это нагрузки от мебели, бытовых приборов и самих жильцов.
В магазинах – от посетителей, персонала, прилавков, стеллажей и оборудования, необходимого для функционирования помещения.
- Допустимые – сочетание внешних сил, приложенных к перекрытию, при котором оно продолжает удовлетворять всем предъявляемым к нему эксплуатационным требованиям без наступления необратимых последствий.
- Постоянные – нагрузки, которые действуют на протяжении всего периода эксплуатации помещения. К таким видам загружения относятся собственный вес плит, масса пирога пола и штамповые нагрузки от конструктивных элементов, без которых эксплуатация помещения не представляется возможной.
- Временные – нагрузки от веса оборудования, мебели, людей и другие виды сил, которые прикладываются к несущему элементу на определённый промежуток времени.
- Предельные – максимальная величина нагрузки, при приложении которой в конструктивном элементе начинают происходить необратимые процессы – пластические деформации, бесконтрольное раскрытие трещин, а также обрушение перекрытия.
В зависимости от функционального назначения помещений, величины полезных нагрузок различаются.
В жилом помещении равномерно распределённые по площади временные нагрузки составляют 150 – 200 кгс/м2, а в общественных зданиях, в зависимости от особенностей технологического процесса они составляют уже 250 – 500 кгс/м2.
Расчёт пролетных конструкций
Расчёт пролётных конструкций ведётся по двум группам предельных состояний:
- 1 группа – подбирается такие параметры жёсткости конструктивного элемента, при которых оно не потеряет прочность под действие сочетания постоянных, временных и особых нагрузок;
- 2 группа – расчёт по деформациям, при котором определяется фактический прогиб перекрытия, после чего это значение сравнивается с предельно допустимыми значениями из СНиП.
На несущую способность плит перекрытий влияет величины постоянных и полезных нагрузок, толщина элемента, длина пролёта и условия эксплуатации помещения.
Как рассчитать значения?
Расчёт нагрузок на плиту перекрытия производится методом суммирования всех приложенных к конструктивному элементу внешних сил, с учётом различных коэффициентов запаса, принимаемых по указанному выше СНиП. Если рассмотреть теоретические выкладки, то расчёт нагрузок делится на следующие категории:
Предельные

Например, на основании представленного ниже расчёта – при приложении суммарной расчётной нагрузки 900 кг/м2 на плиту перекрытия толщиной 200 мм, армированную прутками d10 A500s с шагом 200 мм, достигается фактический изгибающий момент М = 2812,5 кН*см при пролёте 5 м.
А сечение с такими параметрами остаётся в равновесии при достижении момента Мпред = 2988.5 кН*см, что всего на 5,8% выше предельного значения.
Учитывая, что момент в изгибаемом сечении под действием равномерно распределённой нагрузки равняется M = q х l2 / 8, то qпред = 8M/l2, или qпред = 8 х 2998.5 / 25 = 956.32 кг/м2 – при такой внешней силе сечение установленных параметров перестанет удовлетворять предельному равновесию, и данная нагрузка является предельной.
Точечные
Как правило, такие силы не прикладываются к перекрытию отдельно – всегда существуют постоянные нагрузки, и единичное точечное загружение суммируется с ними.
Приложенная точечная нагрузка влияет на значение опорных реакций и величину изгибающего момента в расчётном сечении. Усилия от точечного загружения определяется как произведение силы на плечо (расстояние от ближайшей точки опоры).
Например, если в комнате с пролётом 5 метров стоит декоративная колонна массой 500 кг на расстоянии от стены 2 м, то расчётная нагрузка с учётом коэффициента запаса (gn для постоянных сил = 1,05) составит 525 кг. Момент в данной точке составит 525 кг х 2 м = 1050 кг * м, или 1050 кН * см.
Соответственно, при добавлении равномерно распределённого загружения, описанного выше, стандартное сечение плиты с армированием d10 A500s с шагом 200 мм не будет удовлетворять расчёту прочности, и данное место следует усилить дополнительными стержнями, например, d10 A500s ш. 200 + d12 A500s ш. 200.
Пересчёт на м2

СНиП допускает не производить расчёт временных нагрузок на плиту от конкретных предметов, а учитывать приведённую равномерно-распределённую по площади поверхности силу.
Например, вдоль стены комнаты, на протяжении 3 м стоит гарнитур общей массой 400 кг, напротив – диван массой 200 кг и другие предметы мебели с разными весами. По данному помещению каждый день передвигаются 4 человека с массами тела от 50 до 120 кг.
По факту, точно посчитать нагрузку не представляется возможным, но СП 20.13330.2011 допускает учитывать в статическом расчёте приведённую равномерно распределённую нагрузку для жилых помещений 150 кг/м2.
Пример
Ниже представлен пример сбора нагрузок на перекрытие в частном жилом доме. По условию задачи, габариты комнаты составляют 7 х 4 м, плита перекрытия 200 мм, поверх которой уложена ц/п стяжка толщиной 50 мм по подложке из экструдированного пенополистирола 30 мм, а в качестве чистового пола применяется керамогранитная плитка толщиной 12 мм с клеевым составом 3 мм.
Требуется собрать расчётные нагрузки на данную конструкцию для последующего расчёта. Задача решается с выполнением следующих этапов:
Собственный вес плиты – M1 = S x h x rбет, где:
- S – площадь поверхности перекрытия, равный 5 м х 4 м, или 2 м2,
- h – толщина плиты, которая составляет 200 мм, или 0,2 м,
- rбет – средняя плотность армированного бетона, которая равна 2500 кг/м2.
- M1 = 20 м2 х 0,2 м х 2500 кг/м2 = 10 000 кг.
Масса полов – M2 = mподл + mстяж + mплит, где:
- mподл = S x hподл х rпенопол = 20 м2 х 0,03 м х 40 кг/м2 = 24 кг,
- mстяж = S x hстяж х rц/п р-ра = 20 м2 х 0,05 м х 1800 кг/м2 = 1800 кг,
- mплит = S x hплит х rкерамогр = 20 м2 х 0,015 м х 2400 кг/м2 = 720 кг (значение принимается с учётом слоя плиточного клея).
M2 = 24 кг + 1800 кг + 720 кг = 2544 кг. В жилом помещении рекомендуемая по СНиП временная нагрузка составляет q = 150 кгс/м2.
Таким образом, суммарная полезная нагрузка на плиту составляет F = q x S = 150 х 20 = 3000 кг:
- Общая вертикальная нагрузка, приложенная к плите, равняется Fобщ = M1 + M2 + F = 10000 кг + 2544 кг + 3000 кг = 15544 кг, или 1554,4 кН.
- Как правило, нормативные нагрузки необходимо привести к расчётным величинам, учитывая коэффициенты надёжности. Данный показатель записывается как gn, и для постоянных загружений он составляет 1,1, а для полезной нагрузки – 1,4.
Таким образом, Fобщ расч = (M1 + M2) x gnс пост + F x gn врем = (10000 кг + 2544 кг) х 1,1 + 3000 кг х 1,4 = 13798,4 кг + 4200 кг = 17998.4 кг ~ 18000 кг, или 1800 кН.
Чтобы привести суммарное значение данной величины в равномерно распределённую нагрузку, достаточно разделить его на общую площадь комнаты. То есть Qобщ расч = Fобщ расч / S = 1800 кН / 20 м2 = 90 кН/м2, или 900 кг/м2.
При наличии точечной или штамповой нагрузки от веса какого-либо оборудования, она участвует в расчёте отдельно, формируя линейную, а не квадратичную зависимость изгибающего момента.
В отдельных случаях допускается разложить точечную нагрузку на равномерно распределённую по площади, с учётом повышающего коэффициента, так как железобетон не является упругим материалом, и все усилия в нём перераспределяются в большей части его объёма.
Изгибающий момент
Безбалочная плита перекрытия должна удовлетворять расчёту по прочности, или первой группе предельных состояний. Чтобы определить несущую способность перекрытия, необходимо выполнить следующий алгоритм:
-
Если соотношения габаритов перекрытия а/b или b/a > 2, то такая плита работает по короткой стороне.
Если данные показатель меньше 2, то плита считается опёртой по контуру, и расчёт ведётся относительно того пролёта, в котором возникает наибольший изгибающий момент.
Значение момента прямо пропорционально величине пролёта, поэтому в рассматриваемом примере расчёт ведётся относительно стороны a = 5 м.
- Из плиты выделяется расчётная полоса шириной 1 м, которая будет рассматриваться как изгибаемый линейный элемент, или балка с приложенной к ней равномерно распределённой по длине нагрузкой.
В рассматриваемом примере балка имеет сечение b x h = 1 м х 0,2 м, и к ней приложена нагрузка qрасч = 900 кг/м, или 90 кН/м.
Величина изгибаемого момента для подобной конструкции составляет M = qрасч х l2 / 8, где l – величина пролёта, или 5 м. M = 90 кН/м х 5 х 5 / 8 = 281.25 кН*м, или 2812,5 кН*см.
Величина изгибающего момента может быть отображена на эпюре данного вида усилия, возникающего в конструкции.
Как посчитать несущую способность?
При известной величине изгибающего момента и габаритов (жёсткости сечения) можно определить несущую способность данного пролётного элемента по следующим формулам:
Высота сечения плиты складывается из двух величин h = h0 + a, где h0 – рабочая высота от нижней арматуры, находящейся в зоне растяжения до верхней грани бетона. а – величина защитного слоя бетона. Как правило, этот показатель в тонких плитах варьируется в пределах от 15 до 25 мм. h0 = h – a = 200 мм – 20 мм = 180 мм.
В строительной механике, согласно по СП 63.13330.2018 «Бетонные и железобетонные конструкции», существуют два условия, при которых конструкция достигает предельного равновесия под действием внешних сил.
Rs As = Rbbx, где:
- M = Rbbx (h0 – x/2),
- Rs – предел прочности арматурной стали заданного класса на растяжение,
- Rb – тот же показатель, но для бетона, на сжатие, зависящий от марки материала.
Если в плите принимается наиболее распространённая арматура класса A500s, то Rs = 43,5 кН/см2. Если бетон в рассматриваемом примере имеет класс B30, то Rb = 1,7 кН/см2.
В условии равновесия х – абсолютная величина сжатой зона бетона, которая равняется х = Rs Аs / gb1 Rbb (по СП 63.13330.2018 «Бетонные и железобетонные конструкции»):
- As – площадь всех стержней рабочей арматуры в растянутой зоне сечения плиты,
- gb1 – коэффициент запаса, зависящий от условий работы бетона в конструкции, для стандартных вариантов эксплуатации перекрытия принимается равным 0,9.
Требуемая площадь рабочей арматуры зависит от расчётных параметров сечения и величины внутренних усилий (в плите перекрытия – изгибающего момента).
Аs = gb1Rbbeh0/Rs (по СП 63.13330.2018):
e – безразмерная величина, характеризующая относительную высоту сжатой части бетонного сечения, которая определяется из соотношения e = (1 – (1 – 2am)1/2),
- am – это показатель, описывающий отношение изгибающего момента к прочностным характеристикам жб сечения, определяемый по формуле СП,
- am = M / (gb1 Rbbh02) = 2812,5 / (0,9 х 1,7 х 100 х 324) = 2812,5 кН*см / 49572 = 0,057.
Аs = 0,9 х 1,7 х 100 х 0,057 х 18 / 43,5 = 3,61 см2.
Для предотвращения образования трещин от усадки бетона, в плитах перекрытий шаг рабочей арматуры, чаще всего, назначается 200 мм. Таким образом, в расчётной полосе шириной 1 м располагается 5 рабочих стержней.
В данном примере допускается рассмотреть армирование из 5d10, и реальная площадь стержней составит 3,93 см2, что больше, чем требуемое значение, с учётом повышающих коэффициентов. При известных значениях площади армирования, можно определить величину х: х = Rs Аs / gb1 Rbb = 43,5 х 3,93 / (0,9 х 1,7 х 100) = 1,12 см.
На завершающем этапе из основного условия равновесия определяется предельно допустимый момент, который может возникнуть в сечении плиты перекрытия. M = gb1 Rbbx(h0 – x/2) = 0,9 х 1,7 х 100 х 1,12 х (18 – 1,12/2) = 2988.5 кН*см.
Далее остаётся сравнить предельно допустимый момент 2988.5 кН*см с фактическим усилием, возникающим после приложения нагрузок – 2812,5 кН*см, который оказался меньше, значит, условие прочности выполняется.
В случае, если условие предельного равновесия не достигается, толщина плиты, а также расчётное количество рабочей арматуры должны быть пересмотрены.
Прочность ЖБ элемента
В строительной механике понятия прочности и несущей способности практически не имеют различий. Однако, на практике это не совсем так. Прочность – это способность конструктивного элемента не разрушаться под действием внешних сил. Несущая способность – это способность конструктивного элемента удовлетворять предъявленным к нему эксплуатационным требованиям под действием сочетания нагрузок.
Таким образом, расчёт по предельным состояниям 1 группы, приведённый выше, показывает, что плита перекрытия остаётся в статическом положении не разрушается, (то есть, обеспечивается её прочность) и может эксплуатироваться в нормальных условиях (так как в расчёте были учтены все коэффициенты условий работы). Проведения дополнительных прочностных расчётов не требуется.
Возможные сложности и ошибки
При расчёте сечения плиты перекрытия на прочность, следует учитывать важные нюансы, чтобы не допустить серьёзных ошибок:
Расчёты должны проводиться в строгом соответствии с требованиями нормативных документов.
- При вычислениях все единицы измерения должны быть приведены к единым значениям, а, в противном случае, результат будет далёким от истины.
- При определении изгибающего момента следует учесть характер опирания плиты перекрытия, так как формулы для жёсткой заделки или шарнирного сопряжения отличаются друг от друга.
- При сборе нагрузок не следует забывать коэффициенты надёжности, которые усугубляют теоретическую работу конструкции и приближают её к реальным условиям.
Последствия неверных расчётов могут привести к обрушению строительных конструкций, недопустимым прогибам и другим непоправимым проблемам во время эксплуатации сооружения.
Заключение
Перед назначением толщины и армирования плиты перекрытия необходимо провести расчёт прочности изгибаемого элемента. Вычисления выполняются после сбора постоянных и временных нагрузок и определения внутренних усилий в конструкции.
Если результаты расчёта не удовлетворяют условиям предельного равновесия, необходимо задать другую толщину плиты и провести вычисления заново.
Крайние пролеты
l1
= l01
–
b0
–
bb/2
+ hp/2
=
1,85–0,20–(0,20/2)+(0,06/2)
= 1,58 м,
где b0
– размер
привязки (расстояние от грани стены до
разбивочной оси), b0=200
мм.
Средние пролеты
l2
= l02
–
bb
=
2,10–0,20 = 1,90 м > l1=
1,58 м.
∆l
= 1,90–1,58 = 0,32 м, ∆l,%
=16,8%
< 20%.
2.3. Расчетные нагрузки
а) Постоянная
нагрузка определяется как сумма
собственного веса плиты (gпл)
и веса
конструкций пола и перегородок (gп):
g
= gпл
+ gп,
кН/м²,
где gпл
= γfg
· h
· 10 · p;
p
– плотность железобетона, при тяжелом
бетоне – p=2,5т/м3,
γfg
=1,1;
gn=
γfg
·
gn,n
– собственный вес
плиты gnл
= 1,1 · 0,06
· 10 · 2,5 = 1,65 кН/м²;
– вес пола и
перегородок gn
= 1,1 ·
2,70 = 2,97 кН/м²;
Итого:
g
= 1,65 + 2,97 =
4,62 кН/м²;
б) Временная
нагрузка v
= γfg
· vn
, γfg
= 1,2
v
= 1,2 · 5,0 = 6
кН/м².
Погонная расчетная
нагрузка для полосы плиты шириной 1м
(b
= 1м) при γn=
0,95 равна
q
= γn
(g
+
v)
·
b
= 0,95
·(4,62 + 6) = 10,09 кН/м²
2.4. Статический расчет
Расчетная схема
плиты принята в виде многопролетной
неразрезной балки. Изгибающие моменты
в неразрезной балочной плите с равными
пролетами или отличающимися не более
чем на 20%, как в данном случае ∆l,%=16,8%
< 20%,
определяются
с учетом перераспределения изгибающих
моментов вследствие пластических
деформаций по формулам (7, 9):
– в крайних пролетах
М1
= (q
·
l1²)
/ 11
= (10,09 · 1,58²) /
11 = 2,29 кН ·
м;
– на вторых с края
опорах В
МВ
= − (q
·
l2²)
/ 14
= − (10,09 · 1,9²) /
14 = −2,60 кН ·
м;
– в средних пролетах
М2
= (q
·
l2²)
/ 16
= (10,09 · 1,9²) /
16 = 2,28 кН ·
м;
– на средних опорах
МС
= − (q
·
l2²)
/ 16
= − (10,09 · 1,9²) /
16 = −2,28 кН ·
м.
А 10,09
кН/м
В С

2,60 кН · м МС= 2,28 кН ·
м
Рис. 2.1. Расчетная схема и эпюры изгибающих
моментов монолитной плиты.
2.5. Расчет плиты на прочность
Определяем толщину
плиты по максимальному моменту МВ
= 2,60 кН · м, при ширине плиты b
= 1000 мм. Задаваясь значением ξ
= 0,23, находим αт
=ξ (1 − 0,5 ξ
) = 0,23 (1 – 0,5
· 0,23) = 0,204. Требуемая рабочая высота
сечения плиты будет равна
h0
= М /
(αт·
Rb
· b)
= (2,60 ·106)
/
(0,204 · 7,65 · 1000) = 40,82 мм.
Требуемая толщина
плиты hp
= h0
+ a
= 40,82 + 23 = 63,82 мм. Принимаем hp
= 70 мм.
Расчет арматуры
(на 1 м ширины плиты).
В крайних пролетах
М1
= 2,29 кН · м;
При принятом
размере а
= 23 мм, h0
= hр
− a
= 70 – 23 = 47 мм.
αт
= М1/
(Rb
· b·
h02)
= (2,29 · 106)
/
(7,65 · 1000 · 472)
= 0,136.
Тогда ξ
= 1 − 1 − 2 αт
= 1 − 1 – 2 · 0,136 = 0,147.
Проверяем условие
ξ ≤ ξR,
для чего вычисляем
ξR
= xR
/ h0
= 0,8 =
0,8 = 0,5308;
1
+ ξs,el
1 +
0,001775
ξb,ult
0,0035
в этой формуле:
ξs,el
=
Rs
/ Es
= 355 /
2,0 · 105
= 0,001775, ξb,ult
=
0,0035.
Условие ξ
≤ ξR
выполняется, т.к. ξ
= 0,147 < ξR
= 0,531.
Условие ξ ≤
ξR
выполняется и в других расчетных случаях.
As
= М1/
((1−0,5
ξ)
·Rs
·h0)
= 2,29 ·106
/
((1−0,5·0,147)·355·47
= 148,14 мм²,
или
As
= (Rb/Rs)·ξ
·b·h0
=
(7,65/355)·0,147·1000·47
= 148,88 мм².
Принимаем Ø 6 А400
с шагом 175 мм (Аs
=162 мм²).
На вторых с края
опорах В
МВ
= −2,60 кН · м, а
= 23 мм, h0
= 47 мм.
αт
= МВ
/
(Rb
· b·
h02)
= (2,60 · 106)
/
(7,65 · 1000 · 472)
= 0,154.
ξ
= 1 − 1 − 2 αт
= 1 − 1 – 2 · 0,154 = 0,168; тогда
As
= (Rb/Rs)·ξ
·b·h0
=
(7,65/355)·0,168·1000·47
= 170,2 мм².
Принимаем Ø 6 А400
с шагом 150 мм (Аs
=189 мм²).
В средних пролетах
и на средних опорах
М2
= −МС
= 2,28 кН · м.
αт
= М2
/
(Rb
· b·
h02)
= (2,28 · 106)
/
(7,65 · 1000 · 472)
= 0,135,
ξ
= 1 − 1 − 2 αт
= 1 − 1 – 2 · 0,135 = 0,146,
As
= М2/
((1−0,5
ξ) ·Rs
·h0)
= 2,28 ·106
/
((1−0,5·0,146)·355·47
= 147,4 мм².
Принимаем Ø 6 А400
с шагом 175 мм (Аs
=162 мм²).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
08.04.2015538.11 Кб211А.И.Фирсов с рисунками.doc
- #
- #
2. Расчёт многопустотной плиты по предельным состояниям первой группы
Исходные данные. Многопустотная плита из тяжелого бетона класса В40 опирается поверху на железобетонные ригели каркаса, пролет ригелей – lp=5,9м. Нормативное значение временной нагрузки 3,5кПа. Требуется рассчитать и законструировать плиту перекрытия. Класс рабочей арматуры принять А-V.
2.1 Расчет плиты по предельным состояниям первой группы
2.1.1 Расчётный пролёт и нагрузки
Для установления расчётного пролёта плиты предварительно задаёмся размерами сечения ригеля:
hp=(1/12)*lp=(1/12)*590=50см, bp=0.5*hp=0.4*50=20см.
При опирании на ригель поверху расчётный пролёт плиты составит:
lo=l-bp/2=6,4-0,2/2=6,3м.
Рекомендуемые материалы
Подсчёт нагрузок на 1м2 перекрытия сводим в таблицу 1.
Таблица 1 – Нормативные и расчётные нагрузки на 1м2 перекрытия
|
Нагрузка |
Нормативная нагрузка, Н/м2 |
Коэффициент надёжности по нагрузке |
Расчётная нагрузка, Н/м2 |
ПостояннаяСобственный вес многопустотной плиты с круглыми пустотами |
3000 |
1,1 |
3300 |
|
То же слоя цементного раствора d=20мм (r=2200кг/м3) |
440 |
1,3 |
570 |
|
То же керамических плиток d=13мм (r=1800кг/м3) |
240 |
1,1 |
264 |
Итого |
3680 |
– |
4134 |
Временная |
3500 |
1,2 |
4200 |
|
В том числе длительная |
2450 |
1,2 |
2940 |
|
Кратковременная (30%) |
1050 |
1,2 |
1260 |
Полная нагрузка |
7180 |
– |
8334 |
|
В том числе: Постоянная и длительная |
6130 |
– |
7074 |
На 1м длины плиты шириной плиты 2,1м действуют следующие нагрузки, Н/м: кратковременная нормативная pn=1050*2,1=2205; кратковременная расчетная р=1260*2,1=2646; постоянная и длительная нормативная qn=6130*2,1=12873; постоянная и длительная расчетная q=7074*2,1=14855,4; итого нормативная qn+pn=12873+2205=15078; итого расчетная q+p=14855,4+2646=17501,4.
2.1.2 Усилия от расчётных и нормативных нагрузок
Расчётный изгибающий момент от полной нагрузки:
M=(q+p)*l20*gn/8=17501,4*6,32*0.95/8=82487,4Н.м.
Расчетный изгибающий момент от полной нормативной нагрузки:
Mn=(qn+pn)*l20*gn/8=15078*6,32*0.95/8=71065,4Н.м.
То же, от нормативной постоянной и длительной временной нагрузок:
Mld=qn*l20*gn/8=12873*6,32*0.95/8=60672,9Н.м.
То же, от нормативной кратковременной нагрузки:
Mсd=рn*l20*gn/8=2205*6,32*0.95/8=10392,6Н.м.
Максимальная поперечная сила на опоре от расчетной нагрузки:
Q=(q+p)*l0*gn/2=17501,4*6,3*0.95/2=52372,9Н.
То же, от нормативной нагрузки:
Qn=(qn+pn)*l0*gn/2=15078*6,3*0.95/2=45120,9Н.
То же, от нормативной нагрузки:
Qnld=qn*l0*gn/2=12873*6,3*0.95/2=38522,5Н.
2.1.3 Установление размеров сечения плиты
Плиту рассчитываем как балку прямоугольного сечения с заданными размерами bxh=210х22см (где b – номинальная ширина, h – высота плиты). Проектируем плиту одинадцатипустотной. В расчете поперечное сечение пустотной плиты приводим к эквивалентному двутавровому сечению. Заменяем площадь круглых пустот прямоугольниками той же площади и того же момента инерции.
Вычисляем:
h1=0.9*d=0.9*15.9=14.3см;
hf=hf’=(h-h1)/2=(22-14.3)/2=3.8см;
тогда приведенная толщина ребер равна:
bp=b=bf’-n*h1=207-11*14.3=49,7см,
где bf’=207см – расчетная ширина сжатой полки.
Приведенная толщина бетона плиты:
hred=h-(n*p*d2)/4b=22-(11*p*15.92)/(4*207)=11.5см>10 см.
Рабочая высота сечения h0=22-3=19см.
Толщина верхней и нижней полок hf=(22-15.9).0.5=3см.
Ширина ребер: средних – 2.9см, крайних – 3см.
2.1.4 Характеристики прочности бетона и арматуры
Плита изготавливается из тяжелого бетона класса В40, имеет предварительно напрягаемую рабочую арматуру класса А-VI с электротермическим натяжением на упоры форм. К трещиностойкости плиты предъявляются требования 3-ей категории. Изделие подвергают тепловой обработке при атмосферном давлении.
Бетон тяжёлый класса В40
Призменная прочность бетона нормативная: Rbn=Rb,ser=29МПа, расчётная Rb=22МПа, коэффициент условий работы бетона gb2=0.9; нормативное сопротивление при растяжении Rbtn=Rbt,ser=2.1МПа, расчётное Rbt=1.4МПа; начальный модуль упругости бетона Eb=32.5*103МПа.
Передаточная прочность бетона Rbp устанавливается так, чтобы при обжатии отношение напряжений sbp/Rbp£0.75.
Арматура продольная класса A–VI
Нормативное сопротивление Rsn=Rs,ser=980МПа,
Расчётное сопротивление Rs=225МПа,
Модуль упругости Es=1.9*105МПа.
Предварительное напряжение арматуры назначаем таким образом, чтобы выполнялись условия 
Принимаем ssp=600МПа.
Определяем коэффициент точности натяжения арматуры
где n – число стержней напрягаемой арматуры, принимаем n=8.

При благоприятных влияниях предварительного напряжения gsp=1-0.1=
=0.9. При проверке по образованию начальных трещин в верхней зоне плиты g’sp =1+0.1=1.1. Значение предварительного напряжения с учётом точности натяжения арматуры составит 0.9*600=540МПа.
2.1.5 Расчёт прочности плиты по сечению, нормальному к продольной оси
При расчёте прочности, сечение плиты принимается тавровым (полка нижней растянутой зоны в расчёт не вводится). Размеры сечения показаны на рисунке 2б.
Вычисляем:
Находим
Высота сжатой зоны сечения:

ω=0,85-0,008·Rb=0,85-0,008·22·0,9=0,69
Вычисляем граничную высоту сжатой зоны
ξR=
где σSR=Rs+400- σSP2
σSP=0,6Rsn=0,6·785=471 МПа
σSP2=γsp· σSP·0,7=0,84·471·0,7=276,95 МПа
σSR=680+400-276,95=803,1 МПа
Поскольку соблюдается условие x<xR (0.034<0.43), то расчётное сопротивление арматуры умножается на коэффициент условий работы gs6:
где h=1.15 – коэффициент, принимаемый равным для арматуры класса A-V.
Требуемую площадь сечения рабочей арматуры определяем по формуле:
где h=1-0.5x=1-0.5*0.058=0.971.
Принимаем в качестве предварительно напряжённой продольной рабочей арматуры три стержня арматуры класса A-V 3Æ16мм с общей площадью Asp=6,03см2. Арматура устанавливается в четвертом слева и крайних рёбрах плиты.
2.1.6 Расчёт прочности плиты по наклонным сечениям
По конструктивным требованиям в многопустотных плитах высотой не более 30см поперечная арматура не устанавливается, если она не нужна по расчету. Проверим необходимость постановки поперечной арматуры расчетом. Проверяем условие: Q£ 0.3jw1jb1Rb b h0,
где Q – поперечная сила на опоре от расчетной нагрузки; Q=52,37кН,
jw1=1, так как поперечная арматура отсутствует;
jb1=1-0.01Rb=1-0.01*22=0.78.
Условие:
52,37<0.3*1*0.78*22*10-1*49,7*19,
52,37кН<486,13кН, выполняется,
следовательно, прочность плиты по наклонной полосе между наклонными трещинами обеспечена.
Поперечную арматуру в плите можно не устанавливать, если выполняются условия:
а) Qmax£2.5*Rbt*b*h0; Qmax=Q.
52,37<2.5*1.4*10-1*49,7*19,
52,37кН<330,51кН, условие выполняется.
б) Q1£Mb1/c, Q1=Qmax-q1*c=52,37-11,88*0.475=46,73кН,
где с – проекция наклонного сечения, принимаем:
с=2,5h0=2,5*19=47,5см;
q=gp*b*gf=8,334*1,5*0,95=11,88кН/м,
Мb1=jb4(1+jn)gb2Rbt*b*h02;
jb4=1.5- для тяжелого бетона; jn=0;
где Р=Asp(ssp-100)=5,96*(540-100)*0.1=262кН – усилие предварительного обжатия,
100МПа – минимальное значение суммарных потерь предварительного напряжения.
Принимаем jn=0.5.
Мb1=1,5*(1+0,22)*0,9*1,4*10-1*49,7*192=4137кН*см.
Мb1/с=4137/47,5=87,09кН.
Условие Q1£Мb1/с:
46,73кН<87,09кН выполняется,
следовательно, поперечную арматуру в плите не устанавливаем.
На приопорных участках длиной l/4 арматуру устанавливаем конструктивно Æ4 Вр-I с шагом S=h/2=22/2=11см, в средней части пролёта поперечную арматуру не устанавливаем.
2.2 Расчет плиты по предельным состояниям второй группы
2.2.1 Геометрические характеристики сечения
При расчёте по 2-ой группе предельных состояний в расчёт водится двутавровое сечение плиты (рисунок 2в).
Площадь приведённого сечения:
расстояние от нижней грани до центра тяжести приведённого сечения:
момент инерции сечения:
момент сопротивления сечения:
упругопластический момент сопротивления по растянутой зоне
здесь g=1.5 для двутаврового сечения при 2<bf/b=207/49,7=4,2<6,0.
Упругопластический момент по растянутой зоне в стадии изготовления и обжатия Wpl’=Wpl=20343см3.
Расстояния от ядровых точек – наиболее и наименее удалённой от растянутой зоны (верхней и нижней) – до центра тяжести сечения:
2.2.2 Потери предварительного напряжения
Расчёт потерь выполняем в соответствии с требованиями СНиП 2.03.01-84*. Коэффициент точности натяжения арматуры принимаем gsp=1.0.
Потери s1 от релаксации напряжений при электротермическом натяжении высокопрочных канатов:
s1=0.03*ssp=0.03*600=18МПа.
Потери s2 от температурного перепада между натянутой арматурой и упорами равны нулю, так как при пропаривании форма с упорами нагревается вместе с изделием.
Потери от деформации анкеров s3 и формы s5 при электротермическом способе равны нулю. Поскольку арматура не отгибается, потери от трения арматуры s4 также равны нулю.
Усилие обжатия
Эксцентриситет силы Р1 относительно центра тяжести сечения еор=у0-а=11-3=8см. Определим сжимающие напряжения в бетоне:
где Mg=q*l2/8=(2,07*3,0)*6,42/8=31,8кНм – изгибающий момент в середине пролета плиты от собственного веса,
l=6,4м – расстояние между прокладками при хранении плиты.
Устанавливаем значение передаточной прочности бетона из условия sbp/Rbp£0.75, но не менее 0.5В (В – класс бетона):

0,5 B=0,5*40=20МПа.
Принимаем Rbp=20МПа, тогда:
при расчёте потерь от быстронатекающей ползучести s6 при

Итак, первые потери slos1=s1+s6=18+0,79=18,79МПа.
С учётом потерь slos1:
Р1=Аsp(ssp-slos1)=5,96*(600-18,79)*10-1=346,4МПа.
Отношение 
Из вторых потерь s7…s11 при принятом способе натяжения арматуры учитываются только потери s8 от усадки бетона и потери s9 от ползучести бетона.
Для тяжёлого бетона классов В40 и ниже s8=40МПа.
Так как sbp/Rbp<0.75 то s9=127.9*sbp/Rbp=112,5*0,029=3,26МПа.
Вторые потери slos2=s8+s9=40+3,26=43,26МПа.
Полные потери slos=slos1+slos2=18,79+43,26=62,05МПа<100МПа, принимаем slos=100МПа.
Усилие обжатия с учётом полных потерь:
Р2=Аsp(ssp-slos)=5,96*(600-100)*10-1=298кН.
2.2.3 Расчёт по образованию нормальных трещин
Образование нормальных трещин в нижней растянутой зоне плиты не происходит, если соблюдается условие Mn=71,065кН*м£Mcrc (Mcrc – момент образования трещин):
Поскольку Mn<Mcrc (71,065<79,52), то в нижней зоне плиты трещины не образуются.
Проверим, образуются ли начальные трещины в верхней зоне плиты от усилия предварительного обжатия. Расчётное условие:
здесь Rbt,p=1МПа – нормативное сопротивление бетона растяжению, соответствующее передаточной прочности бетона Rbp=20МПа;
Р1 – принимается с учётом потерь только s1, Р1=346,4кН;
Mg – изгибающий момент в середине пролёта плиты от собственного веса, Mg=31,8кН*м.
Вычисляем: 1.12*346,4*(8-5,72)£1*10-1*20343,5+31,8, 884,57кН*см<2066,2кН*см.
Условие выполняется, значит, начальные трещины в верхней зоне плиты от усилия предварительного обжатия не образуются.
2.2.4 Расчёт прогиба плиты
Для однопролётной шарнирно опертой балочной плиты прогиб можно определить по формуле:
где 1/r – кривизна оси элемента при изгибе. Кривизна оси элемента, где не образуются трещины при длительном действии нагрузки:
где jb1=0.85 – коэффициент, учитывающий снижение жесткости под влиянием неупругих деформаций бетона растянутой зоны;
jb2 – коэффициент, учитывающий снижение жёсткости (увеличение кривизны) при длительном действии нагрузки под влиянием ползучести бетона сжатой зоны при средней относительной влажности воздуха выше 40%, равна 2; jb2 – то же, при кратковременной нагрузке равна 1.
Так как в растянутой зоне плиты трещины не образуются, то кривизна оси (без учета влияния выгиба):
где 
Тогда прогиб будет равен:
От постоянной и длительной временной нагрузок:
Тогда прогиб будет равен:
Тогда полный прогиб будет равен:
2.3 Проверка панели на монтажные нагрузки
Панель имеет четыре монтажные петли из стали класса А-1, расположенные на расстоянии 70см от концов панели (рисунок 3а). С учётом коэффициента динамичности kd=1.4 расчётная нагрузка от собственного веса панели:
где 
Расчётная схема панели показана на рисунке 3б. Отрицательный изгибающий момент консольной части панели:
Этот момент воспринимается продольной монтажной арматурой каркасов. Полагая, что z1=0.9*h0=0.9*19=17.1см, требуемая площадь сечения указанной арматуры составляет:
Если Вам понравилась эта лекция, то понравится и эта – 49 Кавитация.
что значительно меньше принятой конструктивно арматуры 3Æ16 А-II, Аs=5,96см2.
При подъёме панели вес её может быть передан на две петли. Тогда усилие на одну петлю составляет
Площадь сечения арматуры петли
принимаем конструктивно стержни диаметром 14 мм, Аs=1,539см2.


 Полезные – нагрузки, необходимые для обеспечения комфортной эксплуатации помещения, в соответствии с его функциональным назначением.
Полезные – нагрузки, необходимые для обеспечения комфортной эксплуатации помещения, в соответствии с его функциональным назначением.
 Если соотношения габаритов перекрытия а/b или b/a > 2, то такая плита работает по короткой стороне.
Если соотношения габаритов перекрытия а/b или b/a > 2, то такая плита работает по короткой стороне.
 e – безразмерная величина, характеризующая относительную высоту сжатой части бетонного сечения, которая определяется из соотношения e = (1 – (1 – 2am)1/2),
e – безразмерная величина, характеризующая относительную высоту сжатой части бетонного сечения, которая определяется из соотношения e = (1 – (1 – 2am)1/2), Расчёты должны проводиться в строгом соответствии с требованиями нормативных документов.
Расчёты должны проводиться в строгом соответствии с требованиями нормативных документов.











































