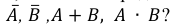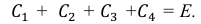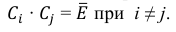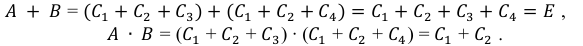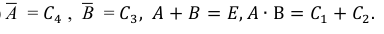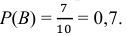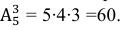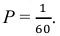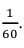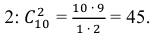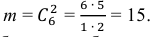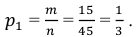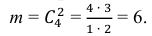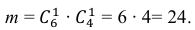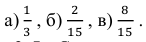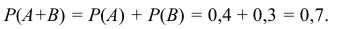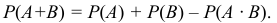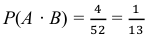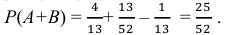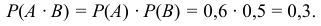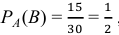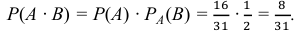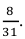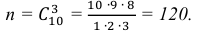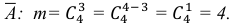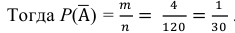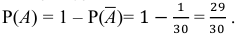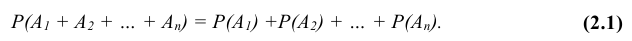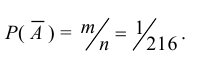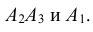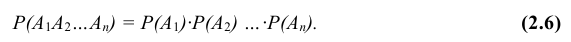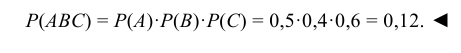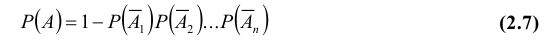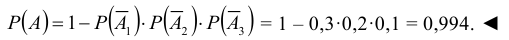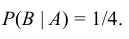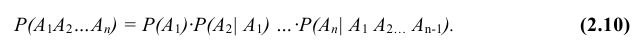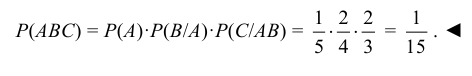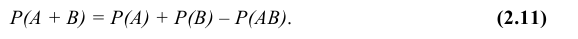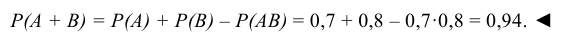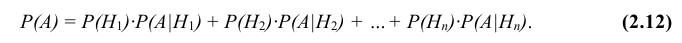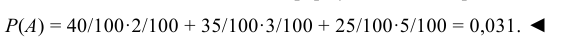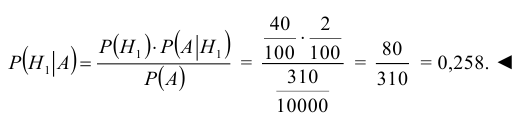На этой странице вы узнаете
- Как кот может быть одновременно жив и мертв?
- Можно ли всегда выигрывать спор с монеткой?
- Если рандомно ответить на вопрос теста, какой шанс угадать ответ?
Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.
Вероятность
Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…
Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.
Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов.
Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат.
Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом.
По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив.
Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным. Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.
Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:
- выпадет орел;
- выпадет решка.

Эти два события образуют множество элементарных событий.
Множество элементарных событий — множество всех возможных результатов случайного эксперимента.
В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации.
Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран.
Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности.
Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу.
(P = frac{m}{n})
Вероятность можно обозначить, как P(x), где х — некоторое событие.
Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.
Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.
Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна (P = frac{2}{2} = 1), то есть мы точно выиграем спор.
Однако вероятность не так проста, и даже здесь подготовила ловушку.
В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет (frac{1}{6000}). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.
Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.
Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?
Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна
(frac{49}{140} = 0,35)
Выразим в процентах:
0,35 * 100% = 35%
Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.
Ответ: 0,35
Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой.
(P = frac{m}{n} * 100%)
Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.
Равновозможные и противоположные события
Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.
Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.
Вероятности появления событий равны.
Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий.
Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.
В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий.
Мы подбросили монету и выпал орел. Следовательно, не выпала решка.
А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными.
Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline{A}).
Заметим, что вероятность события A равняется 12, как и вероятность события (overline{A}). Чему равна их сумма?
)frac{1}{2} + frac{1}{2} = 1)
Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1.
(P(A) + P(overline{A}) = 1)
Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить.
Объединение и пересечение событий
Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим?
Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий.
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег.
Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B).
Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?
Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.

Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B).
Несовместные и совместные события
Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.
Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно.
Несовместные события — такие события, появление одного из которых исключает появление другого.
Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.
Сформулируем определение суммы вероятностей двух несовместных событий.
Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:
(P(A cup B) = P(A) + P(B))
Если существуют несовместные события, то существуют и совместные.
Совместные события — события, наступление одного из которых не исключает наступления другого.
В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят? Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет.
Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”.
Найдем вероятность события А: (frac{1}{6}).
Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac{3}{6} = frac{1}{2})
Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А.
Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги.

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок.
Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:
(P(A cup B) = P(A) + P(B) — P(A cap B))
В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.
Независимые и зависимые события
Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем.
Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac{95}{100} = 0,95).
Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?
Ответим на вопрос: зависят ли булочки друг от друга?
Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.
Независимые события — такие события, появление одного из которых не зависит от появления другого события.
Определим вероятность независимых событий.
Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95.
А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:
(P(A cap B) = P(A) * P(B))
Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025.
В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”.
Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.
Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого.
Но если автоматы стоят рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.
Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

Нужная последовательность может быть в двух случаях:
- сначала вытащат фиолетовый кубик и потом снова фиолетовый;
- сначала вытащат оранжевый кубик, а потом фиолетовый.
Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac{5}{7}). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые.

Вероятность вытащить во второй раз фиолетовый кубик равна (frac{5}{7} * frac{4}{6} = frac{20}{42} = frac{10}{21}).

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac{2}{7}). В мешке останется шесть кубиков, пять из которых будут фиолетовыми.

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac{2}{7} * frac{5}{6} = frac{10}{42} = frac{5}{21}).
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы.
Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.
Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность.
Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:
(P(A cap B) = P(A) * P(B | A))
Формула Бернулли
Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?
Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac{1}{6}).
Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac{5}{6}).
Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k.
Чтобы решить задачу, нужно воспользоваться формулой Бернулли.
(P_n(k) = C_n^k * p^k * q^{n — k})
Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики».
Решим задачу, подставив значения в формулу:
(P_8(3) = C_8^3 * (frac{1}{6})^3 * (frac{5}{6})^5 = frac{8!}{5!3!} * frac{1}{6^3} * frac{5^5}{6^5} = frac{6 * 7 * 8}{1 * 2 * 3} * frac{5^5}{6^8} approx 0,1)
Фактчек
- Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
- События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
- События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
- События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A).
- Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Проверь себя
Задание 1.
Какие события являются несовместными?
- Подбрасывание монетки.
- Брак батареек в одной упаковке.
- “Миша идет” и “Миша стоит”.
- Случайное вытаскивание конфет из вазы.
Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?
- 0,17
- 1
- 0,83
- 1,17
Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?
- 1
- 0,216
- 0,45
- 1,5
Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.
- 0,3
- 0,001
- 2,7
- 0,729
Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой.
- 0,77
- 0,135
- 0,23
- -0,23
Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1
Для двух событий, A и B, «найти вероятность A или B» означает найти вероятность того, что произойдет либо событие A, либо событие B.
Обычно мы записываем эту вероятность одним из двух способов:
- P (A или B) – Письменная форма
- P(A∪B) – Форма записи
То, как мы вычисляем эту вероятность, зависит от того, являются ли события A и B взаимоисключающими или нет. Два события являются взаимоисключающими, если они не могут произойти одновременно.
Если A и B взаимоисключающие , то формула, которую мы используем для вычисления P(A∪B):
Mutually Exclusive Events: P(A∪B) = P(A) + P(B)
Если A и B не исключают друг друга , то формула, которую мы используем для вычисления P(A∪B):
Not Mutually Exclusive Events: P(A∪B) = P(A) + P(B) - P(A∩B)
Обратите внимание, что P(A ∩ B) — это вероятность того, что событие A и событие B произойдут одновременно.
Следующие примеры показывают, как использовать эти формулы на практике.
Примеры: P(A∪B) для взаимоисключающих событий.
Пример 1: Какова вероятность того, что при бросании игральной кости выпадет либо 2, либо 5?
Решение: если мы определим событие A как получение 2, а событие B как получение 5, то эти два события являются взаимоисключающими, потому что мы не можем выбросить 2 и 5 одновременно. Таким образом, вероятность того, что выпадет либо 2, либо 5, рассчитывается как:
Р(А∪В) = (1/6) + (1/6) = 2/6 = 1/3.
Пример 2: Предположим, что в урне 3 красных шара, 2 зеленых шара и 5 желтых шаров. Если мы случайно выберем один шар, какова вероятность того, что вы выберете либо красный, либо зеленый шар?
Решение: если мы определим событие А как выбор красного шара, а событие В как выбор зеленого шара, то эти два события будут взаимоисключающими, потому что мы не можем выбрать одновременно красный и зеленый шар. Таким образом, вероятность того, что мы выберем красный или зеленый шар, рассчитывается как:
P(A∪B) = (3/10) + (2/10) = 5/10 = 1/2.
Примеры: P(A ∪ B) для не взаимоисключающих событий .
В следующих примерах показано, как вычислить P(A∪B), когда A и B не являются взаимоисключающими событиями.
Пример 1. Если мы случайно выберем карту из стандартной колоды из 52 карт, какова вероятность того, что вы выберете пику или даму?
Решение: В этом примере можно выбрать карту, которая является и пикой, и дамой, поэтому эти два события не исключают друг друга.
Если мы допустим, что событие A будет событием выбора пики, а событие B будет событием выбора ферзя, то мы получим следующие вероятности:
- Р(А) = 13/52
- Р(В) = 4/52
- Р(А∩В) = 1/52
Таким образом, вероятность выбора пики или королевы рассчитывается как:
P(A∪B) = P(A) + P(B) – P(A∩B) = (13/52) + (4/52) – (1/52) = 16/52 = 4/13.
Пример 2. Если мы бросим игральную кость, какова вероятность того, что выпадет число больше 3 или четное число?
Решение. В этом примере кости могут выпасть на число, которое одновременно больше 3 и четно, поэтому эти два события не исключают друг друга.
Если мы допустим, что событие А будет событием выпадения числа больше 3, а событие В будет событием выпадения четного числа, то мы получим следующие вероятности:
- Р(А) = 3/6
- Р(В) = 3/6
- Р(А∩В) = 2/6
Таким образом, вероятность того, что кубик выпадет на число больше 3 или на четное число, рассчитывается как:
P(A∪B) = P(A) + P(B) – P(A∩B) = (3/6) + (3/6) – (2/6) = 4/6 = 2/3.
Операции над событиями. Теория вероятностей
Пересечение событий
Пусть есть события A и B, у каждого события есть набор элементарных исходов. Пересечением событий A и B называют то событие, в результате которого произошло и событие A и событие B, то есть случился некоторый элементарный исход, который одновременно принадлежит и событию A и событию B.
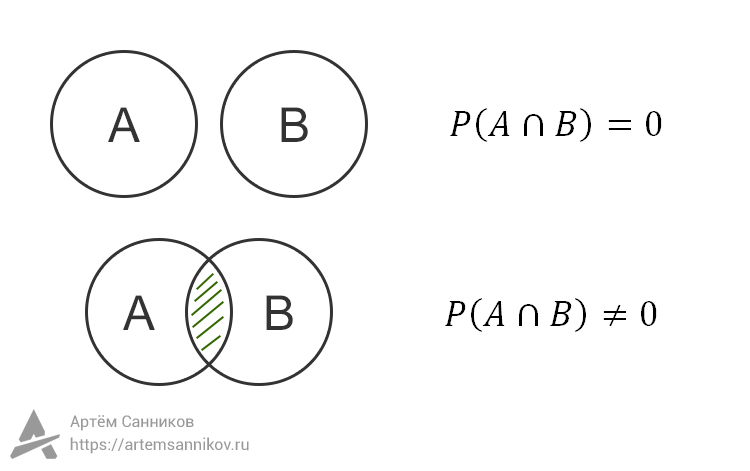
События не пересекаются
Если у событий A и B нет пересечения (отсутствует элементарный исход), то такая вероятность равна нулю.
События пересекаются
Если события A и B пересекаются (имеют некоторое общее количество элементарных исходов), то вероятность этого пересечения нельзя рассчитать по какой-то универсальной формуле. Эту вероятность нужно подсчитывать, рассматривая общие элементарные исходы.
Объединение событий
Объединением событий A и B называют те события, в результате которых произошло или событие A, или событие B, то есть хотя бы одно из двух.
События не пересекаются
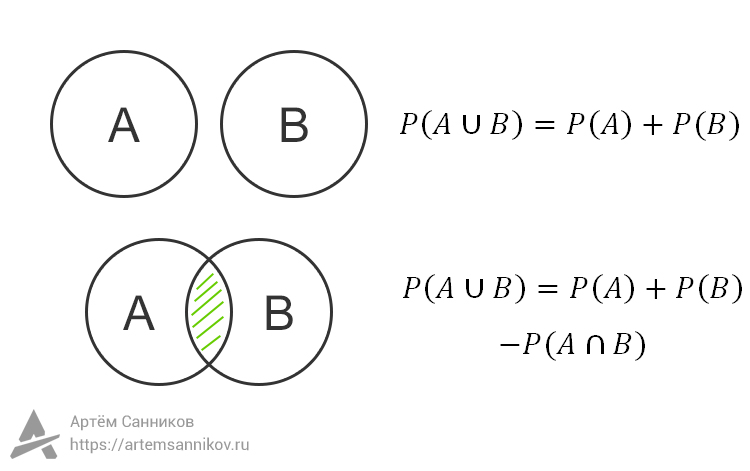
Если события A и B не пересекаются, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B).
События пересекаются
Если события A и B пересекаются, то есть у них есть общие элементарные исходы, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B) — вероятность пересечения событий P(A ∩ B)
Независимые события
События A и B независимы, если наступление одного события не влияет на другое событие.
Практический пример
Будем рассматривать пример с игральным кубиком, для простоты и анализа нашего эксперимента введём следующие обозначения:
- 1 очко = ω1;
- 2 очка = ω2;
- 3 очка = ω3;
- 4 очка = ω4;
- 5 очков = ω5;
- 6 очков = ω6.
Событие A: выпало > 3 очков
Событие B: выпало нечетное число очков
Чтобы приступить к решению задачи выполняем анализ событий.
Анализ события A: этому событию соответствует три элементарных исхода { ω4, ω5, ω6}
Анализ события B: этому событию соответствует три элементарных исхода{ ω1, ω3, ω5}
После анализа событий приступаем к пошаговому решению.
Рассмотрим теперь пересечение события A и B, то есть у нас должно выпасть > 3 очков и при этом число должно быть нечётное. В этом случае у нас есть один элементарный исход: { ω5}.
Отсюда мы можем посчитать вероятность этого события:
- n – элементарный исход, который удовлетворяет нашим условиям;
- N – общее количество исходов.
Далее рассмотрим объединение событий A и B. В данном случае у нас будет следующий набор элементарных условий { ω1, ω3, ω4, ω5, ω6}
Обратите внимание: у нас отсутствует ω2, так как этот исход не фигурирует ни в событии A, ни в событии B.
Поэтому мы можем сказать, что вероятность объединения в этом случае будет:
По факту мы решили задачу, но мы можем её решить намного быстрее, если воспользуемся формулой, которую изучили ранее:
- Вероятность P(A) – выпало > 3 очков
- Вероятность P(B) – выпало нечётное число
- Вероятность P(A ∩ B) – пересечение событий A и B
Метки: Математика, Теория вероятностей.
Как решать задачи на вероятность?
Если вас интересует вопрос заголовка, вы наверняка студент или школьник, столкнувшийся с новым для себя предметом. Задачи теории вероятностей сейчас решают и школьники пятых классов продвинутых школ, и старшеклассники перед ЕГЭ, и студенты буквально всех специальностей – от географов до математиков. Что же это за предмет такой, и как к нему подойти?
Лучшее спасибо – порекомендовать эту страницу
Вероятность. Что это?
Теория вероятностей, как следует из названия, имеет дело с вероятностями. Нас окружают множество вещей и явлений, о которых, как бы ни была развита наука, нельзя сделать точных прогнозов.
Мы не знаем, какую карту вытянем из колоды наугад или сколько дней в мае будет идти дождь, но, имея некоторую дополнительную информацию, можем строить прогнозы и вычислять вероятности этих случайных событий.
Таким образом, мы сталкиваемся с основным понятием случайного события – явления, поведение которого невозможно предсказать, опыта, результат которого заранее невозможно вычислить и т.п. Именно вероятности событий вычисляются в типовых задачах.
Вероятность – это некоторая, строго говоря, функция, принимающая значения от 0 до 1 и характеризующая данное случайное событие. 0 – событие практически невозможно, 1 – событие практически достоверно, 0,5 (или “50 на 50”) – с равной вероятностью событие произойдет или нет.
Подробно решим ваши задачи по теории вероятностей
Алгоритм решения задач на вероятность
Подробнее с основами теории вероятностей можно ознакомиться, например, в онлайн учебнике.
А теперь не будем ходить вокруг да около, и сформулируем схему, по которой следует решать стандартные учебные задачи на вычисление вероятности случайного события, а затем ниже на примерах проиллюстрируем ее применение.
- Внимательно прочитать задачу и понять, что именно происходит (что из какого ящика вытаскивается, что где лежало, сколько приборов работает и т.п.)
- Найти основной вопрос задачи вроде “вычислить вероятность того, что …” и вот это многоточие записать в виде события, вероятность которого надо найти.
- Событие записано. Теперь надо понять, к какой “схеме” теории вероятностей относится задача, чтобы правильно выбрать формулы для решения. Ответьте на тестовые вопросы типа:
- происходит одно испытание (например, выбрасывание двух костей) или несколько (например, проверка 10 приборов);
- если испытаний несколько, зависимы ли результаты одного от других (зависимость или независимость событий);
- событие происходит в единственной ситуации или задача говорит о нескольких возможных гипотезах (например, шар вынимается из любого ящика из трех, или из конкретного).
Чем больше опыт решения задач, тем легче будет определить, какие формулы подходят.
- Выбрана формула (или несколько) для решения. Записываем все данные задачи и подставляем в данную формулу.
- Вуаля, вероятность найдена.
Как решать задачи: классическая вероятность
Пример 1. В группе из 30 студентов на контрольной работе 6 студентов получили «5», 10 студентов – «4», 9 студентов – «3», остальные – «2». Найти вероятность того, что 3 студента, вызванные к доске, получили по контрольной работе «2».
Начинаем решение по пунктам, описанным выше.
- В задаче речь идет о выборе 3 студентов из группы, которые удовлетворяют определенным условиям.
- Вводим основное событие $X$ = (Все 3 студента, вызванные к доске, получили по контрольной работе «2»).
- Так как в задаче происходит только одно испытание и оно связано с отбором/выбором по определенному условию, речь идет о классическом определении вероятности. Запишем формулу: $P=m/n$, где $m$ – число исходов, благоприятствующих осуществлению события $X$, а $n$ – число всех равновозможных элементарных исходов.
- Теперь необходимо найти значения $m$ и $n$ для этой задачи. Сначала найдем число всех возможных исходов – число способов выбрать 3 студентов из 30. Так как порядок выбора не имеет значения, это число сочетаний из 30 по 3: $$n=C_{30}^3=frac{30!}{3!27!}=frac{28cdot 29 cdot 30}{1cdot 2 cdot 3}=4060.$$ Найдем число способов вызвать только студентов, получивших “2”. Всего таких студентов было $30-6-10-9=5$ человек, поэтому $$m=C_{5}^3=frac{5!}{3!2!}=frac{4 cdot 5}{1cdot 2}=10.$$
- Получаем вероятность: $$P(X)=frac{m}{n}=frac{10}{4060}=0,002.$$ Задача решена.
Еще: Решенные задачи на классическое определение вероятности.
Некогда решать? Найди решенную задачу
Готовые решения задач по любым разделам теории вероятностей, более 10000 примеров! Найди свою задачу:
Как решать задачи: формула Бернулли
Пример 2. Какова вероятность того, что при 8 бросаниях монеты герб выпадет 5 раз?
Снова по схеме решения задач на вероятность рассматриваем данную задачу:
- В задаче идет речь о серии одинаковых испытаний – бросаний монеты.
- Вводим основное событие $X$ = (При 8 бросаниях монеты герб выпадет 5 раз).
- Так как в задаче происходит несколько испытаний, и вероятность появления события (герба) одинакова в каждом испытании, речь идет о схеме Бернулли. Запишем формулу Бернулли, которая описывает вероятность того, что из $n$ бросков монет герб выпадет ровно $k$ раз:
$$ P_{n}(k)=C_n^k cdot p^k cdot (1-p)^{n-k}.$$ - Записываем данные из условия задачи: $n=8, p=0,5$ (вероятность выпадения герба в каждом броске равна 0,5) и $k=5$
- Подставляем и получаем вероятность:
$$ P(X)=P_{8}(5)=C_8^5 cdot 0,5^5 cdot (1-0,5)^{8-5}=frac{8!}{5!3!}cdot 0,5^8=frac{6cdot 7 cdot 8}{1cdot 2 cdot 3} cdot 0,5^8= 0,219.$$
Задача решена.
Еще примеры: Решенные задачи на формулу Бернулли
И это все? Конечно, нет.
Выше мы упомянули только малую часть тем и формул теории вероятностей, для более подробного изучения вы можете посмотреть учебник онлайн на данном сайте (или скачать классические учебники по ТВ), ознакомиться со статьями по решению вероятностных задач, бесплатными примерами, воспользоваться онлайн калькуляторами. Удачи!
Лучшее спасибо – порекомендовать эту страницу
Полезные статьи по теории вероятностей
- Как найти математическое ожидание случайной величины?
- Как найти дисперсию случайной величины?
- Как найти вероятность в задачах про выстрелы?
- Как найти вероятность в задачах про подбрасывания монеты?
- Как найти вероятность в задачах про подбрасывание игральных костей?
- Как найти вероятность в задачах про станки?
- Как найти вероятность в задачах про надежность схем и цепей?
- Как найти вероятность наступления хотя бы одного события?
Содержание:
Алгебра событий:
С каждым испытанием связан ряд интересующих нас событий, которые, вообще говоря, могут появляться одновременно. Например, пусть при бросании игральной кости (т. е. кубика, на гранях которого имеются очки 1, 2, 3, 4, 5, 6) событие А есть выпадение одного очка, а событие В есть выпадение нечетного числа очков. Очевидно, эти события не исключают друг друга.
Пусть все возможные результаты испытания осуществляются в ряде единственно возможных частных случаев, взаимно исключающих друг друга (так называемые элементарные события или элементарные исходы). Тогда:
- каждый исход испытания представляется одним и только одним элементарным событием;
- всякое событие А, связанное с этим испытанием, есть множество (совокупность) конечного или бесконечного числа элементарных событий;
- событие А происходит тогда и только тогда, когда реализуется одно из элементарных событий, входящих в это множество.
Пример:
Пусть событие А состоит в выпадении нечетного числа очков при однократном бросании игральной кости.
За элементарные события здесь могут быть приняты следующие результаты испытания: (1), (2), (3), (4), (5), (6). Событие А представляет собой множество событий {(1) (3), (5)}.
По аналогии с теорией множеств строится алгебра событий.
Определение: Под суммой двух событий А и В понимается событие
которое имеет место тогда и только тогда, когда произошло хотя бы одно из событий А и В.
В общем случае, под суммой нескольких событий понимается событие, состоящее в появлении хотя бы одного из этих событий.
Пример:
Пусть событие А есть выигрыш по займу I, а событие В — выигрыш по займу И. Тогда событие А + В есть выигрыш хотя бы по одному займу (возможно, по двум сразу!).
Определение: Произведением двух событий А и В называется событие
состоящее в одновременном появлении как события А, так и события В.
В общем случае, под произведением нескольких событий понимается событие, состоящее в одновременном осуществлении всех этих событий.
Пример:
Пусть события А и В есть успешные прохождения соответственно туров I и II при поступлении в институт. Тогда событие АВ представляет собой успешное прохождение обоих туров.
События А и Б называются несовместными в данном испытании, если произведение их есть событие невозможное, т. е.
АВ = О,
где О — невозможное событие.
Иными словами, два события несовместны, если появление одного из них исключает появление другого и наоборот.
Предмет теории вероятностей
Цель изучения основ теории вероятностей –
математической науки, изучающей закономерности случайных явлений. Случайные явления, как вам известно, – это явления, которые при многократном повторении (например, некоторого опыта) протекают каждый раз по-другому.
Заметим, что этот материал качественно отличается от ранее изученных разделов. Как вы знаете, в курсе политехнического университета, кроме теории вероятностей, рассматривается математический аппарат, позволяющий исследовать так называемые детерминированные явления, т.е. известные явления не содержащие каких – либо неопределенностей. Так вот, эти детерминированные явления, как правило, исследуются с помощью дифференциальных уравнений, описывающих математические модели реальных процессов. При этом предполагается, что параметры, входящие в эти уравнения являются заданными постоянными величинами или меняются по заданным функциональным зависимостям. Внешние возмущения, если таковы имеются, также заданы детерминировано.
Однако при изучении многих явлений такая точка зрения неприемлема, так как может оказаться, что, например, внешние воздействия на систему не детерминированные, а случайные (различные шумы, помехи и т.п.), проявляющие свою закономерность не в единичном явлении, а в их совокупности. В этом случае говорят о массовых случайных явлениях. Это означает, что закономерности, свойственные случайным явлениям, могут проявляться только при большом числе однородных опытов. В этой связи большое значение уделяется методам изучения случайных явлений (эти методы, кстати сказать, называются вероятностными или
статистическими). Другими словами, предметом теории вероятностей, как математической науки, как раз и является изучение закономерностей в массовых случайных явлениях независимо от их природы. Возникновение теории вероятностей относится к середине XVII в. и связано с именами Гюйгенса, Паскаля, Ферма и Якова Бернулли. В переписке Паскаля и Ферма, вызванной задачами, связанными с азартными играми, определились постепенно такие важные понятия, как вероятность и математическое ожидание.
При этом, конечно, нужно отдавать себе ясный отчет, что выдающиеся ученые, занимаясь задачами азартных игр, предвидели и фундаментальную роль науки, изучающей случайные явления. Следующий этап в развитии теории вероятностей связан с именем Якова Бернулли. Его теорема – закон больших чисел – первое теоретическое обоснование накопленных фактов.
Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону, им принадлежит развитие первых аналитических методов теории вероятностей. Новый, наиболее плодотворный период связан с именами Чебышева и его учеников – Маркова и Ляпунова. Этот период становления теории вероятностей стал началом раздела математики.
Дальнейшее развитие теории вероятностей связано с именами советских математиков: Колмогорова, Хинчина, Гнеденко и др. В настоящее время роль теории вероятностей неоспорима.
Элементы теории множеств
Под множеством понимается любая (конечная или бесконечная) совокупность объектов с некоторой общей характеристикой (или, что то же самое – объектов одинаковой природы). Эти объекты, как вам известно еще со школы, называются элементами множества. Множества с конечным числом различных элементов могут быть описаны путем явного перечисления всех этих элементов: обычно, эти элементы заключаются в фигурные скобки. Например, 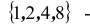
Для некоторых особо важных множеств приняты стандартные обозначения, которых стоит придерживаться.
Так, буквами
- N – множество натуральных чисел
- Z – множество целых чисел
- Q – множество рациональных чисел
- R – множество вещественных (или действительных) чисел
При заданном множестве S включение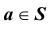
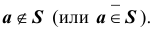
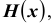
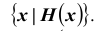
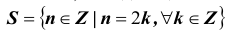
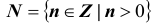
Говорят, что S – подмножество множества T или 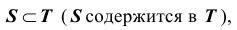
Два множества S и T совпадают (или равны), если у них одни и те же элементы.
Символически это выглядит так:
Заметим, что пустое множество 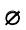
Если 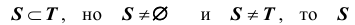
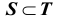
Для множеств A,B,C справедливы следующие соотношения:
( значок 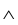
этого множества поставлено в соответствие некоторое число (номер элемента) от 1 до n.
Операции над множествами
Для пояснения некоторых определений и свойств операций над множествами и различных соотношений между ними воспользуемся диаграммами Эйлера – Венна, на которых множества, подлежащие рассмотрению, изображаются в виде совокупности точек на плоскости.
1. Под пересечением (произведение) двух множеств S и T понимается множество:
2. Под объединением (сумма) двух множеств S и T понимается множество :
3. Разностью S T множеств S и T называется совокупность тех элементов, из S , которые не содержатся в T , то есть
4. Если 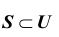
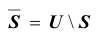
Можно еще много говорить о множествах, их свойствах, операциях над ними и т.п. Остановлюсь лишь на некоторых свойствах, указанных операций, после чего перейдем к новому разделу. Итак, для множеств A,B,C справедливы следующие соотношения:
1. Свойство коммутативности:
2. Свойство дистрибутивности:
3. Свойство ассоциативности:
Элементы комбинаторики
Комбинаторика – это раздел математики, изучающий задачи о расположении или выборе элементов из множеств.
Группы, составленные из каких – либо предметов (любой, но одинаковой природы: буквы, числа, геометрические фигуры, детали и т. д.) называются соединениями (множествами). Сами предметы, их которых составляются соединения, называются элементами
Различают три основных типа соединений: размещения, перестановки и сочетания.
Размещениями из n различных элементов по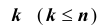
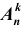
Такие размещения называются размещениями без повторений.
Пример №1
В группе 25 студентов. Выбирают старосту, физорга и профорга. Каково число всех возможных вариантов выбора «треугольника» группы?
Решение. Получаемые комбинации (т.е. соединения) из 25 – и элементов по 3 в каждом являются размещениями, так как в них важен не только состав элементов «треугольника», но и расположение внутри него. Следовательно
Размещение с повторениями из n элементов по k элементов в каждом может содержать любой элемент сколько угодно раз от 1 до k включительно, либо не содержать его вовсе. Другими словами, каждое размещение с повторениями из n элементов по k может состоять не только из k каких угодно, но и как угодно повторяющихся элементов. Число размещений с повторениями вычисляется по формуле
Пример №2
Известно, что 4 студента сдали экзамен. Сколько возможно различных исходов экзамена (распределений оценок)?
Решение. Число элементов n=3 ( «3», «4», «5» ); k = 4. Последовательность, т. е. порядок элементов, существенна, повторения неизбежны.
Следовательно
Пример №3
Сколькими способами 10 пассажиров могут распределиться по 13 вагонам, если для каждого существенным является только № вагона, а не занимаемое место в нем?
Решение. Пусть 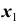
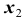
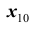
выбранного десятым пассажиром. Соединение (комбинация) 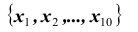
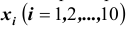
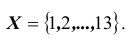
Перестановками из n различных элементов называются такие соединения,
из которых каждое содержит все n элементов и которые отличаются друг от друга лишь порядком расположения элементов. Число таких перестановок из n различных элементов обозначается 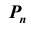
Так как число перестановок из n элементов – это то же самое, что и число размещений из n элементов по n в каждом, то можем записать:
Пример №4
Для проведения испытаний выбрано 5 различных моделей автомобилей. Сколькими способами они могут быть распределены между пятью испытателями?
Решение. Число способов, которыми можно распределить 5 автомобилей, равно числу комбинаций из 5 элементов по пять. Причем, сами комбинации отличаются друг от друга только порядком элементов, т.е. применимы перестановки. Следовательно
Если же среди n элементов имеются одинаковые, то такие перестановки называются перестановками с повторениями. Пусть имеется n элементов, среди которых 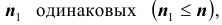
определяется по формуле
Если из n элементов имеется две различные группы, состоящие соответственно из одинаковых элементов:
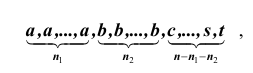
Пример №5
Каким числом способов можно распределить 9 цитрусовых между 9 студентами, если имеются 4 мандарина, 3 апельсина и 2 лимона?
Решение. Пусть m – мандарины, a – апельсины и l – лимоны. Тогда
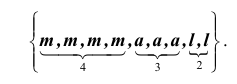
Сочетаниями из n различных элементов по 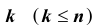
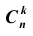
Уверены, вы отлично понимаете, что это определение является определением числа сочетаний без повторений.
Число сочетаний обладает следующими свойствами:
Этим свойством удобно пользоваться в случаях, когда 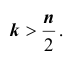
Пример №6
На строительство общежития из 25 студентов требуется выбрать 3 человек. Каково число всех возможных вариантов выбора этой тройки?
Решение. Число возможных вариантов равно числу комбинаций (соединений) из 25 элементов по 3 в каждом. Причем комбинации отличаются друг от друга только составляющими их элементами, а порядок их расположения не имеет
значения. Следовательно
Сочетание с повторениями из n элементов по k в каждом может содержать любой элемент сколько угодно раз от 1 до k включительно, либо не содержать его вовсе. Другими словами, каждое сочетание с повторениями из данных n элементов по k элементов в каждом может состоять не только из k различных элементов, но из k каких угодно и как угодно повторяющихся элементов.
Два сочетания по k элементов не считаются различными сочетаниями, если они отличаются друг от друга только порядком расположения элементов.Число сочетаний с повторениями вычисляется по формуле:
Пример №7
Каким числом способов можно составить расписание занятий из 3-х пар на один день, если изучается 10 предметов, которые могут повторяться в расписании. Расписания считаются различными, если отличаются друг от друга, хотя бы одним предметом (т.е. порядок предметов в расписании роли не играет)?
Решение.
Замечания.
Например. Сколькими способами можно выбрать четырехзначное число, все цифры которого различны?
2. При большом n пользуются приближенной формулой Стирлинга
Алгебра событий. Различные определения вероятности событий
Понятие события является первичным, как, например, в геометрии, понятие точки или прямой, а в математическом анализе – понятие множества.
Случайные события
Под случайным событием понимается все то, о чем имеет смысл говорить, что оно либо происходит, либо не происходит при выполнении определенной системы условий, то есть, всякий факт (явление), который в результате опыта может произойти или не произойти. Опытом (или – испытанием) называется выполнение некоторого комплекса условий. Случайное событие, состоящее только из одного исходы, называется элементарным событием. Элементарное событие, в свою очередь, являющееся результатом опыта, называется также исходом опыта.
Рассмотрим несколько примеров.
- При измерении некоторой величины, результат измерения окажется равным некоторому заданному числу. Это событие.
- В ящике находятся шары, различающиеся лишь цветом: белые, красные, синие. Из ящика наудачу извлекают один шар. Появление при этом шара, например, белого цвета – событие.
- Попадание и промах при выстреле является событием.
Событие называется достоверным (обозначается U ), если оно обязательно происходит в результате данного испытания, т. е. при выполнении определенной совокупности условий S . Например, при бросании игральной кости (всем известного кубика с указанием числа очков на его шести гранях) событие «выпадение на верхней грани по крайней мере одного из шести очков» есть достоверное событие.
Событие называется невозможным (обозначается V ), если оно не может произойти в результате данного опыта. В предыдущем примере событие «выпадение на верхней грани игральной кости дробного числа очков» –
невозможное событие.
События мы будем обозначать заглавными печатными буквами латинского алфавита: A,B,C,…
Пространством 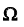
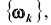
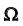
После этого определения, нетрудно сделать вывод, что случайным событием
называется любое подмножество пространства элементарных исходом 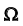
В рассмотренных примерах события являются случайными, их, как уже отмечалось, обозначают заглавными печатными буквами латинского алфавита: A,B,C,… Далее, если рассматривать случай бросания игральной кости, то при одном бросании элементарных исходов всего шесть. Обозначим их через
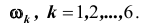
Тогда, например, событие A – выпадение грани с четным числом очков можно записать в виде: 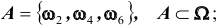
Геометрически событие будем обозначать (согласно Венну) множеством точек плоскости (см. рис.). Любое случайное событие есть подмножество множества
Отношения между событиями
1. Если при появлении события A событие B обязательно происходит, то говорят, что событие A влечет событие B . Обозначение
(Здесь и в дальнейшем будем пользоваться известными символами теории множеств). Например, A- выпадение на верхней грани игральной кости числа очков, кратного 3, а B – выпадение числа очков, кратного 2. Тогда, случай 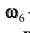
2. Говорят, что события A и B эквивалентны (равноправны) и пишут
3. События A и B называются несовместными в данном испытании,если появление одного из них автоматически исключает появление другого.
В противном случае события A и B называются совместными. Другими словами, в результате испытания возможно их совместное осуществление, т. е. соответствующие множества A и B имеют общие элементы.
Например, при единичном бросании игральной кости событие A – выпадение грани с четным числом очков и событие B – выпадение грани с нечетным числом очков – н е с о в м е с т н ы, а событие C – выпадение числа очков, кратного 3 и D – выпадение числа очков, кратного 2 – с о в м е с т н ы, так как в пространстве элементарных исходов 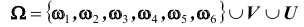
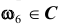
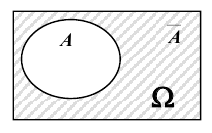
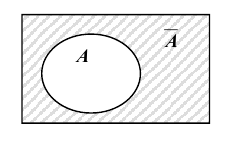
4. Противоположным событием 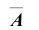
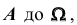
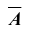
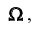
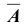
очевидно, что событие B – выпадение грани с нечетным числом очков, является противоположным событием для события A – выпадение грани с четным числом очков, то есть
Операции над событиями
1. Суммой (или объединением) двух событий A и B называется событие 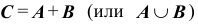
Сумма (объединение) событий 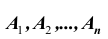
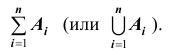
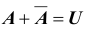
2. Произведением (или пересечением) нескольких событий 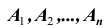
Например, если рассматривать два события A и B , то их произведение 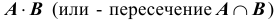
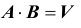
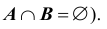
3. Разность событий A и B называется событие, обозначаемое AB и состоящее в том, что A происходит, а B при этом не происходит. Очевидно, что противоположное для A событие 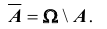
полной группы) событий.
Определение: Система (или – группа) событий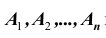
и сумма (объединение) этих событий составляет достоверное событие:
т.е. в результате некоторого опыта хотя бы одно из них обязательно происходит.
Например, при бросании игральной кости события A – выпадение на верхней грани четного числа очков 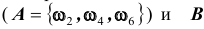
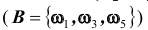
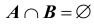
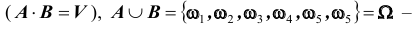
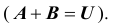
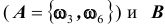
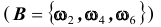
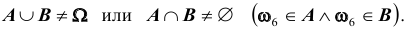
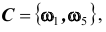
B и C будет такой, что их объединение (сумма) является достоверным событием: 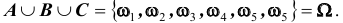
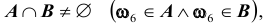
Аксиоматическое определение вероятности
Аксиоматическая теория вероятностей в её современном виде была создана А. Н. Колмогоровым ещё в 1933г. Определение: Вероятностью события A называется числовая функция 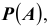
3). Для любой конечной или бесконечной последовательности событий 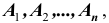
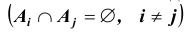
(заметим, что последняя аксиома называется аксиомой сложения). Другими словами, вероятностью 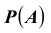
Введенные аксиомы определяют понятие «вероятность события» и
устанавливают основные свойства вероятности. Однако это определение слишком общее и не позволяет производить вычисления. Очевидно, что
Относительная частота. Статистическое определение вероятности. Пусть опыт S повторяется n раз, при этом m раз произошло событие A, т.е. проведена серия из n испытаний.
Определение: Относительной частотой (частостью) 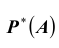
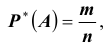
Пример №8
Отдел технического контроля обнаружил 3 нестандартных детали
из 100 случайно отобранных. Тогда
Заметим, что до проведения серии опытов частота 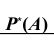
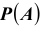
Определение: Статистической вероятностью события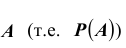
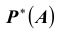
Пример №9
Многократно проводились опыты бросания монеты, в которых подсчитывали число появления герба. Результаты нескольких опытов приведены в таблице
Здесь относительные частоты незначительно отклоняются от числа 0,5, причём тем меньше, чем больше число испытаний. Например, при 4040 испытаниях отклонение равно 0,0069, а при 24 000 испытаний – лишь 0,0005. Приняв во внимание, что вероятность появления герба при бросании монеты равна 0,5, мы вновь убеждаемся, что относительная частота колеблется около вероятности. Статистический способ определения вероятности обладает тем преимуществом, что он опирается на эксперимент. Недостатком же этого определения является необходимость в большом числе опытов для получения достоверных данных.
Классическое определение вероятности
Классическое определение вероятности случайного события вводится, когда пространство элементарных событий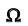
Говорят, что случай 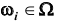
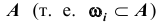
Определение: Вероятностью (классической) события A называется число p 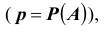
Из этого определения следует, что элементарные случаи ,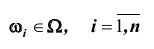
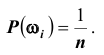
вероятности является то, что:
– конечно. Всегда возникает стремление и желание обобщить это понятие;
- невозможно представить результат испытания в виде совокупности элементарных событий;
- трудно указать основания, считать элементарные события равновозможными (равновероятными).
Наряду с недостатками есть и положительные стороны этого определения.
В частности то, что с помощью классического определения вероятность события можно вычислить, что очень важно, до начала проведения опыта.
Геометрическое определение вероятности
Геометрическое определение вероятности является обобщением классического определения на случай непрерывных множеств с бесконечным числом элементарных исходов. Пусть 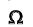
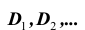
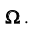
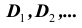
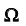
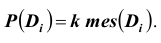
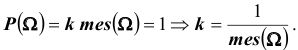
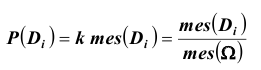
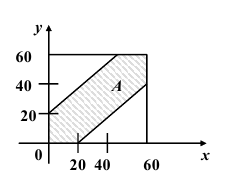
Пример №10
Два партнера договорились о встрече между 12 и 13 часами дня с условием ожидать друг друга не более 20 минут. Найти вероятность их встречи.
Решение. Пусть x – время прихода первого партнера; y – время прихода второго партнера. Тогда, очевидно,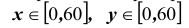
множество всех элементарных исходов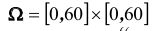
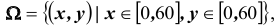
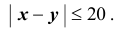
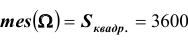
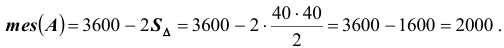
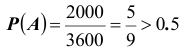
Пример №11
Монета подбрасывается два раза.
а) Опишите полную группу возможных элементарных событий.
б) Если событие А – выпало не менее одного “орла”, В – выпало не менее одной “решки”, укажите, что собой представляют события:
Решение.
В данной задаче испытанием является подбрасывание монеты дважды.
а) Обозначим события:
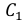
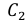
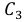
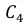
Тогда перечисленные события 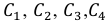
Кроме того, никакие два из указанных событий не могут наступить одновременно. Следовательно, имеет место равенство:
Таким образом, указанные события попарно несовместны. Причём наступление любого из событий 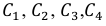
Таким образом, события 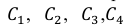
б) Так как 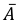
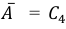
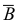
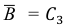
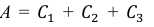
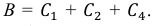
Ответ: а) 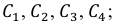
.
Пример №12
В ящике находится 10 шаров: 3 белых и 7 чёрных. Из ящика наугад выбирается один шар. Какова вероятность того, что этот шар:
а) белый,
б) чёрный?
Решение.
В данной задаче полную группу элементарных событий составляют 10 событий, так как выбор любого одного шара можно осуществить 10 способами. Из этих событий только 3 благоприятствуют выбору белого шара и 7 – выбору чёрного. Поэтому, если А – выбор белого шара, то 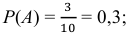
Ответ: а) 0,3 ; б) 0,7.
Пример №13
Из пяти карточек с буквами А, Б, В, Г, Д наугад выбираются одна за другой три карточка и располагаются в ряд (в порядке появления) слева направо. Какова вероятность, что получится слово “ДВА”?
Решение.
Выбор трёх карточек из имеющихся пяти можно осуществить 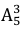
Значит, число всех возможных элементарных событий n = 60. Из этих событий только одно благоприятствует событию – получению слова “ДВА”, следовательно, m = 1. Итак,
Ответ:
Пример №14
В ящике 10 шаров: 6 белых и 4 чёрных. Из ящика наугад вынимают два шара. Какова вероятность того, что
а) оба шара белые?
б) оба шара чёрные?
в) один шар белый, другой чёрный?
Решение.
Число выбора двух шаров из десяти имеющихся определяется числом всевозможных сочетаний из 10 по
Значит, полную группу элементарных событий рассматриваемого испытания (выбор двух шаров из десяти, находящихся в ящике) составляют 45 событий. Следовательно, n = 45.
а) Если из элементарных событий рассматривать только те, которые состоят в выборе двух белых шаров, то находим
Следовательно, вероятность того, что оба шара будут белыми, вычисляется по формуле:
б) Если рассматривать событие – выбор двух чёрных шаров, то число благоприятствующих ему элементарных событий равно:
Значит, вероятность выбора двух чёрных шаров вычисляется по формуле:
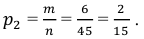
в) Если рассматривать событие – выбор одного белого и одного чёрного шаров, то для него число благоприятствующих элементарных событий равно:
Значит, вероятность выбора одного белого и одного чёрного шаров вычисляется по формуле:
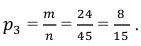
Ответ:
Пример №15
Стрелок стреляет по мишени, разделённой на четыре области. Вероятность попадания в первую область 0,4, во вторую – 0,3.
Найдите вероятность того, что стрелок при одном выстреле попадёт либо в первую область, либо во вторую.
Решение.
Обозначим события:
А – стрелок попадает в первую область, В – стрелок попадает во вторую область. Эти события несовместны, так как они не могут наступить одновременно (попадание пули в одну область мишени исключает её попадание в другую область). Поэтому воспользуемся теоремой 1 (вероятность суммы несовместных событий), откуда находим:
Ответ: 0,7.
Пример №16
Какова вероятность извлечь из колоды в 52 карты фигуру (валет, дама, король, туз) любой масти или карту трефовой масти?
Решение.
Обозначим события: А – извлечение из колоды карты – фигуры, В – извлечение из колоды карты трефовой масти.
Необходимо найти вероятность суммы этих событий. События А и В совместны, так как они могут наступить одновременно, если будет извлечена карта – фигура трефовой масти. Поэтому для подсчёта вероятности суммы этих событий используем теорему 2 (вероятность суммы совместных событий):
В рассматриваемой задаче 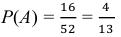
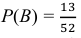
(в колоде 4 карты – фигуры трефовой масти).
Итак, находим:
Ответ: 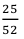
Пример №17
Два орудия стреляют по одной цели. Вероятность попадания для первого орудия равна 0,6, для второго вероятность попадания равна 0,5. Какова вероятность того, что в цель попадут оба орудия?
Решение.
Обозначим события:
А – попадание в цель первого орудия, В – попадание в цель второго орудия.
Отметим, что А и В – события независимые, то есть наступление одного из них не влияет на наступление или ненаступление другого.
Поэтому воспользуемся теоремой 3 (вероятность произведения независимых событий):
Ответ: 0,3.
Пример №18
Для Московской области среднее число дождливых дней в августе равно 15. Какова вероятность, что первые два дня августа не будут дождливыми?
Решение.
Обозначим события: А – 1 августа не будет дождя, В – 2 августа не будет дождя.
Необходимо рассмотреть событие А · В – 1 и 2 августа не будет дождя.
В данной задаче 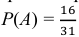
При вычислении Р(В) результат зависит от того, будет ли дождь 1-го августа. Следовательно, необходимо найти условную вероятность 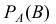
Так как в августе осталось 30 дней, начиная со 2 августа, из них не дождливых дней осталось 15 (ведь один не дождливый день пришёлся по предположению на 1 августа). Итак, по теореме 4 (вероятность произведения зависимых событий) получаем:
Ответ:
Пример №19
В ящике 10 деталей, среди которых 6 стандартных.
Какова вероятность того, что среди трёх наугад взятых деталей окажется хотя бы одна стандартная?
Решение.
События “среди взятых деталей окажется хотя бы одна стандартная” и “среди взятых деталей нет ни одной стандартной” – противоположные события, так как наступление одного из этих событий исключает наступление другого.
Обозначим:
А – среди трёх взятых деталей есть хотя бы одна стандартная, 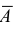
По следствию 2 из теоремы 1 известно, что Р(А) = 1 – 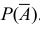
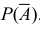
Число нестандартных деталей равно 10 – 6 = 4. Число элементарных исходов, благоприятствующих событию
Тогда
.
Следовательно,
Ответ:
Что такое алгебра событий
Ранее мы познакомились со способами непосредственного вычисления вероятностей простых событий. Однако на практике чаще приходится иметь дело со сложными событиями, которые являются комбинацией простых событий. Для нахождения вероятностей таких событий применяются теоремы сложения и умножения вероятностей. Перед тем, как сформулировать эти теоремы введем понятия суммы событий и произведения событий.
Действия над событиями
Определение: Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из данных событий.
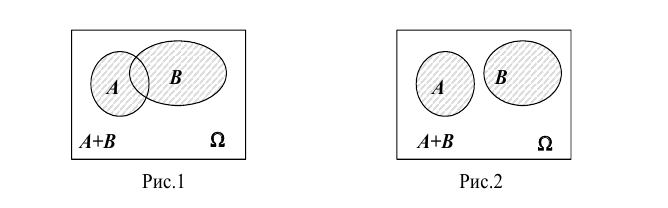
Если А и В – совместные события, то их сумма А + В обозначает наступление события А, или события В, или обоих событий вместе. Если А и В – несовместные события, то их сумма А + В обозначает наступление события А, или события В.
Определение: Произведением нескольких событий называется событие, состоящее в совместном наступлении всех этих событий.
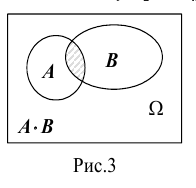
Если А, В, С – совместные события, то их произведение АВС означает одновременное наступление и события А, и события В, и события С.
Пример №20
Экзаменационный билет содержит три вопроса. Рассматриваются следующие события: А – студент, пришедший сдавать экзамен, ответил на первый вопрос, В – на второй вопрос, С – на третий вопрос. Что представляют события: а) А + В; б) АВС, в) А + ВС?
Решение:
а) Событие А + В состоит в том, что студент ответит либо на первый вопрос, либо на второй вопрос, либо на оба вопроса; б) Событие АВС состоит в том, что студент ответит на все три вопроса билета; в) Событие А + ВС состоит в том, что студент ответит либо на первый вопрос, либо на второй и третий вопросы, либо на все вопросы билета. ◄
Теорема сложения вероятностей несовместных событий
Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:
Пример №21
В урне 10 шаров: 2 красных, 3 зеленых и 5 белых. Найти вероятность появления цветного шара.
Решение:
Появление цветного шара означает появление либо красного (событие А), либо зеленого шара (событие В). Вероятность появления красного шара 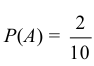
События А и В несовместны, т.к. появление шара одного цвета исключает появление шара другого цвета. Следовательно, теорема сложения применима. Искомая вероятность 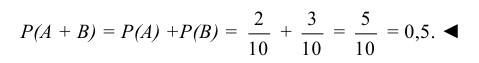
Следствие 1. Сумма вероятностей событий 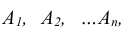
Следствие 2. Сумма вероятностей противоположных событий равна единице: 
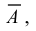
Пример №22
Бросаются три игральных кости. Какова вероятность того, что сумма выпавших очков меньше 18?
Решение:
В результате бросания трех игральных костей могут появиться 16 различных сумм очков от 3 до 18, которые образуют полную группу событий. Для решения задачи следует вычислить вероятность появления 15-ти сумм очков от 3 до 17, а затем сложить их. Это довольно трудоемкая операция.
Поступим по-другому. Событие «сумма выпавших очков меньше 18» и событие «сумма выпавших очков равна 18» являются противоположными. Обозначим их 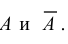
Зная вероятность противоположного события, находим вероятность интересующего нас события: 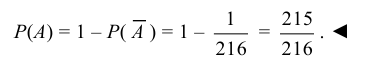
Зависимые и независимые события
Определение: Два события называют независимыми, если вероятность появления одного из них не зависит от того, произойдет другое событие или нет.
Например, опыт состоит в бросании двух монет. Пусть А и В – события, состоящие в том, что герб появится соответственно на первой и второй монете. В данном случае вероятность события А не зависит от того, произошло событие В или нет. Следовательно, событие А независимо от события В.
Определение: Несколько событий называют попарно независимыми, если каждые два из них независимы.
Например, опыт состоит в бросании трех монет. Пусть А, В, С – события, состоящие в том, что герб появится соответственно на первой, второй и третьей монете. В данном случае каждые два из рассматриваемых событий (т.е. А и В, А и С, В и С) – независимы. Следовательно, события А, В и С – попарно независимые. ◄
Определение: Два события называют зависимыми, если вероятность появления одного из них меняется в зависимости от того, произойдет другое событие или нет.
Например, в урне 3 белых и 2 черных шара. Наудачу берут один шар, не возвращая его в урну. Если появился белый шар (событие А), то вероятность появления белого шара во втором испытании (событие В) 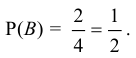
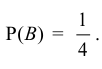
Теорема умножения вероятностей независимых событий
Сформулируем теорему умножения вероятностей независимых событий.
Теорема. Вероятность совместного появления двух независимых событий А и В равна произведению вероятностей этих событий: 
Определение: Несколько событий называют независимыми в совокупности, если каждое из них и любая комбинация остальных событий (содержащих либо все остальные события, либо часть из них) есть события независимые.
Например, если события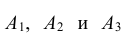
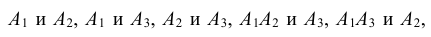
Подчеркнем, что если несколько событий независимы попарно, то из этого еще не следует их независимость в совокупности. В этом смысле требование независимости событий в совокупности сильнее требования их попарной независимости.
Теперь мы можем сформулировать следствие из теоремы умножения вероятностей, обобщающее теорему умножения на несколько событий.
Следствие. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.
Пример №23
Имеется три урны, содержащих по 10 шаров. В первой урне 5 шаров красного цвета, во второй – 4, в третьей – 6. Из каждой урны наудачу вынимают по одному шару. Найти вероятность того, что все три шара окажутся красного цвета.
Решение:
Вероятность того, что из первой урны вынут шар красного цвета (событие А)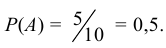
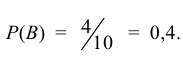
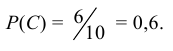
Вероятность появления хотя бы одного события
Теорема. Вероятность появления хотя бы одного из событий 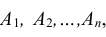
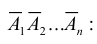
Пример №24
Три стрелка делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,7, второго – 0,8 и третьего – 0,9. Найти вероятность того, что хотя бы один стрелок попадет в мишень.
Решение:
Рассмотрим следующие события: А – хотя бы один стрелок попадет в мишень 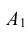
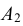
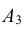
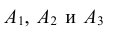
Вероятности событий, противоположных событиям 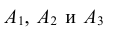
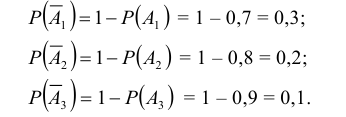
Частный случай. Если события 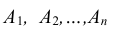

Условная вероятность
Пусть события А и В зависимые. Из определения зависимых событий следует, что вероятность одного из событий зависит от появления или непоявления другого события. Поэтому, если нас интересует вероятность события В, то важно знать, наступило событие А или нет.
Определение: Условной вероятностью 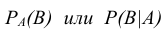
Например, в урне находится пять шаров. Два из них белого цвета, остальные три – черного. Наудачу один за другим берут два шара, не возвращая их обратно в урну. Рассмотрим событие А – «первый вынутый шар оказался белого цвета» и событие В – «второй вынутый шар оказался белого цвета». Найдем условную вероятность события В, при условии, что событие А уже наступило. Если в первый раз был вынут шар белого цвета, то в урне осталось четыре шара, из которых один белого цвета. Следовательно,
Если же вынутый шар возвращается назад в урну, то условия второго испытания остаются неизменными после проведения первого испытания. Тогда 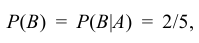
Теорема умножения вероятностей зависимых событий
Пусть события А и В зависимые, причем вероятности Р(А) и Р(В|А) известны. Как найти вероятность совмещения этих событий, т.е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.
Теорема. Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
Следствие. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:
Пример №25
В урне находится пять шаров. Один из них красного цвета, два – зеленого и два – синего. Наудачу один за другим извлекают три шара, не возвращая их обратно в урну. Найти вероятность того, что последовательно будут извлечены красный, зеленый и синий шар.
Решение:
Рассмотрим события: A – первым извлечен шар красного цвета, B – вторым извлечен шар зеленого цвета, C – третьим извлечен шар синего цвета. Вероятность события А: Р(А) = 1/5. Условная вероятность события В при условии, что событие А уже наступило: Р(В|А) = 2/4. Условная вероятность события С при условии, что события А и В уже наступили: Р(С|АВ) = 2/3. Вероятность совместного появления трех зависимых событий А, В и С:
Теорема сложения вероятностей совместных событий
Ранее мы сформулировали теорему сложения вероятностей для несовместных событий. Пусть события А и В совместны, т.е. появление одного из них не исключает появления другого в одном и том же испытании. Даны вероятности этих событий и вероятность их совместного появления. Как найти вероятность события А + В, состоящего в том, что появится хотя бы одно из событий А и В? Ответ на этот вопрос дает теорема сложения вероятностей совместных событий.
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
Пример №26
Два спортсмена-стрелка независимо друг от друга стреляют по одной мишени. Вероятность попадания в мишень первого спортсмена равна 0,7, а второго – 0,8. Какова вероятность того, что мишень будет поражена?
Решение:
Мишень будет поражена в том случае, если в нее попадет либо первый стрелок, либо второй, либо оба вместе, т.е. произойдет событие А + В (событие А – первый стрелок попадет в мишень, событие В – второй стрелок попадет в мишень). Тогда
Формула полной вероятности
Пусть событие А может наступить при условии появления одного из несовместных событий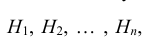
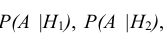
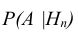
Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий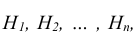
Эту формулу называют «формулой полной вероятности», а события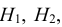
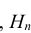
Пример №27
На трех станках различной марки изготавливается определенная деталь. Производительность 1-го станка составляет 40 деталей в смену, 2-го – 35 деталей, 3-го – 25 деталей. Установлено, что 2, 3 и 5% продукции этих станков, соответственно, имеют отклонение от стандарта. В конце смены на контроль взята одна деталь. Какова вероятность того, что она окажется нестандартной?
Решение:
Пусть А – событие, состоящее в том, что наудачу взятая деталь окажется нестандартной. Здесь возможны следующие три гипотезы:
- деталь изготовлена на 1-м станке (гипотеза Н1);
- деталь изготовлена на 2-м станке (гипотеза Н2);
- деталь изготовлена на 3-м станке (гипотеза Н3).
Вероятности этих гипотез: 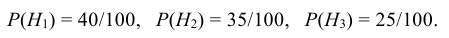
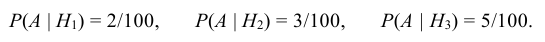
Вероятность гипотез. Формула Байеса
Пусть событие А может наступить при условии появления одного из несовместных событий 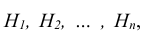
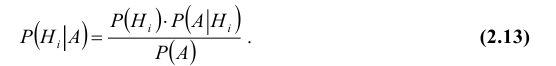
Пример №28
Взятая на контроль деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на первом станке?
Решение:
По условию необходимо переоценить вероятность гипотезы 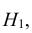
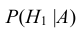
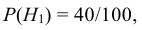
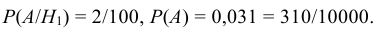
- Свойства вероятности
- Многомерные случайные величины
- Случайные события – определение и вычисление
- Системы случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Генеральная и выборочная совокупности
- Интервальные оценки параметров распределения

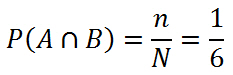
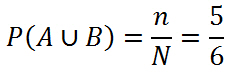
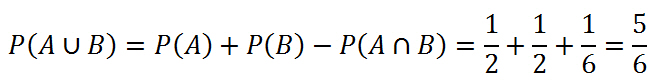
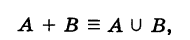
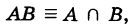
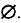
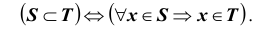
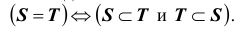
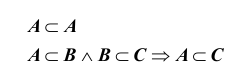
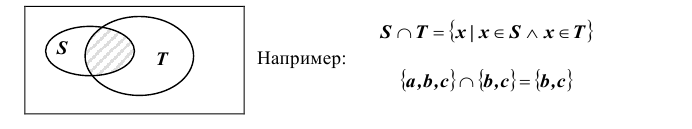


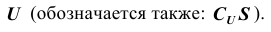

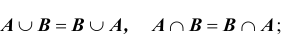
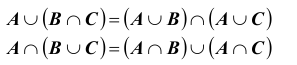
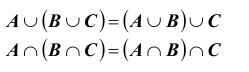
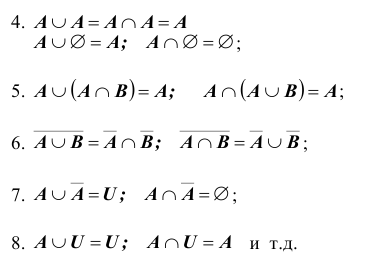
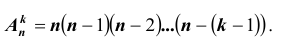
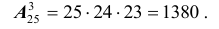
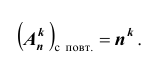
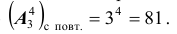
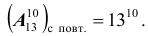

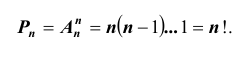
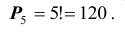
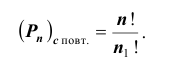
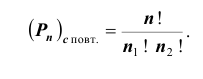
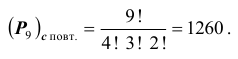
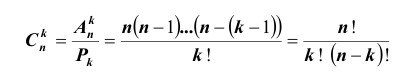
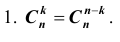
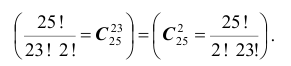
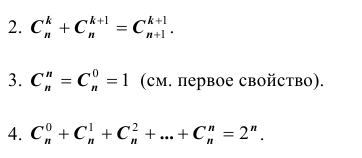
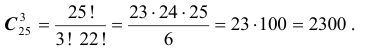
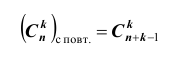
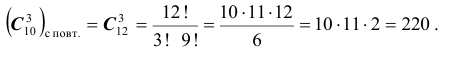
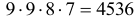
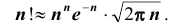
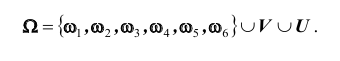
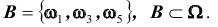
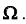
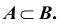
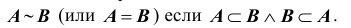
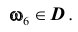
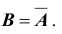
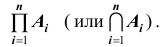
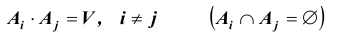
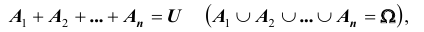
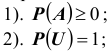
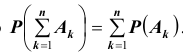
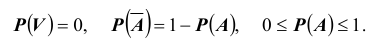
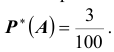

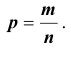
 – конечно. Всегда возникает стремление и желание обобщить это понятие;
– конечно. Всегда возникает стремление и желание обобщить это понятие;