Формула числа сочетаний
Понравилось? Добавьте в закладки
Определение числа сочетаний
Пусть имеется $n$ различных объектов и требуется найти число сочетаний из $n$ объектов по $k$. Будем выбирать комбинации из $k$ объектов всеми возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок (он тут не важен, в отличие от размещений).
Например, есть три ($n=3$) объекта {1,2,3}, составляем сочетания по $k=2$ объекта в каждом. Тогда выборки {1,2} и {2,1} – это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: {1,2}, {1,3}, {2,3}.

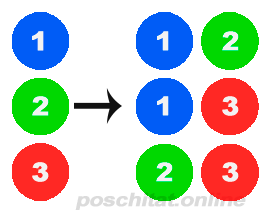
На картинке наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2 (их будет 6, см. калькулятор сочетаний ниже, который даст формулу расчета).
Общая формула, которая позволяет найти число сочетаний из $n$ объектов по $k$ имеет вид:
$$C_n^k=frac{n!}{(n-k)!cdot k!}.$$
Чаще всего сочетания используются в комбинаторных задачах и задачах на расчет вероятности по формуле классической вероятности (см. теорию и примеры).
Смотрите также другие онлайн-калькуляторы
Чтобы вычислить число сочетаний $C_n^k$ онлайн, используйте калькулятор ниже.
Видеоролик о сочетаниях
Не все понятно? Посмотрите наш видеообзор для формулы сочетаний: как использовать Excel для нахождения числа сочетаний, как решать типовые задачи и использовать онлайн-калькулятор.
Расчетный файл из видео можно бесплатно скачать
Понравилось? Добавьте в закладки
Полезные ссылки
- Онлайн учебник по теории вероятностей
- Основные формулы комбинаторики
- Примеры решений задач по теории вероятностей
- Заказать свои задачи на вероятность
Решебник по ТВ
Решебник с задачами по комбинаторике и теории вероятностей:
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.
Описание алгоритма генерации под калькулятором.
![]()
Комбинаторика. Генератор сочетаний из N по M.
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n – m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n – m + i = 5 – 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n – m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5 — последнее сочетание, так как все его элементы равны n – m + i.
Число сочетаний
Пусть имеется n различных объектов. Будем выбирать из них k объектов всевозможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок
(он тут не важен, в отличие от размещений).
Например, есть три объекта {1,2,3}, составляем сочетания по 2 объекта в каждом. Тогда выборки {1,2} и {2,1} – это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: {1,2}, {1,3}, {2,3}.
Общая формула, которая позволяет найти число сочетаний из n объектов по k имеет вид:
Ckn = n!k! ⋅ (n – k)!
Данный онлайн калькулятор позволяет найти число сочетаний из n элементов по k.
Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний – нет), причем именно в k! раз, то есть верна формула связи:
Akn = Ckn ⋅ Pk
Поделиться страницей в социальных сетях:
Онлайн калькулятор для вычисления числа сочетаний из n по k элементов.
Найти число сочетаний.
Скачать калькулятор
Рейтинг: 2.8 (Голосов 29)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Комбинаторика | Число перестановок | Обратная перестановка | Количество инверсий | Число сочетаний с повторениями |
| Порядок перестановки | Элементы комбинаторики | Число размещений | Разложение Бинома | Комбинаторные уравнения |
Число сочетаний
- Главная
- /
- Математика
- /
- Комбинаторика
- /
- Число сочетаний
Для того чтобы найти число сочетаний из n по k без повторений воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Сколько сочетаний будет из
n=
объектов по
k=
?
Ответ:
0
Просто введите общее число объектов (n) и длину одного сочетания (k).
Число сочетаний формула
По данной формуле можно найти только сочетания с неповторяющимися объектами и без учета позиции элемента. То есть у нас есть три объекта: 1 2 3. И нам надо определить все варианты по 2 элемента. Тогда мы получим только три варианта: 1 и 2, 1 и 3, 2 и 3. Варианты 2 и 1, 3 и 1, 3 и 2 считаются идентичными предыдущим. А варианты с повторяющимися объектами (1 и 1, 2 и 2, 3 и 3) не рассматриваются вообще.
Пример
Определим какое количество неповторимых паролей можно создать из 26 букв латинского алфавита, если длина пароля будет 5 символов.
С526 = 26! / (26-5)! ⋅ 5! = 26! / 21! ⋅ 5! = 22⋅23⋅24⋅25⋅26/1⋅2⋅3⋅4⋅5 = 7893600 / 120 = 65780
Итого мы получили 65780 вариантов паролей
