Как найти сокращенную минимальную тупиковую

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Построение минимальных ДНФ

СДНФ, которая строится по таблице булевой функции, зачастую оказывается весьма сложной, т.е. она содержит достаточно много элементарных конъюнкций и литералов. Необходимо уметь находить в определенном смысле минимальную ДНФ, представляющую исходную функцию. Уточним задачу.

Определение 6.5. Булеву функцию называют импликантой булевой функции , если для любых наборов значений переменных из следует .

Замечание 6.7. Напомним, что функции и можно рассматривать как функции от одного и того же числа переменных. Обозначая это число через , можно так уточнить понятие импликанты: функция есть импликанта функции если для каждого набора a из следует . Термин “импликанта” естественным образом ассоциируется и с логической связкой, называемой импликацией, и с одноименной булевой функцией. Действительно, если д импликанта , то из и следует, что , т.е. истинно высказывание

Если функция представлена СДНФ, то любая ее элементарная конъюнкция (констпигпуентпа единицы функции ) будет ее импликантой. Полезно заметить также, что если и — импликанты , то дизъюнкция также является импликантой . Действительно, если , то или . Но тогда, поскольку каждая из этих функций есть импликанта , и есть импликанта .

Из определения 6.5 и понятия равных булевых функций (см. определение 6.2) следует, что булевы функции и равны, если и только если каждая из них служит импликантой другой: .

Определение 6.6. ДНФ называют минимальной, если она содержит наименьшее число литералов среди всех ДНФ, эквивалентных ей.

Обратим внимание на то, что под числом литералов в ДНФ понимают число всех подформул этой ДНФ, которые являются литералами. Так, СДНФ (6.9) содержит 12 литералов (по три литерала в каждой из четырех элементарных конъюнкции).

Пример 6.10. ДНФ не является минимальной, так как ее можно преобразовать к эквивалентной ДНФ, не содержащей ни одного из литералов

Вместо четырех литералов в исходной ДНФ получаем ДНФ, состоящую из одного литерала.
Определение 6.7. Длиной ДНФ называют число входящих в нее элементарных конъюнкций.
ДНФ называют кратчайшей, если она имеет наименьшую длину среди всех эквивалентных ей ДНФ.

Заметим, что кратчайшая ДНФ не обязана быть в то же время минимальной среди всех ДНФ, эквивалентных исходной функции. Но поиск минимальных ДНФ, как мы сейчас увидим, проводится среди кратчайших ДНФ.

Наша задача состоит в том, чтобы описать метод построения минимальной ДНФ, эквивалентной заданной булевой функции. Мы рассмотрим простейший метод такого рода, основанные на алгоритме Квайна — Мак-Клоски. Этот алгоритм исходит обязательно из СДНФ, которая строится по таблице функции так, как это было описано ранее.

---

Алгоритм Квайна–Мак-Клоски

Опишем последовательно этапы, составляющие алгоритм Квайна–Мак-Клоски.

1. Склейка. Пусть и — две элементарные конъюнкции, входящие в исходную СДНФ Ф, которая представляет функцию , причем для некоторого переменного и некоторой элементарной конъюнкции выполняются равенства и . Тогда имеем, согласно тождествам булевой алгебры,

Мы получаем элементарную конъюнкцию , которая содержит на один литерал меньше, чем и , и является, как и обе конъюнкции и , импликантой . Образно говоря, мы “склеили” две импликанты в одну, в которой число литералов на единицу меньше.

Операцию получения по и , описанную выше, можно провести и для любых двух элементарных конъюнкций подобного вида, составляющих любую ДНФ, эквивалентную исходной функции. Такую операцию называют простой склейкой импликант и по переменному .

Установим геометрический смысл простой склейки* (с точки зрения структуры, или “геометрии”, булева куба).

Из доказательства теоремы о представлении булевой функции в виде ДНФ (см. теорему 6.2) мы знаем, что существует взаимно однозначное соответствие между множеством элементарных конъюнкций СДНФ, представляющей функцию , и множеством ее конституент единицы. Это соответствие, напомним, таково, что каждому набору отвечает элементарная конъюнкция , принимающая значение 1 только на наборе . Тогда простая склейка может быть применена только к таким двум элементарным конъюнкциям и , соответствующим наборам , что для некоторого

Это значит, что наборы таковы, что один из них доминирует над другим (они различаются значением только одной компоненты), т.е. они образуют ребро булева куба .

Следовательно, простой склейке, применяемой к элементарным конъюнкциям исходной СДНФ, представляющей функцию , подлежат те и только те элементарные конъюнкции, которые соответствуют элементам какого-либо ребра булева куба, на котором функция принимает единичное значение. Образно говоря, две соседние вершины куба, на которых функция равна 1, псклеиваются” в ребро, их “соединяющее”.

С алгебраической же точки зрения мы из двух элементарных конъюнкций и получаем новую элементарную конъюнкцию , лишенную литерала .

Итак, применяя простую склейку к исходной СДНФ , получаем новую ДНФ ; к ней также применяем простую склейку — получаем ДНФ ; продолжаем выполнять эту операцию до тех пор, пока не окажется, что для некоторого в ДНФ уже нельзя склеить никакие две элементарные конъюнкции. Такое всегда найдется, так как СДНФ состоит из конечного числа элементарных конъюнкций, а они, в свою очередь, состоят из конечного числа литералов. Полученную в результате ДНФ называют сокращенной ДНФ функции , а ее элементарные конъюнкции — простыми импликантами булевой функции .

Замечание 6.8. Понятие простой импликанты определено через процедуру многократного повторения простой склейки. Иногда простую импликанту булевой функции определяют независимо от понятия о склейке как такую элементарную конъюнкцию в составе некоторой ДНФ, представляющей функцию , что удаление из нее любого литерала лишает ее свойства “быть импликантой”. Например, конъюнкция не является простой импликантой мажоритарной функции, так как из ее СДНФ (6.9) можно удалить литерал и получить конъюнкцию , которая будет снова импликантой функции, но уже, как будет показано далее, простой.

Можно доказать, что эти два определения простой импликанты равносильны.

---

Геометрия описанного выше многократного повторения простой склейки, как можно показать, состоит в дальнейшем “склеивании” каждой пары соседних ребер {граней размерности 1), на которых значение функции равно 1, в грани размерности 2, соседних граней размерности 2 в грани размерности 3 и т.д. Разбираемый ниже пример поясняет эту идею.

С геометрической точки зрения склейка первой и третьей конъюнкций в формуле (6.11) означает, что функция принимает единичное значение на ребре [000,100] (рис. 6.6), а склейка второй и четвертой конъюнкций точно так же определяет ребро [001,101], Эти ребра являются соседними, и, кроме того, оказывается, что функция / принимает единичное значение и на другой паре соседних ребер: [000, 001] и [100,101]. Здесь сказывается существенное отличие “геометрии” булева куба от классической: в булевом кубе ребро — это пара вершин, между которыми нет никаких “точек”. Тогда любая пара соседних ребер образует грань размерности 2, любая пара соседних граней размерности 2 образует грань размерности 3 и т.д. Таким образом, если функция принимает единичное значение на двух соседних ребрах булева куба, то она равна 1 в любой точке образуемой ими грани размерности 2, если она равна 1 на двух параллельных соседних гранях размерности 2, то она равна 1 на соответствующей грани размерности 3 и т.д.

Применяя простую склейку к (6.12) (по переменному ), получаем . Побочным результатом склейки явилось и удаление фиктивных переменных функции и .

---

Карты Карно

Для булевых функций от трех и четырех переменных процедура склейки наглядно и просто выполняется на так называемых картах Карио. Форма карт Карно, представляющих собой прямоугольные таблицы, для функции от трех переменных показана на рис. 6.7, а для функции от четырех переменных — на рис. 6.8. На рис. 6.7 строки отмечены наборами значений переменного , а столбцы — , а на рис. 6.8 строки — наборами значений переменных , а столбцы — .

Карта Карно есть не что иное, как форма таблицы для определения булевой функции. Каждая клетка карты задается своим набором значений переменных, причем в клетках, соответствующих конституентам единицы данной функции, ставится единица, тогда как остальные клетки остаются пустыми. Карта Карно устроена так, что наборы, определяющие любые две соседние клетки, различаются в точности в одной позиции (т.е. различаются значениями ровно одной компоненты), причем клетки (одной и той же строки или одного и того же столбца), примыкающие к противоположным сторонам прямоугольника, также являются соседними в только что определенном смысле. Это можно представить себе так, что карта закручивается” в цилиндр” по обоим направлениям, т.е. в “тор”.

С геометрической точки зрения карта Карно есть способ изображения булева куба (размерностей 3 и 4). Любая пара соседних клеток (с учетом “закрученности” карты) определяет некоторое ребро булева куба, а любой прямоугольник, состоящий из клеток (или, как говорят, прямоугольник с площадью ) для некоторого , определяет грань размерности .

Можно построить карты Карно и для размерностей 5 и 6, но они используются весьма редко. Может быть построена и простейшая карта Карно для функции от двух переменных, но для таких функций не возникает нетривиальных задач построения минимальной ДНФ.

Пусть булева функция задана таблицей, представленной в форме карты Карно. Описанный выше итерационный процесс склейки, в результате которого получается сокращенная ДНФ, представляющая функцию , проводится на карте Карно так: любые две соседние клетки, содержащие единицы, обводятся, и “поглотивший” их прямоугольник (он и есть обозначение результата склейки на карте) представляется словом, содержащим “0”, “1” и “×” (“крестик”), причем “крестик” занимает позицию того переменного, по которому произведена склейка (рис. 6.9).

С геометрической точки зрения такой прямоугольник площади 2 соответствует ребру булева куба, в каждой вершине которого функция принимает значение 1. Запись прямоугольника в виде слова можно понимать как обозначение соответствующего ребра. Так, на карте, показанной на рис. 6.9, прямоугольник 11× обозначает ребро [110,111], прямоугольники же 1×1 и ×11 — ребра [101,111] и [011,111] соответственно.

По таким обозначениям легко получить и ту импликанту, которая является результатом простой склейки: для этого достаточно записать литерал (соответственно ), если в i-й позиции стоит 1 (соответственно 0), и пропустить литерал ж», если в i-й позиции стоит “крестик”. Так, по слову 1×0 получим импликанту .

Наличие на карте Карно двух прямоугольников площади 2, находящихся в соседних столбцах или строках, показывает, что функция принимает значение 1 на некоторой паре соседних ребер, т.е. на некоторой грани размерности 2. Тогда они могут быть объединены в один большой прямоугольник площади 4 (рис. 6.10).

Этот прямоугольник можно записать в виде слова хОх, показывая тем самым, что соответствующая грань (размерности 2) образована любой из двух пар соседних ребер: (×00, ×01) (два вертикальных прямоугольника площади 2) или (00×, 10×) (два горизонтальных прямоугольника площади 2).

Точно так же можно объединять в один прямоугольник площади 8 два соседних прямоугольника площади 4 (рис. 6.11).

Если такие большие прямоугольники находить сразу, то “поглощаемые” ими меньшие прямоугольники уже не рассматриваются. Тем самым, находя на карте Карно прямоугольники максимальной площади и не содержащиеся друг в друге, мы находим грани максимальных размерностей и максимальные по включению, такие, на которых заданная функция принимает единичное значение. Поскольку грань размерности имеет вершин, то выделяемые описанным способом прямоугольники могут состоять только из клеток (для некоторого , не превышающего числа переменных). Так, на карте, приведенной на рис. 6.12, получим два прямоугольника площади 4: ×0×0 и 0×0×, соответствующие граням размерности 2, и один прямоугольник 01×1, отвечающий ребру, которое не содержится ни в одной из указанных выше граней. Подчеркнем еще раз, что соседство клеток, прямоугольников и само выделение прямоугольников на карте Карно производится с учетом ее “закрученности”. В этой связи интересен ” прямоугольник” на карте, приведенной на рис. 6.12, обозначенный ×0×0. Он образован двумя парами противоположных угловых клеток.

Таким образом, если на карте Карно сразу выделять все максимальные (в указанном выше смысле) прямоугольники площади (для некоторого и не превышающего числа переменных), то тем самым мы “геометрически” реализуем описанный ранее алгебраический итерационный процесс склейки и в результате получаем все простые импликанты исходной функции (составляющие сокращенную ДНФ). Эти импликанты восстанавливаются по записям прямоугольников точно так же, как описано выше для простой склейки. Так, для карты, приведенной на рис. 6.12, получим сокращенную ДНФ в виде

2. Определение ядра. Говорят, что элементарная конъюнкция покрывает элементарную конъюнкцию (и пишут ), если любой литерал, входящий в , входит в . Так,

, но .

Поскольку вторая конъюнкция содержит литерал , отсутствующий в первой конъюнкции. Легко понять, что если , то (согласно тождествам поглощения).

Каждая входящая в сокращенную ДНФ простая импликанта покрывает некоторую элементарную конъюнкцию исходной С ДНФ. На карте Карно этому отвечает прямоугольник, п закрывающий” соответствующую единицу.

Простую импликанту называют ядровой, если она покрывает некоторую элементарную конъюнкцию исходной СДНФ, не покрываемую никакой другой простой импликантой. На карте Карно прямоугольник, соответствующий ядровой импли-канте, отыскивается очень просто: это такой прямоугольник, удалив который получим единицу, не закрытую никаким другим прямоугольником. Тогда ни одна ядровая импликанта не может быть удалена из искомой минимальной ДНФ исходной функции, т.е. все ядровые импликанты обязательно войдут в минимальную ДНФ.

Множество всех ядровых импликант (склеек) сокращенной ДНФ называют ядром.

---

Пример 6.13. а. У мажоритарной функции все импликанты являются ядровыми. Напротив, у функции, изображенной на карте Карно на рис. 6.13, ядро пусто, т.е. ядровых импликант нет вовсе.

б. На карте Карно на рис. 6.14 в ядро попадают склейки .

Если все простые импликанты оказались в ядре, то сокращенная ДНФ и есть единственная минимальная и кратчайшая ДНФ для данной функции. Именно так обстоит дело с мажоритарной функцией (см. пример 6.12). В противном случае смотрят, не эквивалентна ли ДНФ, построенная как дизъюнкция всех ядровых импликант, исходной СДНФ. Это будет иметь место тогда и только тогда, когда ядровые импликанты покрывают в совокупности все элементарные конъюнкции исходной СДНФ. На карте Карно тогда каждая клетка, содержащая единицу, должна быть закрыта прямоугольником, отвечающим некоторой ядровой импликанте. Если это так, то ДНФ, построенная по ядру, как описано выше, есть минимальная и кратчайшая (склейки ядра закрыли все единицы карты Карно). При этом импликанты, не попавшие в ядро, все оказываются “избыточными”, т.е. их удаление из сокращенной ДНФ не приводит к нарушению эквивалентности этой последней с исходной СДНФ.

В остальных случаях переходят к отысканию так называемых тупиковых ДНФ.

---

3. Перечисление тупиковых ДНФ. Простую импликанту называют избыточной (относительно некоторой ДНФ, содержащей только простые импликанты и эквивалентной исходной СДНФ), если ее можно удалить из этой ДНФ без потери эквивалентности ее исходной СДНФ. Так, сокращенная ДНФ (см. рис. 6.14) содержит избыточные импликанты: импликанта, соответствующая прямоугольнику , или импликанта, соответствующая прямоугольнику , может быть удалена (но не обе сразу!). Это значит, что каждая из этих импликант является избыточной относительно сокращенной ДНФ, но удаление одной из них приводит к новой ДНФ, относительно которой вторая из упомянутых импликант уже не будет избыточной. В том случае, когда каждую элементарную конъюнкцию исходной СДНФ покрывает некоторая ядровая импликанта, импликанты, не вошедшие в ядро, можно удалить одновременно.

Тогда можно представить процесс пошагового удаления избыточных импликант, начиная с сокращенной ДНФ, в результате которого получится некоторая ДНФ, уже не содержащая ни одной избыточной склейки.

Любую ДНФ, эквивалентную исходной СДНФ, содержащую все ядровые импликанты и не содержащую ни одной избыточной импликанты, называют тупиковой.

Заметим, что в силу конечности множества всех импликант тупиковая ДНФ обязательно существует, т.е. в упомянутом выше процессе мы рано или поздно доберемся до такого момента, когда удаление хотя бы одной склейки приведет к тому, что “откроется” какая-то единичная клетка на карте Карно и тем самым будет потеряна эквивалентность полученной таким образом ДНФ исходной СДНФ.

Для СДНФ, карта Карно которой приведена на рис. 6.14, имеются две тупиковые ДНФ (первые три конъюнкции соответствуют ядру):

В общем случае для перечисления всех тупиковых ДНФ может быть использован следующий алгоритм. Мы изложим его в терминах карт Карно и, допуская вольность речи, будем отождествлять максимальные прямоугольники на карте Карно с соответствующими простыми импликантами.

Присвоим каждой простой импликанте сокращенной ДНФ некоторое имя: т.е. обозначим их, например, как . Для любой единицы карты Карно, не покрываемой ядром, перечислим все простые импликанты, которые ее покрывают, записав их в виде элементарной дизъюнкции, в которой переменными считаются введенные выше имена простых импликант. Переменное, именующее данную простую импликанту, принимает, по определению, значение 1, если данная простая импликанта выбирается для покрытия рассматриваемой единицы
карты Карно.

Записав все элементарные дизъюнкции, составим из них КНФ. Рассмотрим карту Карно на рис. 6.13. Обозначив

получим

Тем самым мы образуем вспомогательную функцию (представленную КНФ вида (6.13)), называемую функцией Патрика. Раскрывая скобки в КНФ (6.13) и используя тождества булевой алгебры (в частности, тождество поглощения), получим ДНФ, в которой каждая элементарная конъюнкция соответствует некоторой тупиковой ДНФ и, наоборот, каждой тупиковой ДНФ может быть сопоставлена одна из этих конъюнкций.

Для нашего примера поступим так: вычислим конъюнкцию первой и второй скобки в выражении (6.13), а также третьей и четвертой, пятой и шестой скобок, после чего получим

Используя тождества поглощения, в первой скобке в формуле (6.14) мы можем удалить все члены, содержащие , во второй скобке — все члены, содержащие , в третьей скобке — все члены, содержащие . Проделав это, раскрыв все три скобки и применив еще раз поглощение, окончательно получим

Элементарные конъюнкции в (6.15) определяют тупиковые ДНФ. Более того, так как в данном случае отсутствуют ядровые импликанты, найденные конъюнкции исчерпывают тупиковые ДНФ. Первая тупиковая ДНФ состоит из конъюнкций и , т.е. имеет вид . Точно так же определяются остальные тупиковые ДНФ.

Обоснование описанного выше алгоритма может быть получено из следующих соображений. Функция Патрика, представленная КНФ, принимает значение 1 тогда и только тогда, когда каждая элементарная дизъюнкция принимает значение 1. А элементарная дизъюнкция принимает значение 1 в том и только в том случае, когда хотя бы одно ее переменное принимает значение 1. Согласно определению функции Патрика, это значит, что хотя бы одна простая импликанта выбрана для покрытия соответствующей единицы на карте Карно. Поскольку таким образом перебираются все не покрываемые ядром единицы карты Карно, то гарантируется эквивалентность искомой ДНФ исходной СДНФ. Однако, когда функция Патрика представлена ДНФ и мы выбираем в точности одну из ее элементарных конъюнкций, полагая, что все входящие в нее переменные равны 1, мы тем самым из всех возможных вариантов покрытия каждой единицы на карте Карно выбираем в точности один вариант. Значит, полученная в результате такого выбора ДНФ для исходной (минимизируемой) СДНФ действительно будет тупиковой.

Но нужно заметить, что перечисление тупиковых ДНФ является самым неприятным и трудоемким этапом всего алгоритма минимизации. Если число единичных клеток карты Карно, не покрываемых ядром, достаточно велико, то функция Патрика будет весьма сложной и ее упрощение сопоставимо по трудоемкости со всем процессом минимизации.

---

4. Отыскание среди тупиковых ДНФ кратчайших и минимальных. Среди найденных тупиковых ДНФ находят кратчайшие и минимальные. Можно легко показать, что минимальная ДНФ всегда является кратчайшей, но обратное неверно. Так, и первая ДНФ кратчайшая, но не минимальная. Действительно, легко сообразить, что вторая из записанных ДНФ минимальна. Следовательно, представляемую ею функцию нельзя представить ДНФ, содержащей менее двух элементарных конъюнкций. Но в первой ДНФ три литерала, а во второй — два. Из пяти тупиковых ДНФ, соответствующих функции Патрика (6.15), кратчайшими являются две. Каждая из них минимальна, так как обе они имеют одинаковое число литералов.

Пример 6.14. Рассмотрим карту Карно на рис. 6.15. В результате проведения склейки получим следующую сокращенную ДНФ*:

Ядро составляют склейки (простые импликанты) и .

Шесть клеток, содержащих единицу, на карте Карно остаются непокрытыми ядровыми склейками. Для неядровых склеек (обозначенных ) составляем функцию Патрика в виде

Преобразуя ее аналогично функции (6.13), получаем

Имеем, следовательно, пять тупиковых ДНФ. Запишем их, для наглядности, так:

Из этих пяти тупиковых ДНФ кратчайшими являются первая и вторая. Из них, в свою очередь, минимальной является первая, так как она содержит на один литерал меньше. В итоге получаем минимальную ДНФ в виде

“Обратим еще раз внимание на то, что каждый выделяемый прямоугольник на карте Карно имеет площадь, равную некоторой степени двойки. Поэтому, например, три соседние единичные клетки не могут быть объединены в один прямоугольник, а их “накроют” два прямоугольника площадью 2, пересекающиеся по одной клетке.

В данном случае минимальная ДНФ оказалась единственной, хотя, как это мы видели в ранее разобранных примерах, в общем случае могут существовать несколько минимальных ДНФ.

---

Метод Блейка

Техника карт Карно является удобным и наглядным (при определенных ограничениях на число переменных минимизируемой функции) способом реализации алгоритма Квайна–Мак-Клоски. Но существуют и другие способы проведения склейки, т.е. получения сокращенной ДНФ для исходной функции. Одним из таких способов является чисто алгебраический метод Блейка, состоящий в том, что к любой ДНФ, представляющей функцию, применяются следующие тождества:

Первое из тождеств (6.16) называют тождеством (или правилом) обобщенного склеивания, второе — тождеством (или правилом) поглощения.

“Технология” использования метода Блейка такова: применяют тождество обобщенного склеивания до тех пор, пока не перестанут появляться новые элементарные конъюнкции (вида К1К2). После этого применяют тождество поглощения.

---

Таблицы Квайна

Как только сокращенная ДНФ тем или иным способом найдена, приступают к нахождению ядра. Ядро можно определить (без использования карты Карно) с помощью так называемой таблицы Квайна. Столбцы этой таблицы соответствуют элементарным конъюнкциям исходной СДНФ, а строки — простым импликантам сокращенной ДНФ. На пересечении строки и столбца проставляется знак “+” (плюс), если простая импликанта данной строки покрывает элементарную конъюнкцию данного столбца. Ядро вычисляется так: отмечаем столбцы с единственным знаком “+”, тогда простые импликанты тех и только тех строк, в которые попал этот знак, образуют ядро. Для примера 6.13.6 (см. рис. 6.14) получим таблицу Квайна, изображенную на рис. 6.16. (В целях экономии места элементарные конъюнкции в таблице заменены цифровыми обозначениями соответствующих вершин и граней булева куба — точно так же как при обозначении прямоугольников на картах Карно. Ядровые импликанты выделены жирным шрифтом.)

По таблице Квайна можно составить и функцию Патрика для перечисления тупиковых ДНФ. Для этого нужно отметить все столбцы таблицы, в которых на пересечении со строками, соответствующими ядровым импликантам, не стоит знак “+”. Для разбираемого примера таковым является только последний столбец. Чтобы покрыть соответствующую элементарную конъюнкцию СДНФ, можно выбрать одну из двух простых импликант: или .

---

Построение минимальных ДНФ частичных булевых функций

В заключение рассмотрим очень кратко применение карт Карно к построению минимальных ДНФ частичных булевых функций, т.е. частичных отображений из множества в множество .

Частичная булева функция может быть задана посредством карты Карно, в которой кроме клеток с единицами и пустых клеток будут клетки, заполненные прочерками (–). Такой прочерк означает, что на соответствующем наборе функция не определена.

Склейка для частичной функции (заданной картой Карно) проводится таким образом, что выделяются прямоугольники максимальной площади (содержащие клеток, для некоторого ), каждая клетка которых содержит либо единицу, либо прочерк, причем существует по крайней мере одна единичная клетка.

Пример 6.15. Пусть частичная функция задана картой Карно, приведенной на рис. 6.17. Прямоугольник максимальной площади (равной 4), состоящий из единицы и прочерков, записывается как . Следовательно, минимальная ДНФ для заданной функции будет .

По поводу рассмотренного примера возникает такой вопрос: почему не принят во внимание другой прямоугольник (площади 2), содержащий клетку с единицей и клетку с прочерком: ? Связано это вот с чем. Перед тем как выделять упомянутые выше прямоугольники, мы на самом деле доопределяем исходную частичную функцию (получая обычную булеву функцию) так, чтобы в максимальном числе клеток, в которых стоят прочерки (но не нули!), появились единицы. Точнее говоря, среди прямоугольников (с прочерками), содержащих данную единицу, выбирают для замены прочерков единицами такой, который имеет максимальную площадь. Прочерки же в остальных прямоугольниках заменяют нулями.

В примере 6.15 мы доопределяем исходную функцию так, что получается функция , задаваемая картой Карно, приведенной на рис. 6.18. Эта функция имеет минимальную ДНФ . Следовательно, и частичная исходная функция может быть представлена такой ДНФ, поскольку на всех наборах, на которых она определена, она принимает такое же значение, как и функция .

Конечно, мы могли бы доопределить функцию по-другому, так, чтобы получилась функция , заданная картой Карно, приведенной на рис. 6.19. Ясно, что поэтому и частичная функция может быть определена такой ДНФ. Но эта ДНФ не минимальна для данной частичной (именно частичной!) функции, поскольку первый способ доопределения дал ДНФ, содержащую лишь один литерал.

Таким образом, в отличие от минимизации булевых функций при минимизации частичных булевых функций не следует выделять все максимальные прямоугольники с прочерками, содержащие данную единичную клетку карты Карно, достаточно выбрать произвольно любой из таких прямоугольников. Но, конечно, не нужно забывать о том, что каждая единица на карте должна быть покрыта некоторой склейкой.

Пример 6.16. Для карты на рис. 6.20 следует взять обе склейки на четыре позиции: и , получив для заданной этой картой частичной функции минимальную ДНФ в виде .

Заметим, что без использования склеек с прочерками мы вообще не могли бы минимизировать данную функцию. Нужно также отметить, что не всегда использование “частичности” функции позволяет получить минимальную ДНФ для нее. Так, на представленной на рис. 6.20 карте в случае, если мы переместим нижнюю единицу на строку выше, обычная склейка на две позиции дает лучший результат: , а записанная выше ДНФ уже не будет минимальной (и даже кратчайшей).

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Минимальная ДНФ — наименьшее число литералов (вхождений переменных). Кратчайшая ДНФ — наименьшее число элементарных конъюнкций. Геометрия булева куба. Импликанты и простые импликанты. Сокращенная ДНФ. Избыточные импликанты и тупиковые ДНФ. Методы построения сокращенной ДНФ. Алгоритм Квайна — Мак-Клоски. Склейка. Таблицы Квайна и простые импликанты. Ядровые импликанты. Тупиковые ДНФ и функция Патрика. Выбор кратчайших и минимальных ДНФ.

Каждая функция может быть представлена дизъюнктивной нормальной формой различными способами. например, изменить ДНФ можно, если в одно из ее слагаемых ввести фиктивную переменную с помощью сомножителя x + x. Возникает задача из всех ДНФ найти наиболее простую в том или ином смысле.

Возможны по крайней мере два подхода к оценке сложности ДНФ: по количеству элементарных конъюнкций в ней (это количество называют длиной ДНФ) и по общему количеству литералов, т.е. по сумме длин элементарных конъюнкций, входящих в ДНФ (эту сумму называют сложностью ДНФ). ДНФ называют минимальной, если она имеет наименьшую сложность, и кратчайшей, если она имеет наименьшую длину.

В приведенной терминологии задача состоит в выборе среди всех ДНФ, представляющих данную функцию, наименьших и кратчайших. Решение такой задачи сводится к отбору некоторого ограниченного круга ДНФ, ”подозрительных на минимум“, и последующему перебору отобранных ДНФ. Здесь возможны различные приемы. Чтобы описать и объяснить эти приемы, перейдем к геометрической интерпретации области определения булевой функции — булева куба.

Отдельные элементы, составляющие булев куб Bⁿ, т.е. булевы векторы принято называть вершинами куба. Множество булевых векторов, у которых компоненты заданного набора, например с номерами i₁, …, i_k, имеют определенные значения образуют подалгебру булевой алгебры, называемую гранью булева куба. Грань представляет собой булев куб, но меньшей размерности, равной n − k, где n — размерность булева куба, k — количество фиксированных номеров. Грань размерности 1 называется ребром булева куба. Кортеж номеров фиксированных компонент, определяющий грань куба называют направлением грани. Грани, имеющие одинаковое направление, не пересекаются. Они называются параллельными. Среди паралельных граней выделим соседние, у которых совпадают значения всех фиксированных компонент, кроме одной.

Грани булева куба удобно обозначать, как слово из трех символов 0, 1 и ∗, где 0 и 1 обозначают фиксированные значения компонент, а ∗ указывает меняющиеся компоненты. Например, слово 00 ∗ 1, обозначает ребро четырехмерного булева куба, определяемое условиями x₁ = 0, x₄ = 0, x₄ = 0. Третья компонента, отмеченная звездочкой, варьируется. При таком способе записи размерность грани совпадает с количеством звездочек, грани параллельны, если у них совпадает положение звездочек (например 10 ∗ 0 и 01 ∗ 1). Грани соседние, если их записи раз- личаются только в одной позиции, в которой для одной грани указано значение 0, а для другой 1 (например 01∗0∗1 и 11∗0∗1).

Будем говорить, что булева функция f, определенная на Bn, подчиняется булевой функции g, определенной на том же кубе (или f меньше g), если f(x)≤g(x) для любого x ∈ Bⁿ. В этом случае будем писать f ≤g. Множество вершин куба, в которых функция f принимает значение 1, будем называть уровнем единицы функции, сами эти вершины называют конституентами единицы. Если f ≤ g, то уровень единицы функции f является подмножеством уровня единицы функции g.

Элементарная конъюнкция принимает значение 1 в том и только в том случае, когда каждый литерал в ней принимает значение 1. Часть переменных может не входить в конъюнкцию, т.е. эти переменные будут фиктивными. Варьируя значения фиктивных переменных, получим грань n-мерного булева куба. Таким образом, уровень единицы любой элементарной конъюнк- ции есть некоторая грань булева куба.

Любую ДНФ данной функции f можно интерпретировать как набор граней булева куба, объединение которых совпадает с уровнем единицы функции f. При этом каждая элементар- ная конъюнкция рассматриваемой ДНФ будет подчинена функции f. Любую элементарную конъюнкцию, подчиненную функции f, будем называть импликантой.

Замечание. Далее будем предполагать, что исследуемая функция от n аргументов не меняется, так что можно заранее каждый аргумент функции связать с некоторой переменной, а точнее, с i-м аргументом связывается переменная x_i. Это позволяет не различать булевы функции и формулы, составленные из переменных x₁, . . . , x_n. Именно в этом контексте элементарная конъюнкция трактуется как функция от n аргументов.

Чтобы получить кратчайшую ДНФ заданной функции, надо выбрать минимальное количество импликант (граней булева куба, содержащихся в уровне единицы функции), в совокупности накрывающих уровень 1. Для минимальной ДНФ минимума достигает сумма длин импликант, а для этого надо стремиться увеличить сумму размерностей граней куба, соответствующих элементарным конъюнкциям ДНФ. В самом деле, пусть d_i и n_i, i = 1, k, — длины конъюнкций, составляющих ДНФ, и размерности соответствующих граней булева куба; s — сложность ДНФ; r — сумма размерностей граней, соответствующих конъюнкциям ДНФ. Тогда и мы видим, что увеличение суммы размерностей граней ведет к уменьшению сложности ДНФ.

При небольших размерностях булева куба (до 4) его геометрию можно представить на плоскости с помощью так называемых карт Карно. Представим куб Bn как декартово произведение двух кубов Bk × Bl, где k, l ≤2. Такое произведение можно изобразить таблицей, в которой каждая строка соответствует вершине куба Bk , а каждый столбец — вершине куба Bl . Существенным моментом является такой порядок строк и соответственно столбцов, при котором соседним строкам и столбцам отвечают соседние вершины соответствующего булева куба. А именно, при k, l = 1, берем естественный порядок 0, 1. при k, l = 2 используем порядок 00, 01, 11, 10 (табл. 1.5).

В такой таблице соседние клетки соответствуют соседним вершинам четырехмерного булева куба. Если представить, что эта ”шахматная доска“ склеена по горизонтали и вертикали, т.е. соседними, например, являются (00, 11) и (10, 11), а также (01, 00) и (01, 10), то соседние на доске будет в точности соответствовать соседним на кубе.

На карте Карно ребро — это пара соседних (в том числе и ”через край“) клеток. Легко изобразить на карте Карно и двумерные грани, состоящие из 4-х вершин. это либо квадрат из двух примыкающих пар клеток, либо одна строка, либо один столбец. Трехмерная грань — это две соседние строки или два соседних столбца.

К сожалению, при увеличении размерности такая простая интерпретация исчезает. Например, для пятимерного куба (табл. 1.6), соседние клетки (включая ”соседство через край“) будут соответствовать со- седним вершинам. Но, кроме того, и другие пары клеток, например (01, 001) и (01, 101), не будучи со- седними в таблице, соответствуют соседним верши- нам. Причина в том, что на карте Карно у каждой клетки четыре соседних, в то время как в n-мерном кубе каждая вершина имеет n соседних вершин, которые получаются, если в булевом векторе изменить одну компоненту из n возможных.

Рассмотрим два приема, с помощью которых из имеющейся ДНФ можно получить более простую ДНФ (и в смысле длины, и в смысле сложности).

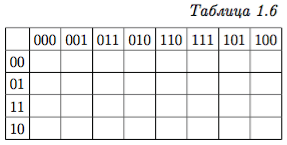
Склейка. Дизъюнктивная нормальная форма данной функции может содержать пару импликант, соответствующих соседним граням булева куба. Но две соседние грани булева куба вместе составляют грань большей размерности. Например, две двумерные грани 01∗∗10 и 01∗∗11 пятимерного куба в совокупности составляют трехмерную грань 01∗∗1∗. Замена в ДНФ двух таких импликант одной более короткой приводит к 0*0* уменьшению и длины, и сложности ДНФ. Такую замену называют склейкой.

Импликанты, соответствующие соседним граням, имеют один и тот же набор переменных, причем они различаются только по одной переменной: в одной импликанте стоит сама переменная, а в другой — ее отрицание. Например, грани 01∗∗10 и 01∗∗11 соответствуют элементарным конъюнкциям x1 x2 x4 x5 и x1 x2 x4 x5 . Изменение ДНФ выполняется в данном случае в соответствии с тождеством x1 x2 x4 x5 + x1 x2 x4x5 = x1 x2 x4 Примеры возможных склеек показаны с помощью карты Карно на рис. 1.3.

Отталкиваясь от совершенной ДНФ, мы можем сперва склеивать различные пары соседних нульмерных граней (вершин) в ребра, затем в соседние ребра в двумерные грани и т.д. Процесс подобной склейки приведет к выявлению граней максимальной размерности, содержащихся в уровне единицы функции. Этим граням соответствуют максимальные импликанты функции (максимальные относительно введенного порядка ≤ на импликантах функции). Такие импликанты называются простыми импликантами. ДНФ данной функции, в которую входят все простые импликанты, называют сокращенной ДНФ.

Отметим, что если исходная ДНФ не является совершенной, то склейка может и не привести к сокращенной ДНФ. Так, если на рис. 1.3 выбрать грани ∗0∗0, 01∗1, 0001, 0100, получим покрытие уровня единицы функции. В соответствующей ДНФ x₂x₄+x₁x₂x₄+x₁x₂x₃x₄+x₁x₂x₃x₄ нельзя склеить какие-либо грани, но эта ДНФ не является сокращенной, так как два последних слагаемых не являются простыми импликантами.

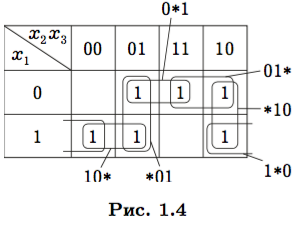Избыточные импликанты. В сокращенной ДНФ одна из импликант может накрываться остальными. Такую импликанту можно удалить из формулы, уменьшая и длину, и сложность ДНФ. Рассмотрим, например, функцию, представленную картой Карно на рис. 1.4. У этой функции максимальными являются шесть импликант 1∗0, 10∗, ∗01, 0∗1, 01∗,01* ∗10. Их сумма даст сокращенную ДНФ. Но из рисунка видно, что, например, импликанта 10∗ накрывается двумя импликантами 1∗0 и ∗01. Значит, эту импликанту можно из ДНФ удалить.

Импликанта в ДНФ, подчиненная сумме остальных импликант этой ДНФ, называется избыточной. Если из сокращенной ДНФ удалить избыточные импликанты, то получим тупиковую ДНФ. По определению, тупиковая ДНФ — это ДНФ, состоящая из простых импликант, ни одна из которых в этой ДНФ не является избыточной. Например, на рис. 1.4 тупиковую ДНФ образуют импли-

канты 1∗0, ∗01, 01∗.

Основной целью каждого метода минимизации ДНФ является выявление всех тупиковых ДНФ. Именно среди них находится минимальная и кратчайшая формы.

Построение сокращенной ДНФ. Один из методов построения сокращенной ДНФ — это метод Квайна — МакКлоски. Его суть в следующем. В качестве исходной выбирается совершенная ДНФ. На первом этапе проводится склейка импликант совершенной ДНФ в ребра, которые добавляются в ДНФ. После того как проведены все склейки вершин, из ДНФ удаляются все избыточные вершины, т.е. те, которые подчиняются добавленным ребрам. На втором этапе проводится склейка всех ребер в четырехмерные грани, которые добавляются к ДНФ. После проведения всех склеек между ребрами удаляются ребра, подчиненные двумерным граням. На третьем этапе выполняется склейка двумерных граней и удаление избыточных двумерных гра- ней. Процесс останавливается, когда между гранями соответствующей размерности не удается провести ни одной склейки. Результатом этих преобразований и будет сокращенная ДНФ.

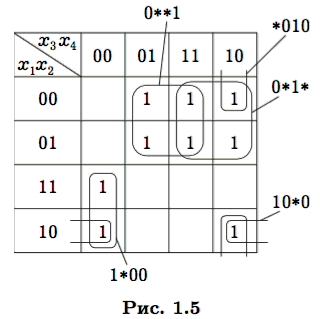Пример 1.6. Рассмотрим функцию, заданную картой Карно на рис. 1.5. Первый этап склейки по методу Квайна приведет к ребрам 1∗00, 10∗0, ∗010, а также четырем ребрам двумерной грани 0∗∗1 и четырем ребрам двумерной грани 0∗1∗. Все исходные импликанты будут удалены как избыточные. На втором этапе мы получим две двумерные грани 0∗∗1 и 0∗1∗. При этом будут удалены 6 ребер, входящих в эти грани. Поскольку склеить две эти грани нельзя, процесс вы- явления простых импликант на этом завершится. Сокращен- ная ДНФ будет содержать пять импликант, соответствующих граням 0∗∗1, 0∗1∗, 1∗00, 10∗0, ∗010. #

Другой метод построения сокращенной ДНФ — метод Блейка, в котором в качестве исходной можно взять любую ДНФ. В этом методе на первом этапе многократно выполняется операция обобщенного склеивания, при которой сумма xK₁ +xK₂ заменяется суммой xK₁ +xK₂ +K₁K₁. Такая операция выполняется до тех пор, пока удается получать новые импликанты вида K₁K₂. После завершения первого этапа выполняется операция поглощения согласно формуле K₁K₂ + K₂ = K₂.

Выявление всех тупиковых ДНФ. Создать список всех тупиковых ДНФ можно, используя следующий прием. Обозначим все простые импликанты символами K₁, K₂, . . . , K_m. Перенумеруем все вершины уровня единицы функции. Пусть первая вершина накрывается склейками K_i1 , K_i2 , . . . , K_ip . Тогда элементарная дизъюнкция K_i1 + K_i2 + . . . + K_ip задает условие, что первая вершина уровня единицы функции накрывается одной из простых импликант. Составив конъюнкцию из указанных элементарных дизъюнкций по всем вершинам уровня единицы функции, мы получим КНФ, представляющее собой логическое условие того, что весь уровень единицы функции накрыт простыми импликантами. Эта КНФ называют функцией Патрика. Преобразуем КНФ в ДНФ, пользуясь свойствами булевых операций (дистрибутив- ностью, коммутативностью, идемпотентностью). В ДНФ каждая элементарная конъюнкция будет описывать набор простых импликант, целиком покрывающих уровень единицы функ- ции, т.е. набор, описывающий конкретную тупиковую ДНФ рассматриваемой функции. Можно показать, что таким образом можно выявить все тупиковые ДНФ.

Среди простых импликант рассматриваемой функции есть те, которые входят в любую тупиковую ДНФ. К таким относится любая импликанта, для которой среди накрываемых вершин есть хотя бы одна, не накрываемая никакой другой импликантой. Например, на рис. 1.5 вершина 1100 накрывается единственной простой импликантой 1∗00. Эта импликанта должна входить в любую тупиковую ДНФ. Импликанты, удовлетворяющие описанному условию, называются ядровыми импликантами. Совокупность ядровых импликант — ядро — постоянная часть всех тупиковых ДНФ. Например, на рис. 1.5 ядро составляют импликанты 0∗∗1, 0∗1∗, 1∗00, а импликанты ∗010 и 10∗0 неядровые. При выявлении тупиковых ДНФ ядровые импликанты и накрываемые ими вершины из функции Патрика можно исключить.

Пример 1.7. У функции, представленной на рис. 1.5 диаграммой Карно, имеется пять простых импликант. Введем обозначения:

K₁ = 0∗∗1, K₂ = 0∗1∗, K₃ = 1∗00, K₄ = 10∗0, K₅ = ∗010.

Тогда функция Патрика для 9 вершин уровня 1 при их нумерации по строкам будет иметь следующий вид:

P = K₁(K₁ + K₂)(K₂ + K₅)K₁(K₁ + K₂)K₂K₃(K₃ + K₄)(K₄ + K₅).

Упростив согласно идемпотентности операций и тождествам поглощения (x(x + y) = x), получим

P = K₁K₂K₃(K₄ + K₅).

Используя дистрибутивность и идемпотентность, приходим к ДНФ:

P = K₁K₂K₃(K₄ + K₅) = K₁K₂K₃K₄ + K₁K₂K₃K₅.

Таким образом, рассматриваемая функция имеет две сокращенные ДНФ, описываемые двумя списками склеек K₁, K₂, K₃, K₄ и K₁, K₂, K₃, K₅. В результате получим

D₁ = x ₁x₄ + x₁x₃ + x₁x ₃x ₄ + x₁x₂x₄, D₂ = x₁ x₄ + x₁x₃ + x₁x3x₄ + x₂x₃x₄.

Видно, что у обоих сокращенных ДНФ есть общая часть — первые три конъюнкции. Это ядро, входящее в каждую сокращенную ДНФ. Его можно исключить из рассмотрения, рассматривая условия накрытия только для тех вершин, которые не накрываются склейками ядра. В данном случае это единственная вершина 1010. При этом функция Патрика будет иметь вид Pˆ = K₄ + K₅. Добавив к каждому слагаемому элементарную конъюнкцию K₁K₂K₃, описывающую ядро, получим полную функцию Патрика. #

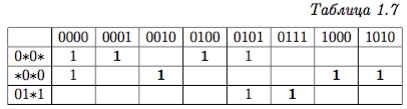
Ядро данной функции можно получить с помощью таблицы Квайна, в которой каждая строка соответствует одной простой импликанте, а каждый столбец — одной вершине уровня единицы функции. В каждой клетке указывается 1, если импликанта накрывает вершину, и пробел в противном случае Например, составим таблицу Квайна функции, представленной картой Карно на рис. 1.3 (табл. 1.7). Чтобы определить ядро функции, необходимо выявить столбцы, в которых находится только одна единица, и пометить соответствующие строки. Импликанты, соответствующие помеченным строкам, образуют ядро. Например, в табл. 1.7 по одной единице содержится в столбцах, отвечающих вершинам 0001, 0010, 0100, 0111, 1000, 1010 (эти единицы выделены полужирным шрифтом). Поскольку в каждой строке содержится хотя бы одна выделенная единица, все простые импликанты ядровые, т.е. рассматриваемая функция имеет единственную тупиковую ДНФ.

Минимальная ДНФ — наименьшее число литералов (вхождений переменных). Кратчайшая ДНФ — наименьшее число элементарных конъюнкций. Геометрия булева куба. Импликанты и простые импликанты. Сокращенная ДНФ. Избыточные импликанты и тупиковые ДНФ. Методы построения сокращенной ДНФ. Алгоритм Квайна — Мак-Клоски. Склейка. Таблицы Квайна и простые импликанты. Ядровые импликанты. Тупиковые ДНФ и функция Патрика. Выбор кратчайших и минимальных ДНФ.

Каждая функция может быть представлена дизъюнктивной нормальной формой различными способами. например, изменить ДНФ можно, если в одно из ее слагаемых ввести фиктивную переменную с помощью сомножителя x + x. Возникает задача из всех ДНФ найти наиболее простую в том или ином смысле.

Возможны по крайней мере два подхода к оценке сложности ДНФ: по количеству элементарных конъюнкций в ней (это количество называют длиной ДНФ) и по общему количеству литералов, т.е. по сумме длин элементарных конъюнкций, входящих в ДНФ (эту сумму называют сложностью ДНФ). ДНФ называют минимальной, если она имеет наименьшую сложность, и кратчайшей, если она имеет наименьшую длину.

В приведенной терминологии задача состоит в выборе среди всех ДНФ, представляющих данную функцию, наименьших и кратчайших. Решение такой задачи сводится к отбору некоторого ограниченного круга ДНФ, ”подозрительных на минимум“, и последующему перебору отобранных ДНФ. Здесь возможны различные приемы. Чтобы описать и объяснить эти приемы, перейдем к геометрической интерпретации области определения булевой функции — булева куба.

Отдельные элементы, составляющие булев куб Bⁿ, т.е. булевы векторы принято называть вершинами куба. Множество булевых векторов, у которых компоненты заданного набора, например с номерами i₁, …, i_k, имеют определенные значения образуют подалгебру булевой алгебры, называемую гранью булева куба. Грань представляет собой булев куб, но меньшей размерности, равной n − k, где n — размерность булева куба, k — количество фиксированных номеров. Грань размерности 1 называется ребром булева куба. Кортеж номеров фиксированных компонент, определяющий грань куба называют направлением грани. Грани, имеющие одинаковое направление, не пересекаются. Они называются параллельными. Среди паралельных граней выделим соседние, у которых совпадают значения всех фиксированных компонент, кроме одной.

Грани булева куба удобно обозначать, как слово из трех символов 0, 1 и ∗, где 0 и 1 обозначают фиксированные значения компонент, а ∗ указывает меняющиеся компоненты. Например, слово 00 ∗ 1, обозначает ребро четырехмерного булева куба, определяемое условиями x₁ = 0, x₄ = 0, x₄ = 0. Третья компонента, отмеченная звездочкой, варьируется. При таком способе записи размерность грани совпадает с количеством звездочек, грани параллельны, если у них совпадает положение звездочек (например 10 ∗ 0 и 01 ∗ 1). Грани соседние, если их записи раз- личаются только в одной позиции, в которой для одной грани указано значение 0, а для другой 1 (например 01∗0∗1 и 11∗0∗1).

Будем говорить, что булева функция f, определенная на Bn, подчиняется булевой функции g, определенной на том же кубе (или f меньше g), если f(x)≤g(x) для любого x ∈ Bⁿ. В этом случае будем писать f ≤g. Множество вершин куба, в которых функция f принимает значение 1, будем называть уровнем единицы функции, сами эти вершины называют конституентами единицы. Если f ≤ g, то уровень единицы функции f является подмножеством уровня единицы функции g.

Элементарная конъюнкция принимает значение 1 в том и только в том случае, когда каждый литерал в ней принимает значение 1. Часть переменных может не входить в конъюнкцию, т.е. эти переменные будут фиктивными. Варьируя значения фиктивных переменных, получим грань n-мерного булева куба. Таким образом, уровень единицы любой элементарной конъюнк- ции есть некоторая грань булева куба.

Любую ДНФ данной функции f можно интерпретировать как набор граней булева куба, объединение которых совпадает с уровнем единицы функции f. При этом каждая элементар- ная конъюнкция рассматриваемой ДНФ будет подчинена функции f. Любую элементарную конъюнкцию, подчиненную функции f, будем называть импликантой.

Замечание. Далее будем предполагать, что исследуемая функция от n аргументов не меняется, так что можно заранее каждый аргумент функции связать с некоторой переменной, а точнее, с i-м аргументом связывается переменная x_i. Это позволяет не различать булевы функции и формулы, составленные из переменных x₁, . . . , x_n. Именно в этом контексте элементарная конъюнкция трактуется как функция от n аргументов.

Чтобы получить кратчайшую ДНФ заданной функции, надо выбрать минимальное количество импликант (граней булева куба, содержащихся в уровне единицы функции), в совокупности накрывающих уровень 1. Для минимальной ДНФ минимума достигает сумма длин импликант, а для этого надо стремиться увеличить сумму размерностей граней куба, соответствующих элементарным конъюнкциям ДНФ. В самом деле, пусть d_i и n_i, i = 1, k, — длины конъюнкций, составляющих ДНФ, и размерности соответствующих граней булева куба; s — сложность ДНФ; r — сумма размерностей граней, соответствующих конъюнкциям ДНФ. Тогда и мы видим, что увеличение суммы размерностей граней ведет к уменьшению сложности ДНФ.

При небольших размерностях булева куба (до 4) его геометрию можно представить на плоскости с помощью так называемых карт Карно. Представим куб Bn как декартово произведение двух кубов Bk × Bl, где k, l ≤2. Такое произведение можно изобразить таблицей, в которой каждая строка соответствует вершине куба Bk , а каждый столбец — вершине куба Bl . Существенным моментом является такой порядок строк и соответственно столбцов, при котором соседним строкам и столбцам отвечают соседние вершины соответствующего булева куба. А именно, при k, l = 1, берем естественный порядок 0, 1. при k, l = 2 используем порядок 00, 01, 11, 10 (табл. 1.5).

В такой таблице соседние клетки соответствуют соседним вершинам четырехмерного булева куба. Если представить, что эта ”шахматная доска“ склеена по горизонтали и вертикали, т.е. соседними, например, являются (00, 11) и (10, 11), а также (01, 00) и (01, 10), то соседние на доске будет в точности соответствовать соседним на кубе.

На карте Карно ребро — это пара соседних (в том числе и ”через край“) клеток. Легко изобразить на карте Карно и двумерные грани, состоящие из 4-х вершин. это либо квадрат из двух примыкающих пар клеток, либо одна строка, либо один столбец. Трехмерная грань — это две соседние строки или два соседних столбца.

К сожалению, при увеличении размерности такая простая интерпретация исчезает. Например, для пятимерного куба (табл. 1.6), соседние клетки (включая ”соседство через край“) будут соответствовать со- седним вершинам. Но, кроме того, и другие пары клеток, например (01, 001) и (01, 101), не будучи со- седними в таблице, соответствуют соседним верши- нам. Причина в том, что на карте Карно у каждой клетки четыре соседних, в то время как в n-мерном кубе каждая вершина имеет n соседних вершин, которые получаются, если в булевом векторе изменить одну компоненту из n возможных.

Рассмотрим два приема, с помощью которых из имеющейся ДНФ можно получить более простую ДНФ (и в смысле длины, и в смысле сложности).

Склейка. Дизъюнктивная нормальная форма данной функции может содержать пару импликант, соответствующих соседним граням булева куба. Но две соседние грани булева куба вместе составляют грань большей размерности. Например, две двумерные грани 01∗∗10 и 01∗∗11 пятимерного куба в совокупности составляют трехмерную грань 01∗∗1∗. Замена в ДНФ двух таких импликант одной более короткой приводит к 0*0* уменьшению и длины, и сложности ДНФ. Такую замену называют склейкой.

Импликанты, соответствующие соседним граням, имеют один и тот же набор переменных, причем они различаются только по одной переменной: в одной импликанте стоит сама переменная, а в другой — ее отрицание. Например, грани 01∗∗10 и 01∗∗11 соответствуют элементарным конъюнкциям x1 x2 x4 x5 и x1 x2 x4 x5 . Изменение ДНФ выполняется в данном случае в соответствии с тождеством x1 x2 x4 x5 + x1 x2 x4x5 = x1 x2 x4 Примеры возможных склеек показаны с помощью карты Карно на рис. 1.3.

Отталкиваясь от совершенной ДНФ, мы можем сперва склеивать различные пары соседних нульмерных граней (вершин) в ребра, затем в соседние ребра в двумерные грани и т.д. Процесс подобной склейки приведет к выявлению граней максимальной размерности, содержащихся в уровне единицы функции. Этим граням соответствуют максимальные импликанты функции (максимальные относительно введенного порядка ≤ на импликантах функции). Такие импликанты называются простыми импликантами. ДНФ данной функции, в которую входят все простые импликанты, называют сокращенной ДНФ.

Отметим, что если исходная ДНФ не является совершенной, то склейка может и не привести к сокращенной ДНФ. Так, если на рис. 1.3 выбрать грани ∗0∗0, 01∗1, 0001, 0100, получим покрытие уровня единицы функции. В соответствующей ДНФ x₂x₄+x₁x₂x₄+x₁x₂x₃x₄+x₁x₂x₃x₄ нельзя склеить какие-либо грани, но эта ДНФ не является сокращенной, так как два последних слагаемых не являются простыми импликантами.

Избыточные импликанты. В сокращенной ДНФ одна из импликант может накрываться остальными. Такую импликанту можно удалить из формулы, уменьшая и длину, и сложность ДНФ. Рассмотрим, например, функцию, представленную картой Карно на рис. 1.4. У этой функции максимальными являются шесть импликант 1∗0, 10∗, ∗01, 0∗1, 01∗,01* ∗10. Их сумма даст сокращенную ДНФ. Но из рисунка видно, что, например, импликанта 10∗ накрывается двумя импликантами 1∗0 и ∗01. Значит, эту импликанту можно из ДНФ удалить.

Импликанта в ДНФ, подчиненная сумме остальных импликант этой ДНФ, называется избыточной. Если из сокращенной ДНФ удалить избыточные импликанты, то получим тупиковую ДНФ. По определению, тупиковая ДНФ — это ДНФ, состоящая из простых импликант, ни одна из которых в этой ДНФ не является избыточной. Например, на рис. 1.4 тупиковую ДНФ образуют импли-

канты 1∗0, ∗01, 01∗.

Основной целью каждого метода минимизации ДНФ является выявление всех тупиковых ДНФ. Именно среди них находится минимальная и кратчайшая формы.

Построение сокращенной ДНФ. Один из методов построения сокращенной ДНФ — это метод Квайна — МакКлоски. Его суть в следующем. В качестве исходной выбирается совершенная ДНФ. На первом этапе проводится склейка импликант совершенной ДНФ в ребра, которые добавляются в ДНФ. После того как проведены все склейки вершин, из ДНФ удаляются все избыточные вершины, т.е. те, которые подчиняются добавленным ребрам. На втором этапе проводится склейка всех ребер в четырехмерные грани, которые добавляются к ДНФ. После проведения всех склеек между ребрами удаляются ребра, подчиненные двумерным граням. На третьем этапе выполняется склейка двумерных граней и удаление избыточных двумерных гра- ней. Процесс останавливается, когда между гранями соответствующей размерности не удается провести ни одной склейки. Результатом этих преобразований и будет сокращенная ДНФ.

Пример 1.6. Рассмотрим функцию, заданную картой Карно на рис. 1.5. Первый этап склейки по методу Квайна приведет к ребрам 1∗00, 10∗0, ∗010, а также четырем ребрам двумерной грани 0∗∗1 и четырем ребрам двумерной грани 0∗1∗. Все исходные импликанты будут удалены как избыточные. На втором этапе мы получим две двумерные грани 0∗∗1 и 0∗1∗. При этом будут удалены 6 ребер, входящих в эти грани. Поскольку склеить две эти грани нельзя, процесс вы- явления простых импликант на этом завершится. Сокращен- ная ДНФ будет содержать пять импликант, соответствующих граням 0∗∗1, 0∗1∗, 1∗00, 10∗0, ∗010. #

Другой метод построения сокращенной ДНФ — метод Блейка, в котором в качестве исходной можно взять любую ДНФ. В этом методе на первом этапе многократно выполняется операция обобщенного склеивания, при которой сумма xK₁ +xK₂ заменяется суммой xK₁ +xK₂ +K₁K₁. Такая операция выполняется до тех пор, пока удается получать новые импликанты вида K₁K₂. После завершения первого этапа выполняется операция поглощения согласно формуле K₁K₂ + K₂ = K₂.

Выявление всех тупиковых ДНФ. Создать список всех тупиковых ДНФ можно, используя следующий прием. Обозначим все простые импликанты символами K₁, K₂, . . . , K_m. Перенумеруем все вершины уровня единицы функции. Пусть первая вершина накрывается склейками K_i1 , K_i2 , . . . , K_ip . Тогда элементарная дизъюнкция K_i1 + K_i2 + . . . + K_ip задает условие, что первая вершина уровня единицы функции накрывается одной из простых импликант. Составив конъюнкцию из указанных элементарных дизъюнкций по всем вершинам уровня единицы функции, мы получим КНФ, представляющее собой логическое условие того, что весь уровень единицы функции накрыт простыми импликантами. Эта КНФ называют функцией Патрика. Преобразуем КНФ в ДНФ, пользуясь свойствами булевых операций (дистрибутив- ностью, коммутативностью, идемпотентностью). В ДНФ каждая элементарная конъюнкция будет описывать набор простых импликант, целиком покрывающих уровень единицы функ- ции, т.е. набор, описывающий конкретную тупиковую ДНФ рассматриваемой функции. Можно показать, что таким образом можно выявить все тупиковые ДНФ.

Среди простых импликант рассматриваемой функции есть те, которые входят в любую тупиковую ДНФ. К таким относится любая импликанта, для которой среди накрываемых вершин есть хотя бы одна, не накрываемая никакой другой импликантой. Например, на рис. 1.5 вершина 1100 накрывается единственной простой импликантой 1∗00. Эта импликанта должна входить в любую тупиковую ДНФ. Импликанты, удовлетворяющие описанному условию, называются ядровыми импликантами. Совокупность ядровых импликант — ядро — постоянная часть всех тупиковых ДНФ. Например, на рис. 1.5 ядро составляют импликанты 0∗∗1, 0∗1∗, 1∗00, а импликанты ∗010 и 10∗0 неядровые. При выявлении тупиковых ДНФ ядровые импликанты и накрываемые ими вершины из функции Патрика можно исключить.

Пример 1.7. У функции, представленной на рис. 1.5 диаграммой Карно, имеется пять простых импликант. Введем обозначения:

K₁ = 0∗∗1, K₂ = 0∗1∗, K₃ = 1∗00, K₄ = 10∗0, K₅ = ∗010.

Тогда функция Патрика для 9 вершин уровня 1 при их нумерации по строкам будет иметь следующий вид:

P = K₁(K₁ + K₂)(K₂ + K₅)K₁(K₁ + K₂)K₂K₃(K₃ + K₄)(K₄ + K₅).

Упростив согласно идемпотентности операций и тождествам поглощения (x(x + y) = x), получим

P = K₁K₂K₃(K₄ + K₅).

Используя дистрибутивность и идемпотентность, приходим к ДНФ:

P = K₁K₂K₃(K₄ + K₅) = K₁K₂K₃K₄ + K₁K₂K₃K₅.

Таким образом, рассматриваемая функция имеет две сокращенные ДНФ, описываемые двумя списками склеек K₁, K₂, K₃, K₄ и K₁, K₂, K₃, K₅. В результате получим

D₁ = x ₁x₄ + x₁x₃ + x₁x ₃x ₄ + x₁x₂x₄, D₂ = x₁ x₄ + x₁x₃ + x₁x3x₄ + x₂x₃x₄.

Видно, что у обоих сокращенных ДНФ есть общая часть — первые три конъюнкции. Это ядро, входящее в каждую сокращенную ДНФ. Его можно исключить из рассмотрения, рассматривая условия накрытия только для тех вершин, которые не накрываются склейками ядра. В данном случае это единственная вершина 1010. При этом функция Патрика будет иметь вид Pˆ = K₄ + K₅. Добавив к каждому слагаемому элементарную конъюнкцию K₁K₂K₃, описывающую ядро, получим полную функцию Патрика. #

Ядро данной функции можно получить с помощью таблицы Квайна, в которой каждая строка соответствует одной простой импликанте, а каждый столбец — одной вершине уровня единицы функции. В каждой клетке указывается 1, если импликанта накрывает вершину, и пробел в противном случае Например, составим таблицу Квайна функции, представленной картой Карно на рис. 1.3 (табл. 1.7). Чтобы определить ядро функции, необходимо выявить столбцы, в которых находится только одна единица, и пометить соответствующие строки. Импликанты, соответствующие помеченным строкам, образуют ядро. Например, в табл. 1.7 по одной единице содержится в столбцах, отвечающих вершинам 0001, 0010, 0100, 0111, 1000, 1010 (эти единицы выделены полужирным шрифтом). Поскольку в каждой строке содер

Минимизация булевых функций

Сокращенная ДНФ

О1 Элементарным произведением назыв конъюнкт, в который любая переменная входит не более 1 раза

О2 Формула (х₁, х₂, … х_п) называется импликантой формулы (х₁, х₂, … х_п), если   элементарное произведение и для соответствующих формулам  и  функций f_ и f_ справедливо неравенство f_f_. Формула (х₁, х₂, … х_п) называется импликантой функции f, если   импликанта совершенной ДНФ, представляющей функцию f. О3. Импликанта (х₁, х₂, … х_п)=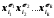 формулы  называется простой, если после отбрасывания любой литеры из  не получается формула, являющаяся импликантой формулы .

О4.Дизъюнкция всех простых импликант данной (функции называется сокращённой ДНФ.

Сокращенная ДНФ -форма записи логической функции с свойствами:

любые два слагаемых различаются как минимум в двух позициях,

ни один из конъюнктов не содержится в другом.

Функцию можно записать с помощью сокращенной ДНФ не единственным способом.

Тупиковая ДНФ

Даже если ДНФ сокращенная, ее можно минимизировать т е уменьшить количество входящих в нее элементарных конъюнкций.

Пример. Пусть сокр ДНФ функции имеет вид:  .

Тогда ее единичное множество может быть представлено в виде:

 .

наборы, входящие в последн подмножество, находятся так же в 1м и во 2м. Так  ( гов, набор 101 покрывается множеством  ), а  . Значит, если убрать из объед составл  , объединение от этого не изменится. Говорят, что множество покрывается объединением   и   

След, импликант xz – лишний. Сокращённая ДНФ, из которой удалены все лишние импликанты, называется  тупиковой.

Отношение покрытия между единичными наборами и импликантами ДНФ задается таблицей покрытия.

Строки табл соотв конъюнкций ДНФ, столбцы – элементы единичного множества. На пересечении строки и ст-ца ставится пометка, если данная конъюнкция=1 данным набором зн арг (иначе говоря данный набор покрывается единичным множеством конъюнкции).

Пример. Пусть ДНФ функции имеет вид:  .

Тогда ее единичное множество может быть представлено в виде:

 .  .

Построим таблицу покрытия.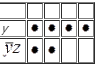

Из табл видно, что 2я строка – лишняя, если ее убрать, все эл един мн-ва останутся покрыты. Зн, импликант  – лишний. Таким обр, ДНФ м упростить, убрав лишний импликант. Она приобр вид  , и в дан сл явл тупиковой, та к оставш импликант – простой. Так быв не всегда.

Замеч1 Чтобы с помощью табл покрытия получить тупиковую ДНФ, надо сначала получить сокращенную ДНФ и именно ее простые импликанты помещаются в таблицу покрытия.

Замеч2 У функции может быть несколько тупиковых ДНФ. Чтобы найти их надо построить сокращенную ДНФ, содержащую все простые импликанты данной функции.

Метод Блейка-Порецкого 

– метод получения сокращенной ДНФ, содержащей все простые импликанты.

позволяет получать сокращенную ДНФ булевой функции f из ее произвольной ДНФ. Базируется на применении формулы обобщенного склеивания:

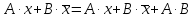
справедливость которой легко доказать. Действительно,

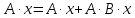
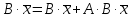Следовательно,

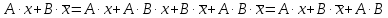
В основе метода: если в произвольной ДНФ булевой функции f произвести все возможные oбобщенные склеивания, а затем выполнить все поглощения, то в результате получится сокращенная ДНФ функции f.

Алгоритм

Пусть дана СДНФ функции.

1. Перенумеруем элементарные конъюнкции.2. Осуществим попарно склеивание каждой конъюнкц с каждой, если это возм. Под полученными конъюнкциями будем фиксировать номера.

3. Допишем к списку получ конъюнк те, кот не участв в склеивании (их номера не фиксир.

4. Вернемся к п.1.В рез получим сокращ ДНФ, содержвсе простые импликанты.

Пример. Дана СДНФ вида:

Получить с пом метода Блейка-Порецкого сокращ ДНФ, содерж все простые импликанты.

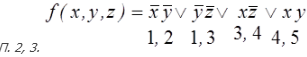
Т к больше склеивания произвести нельзя, сокращенная ДНФ имеет вид: Построим таблицу покрытия

Из табл видно, что 1ю строку удалять нельзя, т к при этом ост не покрыт набор 001. 2ю строку м удалить, т к наборы, составл ед мн=во конъюнк  , содерж также в единич мн-вах др конъюнкций. Анал с 3й строкой. Посл строку также нельзя удалить, та к если это сдел, ост не покрыт набор 111. Таким обр, данн функция имеет 2 тупиковые ДНФ:

Пример 2.

П. 1.  ;

П. 2,

п3.  ;

П.4.  ;

Т к больше склеиваний произвести нельзя, сокращенная ДНФ имеет вид

:  .Построим таблицу покрытия:

Из табл видно, что при удалении любой ее строки появляются единичные наборы, не покрытые никаким единичным множеством.т е , полученная сокращенная ДНФ является тупиковой.

Минимизация ДНФ.

Логическая формула с наименьшим числом логических связей наз минимальной.

О5 Минимальной ДНФ функции называется её тупиковая ДНФ с наименьшим числом вхождений переменных.Так, получим миним дизъюнктивную нормальную форму (МДНФ) и, соотв, – МКНФ.

Процесс отыск мин формы наз минимизац логической функции или просто минимизацией.

Минимизировать функции можно тремя методами:

1) расчетным путем, используя законы алгебры логики

2) графич путем (метод карт Карно или диагр Вейча), используя специальные карты,

3) метод Квайна и его модификации).

Метод Квайна исп при числе перем6, хор алгоритмизируется и программируется. На его осн разраб CАПР и разл станд прогр минимизации логич функц любого числа перем. Но они не всегда доступны и не оправд при малом числе независимых= перем. Метод карт Карно хор раб при числе перем

Метод Квайна

Строим таблицы Квайна (ТК). Заголовками столбцов ТК – конституенты елиницы СДНФ, а заголовками строк  простые импликанты из сокращённой ДНФ. Табл заполняется «+» на пересечениях тех строк и столбцов, для кот конъюнкт, стоящий в заголовке строки, входит в конституенту единицы, являющейся заголовком столбца. В тупиковую ДНФ выбирается миним число тех простых импликант, знаки «+» при которых охватывают все столбцы ТК.

Пр. f(x, y, z) задана СДНФ f(x, y, z)=zxxy. Производя операции склеивания и элементарного поглощения, получим сокращённую ДНФ f(x, y, z)=x. Ее табл Квайна

Минимальное число простых импликант, знаки «+» при которых охватывают все столбцы, образуют импликанты 1й и 3й строки, т е и x. Поэтому x является МДНФ функции.

метод Квайна-Мак-Класки.

1. Представим каждую конституенту булевой функции в виде 2ичного набора длины п.

2. Сгруппируем наборы чтобы в каждую группу попали только те наборы, которые имеют одинаковое число 1, располагая их в порядке возрастания числа единиц.

3. Сравнивая наборы из соседних групп, выделяем пары, отличающиеся только в 1 позиции (те выделяем конституенты, отличающиеся только одной литерой).

4. В обоих выделенных наборах пар заменяем отличающиеся символы (0 и 1) на «-» (тем самым из 2 различных наборов получаем один и тот же набор из 0, 1 и «-», что соответствует тому, что два одинаковых элемент произведения склеили по отличающейся литере, при этом знак «-» соответствует тому, что соотв литера в полученном элемент произведении будет отсутствовать).

Если в результате склеивания получается уже имеющийся набор, то результат склеивания (т е полученный набор) опускается ( согласно закона идемпотентности одинаковые элементарные произведения сливаются в одну). Если в результате склеивания получаются наборы, отличающиеся только в 1 позиции, причём в соотв позиции одного стоит знак «-» (у других  0 или 1), то остальные опускаются (что соответствует элементарному поглощению)

5. После всевозможных склеиваний на очередном этапе, переходим к пункту 2.

Процесс продолжается пока склеивать будет нечего. Простыми импликанты -те элементарные произведения, которые не участвовали в процессе склейки на очередном шаге.

Пр f(x, y, z)=zxxy. f(0, 1, 0)=f(0, 1, 1)=f(1, 0, 1)=f(1, 1, 0)=f(1, 1, 1)=1

непомечены -1- и 1-1. Т е соответствующие им элементарные произведения у и хz являются простыми импликантами функции. Т е, сокращённой ДНФ данной функции является ухz.

Карта Карно 

Карта Карно — это табл истинности, представленная в виде матрицы в 2-мерн виде..Удобна тем, что логические термы, к которым м б применены операции попарного неполного склеивания  и элем поглощ группируются в карте Карно в виде массивов соседних ячеек по вертикали и горизонтали логич 1 или 9, что чел сразу наглядно видно. Карту Карно м рассматривать как развертку на плоскость n-мерн булева куба, причем размерн этого гиперкуба совп с кол перем представл функции. Графич карта Карно изобр в виде прямоуг или квадрата из ячеек, число кот , причем любые две сосед яч по вертикали или горизонтали опис термы, различающиеся только по 1 перем — с логическим отрицанием и без Также соседним явл 1я и послед строки, крайний левый и край правый ст-цы табл, поэтому табл Карно явл фактически разверткой логического гиперкуба на поверхость тороида. 

Карта Карно двух перем: n = 2, число наборов N = 2² = 4

или так

Напр, для функц 2 перем, задан табл истинности: м построить эквивал ей квадрат: Или, если обозн верш соотв элем конъюнкц и выделить верш, конъюнкции кот входят в СДНФ: Или СКНФ:

члены, нах на одной стор квадрата, м б склеены. Соотв, если сост ДНФ, то опер произв только над верш, в кот функция имеет зн 11 (по плам постр СДНФ). Если же составл КНФ, то над верш, в кот функ имеет зн 00 (по п-лам постр СКНФ).При этом, сохр перем, зн кот на стороне постоянно.

Карта Карно 3 перем n = 3, число наборов N = 2³ = 8

или так

3перем

Карта Карно -развертку гиперкуба на пл-ть. Напр, 3мерн куб из предыд прим м развернуть так:

В сл ф 3перем прих иметь дело с трёхмер кубом. Это сложнее и менее нагл, но технич возм. На рис в кач примера показана табл истинности для бул функ 3 перем и соотв ей куб.

Как видно из рис, для трёхмерн сл возм б сложные конфигур. Напр, 4 члена, принадл одной грани куба, объед в один с поглощением 2 переменных:

Пр2

Карта Карно 4 перем :n = 4, N = 16

В этих картах переменные располагаются по-разному, но они обе правильны, т к любые соседние клетки по горизонтали или вертикали отлич только одной из перем

Для функц от 4 перем треб развертка 4-мерн гиперкуба. Карта Карно в таком сл имеет вид:

В данном сл, все крайние яч смежны др др Это м себе представить, натянув эту развертку на тор

В общем сл м сказать, что  членов, принадл одной K–мерн грани гиперкуба, склеив в 1 член, при этом поглощаются  K  перем на одной  K-мерн грани м лежать  вершин. След, в карте Карно выб группы по  смежных ячеек, и в результир ДНФ или КНФ вх только те перем, кот неизм в рамках данной гру. Общее ч-ло членов соотв числу групп в карте Карно, а число неизмен перем обратн образависит от колич элем в группе. Как следст, группы н выбрать как м более большими. 1 комб перем м входить в неск групп.

Если н получ мин ДНФ, то в Карте рассм только те клетки, содержат 1, если н КНФ, то клетки, кот содержат 0.

минимизация: охватить все 1 карты Карно наим числом кубов наиб высокого ранга. Из каждого куба выписать минтерм общих перем. Минтермы объединить дизъюнктивно.

Куб – это прямоуг или квадр контур, содерж клетки только с единицами:

одна 1 – куб “0”-го ранга, т к 2⁰ = 1 две 1 – куб “1”-го ранга, т.к. 2¹ = 2

4 ед – куб “2”-го ранга, т.к. 2² = 4 8 ед – куб “3”-го ранга, т.к. 2³ = 8

16 ед – куб “4”-го ранга, т.к. 2⁴=16 и т.д. Куб не м содержать др число 1 и клетки с 0. Одна и та же 1 одновр м принадл неск кубам, чтобы ранг куба был наиб Тогда форма будет именно минимальной.

Алгоритм минимизации(на прим ДНФ).

1)Объед смежн клетки, содерж 1, в обл так, чтоб одна обл содерж  ( n целое клеток ( крайн строки и столбцы явл сосед меж собой), в обл не д нах клеток, содерж 0;

2)Обл д распол симм оси(ей) (оси распол через каждые 4 клетки);

3)Несмежн обл, распол симм оси, м объед в одну;4)Обл д б как м больше, а кол обл как м меньше;

5)Обл м пересекаться; 6)Возм неск вариантов покрытия.

Далее берём 1ю обл и смотр, какие перем не меняются в пределах этой обл, выпис  конъюнкцию этих перем; если неменяющ перем 0, прост над ней инверсию. Берём след обл, вып то же самое, что и для 1й, и т. д. для всех обл. Конъюнк областей объед дизъюнкцией.

В элем конъюнкции (дизъюнкц), кот соотв 1 контуру, ост только те перем, зн кот не изменяются внутри обвед контура. Перем бул функ вх в элем коньюнкции (для зн фун 1) без инверсии, если их зн на соотв к-тах= 1 и с инверсией – если= 0. Для зн бул функц,= 0, запис элем дизьюнкции, куда перем входят без инверсии, если их зн на соотв к-тах =0 и с инверсией – если= 1.

Примеры 2 перем

МДНФ МКНФ

Пр2

МДНФ:

3 переменных

Составить таблицу истинности функции, написать для нее СДНФ и СКНФ (если возможно);

СДНФ

СКНФ

Карта Карно и покрытия

Отсюда сокращ ДНФ: =

СДНФ

На карте Карно 2 прямоуг. 1й из них объед (как бы закл в скобки) 2 1х мин терма, а 2й — 1е и

3е слаг СДНФ минимизир функц. Мин термы, объед в прямоуг, отлич только в 1 разр. Их неизм часть, кот при минимиз вынос за скобки, и явл минимизируемым знач функции

мин форма . Здесь 1 куб содерж 4 ед (ранг r = 2). Число перем в минтерме n–r = 3–2=1 Из 2 куба n–r=3 –1 = 2.Сост СДНФ и вып склеив минтермов кажд с кажд:

4 переменных

С пом карт Карно по табл истинности для ф 4-х перем найти ее сокращенную ДНФ.

А)

)

Зад 1.2. Полнопределенная булева ф от 4-х перем задана десятичн раб наборами:

РН(4) = 5, 6, 7, 8, 9, 10, 11.Число в скобк указ колич перем. Найти мин форму этой функции.

Реш. Т к ф явл полностью определенной, то запрещ наборами ЗН(4) явл наборы 0 – 4, 12 – 15. Исх из этого, сост табл истинности и осущ минимизацию по карте Карно.

По карте Карно получим результат: f = x₄x₃’ + x₄’x₃(x₁ + x₂)

Найти мин форму полностью определ булевых функций, зад 10-чн раб наборами :

1-1) РН(4) = 0, 1, 5, 7 – 9, 13, 15 1-2) РН(5) = 4, 6, 8, 10, 13, 17, 24, 30

1-3) РН(6) = 1 – 8, 16 – 24, 32 – 40

Карта Карно 5 перем: n = 5, N = 32.

Это 2 16-клеточных карты, отлич только одной (5й) переменной.

Карта Карно 6 перем n = 6, N = 64. Это 4 16-клеточных карты:

ПР2 Минимизировать функцию 4 перем с заданн картой Карно

Проводим 2 контура 2 ранга и получ Цена схемы Ц = 4 + 2 = 6

М в карте Карно объед 0, но при этом получ инверсную функ: . Здесь проведены 2 куба – 3го и 2го ранга. Цена схемы получ меньше. Ц = 2 + 2 = 4 Ее реализ на рис выше справа Отрицание м перенести в пр часть, что не отраж на цене

функция 5 перем

Здесь проводим 3куба : 1 – куб 2 ранга, 2 – куб 3го ранга, 3 – куб 2го ранга. Запис мин форму: . Нах цену Ц =8 +3=11 м найти цену схемы после объеди нулей.

Минимизация не полностью определенных функций

есть ряд функций, зн кот на нек наборах неопр или просто не интерес. Такие наборы наз запрещенными и исп для минимиз, дополним функ 0 или 1 так, чтобы провести куб б высокого ранга. Пусть, напр, имеем функцию 3 перем

Если не использ запрещённые наборы, то карта Карно справа на рис

. Цена схемы Ц = 7+ 3 = 10

Если на запрещенных наборах функцию дополнить 1, то карта Карно принимает вид

Мин форма .Цена Ц = 2. Схемная реализация

получ значит проще.

Пусть необходимо минимизировать булеву функцию, заданную картой Карно (рис. 7)

Если группировать 1 в контурах только по исх зад (рис. 7, а), то мин форма функц б иметь вид:

.

После доопределения функции (рис. 7, б), ее мин ДНФ (это будет уже другая полностью определенная функция  j ) оказ предельно простой.

Ф j , значения кот совпали со зн зад фун F на тех наборах, где F определено, наз эквивал.Таким обр, задача минимиз недоопределенной функ сводится к отысканию такой эквивалентной функции, кот имеет простей форму.

При синтезе комбинационных схем всегда возникает вопрос выявления опасных состязаний. С этой целью на практ польз простым и удоб форм крит Хаффмена: статич опасные состязания в у=ве с минимизир структурой м иметь место, если на карте Карно при охвате соседних клеток контурами склеивания окажутся хотя бы две соседние клетки, не покрытые контуром.

Поэтому устранение опасных состязаний достиг возвращением импликант, кот оказ лишними при переходе от сокр к тупиковой ДНФ

Найти минимальную форму функции y от 4-х арг, заданной десятич рабочими (РН) и запрещенными (ЗН) наборами: РН(4): 1, 2, 9; ЗН(4): 7, 13.

Ф задана только на 5 наборах Доб к 3раб наборам ещё 5 а именно : 0000, 0011, 1000, 1011, 1010. Все ост наборы доопр как запрещ. В рез такого доопр получим прямоуг Карно, сост из 8 эл квадратов Карно. Этому прямоуг соотв функция: y = х3′

Даже если ДНФ сокращ, ее м минимизиро т е уменьшить кол вх в нее элем конъюнкций.

Пр. Пусть сокрашенная ДНФ функции имеет вид:  .

Тогда ее единичное множество м б представлено в виде:

 .

наборы, входящие в последн подмн=во, нахо так же в 1м и во 2м. Так  ( гов, набор 101 покрывается мн=вом  ), а  . Зн, если убрать из объед составл  , объед от этого не изменится. Гот, что мн=во покрывается объединением  и  След, импликант xz – лишний. Сокращенная ДНФ, из кот удалены все лишние импликанты, наз тупиковой.

Задания

4. Найти все сокращённые и минимальные ДНФ переключательной функции f(0, 0, 0)=f(0, 0, 1)=f(1, 0, 1)=f(1, 1, 1)=1. К каким классам Поста принадлежит эта функция?

5. Найти сокращённую, все тупиковые и минимальные ДНФ булевой функции f(х₁, х₂, х₃, х₄), заданной вектором своих значений (1011 1010 1001 1001).

4. Найти все сокращённые и минимальные ДНФ переключательной функции f(0, 1, 1)=f(1, 0, 0)=f(1, 1, 0)=0. К каким классам Поста принадлежит эта функция?

5. Найти сокращённую, все тупиковые и минимальные ДНФ булевой функции f(х₁, х₂, х₃, х₄), заданной вектором своих значений (0110 1010 1100 1100).

4. Найти сокращённую, все тупиковые и минимальные ДНФ булевой функции f(0, 1, 1)=f(1, 1, 0)=f(1, 0, 1)=0. К каким классам Поста принадлежит эта функция?

5. Найти сокращённую, все тупиковые и минимальные ДНФ булевой функции f(х₁, х₂, х₃, х₄), заданной вектором своих значений (1101 1000 1001 0111).

ЛИТЕРАТУРА, ССЫЛКИ

1) Мухаметьянов И.Т. Методические материалы к изучению курса «Дискретная математика».

Часть IV. Булевы функции, ЛФ ПГТУ, 2006

2) https://helpiks.org/9-51416.html