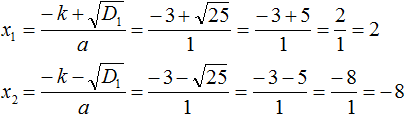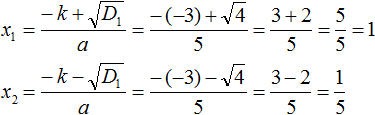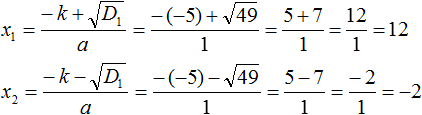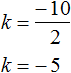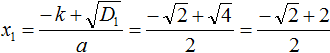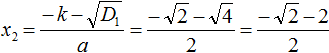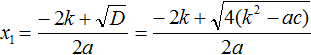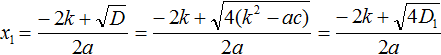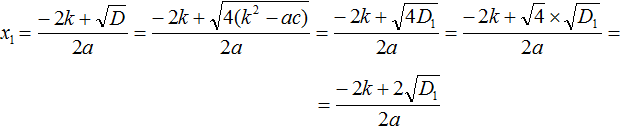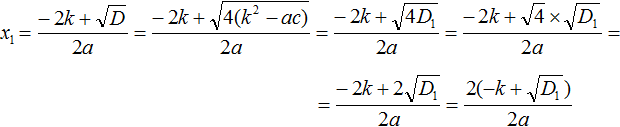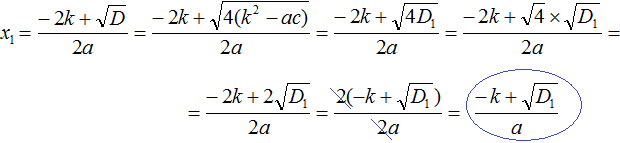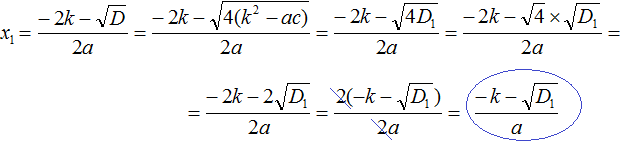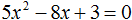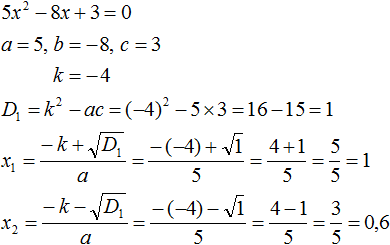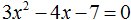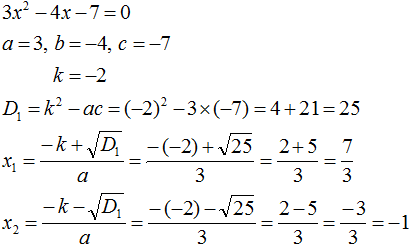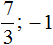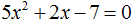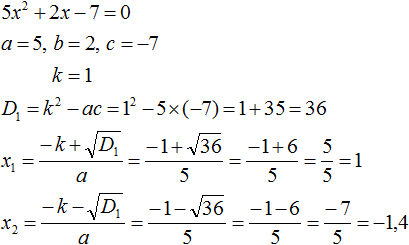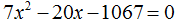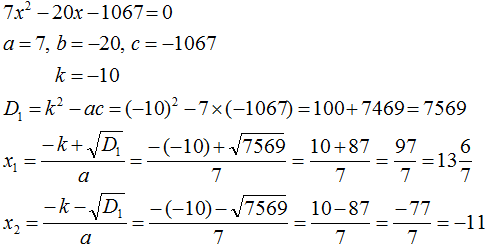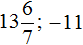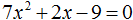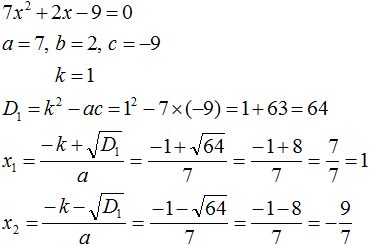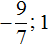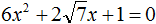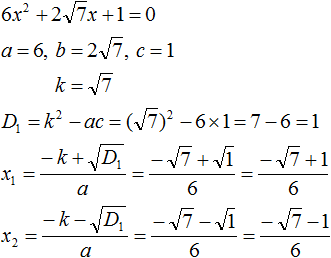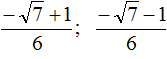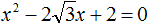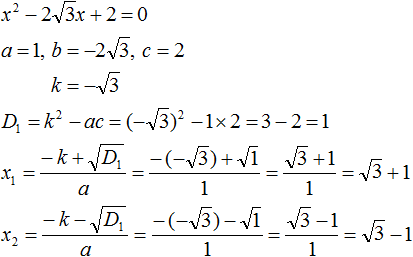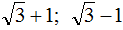Квадратные уравнения
Квадратным называется уравнение, содержащее переменную во второй степени.
В общем виде оно выглядит следующим образом:
(ax^{2} + bx + c = 0,) где (a neq 0, b, c) – некоторые числа.
ДИСКРИМИНАНТ:
Корни уравнения можно определить с помощью дискриминанта (D = b^{2} – 4ac) по формулам:
(leftlbrack begin{matrix} \ x_{1} = frac{- b + sqrt{D} }{2a} \ \ x_{1} = frac{- b – sqrt{D} }{2a} \ \ end{matrix} right. )
– Если дискриминант больше нуля – уравнение имеет два корня.
– Если дискриминант равен нулю – уравнение имеет один корень.
– Если дискриминант меньше нуля – корней нет.
Пример №1:
(x^{2} = 6x – 5)
-
Способ 1:
1. Преобразуем уравнение к стандартному виду, перенеся все слагаемые в левую часть:
(x^{2} – 6x + 5 = 0)
2. Определим дискриминант полученного уравнения:
(D = 6^{2} – 4 cdot 1 cdot 5 = 16 = 4^{2})
3. С помощью дискриминанта найдем корни по формулам:
(leftlbrack begin{matrix} \ x_{1} = frac{6 + 4 }{2} \ \ x_{1} = frac{6 – 4 }{2} \ \ end{matrix} right. ) (leftlbrack begin{matrix} x_{1} = 5 \ {text{ }x}_{2} = 1 \ end{matrix} right. )
Ответ: 5; 1.
СОКРАЩЁННЫЙ ДИСКРИМИНАНТ:
Существует второй способ решения квадратного уравнения. В случае, если коэффициент (b) – четное число, запишем его как (2k). Квадратное уравнение примет следующий вид:
(ax^{2} + 2kx + c = 0),( a neq 0, k, c) – некоторые числа.
Тогда вместо дискриминанта D будем использовать сокращённый дискриминант (frac{D}{4}), а формула его нахождения будет следующей:
(frac{D}{4} = k^{2} – ac)
Корни уравнения определим так же через сокращённый дискриминант:
(leftlbrack begin{matrix} \ x_{1} = frac{- k + sqrt{frac{D}{4}} }{a} \ \ x_{1} = frac{- k – sqrt{frac{D}{4}} }{a} \ \ end{matrix} right. )
-
Способ 2:
1. Преобразуем уравнение к стандартному виду, перенеся все слагаемые в левую часть:
(x^{2} – 6x + 5 = 0)
2. Выделим коэффициент k:
(x^{2} – 2 bullet 3x + 5 = 0)
(k = 3)
3. Определим сокращённый дискриминант полученного уравнения:
(frac{D}{4} = 3^{2} – 1 cdot 5 = 4 = 2^{2})
4. С помощью сокращённого дискриминанта найдем корни по формулам:
(leftlbrack begin{matrix} \ x_{1} = frac{3 + 2 }{1} \ \ x_{1} = frac{3 – 2 }{1} \ \ end{matrix} right. ) (leftlbrack begin{matrix} x_{1} = 5 \ {text{ }x}_{2} = 1 \ end{matrix} right. )
Ответ: 5; 1.
Как мы видим, ответ остался прежним, но числа, используемые при вычислениях, стали меньше. Это значит, что при работе с большими коэффициентами решение через сокращённый дискриминант уменьшает вероятность вычислительной ошибки.
ТЕОРЕМА ВИЕТА:
В некоторых случаях (например, (a = 1)) корни проще искать по теореме Виета, решая подбором систему уравнений:
(left{ begin{matrix} \ x_{1} cdot x_{2} = frac{c}{a} \ \ text{ x}_{1} + x_{2} = – frac{b}{a} \ \ end{matrix} right. )
Важно, что теорему Виета можно использовать при любом ненулевом коэффициенте а, формула представлена в общем виде. Однако если (a = 1,) то чаще всего нужно работать с целыми числами, а не с дробными, что упрощает подбор.
Следствия из теоремы Виета:
Используя теорему Виета, можно увидеть взаимосвязь между коэффициентами b и c и знаками корней уравнения.
Коэффициент c показывает, будут ли одинаковыми знаки корней:
-
Если( c > 0), то корни( x_{1}) и (x_{2} ) имеют одинаковый знак.
-
Если коэффициент (c < 0), корни (x_{1}) и (x_{2}) будут разных знаков.
Коэффициент b показывает, какой именно знак у корней, если он один, либо какой корень положительный, а какой отрицательный, если знаки разные.
-
Если (x_{1} + x_{2} = – b > 0) (т.е. сумма корней положительна), то возможны 2 варианта:
а) либо оба корня положительны;
б) либо модуль положительного корня больше модуля отрицательного.
-
Если( x_{1} + x_{2} = – b < 0) (т.е. сумма корней отрицательна), то опять же есть 2 варианта:
а) либо все корни отрицательны;
б) либо модуль положительного корня меньше модуля отрицательного.
Пример №2:
(x^{2} – 5x + 6 = 0)
1. Составим систему:
(left{ begin{matrix} \ x_{1} cdot x_{2} = 6 \ \ text{ }x_{1} + x_{2} = 5 \ \ end{matrix} right. )
Из следствий из т. Виета видим, что (c > 0), значит у корней одинаковые знаки.
Коэффициент (b > 0), значит оба корня положительные
2. Подберем (x_{1}, x_{2}) так, чтобы оба равенства выполнялись.
Видим, что произведение больше нуля, значит, либо оба числа отрицательные, либо оба положительные. Сумма положительна, значит, оба положительные.
Произведение корней раскладываем всеми способами на множители:
(6 = 2 cdot 3 = 1 cdot 6)
Через сумму делаем проверку:
(2 + 3 = 5)
(1 + 6 = 7)
В данном случае подходят числа
(x_{1} = 2, x_{2} = 3).
Ответ: 2; 3.
ЧАСТНЫЕ СЛУЧАИ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ:
-
Если (a + b + c = 0), то (x_{1} = 1, x_{2} = frac{c}{a})
Пример №3:
(x^{2} + 3x – 4 = 0)
1. Сложим все коэффициенты уравнения, чтобы проверить, является ли это уравнение примером частного случая. Действительно, коэффициенты в сумме дают 0:
(1 + 3 – 4 = 0)
2. Тогда по правилу: (x_{1} = 1, x_{2} = frac{c}{a}) получаем:
(leftlbrack frac{x_{1} = 1}{x_{2} = frac{–4}{1} = –4} right. )
Ответ: 1; -4.
-
Если (a + c = b), то (x_{1} = –1, x_{2} = – frac{c}{a})
Пример №4:
(x^{2} + 9x + 8 = 0)
1. Сложим коэффициенты a и c, чтобы проверить уравнение на соответствие второму частному случаю. Действительно (a + c = b):
(1 + 8 = 9)
2. Тогда по правилу: (x_{1} = –1, x_{2} = – frac{c}{a}) получаем:
(leftlbrack frac{x_{1} = –1}{x_{2} = – frac{8}{1} = –8} right. )
Ответ: – 1; – 8.
НЕПОЛНЫЕ КВАДРАТНЫЕ УРАВНЕНИЯ
Неполное квадратное уравнение вида
(ax^{2} + bx = 0.)
Если отсутствует свободный член, то:
1.Раскладываем левую часть на множители:
(x(ax + b) = 0)
2. Приравниваем каждый из множителей к нулю:
(leftlbrack begin{matrix} \ begin{matrix} \ x = 0 \ ax + b = 0 \ \ end{matrix} \ end{matrix} right. )
3. Решаем каждое из полученных уравнений, получаем:
(leftlbrack begin{matrix} \ x = 0 \ x = – frac{b}{a} \ end{matrix} right. )
Неполное квадратное уравнение вида
(ax^{2} + c = 0.)
Если отсутствует слагаемое с переменной в первой степени, то:
1.Делим левую и правую часть на коэффициент (a neq 0.)
(x^{2} + frac{c}{a} = 0)
2. Смотрим на знак слагаемого без переменной.
Если (frac{c}{a} < 0), то раскладываем по формуле разности квадратов, приравниваем каждую из скобок к нулю и решаем полученные уравнения.
Если (frac{c}{a} = 0), то получаем единственное решение (x = 0.)
Если (frac{c}{a} > 0), то решений нет.
В прошлой статье из серии Антимагия мы показали, как решаются квадратные уравнения в общем виде. Там мы рассмотрели, что такое дискриминант, откуда он появляется и зачем он нужен.
Однако помимо общей формулы для решения квадратных уравнений есть и частные случаи, для которых есть свои более удобные способы решения. В первую очередь это касается случая, когда второй коэффициент в квадратном уравнении чётный.
*********
Например, решим такое уравнение:
Используем уже знакомый нам алгоритм и постараемся выделить слева полный квадрат:
Обратите внимание, как легко удалось это сделать. За счёт того, что второй коэффициент был чётным, мы сразу выделили множитель 2, который отвечает за удвоение в формуле квадрата двучлена. То есть одночлен с x стал равен 2⋅3⋅x, откуда становится очевидным, что второе слагаемое в двучлене это 3.
Теперь проведём наши рассуждения для более общего случая. Пусть у нас второй коэффициент в квадратном уравнении — чётный. Тогда удобно записать наше уравнение в виде:
Решим это уравнение также через выделение полного квадрата:
Однако, пока мы рассмотрели лишь приведённое квадратное уравнение (то есть такое, в котором коэффициент при равен 1). Для неприведённого уравнения алгоритм такой же, только сначала нам нужно будет разделить его на первый коэффициент. После этого повторим алгоритм поиска корней для полученного уравнения.
Квадратный корень удобно упростить:
В итоге получаем следующие корни:
И окончательный результат для корней:
Есть и другой способ получить ту же самую формулу.
Для уравнения ax²+bx+c=0 мы уже знаем формулы корней
Возьмём теперь уравнение ax²+2kx+c=0 и используем для его решения общую формулу корней.
Далее, на примере первого корня, упростим получившиеся дроби:
Для второго корня результат аналогичен:
Выражение k²—ac называется сокращённым дискриминантом или коротко «дэ на четыре» (т.к. оно в 4 раза меньше обычного дискриминанта).
*********
Сокращённый дискриминант старшеклассники используют не часто. Обычно запоминают формулу для простого дискриминанта и не видят необходимости в поиске корней через сокращённый дискриминант. Или же используют более продвинутые способы решения.
Однако, во многих случаях он может быть полезен.
Например, решим такое уравнение через обычный дискриминант:
Сразу намечаются некоторые вычислительные сложности.
Нужно посчитать 38² (это обычно делается столбиком), потом 4⋅9⋅8 (можно в уме, но на практике чаще тоже считают столбиком), потом вычесть результаты (1444—288, тоже столбиком).
Получается дискриминант равен 1156. Но ведь из него ещё нужно правильно извлечь корень! Мало кто помнит квадрат какого числа равен 1156. Приходится дополнительно находить этот корень подбором по соответствующему алгоритму. Получим, что дискриминант равен 34².
Далее находим сами корни:
С сокращённым же дискриминантом вычисления будут гораздо проще:
38 = 2k, т.е. k = 19
19² легко посчитать, т.к. квадраты чисел до 20 часто знают наизусть. Вычитание можно выполнить в уме. А что 289 = 17² мы получаем снова благодаря знанию таблицы квадратов.
И сами корни легко ищутся по формулам:
Ещё отметим, что при расчёте через дискриминант с чётным вторым коэффициентом вам всегда нужно будет сокращать дроби на 2. Это лишнее действие, которое при сокращённом дискриминанте отсутствует.
Конечно, чтобы овладеть этим инструментом нужна практика. Обычно ученики ленятся запоминать эту формулу и просто пытаются всё посчитать через обычный дискриминант. Также поначалу они забывают, что в знаменателе уже нет умножения на 2 или что первое слагаемое в числителе не число b, а k (то есть его половина, b/2). В таком случае важно несмотря на ошибки всё равно пробовать решать через сокращённый дискриминант, даже если не удаётся запомнить формулу с первого раза.
Если в квадратном уравнении ax2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D1 = k2 − ac, а корни по формулам 

Примеры
Решим квадратное уравнение x2 + 6x − 16 = 0. В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k.
Любое четное число n можно представить в виде произведения числа 2 и числа k, то есть 2k.
n = 2k
Например, число 10 можно представить как 2 × 5.
10 = 2 × 5
В этом произведении k = 5.
Число 12 можно представить как 2 × 6.
12 = 2 × 6
В этом произведении k = 6.
Число −14 можно представить как 2 × (−7)
В этом произведении k = −7.
Как видим, сомножитель 2 не меняется. Меняется только сомножитель k.
В уравнении x2 + 6x − 16 = 0 вторым коэффициентом является число 6. Это число можно представить как 2 × 3. В этом произведении k = 3. Теперь можно воспользоваться формулами для чётного коэффициента.
Найдем дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = 32 − 1 × (−16) = 9 + 16 = 25
Теперь вычислим корни по формулам: 

Значит корнями уравнения x2 + 6x − 16 = 0 являются числа 2 и −8.
В отличие от стандартной формулы для вычисления дискриминанта (D=b2 − 4ac), в формуле D1 = k2 − ac не нужно выполнять умножение числа 4 на ac.
И в отличие от формул 



Пример 2. Решить квадратное уравнение 5x2 − 6x + 1=0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3). То есть k = −3. Найдём дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = (−3)2 − 5 × 1 = 9 − 5 = 4
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами 
Пример 3. Решить квадратное уравнение x2 − 10x − 24 = 0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5). То есть k = −5. Найдём дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = (−5)2 − 1 × (−24) = 25 + 24 = 49
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами 
Обычно для определения числа k поступают так: делят второй коэффициент на 2.
Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2k. Чтобы из этого равенства выразить сомножитель k, нужно произведение b разделить на сомножитель 2
Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2
Пример 5. Решить квадратное уравнение
Коэффициент b равен . Это выражение состоит из множителя 2 и выражения
. То есть оно уже представлено в виде 2k. Получается, что
Найдём дискриминант по формуле D1 = k2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами 
При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.
В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен 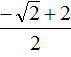
Вычислим второй корень уравнения:
Вывод формул
Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.
Рассмотрим квадратное уравнение ax2 + bx + c = 0. Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k
b = 2k
Заменим в уравнении ax2 + bx + c = 0 коэффициент b на выражение 2k
ax2 + 2kx + c = 0
Теперь вычислим дискриминант по ранее известной формуле:
D = b2 − 4ac = (2k)2 − 4ac = 4k2 − 4ac
Вынесем в получившемся выражении за скобки общий множитель 4
D = b2 − 4ac = (2k)2 − 4ac = 4k2 − 4ac = 4(k2 − ac)
Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k2 − ac.
В выражении 4(k2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k2 − ac. Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.
То есть выражение k2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D1
D1 = k2 − ac
Теперь посмотрим как выводятся формулы 

В нашем уравнении ax2 + bx + c = 0 коэффициент b заменён на выражение 2k. Воспользуемся стандартными формулами для вычисления корней. То есть формулами 

Но ранее было сказано, что выражение k2 − ac обозначается через D1. Тогда в наших преобразованиях следует сделать и эту замену:
Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:
Теперь в получившемся выражении вынесем за скобки общий множитель 2
Сократим получившуюся дробь на 2
Аналогично вывóдится формула для вычисления второго корня:
Задания для самостоятельного решения
Задание 1. Решить уравнение:
Решение:
Ответ: 1; 0,6
Задание 2. Решить уравнение:
Решение:
Ответ:
Задание 3. Решить уравнение:
Решение:
Ответ: 1; −1,4
Задание 4. Решить уравнение:
Решение:
Ответ:
Задание 5. Решить уравнение:
Решение:
Ответ:
Задание 6. Решить уравнение:
Решение:
Ответ:
Задание 7. Решить уравнение:
Решение:
Ответ:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

05
Фев 2014
Категория: Справочные материалы
Об отдельных случаях вычисления дискриминанта
2014-02-05
2021-06-25
Сложно встретить старшеклассника, НЕ умеющего находить корни квадратного уравнения через дискриминант.
Но, к сожалению, в отдельных случаях, получая громоздкий дискриминант, многие начинают паниковать (без калькулятора).
А на ЕГЭ по математике, например, в задачах №11, вам вполне может встретиться причудливый дискриминант.
Нет безвыходных ситуаций!
На чем можно сэкономить силы при вычислении дискриминанта
Прежде чем разбирать примеры, вспомним все же формулу дикриминанта для вычисления корней квадратного уравнения
Тогда корни уравнения находим по формуле
Надеюсь, вы помните, что удобно искать корни уравнения через дискриминант в случае, если имеем дело с полным квадратным уравнением ( и
– ненулевые).
Как решать неполные квадратные уравнения мы уже говорили.
I. Используем формулу «разность квадратов» + показать
II. Используем прием вынесения общего множителя за скобки + показать
III. Формула сокращенного дискриимнанта + показать
IV. Вместо дискриминанта – т. Виета + показать
Автор: egeMax |
комментариев 19
Как найти дискриминант квадратного уравнения
О чем эта статья:
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, содержащее переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим:
13 = 12 — противоречие.
Значит, х = 5 не является корнем уравнения.
Если же х = 4, то при подстановке в уравнение мы получим:
12 = 12 — верное равенство.
Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.
Такое уравнение можно решить с помощью формулы дискриминанта.
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.
Как решать квадратные уравнения через дискриминант
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Определим, чему равны коэффициенты a, b, c.
Вычислим значение дискриминанта по формуле D = b2 − 4ac.
Если дискриминант D 0, то у уравнения две корня, равные
Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:
Примеры решения квадратных уравнений с помощью дискриминанта
Пример 1. Решить уравнение: 3x 2 – 4x + 2 = 0.
- Определим коэффициенты: a = 3, b = -4, c = 2.
- Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 3 * 2 = 16 – 24 = -8.
Ответ: D 2 – 6x + 9 = 0.
- Определим коэффициенты: a = 1, b = -6, c = 9.
- Найдем дискриминант: D = b 2 – 4ac = (-6) 2 – 4 * 1 * 9 = 36 – 36 = 0.
D = 0, значит уравнение имеет один корень:
Ответ: корень уравнения 3.
Пример 3. Решить уравнение: x 2 – 4x – 5 = 0.
- Определим коэффициенты: a = 1, b = -4, c = -5.
- Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 1 * (-5) = 16 + 20 = 36.
D > 0, значит уравнение имеет два корня:
Ответ: два корня x1 = 5, x2 = -1.
Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.
Об отдельных случаях вычисления дискриминанта
Сложно встретить старшеклассника, НЕ умеющего находить корни квадратного уравнения через дискриминант.
Но, к сожалению, в отдельных случаях, получая громоздкий дискриминант, многие начинают паниковать (без калькулятора).
А на ЕГЭ по математике, например, в задачах №11, вам вполне может встретиться причудливый дискриминант.
Нет безвыходных ситуаций!
На чем можно сэкономить силы при вычислении дискриминанта
Прежде чем разбирать примеры, вспомним все же формулу дикриминанта для вычисления корней квадратного уравнения
Тогда корни уравнения находим по формуле
Надеюсь, вы помните, что удобно искать корни уравнения через дискриминант в случае, если имеем дело с полным квадратным уравнением ( и – ненулевые).
I. Используем формулу «разность квадратов» + показать
Допустим, нам нужно решить уравнение
Ясно, что дискриминант следующий:
Не спешим возводить 53 в квадрат! Замечаем, что , поэтому
Корни данного уравнения, думаю, теперь каждый из вас найдет без труда…
II. Используем прием вынесения общего множителя за скобки + показать
Допустим, нам нужно решить уравнение (кстати, оно взято из реальной текстовой задачи из открытого банка заданий ЕГЭ по математике).
Ясно, что дискриминант следующий:
Нет, мы не пойдем напролом!
Замечаем, что , а .
Мы можем вынести за скобку общий множитель
Корни найти – уже не проблема…
III. Формула сокращенного дискриимнанта + показать
Допустим, нам нужно решить уравнение
Вы знаете, что такое ? [spoiler]
Его очень удобно применять в случае четности второго коэффициента (при ).
Вот формулы дискриминанта и корней в этом случае:
для уравнения , где – четное
Тогда корни следующие: , то есть или
Хоть на чуть-чуть, но упростили вычисления. Считаете, что неоправданно, – лишней формулой забивать голову… Выбор за вами.
IV. Вместо дискриминанта – т. Виета + показать
Допустим, нам нужно решить уравнение
Вспоминаем теорему Виета:
Для приведенного квадратного уравнения (т.е. такого, коэффициент при в котором равен единице) сумма корней равна коэффициенту , взятому с обратным знаком, а произведение корней равно свободному члену , то есть ,
Так вот, очевидно, на роль корней уравнения претендуют числа и , так как и
Квадратное уравнение с чётным вторым коэффициентом
Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D1 = k 2 − ac , а корни по формулам и .
Примеры
Решим квадратное уравнение x 2 + 6x − 16 = 0 . В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k .
Любое четное число n можно представить в виде произведения числа 2 и числа k , то есть 2k .
Например, число 10 можно представить как 2 × 5 .
В этом произведении k = 5 .
Число 12 можно представить как 2 × 6 .
В этом произведении k = 6 .
Число −14 можно представить как 2 × (−7)
В этом произведении k = −7 .
Как видим, сомножитель 2 не меняется. Меняется только сомножитель k .
В уравнении x 2 + 6x − 16 = 0 вторым коэффициентом является число 6 . Это число можно представить как 2 × 3 . В этом произведении k = 3 . Теперь можно воспользоваться формулами для чётного коэффициента.
Найдем дискриминант по формуле D1 = k 2 − ac
Теперь вычислим корни по формулам: и .
Значит корнями уравнения x 2 + 6x − 16 = 0 являются числа 2 и −8 .
В отличие от стандартной формулы для вычисления дискриминанта ( D=b 2 − 4ac ), в формуле D1 = k 2 − ac не нужно выполнять умножение числа 4 на ac .
И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.
Пример 2. Решить квадратное уравнение 5x 2 − 6x + 1=0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3) . То есть k = −3 . Найдём дискриминант по формуле D1 = k 2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Пример 3. Решить квадратное уравнение x 2 − 10x − 24 = 0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5) . То есть k = −5 . Найдём дискриминант по формуле D1 = k 2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Обычно для определения числа k поступают так: делят второй коэффициент на 2.
Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2 k . Чтобы из этого равенства выразить сомножитель k , нужно произведение b разделить на сомножитель 2
Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2
Пример 5. Решить квадратное уравнение
Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k . Получается, что
Найдём дискриминант по формуле D1 = k 2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.
В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .
Вычислим второй корень уравнения:
Вывод формул
Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.
Рассмотрим квадратное уравнение ax 2 + bx + c = 0 . Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k
Заменим в уравнении ax 2 + bx + c = 0 коэффициент b на выражение 2k
Теперь вычислим дискриминант по ранее известной формуле:
Вынесем в получившемся выражении за скобки общий множитель 4
Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k 2 − ac .
В выражении 4(k 2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k 2 − ac . Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.
То есть выражение k 2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D1
Теперь посмотрим как выводятся формулы и .
В нашем уравнении ax 2 + bx + c = 0 коэффициент b заменён на выражение 2k . Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k . Также на забываем, что D у нас равно выражению 4(k 2 − ac)
Но ранее было сказано, что выражение k 2 − ac обозначается через D1 . Тогда в наших преобразованиях следует сделать и эту замену:
Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:
Теперь в получившемся выражении вынесем за скобки общий множитель 2
Сократим получившуюся дробь на 2
Аналогично вывóдится формула для вычисления второго корня:
[spoiler title=”источники:”]
[/spoiler]