Загрузить PDF
Загрузить PDF
Соотношение (в математике) — это взаимосвязь между двумя или более числами одного рода. Соотношения сравнивают абсолютные величины или части целого. Соотношения вычисляются и записываются по-разному, но основные принципы одинаковы для всех соотношений.
-
1
Использование соотношений. Соотношения используются как в науке, так и в повседневной жизни для сравнения величин. Простейшие соотношения связывают только два числа, но есть соотношения, сравнивающие три или более значения. В любой ситуации, в которой присутствует более одной величины, можно записать соотношение. Связывая некоторые значения, соотношения могут, например, подсказать, как увеличить количество ингредиентов в рецепте или веществ в химической реакции.[1]
-
2
Определение соотношений. Соотношение — это взаимосвязь между двумя (или более) значениями одного рода. Например, если для приготовления торта необходимы 2 стакана муки и 1 стакан сахара, то соотношение муки к сахару равно 2 к 1.
- Соотношения могут быть использованы и в тех случаях, когда две величины не связаны друг с другом (как в примере с тортом). Например, если в классе учатся 5 девочек и 10 мальчиков, то соотношение девочек к мальчикам равно 5 к 10. Эти величины (число мальчиков и число девочек) не зависят друг от друга, то есть их значения изменятся, если кто-то уйдет из класса или в класс придет новый ученик. Соотношения просто сравнивают значения величин.
-
3
Обратите внимание на разные способы представления соотношений. Соотношения могут быть представлены словами или при помощи математических символов.[2]
- Очень часто соотношения выражены словами (как показано выше). Особенно такая форма представления соотношений применяется в повседневной жизни, далекой от науки.
- Также соотношения можно выразить через двоеточие. При сравнении двух чисел в соотношении вы будете использовать одно двоеточие (например, 7:13); при сравнении трех и более значений ставьте двоеточие между каждой парой чисел (например, 10:2:23). В нашем примере с классом вы можете выразить соотношение девочек и мальчиков так: 5 девочек : 10 мальчиков. Или так: 5:10.
- Реже соотношения выражаются при помощи наклонной черты. В примере с классом оно может быть записано так: 5/10. Тем не менее это не дробь и читается такое соотношение не как дробь; более того, запомните, что в соотношении цифры не представляют собой часть единого целого.
Реклама
-
1
Упростите соотношение. Соотношение можно упростить (аналогично дробям), разделив каждый член (число) соотношения на наибольший общий делитель. Однако при этом не упустите из виду исходных значений соотношения.[3]
- В нашем примере в классе 5 девочек и 10 мальчиков; соотношение равно 5:10. Наибольший общий делитель членов соотношения равен 5 (так как и 5, и 10 делятся на 5). Разделите каждое число соотношения на 5 и получите соотношение 1 девочка к 2 мальчикам (или 1:2). Однако при упрощении соотношения помните об исходных значениях. В нашем примере в классе не 3 ученика, а 15. Упрощенное соотношение сравнивает количество мальчиков и количество девочек. То есть на каждую девочку приходится 2 мальчика, но в классе не 2 мальчика и 1 девочка.
- Некоторые соотношения не упрощаются. Например, соотношение 3:56 не упрощается, так как у этих чисел нет общих делителей (3 — простое число, а 56 не делится на 3).
-
2
Используйте умножение или деление для увеличения или уменьшения соотношения. Распространены задачи, в которых необходимо увеличить или уменьшить два значения, пропорциональных друг другу. Если вам дано соотношение и нужно найти соответствующее ему большее или меньшее соотношение, умножьте или разделите исходное соотношение на некоторое данное число.[4]
- Например, пекарю нужно утроить количество ингредиентов, данных в рецепте. Если по рецепту соотношение муки к сахару составляет 2 к 1 (2:1), то пекарь умножит каждый член соотношения на 3 и получит соотношение 6:3 (6 чашек муки к 3 чашкам сахара).
- С другой стороны, если пекарю необходимо уполовинить количество ингредиентов, данных в рецепте, то пекарь разделит каждый член соотношения на 2 и получит соотношение 1:½ (1 чашка муки к 1/2 чашке сахара).
-
3
Поиск неизвестного значения, когда даны два эквивалентных соотношения. Это задача, в которой необходимо найти неизвестную переменную в одном соотношении при помощи второго соотношения, которое эквивалентно первому. Для решения таких задач пользуйтесь умножением крест-накрест. Запишите каждое соотношение в виде обыкновенной дроби, поставьте между ними знак равенства и перемножьте их члены крест-накрест.[5]
- Например, дана группа учеников, в которой 2 мальчика и 5 девочек. Каково будет число мальчиков, если число девочек увеличить до 20 (пропорция сохраняется)? Во-первых, запишите два соотношения — 2 мальчика:5 девочек и х мальчиков:20 девочек. Теперь запишите эти соотношения в виде дробей: 2/5 и х/20. Перемножьте члены дробей крест-накрест и получите 5x = 40; следовательно, х = 40/5 = 8.
Реклама
-
1
Избегайте сложения и вычитания в текстовых задачах на соотношение. Многие текстовые задачи выглядят примерно так: «В рецепте необходимо использовать 4 клубня картофеля и 5 корнеплодов моркови. Если вы хотите добавить 8 клубней картофеля, то сколько понадобится моркови, чтобы соотношение осталось неизменным?» При решении подобных задач ученики часто допускают ошибку, прибавляя одинаковое количество ингредиентов к исходному числу. Однако, чтобы сохранить соотношение, нужно использовать умножение. Вот примеры правильного и неправильного решения:
- Неверно: «8 – 4 = 4 — так мы добавили 4 клубня картофеля. Значит, нужно взять 5 корнеплодов моркови и к ним добавить еще 4… Стоп! Соотношения так не вычисляют. Стоит попробовать снова».
- Верно: «8 ÷ 4 = 2 — значит, мы умножили количество картофеля на 2. Соответственно, 5 корнеплодов моркови тоже нужно умножить на 2. 5 x 2 = 10 — в рецепт нужно добавить 10 корнеплодов моркови».
-
2
Преобразуйте члены в те же единицы измерения. Некоторые текстовые задачи специально усложняют, добавляя разные единицы измерения. Преобразуйте их, прежде чем вычислять соотношение. Вот пример задачи и решения:
- У дракона есть 500 грамм золота и 10 килограмм серебра. Каково соотношение золота к серебру в сокровищнице дракона?
- Граммы и килограммы — разные единицы измерения, их нужно преобразовать. 1 килограмм = 1000 грамм, соответственно, 10 килограмм = 10 килограмм x 1000 грамм/1 килограмм = 10 x 1000 грамм = 10 000 грамм.
- У дракона в сокровищнице 500 грамм золота и 10 000 грамм серебра.
- Соотношение золота к серебру равно: 500 грамм золота/10 000 грамм серебра = 5/100 = 1/20.
-
3
Записывайте единицы измерения после каждой величины. В текстовых задачах гораздо проще распознать ошибку, если записывать единицы измерения после каждого значения. Помните, что величины с одними и теми же единицами измерения в числителе и знаменателе сокращаются. Сократив выражение, вы получите верный ответ.
- Пример: дано 6 коробок, в каждой третьей коробке находится 9 шариков. Сколько всего шариков?
- Неверно: 6 коробок x 3 коробки/9 шариков = … Стоп, ничего нельзя сократить. Ответ будет таким: «коробки x коробки / шарики». Он не имеет смысла.
- Верно: 6 коробок x 9 шариков/3 коробки = 6 коробок * 3 шарика/1 коробку = 6 коробок * 3 шарика/1 коробку = 6 * 3 шарика/1 = 18 шариков.
Реклама
Источники
Об этой статье
Эту страницу просматривали 225 265 раз.
Была ли эта статья полезной?
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Отношение чисел
Поддержать сайт
Прежде чем обсуждать пропорции необходимо разобраться, что такое отношение двух чисел.
Если вам знакомо понятие отношение чисел, можете смело переходить к теме
пропорции.
Что называют отношением двух чисел
Запомните!
Отношение двух чисел — это их частное.
Отношение двух чисел показывает:
- во сколько раз одно число больше другого;
- какую часть одно число составляет от другого.
Покажем на примере, где используется понятие отношение двух чисел.
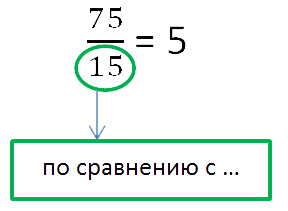
В городе Липецк проводятся соревнования на велосипедах. В прошлом году участников было 15.
В этом году — 75. Во сколько раз увеличилось количество участников в этом году по
сравнению с предыдущим годом?
Прежде чем решать задачу, подчёркиваем важные данные.
Запишем отношение количества участников в этом году к количеству участников в предыдущем.
Запомните!
При записи отношения двух чисел в знаменатель дроби (вниз) записывается
то число, с которым сравнивают.
Обычно это число идёт после слов «по сравнению с …» или
предлога «к …».
Запомните!
Если умножить или разделить оба члена отношения на одно и то же число, неравное нулю, то получится отношение, равное данному.
При внимательном изучении правила выше, можно подметить, что правило записанное выше,
есть нечто иное как основное свойство дроби, по которому мы их легко сокращаем.
Отношение 16 к 10:
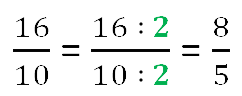
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
25 апреля 2023 в 20:44
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
Максим Тагиров
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
У этого термина существуют и другие значения, см. Отношение.
Соотноше́ние, в математике (отношение[1], пропорция) — это количественная характеристика взаимосвязи между двумя однородными числовыми величинами[2].
Обычно выражается как «a к b» или 
Иногда представляется арифметически как результат (не обязательно целочисленный) деления двух числовых значений[3], непосредственно отображающий, сколько раз первое число содержит второе[4]. Проще говоря, соотношение показывает, для какого количества чего-то одного сколько есть чего-то другого. Например, предположим, что у кого-то есть 8 апельсинов и 6 лимонов в вазе для фруктов, соотношение апельсинов и лимонов составит 8:6 (или, что то же самое, 4:3), а соотношение лимонов и апельсинов составит 3:4. Кроме того, количество апельсинов относительно общего количества фруктов составит 4:7 (что эквивалентно 8:14). Соотношение 4:7 можно преобразовать в дробь 4/7, показывающую, какую долю от общего числа фруктов составляют апельсины.
Обозначения и термины[править | править код]
Соотношение чисел A и B можно представить как:[3]
- отношение A к B;
- пропорцию A : B;
причём, как правило, соотношения записывают как отношения целых чисел, и в этом случае соотношение чисел A и B также представляет собой долю числа A, являющуюся рациональным числом.
Числа A и B в данном контексте иногда называют членами (terms), где A — антецедент, а B — консеквент.
Пропорция, выражающая равенство соотношений A : B и C : D, записывается как A : B = C : D или A : B ∷ C : D. Читается:
- A относится к B как C относится к D.
И в данном случае A, B, C, D называются членами пропорции. A и D — крайние члены пропорции, а B и C — средние члены.
Иногда в соотношениях могут записывать три и более членов. Например, размеры предмета с сечением два к четырём и длиной десять сантиметров составят 2 : 4 : 10. Равенство трёх и более соотношений называется непрерывной пропорцией (англ. continued proportion — ряд отношений).[3]
История и этимология[править | править код]
Невозможно проследить истоки концепции соотношения, поскольку идеи, из которых она развилась, должны были быть известны дописьменным культурам. Например, идея того, что одна деревня вдвое больше другой, настолько базовая, что была бы понятна даже в доисторическом обществе.[5]
Для обозначения отношения греки использовали термин др.-греч. λόγος, которое латиняне передавали как ratio («разумное основание»; как в слове «рациональный») или как proportio. (Рациональное число можно представить как результат отношения двух целых чисел.) Более современная интерпретация античного значения ближе к «вычисление» или «расчёт».[4] Боэций («Основы арифметики», «Основы музыки», начало VI в.) использовал слово proportio (наряду с ratio, comparatio и habitudo) для обозначения отношения и proportionalitas (перевод др.-греч. ἀναλογία) для обозначения пропорции (отношения отношений)[6]. Такое терминоупотребление (в связи с широчайшей распространённостью «Арифметики» и «Музыки» Боэция) практиковалось и в Средние века.
Евклид объединил в «Началах» результаты из более ранних источников. Пифагорейцы развили теорию соотношения и пропорции в приложении к числам[7]. Пифагорейская концепция числа включала только рациональные числа, что вызвало сомнения в применимости теории в геометрии, где, как также обнаружили пифагорейцы, существуют несоизмеримые размеры, соответствующие иррациональным числам. Открытие теории отношений, не предполагавшей соизмеримость, вероятно, принадлежит Евдоксу Книдскому. В Книге VII «Начал» приведена и более ранняя теория отношений соизмеримых величин[8].
Существование нескольких теорий выглядит ненужным усложнением для современного взгляда, поскольку соотношения, во многом, определяются результатом деления. Однако, это довольно недавнее открытие, что можно увидеть на примере того, что современные учебники по геометрии до сих пор используют различную терминологию для соотношений (ratio) и результатов деления (quotient, частное). Причин для этого две. Во-первых, существовало вышеупомянутое нежелание признавать иррациональные числа как истинные числа. Во-вторых, нехватка широко используемых символов (обозначений) для замены уже устоявшейся терминологии соотношений задержало полное принятие дробей как альтернативы вплоть до XVI века.[9]
Определения Евклида[править | править код]
В книге V «Начал» Евклида 18 определений, касающихся соотношений[10]. Кроме того, Евклид использует идеи, которые были в настолько широком употреблении, что он не даёт им определений. Первые два определения гласят, что часть количества есть другое количество, которое «измеряет» его, и наоборот, кратное для количества есть другое количество, измеряемое им. В современных терминах, это означает, что кратное для количества есть это количество, умноженное на целое число, большее единицы, а часть количества (то есть делитель) при умножении на число, большее единицы, даёт то количество.
Эвклид не даёт определения слова «измерять». Тем не менее, можно предположить, что, если количество принимается за единицу измерения, а другое количество представлено как общее количество таких единиц измерения, то первое количество измеряет второе. Заметим, эти определения повторяются почти слово в слово как определения 3 и 5 в книге VII.
Определение 3 разъясняет, что такое соотношение в общем смысле. Оно не является математически строгим и некоторые исследователи приписывают его редакторам, а не самому Евклиду.[11] Евклид определяет соотношение между двумя количествами одного вида, например двух отрезков или двух площадей, но не соотношение длины к площади. Определение 4 указывает это ещё более строго. Оно утверждает, что соотношение между двумя количествами существует, если есть кратное для каждого, превышающее другое. В современных терминах: соотношение между количествами p и q существует, если существуют целые числа m и n такие, что mp>q и nq>p. Это условие известно как аксиома Архимеда.
Определение 5 наиболее сложное и трудное для понимания. Оно объясняет, что означает равенство для двух соотношений. Сегодня можно просто заявить, что соотношения равны, если равны результаты деления членов, но Евклид не признавал существование результатов деления для несоизмеримых величин, поэтому для него такое определение было бы бессмысленным. Поэтому требовалось более тонкое определение для случая количеств, не измеряющих друг друга напрямую. Хотя может быть невозможно присвоить соотношению рациональное значение, но вполне возможно сравнить соотношение с рациональным числом. А именно, для двух количеств p и q, а также рационального числа m/n, мы можем сказать, что соотношение p к q меньше, равно или больше m/n, когда np меньше, равно или больше mq, соответственно. Евклидово определение равенства можно сформулировать так: два соотношения равны, когда они одинаково себя ведут, будучи одновременно меньше, равны или больше любого рационального числа. В современной нотации это выглядит так: для данных количеств p, q, r и s выполняется p:q::r:s, если для любых положительных целых чисел m и n выполняется отношение np<mq, np=mq, np>mq в соответствии с nr<ms, nr=ms, nr>ms. Есть примечательное сходство между этим определением и теорией Дедекиндова сечения, используемого в современной теории иррациональных чисел[12].
Определение 6 гласит, что количества с одинаковым соотношением пропорциональны или состоят в пропорции. Евклид использует греческое слово ἀναλόγον (analogon), с тем же корнем, что и λόγος, от которого произошло слово «аналог».
Определение 7 объясняет, что значит для соотношения быть меньше или больше другого, и основывается на идеях из определения 5. В современной нотации: для данных количеств p, q, r и s выполняется p:q>r:s, если существуют положительные целые числа m и n такие, что np>mq и nr≤ms.
Как и в случае с определением 3, определение 8 некоторыми исследователями рассматривается как позднее включение редакторов. Оно гласит, что три члена p, q и r находятся в пропорции, если p:q::q:r. Это расширяется на 4 члена p, q, r и s как p:q::q:r::r:s и т. д. Последовательности, обладающие таким свойством, что соотношения последовательных членов равны, называются геометрическими прогрессиями. Определения 9 и 10 применяют это, говоря, что, если p, q и r состоят в пропорции, то p:r есть двойное отношение (duplicate ratio, отношение квадратов) для p:q, а если p, q, r и s находятся в пропорции, то p:s есть тройное отношение (triplicate ratio, отношение кубов) для p:q. Если p, q и r находятся в пропорции, то q называется средним пропорциональным (или геометрическим средним) для p и r. Подобным образом, если p, q, r и s находятся в пропорции, то q и r называют средними пропорциональными для p и s.
Процентное соотношение[править | править код]
Если умножить все количества в соотношении на одно и то же число, то соотношение не изменится. Например, соотношение 3:2 есть то же самое, что 12:8. Обычно члены пропорции уменьшают до наименьшего общего знаменателя либо выражают их в долях ста (процент). Иногда для удобства сравнения соотношения представляют в виде n:1 или 1:n.
Если смесь содержит вещества A, B, C и D в соотношении 5:9:4:2, то в ней 5 частей A приходится на каждые 9 частей B, 4 части C и 2 части D. Поскольку 5+9+4+2=20, то всего смесь содержит 5/20 A (5 частей из 20), 9/20 B, 4/20 C и 2/20 D. Если эти числа, деленные на общую сумму, умножить на 100, то получаем проценты: 25 % A, 45 % B, 20 % C и 10 % D (эквивалентно написанию соотношения в виде 25:45:20:10).
Пропорции[править | править код]
Если в какой-то ситуации рассматриваются две или более величины, состоящие в пропорциональном соотношении — допустим, если в корзине находятся два яблока и три апельсина и только они — то можно сказать, что «целое» содержит пять частей, состоящих из двух частей яблок и трёх частей апельсинов. В данном случае 
, или 40 % целого, — это яблоки, а 
, или 60 % целого, — это апельсины. Такое сравнение определённого количества с «целым» иногда называют пропорцией. Пропорции иногда выражают в процентах, как указано выше.
Другие применения[править | править код]
- Соотношения часто используются для простых растворов в химии и биологии (степень разбавления).
- Шансы выигрыша в играх выражают в виде соотношения.
- Соотношения также могут рассматривать между величинами, измеряемыми в разных единицах измерения.
См. также[править | править код]
- Двойное отношение,
- Дробь (математика)
- Интервал (музыка)
- Отношение
- Отношение цена/производительность
- Пропорциональность
Примечания[править | править код]
- ↑ Отношение, в математике // Новый энциклопедический словарь: В 48 томах (вышло 29 томов). — СПб., Пг., 1911—1916.
- ↑ Wentworth, p. 55
- ↑ 1 2 3 New International Encyclopedia
- ↑ 1 2 Penny Cyclopedia, p. 307
- ↑ Smith, p. 477
- ↑ А. М. С. Боэций. Основы музыки / Подготовка текста, перевод с латинского и комментарий С. Н. Лебедева. М.: Научно-издательский центр «Московская консерватория», 2012, pp. xxxiv-xxxv, 276.
- ↑ Heath, 1908, p. 112.
- ↑ Heath, 1908, p. 113.
- ↑ Smith, p. 480
- ↑ Heath, 1908, reference for section.
- ↑ «Geometry, Euclidean» Encyclopædia Britannica Eleventh Edition p682.
- ↑ Heath, 1908, p. 125.
Литература[править | править код]
- Отношение // Большая Советская энциклопедия (в 30 т.) / А. М. Прохоров (гл. ред.). — 3-е изд. — М.: Сов. энциклопедия, 1974. — Т. XVIII. — С. 629. — 632 с.
- Отношение, в математике // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- «Ratio» The Penny Cyclopædia vol. 19, The Society for the Diffusion of Useful Knowledge (1841) Charles Knight and Co., London pp. 307ff
- «Proportion» New International Encyclopedia, Vol. 19 2nd ed. (1916) Dodd Mead & Co. pp270-271
- «Ratio and Proportion» Fundamentals of practical mathematics, George Wentworth, David Eugene Smith, Herbert Druery Harper (1922) Ginn and Co. pp. 55ff
- The thirteen books of Euclid’s Elements, vol 2 / trans. Sir Thomas Little Heath. — Cambridge Univ. Press, 1908. — P. 112ff.
- D.E. Smith, History of Mathematics, vol 2 Dover (1958) pp. 477ff
Соотношение 1: упростить
:
Соотношение 2: сравнить
:
Результат упрощения
Результат сравнения
Вы можете использовать этот инструмент для получения наиболее упрощенного соотношения или для сравнения двух одинаковых соотношений.
Соотношение
Соотношение в математике — это термин, который используется для сравнения двух или более чисел. Он используется, чтобы указать, насколько велика или мала величина по сравнению с другой. В отношении две величины сравниваются с помощью деления. Здесь делимое называется «антецедентом», а делитель — «консеквентом». Например, в группе из 30 человек 17 из них предпочитают ходить по утрам, а 13 — ездить на велосипеде. Чтобы представить эту информацию в виде соотношения, запишем его как 17:13. Здесь символ ‘:’ читается как «есть к». Таким образом, отношение людей, предпочитающих ходить пешком, к людям, предпочитающим езду на велосипеде, читается как «17 к 13».
Что такое соотношение?
Соотношение определяется как сравнение двух величин в одних и тех же единицах измерения, которое показывает, сколько одного количества присутствует в другом количестве. Коэффициенты можно разделить на два типа. Одно из них — соотношение части к части, а другое — соотношение части к целому. Соотношение частей к частям показывает, как связаны две различные сущности или группы. Например, соотношение мальчиков и девочек в классе составляет 12: 15, тогда как соотношение частей к целому обозначает соотношение между определенной группой и целым. Например, из каждых 10 человек 5 любят читать книги. Таким образом, соотношение части к целому составляет 5: 10, что означает, что каждые 5 человек из 10 любят читать книги.
Формула соотношения
Мы используем формулу соотношения при сравнении соотношения между двумя числами или величинами. Общая форма представления соотношения между двумя величинами, скажем, «a» и «b», — это a: b, которое читается как «a равно b».
Форма дроби, представляющая это соотношение, — a/b. Чтобы еще больше упростить соотношение, мы следуем той же процедуре, которую используем для упрощения дроби. a:b = a/b. Давайте разберемся в этом на примере.
Пример. В классе из 50 учеников 23 девочки, а остальные мальчики. Найдите соотношение количества мальчиков к количеству девочек.
Общее количество студентов = 50; Количество девушек = 23.
Общее количество мальчиков = Общее количество учеников — Общее количество девочек
= 50 — 23
= 27
Таким образом, желаемое соотношение (Количество мальчиков: Количество девочек) равно 27:23.
Расчет коэффициентов
Для того чтобы рассчитать соотношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления пышных блинов необходимо 15 стаканов муки и 20 стаканов сахара, давайте рассчитаем соотношение муки и сахара, используемых в рецепте.
- Шаг 1: Найдите величины обоих сценариев, для которых мы определяем соотношение. В данном случае это 15 и 20.
- Шаг 2: Запишите его в форме дроби a /b. Итак, мы записываем это как 15/20.
- Шаг 3: По возможности еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 15/20 может быть упрощено до 3/4.
- Шаг 4: Поэтому соотношение муки к сахару можно выразить как 3:4.
Используйте бесплатный онлайн-калькулятор коэффициентов, чтобы проверить свои ответы при расчете коэффициентов.
Как упростить соотношения?
Соотношение выражает, сколько требуется одного количества по сравнению с другим количеством. Два термина в соотношении могут быть упрощены и выражены в их низшей форме. Соотношения, выраженные в их наименьших выражениях, легко понять и могут быть упрощены так же, как мы упрощаем дроби. Чтобы упростить соотношение, мы используем следующие шаги. Давайте разберемся в этом на примере. Например, давайте упростим соотношение 18:10.
- Шаг 1: Запишите заданное соотношение a:b в виде дроби a/b. Записав соотношение в виде дроби, мы получим 18/10.
- Шаг 2: Найдите наибольший общий коэффициент ‘a’ и ‘b’. В этом случае GCF из 10 и 18 равен 2.
- Шаг 3: Разделите числитель и знаменатель дроби на GCF, чтобы получить упрощенную дробь. Здесь, разделив числитель и знаменатель на 2, мы получаем, (18÷2)/(10÷2) = 9/5.
- Шаг 4: Представьте эту дробь в форме соотношения, чтобы получить результат. Таким образом, упрощенное соотношение составляет 9:5.
Используйте бесплатный онлайн-калькулятор коэффициентов упрощения, чтобы проверить свои ответы.
Советы и рекомендации по соотношению:
- В случае, если оба числа «a» и «b» равны в соотношении a: b, то a: b = 1.
- Если a > b в соотношении a : b, то a : b > 1.
- Если a < b в соотношении a : b, то a : b < 1.
- Перед их сравнением необходимо убедиться в том, что единицы измерения двух величин одинаковы.
Эквивалентные Соотношения
Эквивалентные соотношения аналогичны эквивалентным дробям. Если предшествующий (первый член) и последующий (второй член) данного соотношения умножаются или делятся на одно и то же число, отличное от нуля, это дает эквивалентное соотношение. Например, когда антецедент и следствие соотношения 1:3 умножаются на 3, мы получаем, (1 × 3) : (3 × 3) или 3: 9. Здесь 1:3 и 3:9 являются эквивалентными соотношениями. Аналогично, когда оба члена соотношения 20:10 делятся на 10, это дает 2:1. Здесь 20:10 и 2:1 являются эквивалентными соотношениями. Бесконечное число эквивалентных соотношений любого заданного соотношения может быть найдено путем умножения предшествующего и последующего на положительное целое число.
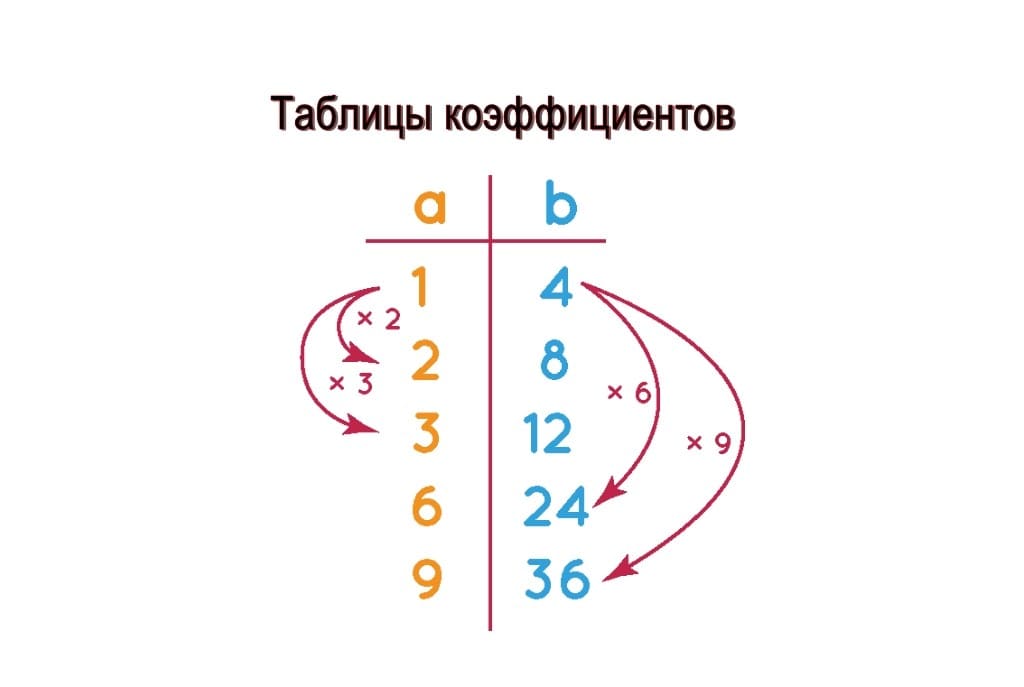
Таблица коэффициентов
Таблица коэффициентов — это список, содержащий эквивалентные коэффициенты любого заданного соотношения в структурированном виде. В следующей таблице соотношений приведено соотношение между соотношением 1:4 и четырьмя его эквивалентными соотношениями. Эквивалентные соотношения связаны друг с другом умножением числа. Эквивалентные соотношения получаются путем умножения или деления двух членов соотношения на одно и то же число. В примере, показанном на рисунке, давайте возьмем соотношение 1:4 и найдем четыре эквивалентных соотношения, умножив оба члена соотношения на 2, 3, 6 и 9. В результате мы получаем 2:8, 3:12, 6:24, и 9:36.
Используйте бесплатный онлайн-калькулятор эквивалентных коэффициентов, чтобы проверить свои ответы.
Примеры соотношения
-
Пример 1. В школьном зале 49 мальчиков и 28 девочек. Выразите соотношение числа мальчиков к числу девочек.
Решение:
Учитывая, что количество мальчиков = 49, а количество девочек = 28. GCF 49 и 28 равен 7. Теперь, для упрощения, разделите два термина на их GCF, который равен 7. Это означает, (49 ÷ 7)/(28 ÷ 7) = 7/4. Следовательно, соотношение числа мальчиков к числу девочек = 7:4.
-
Пример 2: В музыкальном классе 30 учеников. 10 из них были взрослыми, а остальные — детьми. Каково соотношение числа детей к общему числу учащихся в музыкальном классе?
Решение:
Учитывая, что общее количество учащихся в музыкальном классе = 30, а общее количество взрослых = 10. Следовательно, количество детей, посещавших музыкальный класс = 30 -10, что равно 20. Отношение общего числа детей к общему числу учащихся в музыкальном классе = 20: 30, что в упрощенном виде дает 2:3.
-
Пример 3: Упростите заданное соотношение, 87:75.
Решение:
Чтобы упростить данное соотношение, мы сначала найдем GCF 87 и 75, что равно 3. Затем мы разделим каждый член на 3. Это означает, (87 ÷ 3)/(75 ÷ 3) = 29/25. Таким образом, соотношение 87:75 в простейшей форме равно 29:25.
Как ваш ребенок может овладеть математическими понятиями?
Математическое мастерство приходит с практикой и пониманием того, «Почему» стоит за «Что». Почувствуйте разницу в математике.
FAQ по соотношению
Что такое соотношение в математике?
Соотношение может быть определено как соотношение или сравнение между двумя числами одной и той же единицы измерения, чтобы проверить, насколько одно число больше другого. Например, если количество баллов, набранных в тесте, равно 7 из 10, то отношение полученных баллов к общему количеству баллов записывается как 7:10.
Каковы способы написания соотношения?
Соотношение может быть записано путем разделения двух величин с помощью двоеточия (:) или оно может быть записано в дробной форме. Например, если есть 4 яблока и 8 дынь, то соотношение яблок и дынь можно записать как 4: 8 или 4/8, что может быть дополнительно упрощено как 1: 2.
Как рассчитать Соотношение между двумя числами?
Для того чтобы рассчитать соотношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления крема для глазури необходимо 14 чашек сливочного масла и 28 чашек сахара, каково соотношение масла и сахара?
- Шаг 1: Обратите внимание на количество обоих ингредиентов, для которых мы определяем соотношение. В данном случае это 14 и 28.
- Шаг 2: Запишите его в форме дроби a /b. Итак, мы записываем это как 14/28.
- Шаг 3: По возможности еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 14/28 может быть упрощено до 1/2.
- Шаг 4: Поэтому соотношение сливочного масла к сахару можно выразить как 1:2.
Как найти эквивалентные соотношения?
Два коэффициента считаются эквивалентными, если при упрощении они представляют одно и то же значение. Эта концепция аналогична эквивалентным дробям. Например, когда соотношение 1: 4 умножается на 2, это означает умножение обоих членов в соотношении на 2. Таким образом, мы получаем, (1 × 2)/ (4 × 2) = 2/8 или 2: 8. Здесь 1:4 и 2:8 являются эквивалентными соотношениями. Аналогично, соотношение 30: 10 при делении на 10 дает соотношение 3:1. Здесь 30:10 и 3:1 являются эквивалентными соотношениями. Таким образом, эквивалентные соотношения можно найти с помощью операции умножения или деления в зависимости от чисел.
Что такое Таблица коэффициентов?
Таблица коэффициентов показывает список эквивалентных коэффициентов, которые получаются либо путем умножения, либо деления обеих величин на одно и то же значение. Например, если таблица коэффициентов начинается с соотношения 1 : 3, то последующие строки будут иметь 2:6, 3:9, 4:12, и так далее. Когда эти соотношения упрощены, они представляют одно и то же значение, то есть 1:3.
Что такое Золотое сечение?
Золотое сечение — это отдельное число, значение которого приблизительно равно 1,618. Символом для этого является греческая буква «phi», представленная как ϕ. Это особый атрибут, который используется в искусстве, геометрии и архитектуре, потому что считается, что золотое сечение создает наиболее приятную и красивую форму.Это также известно как божественная пропорция, которая существует между двумя величинами, и соотношение для расчета золотого сечения представлено как ϕ = a /b = (a + b)/a = 1,61803398875… где a и b — размеры двух величин, а a — большее между ними.
Почему важны Коэффициенты?
Соотношения важны, потому что они позволяют нам выражать величины таким образом, чтобы их было легче интерпретировать. Это инструмент, который используется для сравнения размеров двух или более величин по отношению друг к другу. Например, если в классе 30 девочек и 20 мальчиков. Мы можем представить количество девочек к числу мальчиков с помощью соотношения, которое в данном случае равно 3: 2.
Какова формула соотношения?
Формула соотношения используется для сравнения соотношения между двумя числами или величинами. Общая форма представления соотношения между двумя величинами, скажем, «a» и «b», — это a: b, которое читается как «a равно b».
Что такое Соотношение и Пропорция?
Соотношение — это соотношение или сравнение между двумя величинами одной и той же единицы измерения, чтобы проверить, насколько одно число больше другого. Он записывается как a/b или a: b, где b не равно нулю. Пропорция — это равенство двух соотношений. Пропорции используются для записи эквивалентных соотношений, которые помогают решить неизвестные величины. Например, пропорция выражается следующим образом: a: b = c: d
Как сравнить коэффициенты?
Существуют различные методы сравнения коэффициентов. Например, давайте сравним 1: 2 и 2: 3 с помощью метода LCM.
- Шаг 1: Запишите соотношения в виде дроби. Здесь это означает 1/2 и 2/3.
- Шаг 2: Уменьшите фракции по отдельности. Здесь обе фракции 1/2 и 2/3 уже находятся в их уменьшенной форме.
- Шаг 3: Теперь сравните 1/2 и 2/3, найдя LCM (наименьшее общее кратное) знаменателей. LCM 2 и 3 равно 6.
- Шаг 4: Сделайте знаменатели равными, умножив числитель и знаменатель первой дроби на 3, то есть, (1 × 3)/(2 × 3) = 3/6. Затем умножьте числитель и знаменатель второй дроби на 2, то есть, (2 × 2)/(3 × 2) = 4/6.
- Шаг 5: Теперь 3/6 и 4/6 можно легко сравнить. Это показывает, что 4/6 больше, чем 3/6. Следовательно, 2:3 > 1:2.
Как преобразовать соотношения в дроби?
Соотношения могут быть записаны в виде дробей очень простым способом. Предшествующее записывается как числитель, а последующее записывается как знаменатель. Например, если мы возьмем соотношение 3: 5. Здесь 3 — это предшествующее, а 5 — последующее. Итак, мы можем записать это как 3/5.
Как преобразовать дроби в соотношения?
Дроби могут быть записаны в виде соотношений после упрощения. Это означает, что мы сначала уменьшаем данную дробь до ее наименьших членов, а затем записываем числитель в качестве предшествующего, а знаменатель — в качестве последующего. Например, доля 16/48 сначала будет уменьшена до 1/3, а затем она может быть выражена в виде соотношения 1:3.
Как перевести коэффициенты в десятичные дроби?
Соотношения можно легко преобразовать в десятичные дроби, записав соотношение в виде дроби, а затем дробь преобразуется в десятичную дробь путем деления числителя на знаменатель. Например, 3:7 может быть записано как 3/7. Теперь 3/7 = 0,428.
Как преобразовать коэффициенты в проценты?
Коэффициенты можно преобразовать в проценты, выполнив следующие действия. Например, давайте преобразуем 5: 6 в виде процента.
- Шаг 1: Запишите соотношение в виде дроби. Здесь 5: 6 может быть записано как 5/6.
- Шаг 2: Умножьте эту дробь на 100 и добавьте символ процента. В этом случае 5/6 × 100 = 83,33%.
Соотношением называют некоторую взаимосвязь между сущностями нашего мира. Это могут быть числа, физические величины, предметы, продукты, явления, действия и даже люди.
В повседневной жизни, когда речь заходит о соотношениях, мы говорим «соотношения того-то и того-то». Например, если в вазе лежит 4 яблока и 2 груши, то мы говорим «соотношения яблок и груш» или если поменять местами яблоки и груши, то «соотношения груш и яблок».
В математике соотношение чаще употребляется как «отношение того-то к тому-то». Например, соотношение четырёх яблок и двух груш, которые мы рассматривали выше, в математике будет читаться как «отношение четырех яблок к двум грушам» или если поменять местами яблоки и груши, то «отношение двух груш к четырем яблокам».
Соотношение выражается, как a к b (где вместо a и b любые числа), но также можно встретить запись, которая составлена с помощью двоеточия как a : b. Прочитать эту запись можно различными способами:
- a к b
- a относится к b
- отношение a к b
Запишем соотношение четырех яблок и двух груш с помощью символа соотношения:
4 : 2
Это соотношение можно прочитать как «четыре к двум» либо «соотношение четырех яблок и двух груш» либо «четыре яблока относится к двум грушам»
Если же поменяем местами яблоки и груши, то будем иметь соотношение 2 : 4. Это соотношение можно прочитать как «два к четырем» либо «две груши к четырем яблокам» либо «две груши относятся к четырем яблокам».
В дальнейшем соотношение мы будем называть просто отношением.
Что такое отношение?
Отношение, как было сказано ранее, записывается в виде a : b. Также его можно записать в виде дроби 
. А мы знаем, что такая запись в математике означает деление. Тогда результатом выполнения отношения будет частное чисел a и b.
Отношением в математике называют частное двух чисел.
Отношение позволяет узнать сколько количества одной сущности приходится на единицу другой. Вернемся к отношению четырех яблок к двум грушам (4 : 2). Это отношение позволит нам узнать, сколько яблок приходится на единицу груши. Под единицей подразумевается одна груша. Сначала запишем отношение 4 : 2 в виде дроби:
Данное отношение представляет собой деление числа 4 на число 2. Если выполнить это деление, мы получим ответ на вопрос сколько яблок приходится на единицу груши
Получили 2. Значит четыре яблока и две груши (4 : 2) соотносятся (взаимосвязаны друг с другом) так, что на одну грушу приходится два яблока
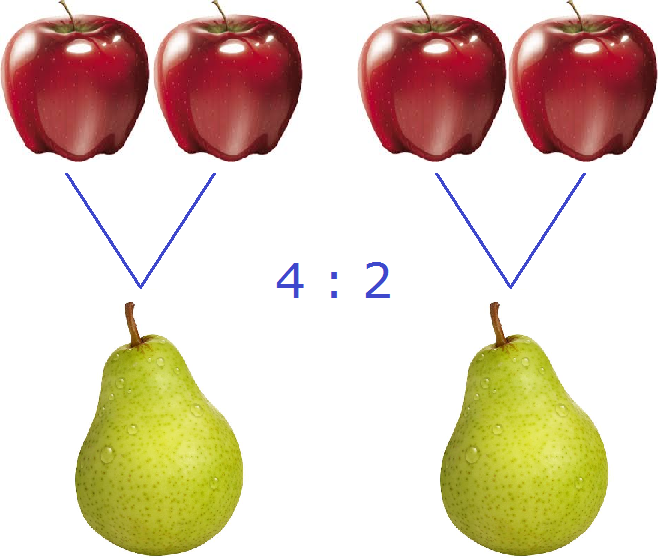
На рисунке показано, как четыре яблока и две груши соотносятся между собой. Видно, что на каждую грушу приходятся два яблока.
Отношение можно перевернуть, записав как 
. Тогда у нас получится соотношение двух груш и четырех яблок или «отношение двух груш к четырем яблокам». Это отношение покажет, сколько груш приходится на единицу яблока. Под единицей яблока подразумевается одно яблоко.
Чтобы найти значение дроби нужно вспомнить, как делить меньшее число на большее
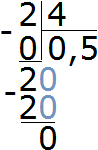
Получили 0,5. Переведём эту десятичную дробь в обыкновенную:
Сократим полученную обыкновенную дробь на 5
Получили ответ 
(половину груши). Значит две груши и четыре яблока (2 : 4) соотносятся (взаимосвязаны друг с другом) так, что на одно яблоко приходится половина груши
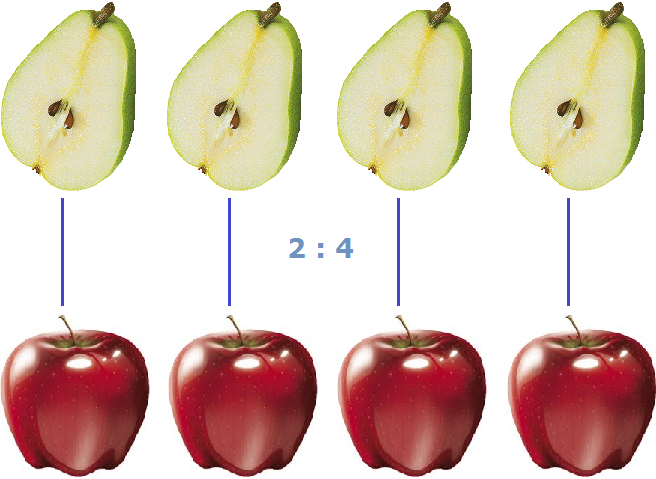
На рисунке показано, как две груши и четыре яблока соотносятся между собой. Видно, что на каждое яблоко приходится половинка груши.
Числа, из которых составлено отношение, называют членами отношения. Например, в отношении 4 : 2 членами являются числа 4 и 2.
Рассмотрим другие примеры соотношений. Для приготовления чего-либо составляется рецепт. Рецепт строят из соотношений между продуктами. Например, для приготовления овсяной каши обычно требуется стакан хлопьев на два стакана молока или воды. Получается соотношение 1 : 2 («один к двум» или «один стакан хлопьев на два стакана молока»).
Преобразуем соотношение 1 : 2 в дробь, получим . Вычислив эту дробь, получим 0,5. Значит один стакан хлопьев и два стакана молока соотносятся (взаимосвязаны друг с другом) так, что на один стакан молока приходится половина стакана хлопьев.
Если перевернуть соотношение 1 : 2 то получится соотношение 2 : 1 («два к одному» или «два стакана молока на один стакан хлопьев»). Преобразуем соотношение 2 : 1 в дробь, получим 
. Вычислив эту дробь, получим 2. Значит два стакана молока и один стакан хлопьев соотносятся (взаимосвязаны друг с другом) так, что на один стакан хлопьев приходятся два стакана молока.
Пример 2. В классе 15 школьников. Из них 5 – это мальчики, 10 – девочки. Можно записать соотношение девочек и мальчиков 10 : 5 и преобразовать это соотношение в дробь 
. Вычислив эту дробь получим 2. То есть девочки и мальчики соотносятся между собой так, что на каждого мальчика приходятся две девочки
На рисунке показано, как десять девочек и пять мальчиков соотносятся между собой. Видно, что на каждого мальчика приходятся две девочки.
Соотношение не всегда можно обращать в дробь и находить частное. В некоторых случаях это будет нелогично.
Так, если перевернуть отношение получится 
, а это уже отношение мальчиков к девочкам. Если вычислить эту дробь получается 0,5. Получается, что пять мальчиков относятся к десяти девочкам так, что на каждую девочку приходится половина мальчика. Математически это конечно верно, но с точки зрения реальности не совсем разумно, ибо мальчик это живой человек и его нельзя просто так взять и разделить, как грушу или яблоко.
Умение построить правильное отношение — важный навык при решении задач. Так в физике, отношение пройденного расстояния ко времени есть скорость движения.
Расстояние обозначается через переменную S, время — через переменную t, скорость — через переменную v. Тогда фраза «отношение пройденного пути ко времени есть скорость движения» будет описываться следующим выражением:
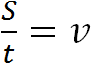
Предположим, что автомобиль проехал 100 километров за 2 часа. Тогда отношение пройденных ста километров к двум часам будет скоростью движения автомобиля:
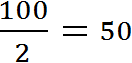
Скоростью принято называть расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. А отношение, как было сказано ранее, позволяет узнать сколько количества одной сущности приходится на единицу другой. В нашем примере отношение ста километров к двум часам показывает сколько километров приходится на один час движения. Видим, что на каждый час движения приходятся 50 километров
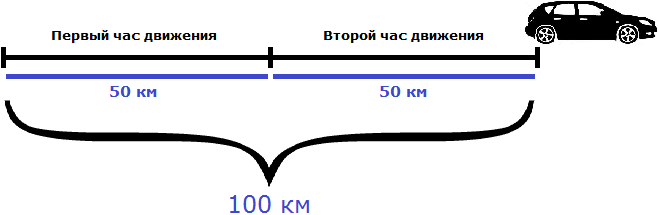
Поэтому скорость измеряется в км/ч, м/мин, м/с. Символ дроби ( / ) указывает на отношение расстояния ко времени: километров в час, метров в минуту и метров в секунду соответственно.
Пример 2. Отношение стоимости товара к его количеству есть цена одной единицы товара
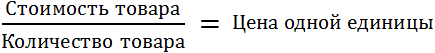
Если мы взяли в магазине 5 шоколадных батончиков и их общая стоимость составила 100 рублей, то мы можем определить цену одного батончика. Для этого нужно найти отношение ста рублей к количеству батончиков. Тогда получим, что на один батончик приходятся 20 рублей
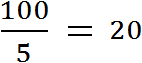
Сравнение величин
Ранее мы узнали, что отношение между величинами разной природы образуют новую величину. Так, отношение пройденного расстояния ко времени есть скорость движения. Отношение стоимости товара к его количеству есть цена одной единицы товара.
Но отношение можно использовать и для сравнения величин. Результат выполнения такого отношения есть число, показывающее во сколько раз первая величина больше второй или какую часть первая величина составляет от второй.
Чтобы узнать во сколько раз первая величина больше второй, в числитель отношения нужно записать большую величину, а в знаменатель меньшую величину.
Чтобы узнать какую часть первая величина составляет от второй, в числитель отношения нужно записать меньшую величину, а в знаменатель большую величину.
Рассмотрим числа 20 и 2. Давайте узнаем во сколько раз число 20 больше числа 2. Для этого находим отношение числа 20 к числу 2. В числителе отношения записываем число 20, а в знаменателе — число 2
Значение данного отношения равно десяти
Отношение числа 20 к числу 2 есть число 10. Это число показывает во сколько раз число 20 больше числа 2. Значит число 20 больше числа 2 в десять раз.
Пример 2. В классе 15 школьников. 5 из них это мальчики, 10 – девочки. Определить во сколько раз девочек больше мальчиков.
Записываем отношение девочек к мальчикам. В числителе отношения записываем количество девочек, в знаменатель отношения — количество мальчиков:
Значение данного отношения равно 2. Значит в классе из 15 человек девочек в два раза больше мальчиков.
Здесь уже не стоит вопрос о том, сколько девочек приходятся на одного мальчика. В данном случае отношение используется для сравнения количества девочек с количеством мальчиков.
Пример 3. Какую часть число 2 составляет от числа 20.
Находим отношение числа 2 к числу 20. В числителе отношения записываем число 2, а в знаменателе — число 20
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее
Значение отношения числа 2 к числу 20 есть число 0,1
В данном случае десятичную дробь 0,1 можно перевести в обыкновенную. Такой ответ будет проще для восприятия:
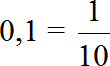
Значит число 2 от числа 20 составляет одну десятую часть.
Можно сделать проверку. Для этого найдём 
от числа 20. Если мы всё сделали правильно, то должны получить число 2
20 : 10 = 2
2 × 1 = 2
Получили число 2. Значит одна десятая часть от числа 20 есть число 2. Отсюда делаем вывод, что задача решена верно.
Пример 4. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества школьников составляют мальчики.
Записываем отношение мальчиков к общему количеству школьников. В числителе отношения записываем пять мальчиков, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 5 нужно разделить на число 15
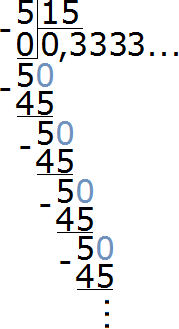
При делении 5 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную
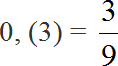
Сократим полученную дробь на 3
Получили окончательный ответ 
. Значит мальчики составляют одну треть от всего класса
На рисунке видно, что в классе из 15 школьников треть класса составляют 5 мальчиков.
Если для проверки найти от 15 школьников, то мы получим 5 мальчиков
15 : 3 = 5
5 × 1 = 5
Пример 5. Во сколько раз число 35 больше числа 5 ?
Записываем отношение числа 35 к числу 5. В числитель отношения нужно записать число 35, в знаменатель — число 5, но не наоборот
Значение данного отношения равно 7. Значит число 35 в семь раз больше числа 5.
Пример 6. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества составляют девочки.
Записываем отношение девочек к общему количеству школьников. В числителе отношения записываем десять девочек, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае, число 10 нужно разделить на число 15
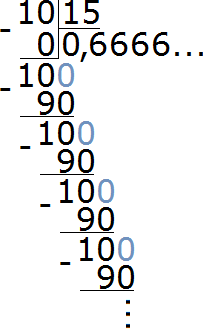
При делении 10 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную
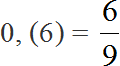
Сократим полученную дробь на 3
Получили окончательный ответ 
. Значит девочки составляют две трети от всего класса
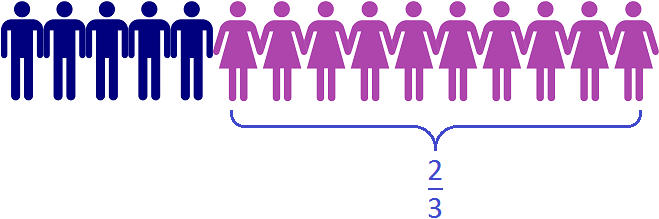
На рисунке видно, что в классе из 15 школьников две трети класса составляют 10 девочек.
Если для проверки найти от 15 школьников, то получим 10 девочек
15 : 3 = 5
5 × 2 = 10
Пример 7. Какую часть 10 см составляют от 25 см
Записываем отношение десяти сантиметров к двадцати пяти сантиметрам. В числителе отношения записываем 10 см, в знаменателе — 25 см
Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 10 нужно разделить на число 25
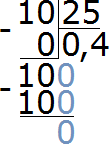
Переведём полученную десятичную дробь в обыкновенную
Сократим полученную дробь на 2
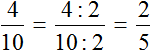
Получили окончательный ответ 
. Значит 10 см составляют от 25 см.
Пример 8. Во сколько раз 25 см больше 10 см
Записываем отношение двадцати пяти сантиметров к десяти сантиметрам. В числителе отношения записываем 25 см, в знаменателе — 10 см
Найдём значение данного отношения
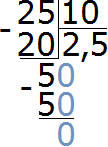
Получили ответ 2,5. Значит 25 см больше 10 см в 2,5 раза (в два с половиной раза)
Важное замечание. При нахождении отношения одноименных физических величин эти величины обязательно должны быть выражены в одной единице измерения, в противном случае ответ будет неверным.
Например, если мы имеем дело с двумя длинами и хотим узнать во сколько раз первая длина больше второй или какую часть первая длина составляет от второй, то обе длины сначала нужно выразить в одной единице измерения.
Пример 9. Во сколько раз 150 см больше 1 метра?
Сначала сделаем так, чтобы обе длины были выражены в одной единице измерения. Для этого переведем 1 метр в сантиметры. Один метр это сто сантиметров
1 м = 100 см
Теперь находим отношение ста пятидесяти сантиметров к ста сантиметрам. В числителе отношения записываем 150 сантиметров, в знаменателе — 100 сантиметров
Найдём значение данного отношения
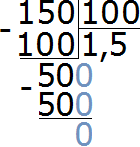
Получили ответ 1,5. Значит 150 см больше 100 см в 1,5 раза (в полтора раза).
А если бы не стали переводить метры в сантиметры и сразу попытались найти отношение 150 см к одному метру, то у нас получилось бы следующее:
Получилось бы, что 150 см больше одного метра в сто пятьдесят раз, а это неверно. Поэтому обязательно нужно обращать внимание на единицы измерения физических величин, которые участвуют в отношении. Если эти величины выражены в разных единицах измерения, то для нахождения отношения этих величин, нужно перейти к одной единице измерения.
Пример 10. В прошлом месяце зарплата человека составляла 25000 рублей, а в текущем месяце зарплата выросла до 27000 рублей. Определить во сколько раз выросла зарплата
Записываем отношение двадцати семи тысяч к двадцати пяти тысячам. В числителе отношения записываем 27000, в знаменателе — 25000
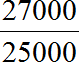
Найдём значение данного отношения
Получили ответ 1,08. Значит зарплата выросла в 1,08 раза. В будущем, когда мы познакомимся с процентами, такие показатели как зарплата будем выражать в процентах.
Пример 11. Ширина многоквартирного дома 80 метров, а высота 16 метров. Во сколько раз ширина дома больше его высоты?
Записываем отношение ширины дома к его высоте:
Значение данного отношения равно 5. Значит ширина дома в пять раз больше его высоты.
Свойство отношения
Отношение не изменится если его члены умножить или разделить на одно и тоже число.
Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.
Вернемся к отношению девочек к мальчикам (10 : 5). Данное отношение показало, что на каждого мальчика приходится две девочки. Проверим, как работает свойство отношения, а именно попробуем умножить или разделить его члены на одно и то же число.
В нашем примере удобнее разделить члены отношения на их наибольший общий делитель (НОД).
НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5
Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5 показывает, что на одного мальчика приходятся две девочки.
На рисунке показано отношение 2 : 1 (два к одному). Как и в прошлом отношении 10 : 5 на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.
Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?
В обоих классах девочек в два раза больше мальчиков, поскольку отношения 
и 
равны одному и тому же числу.
Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.
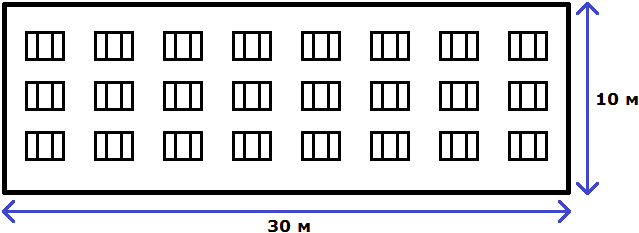
Чтобы нарисовать на бумаге похожий дом, нужно рисовать его в таком же отношении 30 : 10.
Разделим оба члена этого отношения на число 10. Тогда получим отношение 3 : 1. Это отношение равно 3, как и предыдущее отношение равно 3
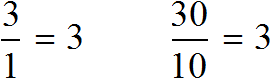
Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров
3 м = 300 см
1 м = 100 см
Имеем отношение 300 см : 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см : 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см
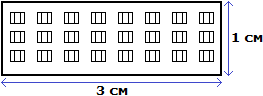
Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный
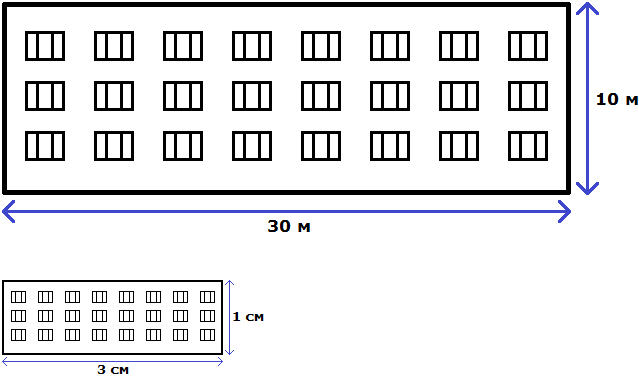
Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.
Эти 40 метров можно понимать, как 40 частей. Отношение 30 : 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.
Далее члены отношения 30 : 10 были разделены на 10. В результате получилось отношение 3 : 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.
Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3 : 1 всего четыре части
40 м : 4 = 10 м
Далее с помощью умножения определяют сколько метров приходятся на ширину и высоту. Члены, которые даны в отношении используют в качестве сомножителя.
Определим сколько метров приходится на ширину:
10 м × 3 = 30 м
Определим сколько метров приходится на высоту:
10 м × 1 = 10 м
Несколько членов отношения
Если в отношении дано несколько членов, то их можно понимать как части от чего-либо.
Пример 1. Куплено 18 яблок. Эти яблоки разделили между мамой, папой и дочкой в отношении 2 : 1 : 3. Сколько яблок получил каждый?
Отношение 2 : 1 : 3 говорит о том, что мама получила 2 части, папа — 1 часть, дочка — 3 части. Другими словами, каждый член отношения 2 : 1 : 3 это определенная часть от 18 яблок:
Если сложить члены отношения 2 : 1 : 3, то можно узнать сколько всего частей имеется:
2 + 1 + 3 = 6 (частей)
Узнаем сколько яблок приходится на одну часть. Для этого 18 яблок разделим на 6
18 : 6 = 3 (яблока на одну часть)
Теперь определим сколько яблок получил каждый. Умножая три яблока на каждый член отношения 2 : 1 : 3, можно определить сколько яблок получила мама, сколько получил папа и сколько получила дочка.
Узнаем сколько яблок получила мама:
3 × 2 = 6 (яблок)
Узнаем сколько яблок получил папа:
3 × 1 = 3 (яблока)
Узнаем сколько яблок получила дочка:
3 × 3 = 9 (яблок)
Пример 2. Новое серебро (альпака) — это сплав никеля, цинка и меди в отношении 3 : 4 : 13. Сколько килограммов каждого металла нужно взять, чтобы получить 4 кг нового серебра?
4 килограмма нового серебра будет содержать 3 части никеля, 4 части цинка и 13 частей меди. Сначала узнаем сколько всего частей будет в четырех килограммах серебра:
3 + 4 + 13 = 20 (частей)
Определим сколько килограммов будет приходиться на одну часть:
4 кг : 20 = 0,2 кг
Определим сколько килограммов никеля будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:
0,2 кг × 3 = 0,6 кг никеля
Теперь определим сколько килограммов цинка будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:
0,2 кг × 4 = 0,8 кг цинка
Теперь определим сколько килограммов меди будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:
0,2 кг × 13 = 2,6 кг меди
Значит, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.
Пример 3. Латунь — это сплав меди и цинка, массы которых относятся как 3 : 2. Для изготовления куска латуни требуется 120 г меди. Сколько требуется цинка для изготовления этого куска латуни?
Определим сколько граммов сплава приходится на одну часть. В условии сказано, что для изготовления куска латуни требуется 120 г меди. Также сказано, что три части сплава содержат медь. Если разделить 120 на 3, мы узнаем сколько граммов сплава приходится на одну часть:
120 : 3 = 40 граммов на одну часть
Теперь определим сколько требуется цинка для изготовления куска латуни. Для этого 40 граммов умножим на 2, поскольку в отношении 3 : 2 указано, что две части содержат цинк:
40 г × 2 = 80 граммов цинка
Пример 4. Взяли два сплава золота и серебра. В одном количество этих металлов находится в отношении 1 : 9, а в другом 2 : 3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золото и серебро относилось бы как 1 : 4?
Решение
15 кг нового сплава должны состоять в отношении 1 : 4. Это отношение говорит о том, что на одну часть сплава будет приходиться золото, а на четыре части будет приходиться серебро. Всего же частей пять. Схематически это можно представить следующим образом
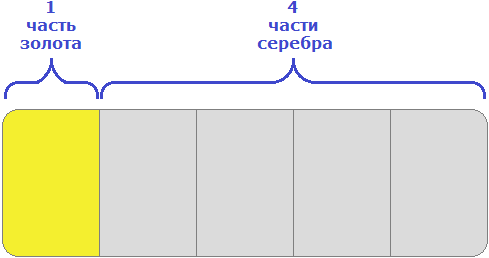
Определим массу одной части. Для этого сначала сложим все части (1 и 4), затем массу сплава разделим на количество этих частей
1 + 4 = 5
15 кг : 5 = 3 кг
Одна часть сплава будет иметь массу 3 кг. Тогда в 15 кг нового сплава будет содержáться 3 × 1 = 3 кг золота и серебра 3 × 4 = 12 кг серебра.
Поэтому для получения сплава массой 15 кг нам нужно 3 кг золота и 12 кг серебра.
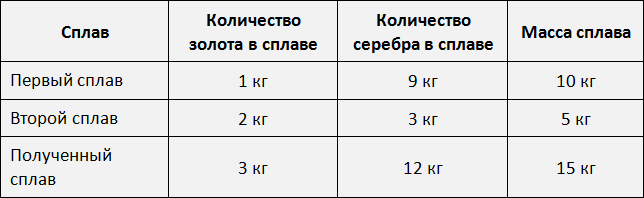
Теперь ответим на вопрос задачи — «Сколько нужно взять каждого сплава?»
Первого сплава мы возьмем 10 кг, поскольку золото и серебро в нём находятся в отношении 1 : 9. То есть этот первый сплав даст нам 1 кг золота и 9 кг серебра.
Второго сплава мы возьмем 5 кг, поскольку золото и серебро находятся в нём в отношении 2 : 3. То есть этот второй сплав даст нам 2 кг золота и 3 кг серебра.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
