Плотность и удельный вес являются физическими величинами, описывающими объемные характеристики данного вещества. В этом посте вы узнаете больше о плотности и удельном весе.
Плотность определяет массу вещества в единице объема, а удельный вес также является плотностью по сравнению с плотностью другого вещества в качестве эталона. Удельный вес – это отношение массы единицы объема материала к массе единицы объема другого эталонного вещества. Однако и плотность, и удельный вес взаимосвязаны.
Вода используется в качестве эталонного вещества для твердых и жидких тел для измерения удельного веса. Сухой воздух используется в качестве эталонного вещества для газов для измерения удельного веса. Следующий раздел будет знать соотношение и различия между плотностью и удельным весом.
Отношение плотности и удельного веса
Удельный вес и плотность взаимосвязаны друг с другом. Отношение между плотностью и удельным весом определяется как
п∝SG; где ρ — плотность, SG — удельный вес.
Приведенное выше выражение объясняет, что изменение плотности прямо соответствует удельному весу. Если плотность увеличивается, удельный вес также увеличивается.
Мы также можем приблизительно проверить плотность данного твердого вещества или жидкости, используя значение удельного веса, рассчитанное по отношению к воде.
- Для любого вещества, измеренный удельный вес которого меньше одного среднего, плотность этого вещества меньше, чем у воды, и оно плавает на воде.
- Предположим, что если показатель удельного веса больше 1, то плотность больше, чем у воды, и он тонет в воде.
Поскольку в большинстве случаев в качестве эталонного вещества используется вода, значения удельного веса и плотности практически равны. Из точного расчета установлено, что плотность немного меньше удельного веса.
Разница плотности и удельного веса
Поскольку мы знаем определения плотности и удельного веса, они кажутся одинаковыми, но есть некоторые различия в их основных характеристиках, а также в их измерениях. Некоторые различия между плотностью и удельным весом приведены в таблице ниже.
| Плотность | Удельный вес | |
| Определение | Плотность определяет вес данного вещества в единице объема. | Удельный вес определяет отношение плотностей двух веществ, при котором одно из них называют эталонным веществом. |
| Единица СИ | Плотность id обозначается символом ρ, а единицей плотности в системе СИ является кг/м.3. | Удельный вес не имеет единиц СИ, потому что мы берем плотность двух эквивалентных веществ, в которых единицы уравновешиваются. |
| Представление | Плотность представляет собой абсолютное значение вещества в одном измерении. | Удельный вес представляет собой относительное значение в одном измерении. |
| Термины, использованные при расчете | Для расчета важны только масса вещества и объем. | Для расчета удельной плотности плотности данного вещества и плотности эталонного вещества необходимо. Поэтому важно знать массу и объем, если плотность не задана. |
| Приложения | Плотность имеет приложения в области науки и промышленности, а также широко используется в повседневной жизни. | Удельный вес имеет применение только в научных и промышленных областях. Он не так часто используется в повседневной жизни. |
Как плотность влияет на удельный вес?
Мы знаем, что плотность и удельный вес взаимосвязаны, так что любое изменение плотности обязательно повлияет на удельный вес.
Плотность очень чувствительна к температуре и давлению. Значение плотности изменяется линейно при небольших изменениях температуры и давления. Поскольку удельный вес соответствует плотности, изменение плотности при изменении температуры и давления обеспечивает изменение удельного веса.
Плотность пропорциональна изменению давления и обратно пропорциональна температуре. Это означает, что увеличение давления увеличивает плотность при постоянной температуре, следовательно, увеличивает удельный вес.
Изображение кредита: Wikimedia Commons
Формула плотности и удельного веса
Удельный вес дает плотность данного вещества по отношению к другому веществу; формула дает это.
Плотность данного вещества определяется отношением его массы к объему как
р = м / В
Вместе мы можем записать удельный вес как
Приведенное выше выражение дает формулу, описывающую, как плотность и удельный вес связаны друг с другом.
Как найти плотность по удельному весу?
Если у вас есть удельный вес вещества, вы можете легко найти плотность. Шаги, которые необходимо выполнить, приведены ниже.
- Шаг 1: Найдите плотность воды при данных температуре и давлении.
- Шаг 2: подставьте значения в выражение удельного веса.
- Шаг 3: перемножить значения удельного веса и плотности эталонного объекта, что дает плотность искомого вещества.
Удельный вес твердого вещества 14.87; найти его плотность.
Так как данный объект твердый, эталонным веществом будет вода.
Плотность воды 1000кг/м3. Подставляя, получаем
14.87 =
ρsub=14.87×1000кг/м3
ρsub=14870кг/м3
Как рассчитать плотность газа по удельному весу?
Сухое вещество считается эталонным веществом для определения плотности газа. Шаги, приведенные ниже, помогут вам найти плотность по удельному весу..
- Шаг 1: сначала найдите плотность сухого воздуха.
- Шаг 2: умножьте плотность сухого воздуха и дайте удельный вес вещества, что даст вам плотность данного вещества.
ρгаз=SG×ρвоздух
Пример, приведенный ниже, поможет вам ясно понять.
Найдите плотность газа, удельный вес которого равен 0.00126.
Плотность воздуха 1.20 кг/м.3
ρгаз=SG×ρвоздух
ρгаз=0.00126×1.20 кг/м3
ρгаз= 1.512 × 10-3кг / м3.
Как найти плотность с относительной плотностью?
Относительная плотность определяет отношение плотностей двух веществ относительно друг друга. Можно также сказать, что это отношение плотностей вещества, находящегося вблизи другого вещества.
В некоторых контекстах относительная плотность также упоминается как удельный вес. если ты знать относительную плотность объекта, то плотность можно рассчитать по формуле;
Задача, решаемая ниже, объясняет, как рассчитать плотность по относительной плотности.
Некоторые решенные задачи на плотность и удельный вес
Рассчитайте удельный вес железных стержней в воде плотностью 7870 кг/м.3.
Решение:
Поскольку железный стержень находится в воде, плотность воды составляет 1000 кг/м.3.
Удельный вес определяется выражением
Подставив в уравнение значение плотности железного стержня и воды,
СГ=7870/1000
СГ=7.87
Рассчитайте удельный вес тела в воде массой 55 г и объемом 22 м.3.
Решение:
Дано – масса предмета m=50г
Объем объекта V=22м3.
Плотность воды=1000кг/м3.
Плотность данного объекта определяется выражением
Подставляя значения
ρоб=2.27 г/м3=2270кг/м3.
Удельный вес
СГ=2.27.
Объект погружен в масло с относительной плотностью 2.3. Та же нефть плавает в воде с удельным весом 0.92. Вычислите плотность тела в масле.
Решение:
Дано – относительная плотность объекта по нефти RD=2.3
Удельный вес масла SG=0.92
Плотность воды ρw=1000кг/м3
Плотность масла рассчитывается как
ρмасло=SG×ρw
ρмасло=0.92×1000 кг/м3
ρмасло=920кг/м3.
Плотность объекта рассчитывается как
ρоб=РГ× рмасло
ρоб=2.3×920
ρоб=2116кг/м3.
Вычислите удельный вес газа плотностью 1.5 кг/мXNUMX.3.
Решение:
Поскольку просят рассчитать удельный вес газа, эталонной средой должен быть сухой воздух плотностью 1.205 кг/м3 при нормальной температуре и давлении.
Плотность газа равна 1.
Удельный вес данного газа равен
СГ=1.244.
Вычислите плотность и удельный вес вещества в воде, масса которого 63 г, а объем 28 м.3.
Решение:
Дано -масса вещества m=63г
Объем вещества V=28м3
Нам предоставлены только масса и объем вещества, а плотность необходимо вычислить по формуле.
ρниже=2.25 г/м3=2250кг/м3
Удельный вес вещества находится по формуле
SG = гидроразрыва { rho_ {суб}} { rho_ {вода}}
SG=frac{2250кг/м^3}{1000кг/м^3}
СГ=2.25.
Заключение
Из этого поста вы узнали, как плотность и удельный вес зависят друг от друга. И найти удельный вес, зная, что один из них плотность вещества и эталонного вещества является обязательным.
Каково соотношение между высотами столбов жидкостей разной плотности в сообщающихся сосудах и их плотностями?
Вопрос посетителя
Каково соотношение между высотами столбов жидкостей разной плотности в сообщающихся сосудах и их плотностями?
Ответ эксперта
hв/hр =pр/pв во сколько раз плотность одной жидкости больше плотности другой жидкости, во столько раз меньше высота ее столба при равенстве давлений.
Сообщающиеся сосуды, теория и онлайн калькуляторы
Сообщающиеся сосуды
Определение сообщающихся сосудов
Определение
Соединенные между собой сосуды называют сообщающимися.
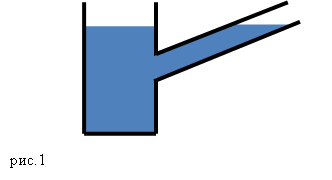
В таких сосудах жидкость имеет возможность перетекать из одной емкости в другую (рис.1). Форма сообщающихся сосудов может быть самая разная.
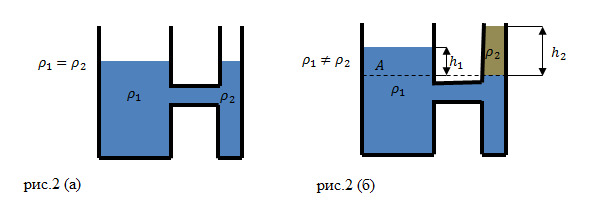
Допустим, что в сообщающиеся сосуды налита однородная жидкость, то в этих сосудах жидкость устанавливается на одном уровне, если давление над поверхностью жидкости одинаково, и не важно какую форму имеют сосуды. В неподвижной жидкости давление ($p$) на одном уровне в сообщающихся сосудах является равным, так как мы знаем, что:
[p=rho gh left(1right),]
где $rho $ – плотность жидкости; $g$ – ускорение свободного падения; $h$ – высота столба жидкости. Так как давление на одном уровне жидкости одинаково, то равными будут и высоты столбов жидкости.
Жидкости разной плотности в сообщающихся сосудах
Допустим, что в сообщающиеся сосуды налили жидкость разной плотности (рис.2(б)). В состоянии равновесия жидкостей, их уровни не будут находиться на одном уровне (высоты столбов жидкости равными не будут).
Жидкости в сосудах находятся в равновесии. Давления на уровне A (граница раздела разных жидкостей) (рис. 2 (б)) равны:
[{rho }_1gh_1={rho }_2gh_2left(2right),]
где ${rho }_1$ и ${rho }_2$ – плотности жидкостей. Найдем отношение высот столбов жидкостей в сосудах:
[frac{h_1}{h_2}=frac{{rho }_2}{{rho }_1}left(3right).]
Формула (3) говорит о том, что в сообщающихся сосудах высоты столбиков жидкости над уровнем их раздела обратно пропорциональны плотностям этих жидкостей. При одинаковом давлении над поверхностями жидкостей, высота столба жидкости с меньшей плотностью будет больше, чем высота столба более плотной жидкости.
Гидравлический пресс и другие примеры использования сообщающихся сосудов
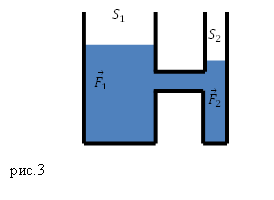
В технике сообщающиеся сосуды используют часто. Например, существует такое устройство, как гидравлический пресс. Его изготавливают из двух цилиндров разного радиуса, в которых находятся поршни (рис.3). Сообщающиеся сосуды пресса обычно заполняют минеральным маслом.
Пусть площадь первого поршня, к которому прикладывают силу ${overline{F}}_1,$ равна $S_1$, площадь второго $S_2$, к нему приложена сила ${overline{F}}_2$. Давление, которое создает первый поршень равно:
[p_1=frac{F_1}{S_1}left(4right).]
Второй поршень давит на жидкость:
[p_2=frac{F_2}{S_2}left(5right).]
Если система находится в состоянии равновесия, то по закону Паскаля давления $p_1$ и $p_2$ равны:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(6right).]
Получим:
[F_1=F_2frac{S_1}{S_2}(7)]
величина первой силы больше модуля силы $F_2$ в $frac{S_1}{S_2}$ раз. Это означает, что при помощи гидравлического пресса, прикладывая небольшую силу к поршню малого сечения, можно получить большую по величине силу, которая будет действовать на большой поршень.
По принципу сообщающихся сосудов, в особенности раньше, действовал водопровод. Такой водопровод сейчас еще можно наблюдать на дачных участках. На относительно большой высоте устанавливается бак с водой, от бака идут водопроводные трубы, закрываемые кранами. Давление у кранов соответствует давлению столба воды, который равен разности высот уровень крана – уровень воды в баке.
Принципом сообщающихся сосудов пользовались, когда проектировали фонтаны, работающие без насосов, шлюзы на реках и каналах.
Примеры задач с решением
Пример 1
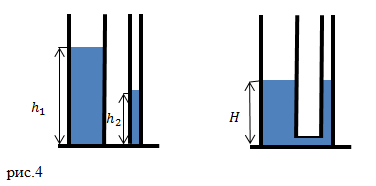
Задание. Имеются два цилиндрических сосуда. Высота столба жидкости в одном равна $h_1$, в другом $h_2$. Эти сосуды соединяют трубкой. Насколько изменится высота столба жидкости в левом сосуде, если площадь поперечного сечения его $S_1>S_2$ , $S_2$ – площадь сечения правого сосуда. Объемом трубки пренебречь.
Решение. После того как сосуды соединили, они стали сообщающимися. Часть жидкости из левого сосуда перетечет в правый. Так как жидкость в правом и левом сосудах одна и та же, то уровни жидкости в обоих сосудах будут находиться на одном уровне, то есть высота столбиков жидкости станет равна $H$ в обоих коленах емкости. Определим, какой объем воды перетечет из левого колена в правое:
[Delta V_1=left(h_1-Hright)S_{1 }left(1.1right),]
где $S_{1 }$ – площадь поперечного сечения левого сосуда (сосуда из которого вытекает жидкость). В правом сосуде эта жидкость займет объем равный:
[Delta V_2=left(H-h_2right)S_{2 }left(1.2right),]
где $S_{2 }$ – площадь поперечного сечения правого сосуда. Так как мы считаем, что жидкость не сжимаема, то имеем:
[Delta V_1=Delta V_2left(1.3right).]
Приравниваем правые части выражений (1.2) и (1.1), выражаем высоту столбиков жидкости в правой и левой части сообщающихся сосудов:
[left(h_1-Hright)S_{1 }=left(H-h_2right)S_{2 }to H=frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }} left(1.4right).]
Используя выражение (1.4), изменение высоты жидкости в левом колене, получим равным:
[Delta h=h_1-H=h_1-frac{h_1S_{1 }+S_{2 }h_2}{S_1+S_{2 }}=frac{h_1S_1+h_1S_2-h_1S_{1 }-S_{2 }h_2}{S_1+S_{2 }}=]
[=frac{h_1S_2-S_{2 }h_2}{S_1+S_{2 }}=frac{h_1-h_2}{S_1+S_{2 }}S_2.]
Ответ. $Delta h=frac{h_1-h_2}{S_1+S_{2 }}S_2$
Пример 2
Задание. Какой будет сила давления на большой поршень (площадью $S_1$) гидравлического пресса, если площадь его малого поршня равна $S_2$, при этом на него действует сила равная $F_2$?
Решение. В теоретическом разделе сказано, что гидравлический пресс представляет собой систему из сообщающихся сосудов (рис.3). Из закона Паскаля следует, что, прикладывая небольшую силу ($F_2$) к поршню малого сечения ($S_2$) пресса, можно получить большую по величине силу, которая будет действовать на большой поршень ($S_1$):
[F_1=F_2frac{S_1}{S_2}(2.1)]
Ответ. $F_1=F_2frac{S_1}{S_2}$
Читать дальше: условия плавания тел.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
вопрос по теме погружение в жидкость
Профи
(950),
закрыт
11 лет назад
Андрей Галыгин
Гуру
(2999)
12 лет назад
1. Если плотность тела больше плотности жидкости, то тело в жидкости тонет.
2. Если плотность тела равна плотности жидкости, то тело плавает в жидкости не всплывая и не тоня (в смысле не погружаясь на дно) . Причем без разницы, где тело находится в жидкости и на какой глубине.
3. Если плотность тела меньше плотности жидкости, то тело, помещенное в жидкость, будет всплывать. А когда всплывет, будет плавать на ее поверхности, частично погрузившись в жидкость. Глубина погружения будет определяться отношением плотностей тела/жидкость. Так, если весота тела H, его плотность ρ(т) , плотность жидкости ρ(ж) , то высота выступающей над жидкостью части тела h равна: h=(ρ(ж) -ρ(т)) /ρ(ж) * Н
.Профи (950)
12 лет назад
в формуле: *Н это в числитель или знамменатель дроби? а так спасибо!
Найти массу, плотность или объем онлайн
На данной странице калькулятор поможет найти плотность, массу или объем вещества онлайн. Для расчета введите значения в калькулятор.
Объем, масса и плотность
Найти
Масса:
Объем:
Плотность:
Ответы:
Формула для нахождения массы тела через плотность и объем:
m – масса; V – объем; p – плотность.
Формула для нахождения объема тела через плотность и массу:
m – масса; V – объем; p – плотность.
Формула для нахождения плотности тела через объем и массу:
m – масса; V – объем; p – плотность.