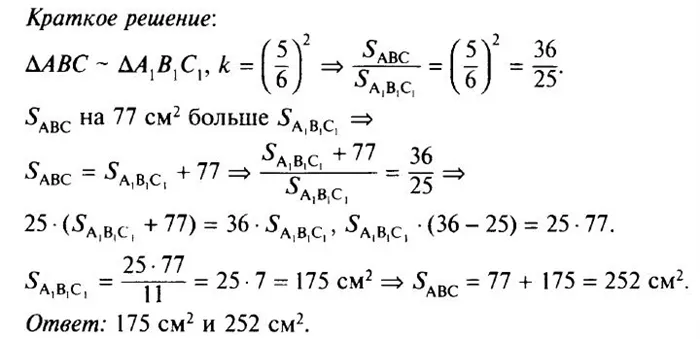Площадь прямоугольного треугольника
О чем эта статья:
площадь, 8 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
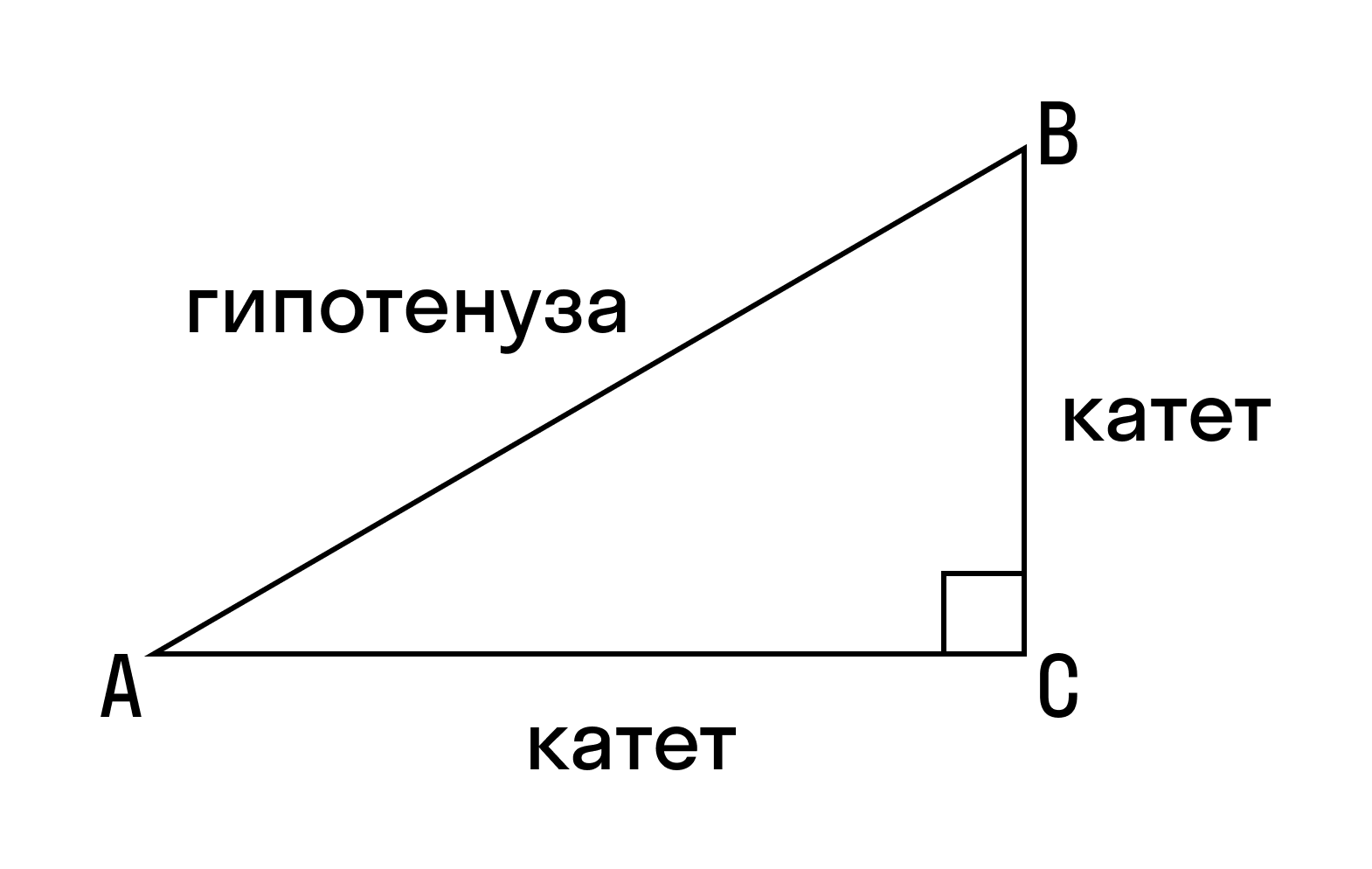
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Формула для нахождения площади прямоугольного треугольника через гипотенузу
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
где с — гипотенуза,
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через катет и угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!
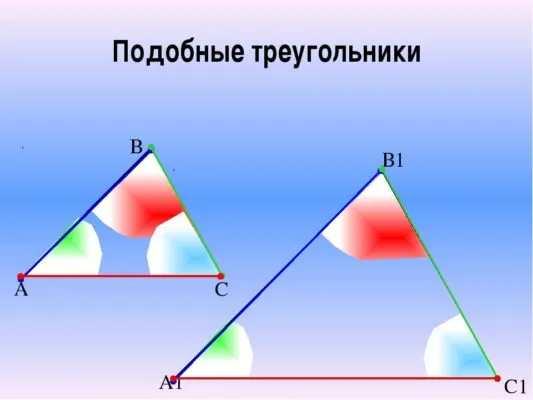
Подобные треугольники
Определение
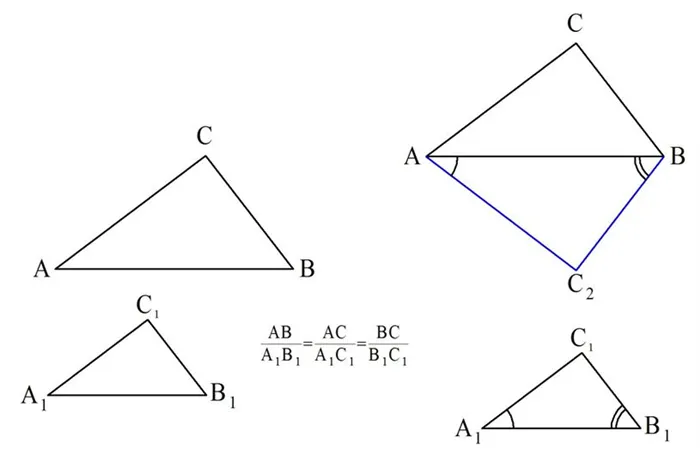
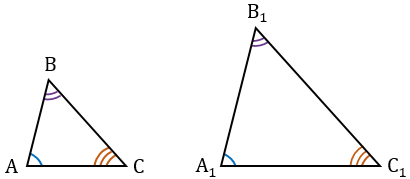
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k , равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники» .
Отношение площадей подобных треугольников
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На данном уроке мы введем понятие подобных треугольников и рассмотрим теорему об отношении их площадей. Затем будет рассмотрен ряд примеров на применение этой теоремы.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Измерение»
[spoiler title=”источники:”]
http://interneturok.ru/lesson/geometry/8-klass/podobnye-treugolniki/otnoshenie-ploschadey-podobnyh-treugolnikov
[/spoiler]
Если стороны одного треугольника равны 8 см, 10 см и 6 см, а стороны другого треугольника равны 12 см, 15 см и 9 см, найдите отношение площадей этих двух треугольников.
Подобные треугольники
Подобные треугольники — это треугольники, углы которых равны между собой, а одна сторона пропорциональна другой.
Коэффициентом подобия является k, который равен отношению сходных сторон подобных треугольников.
Стороны (или сопряженные стороны) подобных треугольников являются противоположными сторонами равных углов.
Признаки подобия треугольников
I Принцип подобия треугольников
Если два угла треугольника равны двум углам другого треугольника, то эти треугольники одинаковы.
II Принцип подобия треугольников
Если две стороны треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные в этих сторонах, равны, то эти треугольники одинаковы.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то эти треугольники одинаковы.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
1. линия, параллельная одной стороне треугольника, пересекает подобный ей треугольник.
2. треугольники, образованные отрезком диагонали и основанием трапеции, подобны. Степень сходства
3. в прямоугольном треугольнике высота, проведенная из вершины прямого угла, делит треугольник на два треугольника, подобных исходному треугольнику.
Здесь вы найдете подборку задач, похожих на «Подобные треугольники».
Работа. Прямая, параллельная AB в BCABC, пересекает BC и AC в точках E и P. Найдем, что EC = 2, BE = 3 и EP = 3,2. Какова длина отрезка AB?
Подобие
Идентичные треугольники — это треугольники, у которых длины всех сторон пропорциональны друг другу, а углы равны. Отношение соответствующих сторон подобных треугольников всегда равно одному и тому же числу, которое называется коэффициентом подобия.
Рисунок 1. Подобные треугольники
Коэффициенты подобия часто используются для решения задач на подобие треугольников, так как коэффициенты можно найти из оснований после того, как неизвестные стороны представлены известными сторонами. Сходство представлено буквой k.
Не обязательно концентрироваться на треугольниках. Все фигуры в геометрии имеют сходство, хотя символ сходства появляется только на них. То же самое справедливо и для эквивалентности формы. Все фигуры в геометрии эквивалентны, так как эквивалентность является частным случаем сходства с коэффициентом k=1.
Рисунок 2.Похожие элементы
Признаки подобия
В настоящее время для любого треугольника существует три варианта подобия.
- По двум углам. Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
- По сторонам и углу между ними. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами равны, то такие треугольники подобны.
- По трем сторонам. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Чтобы доказать пропорциональность сторон, необходимо вычислить отношение длин каждой стороны. Тот же результат применим и к аналоговой стороне.
Аналоговые треугольники также имеют аналоговые треугольники и все характерные части, такие как высоты, медианы и биссектрисы. Коэффициенты сходства одинаковы для всех сегментов треугольника. Этот факт необходимо помнить. Это важно для решения многих задач и извлечения формул, поскольку существуют площади подобных треугольников.
Площади подобных треугольников
Рассмотрим два одинаковых треугольника ABC и $A_1B_1C_1$. Площадь треугольника равна половине произведения его основания и высоты.
$ S =.<1over<2>> h * AB $, тогда площадь второго треугольника:.
Деление одной поверхности на вторую поверхность дает следующее соотношение.
$> = over> $ Вспоминая, что отношение сторон подобных треугольников равно коэффициенту подобия, получаем.
$> = k * k = k ^ 2 $- т.е. области подобных треугольников взаимосвязаны в соотношении, равном коэффициенту подобия квадратов.
Проведите перпендикуляр к вертикальному прямоугольному треугольнику (рис. 166, а). Сделайте из него квадрат со сторонами квадрата. Итак: ^
Работа по теме урока
(Учитель делит класс на группы для решения творческой работы. По завершении задаются и обсуждаются решения).
Работа. Треугольники ABC и A1B1C1 подобны коэффициенту K. Найдите причину в их районе.
Заключение Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Закрепление изученного материала
- Работа в рабочих тетрадях. Решить задачу № 54. (Учащиеся самостоятельно решают задачу, по окончании работы один ученик вслух читает задачу и ее решение. Учащиеся его слушают, а затем исправляют ошибки.)
- Решить задачу № 545 (работа в парах). (После завершения работы заслушиваются и обсуждаются варианты решений.)
Вопрос нет. 545
- Чему равно отношение площадей подобных треугольников, если их сходственные стороны относятся как 6 : 5?
- Верно ли составлено уравнение исходя из условий задачи?
- Решить задачи № 547, 548 (работа в группах). (После завершения работы заслушиваются и обсуждаются варианты решений.)
Самостоятельная работа
I уровень сложности
II уровень сложности
III уровень сложности
Научитесь правильно писать задачи, делайте записи короткими и не тратьте время на то, чтобы написать все идеи и названия теорий.
Самый главный «секрет» подобия треугольников
Плита научила вас находить подобные треугольники, но как теперь использовать те, которые вы нашли?
А что бы вы хотели с ним сделать? Что же тогда …
Все элементы одного треугольника ровно в ዄ (⌘ displaystyle 2 ) (или во столько раз, во сколько получится) больше элементов других треугольников.
Не только стороны, но и высоты, дихотомии, интерстиции, зарегистрированные, граничные лучи цикла и т.д.
Есть важное исключение: площадь.
Открыть ответы…
Чтобы открыть все выпуски всех учебников, охваченных синим баннером (например, этот), зарегистрируйтесь следующим образом.
Чтобы управлять им, просто разделите длину сторон между ними. Разделите наибольшую сторону одного треугольника на другую и наименьшую сторону на наименьшую. Если результат одинаков для всех трех сторон, то треугольники подобны.
Второй и третий признаки подобия треугольников
Существуют еще два подобия треугольника, которые реже используются при решении задач. Идите прямо от первого участка.
Докажите второе сходство. Пусть DABC и DA1В1Больше.1, мы удовлетворяем соотношению:.
Докажите, что они похожи. Для этого мы построим еще один DABC2которая имеет общие аспекты с DABC.2 Выберите точку C так, чтобы условие было выполнено.
DM1В1Больше.1 Затем слегка постучите.2 Поскольку два угла одинаковы, они подобны. Поэтому необходимо применить следующие уравнения
Но потом ДАБК и ДАБК2 равны, так как углы, образованные двумя сторонами и двумя сторонами, одинаковы.
В результате, DB и DA1В1Больше.1 имеют два одинаковых угла, т.е. похожи друг на друга
Выпуск. На стороне угла отмечены точки a и b, так что ab = 5 см и ag = 16 см. На другой стороне того же угла отмечены точки c и d, такие, что AD = 8 см и AF = 10 см. Похожи ли ΔACD и D AFB?
Рассмотренные треугольники имеют общий угол.
Отношения одинаковы, поэтому треугольники симметричны.
ПРИМЕЧАНИЯ. В этом случае важно понять, какую сторону нужно разделить. У DGD стороны AC и AD равны 16 и 8 см. У DAFB стороны AF и AB равны 10 и 5 см. Наибольшая сторона одного треугольника делится на наибольшую сторону другого треугольника, т.е. 16 x 10, или 8 на 8. Сходство и взятое число — это просто коэффициент сходства.
Рассмотрим третье свойство подобия треугольников.
Давайте докажем это. Пусть DABC и DA1В1Больше.1 Это соизмеримо с их сторонами:.
Мы видим, что DABC2 И да1В1Больше.1 Они похожи, потому что два угла одинаковы. Тогда пропорции верны:.
Отношение площадей подобных треугольников
Если треугольники подобны, то их стороны зависят от коэффициента K. Здесь K — коэффициент. И как соотносятся между собой их высоты, промежуточные и другие характерные длины? Легко предположить, что они также зависят от коэффициента K.
Докажем это на примере высоты. Предположим, что у нас есть аналогичные DABC и DA1В1Больше.1и их коэффициент сходства равен k.
ch и c, которые построены на этих высотах1н1:.
Аналогично, мы можем доказать, что длины и расщепления промежуточных продуктов отличаются по времени k.
В чем причина одинаковой площади треугольника? Получается, что дважды по k. Докажите это.
Пусть DABC и DA1В1Больше.1 аналогично коэффициенту сходства k. Снова постройте высоты Ch и Ch1:.
Запишите очевидное уравнение: .
В результате площади одного и того же треугольника могут отличаться на коэффициент k 2.
Задание. Площадь DABC равна 10, и мы знаем, что отрезок AB равен 5. Сторона DE, которая подобна AB, равна 15. чтобы вычислить площадь DEF, DEF DB подобна DAB.
Решение. Согласно описанию проблемы, мы находим сходство между DABC и DDEF следующим образом
Задание. Два подобных треугольника имеют площади 75 м 2 и 300 м 2. Одна сторона второго треугольника равна 9 м. Вычислите одинаковую сторону первого треугольника.
Решение. Если известны площади треугольников, то коэффициент подобия легко найти.
Если коэффициент подобия равен 2, то сторона первого треугольника меньше стороны второго.
Коэффициенты подобия часто используются для решения задач на подобие треугольников, так как коэффициенты можно найти из оснований после того, как неизвестные стороны представлены известными сторонами. Сходство представлено буквой k.
Как найти отношение площадей двух треугольников, если стороны одного равны 5 см, 8 см, 12 см, а стороны другого 15 см, 24 см, 36 см?
Как найти отношение двух треугольников, если одна сторона равна 5 см, 8 см или 12 см, а другая сторона равна 15 см, 24 см или 36 см.
Треугольники, приведенные в задаче, подобны. Это объясняется тем, что их стороны соизмеримы.
Два треугольника подобны, если три стороны одного треугольника подобны другой стороне.
Площадь подобных треугольников равна квадрату их подобия.
Площадь этих треугольников объясняется следующими причинами.
Найдите отношение двух треугольников, если одна сторона равна 5 см, 8 см или 12 см, а другая сторона равна 15 см, 24 см или 36 см.
Если стороны одного треугольника равны 8 см, 10 см и 6 см, а стороны другого треугольника равны 12 см, 15 см и 9 см, найдите отношение площадей этих двух треугольников.
Если стороны одного треугольника равны 12 см и 21 см 27 см, а другого треугольника — 4 см 7 см и 9 см, найдите причину возникновения двух треугольников.
На этой странице вы найдете ответ на вопрос, как найти отношение двух треугольников, если одна сторона равна 5 см, 8 см и 12 см, а другая 15 см, 24 см, 36 см и 36 см. Он относится к категории геометрии. Сложность вопроса соответствует базовым знаниям учащихся в классе5-9.Для получения дополнительной информации воспользуйтесь поисковой системой, чтобы найти другие вопросы, связанные с этим. Кроме того, нажмите на кнопку в верхней части страницы и задайте новый вопрос, используя ключевые слова, соответствующие критериям. Поговорите с посетителями вашей страницы и обсудите эту тему. Возможно, их ответы помогут вам найти информацию, которую вы ищете.
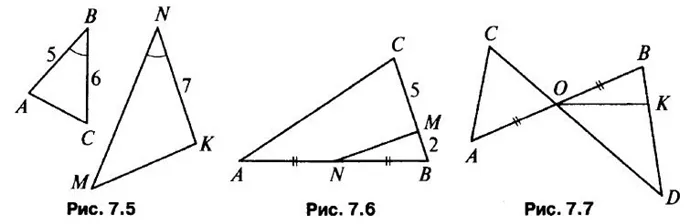
ДОКАЗАТЕЛЬСТВО: Предположим, что отрезки AC и BD пересекаются в точке o треугольника. Первое начало согласно треугольнику aob = sod (угол aob, угол SOD перпендикулярны, bo = od, ao = os, где o — середина ac и ua) треугольник abc = треугольник SOD (ac) является общим …
AC = 16 + 2 = 18 (см) BC = 18-8 = 10 (см) P = 16 + 18 + 10 = 44 (см) Ответ: 44 см.
Да, потому что это проекция и поэтому может иметь отображение.
AC = AD + DC = 6 + 8 = 14.Построим график CH, который является высотой ABC. Это также высота треугольника ABD. Sabc = 1/2 AC-BHBH = 2Sabc / AC = 2-42/14 = 6Sabd = 1/2 AB-BH = 1/2-6-6 = 18Sq.
Решение. Эта диаграмма показывает, что ∠BCA = CESCE и ∠A = ∠E = 90°. Это означает, что BCABC и CESCE похожи, потому что у них два одинаковых угла. Стороны AB и EC похожи, используйте их для нахождения коэффициентов подобия.
Применение площадей
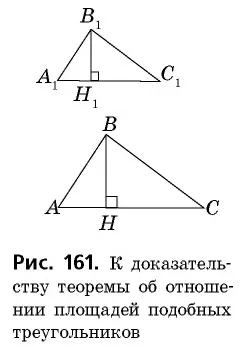
Теорема (Соотношение площадей подобных треугольников).
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Предположим, мы докажем, что с этим коэффициентом.
Проведем в данных треугольниках высоты
Прямоугольные треугольники Это означает, что
Средняя линия отсекает от данного треугольника треугольник с площадью 8
Давайте сделаем сторону, параллельную
Треугольники подобны по двум сторонам и углу между ними, причем Тогда по доказанной теореме откуда Ответ:
Метод площадей
Понятие площади и формула для ее вычисления также могут быть применены к задачам, в которых условия не относятся к площадям. Рассмотрим такой пример.
Стороны прямоугольника равны 16 см и 12 см. Высота прямоугольника, начерченного по самой длинной стороне, равна 3 см. Найдите высоту меньшего из них.
Предположим, что вам дан прямоугольник со сторонами, высоты которых нарисованы, а длины нужно найти (рис. 163).
Используйте формулу для площади прямоугольника
Итак.
Для решения этой задачи площадь прямоугольника вычислялась двумя разными способами. Поскольку площадь полигона определялась однозначно, независимо от метода расчета, полученное уравнение было уравнено, чтобы соотнести известные значения с требуемыми. Этот метод, использующий площадь в качестве вспомогательного размера, называется методом вспомогательной площади или просто методом площади.
Отметим, что для прямоугольного типа площади следует сделать важный вывод: в прямоугольниках высота, нарисованная на малой стороне, больше, а высота, нарисованная на большой стороне, меньше.
Метод сайта используется как для вычислительных задач, так и для доказательств утверждений.
Сумма расстояний от внутренних точек равностороннего треугольника до его сторон равна высоте треугольника, независимо от выбора точек. Доказательство.
Пусть точка находится на расстоянии одной стороны от этой точки до стороны треугольника (рис. 164).
Точка соединения равна сумме площадей треугольника и возвышения. У нас есть:.
Отсюда т.е. сумма рассматриваемых расстояний равна высоте треугольника и не зависит от выбора точки
Другие доказательства теоремы Пифагора
Исторически появление и доказательство теоремы Пифагора связано с вычислением площадей. Таким образом, классическая формулировка этой теоремы относится не к квадратам сторон прямоугольного треугольника, а к площади соответствующей фигуры.
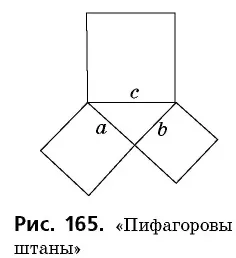
- площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
Рисунок 165, на котором наглядно представлена эта формулировка, стал отличительным символом геометрии и был назван школьниками прошлого века «пифагорейскими брюками».
Ученики на всю жизнь запомнили забавные стихи о пифагорейских брюках.
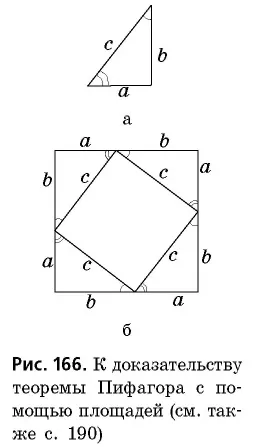
Используйте площадь для доказательства теоремы Пифагора.
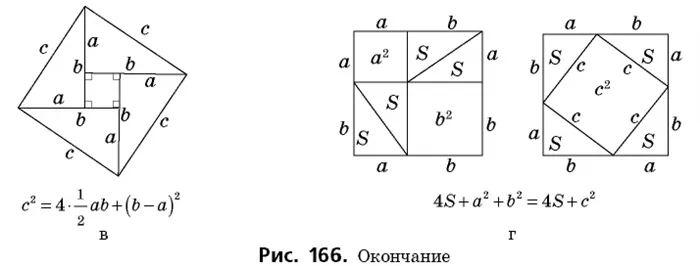
Проведите перпендикуляр к вертикальному прямоугольному треугольнику (рис. 166, а). Сделайте из него квадрат со сторонами квадрата. Итак: ^
т.е.
На рисунках 166, C и D показаны другие способы доказательства теоремы Пифагора с помощью площадей. В работе индийского математика XII века Бхаскари, один из них: «Смотрите!». сопровождается только словом «Смотри!». В целом, в настоящее время существует более 150 различных способов доказательства этой знаменитой теоремы. Однако каждый из вас может изобрести свой собственный метод.
Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, содержащей стороны
Сумма углов многоугольника Сумма углов выпуклости
Сумма внешних углов выпуклой фигуры
Внешние углы выпуклого многоугольника
Если все вершины лежат на окружности, многоугольник регистрируется как окружность.
Полигон описан как зарегистрированный.
Если все стороны принадлежат этому циклу, то многоугольник называется циклом периметра многоугольника.
Аксиомы площади
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата со стороной, равной единице длины, равна единице площади
План урока:
Пропорциональные отрезки
Определение подобных треугольников
Первый признак подобия треугольников
Второй и третий признаки подобия треугольников
Отношение площадей подобных треугольников
Пропорциональные отрезки
Если известна длина двух отрезков, то можно узнать, во сколько раз один из них больше другого. Например, если некоторый отрезок NM = 24 см, а другой отрезок KP = 4 см, то можно утверждать, что NM в 6 раз длиннее, так как
Величину NM/KP именуют отношением отрезков NM и KP. Надо заметить, что в ряде случаев отношение отрезков можно найти, не зная их длины. Пусть в ∆МКР проведена медиана МН. Очевидно, что отрезок КР будет вдвое длиннее КН, ведь Н – середина КР:
Другой пример – это отношение между диагональю квадрата и его стороной.
Используя теорему Пифагора, несложно показать, что в любом квадрате АВСD
Наконец, в прямоугольном треуг-ке, один из углов которого равен 30°, гипотенуза всегда вдвое длиннее меньшего из катетов:
Если отношение отрезка AB к А1В1 равно отношению отрезка СD к С1D1, то говорят, что отрезки AB и CD пропорциональны отрезкам А1В1 и С1D1. Например, пусть
Получается, AВ и CD пропорциональны А1В1 и С1D1. Важно отметить, что пропорциональны могут быть также сразу три и более отрезка.
Определение подобных треугольников
В жизни нередко можно наблюдать объекты, у которых совпадает форма, но отличаются размеры. В качестве примера можно привести мяч для настольного тенниса и баскетбольный мяч. Оба этих предмета имеют форму шара, на баскетбольный мяч значительно больше. Другой пример – настоящий танк и игрушка, изображающая его. Часто подобны друг другу матрешки, которые вкладываются друг в друга – все они выглядят одинаково, а отличаются только общим размером. Наконец, подобны и знаменитые египетские пирамиды:
Такие объекты в геометрии именуют подобными. Подобны друг другу любые две окружности и любые два квадрата. Но особо важную роль в геометрии играют подобные треугольники. Рассмотрим это понятие подробнее.
Пусть есть два треуг-ка, ∆AВС и ∆А1В1С1, у которых соответственно равны углы:
Стороны, которые лежат против одинаковых углов в таких треуг-ках, именуют сходственными. Ими являются стороны AВ и А1В1, ВС и В1С1, АС и А1С1.
Можно дать такое определение подобных треугольников:
Таким образом, подобие треугольников (оно обозначается символом ∾) обозначает выполнение сразу нескольких равенств:
Отношение между сходственными сторонами подобных треуг-ков именуется коэффициентом подобия и обозначается буквой k:
Грубо говоря, подобие треуг-ков означает, что их форма одинакова, но один из них в несколько раз больше или меньше другого. Чтобы получить, из одного треуг-ка другой, равный ему по размерам, его надо просто «масштабировать». Например, на этом рисунке все стороны исходного треуг-ка просто увеличили в три раза:
Это значит, что коэффициент подобия в данном случае равен 3. Однако важно понимать, что в различных геометрических задачах подобные треуг-ки также могут быть повернуты друг относительно друга:
Задание. ∆AВС подобен ∆DEF. Известно, что
Найдите длину ЕF.
Решение. Как только в задаче появляются подобные треуг-ки, стоит сразу же определить их коэффициент подобия, а для этого надо разобраться, какие стороны будут сходственными. Так как∠А = ∠Е, то лежащие против них стороны DF и ВС– сходственные. Их отношение и будет равно коэффициенту подобия:
Получили, что стороны ∆DEF вдвое длиннее сходственных им сторон ∆AВС. У подобных треуг-ков углы одинаковы, поэтому∠С = ∠D. Отсюда следует, что стороны AВ и ЕF сходственны, а потому ЕF вдвое больше:
Задание. ∆AВС и∆DEF – подобные. Известно, что
Найдите длину ЕF.
Решение. По сравнению с предыдущей задачей изменилось только одно условие, теперь∠А = ∠D. Однако это меняет сходственные стороны. Из подобия треуг-ков следует, что∠С = ∠Е. Тогда сходственными оказываются уже стороны AВ и DF. Найдем коэффициент подобия треугольников:
Сходственными являются также стороны ВС и ЕF (ведь∠А = ∠D), поэтому ЕF в 1,25 раза длиннее:
Эти две задачи показывают, как важно правильно определять сходственные стороны подобных треугольников.
Естественно, что все равные друг другу треуг-ки являются одновременно и подобными, причем их коэффициент подобия равен единице.
Задание. Докажите, что у подобных треуг-ков отношение их периметров равно коэффициенту подобия.
Решение. Пусть подобны ∆ AВС и ∆А1В1С1, причем
Периметр ∆AВС можно вычислить так:
Мы доказали утверждение, сформулированное в условии.
Первый признак подобия треугольников
Оказывается, для того, чтобы доказать подобие треуг-ков, не требуется сравнивать все их углы и находить соотношение всех сторон. Существуют три простых признака подобия треугольников.
Однако прежде, чем сформулировать их, нам придется доказать отдельное утверждение, которое известно как обобщенная теорема Фалеса («обычную», не обобщенную теорему мы уже изучали ранее).
Если прямые ВВ1 и СС1 (показаны красным цветом)параллельны, то отрезки AВ и АС пропорциональны отрезкам AВ1 и АС1, то есть справедливо соотношение:
Доказывать будем от противного. Пусть отрезки AВ и АС непропорциональны AВ1 и АС1. Тогда отметим наАС такую точку Н, которая разобьет АС на пропорциональные отрезки, то есть
Естественно, эта точка не будет совпадать с С1. Рассмотрим случай, когда она окажется правее, чем С1:
Теперь поступим следующим образом. Проведем через стороны угла большое число прямых, параллельных ВС, которые будут разбивать АС на одинаковые отрезки. По теореме Фалеса эти же прямые отсекут одинаковые отрезки и на AВ. При этом мы проведем настолько много параллельных прямых, что хотя бы одна из них пересечет отрезок С1Н:
Пусть эта прямая пересечет отрезок С1Н в некоторой точке С2, а сторону AВ в точке В2. Ясно, что отрезки AВ и АВ2 пропорциональны отрезкам АС и АС2, так как они состоят из одинакового количества одинаковых отрезков. Например, на построенном рисунке отношение AB2 к AB равно 5/8, так как AB2 состоит из 5 отрезков, отсеченных зелеными параллельными прямыми, а AB состоит из 8 таких отрезков. Аналогично и отношение АС2 к АС также равно 5 к 8. Таким образом, можно записать:
Здесь мы рассмотрели случай, когда точка Н лежит правее С1, то есть АН >C1. Случай, когда АН <АС1, рассматривается аналогично, и также получается противоречие. Эти противоречия означают, что на самом деле точка Н должна совпадать с С1, то есть справедливо равенство
ч.т. д.
Теперь, доказав обобщенную теорему Фалеса, мы можем перейти к первому признаку подобия треугольников.
Действительно, пусть есть ∆AВС и ∆А1В1С1, у которых
Так как сумма углов у любого треуг-ка постоянна и составляет 180°, то должны быть одинаковы и третьи углы:
При таком наложении прямые ВС и В1С1 окажутся параллельными, так как соответственные углы ∠В1С1А и ∠ВСА одинаковы. Но параллельные прямые должны отсекать на сторонах угла пропорциональные отрезки, то есть
У ∆AВС и ∆А1В1С1 углы одинаковы, а лежащие напротив них стороны пропорциональны, следовательно, это подобные треуг-ки.
Задание. Прямая, параллельная стороне AВ ∆AВС, пересекает стороны ВС и АС в точках Е и Р. Известно, что ЕС = 2, ВЕ = 3, ЕР = 3,2. Какова длина AВ?
Решение. В данной задаче есть только два треуг-ка, ∆AВС и ∆РЕС. Докажем их подобие. У них есть общий∠С, а ∠СЕР = ∠СВА, ведь это односторонние углы при параллельных прямых ЕР и AВ. Отсюда следует, что ∆AВС∾∆РЕС. Значит, ∠А = ∠СРЕ.
Далее надо найти коэффициент подобия. Стороны СЕ и ВС лежат против равных углов∠А и ∠СРЕ, поэтому они сходственные.
Задание. По данным рисунка найдите длину КЕ:
Решение. На рисунке показано, что ∠ВСА = ∠СКЕ, а∠А = ∠Е = 90°. То есть у ∆AВС и ∆СКЕ есть два одинаковых угла, и, следовательно, они подобны. Сходственными будут являться стороны AВ и ЕС, с их помощью найдем коэффициент подобия:
Задание. Основания трапеции имеют длины 5 и 8 см. Длины ее боковых сторон составляют 3,6 и 3,9 см. Продолжения боковых сторон пересекаются в точке М. Определите расстояние от М до вершин меньшего основания.
Решение. Для начала выполним построение:
Отрезки ВС и АD параллельны, так как они являются основаниями трапеции. Отсюда получаем равенство соответственных углов:
Теперь посмотрим на ∆АМD и ∆ВМС. МЫ только что выяснили, что у них есть одинаковые углы (∠МВС и ∠МАD), а ∠М является общим для них. Тогда получаем, что эти треуг-ки подобны. Стороны ВС и AD будут сходственными, так как лежат против одного и того же ∠М, поэтому по их длине можно найти коэффициент подобия:
Для нахождения МВ обозначим его длину как х. Тогда отрезок АМ будет иметь длину х + 3,9. Но из подобия треуг-ков следует такое соотношение:
Подставив сюда значение k и выраженные через х длины АМ и МВ, получим уравнение:
МС можно найти таким же путем, обозначив его длину как у. Тогда отрезок МD будет равен у + 3,6, и можно составить уравнение:
Второй и третий признаки подобия треугольников
Существует ещё два признака подобия треуг-ков, которые в решении задач используются значительно реже. Они выводятся непосредственно из первого признака.
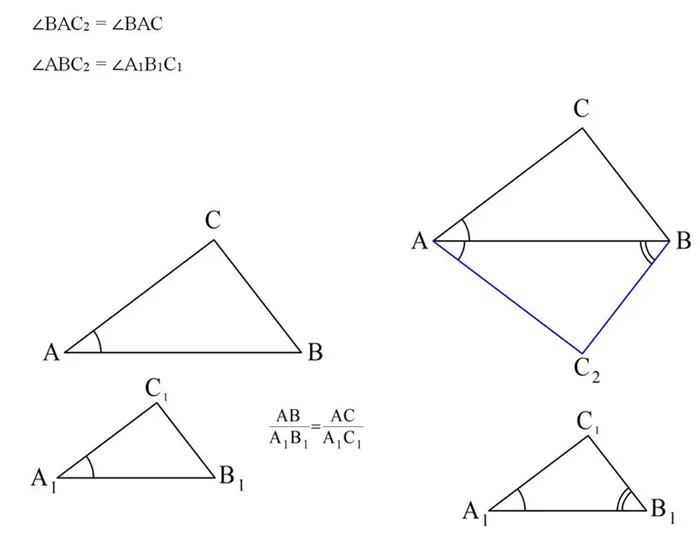
Докажем второй признак подобия. Пусть есть ∆AВС и ∆А1В1С1, для которых выполняются соотношения:
Необходимо доказать, что они подобны. Для этого построим ещё один ∆AВС2, который будет иметь общую сторону с ∆AВС, причем точку С2 мы выберем так, что будут выполняться условия:
∆А1В1С1 и ∆AВС2 будут подобными, ведь у них одинаковы два угла. Значит, будет выполняться соотношение
Но тогда ∆AВС и ∆AВС2 будут равными, ведь у них одинаковы две стороны и угол, образованный этими сторонами:
В итоге у ∆AВС и ∆А1В1С1 оказываются два одинаковых угла, то есть они подобны друг другу
ч. т. д.
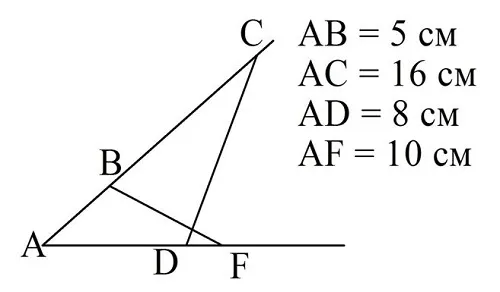
Задание. На стороне угла отмечены точки A и В так, что AВ = 5 см и АС = 16 см. На другой стороне этого же угла отмечены точки С и D так, что AD = 8 cм и AF = 10 см. Подобны ли ∆АСD и ∆AFB?
Решение.
У рассматриваемых треуг-ков есть общий угол ∠А. Найдем отношение сторон, прилегающих к этому углу.
Отношения одинаковы, значит, треуг-ки подобны.
Примечание. В данном случае важно понимать, какие стороны надо делить друг на друга. У ∆АСD известны стороны АС и АD, равные 16 и 8 см. У ∆AFB известны AF и AB, которые составляют 10 и 5 см. Делить надо большую сторону одного треуг-ка на большую сторону другого треуг-ка, то есть 16 на 10. Потом же делим меньшие стороны, то есть 8 на 5.Если получили одно и тоже число, то это значит, что рассмотренные треуг-ки подобны, причем полученное число как раз и является коэффициентом подобия.
Рассмотрим третий признак подобия треуг-ков.
Докажем его. Пусть у ∆AВС и ∆А1В1С1 пропорциональны их стороны:
Можно заметить, что ∆AВС2 и ∆А1В1С1 подобны, ведь у них совпадают два угла. Тогда верны соотношения:
Самая левая дробь в обоих случаях одинакова, а в других отличны лишь числители. Значит, эти числители одинаковы:
Но тогда у ∆AВС и ∆AВС2 совпадают все стороны, то есть эти треуг-ки равные. Следовательно. Так как ∆AВС2 подобен ∆А1В1С1, то и равный ему ∆AВС также подобен ∆А1В1С1
ч. т. д.
Задание. Подобны ли ∆AВС и ∆DEF, если их стороны имеют длины:
Решение.
Для проверки достаточно просто поделить длины сторон друг на друга. При этом большую сторону одного треуг-ка будем делить на большую сторону другого, а меньшую – на меньшую. Если в результате отношение всех трех сторон будет одинаково, то можно утверждать, что треуг-ки подобны:
Все три раза мы получали число 2, именно оно и является коэффициентом подобия треуг-ков.
Отношение площадей подобных треугольников
Если треуг-ки подобны, то их стороны отличаются в k раз, где k– коэффициент подобия. А как соотносятся друг с другом длины их высот, медиан и других характерных отрезков. Несложно догадаться, что они также отличаются в k раз.
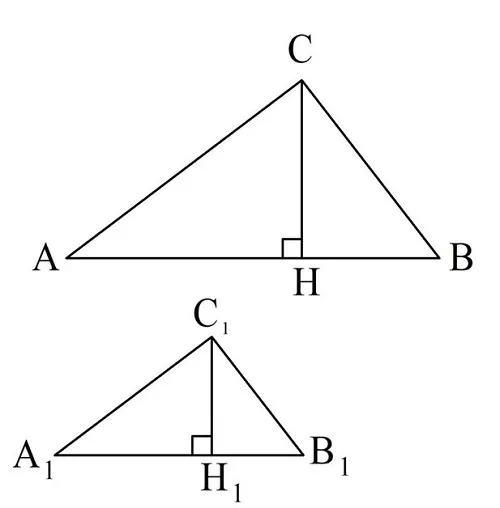
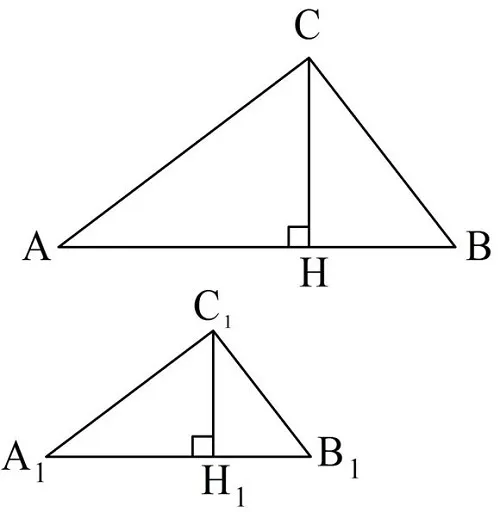
Докажем это на примере высот. Пусть есть подобные ∆AВС и ∆А1В1С1, причем их коэффициент подобия равен k:
Проведем в них высоты СН и С1Н1:
Теперь сравним ∆АСН и ∆А1С1Н1. Из подобия ∆AВС и ∆А1В1С1 следует, что
Аналогично можно доказать, что в k раз будут отличаться длины медиан и биссектрис.
А каким будет отношение площадей подобных треугольников?Оказывается, что они отличаются уже в k2 раз. Докажем это.
Пусть ∆AВС и ∆А1В1С1 подобны с коэффициентом подобия k. Снова проведем в них высоты СН и СН1:
Запишем очевидные равенства:
В итоге получили, что площади подобных треугольников отличаются в k2 раз.
Задание. Известно, у ∆AВС площадь составляет 10, а отрезок AВ имеет длину 5. ∆DEF подобен ∆AВС, причем сторона DE, сходственная AВ, равна 15. Вычислите площадь ∆DEF.
Решение. По условию задачи легко найти коэффициент подобия ∆AВС и ∆DEF, надо лишь поделить одну сходственную сторону на другую:
Задание. Площади двух подобных треуг-ков составляют 75 м2 и 300 м2. Одна из сторон второго треуг-ка равна 9 м. Вычислите сходственную ей сторону первого треуг-ка.
Решение. Зная площади треуг-ков, легко найдем коэффициент их подобия:
Если коэффициент равен 2, то стороны первого многоугольника вдвое меньше сторон второго, поэтому интересующая нас сторона равна
9:2 = 4,5 м
Ответ: 4,5 м.
ВИДЕОУРОК
Две фигуры подобны, если каждой точке одной
фигуры можно сопоставить точку другой фигуры так, что для любых двух точек А и В одной
фигуры и сопоставимых им точек А1 и В1 другой фигуры выполняется условие
где k – одно и то же положительное число для всех точек.
Число k – коэффициент подобия фигур.
Признаки подобия прямоугольных
треугольников.
Два прямоугольных
треугольника подобны между собой, если:
– острый угол
одного треугольника равен острому углу другого треугольника;
– катеты одного
треугольника пропорциональны катетам другого треугольника;
– гипотенуза и
катет одного треугольника пропорциональны гипотенузе и катету другого
треугольника.
Отношение периметров
подобных прямоугольных треугольников равно отношению сходственных сторон
(коэффициенту подобия):
Отношение площадей
подобных прямоугольных треугольников равно квадрату отношения соответствующих
сторон (квадрату коэффициента подобности).
Высота
прямоугольного треугольника, проведённая из вершины прямого угла, делит
треугольник на два подобных треугольника, каждый из которых подобен данному
треугольнику.
ПРИМЕР:
∆ АВС, ∠ С = 90°, СМ – высота,
∆ АМС ∼ ∆ СМВ.
При проведении всех
трёх средних линий образуется 4 равных
треугольника, подобных исходному с коэффициентом 1/2.
ЗАДАЧА:
Параллельные прямые ВС и DЕ пересекают стороны угла А, изображённого
на рисунку.
АВ = 6 см,
АС = 4 см,
СE = 2 см.
Найдите длину отрезка АD.
РЕШЕНИЕ:
∆ ABC
~ ∆ ADE, тогда
ОТВЕТ: 9 см
ЗАДАЧА:
По данным, изображённым на
рисунку, найдите высоту дерева.
РЕШЕНИЕ:
ЗАДАЧА:
Середина боковой стороны равнобедренного треугольника удалена
от его основания на 9 см. Найдите расстояние от точки пересечения медиан треугольника
до его основания.
РЕШЕНИЕ:
Начертим чертёж.
Треугольники АМD и АКL – подобные.
MD = 6 (см).
ЗАДАЧА:
Отрезки АС и СD, изображённые на
рисунку,
параллельны,
∠
АВС = 90°, АВ
= 24 см,
ВО = 10
см, СО = 5 см.
Найдите длину отрезка АD.
РЕШЕНИЕ:
СD ∥
АВ, ∠ АВС = 90°,
АВ = 24 см,
ВО = 10 см,
СО = 5 см.
Так как
СD ∥
АВ і
AВ ⊥ ВС, то
DС ⊥ ВС, то есть
∠ ВСD = 90°.
Из ∆ AВО (∠ В = 90°):
∠ АОВ = ∠ DОС как вертикальные.
∆ DСО ~ ∆ AВО,
Поэтому,
AD = AO + OD =
= 26 + 13 = 39 см.
ОТВЕТ: 39 см
ЗАДАЧА:
В треугольнике АВС отрезок ВК –
высота, отрезок АМ – биссектриса,
ВК = 26 см,
АВ : АС
= 6 : 7.
Из точки М опущен
перпендикуляр МD на сторону
АС. Найдите отрезок МD.
РЕШЕНИЕ:
Начертим чертёж.
По свойству биссектрисы треугольника имеем:
ВМ : МС = АВ : АС = 6 : 7.
Пусть ВМ = 6х,
тогда
МС = 7х,
ВС = 6х + 7х = 13х.
По условию, ВК ⊥
АС и
МD ⊥ АС.
Поэтому ВК
∥ МD и
∆ СВК ~ ∆ СМD.
Откуда:
ВК : МD = ВС : МС,
26 : МD = 13х : 7х.
ОТВЕТ: 14 см
ЗАДАЧА:
Окружность, центр которой принадлежит гипотенузе прямоугольного
треугольника, касается большого катета и проходит через вершину противоположного
острого угла. Найдите радиус окружности, если катеты равны 5
см и
12
см.
РЕШЕНИЕ:
Пусть треугольник АСВ (∠ С = 90°) – данный прямоугольный
треугольник,
АС = 5 см, ВС = 12
см,
О –
центр окружности,
ОD ⊥ ВС, D –
точка касания окружности с центром О до катета ВС,
ОD = ОА –
радиус окружности.
Из прямоугольного треугольника АСВ имеем:
Поэтому ОD
∥ АС и треугольники АСВ и ОDВ подобные.
Нехай
ОD = ОА = х.
Тогда ОВ = 13 – х.
Получим:
ОВ : ОD = АВ : АС,
(13 – х) : х = 13 : 5,
(13 – х) ∙ 5
= 13x,
65 – 5х = 13х, 18х = 65,
х = 65 : 18, х = 311/18,
Поэтому, радиус окружности равен 311/18
см.
ОТВЕТ: 311/18 см
ЗАДАЧА:
Катет прямоугольного треугольника равен 8 см,
а гипотенуза – 16 см. Найдите проекцию данного катета на гипотенузу.
РЕШЕНИЕ:
Начертим чертёж.
∆ АВС ~ ∆ ВDС, поэтому
ЗАДАЧА:
Боковая сторона равнобедренного треугольника точкою касания
вписанной окружности делится в отношении
8
: 9, считая
от вершины угла при основании треугольника. Найдите площадь треугольника, если
радиус вписанной окружности равен 16 см.
РЕШЕНИЕ:
Пусть АВС – равнобедренный
треугольник (АВ = ВС) с центром вписанной окружности О,
К – точка касания окружности до стороны ВС,
ОК = 16 см,
СК : КВ
= 8 : 9.
Пусть СК = 8х,
тогда
ВК = 9х,
ВС = 8х + 9х = 17х (см).
Проведем высоту ВD треугольника. Треугольник ОКВ прямоугольный
(∠ К = 90°), тому
По свойству касательных, проведённых из одной точки до окружности,
СD = СК = 8х.
Из подобности прямоугольных треугольников ВОК и ВСD (у них общий острый угол) получим:
256 + 81х2 = 1156,
81х2 = 900, х2 = 900/81,
х =
10/3.
DС = 8х = 10/3 ∙ 8
= 80/3 (см).
ВС = 17х
= 17 ∙ 10/3 = 170/3 (см).
Р = 2 ∙ (80/3 + 170/3) = 500/3 (см).
S∆ABC = 1/2 р ∙ r = 1/2 ∙ 500/3 ∙16
=
= 4000/3 = 13331/3 (см2).
ОТВЕТ: 13331/3 см2
ЗАДАЧА:
Центр окружности, вписанной в равнобедренный треугольник,
делить его высоту, проведённую до основания, на отрезки, длины которых равны 10
см и
26
см. Найдите площадь данного треугольника.
РЕШЕНИЕ:
Пусть АВС – заданный равнобедренный треугольник (АВ = ВС),
О –
центр вписанной окружности,
ВD –
высота треугольника,
ОD = 10 см, ОВ = 26 см,
К – точка касания кола до боковой стороны АВ,
ОК = ОD = 10 см.
Из прямоугольного
треугольника ВКО (∠ К = 90°) имеем:
ВD = ВО + ОD =
= 26 + 10 = 36 (см).
Из подобных прямоугольных треугольников
АВD і ОВК имеем:
АD : ВD = КО : КВ,
АD : 36
= 10 : 24
Находим площадь треугольника АВС.
SABC = 1/2 AC ∙
BD =
= AD ∙
BD
=
=
15 ∙ 36 = 540 (см2).
ОТВЕТ: 540 см2
ЗАДАЧА:
На медиане ВD равнобедренного
треугольника АВС (АС = ВС) взята точка
К такая, что
КD = 2ВК.
Прямая АК пересекает сторону ВС в точке
М.
Найдите площадь треугольника АМС, если площадь треугольника АВС равна 20.
РЕШЕНИЕ:
Начертим чертёж.
ВD –
медиана треугольника АВС, проведённая к его основанию, следовательно, ВD является высотой
и биссектрисой. Проведём прямую ВF параллельную АС до пересечения её с продолжением АМ в точке F.
Пусть
АD = DС = х, АС = 2х.
Треугольник АКD подобен
треугольнику FКВ по двум углам
(∠ КAD
= ∠ КFB, ∠ AKD = ∠ FKB),
следовательноотсюда
BF = 1/2 AD = 1/2 x.
Треугольник АMC подобен
треугольнику FMB
(∠ AMC
= ∠ FMB, ∠ MAC = ∠ MFB),
поэтому
отсюда
BF = 1/2 AD = 1/2 x.
Треугольник АMC подобен
треугольнику FMB
(∠ AMC
= ∠ FMB, ∠ MAC = ∠ MFB),
поэтому
Треугольники АВС и АМС имеют
одинаковую высоту, проведённую из вершины
А. Следовательно их площади относятся также, как
стороны к которым эта высота проведена.
отсюда получим, что
SAМC = 4/5 SAВС =
= 4/5∙ 20 = 16.
ЗАДАЧА:
Диагональ равнобедренной трапеции перпендикулярна до боковой
стороны, а основание равно 28 см и 100
см. Найдите длины отрезков, на которые высота трапеции, проведённая из вершины
тупого угла, делит диагональ.
РЕШЕНИЕ:
Пусть АВСD (АВ ∥ СD) – равнобедренная трапеция,
ВЕ и СК – высоты,
АС ⊥ СD,
ВС = 28 см,
АD = 100 см,
О –
точка пересечения прямых АС и ВЕ.
Проведём медиану СМ треугольника АСD (∠ С
= 90°). По свойству медианы, проведённой из вершины прямого угла
прямоугольного треугольника, получим
СМ = АМ = МD = 50 (см).
MK = MD – KD =
= 50 – 36
= 14 (см).
Из треугольника
МКС (∠ К = 90°) имеем:
Из треугольника АКС (∠ К = 90°) имеем:
∆ AOE ~ ∆ СOB,
(∠ OAE = ∠ OCB, ∠ OBC = ∠ OEA), тому
откуда
Пусть АО = 9х (см), тогда
ОС = 7х (см).
АО + ОС = АС,
9х + 7х = 80, х = 5 (см).
АО = 45 см, ОС = 35 см.
ОТВЕТ: 45 см, 35 см
ЗАДАЧА:
Два равных равнобедренных прямоугольных
треугольника с катетами а расположены так, что катет ВС ∆ АВС параллельный гипотенузе А1В1 ∆ А1В1C1. Вершины В и С соответственно лежат на катетах А1C1 и В1C1. Определите площадь трапеции BCMN.
РЕШЕНИЕ:
Из ∆ АВN выходит, что
MN = AM = a – MC.
∆ А1C1B1 ~ ∆ BCC1, поэтому
то есть
Откуда
MC = a(√͞͞͞͞͞2– 1);
MN = a(2
– √͞͞͞͞͞2 );
Поэтому,
Задания к уроку 15
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Единицы измерения площади
- Урок 2. Площадь прямоугольника
- Урок 3. Площадь квадрата
- Урок 4. Площадь треугольника
- Урок 5. Площадь прямоугольного треугольника
- Урок 6. Площадь равнобедренного треугольника
- Урок 7. Площадь параллелограмма
- Урок 8. Площадь ромба
- Урок 9. Площадь трапеции
- Урок 10. Площадь равнобедренной трапеции
- Урок 11. Площадь прямругольной трапеции
- Урок 12. Площадь круга и его частей
- Урок 13. Подобие разносторонних треугольников
- Урок 14. Подобие равнобедренных треугольников
- Урок 16. Площадь многоугольника
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Отношение площадей подобных треугольников
Теорема
Доказательство
Дано: 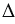
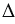
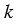
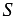
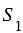
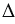
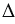
Доказать: 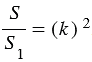
Доказательство:
1. 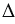
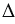
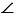
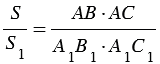
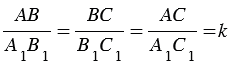
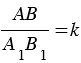
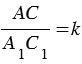
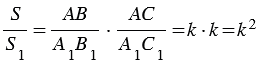
Теорема доказана.
Советуем посмотреть:
Пропорциональные отрезки
Определение подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 543,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 544,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 545,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 546,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 622,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 627,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1077,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1143,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1209*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1308,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник