Сначала вариант, предложенный FEBUSoм.
Обозначим высоту трапеции h.
Тогда площадь трапеции равна (1/2)*(3+4)*h=3,5*h.
Высота треугольника АМD (проведённавя из точки М к основанию АD) равна h/2.
Площадь треугольника АМD (1/2)*4*(h/2)=h.
Площадь треугольника ECD (1/2)*(4/2)*h=h.
Если из площадей этих треугольников вычесть площадь треугольника ОЕD, то площади остатков (четырёхугольника АМОЕ и треугольника СОD) будут равны.
Продолжим отрезок DM за точку М и верхнее основание ВС за точку В. Точку пересечения продолжений обозначим К.
Очевидно, что треугольники AMD и MBK – равны. КС=3+4=7.
Очевидно, что треугольники КОС и ОЕD подобны, коэффициент подобия равен 7:2. Значит высоты треугольников КСО и ЕОD, проведённые из точки О к основаниям трапеции, также относятся как 7:2.
Высота треугольника ОЕD (проведённавя из точки О к основанию ED) равна (2/(2+7))*h=(2/9)*h.
Площадь четырёхугольника АМОЕ равна h-(2/9)*h=(7/9)*h, что составляет от площади трапеции (7/9)*h/(3,5*h)=2/9.
Задача, в редакции Mefody66 совершенно аналогична и решается точно так же. Только он при записи задачи пропустил важнейшее условие, а именно длину верхнего основания, поэтому задача не могла быть решена. Кстати, если бы была указана длина верхнего основания (CD) то не было бы необходимости в том, чтобы трапеция была равнобочной.
Допустим, что верхнее основание составляет некую долю k (k<1)от нижнего основания.
Пусть нижнее основание равно х, тогда верхнее равно kx. Обозначим высоту трапеции h.
Продлим отрезок АN за точку N и отрезок DC за точку С. В пересечении этих продолжений поставим точку К. Далее полная аналогия. Треугольники NKC и АВN равны, КС=АВ=х. Тогда KD=х+kx=(k+1)*x.
Треугольники KDP и APM подобны, коэффициент подобия равен (k+1)*x/(х/3)=3*(k+1).
Высота треугольника АРМ равна (1/(3*(k+1)+1))*h=h/(3*k+4), а площадь (1/2)*(х/3)*h/(3*k+4)=х*h/(18k+24).
Высота треугольника ANB равна h/2, а площадь (1/2)*х*(h/2)=х*h/4.
Отношение площадей S(APM) : S(ANB) равно (х*h/(18k+24))/(х*h/4)=1/(4,5*k+6).
Трапеция, ее свойства, формулы площади, высоты, сторон.
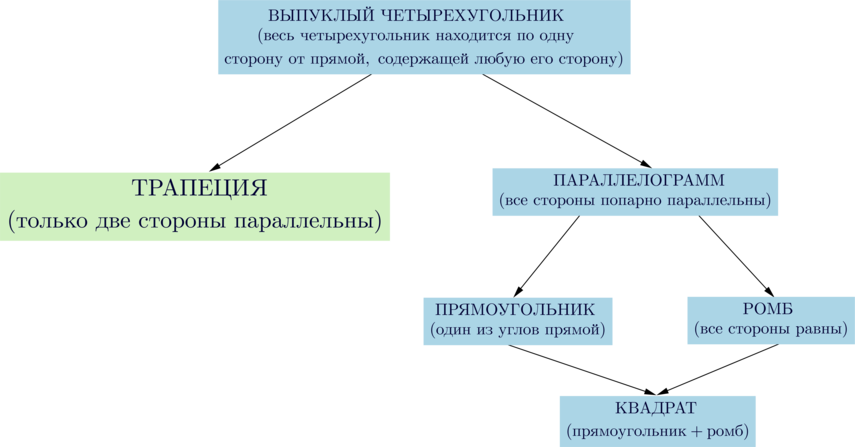
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция (понятие, определение)
Видеоурок “Трапеция”
Виды трапеций
Элементы трапеции: основания, боковые стороны, средняя линия и высота
Свойства трапеции
Свойства равнобедренной трапеции
Формулы трапеции
Трапеция (понятие, определение):
Трапеция (от др.-греч. τραπέζιον – «столик» от τράπεζα – «стол») – это выпуклый четырёхугольник, у которого две стороны параллельны, а другие две стороны не параллельны.
Трапеция – это выпуклый четырехугольник, у которого только одна пара сторон параллельна.
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, и стороны не равны между собой.
Рис. 1. Трапеция
Выпуклым четырёхугольником называется четырёхугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
@ https://youtu.be/Q4EpXexoMrM
Виды трапеций:
Равнобедренная трапеция или равнобокая трапеция – это трапеция, у которой боковые стороны равны.
Рис. 2. Равнобедренная трапеция
Прямоугольная трапеция – это трапеция, один из углов при боковой стороне которой прямой.
Прямоугольная трапеция – это трапеция, имеющая прямые углы при боковой стороне.
Рис. 3. Прямоугольная трапеция
Элементы трапеции: основания, боковые стороны, средняя линия и высота:
Параллельные стороны трапеции называются основаниями трапеции, а две другие – непараллельные – боковыми сторонами.
Рис. 4. Трапеция
AD и BC – основания трапеции, AB и CD – боковые стороны трапеции.
AD – большее основание трапеции, BC – меньшее основание трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, называется средняя линия.
Рис. 5. Трапеция и срединная линия
Расстояние между основаниями трапеции называется высотой трапеции.
Рис. 6. Трапеция
Высота трапеции (h) определяется формулой:
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
Свойства трапеции:
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Рис. 7. Трапеция и срединная линия
MN || BC, MN || AD,
l = (a + b) / 2
2. Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований и лежит на средней линии.
Рис. 8. Трапеция
MN = (b – a) / 2
3. Сумма внутренних углов трапеции (и любого другого четырёхугольника) равна 360° .
Сумма углов, прилежащих к боковой стороне трапеции, равна 180° .
Рис. 9. Трапеция
4. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
Рис. 9. Трапеция
5. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

AB = BK
6. Если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Рис. 11. Трапеция
∠BAD + ∠CDA = 90°, MN = (AD – DC) / 2
7. В трапецию можно вписать окружность, если сумма длин оснований трапеции равна сумме длин её боковых сторон.
Рис. 12. Трапеция
AB + CD = AD + BC
В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
Рис. 13. Трапеция
Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований).
Рис. 14. Трапеция
MN = (AB + CD) / 2,
MN = (AD + BC) / 2
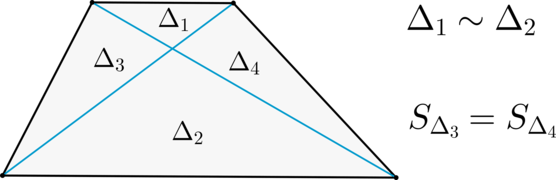
8. Диагонали трапеции делят ее на 4 треугольника.
Два из них, прилежащие к основаниям, подобны.
Два других, прилежащие к боковым сторонам, имеют одинаковую площадь.
Рис. 15. Трапеция
Треугольники BCO и AOD подобны. Коэффициент подобия треугольников (k) находится как отношение оснований трапеции. k = AD / BC. Отношение площадей этих подобных треугольников есть k2.
Треугольники ABO и CDO имеют одинаковую площадь.
9. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями.
Рис. 16. Трапеция
BC : AD = OC : AO = OB : DO
10. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c 2 + d 2
где b – большее основание трапеции, a – меньшее основание трапеции, c и d – боковые стороны трапеции.
11. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основания трапеции, так же делит диагонали пополам.
Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия
Рис. 17. Трапеция
AK = KB, AM = MC, BN = ND, CL = LD,
KL – средняя линия, UV – отрезок, который соединяет основания трапеции
12. Средняя линия разбивает трапецию на две трапеции, площади которых соотносятся как:
где b – большее основание трапеции, a – меньшее основание трапеции, S1 и S2 – площади образованных трапеций, в результате разделения средней линией.
Рис. 18. Трапеция
S1 – площадь трапеции MBCN,
S2 – площадь трапеции AMND
Свойства равнобедренной трапеции:
1. Прямая, которая проходит через середины оснований, перпендикулярна основаниям, тем самым, является осью симметрии равнобедренной трапеции.
2. Высота, опущенная из вершины на большее основание равнобедренной трапеции, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
3. Углы при любом основании равнобедренной трапеции равны.
4. Сумма противоположных углов равнобедренной трапеции равна 180°.
5. Длины диагоналей равнобедренной трапеции равны.
6. Вокруг равнобедренной трапеции можно описать окружность.
7. При перпендикулярности диагоналей в равнобедренной трапеции ее высота равна полусумме оснований.
Формулы трапеции:
Пусть a – большее основание трапеции, b – меньшее основание трапеции, c – левая сторона трапеции, d – правая сторона трапеции, α и β – углы при нижнем основании трапеции, d1 и d2 – диагонали трапеции, m – средняя линия трапеции, h – высота трапеции, γ и δ – углы между диагоналями трапеции, S – площадь трапеции, P – периметр трапеции.
Формулы для определения сторон трапеции:
Через среднюю линию и одно из оснований трапеции:
a = 2m – b
b = 2m – a
Через высоту и углы при нижнем основании трапеции:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
Через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
Через высоту и углы при нижнем основании трапеции:
Формулы для определения средней линии трапеции:
Через длины оснований трапеции:
Через площадь и высоту трапеции:
Формулы для определения высоты трапеции:
Через сторону и прилегающий угол при нижнем основании трапеции:
h = c·sin α = d·sin β
Через диагонали трапеции и углы между ними:
Через диагонали трапеции, углы между ними и среднюю линию трапеции:
Через площадь и длины оснований трапеции:
Через площадь и длину средней линии трапеции:
Формула для определения периметра трапеции:
P = a + b + c + d
Формулы для определения площади трапеции:
Через основания и высоту трапеции:
Через среднюю линию и высоту трапеции:
S = m · h
Через диагонали трапеции и угол между ними:
Через все стороны трапеции:
С помощью формулы Герона для трапеции:
Как называется объемная трапеция?
Если трапецию изобразить в объеме, то такая фигура будет напоминать усеченную пирамиду.
В правильной усеченной пирамиде боковые грани являются равнобокими трапециями.
Квадрат
Овал
Полукруг
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Трапеция
Тупой угол
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Видео https://youtu.be/Q4EpXexoMrM
Коэффициент востребованности
6 463
Вдохновение нужно в геометрии не меньше, чем в поэзии.
В школьной геометрии весьма часто встречаются задачи, связанные с вычислением площади трапеции. К настоящему времени имеется немало учебного материала на эту тему. Некоторые из новых разработок автора изложены в настоящей статье.
Основные понятия и определения
Пусть в трапеции основаниями являются стороны
и
. Обозначим через
перпендикуляр, опущенный на основание
, и пусть диагонали трапеции
и
в точке пересечения образуют угол
. Тогда для вычисления площади
, как правило, используются формулы:
и
.
Если через вершины трапеция можно провести окружность, то для вычисления
применяется формула Брахмагупты:
, (1)
где полупериметр трапеции. Отметим, что такая окружность существует тогда и только тогда, когда трапеция является равнобедренной (иначе – равнобочной, равнобокой).
Так как в равнобедренной трапеции боковые стороны
и
равны, то формула (1) принимает вид
. (2)
Если в равнобедренную трапецию можно вписать окружность, то
. В таком случае
или
, а из формулы (2) вытекает более простая формула
. (3)
Рассмотрим более сложные приемы, которые используются для вычисления площади трапеции .
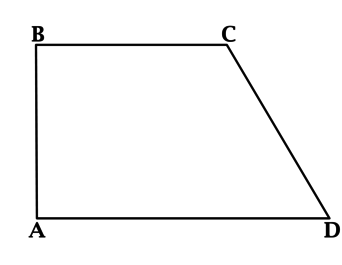
Пусть задана трапеция . Проведем через вершину
прямую, параллельную диагонали
, и обозначим через
точку пересечения этой прямой с продолжением основания
(рис. 1).
Теорема 1. Площади трапеции и треугольника
равны, т.е.
.
Доказательство. Так как (по определению) и
(по построению), то
и
. Обозначим
.
Известно, что и
. Поскольку
, то
. Теорема доказана.
Применяя формулу Герона для вычисления , получаем
, (4)
где . При выводе формулы (4) учитывался тот факт, что
,
и
.
Формулой (4) удобно пользоваться в том случае, когда требуется найти площадь трапеции по двум ее основаниям и обеим диагоналей.
Теорема 2. Если ,
и
, то
. (5)
Доказательство. Треугольники ,
и
, приведенные на рис. 1, являются подобными. В этой связи, используя свойства подобных треугольников, можно записать
и
.
Так как , то
. Следовательно, теорема доказана.
Если обе части равенства (5) возвести в квадрат, то получим
. (6)
Так как для произвольной трапеции имеет место равенство
, то из формулы (6) вытекает
и
.
Приведем весьма интересное, однако малоизвестное, свойство произвольной трапеции . Пусть средняя линия
разбивает трапецию
на две трапеции:
и
. Тогда справедлива следующая теорема.
Теорема 3. Если и
, то
. (7)
Доказательство теоремы приведено в учебном пособии автора «Математика для старшеклассников: дополнительные разделы школьной программы» (М.: Ленанд / URSS, 2014).
Примеры решения задач
Пример 1. Найти , если основания трапеции
,
и диагонали
и
.
Решение. Воспользуемся формулой (4), где
.
В таком случае
.
Ответ: .
Пример 2. В равнобедренной трапеции диагонали взаимно перпендикулярны и
. Найти
.
Решение. Так как трапеция является равнобедренной, то
. Пусть
(рис. 1). Тогда
,
и
. Отсюда следует, что
является равнобедренным и прямоугольным с гипотенузой
или
. Далее по теореме Пифагора получаем
или
.
Поскольку или
и
, то
. Однако
(теорема 1), поэтому
.
Ответ: .
Пример 3. Трапеция разделена диагоналями
и
на четыре части. Найти площадь ее большей части, если
и
.
Решение. Обозначим и
(рис. 1). Так как треугольники
и
являются подобными, то
.
Однако по условию , поэтому
или
. Принимая во внимание теорему 2, имеем
. Так как
и
, то
,
или
. В таком случае
.
Ранее было установлено, что и
. Поскольку
и
, то
и
.
Ответ: .
Пример 4. В трапеции известно:
,
и
, где отрезок
соединяет середины оснований
и
. Найти
.
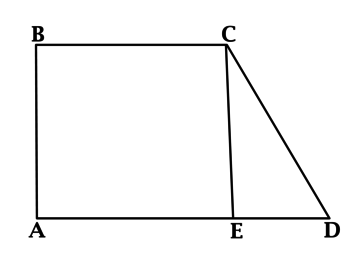
Решение. На рис. 2 изображена трапеция , где
и
. Так как
и
, то
. Поскольку
, то
медиана
.
По известной формуле вычисления медианы по трем сторонам треугольника имеем
.
Отсюда следует или
.
Так как ,
и
, то
является прямоугольным и
. Согласно теореме 1, здесь имеем
.
Ответ: .
Пример 5. В трапеции стороны
,
,
и
. Найти
.
Решение. На рис. 3 приведена трапеция , в которой на основание
опущены перпендикуляры
и
. Так как
и
, то
и
.
Обозначим . Поскольку
,
и
, то
или
Так как ,
и
, то получаем уравнение
. Отсюда следует
.
Если , то
. Так как
,
и
, то
.
Ответ: .
Пример 6. Стороны равнобедренной трапеции равны
,
и
. Найти
.
Решение. Так как ,
,
и
, то для трапеции
выполняется равенство
. Наличие такого равенства свидетельствует о том, что в данную трапецию можно вписать окружность. В этой связи для нахождения
можно использовать формулу (3), т.е.
.
Ответ: .
Пример 7. Задана трапеция , в которой точка
делит боковую сторону
пополам и
. Найти
.
Решение. Проведем через точку отрезок прямой
. Так как
(по условию), то
и
.
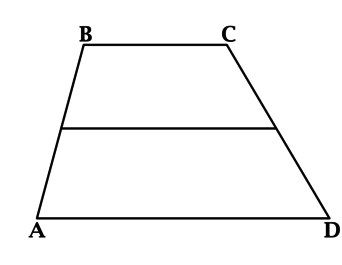
Далее, проведем в трапеции среднюю линию
и получим два равновеликих параллелограмма
и
. Так как
и
, то
.
Поскольку , то
.
Ответ: .
Пример 8. В равнобедренной трапеции дано:
,
биссектриса угла при основании,
и
. Найти
.
Решение. В трапеции продолжим биссектрису
до пересечения в точке
с продолжением верхнего основания
(рис. 5).
Так как трапеция является равнобедренной и , то
. Поскольку
биссектриса, то
.
Однако (как накрест лежащие углы при параллельных основаниях), поэтому
и
является равнобедренным. Отсюда следует, что
и
.
Нетрудно видеть, что треугольники и
подобны. Так как
и
, то коэффициент подобия
. Поэтому
или
. Так как
, то
.
Поскольку трапеция является равнобедренной, в которой
,
,
и полупериметр
, то согласно формуле (2) получаем
.
Ответ: .
Пример 9. В трапеции основания
и
. Найти отношение площадей фигур (трапеций), на которые исходная трапеция разбивается средней линией
.
Решение. Если воспользоваться формулой (7), в которой и
, то получим
.
Ответ:
Также рекомендуем посмотреть наш новый видеоурок по теме нахождения площади плоских фигур, в том числе трапеции:
Для самостоятельной и качественной подготовки к вступительным испытаниям по математике в области решения задач школьной геометрии можно эффективно использовать учебные пособия, приведенные в списке рекомендованной литературы.
Рекомендуемая литература
1. Готман Э.Г. Задачи по планиметрии и методы их решения. – М.: Просвещение, 1996. – 240 с.
2. Амелькин В.В., Рабцевич В.Л., Тимохович В.Л. Планиметрия: Теория и задачи. Мн.: Асар, 2005. – 320 с.
3. Супрун В.П. Математика для старшеклассников: дополнительные разделы школьной программы. – М.: Ленанд / URSS, 2014. – 216 с.
Остались вопросы?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© devblog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Трапеция. Формулы, признаки и свойства трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции – параллельные стороны
- Боковые стороны – две другие стороны
- Средняя линия – отрезок, соединяющий середины боковых сторон.
Виды трапеций:
- Равнобедренная трапеция – трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – трапеция, у которой одна из боковых сторон перпендикулярна основам
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m – b
b = 2m – a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a – h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a – c·cos α – d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
Средняя линия трапеции
Определение.
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
2. Формула определения длины средней линии через площадь и высоту:
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 – 2ad·cos β
d2 = √a2 + c2 – 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab – | a(d 2 – c2) |
| a – b |
| d2 = | √ | c2 + ab – | a(c2 – d 2) |
| a – b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a – h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a – h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab – d22
d2 = √c2 + d 2 + 2ab – d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 – | ( | (a – b)2 + c2 – d 2 | ) | 2 |
| 2 | 2(a – b) |
5. Формула Герона для трапеции
| S = | a + b | √(p – a)(p – b)(p – a – c)(p – a – d) |
| |a – b| |
где
| p = | a + b + c + d | – полупериметр трапеции. |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p – a)(p – c)(p – d1) |
где
a – большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Произвольная трапеция
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства трапеции:
(blacktriangleright) Сумма углов при боковой стороне равна (180^circ).
(blacktriangleright) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
(blacktriangleright) Средняя линия трапеции – отрезок, соединяющий середины боковых сторон. Средняя линия параллельна основаниям и равна их полусумме.
Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Задание
1
#3091
Уровень задания: Равен ЕГЭ
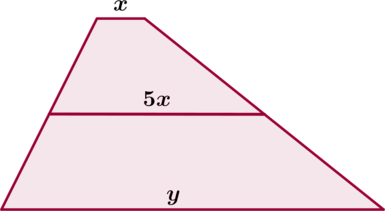
Одно из оснований трапеции в (5) раз меньше ее средней линии. Во сколько раз оно меньше другого основания трапеции?
Обозначим меньшее основание трапеции за (x), большее – за (y). Тогда (5x) – длина средней линии трапеции. Так как средняя линия равна полусумме оснований, то [x+y=2cdot 5xquadLeftrightarrowquad y=9x.] Следовательно, меньшее основание в 9 раз меньше большего.
Ответ: 9
Задание
2
#1694
Уровень задания: Равен ЕГЭ
В трапеции (ABCD): (CD = BC), (angle BCD = 140^circ), (angle ABD = 100^circ). Найдите модуль разности острых углов трапеции.
(triangle BCD) – равнобедренный (Rightarrow) (angle CBD = angle CDB = 20^circ); (angle BAD = 180^circ – angle ABD – angle CBD = 180^circ – 100^circ – 20^circ = 60^circ); (angle ADC = 180^circ – 140^circ = 40^circ). Тогда (|angle ADC – angle BAD| = |40^circ – 60^circ| = |-20^circ| = 20^circ).
Ответ: 20
Задание
3
#290
Уровень задания: Равен ЕГЭ
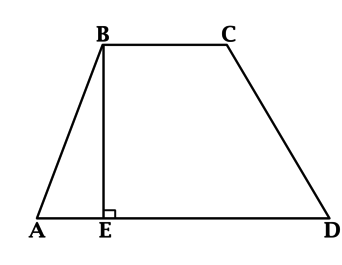
В трапеции (ABCD) с основаниями (BC = 5) и (AD = 2cdot BC) проведена высота (BE). Найдите отношение площади трапеции к длине этой высоты.
Площадь трапеции равна произведению полусуммы оснований на высоту. Полусумма оснований трапеции (ABCD) равна (0,5(5 + 2cdot 5) = 7,5). Площадь трапеции (ABCD) равна (7,5 BE), тогда (dfrac{S_{ABCD}}{BE} = 7,5).
Ответ: 7,5
Задание
4
#292
Уровень задания: Равен ЕГЭ
В трапеции (ABCD) с основаниями (BC = 4) и (AD > BC) угол (A) – прямой. Известно, что (CD = 6), (angle D = 60^{circ}). Найдите среднюю линию трапеции (ABCD).
Из точки (C) опустим высоту (CE). В прямоугольном треугольнике (CDE): (angle ECD = 30^{circ}). В прямоугольном треугольнике катет, лежащий против угла в (30^{circ}) равен половине гипотенузы, тогда (DE = 0,5cdot CD = 3). При этом (ABCE) – прямоугольник, (AE = BC = 4), тогда (AD = AE + ED = 4 + 3 = 7).
В трапеции средняя линия равна полусумме оснований. (0,5(BC + AD) = 0,5(4 + 7) = 5,5), значит, длина средней линии равна (5,5).
Ответ: 5,5
Задание
5
#293
Уровень задания: Равен ЕГЭ
В трапеции (ABCD) средняя линия составляет (dfrac{4}{5}) одного из оснований. Найдите отношение длины другого основания к длине средней линии.
Средняя линия трапеции равна полусумме оснований. Полусумма оснований трапеции (ABCD) составляет (0,8) одного из оснований, тогда сумма оснований трапеции (ABCD) составляет (2cdot 0,8 = 1,6) этого основания, обозначим его за (AD). Тогда (BC + AD = 1,6AD), откуда (BC = 0,6AD). Средняя линия равна (0,8AD), тогда отношение длины основания (BC) к длине средней линии равно (0,6 : 0,8 = 0,75).
Ответ: 0,75
Задание
6
#294
Уровень задания: Равен ЕГЭ
Основания (AD) и (BC) трапеции (ABCD) равны соответственно (20) и (12), одна из боковых сторон равна (10), площадь трапеции (ABCD) равна (80). Найдите острый угол трапеции (ABCD), который образует эта боковая сторона с одним из оснований. Ответ дайте в градусах.
Пусть (AB = 10), (BE) – перпендикуляр к (AD), точка (E) лежит на (AD).
Площадь трапеции равна произведению полусуммы оснований на высоту, тогда (80 = 0,5(20 + 12)cdot BE).
(BE = 5 = 0,5cdot AB). Треугольник (ABE), – прямоугольный, причём (BE = 0,5cdot AB), тогда угол, лежащий против катета (BE), равен (30^{circ}).
(angle BAE = 30^{circ}) – единственный острый угол трапеции (ABCD), который образует (AB) с одним из оснований.
Ответ: 30
Задание
7
#1693
Уровень задания: Равен ЕГЭ
В трапеции (ABCD) диагонали пересекаются в точке (O). Площадь (triangle AOD) относится к площади (triangle ODC), как (8:3). В каком отношении состоит меньшее основание (BC) трапеции (ABCD) к большему основанию (AD)?
Высота, опущенная из вершины (D) на сторону (AO) в (triangle AOD) и на сторону (OC) в (triangle ODC) будет одной и той же. Значит, (frac{S_{triangle DOC}}{S_{triangle AOD}} = frac{OC}{AO} = frac{BC}{AD} = frac{3}{8} = 0,375).
Ответ: 0,375
Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция». Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.
Как подготовиться к экзамену?
Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.
Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или «Равнобедренная трапеция», который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».
«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни