Как найти соотношение сторон в равнобедренном треугольнике

Все формулы для треугольника

1. Как найти неизвестную сторону треугольника

Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.

a , b , c – стороны произвольного треугольника

α , β , γ – противоположные углы

Формула длины через две стороны и угол (по теореме косинусов), ( a ):

* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение

Формула длины через сторону и два угла (по теореме синусов), ( a):

2. Как узнать сторону прямоугольного треугольника

Есть следующие формулы для определения катета или гипотенузы

a , b – катеты

c – гипотенуза

α , β – острые углы

Формулы для катета, ( a ):

Формулы для катета, ( b ):

Формулы для гипотенузы, ( c ):

Формулы сторон по теореме Пифагора, ( a , b ):

3. Формулы сторон равнобедренного треугольника

Вычислить длину неизвестной стороны через любые стороны и углы

b – сторона (основание)

a – равные стороны

α – углы при основании

β – угол образованный равными сторонами

Формулы длины стороны (основания), (b ):

Формулы длины равных сторон , (a):

4. Найти длину высоты треугольника

Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).

Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.

H – высота треугольника

a – сторона, основание

b, c – стороны

β , γ – углы при основании

p – полупериметр, p=(a+b+c)/2

R – радиус описанной окружности

S – площадь треугольника

Формула длины высоты через стороны, ( H ):

Формула длины высоты через сторону и угол, ( H ):

Формула длины высоты через сторону и площадь, ( H ):

Формула длины высоты через стороны и радиус, ( H ):

Равнобедренный треугольник: свойства, признаки и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение равнобедренного треугольника

Какой треугольник называется равнобедренным?

Равнобедренным называется треугольник, у которого две стороны равны.

Давайте посмотрим на такой треугольник:

На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.

А вот как называются стороны равнобедренного треугольника:

AB и BC — боковые стороны,

AC — основание треугольника.

Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.

Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.

Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.

Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.

Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.

Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».

В данном треугольнике медианой является отрезок BH.

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.

Высотой в представленном равнобедренном треугольнике является отрезок BH.

Признаки равнобедренного треугольника

Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.

1. Если у треугольника два угла равны, то этот треугольник — равнобедренный.
2. Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
3. Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
4. Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!

Свойства равнобедренного треугольника

Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!

Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, AH = HC и BH — медиана.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.

Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.

Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).

Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.

Во-вторых, AH = HC и BH — медиана.

Примеры решения задач

Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.

Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.

Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.

Значит, ∠A = ∠C = 80°.

Не должно вас удивить и то, что сумма углов треугольника равна 180°.

∠B = 180° − 80° − 80° = 20°.

Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.

Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.

А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.

Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.

Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.

Равнобедренные треугольники

Равнобедренный треугольник – это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.

1. В равнобедренном треугольнике углы при основании равны.

2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.

6. В равнобедренном треугольнике:

– биссектрисы, проведенные из вершин при основании, равны;

– высоты, проведенные из вершин при основании, равны;

– медианы, проведенные из вершин при основании, равны.

7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.

8. Вписанная окружность точкой касания делит основание пополам.

Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.

Внешний угол треугольника равен сумме двух углов, не смежных с ним.

$∠BCD$ – внешний угол треугольника $АВС$.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$.

Для острого угла $В$: $АС$ – противолежащий катет; $ВС$ – прилежащий катет.

Для острого угла $А$: $ВС$ – противолежащий катет; $АС$ – прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом ($ctg$) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

1. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
2. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
3. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

$cos BOA= – cos BOC;$

$ctg BOA= – ctg BOC.$

В треугольнике $ABC$ $AB=BC, AH$ — высота, $AC=34, cos ∠BAC=0.15$. Найдите $CH$.

Так как треугольник $АВС$ равнобедренный, то $∠A=∠С$ (как углы при основании)

Косинусы равных углов равны, следовательно, $cos∠BAC=cos∠ВСА=0.15$

Рассмотрим прямоугольный треугольник $АНС$.

Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Распишем косинус $∠НСА$ (он же $∠ВСА$) по определению:

Из последнего равенства найдем $НС$, для этого $0.15$ представим в виде обыкновенной дроби и воспользуемся свойством пропорции:

Если на сторонах $ВС, АВ$ и продолжении стороны $АС$ треугольника $АВС$ за точку $С$ отмечены соответственно $А_1,С_1,В_1$, лежащие на одной прямой, то

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

В треугольнике $АВС$ $ВС=16, sin∠A=<4>/<5>$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.

Воспользуемся теоремой синусов:

Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности

Далее подставим числовые данные и найдем $R$

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/chto-takoe-ravnobedrennyj-treugolnik

http://examer.ru/ege_po_matematike/teoriya/ravnobedrennye_treugolniki

[/spoiler]

Как посчитать стороны равнобедренного треугольника

Чтобы посчитать чему равны стороны равнобедренного треугольника воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Как посчитать сторону a равнобедренного треугольника

Если известна сторона b и угол α

Если известна сторона b и угол β

Если известна сторона b и высота h

Как посчитать сторону b (основание) равнобедренного треугольника

Если известна сторона a и угол α

Если известна сторона a и угол β

Если известна сторона a и высота h

См. также

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 апреля 2023 года; проверки требуют 7 правок.

Равнобедренный треугольник — треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием. Каждый правильный треугольник также является равнобедренным, но обратное утверждение неверно^[1].

Терминология[править | править код]

Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании^[1].

Евклид определил равнобедренный треугольник как треугольник, который имеет две равные стороны, но современная трактовка^[2] предпочитает определение, где треугольник имеет хотя бы две равные стороны, определяя таким образом равносторонний треугольник как частный случай равнобедренного.

Симметрия[править | править код]

Треугольник с двумя равными сторонами имеет одну ось симметрии, которая проходит через вершинный угол и середину основания. Эта ось симметрии совпадает с биссектрисой вершинного угла, медианой, проведённой к основанию, высотой, проведённой из вершинного угла и с серединным перпендикуляром^{[3][уточнить]}.

Свойства[править | править код]

Основной источник: ^[1]

В равнобедренном треугольнике углы при основании равны. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.

Биссектриса, медиана, высота и серединный перпендикуляр, проведённые к основанию, совпадают между собой. Центры вписанной и описанной окружностей лежат на этой линии.

Пусть a — длина равных боковых сторон, b — длина основания, h — высота к основанию, R — радиус описанной окружности

Радиус вписанной окружности может быть выражен пятью способами в зависимости от того, какие два параметра равнобедренного треугольника известны:

• 
• 
• 
• 
• 

Углы могут быть выражены следующими способами:

Периметр равнобедренного треугольника находится следующими способами:

Площадь треугольника находится следующими способами:

Теорема Лемуса-Штейнера[править | править код]

Основной источник: ^[4]

Доказан этот признак равнобедренного треугольника был только в XIX веке двумя математиками, Лемусом и Штейнером, которые обменивались письмами в течение нескольких лет.

См. также[править | править код]

• Теорема о равнобедренном треугольнике
• Равнобедренный прямоугольный треугольник

Примечания[править | править код]

Литература[править | править код]

• Выгодский М. Я. Справочник по элементарной математике. — 25-е изд. — М.: Наука, 1978. — 336 с.
  • Переиздание: М.: АСТ, 2006, ISBN 5-17-009554-6, 509 с.

Равнобедренный треугольник. Онлайн калькулятор

Определение равнобедренного треугольника

Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.

Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).

Угол между боковыми сторонами равнобедненного треугольника (( small angle A ) ) называется вершинным углом. Углы между основанием и боковыми сторонами (( small angle B, angle C ) ) называются углами при основании.

Существует более общее определение равнобедненого треугольника:

Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.

Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.

Теорема о равнобедренном треугольнике

Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.

Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что ( small angle B= angle C. ) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол ( small angle A ) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:

Из ( small AB=AC) и ( small AD=AE ) следует:

Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: ( small CE=BD,) ( small CD=BE ,) сторона ( small BC ) общая. Отсюда следует, что

Из (2) и (4) следует, что ( small angle B= angle C. )

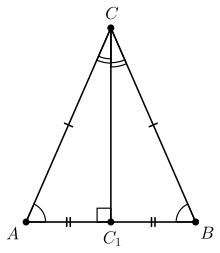
Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису ( small AH ) треугольника. Тогда ( small angle CAH=angle BAH. ) Докажем, что ( small angle B= angle C. ) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle CAH=angle BAH. ) Отсюда следует: ( small angle B= angle C. )

Свойства равнобедренного треугольника

Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.

Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона ( small AH ) общая, ( small angle 1=angle 2. ) Тогда ( small CH=HB, ) ( small angle 3=angle 4. ) Равенство ( small CH=HB ) означает, что ( small AH ) является также медианой треугольника ABC. Углы ( small angle 3) и ( angle 4 ) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда ( small AH ) является также высотой треугольника ( small ABC. ) Поскольку высота ( small AH ) перпендикулярна к ( small BC ) и ( small CH=HB, ) то ( small AH ) является также серединным перпендикуляром к основанию равнобедренного треугольника.

Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.

Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:

Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.

Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.

Признаки равнобедренного треугольника

Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.

Признак 1 следует из определения 1.

Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.

Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).

Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и медианой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small CH=HB. ) Треугольники ( small AHC ) и ( small AHB ) равны по двум сторонам и углу между ними (первый признак равенства треугольников): ( small AH ) − общая сторона, ( small CH=HB, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )

Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство. Пусть в треугольнике ( small ABC ) ( small AH ) является высотой и биссектрисой (Рис.4). Тогда ( small angle 3=angle4=90°, ) ( small angle 1=angle2. ) Треугольники ( small AHC ) и ( small AHB ) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): ( small AH ) − общая сторона, ( small angle 1=angle 2, ) ( small angle 3=angle4. ) Следовательно ( small AB=AC. )

Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.

Доказательство (Вариант 1). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой (Рис.5). Тогда

Применим теорему синусов для треугольника ( small AHC ):

Применим теорему синусов для треугольника ( small AHB ):

тогда, из (5), (6), (7) получим:

Следовательно ( small sin angle C= sin angle B. ) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) ( small angle C= angle B, ) 2) ( small angle C= 180° – angle B. ) Поскольку сумма двух углов треугольника меньше 180°: ( small angle C + angle B< 180° ) второй вариант исключается. Т.е. ( small angle C= angle B ) и по признаку 2 треугольник является равнобедренным.

Доказательство (Вариант 2). Пусть в треугольнике ( small ABC ) ( small AH ) является биссектрисой и медианой, т.е. ( small angle 1=angle 2, ) ( small CH=HB ) (Рис.6). На луче ( small AH ) отложим отрезок ( small HD ) так, чтобы ( small AH=HD. ) Соединим точки ( small C ) и ( small D. )

Треугольники ( small AHB ) и ( small DHC ) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: ( small AH=HD, ) ( small CH=HB, ) ( small angle 4=angle 5 ) (углы 4 и 5 вертикальные). Тогда ( small AB=CD, ) ( small angle 6=angle 2. ) Отсюда ( small angle 6=angle 1. ) Получили, что треугольник ( small CAD ) равнобедренный (признак 2). Тогда ( small AC=CD. ) Но ( small AB=CD ) и, следовательно ( small AB=AC. ) Получили, что треугольник ( small ABC ) равнобедренный.

1. Признак равенства равнобедренных треугольников по основанию и боковой стороне

Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.

Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.

2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине

Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.

Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.

3. Признак равенства равнобедренных треугольников по основанию и углу при основании

Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.

Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.

Задачи и решения

Задача 1. Известны основание ( small a=5 ) и высота ( small h=6 ) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.

Решение. Найдем боковые стороны ( small b ) и ( small c ) равнобедренного треугольника. Воспользуемся теоремой Пифагора:

Откуда:

Подставляя значения ( small a ) и ( small h ) в (9), получим:

Боковая сторона ( small c ) равнобедренного треугольника равна:

Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:

Подставляя значения ( small a=5, ) ( small b=6.5 ) и ( small c=6.5 ) в (10), получим:

Найдем угол ( small B ) равнобедренного треугольника:

Подставляя значения ( small a=5, ) ( small h=6 ) в (11), получим:

Тогда угол ( small C ) равнобедренного треугольника равен:

Поскольку сумма всех углов треугольника равна 180°, то имеем:

Площадь треугольника можно вычислить из формулы:

Подставляя значения ( small a=5, ) ( small h=6 ) в (12), получим:

Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1)
P=2a+b

Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис.88.2)
h_b=m_b=l_b=√(a^2-(b/2)^2 )=√(4a^2-b^2 )/2

Остальные две высоты равны друг другу и считаются через формулу с произведением разностей полупериметров и сторон, где приравнены боковые стороны. (рис.88.8)
h_a=(b√((4a^2-b^2)))/2a

Зная высоту, найти площадь равнобедренного треугольника можно, подставив полученное выражение в формулу, по которой площадь равна половине основания, умноженной на его высоту.
S=hb/2=(b√(4a^2-b^2 ))/4

Углы в равнобедренном треугольнике распределяются следующим образом – углы при основании друг другу конгруэнтны, также как и боковые стороны, а в сумме все три угла дают 180 градусов, поэтому найти их можно двумя видами разности.
α=(180°-β)/2
β=180°-2α

Если ни один из углов не дан, но есть все стороны, то можно воспользоваться теоремой косинусов, чтобы найти любой угол.
cos⁡α=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a
cos⁡β=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 )

Медиана и биссектриса, опущенные на основание, вычисляются по формуле высоты, приведенной выше, а оставшиеся две медианы (равно как и две биссектрисы) равны друг другу, поскольку строятся на равных боковых сторонах. Вычислить медиану можно, упростив формулу произвольного треугольника. (рис. 88.3)
m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2

В формуле биссектрисы аналогично приравниваются боковые стороны, и ее становится возможным вычислить по упрощенной схеме. (рис. 88.4)
l_a=√(ab(2a+b)(a+b-a) )/(a+b)=(b√(a(2a+b) ))/(a+b)

Средняя линия равнобедренного треугольника, параллельная основанию, равна его половине, а средние линии, параллельные боковым сторонам, равны между собой и также равны половинам самих боковых сторон. (рис. 88.5)
M_b=b/2
M_a=a/2

Радиус окружности, вписанной в равнобедренной треугольник, является производной формулы для произвольного треугольника, и рассчитать его можно, зная боковую сторону и основание. (рис. 88.6)
r=b/2 √((2a-b)/(2a+b))

Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы и выглядит упрощенно следующим образом. (рис. 88.7)
R=a^2/√(4a^2-b^2 )