Как найти соотношение токов

Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.

В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.

Закон Ома

Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:

U = I × R

или

I = V/R

или

R = V/I

Где:

• V – напряжение в вольтах (В);
• I – сила тока в амперах (А);
• R – сопротивление в омах (Ом);

Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.

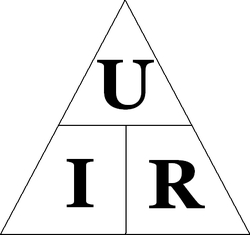
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».

• Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
• Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление:  I = V/R .
• Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .

Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.

Закон Ома для цепи

Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).

Итак, закон Ома для рассматриваемого участка цепи имеет вид:

φ1-φ2=I*R, где

• I – ток, протекающий по участку цепи.
• R – сопротивление этого участка.
• φ1-φ2 – разность потенциалов между точками 1-2.

Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).

В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:

• U1=I*R1
• U2=I*R2
• Un=I*Rn
• U=I*(R1+R2+…+Rn

Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:

U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn

Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.

Для ЭДС

Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:

Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.

Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.

Для полной цепи

Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.

Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.

Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

Для замкнутой цепи

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

• Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
• В сверхпроводниках;
• Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
• В вакуумных и газовых радиолампах;
• В диодах и транзисторах.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

• I = I1= I2 ;
• U = U1+ U2 ;
• R = R1+ R2

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

• I = I1+ I2 … ;
• U = U1= U2 … ;
• 1 / R = 1 / R1+ 1 / R2 + …

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что  делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.

Онлайн калькулятор закона Ома позволяет определять связь между силой тока, электрическим напряжением и сопротивлением проводника в электрических цепях.

Для расчета, вам понадобится воспользоваться отдельными графами:
– сила тока вычисляется в Ампер, исходя из данных напряжения (Вольт) и сопротивления (Ом);
– напряжение вычисляется в Вольт, исходя из данных силы тока (Ампер) и электрического сопротивления (Ом);
– электрическое сопротивление вычисляется в Ом, исходя из данных силы тока (Ампер) и напряжения (Вольт);
– мощность вычисляется в Ватт, исходя из данных силы тока (Ампер) и напряжения (Вольт).

Расчет силы тока по мощности, напряжению, сопротивлению

Бесплатный калькулятор расчета силы тока по мощности и напряжению/сопротивлению – рассчитайте силу тока в однофазной или трехфазной сети в ОДИН КЛИК!

Если вы хотите узнать как рассчитать силу тока в цепи по мощности, напряжению или сопротивлению, то предлагаем воспользоваться данным онлайн-калькулятором. Программа выполняет расчет для сетей постоянного и переменного тока (однофазные 220 В, трехфазные 380 В) по закону Ома. Рекомендуем без необходимости не изменять значение коэффициента мощности (cos φ) и оставлять равным 0.95. Знание величины силы тока позволяет подобрать оптимальный материал и диаметр кабеля, установить надежные предохранители и автоматические выключатели, которые способны защитить квартиру от возможных перегрузок. Нажмите на кнопку, чтобы получить результат.

Смежные нормативные документы:

• СП 256.1325800.2016 «Электроустановки жилых и общественных зданий. Правила проектирования и монтажа»
• СП 31-110-2003 «Проектирование и монтаж электроустановок жилых и общественных зданий»
• СП 76.13330.2016 «Электротехнические устройства»
• ГОСТ 31565-2012 «Кабельные изделия. Требования пожарной безопасности»
• ГОСТ 10434-82 «Соединения контактные электрические. Классификация»
• ГОСТ Р 50571.1-93 «Электроустановки зданий»

Формулы расчета силы тока

Электрический ток — это направленное упорядоченное движение заряженных частиц.
Сила тока (I) — это, количество тока, прошедшего за единицу времени сквозь поперечное сечение проводника. Международная единица измерения — Ампер (А / A).

— Сила тока через мощность и напряжение (постоянный ток): I = P / U
— Сила тока через мощность и напряжение (переменный ток однофазный): I = P / (U × cosφ)
— Сила тока через мощность и напряжение (переменный ток трехфазный): I = P / (U × cosφ × √3)
— Сила тока через мощность и сопротивление: I = √(P / R)
— Сила тока через напряжение и сопротивление: I = U / R

• P – мощность, Вт;
• U – напряжение, В;
• R – сопротивление, Ом;
• cos φ – коэффициент мощности.

Коэффициент мощности cos φ – относительная скалярная величина, которая характеризует насколько эффективно расходуется электрическая энергия. У бытовых приборов данный коэффициент практически всегда находится в диапазоне от 0.90 до 1.00.

Источник

Найти отношение сил токов

Три проводника, изготовленные из одного материала одинаковой длины, но разного диаметра: d₂=2d₁, d₃=3d₁, соеддинены параллельно. Силы токов в проводниках I₁:I₂:I₃ относятся как .

Как дальше применить то, что прооводники соединены параллельно?

Расчет токов в ветвях схемы, методом контурных токов
1. Выполнить расчет токов в ветвях схемы , методом контурных токов. (ВЫПОЛНЕНО приложена.

Найти угловое ускорение цилиндра и отношение сил натяжений T2/T1
В установке, показанной на рисунке, известны масса однородного сплошного цилиндра m, его радиус R и.

Найти отношение амплитуд плотностей токов проводимости и смещения
Помогите, пожалуйста с задачкой) Плоская электромагнитная волна с частотой 10 МГц распространяется.

Сообщение от Лёха666

Ну что ж, изрядно. Теперь, вспомним, что при параллельном подсоединении сопротивлений напряжение на них одно и тоже. Тогда:

Сообщение от Sergeiy_98
Сообщение от IGPIGP

Сообщение от Лёха666
Сообщение от IGPIGP

Сообщение от Лёха666
Сообщение от Лёха666

Лёха666, я надеюсь ро это удельное сопротивление? Потому как остальное верно. Удельная проводимость обозначается сигма, тогда:

удельная проводимость и удельное сопротивление обратные величины.
А вообще, ответ задачи даже от этого не зависит. Важно, что сопротивление для одинаковых материалов и длин, обратно пропорционально квадратам диаметров круглых проводников. Значит ток, прямо пропорционален квадратам диаметров.

Заказываю контрольные, курсовые, дипломные работы и диссертации здесь.

Определите отношение оптических сил собирающей и рассеивающей линз
Здравствуйте, дамы и господа! У меня есть задачка, которую решил, но не знаю правильно ли.

Отношение моментов сил, у тела с грузом, вращающегося вокруг оси
Мне благополучно набросали задачу и с спокойным сердцем ушли домой, условие записано очень.

При какой массе бруска отношение сил будет равно 5?
На горизонтальной поверхности стола находятся связанные нитью бруски массой 0.5 кг и неизвестной.

Найти отношение длин математических маятников, отношение периодов которых равно 2
6) Найти отношение длин математических маятников, отношение периодов которых равно 2.

Вычислить проекции сил и моменты сил относительно осей координат
Вычислить проекции сил и моменты сил относительно осей координат. Правильно ли решено?

Источник

Закон Ома: как связаны между собой напряжение, ток и сопротивление

Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».

Напряжение, ток и сопротивление

Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.

Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.

Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.

Единицы измерения: вольт, ампер и ом

Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:

Величина	Символ	Единица измерения	Сокращение единицы измерения
Ток	I	Ампер	А
Напряжение	V	Вольт	В
Сопротивление	R	Ом	Ом

Единицы измерения тока, напряжения, сопротивления

«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.

Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.

Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.

Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.

Кулон и электрический заряд

Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.

Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.

Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.

Формула закона Ома

Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:

В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:

Анализ простых схем с помощью закона Ома

Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:

Рисунок 1 – Пример простой схемы

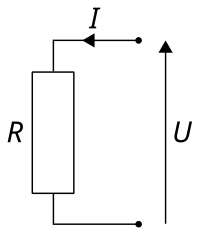
В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.

В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы

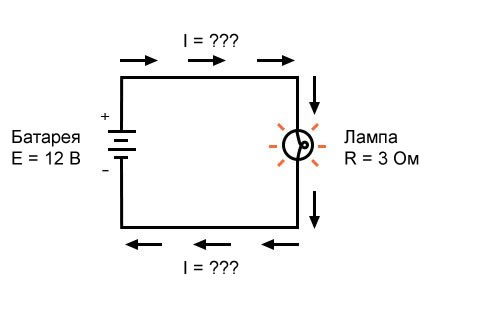
Какая величина тока (I) в этой цепи?

Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи

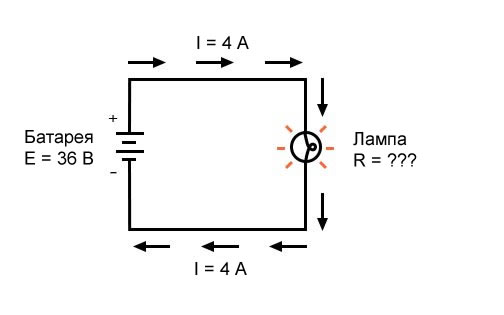
Какое сопротивление (R) оказывает лампа?

В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы

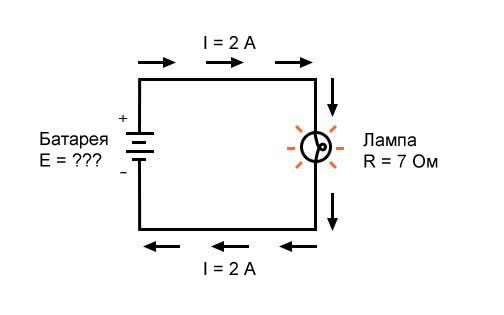
Какое напряжение обеспечивает батарея?

[E = IR = (2 А)(7 Ом) = 14 В]

Метода треугольника закона Ома

Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Рисунок 5 – Треугольник закона Ома

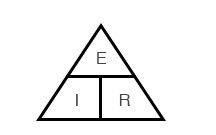
Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Рисунок 6 – Закон Ома для определения R

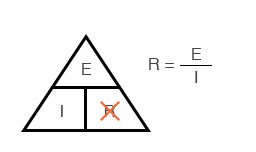
Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Рисунок 7 – Закон Ома для определения I

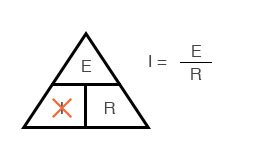
Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

Рисунок 8 – Закон Ома для определения E

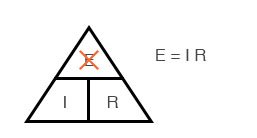
В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!

Источник

Закон Ома для участка цепи и полной цепи: формулы и определения

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

1. I — сила тока (в системе СИ измеряется — Ампер)
   • Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
   • Формула: I=frac
   • U — напряжение (в системе СИ измеряется — Вольт)
     • Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
     • Формула: U=IR
   • R— электрическое сопротивление (в системе СИ измеряется — Ом).
     • Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
     • Формула R=frac

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).

Закон Ома для полной цепи

Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

Формула I=frac <varepsilon>

• varepsilon — ЭДС источника напряжения, В;
• I — сила тока в цепи, А;
• R — сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

Как запомнить формулы закона Ома

Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

.

• U — электрическое напряжение;
• I — сила тока;
• P — электрическая мощность;
• R — электрическое сопротивление

Смотри также:

Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

Источник

Классическая электродинамика
Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника (или электрического напряжения) с силой тока, протекающего в проводнике, и сопротивлением проводника. Установлен Георгом Омом в 1826 году (опубликован в 1827 году) и назван в его честь.

В своей работе^[1] Ом записал закон в следующем виде:

где:

• X — показания гальванометра (в современных обозначениях, сила тока I);
• a — величина, характеризующая свойства источника напряжения, постоянная в широких пределах и не зависящая от величины тока (в современной терминологии, электродвижущая сила (ЭДС) ε);
• l — величина, определяемая длиной соединяющих проводов (в современных представлениях соответствует сопротивлению внешней цепи R);
• b — параметр, характеризующий свойства всей электрической установки (в современных представлениях, параметр, в котором можно усмотреть учёт внутреннего сопротивления источника тока r).

Формула (1) при использовании современных терминов выражает закон Ома для полной цепи:

где:

Из закона Ома для полной цепи вытекают следующие следствия:

Часто^[2] выражение

где есть напряжение, или падение напряжения (или, что то же, разность потенциалов между началом и концом участка проводника), тоже называют «законом Ома».

Таким образом, электродвижущая сила в замкнутой цепи, по которой течёт ток в соответствии с (2) и (3) равняется:

То есть сумма падений напряжения на внутреннем сопротивлении источника тока и на внешней цепи равна ЭДС источника. Последний член в этом равенстве специалисты называют «напряжением на зажимах», поскольку именно его показывает вольтметр, измеряющий напряжение источника между началом и концом присоединённой к нему замкнутой цепи. В таком случае оно всегда меньше ЭДС.

К другой записи формулы (3), а именно:

применима другая формулировка:

Выражение (5) можно переписать в виде

где коэффициент пропорциональности G назван проводимость или электропроводность. Изначально единицей измерения проводимости был «обратный ом» — Мо^[3], в Международной системе единиц (СИ) единицей измерения проводимости является си́менс (русское обозначение: См; международное: S), величина которого равна обратному ому.

Мнемоническая диаграмма для закона Ома

В соответствии с этой диаграммой формально может быть записано выражение:

которое всего лишь позволяет вычислить (применительно к известному току, создающему на заданном участке цепи известное напряжение), сопротивление этого участка. Но математически корректное утверждение о том, что сопротивление проводника растёт прямо пропорционально приложенному к нему напряжению и обратно пропорционально пропускаемому через него току, физически ложно.

В специально оговорённых случаях сопротивление может зависеть от этих величин, но по умолчанию оно определяется лишь физическими и геометрическими параметрами проводника:

где:

•  — удельное электрическое сопротивление материала, из которого сделан проводник,
•  — его длина
•  — площадь его поперечного сечения

Закон Ома и ЛЭП

Одним из важнейших требований к линиям электропередачи (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами, задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока = при минимальных потерях мощности в линии передачи где причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением

Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное увеличение ЭДС. Однако ЭДС ограничивается электрической прочностью обмотки генератора, поэтому повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в линии возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому наибольшее практически используемое напряжение в дальних ЛЭП обычно не превышает миллиона вольт.

Кроме того, любой проводник, как показал Дж. Максвелл, при изменении силы тока в нём излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

Закон Ома в дифференциальной форме

Сопротивление зависит как от материала, по которому течёт ток, так и от геометрических размеров проводника.

Полезно переписать закон Ома в так называемой дифференциальной форме, в которой зависимость от геометрических размеров исчезает, и тогда закон Ома описывает исключительно электропроводящие свойства материала. Для изотропных материалов имеем:

где:

Все величины, входящие в это уравнение, являются функциями координат и, в общем случае, времени. Если материал анизотропен, то направления векторов плотности тока и напряжённости могут не совпадать. В этом случае удельная проводимость является симметричным тензором ранга (1, 1), а закон Ома, записанный в дифференциальной форме, приобретает вид

Раздел физики, изучающий течение электрического тока (и другие электромагнитные явления) в различных средах, называется электродинамикой сплошных сред.

Закон Ома для переменного тока

Вышеприведённые соображения о свойствах электрической цепи при использовании источника (генератора) с переменной во времени ЭДС остаются справедливыми. Специальному рассмотрению подлежит лишь учёт специфических свойств потребителя, приводящих к разновременности достижения напряжением и током своих максимальных значений, то есть учёт фазового сдвига.

Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными:

где:

При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как

Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Нелинейность цепи приводит к возникновению гармоник (колебаний с частотой, кратной частоте тока, действующего на цепь), а также колебаний с суммарными и разностными частотами. Вследствие этого закон Ома в нелинейных цепях, вообще говоря, не выполняется.

Трактовка и пределы применимости закона Ома

Закон Ома, в отличие от, например, закона Кулона, является не фундаментальным физическим законом, а лишь эмпирическим соотношением, хорошо описывающим наиболее часто встречаемые на практике типы проводников в приближении небольших частот, плотностей тока и напряжённостей электрического поля, но перестающим соблюдаться в ряде ситуаций.

В классическом приближении закон Ома можно вывести при помощи теории Друде:

Здесь:

Проводники и элементы, для которых соблюдается закон Ома, называются омическими.

Закон Ома может не соблюдаться:

• При высоких частотах, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.
• При низких температурах для веществ, обладающих сверхпроводимостью.
• При заметном нагреве проводника проходящим током, в результате чего зависимость напряжения от тока (вольт-амперная характеристика) приобретает нелинейный характер. Классическим примером такого элемента является лампа накаливания.
• При приложении к проводнику или диэлектрику (например, воздуху или изоляционной оболочке) высокого напряжения, вследствие чего возникает пробой.
• В вакуумных и газонаполненных электронных лампах (в том числе люминесцентных).
• В гетерогенных полупроводниках и полупроводниковых приборах, имеющих p-n-переходы, например, в диодах и транзисторах.
• В контактах металл-диэлектрик (вследствие образования пространственного заряда в диэлектрике)^[4].

Примечания

Ссылки

• Закон Ома // Элементы.ru. Природа науки, Энциклопедия

Электрическая мощность и закон Ома

Для анализа и расчета параметров нагревателей, как правило, мы используем различные методы, в частности закон Ома. Этот закон используется в основном для определения неизвестных величин, таких как напряжение, ток, сопротивление и мощность, которые связаны с одним или несколькими элементами электронной схемы. Закон Ома – основной закон теории электрических цепей, который определяет линейную зависимость между напряжением, током и сопротивлением. В данной статье мы постараемся  подробно рассказать о законе Ома и его практическом применении.

Закон Ома

Закон Ома – это основной, главный и важный закон теории электрических цепей, который исследует взаимосвязь между напряжением, током и сопротивлением. В нем говорится, что при постоянной температуре ток, протекающий по цепи, прямо пропорционален напряжению или разности потенциалов в этой цепи.

В алгебраической форме, V∝ I

V = IR

Где

I – ток, протекающий по цепи, измеряется в амперах.

V — напряжение, приложенное к цепи, измеряется в вольтах.

А R — это константа пропорциональности, называемая сопротивлением, которое измеряется в омах.

Это сопротивление также указывается в килоомах, мегаомах и т. д.

Следовательно, закон Ома гласит, что ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению в этой цепи. Закон Ома можно применить как к отдельным частям, так и ко всей цепи.

Математически ток, I = V/R

Напряжение, V = IR

Сопротивление, R = V/I

Треугольник закона Ома

Ниже показано, что отношение между различными величинами в законе Ома называется треугольником закона Ома. Это простой метод описания, а также простой для запоминания соотношения между напряжением, током и сопротивлением.

На приведенном выше рисунке показан треугольник закона Ома, где отдельные термины, такие как напряжение, ток и сопротивление, и их формулы представлены из основного уравнения закона Ома. На приведенном выше рисунке один параметр вычисляется из оставшихся двух параметров. Таким образом, можно сделать вывод, что при высоком сопротивлении ток будет низким, а ток будет высоким, когда сопротивление низкое, при любом приложенном напряжении.

Электрическая мощность

Электрическая мощность дает скорость, с которой энергия передается по цепи. Электрическая мощность измеряется в ваттах. Эта мощность потребляется, когда напряжение вызывает протекание тока в цепи.

Следовательно, электрическая мощность есть произведение напряжения и силы тока.

Математически P = VI

По закону Ома V = IR и I = V/R

Подставляя в уравнение мощности

P = I² R

P = V²/ R

Следовательно, электрическая мощность, P =VI или I ² R или V ² / R

Это три основные формулы для нахождения электрической мощности в цепи. Таким образом, мощность может быть рассчитана, когда известна любая из двух величин.

Треугольник мощности

Подобно треугольнику закона Ома, на рисунке ниже показан треугольник мощности, чтобы показать соотношение между мощностью, напряжением и током. Уравнения отдельных параметров легко запоминаются по этому рисунку. Округлите и скройте параметр, который необходимо измерить, а положение оставшихся двух параметров дает уравнение для поиска скрытого или округленного параметра, как показано на рисунке ниже.

Круговая диаграмма закона Ома

В дополнение к двум вышеупомянутым концепциям существует еще один метод определения параметров схемы с использованием закона Ома, который представляет собой круговую диаграмму закона Ома. Используя круговую диаграмму закона Ома, можно легко запомнить все уравнения для нахождения напряжения, тока, сопротивления и мощности, которые необходимы для упрощения электрических цепей, которые могут быть простыми или сложными.

На приведенном выше рисунке показана круговая диаграмма, которая показывает взаимосвязь между мощностью, напряжением, током и сопротивлением. Эта диаграмма разделена на четыре блока для мощности, напряжения, сопротивления и тока. Каждый блок состоит из трех формул с двумя известными значениями для каждой формулы. Из диаграммы для нахождения каждого параметра в цепи мы можем использовать любую из трех доступных формул.

Графическое представление закона Ома

Для лучшего понимания этой концепции ниже приведена экспериментальная установка, в которой регулируемый источник напряжения с шестью ячейками (по 2 В каждая) подключен к нагрузочному резистору через переключатель выбора напряжения. Измерительные приборы, такие как вольтметр и амперметр, также подключены к цепи для измерения напряжения и тока в цепи.

Регулируемый источник напряжения с нагрузочным резистором

Сначала подключите резистор 10 Ом и установите переключатель в положение «1». Тогда амперметр показывает 0,2 А, а вольтметр показывает 2 В, потому что I = V/R, т. е. I = 2/10 = 0,2 А. Затем измените положение селекторного переключателя на вторую ячейку, чтобы подать 4 В на нагрузку и запишите показания амперметра. По мере того, как селектор будет постепенно изменяться от первого положения к последнему, мы получим текущие значения, такие как 0,2, 0,4, 0,6, 0,8, 1, 1,2 для значений напряжения 2, 4, 6, 8, 10 и 12 соответственно.

Точно так же поместите резистор 20 Ом вместо резистора 10 Ом и выполните ту же процедуру, что и выше. Мы получим значения тока 0,1, 0,2, 0,3, 0,4, 0,5, 0,6 для значений напряжения 2, 4, 6, 8, 10 и 12В соответственно. Постройте график этих значений, как показано ниже.

Графическое представление закона Ома

На приведенном выше графике для данного напряжения ток меньше, когда сопротивление больше. Рассмотрим случай приложенного напряжения 12 В, когда значение тока составляет 1,2 А при сопротивлении 10 Ом и 0,6 Ом при сопротивлении 20 Ом. Точно так же при одном и том же токе напряжение тем больше, чем больше сопротивление. Из приведенных выше результатов следует, что отношение напряжения к току постоянно, когда сопротивление постоянно. Следовательно, зависимость между напряжением и током является линейной, и наклон этой линейной кривой становится тем круче, чем больше сопротивление.

Пример применения закона Ома

Рассмотрим приведенную ниже схему, в которой батарея на 6 В подключена к нагрузке 6 Ом. Амперметр и вольтметры подключены к цепи для измерения тока и напряжения практически. Но используя закон Ома мы можем найти силу тока и мощность следующим образом.

Из закона Ома

V = IR

I = V/R

I = 6/6

I = 1 А

Мощность, P = VI

P = 6×1

P = 6 Вт

Но практически амперметр не показывает точное значение из-за внутреннего сопротивления батареи. Включив внутреннее сопротивление батареи (предположим, что батарея имеет внутреннее сопротивление 1 Ом), текущее значение рассчитывается следующим образом.

Общее сопротивление цепи 6+1=7 Ом.

Ток, I = V/R

I = 6/7

I = 0,85 Ампер

Цепь фар в автомобиле

На приведенном ниже рисунке показана схема фар легкового автомобиля без схемы управления. С применением закона Ома мы можем узнать ток, протекающий через каждую лампу. Как правило, каждая лампочка подключается параллельно к аккумулятору, что позволяет другим элементам светиться, даже если какой-то из них поврежден. К этим параллельным лампам подводится батарея 12 В, где лампы имеют сопротивление 2,4 каждая (считается в данном случае).

Общее сопротивление цепи равно R = R1x R2/(R1 + R2), так как они соединены параллельно.

R = 5,76/4,8 = 1,2

Тогда ток, протекающий по цепи, равен I = V/R.

I = 12/1,2

I = 10А.

Ток, протекающий через отдельную лампу, равен I1 = I2 = 5 А (из-за одинаковых сопротивлений).

Закон Ома для цепей переменного тока

В общем, закон Ома можно применить и к цепям переменного тока . Если нагрузка индуктивная или емкостная, то также учитывается реактивное сопротивление нагрузки. Следовательно, с некоторыми изменениями закона Ома, учитывающими влияние реактивного сопротивления, его можно применять к цепям переменного тока. Из-за индуктивности и емкости в переменном токе будет значительный фазовый угол между напряжением и током. А также сопротивление переменному току называется импедансом и обозначается как Z.

Таким образом, закон Ома для цепей переменного тока задается как

E = IZ

I = E/Z

Z = E/I

Где E – напряжение в цепи переменного тока,

I – текущий ток,

Z — импеданс.

Все параметры в приведенном выше уравнении представлены в комплексной форме, которая включает фазовый угол. Подобно круговой диаграмме цепи постоянного тока, круговая диаграмма закона Ома для цепи переменного тока приведена ниже.

Пример закона Ома (цепи переменного тока)

Рассмотрим приведенную ниже схему, в которой нагрузка переменного тока (сочетание резистивной и индуктивной) подключена к источнику переменного тока 10 В, 60 Гц. Нагрузка имеет сопротивление 5 Ом и индуктивность 10 мГн.

Тогда значение импеданса нагрузки Z = R + jX _L

Z = 5 + j (2∏ × f × L)

Z = 5+ j (2×3,14×60×10×10-3)

Z = 5 + j3,76 Ом или 6,26 Ом при фазовом угле -37,016

Ток, протекающий по цепи, равен

I = V/Z = 10/(5+ j3,76) = 1,597 А при фазовом угле -37,016

Для расчета параметров сети для подключения нагревателей вы можете воспользоваться данными в данной статье основными формулами, или же просто позвоните нашим специалистам компании Термоэлемент по телефону и получите полную бесплатную консультацию и помощь с выбором нужных параметров нагревателей для вашей задачи по нагреву.