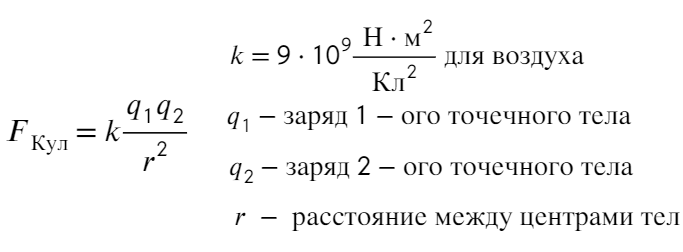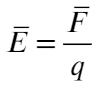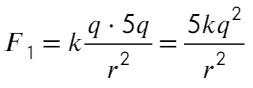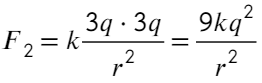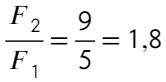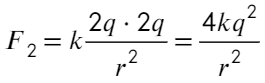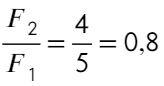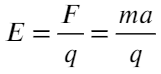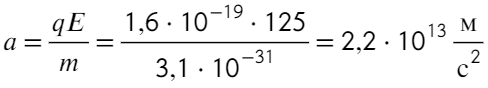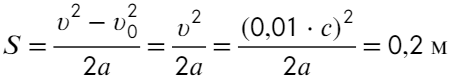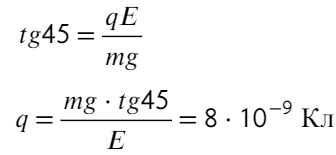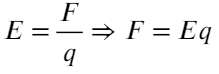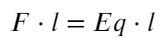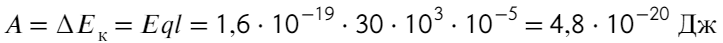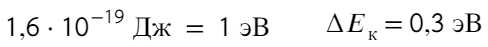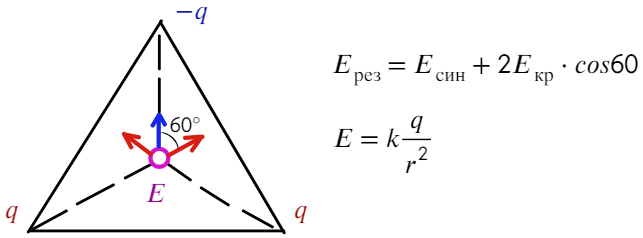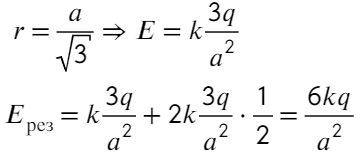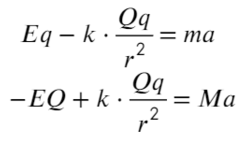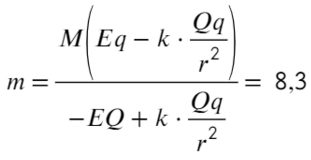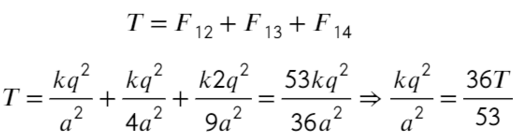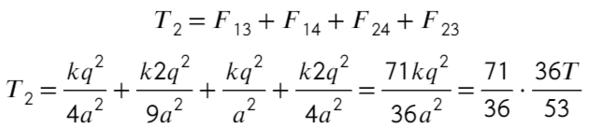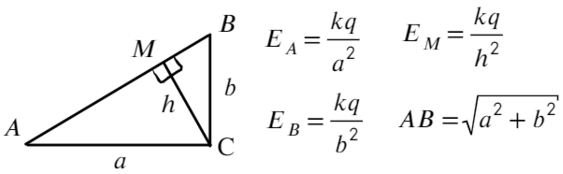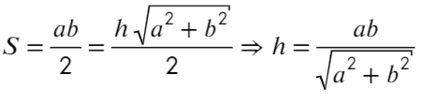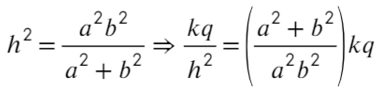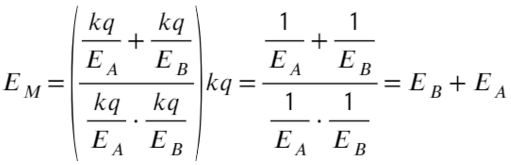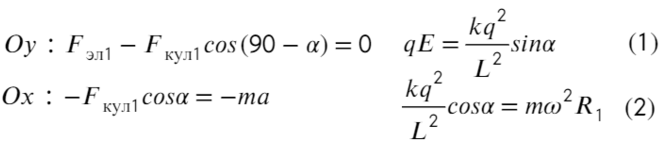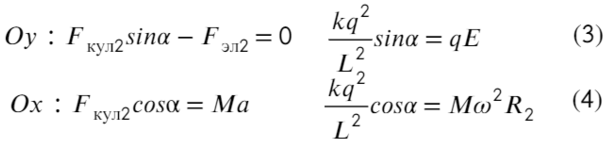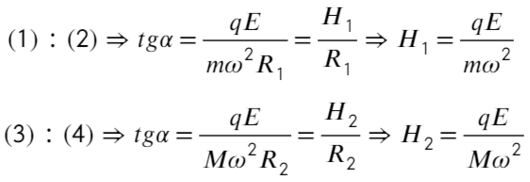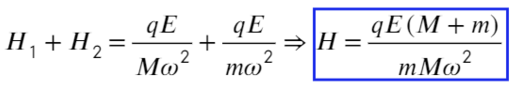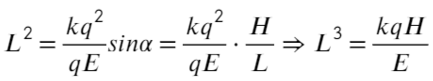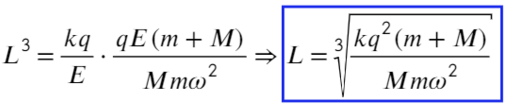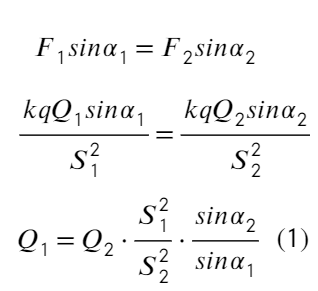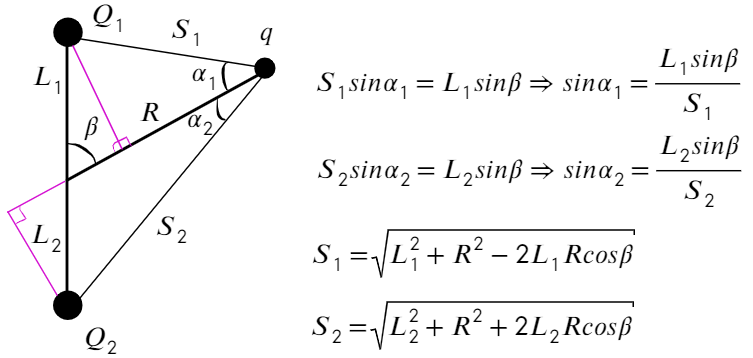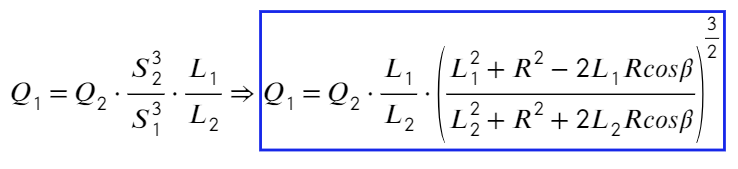Как найти соотношения зарядов - Сайт, где вы сможете решить свои вопросы

Закон Кулона

Закон сохранения электрического заряда

Напряженность

Принцип суперпозиции

Электрическое поле

Потенциал электростатического поля

Разность потенциалов

Теория

Совсем чуть−чуть.

Закон Кулона — сила, с которой два точечных заряда действуют друг на друга. Она обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов.

Заряды с одинаковым знаком отталкиваются, с разными — притягиваются. По III з. Ньютона сила действия одного заряда равна силе действия другого:

Наглядно рассказывается об этом в видео.
А напряженность — силовая характеристика электрического поля. По-простому: электрическое поле действует на заряд, и вот сила, с которой поле действует на заряд, и есть напряженность.

Напряженность НЕ зависит от величины заряда, помещенного в поле!

Задачи

Задача 1 Два одинаковых маленьких положительно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.

Скажем, что заряд одного шарика q, другого 5q. Тогда сила Кулона между ними:

А если теперь соединить два шарика, то общий заряд разделится пополам (на каждый шарик). Общий заряд 5q + q = 6q, тогда на каждом шарике окажется по 3q. Тогда сила Кулона:

Отношение получится таким:

Ответ: 1,8

Задача 2 Два одинаковых маленьких разноименно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 4 раза. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₁ к F₂.

Та же самая задача? А вот и нет, одно слово другое: разноименно вместо положительных. Это значит, что один шарик будет заряжен положительно, другой отрицательно. По сравнению с первым случаем сила Кулона никак не изменится по модулю (только по нарпавлению).

А вот после соприкосновения изменится. Общий заряд: 5q − q = 4q или q − 5q = − 4q, тогда на каждый шар пойдет по 2q:

Отношение:

Ответ: 0,8

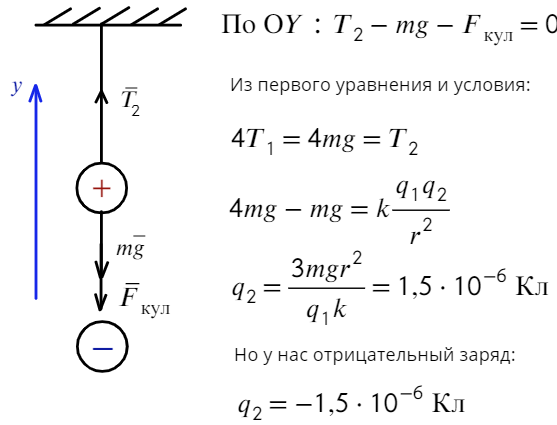
Задача 3 На нерастяжимой нити висит шарик массой 100 г, имеющий заряд 20 мкКл. Как необходимо зарядить второй шарик, который подносят снизу к первому шарику на расстояние 30 см, чтобы сила натяжения: а) увеличилась в 4 раза; б) рассмотреть случай невесомости?

В начальный момент времени на шарик действуют две силы:

а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:

б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:

Ответ: −1,5 мкКл, 500 нКл.

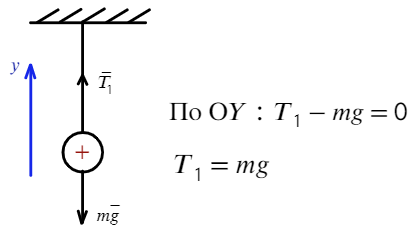
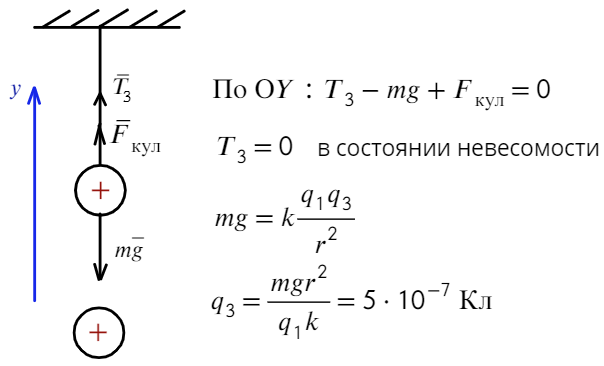
Задача 3 Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света.

В задаче говорится про электрон, значит, его массу m = 9,1×10⁻³¹ кг и заряд q = 1,6 × 10⁻¹⁹ Кл можно посмотреть в справочных данных.

Найдем ускорение электрона в электрическом поле:

Остается найти пройденный путь в равноускоренном движении при нулевой начальной скорости:

Ответ: 0,2 м

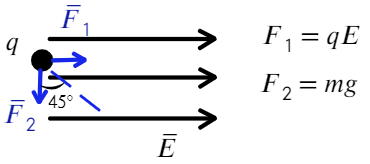
Задача 4 Полый заряженный шарик массой m = 0,4 г. движется в однородном горизонтальном электрическом поле из состояния покоя. Модуль напряженности электрического поля E = 500 кВ/м. Траектория шарика образует с вертикалью угол α = 45°. Чему равен заряд шарика?

Для начала разберемся, какие силы действуют на заряд:

Заряд движется под углом 45 градусов, значит, отношением сил будет тангенс 45°:

Ответ: 8×10⁻⁹ Кл

Задача 5 При нормальных условиях электрический «пробой» сухого воздуха наступает при напряжённости электрического поля 30 кВ/см. В результате «пробоя» молекулы газа, входящие в состав воздуха, ионизируются и появляются свободные электроны. Какую кинетическую энергию приобретёт такой электрон, пройдя в электрическом поле расстояние 10⁻⁵ см? Ответ выразите в электронвольтах. (ЕГЭ)

Задача кажется весьма тяжелой, но это обманчиво. Воспользуемся знакомой формулой напряженности:

Домножим на длину обе части, тогда слева получится работа, а работа — это изменение энергии:

Переводить сантиметры не обязательно, они сократятся. Чтобы перевести джоули в электронвольты, нужно разделить на 1,6 × 10⁻¹⁹

Ответ: 0,3 эВ

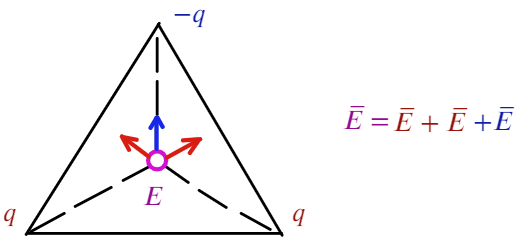
Задача 6 В вершинах равностороннего треугольника со стороной «а» находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника.

Покажем, как направлена напряженность: для двух положительных зарядов — от них (красные стрелочки), для отрицательного заряда — к нему (синяя стрелочка).

Угол между синим вектором и красным составляет 60°. Если продлить красный вектор до стороны, получится прямоугольный треугольник. Тогда, чтобы посчитать результирующую напряженность, спроецируем красные векторы на синий:

Остается разобрать на каком расстоянии находятся заряды от центра треугольника. Высоту треугольника можно найти по т. Пифагора, равна она а√3/2. А расстояние тогда составит 2/3 от высоты:

Ответ: 6kq/a²

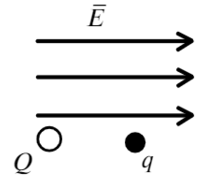
Задача 6 Два шарика с зарядами Q = –1 нКл и q = 5 нКл соответственно, находятся в однородном электрическом поле с напряженностью Е = 18 В/м, на расстоянии r = 1 м друг от друга. Масса первого шарика равна M = 5 г. Определите, какую массу должен иметь второй шарик, чтобы они двигались с прежним между ними расстоянием и с постоянным по модулю ускорением. (ЕГЭ – 2016)

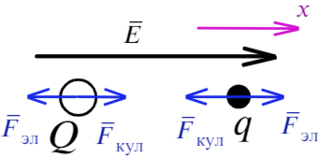
Направим ось X вправо и покажем, какие силы действуют на каждый заряд.

На положительный заряд электрическая сила действует по линиям напряженности, для отрицательного заряда все наоборот. Силы кулона направлены к зарядам, они разноименные. Составим уравнение для каждого заряда:

Сумма всех сила равна ma, потому что в условии сказано, что шарики двигаются с постоянным ускорением, а чтобы расстояние не менялось, двигаться они должны в одном направлении.

Разделим одно уравнение на другое и выразим массу:

Ответ: 8,3 гр.

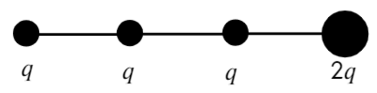
Задача 7 Четыре маленьких одинаковых шарика, связанных нерастяжимыми нитями одинаковой длины, заряженызарядами q, q, q и 2q. Сила натяжения нити, связывающей первый и второй шарики, равна T. Найти силу натяжения нити, связывающейвторой и третий шарики. (Росатом)

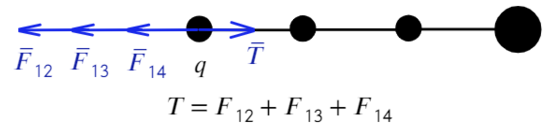
Покажем, каким силам противодействует сила натяжения Т. Воспользуемся принципом суперпозиции и законом Кулона:

Сила натяжения Т удерживает первый шарик, других сил для него нет, значит, больше ничего для первого случая не требуется.

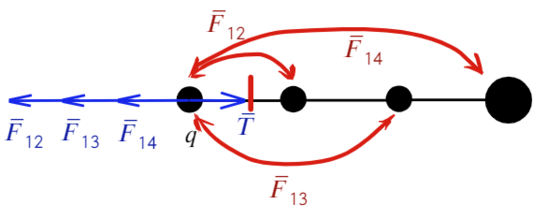
Как проще это запомнить: проводим линию перпендикулярно той нити, о которой говорим (красная черточка), после записываем только те силы между шариками, которые появляются по разные стороны от проведенной линии:

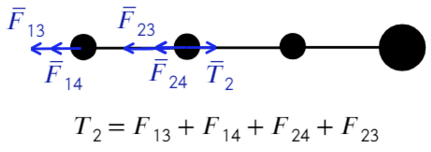
Теперь также составим уравнения для силы натяжения между вторым и третьим шариком:

Распишим каждое уравнение по закону кулона, скажем, что расстояние между соседними шариками равно «а»:

Второе уравнение с подстановкой выражения из первого:

Ответ: 71T/53

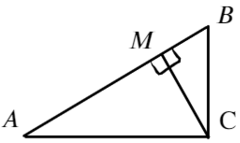
Задача 8 Точечный заряд, расположенный в точке C, создаёт в точках A и B поле с напряжённостью Ea и Eb соответственно (см. рисунок; угол ACB — прямой). Найти напряжённость электрическогополя, создаваемого этим зарядом в точке M, являющейся основанием перпендикуляра, опущенного из точки C на прямую AB. (Росатом)

Запишем, чему равна напряженность в каждой из этих точек, взяв длины отрезков за a; b; h:

Площадь прямоугольного треугольника можно найти как полупроизведение катетов или как полупроизведение высоты и основания:

Возведем в квадрат получившиеся уравнение, а дальше смертельный номер: возводим в −1 степень и домножаем обе части на kq:

Выразим a² и b² через напряженность:

Ответ: Ea+Eb

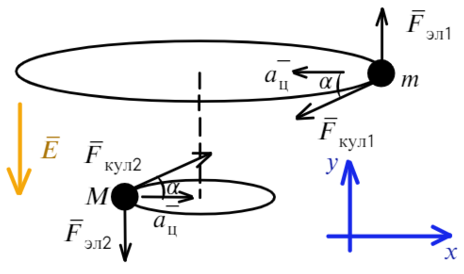
Задача 9 Частицы с массами M и m, и зарядами q и −q соответственно вращаются с угловой скоростью ω по окружностям вокруг оси, направленной по внешнемуоднородному электрическому полю с напряжённостью E (рис.). Найдите расстояние L между частицами и расстояние H между плоскостями их орбит. (Всеросс. 2008)

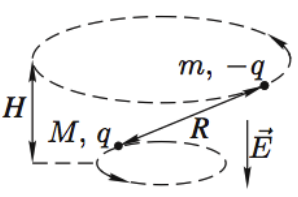
Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:

Запишем уравнения по осям на верхнюю частицу:

На нижнюю частицу:

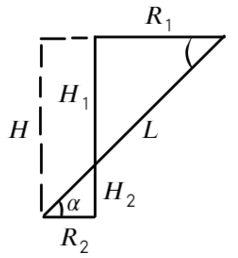
Построим два треугольника, которые показывают расстояние между частицами и высоту между ними.

Разделим уравнения друг на друга, а также выразим тангенс угла из этих треугольников:

Сложим два уравнения, чтобы найти расстояние между плоскостями:

Пункт «а» решили, теперь с расстоянием разберемся: выразим из ур-ия (1) длину, а дальше из треугольника выразим синус угла альфа:

Вместо Н подставим то, что мы нашли:

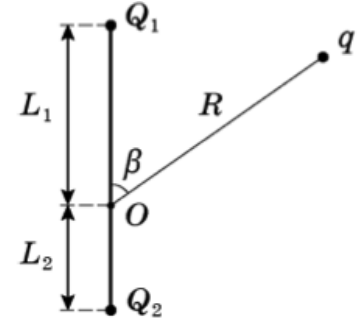
Задача 10 В точке O к стержню привязана непроводящая нить длиной R c зарядом q на конце. Известный эталонный заряд Q₂ и измеряемый заряд Q₁ установлены на расстояниях L₂ и L₁ от точки O. Все заряды одногознака и могут считаться точечными. Найдите величину заряда Q₁, если в состоянии равновесия нить отклонена на угол β от отрезка, соединяющегозаряды Q₂ и Q₁. (Всеросс. 2018)

Проведем оси, подпишем расстояние от Q₁ до q и от Q₂ до q. Запишем ур-ия сил на каждую ось:

Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:

Из прямоугольных треугольников можно получить такие соотношения, а также из теоремы косинусов выразить S₁ и S₂:

Подставим в ур-ие (1):

В качестве закрепления материала решите несколько похожих задач с ответами.

Будь в курсе новых статеек, видео и легкого технического юмора.

Источник

1.1.Основные понятия и соотношения Электрический заряд

В
природе существуют два вида электрических
зарядов: положительные и отрицательные.
Выбор названия был исторической
случайностью.

Как
положительные, так и отрицательные
заряды состоят из равных элементарных
зарядов величиной е
=
1,602189210^-19
Кл. Материальными носителями таких
зарядов являются микрочастицы. В
частности, материальным носителем
отрицательного элементарного заряда
является электрон, а положительного –
протон.

Экспериментально
установлен закон сохранения заряда. В
электрически изолированной системе
полный электрический заряд, т.е.
алгебраическая сумма положительного
и отрицательного зарядов, остается
постоянным.

При
этом под электрически изолированной
понимается такая система, через границы
которой не может проникнуть никакой
заряд. Соответствующие исследования
показали, что этот закон удовлетворяет
условию релятивистской инвариантности,
причем не только в том смысле, что
приведенная выше формулировка справедлива
в любой заданной инерциальной системе
отсчета, но и в более строгом смысле:
расположенные в различных системах
отсчета наблюдатели, измеряя заряд,
получают одно и то же число. Другими
словами, полный электрический заряд
изолированной системы является
релятивистски инвариантным числом.
Отсюда следует, что величина заряда
материального носителя не
зависит от
скорости его движения.

Непрерывное распределение заряда

В
большинстве макроскопических явлений
участвует громадное число элементарных
электрических зарядов. Так на каждой
из обкладок плоского конденсатора
емкостью 10 мкФ при разности потенциалов
100В
содержится около 710¹⁵
нескомпенсированных элементарных
зарядов. При этом их дискретность никак
не проявляется. Поэтому можно считать,
что заряд как бы непрерывно распределен
на обкладках. Различают объемную,
поверхностную и линейную плотности
зарядов.

Объемной
плотностью зарядов
называется отношение зарядаQ
к объемуV,
в котором этот заряд находится:

, (1)

где
– элементарные заряды в объеме(с учетом их знака);– физически малый объем, но не бесконечно
малый в математическом смысле. Физически
малый – это значит, что его положение в
пространстве достаточно точно
характеризуется координатами какой-то
точки, расположенной внутри него. Однако
в этом объеме должно находиться такое
достаточно большое количество элементарных
зарядов, чтобы небольшое изменение их
числа не приводило к существенному
изменению плотности, вычисляемой по
формуле (1).

Поверхностная
плотность зарядов 
определяется формулой

, (2)

где
– бесконечно малая в физическом смысле
площадь, по которой распределяется
заряд.Линейная
плотность зарядов

– это отношение заряда к бесконечно
малой в физическом смысле длине, по
которой распределен заряд:

. (3)

Взаимодействие между покоящимися электрическими зарядами

Для
точечных зарядов, находящихся в вакууме,
взаимодействие описывается экспериментальным
законом Кулона, который в системе СИ
имеет вид

(4)

где
и– модули взаимодействующих зарядов;– радиус-вектор, определяющий положение
точечного зарядав поле точечного заряда,.

–
сила, действующая на заряд
со стороны заряда.
Величинаназывается электрической постоянной.
На зарядсо стороны заряда,
согласно третьему закону Ньютона,
действует сила.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

Beam of electrons moving in a circle in a Teltron tube, due to the presence of a magnetic field. Purple light is emitted along the electron path, due to the electrons colliding with gas molecules in the bulb. Mass-to-charge ratio of the electron can be measured in this apparatus by comparing the radius of the purple circle, the strength of the magnetic field, and the voltage on the electron gun. The mass and charge cannot be separately measured this way—only their ratio.

Mass-to-charge ratio
Common symbols	m/Q
SI unit	kg/C
In SI base units	kg⋅A^-1⋅s^-1
Dimension	${displaystyle {mathsf {MI^{-1}T^{-1}}}}$

The mass-to-charge ratio (m/Q) is a physical quantity relating the mass (quantity of matter) and the electric charge of a given particle, expressed in units of kilograms per coulomb (kg/C). It is most widely used in the electrodynamics of charged particles, e.g. in electron optics and ion optics.

It appears in the scientific fields of electron microscopy, cathode ray tubes, accelerator physics, nuclear physics, Auger electron spectroscopy, cosmology and mass spectrometry.^[1] The importance of the mass-to-charge ratio, according to classical electrodynamics, is that two particles with the same mass-to-charge ratio move in the same path in a vacuum, when subjected to the same electric and magnetic fields.

Some disciplines use the charge-to-mass ratio (Q/m) instead, which is the multiplicative inverse of the mass-to-charge ratio. The CODATA recommended value for an electron is Q/m = −1.75882001076(53)×10¹¹ C⋅kg⁻¹.^[2]

Origin[edit]

When charged particles move in electric and magnetic fields the following two laws apply:

Lorentz force law:
Newton’s second law of motion:

${displaystyle mathbf {F} =mmathbf {a} =m{frac {mathrm {d} mathbf {v} }{mathrm {d} t}}}$

where F is the force applied to the ion, m is the mass of the particle, a is the acceleration, Q is the electric charge, E is the electric field, and v × B is the cross product of the ion’s velocity and the magnetic flux density.

This differential equation is the classic equation of motion for charged particles. Together with the particle’s initial conditions, it completely determines the particle’s motion in space and time in terms of m/Q. Thus mass spectrometers could be thought of as “mass-to-charge spectrometers”. When presenting data in a mass spectrum, it is common to use the dimensionless m/z, which denotes the dimensionless quantity formed by dividing the mass number of the ion by its charge number.^[1]

Combining the two previous equations yields:

${displaystyle left({frac {m}{Q}}right)mathbf {a} =mathbf {E} +mathbf {v} times mathbf {B} .}$

This differential equation is the classic equation of motion of a charged particle in a vacuum. Together with the particle’s initial conditions, it determines the particle’s motion in space and time. It immediately reveals that two particles with the same m/Q ratio behave in the same way. This is why the mass-to-charge ratio is an important physical quantity in those scientific fields where charged particles interact with magnetic or electric fields.

Exceptions[edit]

There are non-classical effects that derive from quantum mechanics, such as the Stern–Gerlach effect that can diverge the path of ions of identical m/Q.

Symbols and units[edit]

The IUPAC recommended symbol for mass and charge are m and Q, respectively,^[3]^[4] however using a lowercase q for charge is also very common. Charge is a scalar property, meaning that it can be either positive (+) or negative (−). The Coulomb (C) is the SI unit of charge; however, other units can be used, such as expressing charge in terms of the elementary charge (e). The SI unit of the physical quantity m/Q is kilogram per coulomb.

Mass spectrometry and m/z[edit]

The units and notation above are used when dealing with the physics of mass spectrometry; however, the m/z notation is used for the independent variable in a mass spectrum.^[5] This notation eases data interpretation since it is numerically more related to the dalton.^[1] For example, if an ion carries one charge the m/z is numerically equivalent to the molecular or atomic mass of the ion in daltons (Da), where the numerical value of m/Q is abstruse. The m refers to the molecular or atomic mass number and z to the charge number of the ion; however, the quantity of m/z is dimensionless by definition.^[5] An ion with a mass of 100 Da (daltons) (m = 100) carrying two charges (z = 2) will be observed at m/z 50. However, the empirical observation m/z 50 is one equation with two unknowns and could have arisen from other ions, such as an ion of mass 50 Da carrying one charge. Thus, the m/z of an ion alone neither infers mass nor the number of charges. Additional information, such as the mass spacing between mass isotopomers or the relationship between multiple charge states, is required to assign the charge state and infer the mass of the ion from the m/z. This additional information is often but not always available. Thus, the m/z is primarily used to report an empirical observation in mass spectrometry. This observation may be used in conjunction with other lines of evidence to subsequently infer the physical attributes of the ion, such as mass and charge. On rare occasions, the thomson has been used as a unit of the x-axis of a mass spectrum.

History[edit]

In the 19th century, the mass-to-charge ratios of some ions were measured by electrochemical methods. In 1897, the mass-to-charge ratio of the electron was first measured by J. J. Thomson.^[6] By doing this, he showed that the electron was in fact a particle with a mass and a charge, and that its mass-to-charge ratio was much smaller than that of the hydrogen ion H⁺. In 1898, Wilhelm Wien separated ions (canal rays) according to their mass-to-charge ratio with an ion optical device with superimposed electric and magnetic fields (Wien filter). In 1901 Walter Kaufman measured the increase of electromagnetic mass of fast electrons (Kaufmann–Bucherer–Neumann experiments), or relativistic mass increase in modern terms. In 1913, Thomson measured the mass-to-charge ratio of ions with an instrument he called a parabola spectrograph.^[7] Today, an instrument that measures the mass-to-charge ratio of charged particles is called a mass spectrometer.

Charge-to-mass ratio[edit]

B is uniform throughout; E exists only where shown.

The charge-to-mass ratio (Q/m) of an object is, as its name implies, the charge of an object divided by the mass of the same object. This quantity is generally useful only for objects that may be treated as particles. For extended objects, total charge, charge density, total mass, and mass density are often more useful.

Derivation:

${displaystyle qvB=mv{frac {v}{r}}}$

${displaystyle {frac {q}{m}}={frac {v}{Br}}}$

(1)

Since ${displaystyle F_{text{electric}}=F_{text{magnetic}}}$ ,

${displaystyle v={frac {E}{B}}}$

(2)

Equations (1) and (2) yield

${displaystyle {frac {q}{m}}={frac {E}{B^{2}r}}}$

Significance[edit]

In some experiments, the charge-to-mass ratio is the only quantity that can be measured directly. Often, the charge can be inferred from theoretical considerations, so the charge-to-mass ratio provides a way to calculate the mass of a particle.

Often, the charge-to-mass ratio can be determined by observing the deflection of a charged particle in an external magnetic field. The cyclotron equation, combined with other information such as the kinetic energy of the particle, will give the charge-to-mass ratio. One application of this principle is the mass spectrometer. The same principle can be used to extract information in experiments involving the cloud chamber.

The ratio of electrostatic to gravitational forces between two particles will be proportional to the product of their charge-to-mass ratios. It turns out that gravitational forces are negligible on the subatomic level, due to the extremely small masses of subatomic particles.

Electron[edit]

The electron charge-to-mass quotient, ${displaystyle -e/m_{e}}$ , is a quantity that may be measured in experimental physics. It bears significance because the electron mass m_e is difficult to measure directly, and is instead derived from measurements of the elementary charge e and $e/m_{e}$ . It also has historical significance; the Q/m ratio of the electron was successfully calculated by J. J. Thomson in 1897—and more successfully by Dunnington, which involves the angular momentum and deflection due to a perpendicular magnetic field. Thomson’s measurement convinced him that cathode rays were particles, which were later identified as electrons, and he is generally credited with their discovery.

The CODATA recommended value is −e/m_e = −1.75882001076(53)×10¹¹ C⋅kg⁻¹.^[2] CODATA refers to this as the electron charge-to-mass quotient, but ratio is still commonly used.

There are two other common ways of measuring the charge-to-mass ratio of an electron, apart from Thomson and Dunnington’s methods.

The magnetron method: Using a GRD7 Valve (Ferranti valve),^{[dubious – discuss]} electrons are expelled from a hot tungsten-wire filament towards an anode. The electron is then deflected using a solenoid. From the current in the solenoid and the current in the Ferranti Valve, e/m can be calculated.^{[citation needed]}
Fine beam tube method: A heater heats a cathode, which emits electrons. The electrons are accelerated through a known potential, so the velocity of the electrons is known. The beam path can be seen when the electrons are accelerated through a helium (He) gas. The collisions between the electrons and the helium gas produce a visible trail. A pair of Helmholtz coils produces a uniform and measurable magnetic field at right angles to the electron beam. This magnetic field deflects the electron beam in a circular path. By measuring the accelerating potential (volts), the current (amps) to the Helmholtz coils, and the radius of the electron beam, e/m can be calculated.^[8]

Zeeman Effect[edit]

The charge-to-mass ratio of an electron may also be measured with the Zeeman effect, which gives rise to energy splittings in the presence of a magnetic field B:

${displaystyle Delta E={frac {ehbar B}{2m}}(m_{j,f}g_{J,f}-m_{j,i}g_{J,i})}$

Here m_j are quantum integer values ranging from −j to j, with j as the eigenvalue of the total angular momentum operator J, with^[2]

where S is the spin operator with eigenvalue s and L is the angular momentum operator with eigenvalue l. g_J is the Landé g-factor, calculated as

${displaystyle g_{J}=1+{frac {j(j+1)+s(s+1)-l(l+1)}{2j(j+1)}}}$

The shift in energy is also given in terms of frequency υ and wavelength λ as

${displaystyle Delta E=hDelta nu =hcDelta left({frac {1}{lambda }}right)=hc{frac {Delta lambda }{lambda ^{2}}}}$

Measurements of the Zeeman effect commonly involve the use of a Fabry–Pérot interferometer, with light from a source (placed in a magnetic field) being passed between two mirrors of the interferometer. If δD is the change in mirror separation required to bring the mth-order ring of wavelength λ + Δλ into coincidence with that of wavelength λ, and ΔD brings the (m + 1)th ring of wavelength λ into coincidence with the mth-order ring, then

${displaystyle Delta lambda =lambda ^{2}{frac {delta D}{2DDelta D}}.}$

It follows then that

${displaystyle hc{frac {Delta lambda }{lambda ^{2}}}=hc{frac {delta D}{2DDelta D}}={frac {ehbar B}{2m}}(m_{j,f}g_{J,f}-m_{j,i}g_{J,i}),.}$

Rearranging, it is possible to solve for the charge-to-mass ratio of an electron as

${displaystyle {frac {e}{m}}={frac {4pi c}{B(m_{j,f}g_{J,f}-m_{j,i}g_{J,i})}}{frac {delta D}{DDelta D}},.}$

References[edit]

^ ^a ^b ^c IUPAC, Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”) (1997). Online corrected version: (2006–) “mass-to-charge ratio, m/z in mass spectrometry”. doi:10.1351/goldbook.M03752
^ ^a ^b ^c “2018 CODATA Value: electron charge to mass quotient”. The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 2019-10-22.
^ International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. p. 4. Electronic version.
^ International Union of Pure and Applied Chemistry (1993). Quantities, Units and Symbols in Physical Chemistry, 2nd edition, Oxford: Blackwell Science. ISBN 0-632-03583-8. p. 14. Electronic version.
^ ^a ^b Compiled by A. D. McNaught and A. Wilkinson (1997). “Mass-to-charge ratio in mass spectrometry, mz”. IUPAC. Compendium of Chemical Terminology, 2nd ed. (the –”––Gold Book”). Oxford: Blackwell Scientific Publications. doi:10.1351/goldbook.M03752. ISBN 978-0-9678550-9-7.
^ J. J. Thomson (1856–1940) Philosophical Magazine, 44, 293 (1897).
^ Joseph John Thomson (1856–1940) Proceedings of the Royal Society A 89, 1–20 (1913) [as excerpted in Henry A. Boorse & Lloyd Motz, The World of the Atom, Vol. 1 (New York: Basic Books, 1966)]
^ PASCO scientific, Instruction Manual and Experimental guide for the PASCO scientific Model SE-9638, pg. 1.

Bibliography[edit]

Szilágyi, Miklós (1988). Electron and ion optics. New York: Plenum Press. ISBN 978-0-306-42717-6.
Septier, Albert L. (1980). Applied charged particle optics. Boston: Academic Press. ISBN 978-0-12-014574-4.
International vocabulary of basic and general terms in metrology =: Vocabulaire international des termes fondamentaux et généraux de métrologie. International Organization for Standardization. 1993. ISBN 978-92-67-01075-5.CC.
IUPAP Red Book SUNAMCO 87-1 “Symbols, Units, Nomenclature and Fundamental Constants in Physics” (does not have an online version).
Symbols Units and Nomenclature in Physics IUPAP-25 IUPAP-25, E.R. Cohen & P. Giacomo, Physics 146A (1987) 1–68.

External links[edit]

BIPM SI brochure
AIP style manual
NIST on units and manuscript check list
Physics Today’s instructions on quantities and units

Источник

История открытия

Взаимодействия двух точечных зарядов рассмотренным выше законом в первый раз были доказаны в 1785 Шарлем Кулоном. Доказать правдивость сформулированного закона физику удалось с использованием крутильных весов, принцип действия которых также был представлен в статье.

Кулон также доказал, что внутри сферического конденсатора нет электрического заряда. Так он пришёл к утверждению, что величину электростатических сил можно менять путём изменения расстояния между рассматриваемыми телами.

Таким образом, закон Кулона по-прежнему является главнейшим законом электростатики, на основе которого было сделано немало величайших открытий. В рамках данной статьи была представлена официальная формулировка закона, а также подробно описаны его составляющие части.

Формулировка

Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.

Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F1|=|F2|=(ke*q1*q2) / r2

Рис. 3. Взаимодействие точечных зарядов

Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.

Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.

Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:

соблюдение точечности зарядов;
неподвижность заряженных тел;
закон выражает зависимости между зарядами в вакууме.

Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.

Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 — 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.

Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 1018 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.

Кулоновские силы подпадают под действие третьего закона Ньютона: F1 = – F2. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m1* m2 ) / r2 , где m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними.

Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.

Физический смысл, что можно определить с его помощью

Теорема 1

Сила взаимодействия F между двумя неподвижными телами с зарядом (q1 и q2), находящимися в вакуумном пространстве, является прямо пропорциональной произведению модулей данных зарядов и обратно пропорциональной расстоянию r в квадрате (r²). Это формула для материальных точек.

Практическая вся электротехника в современном мире строится на законах взаимодействия сил закона Кулона. Благодаря тому, что Кулон открыл свой закон начала развиваться наука, которая изучает электромагнитные взаимосвязи.

Также электрическое поле базируется на представлении о силах закона Кулона. Доказано, что электрическое поле неделимо связано с зарядами простейших частиц.

Облака в грозу — скопление зарядов электрических. Индуцированные заряды с поверхности земли притягиваются к ним, поэтому появляются молнии. Открытие закона Кулона позволило создать эффективные отводы для молний, чтобы защитить многие здания и электротехнические постройки.

На основе законов электростатики было изобретено множество нужных в жизни и в производстве вещей. Например:

Конденсатор.
Самые разные диэлектрики.
Материалы-антистатики для того, чтобы защитить чувствительные детали электроники.
Производство одежды для защиты сотрудников электронной промышленности и т.д.

Также на основе закона Кулона формируется работа ускорителей частиц с зарядом. В частности, можно говорить о том, что закон Кулона помогает функционировать Большому адронному коллайдера.

Ускорение заряженных частиц до скоростей, близких к околосветовым, происходит за счет воздействия электромагнитного поля, которое создается катушками, расположенными вдоль трассы. От столкновения происходит распад простейших частиц, следы которых закрепляются электронными приборами. На основании данных показаний, с помощью закона Кулона, ученые могут сделать вывод о структуре элементарных частиц материи.

Действие электрического поля на электрические заряды

Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.

Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.

Свойства электрического поля заключаются в том, что оно:

материально;
создается зарядом;
обнаруживается по действию на заряд;
непрерывно распределено в пространстве;
ослабевает с увеличением расстояния от заряда.

Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.

Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:

где ( vec{E} ) – напряженность электрического поля, ( q ) – заряд.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.

Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:

сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
записать для заряда условие равновесия или основное уравнение динамики материальной точки;
выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
записать математически все вспомогательные условия;
решить полученную систему уравнений относительно неизвестной величины;
проверить решение

Где закон Кулона применяется на практике

Основной закон электростатики — это важнейшее открытие Шарля Кулона, которое нашло своё применение во многих областях.

Работы известного физика использовались в процессе изобретения различных устройств, приборов, аппаратов. К примеру, молниеотвод.

При помощи молниеотвода жилые дома, здания защищают от попадания молнии во время грозы. Таким образом, повышается степень защиты электрического оборудования.

Молниеотвод работает по следующему принципу: во время грозы на земле постепенно начинают скапливаться сильные индукционные заряды, которые поднимаются вверх и притягиваются к облакам. При этом на земле образуется немаленькое электрическое поле. Вблизи молниеотвода электрическое поле становится сильнее, благодаря чему от острия устройства зажигается коронный электрический заряд.

Далее образованный на земле заряд начинает притягиваться к заряду облака с противоположным знаком, как и должно быть согласно закону Шарля Кулона. После этого воздух проходит процесс ионизации, а напряжённость электрического поля становится меньше возле конца молниеотвода. Таким образом, риск попадания молнии в здание минимален.

Обратите внимание! Если в здание, на котором установлен молниеотвод, попадёт удар, то пожара не произойдёт, а вся энергия уйдёт в землю.

На основе закона Кулона было разработано устройство под названием “Ускоритель частиц”, которое пользуется большим спросом сегодня.

В данном приборе создано сильное электрическое поле, которое увеличивает энергию попадающих в него частиц.

Формулы с пояснениями

Как и силы тяготения, электрические силы (кулоновские) для области применения закона – консервативны, имеют потенциальную энергию, функцию расстояний наблюдаемых частиц. Силовой характеристикой распределения в пространстве поля и его действием на заряд служит напряженность E (векторная). Основные свойства поля и зарядов (притягивающие или отталкивающие) определяет и устанавливает в электростатике ряд формул.

Напряженность пропорциональна силе F, влияющей на q (малый точечный заряд «пробный»), обратно пропорциональна заряду.

Определение напряженности поля E на отрезке r от заряда q выводится из закона Кулона:

Консервативное поле обладает потенциальной энергией (W), такой существующей функцией от соотносительных расстояний для рассматриваемых заряженных частиц. Для поля с напряженностью E заряд q имеет потенциальную энергию (W):

здесь d — расстояние до плоскости, где принята W=0. Нулевой уровень W выбирается произвольно, следовательно, потенциал ? является относительной величиной. Для поля притяжения (механика) тела стремятся к положению с min потенциальной энергией (W), в электростатике по-другому.

Под действием сил поля (электрического) заряженный (+) объект перемещается из точки 2 с > потенциалом (?) в точку 1 с < потенциалом (?), отрицательно же заряженный движется наоборот.

Характеризуя электрическое поле, представляя его, определяют силовую (напряженность E) и энергетическую (потенциальную W) стороны.

Работа (A), выполняемая электростатической силой при перемещении единичного положительного заряда q из некоторой точки в конечную, определяет напряжение (разность потенциалов этих точек) поля.

Зависимость напряженности и разности потенциалов:

где U; напряжение между точками, которые связаны c перемещением Δd, совпадающим по направлению с вектором E.

Электростатика находит применение в многочисленных сферах, в технике, медицине. Электромагнитная теория объяснила многие процессы, безукоризненно описала области явлений, для раскрытия которых была создана. Но дальнейшие исследования сверх микроскопических частиц в атомно-ядерных масштабах, развитие науки показало, что эта сложившаяся картина мира несовершенна. Позднее появлялись другие гипотезы, родилась новая квантово-полевая (релятивистская) теория существования материи, пока до конца непознанная. Но знать и применять практически законы, управляющие известными окружающими нас явлениями и процессами, для соответствующих объектов совершенно необходимо.

Электрический заряд и его свойства

Многие объекты наэлектризовываются, содержат избыток заряженных частиц, они получают электрические заряды. Это величина элементарных зарядов (количество электричества), определяющее электромагнитное воздействие в пространстве поля. Обладают следующими свойствами:

Заряд передается другому телу. Заряжаемый объект при различных обстоятельствах может обладать неодинаковым зарядом. Электризация (переход электронов) тел происходит при соприкосновении или трении.
Передаваемый min возможный заряд (e) электрона называют элементарным, он не делим, в СИ округленно определен:
Протон несет наименьший такой же, но положительный электрический заряд.
Электрический заряд q для объекта считается кратной N раз величиной к e: q=Ne, где N – целое натуральное число.
Заряд тела – сумма электрических зарядов в нем (алгебраическая).

Таблица перевода единицы измерения Кулон, калькулятор онлайн, конвертер

Все Все Абсолютная электромагнитная система СГСМ Абсолютная электромагнитная система СГСМ Внесистемные единицы Внесистемные единицы Международная система (СИ) Международная система (СИ) Единицы электрического заряда в системе СГСЭ Единицы электрического заряда в системе СГСЭ

Кулон в Абкулон	0.1
Кулон в Ампер/мин	0.016667
Кулон в Ампер/сек	1
Кулон в Ампер/час	0.000278
Кулон в Единица заряда СГСМ	0.1
Кулон в Килокулон	0.001
Кулон в Мегакулон	1 * 10-6
Кулон в Микрокулон	1 000 000
Кулон в Милликулон	1 000
Кулон в Нанокулон	10 * 108
Кулон в Пикокулон	10 * 1011
Кулон в Статкулон	3 * 109
Кулон в Фарадей	1.04 * 10-5
Кулон в Франклин	3 * 109
Кулон в Элементарный электрический заряд	6.24 * 1018

Кратные и дольные единицы кулона:

Кратные и дольные единицы образуются с помощью стандартных приставок СИ.

Кратные	Дольные
величина	название	обозначение	величина	название	обозначение
101 Кл	декакулон	даКл	daC	10−1 Кл	децикулон	дКл	dC
102 Кл	гектокулон	гКл	hC	10−2 Кл	сантикулон	сКл	cC
103 Кл	килокулон	кКл	kC	10−3 Кл	милликулон	мКл	mC
106 Кл	мегакулон	МКл	MC	10−6 Кл	микрокулон	мкКл	µC
109 Кл	гигакулон	ГКл	GC	10−9 Кл	нанокулон	нКл	nC
1012 Кл	теракулон	ТКл	TC	10−12 Кл	пикокулон	пКл	pC
1015 Кл	петакулон	ПКл	PC	10−15 Кл	фемтокулон	фКл	fC
1018 Кл	эксакулон	ЭКл	EC	10−18 Кл	аттокулон	аКл	aC
1021 Кл	зеттакулон	ЗКл	ZC	10−21 Кл	зептокулон	зКл	zC
1024 Кл	иоттакулон	ИКл	YC	10−24 Кл	иоктокулон	иКл	yC

Формула Кулона для среды

Стоит отметить, что закон Кулона может быть применим для вычисления взаимосвязи точечных зарядов и шарообразных тел при распределении зарядов равномерно по их объему и поверхности.

В результате экспериментов было доказано, что при всех равных показателях сила электростатического взаимодействия будет зависеть от среды, в которой существуют данные заряды. Коэффициент пропорциональности k в кулоновском законе будет представлен в виде: k=k1e.

В данной формуле:

k1 — коэффициент, зависящий только от того, какую систему единиц вы выберете при расчетах;
e является постоянной величиной, характеризует свойства среды (электрические), носит название «относительная диэлектрическая проницаемость среды». В условиях вакуума e=1.

В системе единиц СИ один заряд (кулон — Кл) будет определяться через единицу силы тока (ампер — А), а также единицу времени (секунда — с).

Таким образом будет выведена формула 1Кл=1А×1с.

Коэффициент k1 будет определяться в данной системе как:

k1=14πe0=8,988×109H×m2Кл2.

Показатель электрической постоянной равен e0=8,85×10-12Кл(вквадрате) H×m2.

Закон Кулона для однородной и изотропной сред будет писаться в таком виде:

F=14πe0q1q2er2r1r2

Закон Кулона для зарядов в вакууме

Сила отталкивания в вакууме рассчитывается с учетом эффекта поляризации (по квантовой электродинамике).
Что это означает? Что необходимо учитывать условное сопротивление электронно-позитронных пар, экранирующих непосредственно заряд.
И оно увеличивается при большем расстоянии.
То есть эффективный заряд электрона считается убывающей функцией по логарифмическому соотношению к расстоянию.

Но при этом формой, массой и габаритами точечного заряда в данном правиле также пренебрегают, оценивая их в условную единицу.
На практике, поправку с учетом эффекта поляризации делать не нужно, так как она играет роль только для микрочастиц размером в несколько атомов.

Примеры практического использования

Уже было сказано про то, что закон Кулона повлиял на формирование целого ряда научных дисциплин, помог в производстве разных материалов. В современном мире нет ни одной области электротехники, в которой не работал бы кулоновский закон. Особенно это касается областей электростатики. Их работа напрямую зависит от закона Кулона. Рассмотрим примеры практического использования закона:

Самый простой способ использования данного закона — введение диэлектрика. Сила взаимосвязи зарядов в вакуумном пространстве будет всегда большей по силе, чем взаимосвязь этих же зарядов, но в условиях, когда между зарядами располагается любой диэлектрик.

Диэлектрическая проницаемость среды является той величиной, которая помогает определить силовые значения количественно, не завися от расстояния между этими зарядами, а также от их величины. Будет достаточно разделить силу взаимосвязи зарядов в вакуумном пространстве на диэлектрический показатель проницаемости внесенного диэлектрика — так получится сила взаимосвязи в присутствии любого диэлектрика.

Благодаря закону Кулона стала возможной работа сложных исследовательских комплексов. Например, ускорителя частиц с зарядами. Фундамент работоспособности ускорителей частиц строится на явлении взаимосвязи электрического поля, а также заряженных частиц.

Электрическое поле делает работу в ускорителе, увеличивая постепенно энергию частицы. Можно принять частицу с ускорением за точечный заряд, действие самого ускоряющего электрического поля ускорителя — за сумму сил со стороны всех остальных точечных зарядов. В таком случае закон Кулона полностью можно считать соблюденным.

Также закон Кулона способствует работе защитных сооружений электротехнического толка. У каждой электротехнической станции всегда устанавливается молниеотвод. А его работа невозможно без соблюдений условий закона Кулона.

В период гроз на планете формируются большие индуцированные заряды — по закону Кулона они должны притягиваться по направлению к грозовому облаку. В результате разряда молнии вокруг молниеотвода воздух ионизируется.

Из-за этого напряжение электрического поля рядом с верхушкой острого кончика молниеотвода уменьшается, а индуцированные заряды не накапливаются на поверхности здания, поэтому вероятность повторного попадания молнии снижается. Если молния все же попадет в молниеотвод, то сила заряда будет направлена в землю, что не причинит вред установке.

Закон Кулона для зарядов в веществе

Действие тел друг на друга, размещенных в каком-нибудь веществе, будет ниже, чем в вакууме.
Сила взаимодействия точечных зарядов рассчитывается аналогично, но добавляются 2 дополнительные составляющие:

объем вещества (который условно взаимодействует с телами);
проницаемость вещества (диэлектрическая).

Закон Кулона в диэлектриках

Диэлектрик приравнивается к среде, в которой из-за поляризации он снижает силу Кулона.
Уменьшение F пропорционально диэлектрической проницаемости.
Для воздуха он близок к 1, поэтому закон в этом случае рассчитывается точно так же, как и для вакуума.
Но нивелируется факт, что модуль рассматриваемого заряда может передавать заряженные частицы непосредственно диэлектрику (процесс формирования статического заряда).
И это актуально только в том случае, если данный процесс постоянный.
Если же телу придали заряд, а в дальнейшем извлекли из электромагнитного поля, то уровень заряженности постепенно меняется.
Соответственно, если между телами находится диэлектрик, чья проницаемость близка или равна бесконечности, то взаимодействия между ними не будет.
Увеличение заряда до бесконечности тоже не меняет данную формулу.

Закон Амонтона-Кулона

Познакомимся с законом, который позволяет вычислять силу трения. Он был открыт французом Г.Амонтоном и проверен его соотечественником Ш.Кулоном, поэтому называется законом Амонтона-Кулона.

Рассмотрим тело, лежащее на опоре (см. левую часть чертежа). Тело действует на опору своим весом W, который направлен вниз. По третьему закону Ньютона опора реагирует

на тело силой R, равной по модулю весу тела и противоположно направленной. По правилу параллелограмма силу реакции
R можно представить суммой силы нормальной реакции N о перпендикуляру к поверхности и силы тангенциальной реакции
T вдоль поверхности. Эта составляющая реакции – сила трения покоя.

Если мы расположим опору горизонтально, то она тоже будет реагировать на тело согласно третьему закону Ньютона (см. среднюю часть чертежа). В этом случае, как и ранее, сила реакции опоры R будет равной по модулю весу тела W и противоположно направленной. Наряду с этим, сила реакции одновременно будет и силой нормальной реакции, а сила тангенциальной реакции, сила трения, будет отсутствовать.

Если теперь к телу приложить внешнюю силу F, направленную вдоль поверхности, то мы снова вызовем появление силы тангенциальной реакции. В этом случае она будет силой трения скольжения
(см. правую часть чертежа).

Опыты показывают: при движении одного тела по поверхности другого модуль силы трения скольжения пропорционален модулю силы нормальной реакции опоры, выражаясь законом Амонтона-Кулона

Fтр – модуль силы трения скольжения, Н N – модуль силы нормальной реакции опоры, Н m – коэффициент трения скольжения

Иначе говоря, закон Амонтона-Кулона указывает на пропорциональность двух сил: тангенциальной реакции опоры (силы трения скольжения) и нормальной реакции опоры (силы давления).

Опыты показывают: закон Амонтона-Кулона можно применять как для расчёта силы трения скольжения, так и максимальной силы трения покоя. Коэффициенты трения скольжения (максимальные коэффициенты трения покоя) определяются экспериментально и могут быть, например, такими:

Дерево по дереву: 0,25	Резина по бетону: 0,75
Дерево по металлу: 0,2 – 0,5	Резина по льду: 0,15 – 0,25

Физический смысл коэффициента трения заключается в том, что он показывает долю возникающей силы трения скольжения (или максимальной силы трения покоя) от силы нормальной реакции опоры.

Задача

Рабочий прижимает брусок к стене, как показано на рисунке. Как нужно изменить вектор силы, чтобы брусок не скользил по стене?

Решение.

В левой части чертежа показано, что рука прижимает брусок. В правой части показано, как он передаёт силу руки на стену. По третьему закону Ньютона возникает ответная сила реакции, которую представим нормальной и тангенциальной силами:

Проектируя последнее равенство на оси, получим следующие уравнения:

Чтобы брусок не скользил по стене, модуль действующей силы трения должен быть меньше её расчётного значения: T < mN . Тогда имеем:

F·sin(a) < m·F·cos(a) => tg(a) < m

Ответ: рабочий должен уменьшить угол a так, чтобы его тангенс был меньше коэффициента трения скольжения бруска по стене; покой или скольжение бруска не зависят от модуля силы давления на брусок.

Закон Кулона и связь с гравитацией

Мы уже упоминали Шарля Кулона. В честь него названа единица измерения заряда — Кулон. Он придумал закон о взаимодействии зарядов.

Закон Кулона

k — коэффициент пропорциональности

(Н · м2)/Кл2

(Н · м2)/Кл2 — электрическая постоянная

— диэлектрическая проницаемость среды — показывает во сколько раз сила электростатического взаимодействия в вакууме больше силы в среде (в вакууме равна 1)

q1 — заряд первого тела [Кл]

q2 — заряд второго тела [Кл]

r — расстояние между телами [м]

F — сила электростатического взаимодействия (кулоновская) [Н]

Мы уже знаем, что заряды бывают положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные — притягиваются. Это значит, что сила направлена туда же, куда заряд будет стремиться двигаться.

Например, у положительного заряда сила будет направлена в сторону отрицательного, если он есть где-то поблизости, и от положительного, так как одноименные заряды отталкиваются.

Согласно третьему закону Ньютона, силы одной природы возникают попарно, равны по величине, противоположны по направлению. Если взаимодействуют два неодинаковых заряда, сила, с которой больший заряд действует на меньший (В на А) равна силе, с которой меньший действует на больший (А на В).

Интересно, что у различных законов физики есть некоторые общие черты. Вспомним закон тяготения. Сила гравитации также обратно пропорциональны квадрату расстояния, но уже между массами. И невольно возникает мысль, что в этой закономерности таится глубокий смысл. До сих пор никому не удалось представить тяготение и электричество, как два разных проявления одной и той же сущности.

Сила и тут изменяется обратно пропорционально квадрату расстояния, но разница в величине электрических сил и сил тяготения поразительна. Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Нельзя говорить, что одно действует сильнее другого, ведь все зависит от того, какова масса и каков заряд.

Рассуждая о том, насколько сильно действует тяготение, мы не вправе говорить: «Возьмем массу такой-то величины», потому что мы выбираем ее сами. Но если мы возьмем то, что предлагает нам сама Природа: ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами — с любыми нашими мерами, вот тогда мы можем сравнивать.

Мы возьмем элементарную заряженную частицу, например, электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.

Закон всемирного тяготения

F — сила тяготения [Н]

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

G = 6,67 · 10−11м3 · кг−1 · с−2

Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Да, это огромное число! Исследователи перебирали все большие числа, чтобы понять — откуда это взялось. Одно из таких больших чисел — это отношение диаметра Вселенной к диаметру протона — как ни удивительно, это тоже число с 42 нулями. Нормально так перебрали.

Если вы смотрели Рика и Морти, то знаете о теории параллельных вселенных и о том, что эти вселенные расширяются. Из-за расширения вселенной постоянная сила тяготения меняется. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная сила тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.

От расширяющихся вселенных и мультиков перейдем к чему-то более приземленному — к задачам.

Задачка раз

Расстояние между двумя точечными электрическими зарядами уменьшили в 3 раза, каждый из зарядов увеличили в 3 раза. Во сколько раз увеличился модуль сил электростатического взаимодействия между ними?

Решение:

Возьмем закон Кулона.

Если расстояние уменьшилось в 3 раза, то знаменатель уменьшился в 9 раз. Каждый из зарядов увеличился в три раза, значит числитель увеличился в 9 раз. Уменьшаем знаменатель в 9 раз, тем самым увеличивая всю дробь в 9 раз, увеличиваем числитель в 9 раз, получаем, что вся дробь увеличилась в 81 раз. И это ответ.

Ответ: модуль сил электростатического взаимодействия увеличится в 81 раз.

Задачка два

Два одинаковых маленьких отрицательно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F1. Модули зарядов шариков отличаются в 5 раз.

Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F2. Определите отношение F2 к F1.

Решение:

Для начала найдем заряд шариков после соприкосновения.

По закону Кулона найдем силу F1:

Теперь по закону Кулона найдем силу F2:

И находим отношение сил

Ответ: отношение сил равно 1,8.

Ограничение в применении

Закон Кулона является основной любых электромагнитных взаимодействий.
Но действует только на сравнительно небольших расстояниях.
Минимальное — это 10-16 метров, максимальное — несколько километров.
И рассчитывается только для не движущихся тел, расстояние между которыми не меняется.
И условное действие всех окружающих сил приравнено к нулю (за исключением поляризации среды, в которой и находятся тела с зарядом).
Соответственно, сумма моментов тоже приравнивается к нулю и не учитывается в формуле.
Но также известно, что при избыточно высоких зарядах (когда между телами формируется облако плазмы) сила взаимодействия растет в геометрической прогрессии.
Но по какой именно формуле — ученым ещё не удалось установить.
И здесь же можно заметить практическое значение силы Кулона.
Молния возникает только между землей и грозовыми тучами, которые расположены над уровнем почвы менее чем в 2 километра.
Тогда как поля заряженных ионов, находящихся в более высоких слоях атмосферы, взаимодействуют только между собой.
В противном бы случае Земля являлась бы необитаемой планетой.
Также закон не может применяться, если заряды помещаются в среду, не являющейся диэлектриком, так как имеющийся потенциал мгновенно нивелируется.
Поэтому его нельзя использовать, к примеру, для расчета потенциально опасного расстояния между трансформатором и человеком.

Источники

https://ElectroInfo.net/informacija/zakon-kulona-formula-opredelenie-sila-vzaimodejstvija-zarjadov-kojefficient-primenenie-na-praktike.html
https://wika.tutoronline.ru/fizika/class/10/opredelenie-i-formula-zakona-kulona
https://fizi4ka.ru/egje-2018-po-fizike/jelektricheskoe-pole.html
https://odinelectric.ru/knowledgebase/zakon-kulona-opredelenie-i-formula
https://nauka.club/fizika/teoriya-i-formuly-elektrostatiki-kratko-o-glavnom.html
https://www.calc.ru/Kulon.html
https://MasterServisNsk.ru/poleznoe/1-kulon-raven.html
https://electrically.ru/teoriya/zakon-kulona
https://rentps3.ru/tehnika/zakon-kulona-amontona.html
https://skysmart.ru/articles/physics/zakon-sohraneniya-elektricheskogo-zaryada

Как вам статья?

Павел

Бакалавр “210400 Радиотехника” – ТУСУР. Томский государственный университет систем управления и радиоэлектроники

Написать

Пишите свои рекомендации и задавайте вопросы

Источник

Между заряженными телами существует сила взаимодействия, благодаря которой они могут притягиваться или отталкиваться друг от друга. Закон Кулона описывает данную силу, показывает степень её действия в зависимости от размеров и формы самого тела. Об этом физическом законе пойдёт речь в данной статье.

Содержание

1 Неподвижные точечные заряды
2 Крутильные весы Шарля Кулона
3 Коэффициент пропорциональности k и электрическая постоянная
4 Направление силы Кулона и векторный вид формулы
5 Где закон Кулона применяется на практике
6 Направление сил в законе Кулона
7 История открытия закона

Неподвижные точечные заряды

Закон Кулона применим к неподвижным телам, размер которых намного меньше их расстояния до других объектов. На таких телах сосредоточен точечный электрический заряд. При решении физических задач размерами рассматриваемых тел пренебрегают, т.к. они не имеют особого значения.

На практике покоящиеся точечные заряды изображаются следующим образом:

В данном случае q₁ и q₂ — это положительные электрические заряды, и на них действует сила Кулона (на рисунке не показана). Размеры точечных объектов не имеют значения.

Обратите внимание! Покоящиеся заряды располагаются друг от друга на заданном расстоянии, которое в задачах обычно обозначается буквой r. Далее в статье данные заряды будем рассматривать в вакууме.

Крутильные весы Шарля Кулона

Это прибор, разработанный Кулоном в 1777 году, помог вывести зависимость силы, названной в последствии в его честь. С его помощью изучается взаимодействие точечных зарядов, а также магнитных полюсов.

Крутильные весы имеют небольшую шёлковую нить, расположенную в вертикальной плоскости, на которой висит уравновешенный рычаг. На концах рычага расположены точечные заряды.

Под действием внешних сил рычаг начинает совершать движения по горизонтали. Рычаг будет перемещаться в плоскости до тех пор, пока его не уравновесит сила упругости нити.

В процессе перемещений рычаг отклоняется от вертикальной оси на определённый угол. Его принимают за d и называют углом поворота. Зная величину данного параметра, можно найти крутящий момент возникающих сил.

Крутильные весы Шарля Кулона выглядят следующим образом:

Коэффициент пропорциональности k и электрическая постоянная

В формуле закона Кулона есть параметры k — коэффициент пропорциональности или — электрическая постоянная. Электрическая постоянная представлена во многих справочниках, учебниках, интернете, и её не нужно считать! Коэффициент пропорциональности в вакууме на основе можно найти по известной формуле:

$k = frac {1}{4cdot picdot varepsilon_0}$

Здесь $varepsilon_0=8.85cdot 10^{-12} frac {C^2}{Hcdot m^2}$ — электрическая постоянная,

— число пи,

$k=9cdot 10^{9} frac {Hcdot m^2}{C^2}$ — коэффициент пропорциональности в вакууме.

Дополнительная информация! Не зная представленные выше параметры, найти силу взаимодействия между двумя точечными электрическими зарядами не получится.
Формулировка и формула закона Кулона

Чтобы подытожить вышесказанное, необходимо привести официальную формулировку главного закона электростатики. Она принимает вид:

Сила взаимодействия двух покоящихся точечных зарядов в вакууме прямо пропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними. Причём произведение зарядов необходимо брать по модулю!

$F=kcdot frac {|q_1|cdot |q_2|}{r^2}$

В данной формуле q₁ и q₂— это точечные заряды, рассматриваемые тела; r² — расстояние на плоскости между этими телами, взятое в квадрате; k — коэффициент пропорциональности ( $9cdot 10^{9} frac {Hcdot m^2}{C^2}$ для вакуума).

Направление силы Кулона и векторный вид формулы

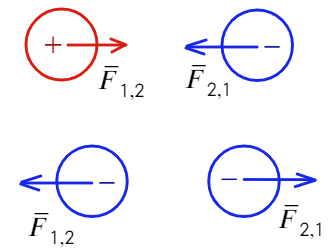
Для полного понимания формулы закон Кулона можно изобразить наглядно:

F_1,2— сила взаимодействия первого заряда по отношению ко второму.

F_2,1— сила взаимодействия второго заряда по отношению к первому.

Также при решении задач электростатики необходимо учитывать важное правило: одноимённые электрические заряды отталкиваются, а разноимённые притягиваются. От этого зависит расположение сил взаимодействия на рисунке.

Если рассматриваются разноимённые заряды, то силы их взаимодействия будут направлены навстречу друг другу, изображая их притягивание.

Формула основного закона электростатики в векторном виде можно представить следующим образом:

$vec F_1_2=frac {1}{4cdot picdot varepsilon_0}cdot frac {q_1cdot q_2}{r_1_2^3}cdot vec r_1_2$

— сила, действующая на точечный заряд q1, со стороны заряда q2,

— радиус-вектор, соединяющий заряд q2 с зарядом q1,

Важно! Записав формулу в векторном виде, взаимодействующие силы двух точечных электрических зарядов надо будет спроецировать на ось, чтобы правильно поставить знаки. Данное действие является формальностью и часто выполняется мысленно без каких-либо записей.

Где закон Кулона применяется на практике

Обратите внимание! Если в здание, на котором установлен молниеотвод, попадёт удар, то пожара не произойдёт, а вся энергия уйдёт в землю.

В данном приборе создано сильное электрическое поле, которое увеличивает энергию попадающих в него частиц.

Направление сил в законе Кулона

Как и говорилось выше, направление взаимодействующих сил двух точечных электрических зарядов зависит от их полярности. Т.е. одноимённые заряды будут отталкиваться, а разноимённые притягиваться.

Кулоновские силы также можно назвать радиус-вектором, т.к. они направлены вдоль линии, проведённой между ними.

В некоторых физических задачах даются тела сложной формы, которые не получается принять за точечный электрический заряд, т.е. пренебречь его размерами. В сложившейся ситуации рассматриваемое тело необходимо разбить на несколько мелких частей и рассчитывать каждую часть по отдельности, применяя закон Кулона.

Полученные при разбиении вектора сил суммируются по правилам алгебры и геометрии. В результате получается результирующая сила, которая и будет являться ответом для данной задачи. Данный способ решения часто называют методом треугольника.

История открытия закона

Источник

Теория

Задачи

1.1.Основные понятия и соотношения Электрический заряд

Непрерывное распределение заряда

Взаимодействие между покоящимися электрическими зарядами

Origin[edit]

Exceptions[edit]

Symbols and units[edit]

Mass spectrometry and m/z[edit]

History[edit]

Charge-to-mass ratio[edit]

Significance[edit]

Electron[edit]

Zeeman Effect[edit]

See also[edit]

References[edit]

Bibliography[edit]

External links[edit]

История открытия

Формулировка

Физический смысл, что можно определить с его помощью

Действие электрического поля на электрические заряды

Где закон Кулона применяется на практике

Формулы с пояснениями

Электрический заряд и его свойства

Таблица перевода единицы измерения Кулон, калькулятор онлайн, конвертер

Кратные и дольные единицы кулона:

Формула Кулона для среды

Закон Кулона для зарядов в вакууме

Примеры практического использования

Закон Кулона для зарядов в веществе

Закон Кулона в диэлектриках

Закон Амонтона-Кулона

Закон Кулона и связь с гравитацией

Задачка раз

Задачка два

Ограничение в применении

Неподвижные точечные заряды

Крутильные весы Шарля Кулона

Направление силы Кулона и векторный вид формулы

Где закон Кулона применяется на практике

Направление сил в законе Кулона

История открытия закона

Вам также может понравиться

Псевдоптоз молочной железы как исправить

Пустота под плиткой на полу как исправить

Как найти массу в физике через объем

Добавить комментарий Отменить ответ