Как найти соответственные стороны подобных треугольников

22
Авг 2013

Категория: Справочные материалы

Подобные треугольники

2013-08-22
2014-01-31

Автор: egeMax |

комментариев 50

Подобные треугольники

3 октября 2022

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Подобные треугольники — ключевая тема геометрии 8 класса. Они будут преследовать нас до самого конца школы. И сегодня мы разберём всё, что нужно знать о них.

План такой:

1. Основное определение
2. Лемма о подобных треугольниках
3. Свойства подобных треугольников
4. Разбор задач

1. Основное определение

Определение. Треугольники называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны соответственным сторонам другого.

Рассмотрим треугольники $ABC$ и $MNK$:

У них есть равные углы: $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. И пропорциональные стороны:

[frac{AB}{MN}=frac{BC}{NK}= frac{AC}{MK}= frac{color{red}{3}}{color{red}{2}}]

Следовательно, треугольники $ABC$ и $MNK$ подобны. Записывается это так:

[Delta ABCsim Delta MNK]

Число $k={color{red}{3}}/{color{red}{2}};$ называется коэффициентом подобия. К нему мы ещё вернёмся.

Пропорциональные стороны подобных треугольников (например, $AB$ и $MN$, либо $BC$ и $NK$) в некоторых учебниках называют сходственными. На практике этот термин применяется редко. Мы будем говорить просто «соответственные стороны».

Дальше идёт очень важное замечание.

1.1. Обозначение подобных треугольников

В геометрии один и тот же треугольник можно называть по-разному. Например, $Delta ABC$, $Delta BCA$ или $Delta CAB$ — это всё один и тот же треугольник. То же самое касается и углов.

Но в подобных треугольниках есть негласное правило:

При обозначении подобных треугольников порядок букв выбирают так, чтобы равные углы перечислялись в одной и той же последовательности.

Вернёмся к нашим треугольникам $ABC$ и $MNK$:

Поскольку $anglecolor{red}{A}=anglecolor{red}{M}$ и $anglecolor{blue}{B}=anglecolor{blue}{N}$, можно записать $Deltacolor{red}{A}color{blue}{B}Csim Deltacolor{red}{M}color{blue}{N}K$. Или $Delta Ccolor{red}{A}color{blue}{B}sim Delta Kcolor{red}{M}color{blue}{N}$. Но никак не $Deltacolor{red}{A}color{blue}{B}Csim Delta Kcolor{red}{M}color{blue}{N}$.

Да, это негласное правило. И если вы нарушите последовательность букв, это не ошибка. Никто не снизит вам за это баллы. А если снизит — добро пожаловать на апелляцию.

Правильная запись позволяет быстро и безошибочно выписывать пропорциональные стороны треугольников. Рассмотрим два подобных треугольника:

[Delta ABCsim Delta MNK]

Берём две первые буквы из каждого треугольника: ${AB}/{MN};$. Затем две последние буквы: ${BC}/{NK};$. Наконец, вычёркиваем «центральную» букву: ${AC}/{MK};$.

Приравниваем полученные три дроби:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Вот и всё! Даже рисунок не нужен! Этот приём настолько прост и эффективен, что его в обязательном порядке изучают на моих занятиях, курсах и вебинарах.

В будущем мы увидим, что подобные треугольники чаще всего ищут как раз для составления таких пропорций.

2. Лемма о подобных треугольниках

Подобные треугольники появляются всякий раз, когда прямая, параллельная стороне треугольника, пересекает его стороны.

Теорема 1. Прямая, пересекающая две стороны треугольника и параллельная третьей стороне, отсекает треугольник, подобный исходному.

Доказательство. Рассмотрим треугольник $ABC$. Пусть прямая $MNparallel AB$ отсекает треугольник $MNC$:

Докажем, что $Delta ABCsim Delta MNC$. Рассмотрим треугольники $ABC$ и $MNC$. У них есть общий угол $ACB$.

Углы $ABC$ и $MNC$ — соответственными при $MNparallel AB$ и секущей $BC$. Следовательно, они равны: $angle ABC=angle MNC$.

Аналогично равны углы $BAC$ и $NMC$. Следовательно, треугольники $ABC$ и $MNC$ имеют три соответственно равных угла.

Докажем теперь, что соответственные стороны пропорциональны. Т.е. докажем пропорцию

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Рассмотрим угол $ACB$. Параллельные прямые $AB$ и $MN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AC}{MC}=frac{BC}{NC}]

Это равенство — второе в искомом:

[frac{AB}{MN}= color{red}{frac{BC}{NC}=frac{AC}{MC}}]

Осталось доказать первое равенство. Дополнительное построение: прямая $KNparallel AC$:

Поскольку $AMparallel KN$ (по построению) и $AKparallel MN$ (по условию), четырёхугольник $AKNM$ — параллелограмм. Поэтому $AK=MN$.

Рассмотрим угол $ABC$. Параллельные прямые $AC$ и $KN$ пересекают стороны этого угла. По теореме о пропорциональных отрезках:

[frac{AB}{AK}=frac{BC}{NC}]

Учитывая, что $AK=MN$, получаем

[frac{AB}{MN}=frac{BC}{NC}=frac{AC}{MC}]

Итак, соответственные углы треугольников $ABC$ и $MNC$ равны, а их стороны пропорциональны. Следовательно, по определению подобных треугольников

[Delta ABCsim Delta MNC]

Что и требовалось доказать.

Эта лемма — не признак подобия. Это самостоятельная теорема, которая ускоряет решение многих задач.

Признаки подобия разобраны в отдельном уроке — см. «Признаки подобия треугольников».

Частный случай этой леммы — средняя линия. Она отсекает треугольник со сторонами в два раза меньше, чем у исходного:

Оформляется это так. Поскольку $AM=MC$ и $BN=NC$, то $MN$ — средняя линия треугольника $ABC$. Следовательно, прямые $AB$ и $MN$ параллельны, откуда

[Delta ABCsim Delta MNC]

3. Свойства подобных треугольников

Два важнейших свойства: связь периметров и связь площадей.

3.1. Периметры подобных треугольников

Теорема 2. Отношение периметров подобных треугольников равно коэффициенту подобия.

Доказательство. Рассмотрим подобные треугольники $ABC$ и $MNK$:

Запишем равенство из определения подобия. Поскольку $Delta ABCsimDelta MNK$, стороны этих треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

Здесь число $color{red}{k}$ — коэффициент подобия. Полученное тройное равенство можно переписать так:

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}; frac{AC}{MK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB&=color{red}{k}cdot MN \ BC &=color{red}{k}cdot NK \ AC &=color{red}{k}cdot MK \ end{align}]

Периметр треугольника $MNK$:

[{{P}_{Delta MNK}}=MN+NK+MK]

Периметр треугольника $ABC$:

[begin{align}{{P}_{Delta ABC}} &=AB+BC+CD= \ &=color{red}{k}cdot MN+color{red}{k}cdot NK+color{red}{k}cdot MK= \ &=color{red}{k}cdot left( MN+NK+MK right)= \ &=color{red}{k}cdot {{P}_{Delta MNK}} end{align}]

Итого получаем равенство

[{{P}_{Delta ABC}}=color{red}{k}cdot {{P}_{Delta MNK}}]

Обычно именно в таком виде это равенство и применяют. Но можно записать его и как отношение:

[frac{{{P}_{Delta ABC}}}{{{P}_{Delta MNK}}}=color{red}{k}]

В любом случае, мы получили отношение, которое и требовалось доказать.

3.2. Площади подобных треугольников

Теорема 3. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Доказательство. Первые шаги очень похожи на доказательство предыдущей теоремы. Вновь рассмотрим подобные треугольники $ABC$ и $MNK$:

Поскольку $Delta ABCsimDelta MNK$, углы $ABC$ и $MNK$ равны. Следовательно, равны синусы этих углов:

[begin{align}angle ABC &=angle MNK=color{blue}{alpha} \ sin angle ABC &=sin angle MNK=sin color{blue}{alpha} end{align}]

Кроме того, стороны подобных треугольников пропорциональны:

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}=color{red}{k}]

В частности, из этого равенства следует, что

[frac{AB}{MN}=color{red}{k}; frac{BC}{NK}=color{red}{k}]

Или, что то же самое:

[begin{align}AB &= color{red}{k}cdot MN \ BC &= color{red}{k}cdot NK \ end{align}]

Площадь треугольника $MNK$:

[{{S}_{Delta MNK}}=frac{1}{2}cdot MNcdot NKcdot sin color{blue}{alpha} ]

Площадь треугольника $ABC$:

[begin{align}{{S}_{Delta ABC}} &=frac{1}{2}cdot ABcdot BCcdot sincolor{blue}{alpha} = \ &=frac{1}{2}cdotcolor{red}{k}cdot MNcdotcolor{red}{k}cdot NKcdot sincolor{blue}{alpha} = \ &={color{red}{k}^{2}}cdot frac{1}{2}cdot MNcdot NKcdot sin alpha = \ &={color{red}{k}^{2}}cdot {{S}_{Delta MNK}} end{align}]

Получаем равенство

[{{S}_{Delta ABC}}={color{red}{k}^{2}}cdot {{S}_{Delta MNK}}]

Перепишем в виде отношения:

[frac{{{S}_{Delta ABC}}}{{{S}_{Delta MNK}}}={color{red}{k}^{2}}]

Что и требовалось доказать.

Для доказательства теоремы мы использовали формулу площади треугольника:

[{{S}_{Delta }}=frac{1}{2}absin alpha ]

Тригонометрию проходят после подобия, поэтому мы опираемся на ещё не изученный материал.

Впрочем, ничто не мешает взять уже известную формулу:

[{{S}_{Delta }}=frac{1}{2}ah]

Здесь $a$ — сторона треугольника, $h$ — высота, проведённая к этой стороне. Дело в том, что высоты в подобных треугольниках тоже пропорциональны. И не только высоты. Назовём это Свойством 3.3.:)

3.3. Элементы подобных треугольников

Теорема 4. Отношение высот, биссектрис и медиан, проведённых к соответствующим сторонам подобных треугольников, равно коэффициенту подобия.

Проиллюстрируем это на высотах. Пусть треугольники $ABC$ и $MNK$ подобны:

В этом случае высоты $CDbot AB$ и $KLbot MN$ относятся как

[frac{CD}{KL}=frac{AB}{MN}= color{red}{k}]

Для доказательства этой теоремы нужно знать признаки подобия. Поэтому оставим его до следующего урока. А сейчас переходим к задачам.

4. Задачи на подобие

Здесь разобрано пять задач на подобие треугольников. Все они довольно простые. За сложными задачами добро пожаловать в задачник.:)

Задача 1. Готовые треугольники

Известно, что треугольники $ABC$ и $MNK$ подобны, причём $angle A=angle M$, $angle B=angle N$, $angle C=angle K$. Кроме того, стороны $AB=6$, $BC=7$, $AC=10$ и $MN=9$. Найдите стороны $NK$ и $MK$.

Решение. Построим треугольники $ABC$ и $MNK$, отметим известные стороны:

Из условия $Delta ABCsim Delta MNK$ следует, что верно равенство

[frac{AB}{MN}=frac{BC}{NK}=frac{AC}{MK}]

Подставим в это равенство всё, что нам известно:

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}=frac{color{red}{10}}{MK}]

Опустим последнюю дробь и получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{7}}{NK}]

Найдём сторону $NK$:

[NK=frac{color{red}{9}cdot color{red}{7}}{color{red}{6}}=10,5]

Аналогично, убирая среднюю дробь, получим пропорцию

[frac{color{red}{6}}{color{red}{9}}=frac{color{red}{10}}{MK}]

Найдём сторону $MK$:

[NK=frac{color{red}{9}cdot color{red}{10}}{color{red}{6}}=15]

Ответ: $NK=10,5$, $MK=15$.

Задача 2. Прямая, параллельная стороне

Прямая, параллельная стороне $AC$ треугольника $ABC$, пересекает сторону $AB$ в точке $D$, а сторону $BC$ — в точке $E$. Найдите:

а) Отрезок $BD$, если $AB=16$, $AC=20$, $DE=15$.

б) Отрезок $AD$, если $AB=28$, $BC=63$, $BE=27$.

Решение. Для начала построим рисунок. Он будет общий для обоих пунктов.

Из условия следует, что прямая $DE$ пересекает стороны треугольника $ABC$:

Поскольку $DEparallel AC$, по лемме о подобных треугольниках прямая $DE$ отсекает от треугольника $ABC$ новый треугольник, подобный исходному:

[Delta ABCsim Delta DBE]

Из подобия треугольников $ABC$ и $DBE$ следует равенство

[frac{AB}{DB}=frac{BC}{BE}=frac{AC}{DE}]

Решаем пункт а). Подставляем в это равенство всё, что нам известно:

[frac{color{red}{16}}{DB}=frac{BC}{BE}=frac{color{red}{20}}{color{red}{15}}]

Вычёркиваем среднюю дробь и получаем пропорцию

[frac{color{red}{16}}{DB}=frac{color{red}{20}}{color{red}{15}}]

Отсюда легко найти $DB$ (или, что то же самое, $BD$):

[DB=frac{color{red}{16}cdotcolor{red}{15}}{color{red}{20}}=12]

Аналогично решаем пункт б). Подставляем в исходное равенство известные величины:

[frac{color{red}{28}}{DB}=frac{color{red}{63}}{color{red}{27}}=frac{AC}{DE}]

Первые две дроби образуют пропорцию, из которой вновь легко найти $DB$:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=12]

Осталось найти $AD$:

[begin{align}AD &=AB-BD= \ &=color{red}{28}-color{red}{12}=16 end{align}]

Ответ: а) $BD=12$; б) $AD=16$.

Важное замечание по работе с пропорциями. Ни в коем случае не нужно перемножать числа в числителе.

Напротив: нужно разложить их на множители и сократить!

Взгляните:

[DB=frac{color{red}{28}cdotcolor{red}{27}}{color{red}{63}}=frac{4cdotcolor{blue}{7}cdot 3cdotcolor{green}{9}}{color{blue}{7}cdotcolor{green}{9}}=12]

Так вы сэкономите время, избежите умножения столбиком и защитите себя от множества ошибок. Никогда не умножайте большие числа, если дальше их нужно будет сокращать.

Задача 3. Доказательство подобия

Точки $M$ и $K$ — середины сторон $CD$ и $AD$ квадрата $ABCD$ соответственно. Докажите, что треугольники $MDK$ и $BCD$ подобны.

Решение. Сделаем первоначальный рисунок по условию задачи:

Здесь нет прямых, параллельных сторонам треугольника, поэтому лемма о подобных треугольниках не поможет. Докажем подобие по определению.

Сначала разберёмся с углами. Поскольку $ABCD$ — квадрат, и $KD=MD$ — половина стороны квадрата, треугольники $MDK$ и $BCD$ — прямоугольные и равнобедренные.

Все острые углы треугольников $MDK$ и $BCD$ равны 45°. Можем записать это так:

[begin{align}angle BCD &=angle MDK={90}^circ \ angle CBD &=angle DMK={45}^circ \ angle CDB &=angle DKM={45}^circ \ end{align}]

Дополнительное построение: диагональ квадрата $color{red}{AC}$:

Рассмотрим треугольник $ACD$. Отрезок $KM$ — средняя линия, поэтому $KM={color{red}{AC}}/{2};$. С другой стороны, $AC=BD$ как диагонали квадрата. Поэтому верно равенство

[frac{KM}{BD}=frac{KM}{color{red}{AC}}=frac{1}{2}]

Но тогда выполняется следующее равенство:

[frac{MD}{BC}=frac{DK}{CD}=frac{MK}{BD}=frac{1}{2}]

А это вместе с равенством углов как раз и означает, что треугольники $MDK$ и $BCD$ подобны:

[Delta MDKsim Delta BCD]

Доказательство завершено.

Мы доказали подобие треугольников по определению. Если пользоваться признаками подобия, всё будет намного быстрее. Но пока мы не вправе пользоваться этими признаками.

Задача 4. Вписанный ромб

В треугольник $ABC$ вписан ромб $BDEK$ так, как показано на рисунке. Найдите сторону ромба, если $AB=10$, $BC=15$.

Решение. Пусть искомая сторона ромба равна $color{red}{x}$. Из условия задачи получим такой рисунок:

Зная, что $AB=10$ и $BC=15$, выразим $AK$ и $CD$:

[begin{align}AK &=10-color{red}{x} \ CD &=15-color{red}{x} \ end{align}]

Далее рассмотрим треугольник $ABC$. Поскольку $BDEK$ — ромб, то $KEparallel BC$. По лемме о подобных треугольниках имеем:

[Delta ABCsim Delta AKE]

В подобных треугольниках подобные стороны пропорциональны, поэтому

[frac{AB}{AK}=frac{BC}{KE}=frac{AC}{AE}]

Подставим в это равенство всё, что нам известно или выражено через $color{red}{x}$:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}=frac{AC}{AE}]

Последняя дробь оказалась бесполезной. Вычеркнем её и получим пропорцию:

[frac{10}{10-color{red}{x}}=frac{15}{color{red}{x}}]

Применяем основное свойство пропорции и уравнение:

[begin{align}10cdotcolor{red}{x} &=15cdot left( 10- color{red}{x} right) \ 2cdotcolor{red}{x} &=3cdot left( 10- color{red}{x} right) \ &cdots\ color{red}{x} &=6 end{align}]

Это и есть искомая сторона ромба. Она равна $color{red}{x}=6$.

Ответ: $BD=6$.

Задача 5. Свойства биссектрисы

В треугольнике $ABC$ стороны $AB=8$, $BC=12$, угол $ABC={120}^circ $. Отрезок $BD$ — биссектриса. Найдите длину $BD$.

Решение. Из условия задачи можно сделать вот такой рисунок:

Поскольку $BD$ — биссектриса угла в треугольнике, точка $D$ делит сторону $AC$ на отрезки, пропорциональные сторонам $AB$ и $BC$. Это можно записать так:

[frac{AD}{CD}=frac{AB}{CB}=frac{color{red}{8}}{color{red}{12}}=frac{color{red}{2}}{color{red}{3}}]

Обозначим пропорциональные отрезки переменными. Пусть $AD=color{blue}{2x}$, $CD=color{blue}{3x}$.

Дополнительное построение: прямая $DMparallel AB$:

Рассмотрим угол $ACB$. Поскольку $DMparallel AB$, по теореме о пропорциональных отрезках получаем, что

[frac{BM}{CM}=frac{AD}{CD}=frac{color{red}{2}}{color{red}{3}}]

Вновь обозначим пропорциональные отрезки переменными. Пусть $BM=color{blue}{2y}$, $CM=color{blue}{3y}$. Но тогда

[BC=BM+MC=color{blue}{5y}=color{red}{12}]

Получаем, что $color{blue}{y}=color{red}{2,4}$. Отсюда легко найти длину $BM$:

[BM=color{blue}{2y}=2cdotcolor{red}{2,4}= color{red}{4,8}]

Далее заметим, что если угол $ABC$ равен 120°, то

[angle ABD=angle CBD={60}^circ ]

С другой стороны, прямые $AB$ и $MD$ параллельны по построению. Прямая $BD$ — секущая для этих параллельных прямых.

Следовательно, углы $ABD$ и $BDM$ — внутренние накрест лежащие, поэтому

[angle BDM=angle ABD={60}^circ ]

Рассмотрим треугольник $BDM$. В нём есть два угла по 60°. Следовательно, это равносторонний треугольник:

[BD=BM=color{red}{4,8}]

Мы нашли длину отрезка $BD$. Задача решена.

Ответ: $BD=4,8$.

Итак, с определением разобрались. В следующем уроке разберём признаки подобия.:)

Смотрите также:

1. Как применяется теорема косинусов и подобие треугольников для решения широкого класса задач в планиметрии.
2. Теорема менелая
3. Комбинаторика в задаче B6: легкий тест
4. Введение системы координат
5. Четырехугольная пирамида: как найти координаты вершин
6. Нестандартная задача B5 на площадь круга

Подобные треугольники в евклидовой геометрии — треугольники, углы у которых соответственно равны, а стороны соответственно пропорциональны. Являются подобными фигурами.

В данной статье рассматриваются свойства подобных треугольников в евклидовой геометрии. Некоторые утверждения являются неверными для неевклидовых геометрий.

Признаки подобия треугольников[править | править код]

Признаки подобия треугольников — геометрические признаки, позволяющие установить, что два треугольника являются подобными без использования всех элементов определения.

Первый признак[править | править код]

то есть:

Дано: и

Доказать:

Следствия первого признака подобия[править | править код]

• Если три стороны исходного треугольника попарно параллельны (дважды антипараллельны или перпендикулярны) трем сторонам другого треугольника, то указанные два треугольника подобны. Примеры применения этого следствия см. ниже в разделах: «Примеры подобных треугольников» и «Свойства параллельности (антипараллельности) сторон родственных треугольников».
• Под дважды антипараллельными сторонами понимается следующее. Например, стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат. В таком случае соответствующие стороны ортотреугольника ортотреугольника (дважды ортотреугольника) дважды антипараллельны соответствующим сторонам исходного треугольника, то есть просто параллельны. Следовательно, подобны, например, ортотреугольник ортотреугольника и исходный треугольник как треугольники с параллельными сторонами.

Второй признак[править | править код]

Дано: и

Доказать:

Третий признак[править | править код]

Дано: и = = .

Доказать:

Признаки подобия прямоугольных треугольников[править | править код]

1. По острому углу — см. первый признак;
2. По двум пропорциональным катетам — см. второй признак;
3. По пропорциональному катету и гипотенузе — см. третий признак.

Свойства подобных треугольников[править | править код]

• Отношение площадей подобных треугольников равно квадрату коэффициента подобия
• Отношение периметров и длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.

Примеры подобных треугольников[править | править код]

Подобны следующие виды треугольников:

• Дополнительный треугольник и антидополнительный треугольник подобны; соответственные их стороны параллельны.
• Треугольник ABC подобен своему дополнительному треугольнику; соответственные их стороны параллельны и относятся как 2:1.
• Треугольник ABC подобен своему антидополнительному треугольнику; соответственные их стороны параллельны и относятся как 1:2.
• Исходный треугольник по отношению к ортотреугольнику является треугольником трёх внешних биссектрис^[1].
• Ортотреугольник и тангенциальный треугольник подобны (Зетель, следствие 1, § 66, с. 81).
• Ортотреугольник ортотреугольника и исходный треугольник подобны.
• Треугольник трёх внешних биссектрис треугольника трех внешних биссектрис и исходный треугольник подобны.
• Пусть точки касания вписанной в данный треугольник окружности соединены отрезками, тогда получится треугольник Жергонна, и в полученном треугольнике проведены высоты. В этом случае прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно ортотреугольник треугольника Жергонна и исходный треугольник подобны.
• Выше указанные свойства подобия родственных треугольников являются следствием ниже перечисленных свойств параллельности сторон родственных треугольников.
• Теорема: окружностно-чевианный треугольник подобен подерному^[2]. Здесь использованы определения:
  • Треугольник с вершинами во вторых точках пересечения прямых, проведённых через вершины и данную точку, с описанной окружностью, называют окружностно-чевианным треугольником.
  • Треугольник с вершинами в проекциях данной точки на стороны называется подерным или педальным треугольником этой точки.

Свойства параллельности (антипараллельности) сторон родственных треугольников[править | править код]

• Соответственные стороны дополнительного треугольника, антидополнительного треугольника и исходного треугольника попарно параллельны.
• Стороны данного остроугольного треугольника антипараллельны соответствующим сторонам ортотреугольника, против которых они лежат.
• Стороны тангенциального треугольника антипараллельны соответствующим противоположным сторонам данного треугольника (по свойству антипараллельности касательных к окружности).
• Стороны тангенциального треугольника параллельны соответствующим сторонам ортотреугольника.
• Пусть точки касания вписанной в данный треугольник окружности соединены отрезками, тогда получится треугольник Жергонна, и в полученном треугольнике проведены высоты. В этом случае прямые, соединяющие основания этих высот, параллельны сторонам исходного треугольника. Следовательно ортотреугольник треугольника Жергонна и исходный треугольник подобны.

Подобие в прямоугольном треугольнике[править | править код]

Треугольники, на которые высота, опущенная из прямого угла, делит прямоугольный треугольник, подобны всему треугольнику по первому признаку, а значит:

• Высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому проекций катетов на гипотенузу,
• Катет равен среднему геометрическому гипотенузы и проекции этого катета на гипотенузу.

Связанные определения[править | править код]

• Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
• Сходственные стороны подобных треугольников — стороны, лежащие напротив равных углов.

См. также[править | править код]

• Неравенство Пидо
• Подобие
• Признаки равенства треугольников
• Решение треугольников
• Среднее геометрическое
• Треугольник

Примечания[править | править код]

Литература[править | править код]

• Геометрия 7-9/Л. С. Атанасян и др. — 12-е изд. — М.: Просвещение, 2002. — 384 c.:
• Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. 153 с.

Ссылки[править | править код]

• Видео. Подобные треугольники
• Подобие треугольников
• Признаки подобия из учебника за восьмой класс

В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).

В треугольниках ABC и DEF (черт. 152), в которых

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.

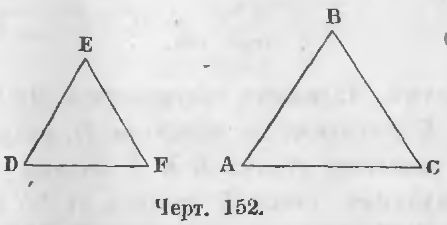
Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.

Если в двух треугольниках (черт. 152) ABC и DEF углы равны

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

и соответственные стороны пропорциональны

AB/DE = AC/DF = BC/EF

то треугольники называются подобными.

Подобие обычно выражают знаком ∼.

Подобие двух треугольников изображают письменно:

ABC ∼ DEF.

Случаи подобия треугольников

Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.

Дано. В треугольниках ABC и DEF углы равны (черт. 153).

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:

AB/DE = AC/DF = BC/EF

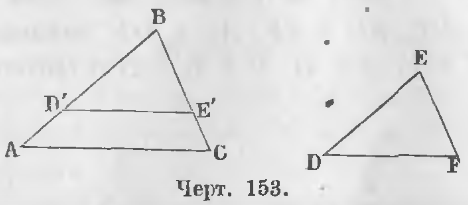
Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,

∠D’ = ∠D, ∠D = ∠A

откуда

∠D’ = ∠A.

Если соответственные углы равны, то D’E || AC.

По теореме 86 имеют место равенства

AC/D’E’ = AB/BD’ = BC/BE’

Так как BD’ = ED, BE’ = EF, D’E’ = DF, то

AC/DF = AB/ED = BC/EF (ЧТД).

Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.

Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).

A = D, B = E

то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).

Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.

Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.

∠B = ∠E и AB/DE = BC/EF.

Требуется доказать, что треугольники подобны.

Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆BD’E’ = ∆DEF, следовательно,

∠D’ = ∠D, ∠E’ = ∠F.

Так как имеет место пропорция

AB/BD’ = BC/BE’

то сторона D’E’ || AC (теорема 87).

Поэтому ∠D’ = ∠A, ∠C = ∠E’.

Следовательно,

∠A = ∠D, ∠C = ∠F, ∠B = ∠E

т. е. три угла одного равны трем углам другого треугольника.

В этом же случае треугольники ABC и DEF подобны (ЧТД).

Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.

Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:

AB/ab = BC/bc = AC/ac (1)

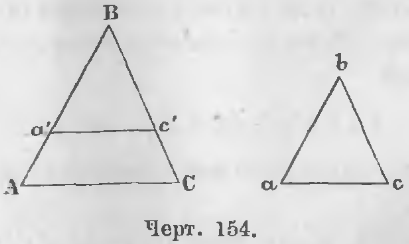
Требуется доказать, что у них углы равны, т. е.

A = a, B = b, C = c.

Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:

AB/Ba’ = BC/Bc’ = AC/a’c’

Так как Ba’ = ba, то рядом с этими имеют место отношения:

AB/ab = BC/Bc’ = AC/a’c’ (2)

Сопоставляя отношения (1) и (2), заключаем, что

Bc’ = bc, a’c’ = ac,

следовательно, два треугольника a’Bc’ и abc равны, откуда

∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c

а так как

∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,

следовательно, углы двух треугольников ABC и abc равны (ЧТД).

Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.

Доказательство. Здесь могут быть два случая:

1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.

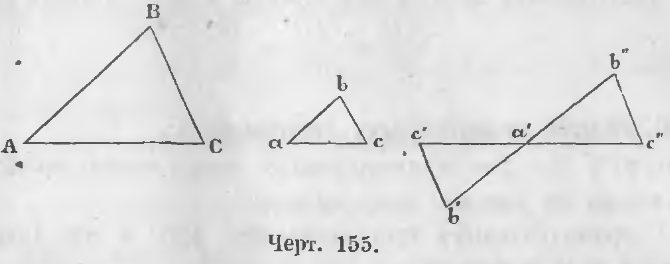
2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.

AB || a’b’, AC || a’c’, BC || b’c’.

Углы же между параллельными сторонами обращены в разные стороны.

В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b” = a’b’ и a’c” = a’c’.

Треугольники a’b”c” и a’b’c’ равны. Треугольник a’b”c” подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,

∆ABC ~ a’b”c”, следовательно, ∆ABC ~ a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’

Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.

Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:

ab ⊥ AB, ac ⊥ AC, bc ⊥ BC

Требуется доказать, что треугольники подобны.

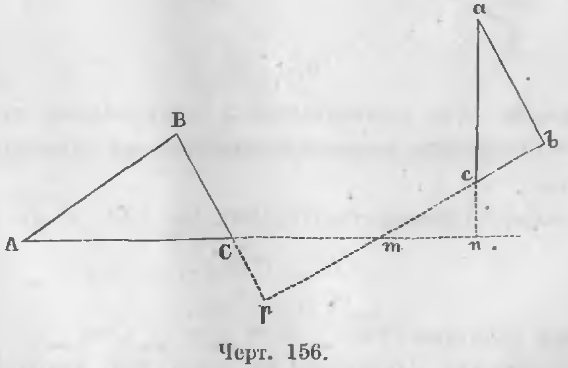
Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо

n = p как прямые

Углы при точке m равны как вертикальные,

а следовательно, и третьи углы равны ∠pCm = ∠mcn.

Так как

∠pCm = ∠ACB, ∠mcn = ∠acb

следовательно,

∠ACB = ∠acb

Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция

AB/ab = AC/ac = BC/bc

Подобие прямоугольных треугольников

Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.

Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

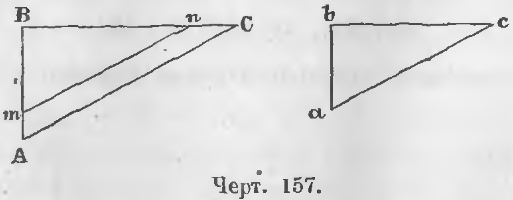
Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

AC/ac = AB/ab (a)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

AC/mn = AB/Bm (b)

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac. У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

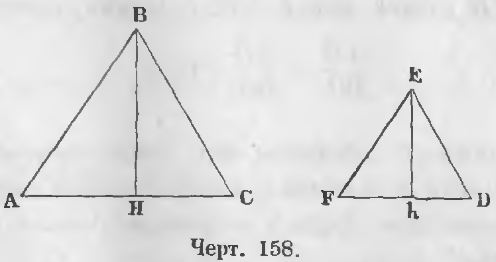
Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

AB/FE = BH/Eh (ЧТД).

Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠α = ∠β

Требуется доказать, что AB/BC = AD/DC.

Доказательство. Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠β как соответственные углы,
∠FAB = ∠α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

FB/BC = AD/DC

Заменяя FB равным отрезком AB, получим пропорцию:

AB/BC = AD/DC (ЧТД).

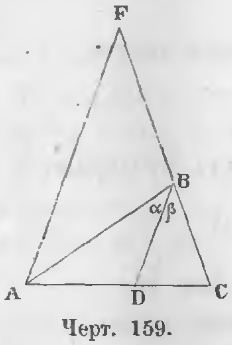
Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

AB/BC = AD/DC (a)

Требуется доказать, что ∠α = ∠β.

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

FB/BC = AD/DC (b)

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

∠AFB = ∠FAB.

Так как ∠α = ∠FAB, ∠β = ∠AFB, то и

∠α = ∠β (ЧТД).

Отношения в прямоугольном треугольнике

Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.

Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.

Требуется доказать, что AD/BD = BD/DC.

Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠α = d, ∠α +∠β = d вытекает

A + α = α + β, или A = β, следовательно и C = α.

Из подобия треугольников ABD и BDC вытекает пропорция

AD/BD = BD/DC (ЧТД).

Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α, которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.

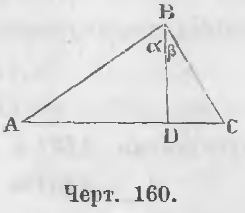
Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.

Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ABC = ∠ADB как прямые, ∠A общий, следовательно,

∠C = ∠α

Из подобия треугольников вытекает пропорция:

AD/AB = AB/AC (a)

b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,

∠A = ∠β, откуда
DC/BC = BC/AC (b)

Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.

Из предыдущих пропорций (a) и (b) вытекают равенства:

AB² = AD · AC
BC² = DC · AC

Складывая их, получим:

AB² + BC² = AD · AC + DC · AC или
AB² + BC² = AC (AD + DC) = AC · AC = AC², т. е.
AC² = AB² + BC²

откуда

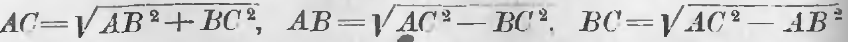
a) Гипотенуза равна корню квадратному из суммы квадратов катетов.

b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.

Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.

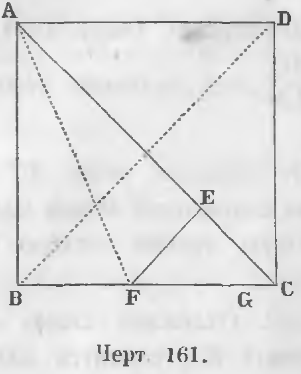
Дано. В квадрате ABCD проведена диагональ AC (черт. 161).

Требуется доказать, что отношение AC/AD есть величина несоизмеримая.

Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.

a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо

AB + BC > AC.

Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC < BC.

b) Наложим первый остаток EC на отрезок BC. Для этого из точки E восставим перпендикуляр EF и соединим точку F с A.

c) Треугольник FEC равнобедренный, ибо ∠EFC = ∠BAC как углы с перпендикулярными сторонами

∠BAC = ∠ECF, следовательно,
∠EFC = ∠ECF

На этом основании стороны EF и EC равны:

EF = EC (1)

Треугольники ABF и AEF равны, ибо они прямоугольны и у них

AF сторона общая
AB = AE по построению, следовательно,
BF = EF (2)

Таким образом из равенств (1) и (2) выходит, что

EC = EF = BF

Не трудно видеть, что первый остаток укладывается в отрезке BC не более двух раз. Отложив EC два раза на отрезке BC, найдем точку G и второй остаток GC. Таким образом, остаток после наложения сторон квадрата на диагональ укладывается в стороне квадрата не более двух раз.

d) Наложим второй остаток GC на первый EC.

В прямоугольном и равнобедренном треугольнике FEC соотношение между отрезками GC, FC и EC то же самое как и соотношение между данными отрезками EC, AC и BC в треугольнике ABC, ибо треугольник FEC прямоугольный и равнобедренный, следовательно, при дальнейшем наложении мы будем снова получать остаток. Продолжая так поступать, мы всегда будем получать остатки, поэтому общей меры мы никогда не получим, следовательно, отрезки AC и BC несоизмеримы.

Обозначив длину диагонали черед l, длину стороны квадрата через a, последовательные величины остатков через d₁, d₂ и т. д., т. е. положив

AC = l, BC = a, CE = d₁, GC = d₂ и т. д.

имеем равенства:

l = a + d₁, a = 2d₁ + d₂, d₁ = 2d₂ + d₃ и т. д.

откуда

l/a = 1 + d₁/a
a/d₁ = 2 + d₂/d₁ или d₁/a = ½ + d₂/d₁
d₁/d₂ = 2 + d₃/d₂ или d₂/d₁ = ½ + d₃/d₂

следовательно,

l/a = 1 + ½ + ½ + …

Отношение между длинами l и a выражается бесконечной непрерывной дробью. Несоизмеримость впрочем прямо вытекает из выражения диагонали квадрата по катетам.

Действительно,

AC² = AB² + BC².

Так как AB = BC, то AC² = 2AB², откуда AC = AB√2 и AC/AB = √2 величина несоизмеримая.

Соотношение между сторонами остроугольного и тупоугольного треугольника

Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.

Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.

Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.

Требуется доказать, что AB² = BC² + AC² – 2AC · DC.

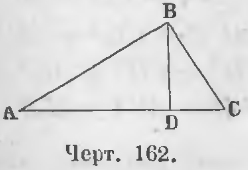
Доказательство. Для прямоугольного треугольника ABD имеем равенство:

AB² = BD² + AD² (a)
AD = AC – DC, AD² = (AC – DC)² = AC² + DC² – 2AC · DC

Из прямоугольного треугольника BDC имеем:

BD² = BC² – DC²

Вставляя величины BD² и AD² в равенство (a), получим:

AB² = BC² – DC² + AC² + DC² – 2AC · DC, откуда
AB² = BC² + AC² – 2AC · DC (ЧТД).

2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.

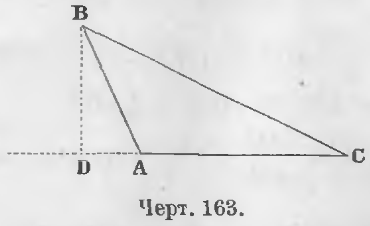
Доказательство. Из прямоугольного треугольника ABD имеем:

AB² = BD² + DA²

Из прямоугольного треугольника BCD имеем:

BD² = BC² – CD²

следовательно,

AB² = BC² – CD² + DA².

Так как

DA = CD – AC
DA² = (CD – AC)² = CD² + AC² – 2CD · AC, то
AB² = BC² – CD² + CD² + AC² – 2CD · AC, откуда
AB² = BC² + AC² – 2CD · AC (ЧТД).

Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.

Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.

Требуется доказать, что

AB² = AC² + BC² + 2AC · CD

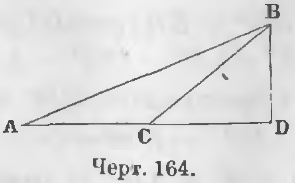
Доказательство. Из тупоугольного треугольника ABC имеем:

AB² = BD² + AD² (a)
AD = AC + CD, AD² = AC² + CD² + 2AC · CD

Из прямоугольного треугольника BCD вытекает, что

BD² = BC² – CD²

Заменяя AD² и BD² в равенстве (a), получим:

AB² = BC² – CD² + AC² + CD² + 2AC · CD

откуда

AB² = BC² + AC² + 2AC · CD (ЧТД).

Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.

Дан параллелограмм ABCD (черт. 165) и проведены его диагонали AC и BD.

Требуется доказать, что

AC² + BD² = AB² + BC² + CD² + AD²

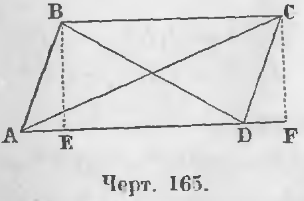
Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:

BD² = AB² + AD² – 2AD · AE (1)

Из тупоугольного треугольника ACD равенство:

AC² = CD² + AD² + 2AD · DF (2)

Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.

Сложив равенства (1) и (2), имеем:

BD² + AC² = AB² + AD² + CD² + AD²

Так как AD = BC, то

BD² + AC² = AB² + BC² + CD² + AD² (ЧТД).

Теорема 107. Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.

Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).

Требуется доказать, что

AB² + BC² = 2AD² + 2BD²

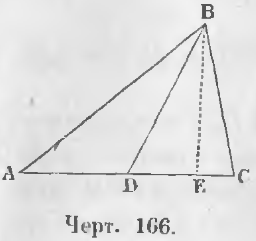
Доказательство. Проведем высоту BE.

Из прямоугольных треугольников ABE и BCE вытекают равенства:

AB² = BE² + AE²
BC² = BE² + CE²

Сложив их, находим:

AB² + BC² = 2BE² + AE² + CE² (a)

Так как AE = AD + DE = CD + DE, CE = CD – DE, то

AE² = (CD + DE)² = CD² + DE² + 2CD · DE
CE² = (CD – DE)² = CD² + DE² – 2CD · DE

откуда

AE² + CE² = 2CD² + 2DE² (b)

Заменяя в равенстве (a) сумму AE² + CE² из равенства (b), имеем:

AB² + BC² = 2BE² + 2CD² + 2DE².

Из прямоугольного треугольника BDE видно, что

BE² = BD² – DE²

следовательно

AB² + BC² = 2BD² – 2DE² + 2CD² + 2DE²

откуда

AB² + BC² = 2BD² + 2CD² (ЧТД).

Коэффициент подобия треугольников – что это? Как его найти? Коэффициент подобия треугольников, определение. Подобные треугольники имеют равные углы и пропорциональные сходственные стороны. Сходственные стороны (другое название – соответственные) – это стороны, которые лежат напротив равных углов. На рисунке представлены подобные треугольники ABC и A1B1C1. Для их сторон выполняется следующее равенство: Величина, которая равна отношению сходственные сторон треугольников, называется коэффициентом подобия. Коэффициент подобия треугольников обозначается буквой k, k > 0. Таким образом, приведённое выше равенство можно записать в виде: Найти коэффициент подобия треугольников можно несколькими способами. 1) Через отношение сходственных сторон (например, AB / A1B1). 2) Этот коэффициент также равен отношению периметров подобных треугольников. P(ABC) = A + B + C, P(A1B1C1) = A1 + B1 + C1. k = P(ABC) / P(A1B1C1). 3) Через площади подобных треугольников. k² = S(ABC) / S(A1B1C1). 4) Отношение длин высот, медиан, биссектрис подобных треугольников также равно коэффициенту подобия. Пример. Даны подобные треугольники DEC и AON. Коэффициент подобия = 1,5, а сторона DE = 12 см. Требуется найти сторону AO. _ По определению коэффициента подобия k = DE / AO = 1,5. Так как DE = 12 см, то можно записать: 12 / AO = 1,5. AO = 12 / 1,5 = 8 см. Значит, длина стороны AO составляет 8 см. модератор выбрал этот ответ лучшим smile­6008 [28.5K] 3 года назад  Для того чтобы найти коэффициент подобия треугольников необходимо сначала определиться что же это понятие значит. Итак, подобный треугольник, это треугольник, геометрическая фигура, у которой одинаковые углы и одинаковые стороны, которые находятся напротив друг друга. То есть называются подобными. Для того чтобы найти коэффициент подобия треугольников обратимся к формуле. Для вычисления коэффициент используют разные способы расчёта. Проще всего найти коэффициент, если вычислить площади треугольников. Другой способ расчёта коэффициента примениние расчёта через отношение сходственных сторон подобных треугольников. Дубло­н [176K] 2 месяца назад  Говоря о коэффициенте подобия треугольников, необходимо знать, что есть подобные фигуры, а точнее подобные треугольники. Под таковыми являются треугольники, чьи углы равные, а сходственные стороны этих треугольников пропорциональны. Так вот, отношение этих сходственных сторон и есть коэффициент подобия. Коэффициент подобия можно определить, зная величину как сходственных сторон, так и величину периметров подобных треугольников, так и величину площади подобных треугольников. Бутаф­ога [31.1K] 2 месяца назад  Говоря простым языком, подобные треугольники называют такие геометрические фигуры, у которых углы одинаковые, а стороны пропорциональные. Стоит отметить как понятие соответственных сторон, лежащих напротив одинаковых углов. Отсюда вытекает коэффициент подобия, равный отношению соответственных сторон подобных треугольников. Корне­тОбол­енски­й [160K] 3 месяца назад  Подобными называются фигуры, одинаковые по форме, но разные по размеру. Треугольники считаются подобными, если у них углы равны, а их соответственные стороны пропорциональны друг другу. Рассмотрим рисунок: Изображённые на нем треугольники подобны, поскольку у них соответствующие углы равны между собой, а соответственные (второе название сходственные) стороны пропорциональны. Коэффициент подобия равняется отношению сходственных сторон имеющихся подобных треугольников, т.е. сторон, лежащих напротив равных углов. Простыми словами, Коэффициент подобия показывает, в какое количество раз один треугольник больше другого, обозначается буквой k, при этом k>0. Т.е. коэффициент подобия всегда является положительной величиной. Коэффициент подобия можно найти несколькими способами: поделить одну сходственную сторону на другую. Это правило работает, если известны длины сторон треугольников. Можно вычислить также коэффициент подобия треугольников в случае, если по условию задачи известны их площади. Существует свойство подобных треугольников, говорящее, что отношение их площадей равняется коэффициента подобия, умноженному на себя, т.е. собственному квадрату. Тогда, разделив значения площадей у подобных треугольников и, извлекши квадратный корень из результата, получим коэффициент подобия. Также k находится через отношение длин медиан, биссектрис или серединных перпендикуляров, проведенных к соответственным сторонам, если длины этих медиан, серединных перпендикуляров или биссектрис известны по условию задачи. Если известны периметры подобных треугольников, то их отношение будет давать всё тот же коэффициент подобия. Если в подобные треугольники вписаны окружности, то отношение их радиусов или диаметров также даст коэффициент подобия. У подобных треугольников отношение диаметров или радиусов описанных вокруг них окружностей равно коэффициенту подобия. Если по условиям задачи известны диаметры или радиусы этих окружностей, либо есть возможность каким-либо способом вычислить из площадей окружностей, то коэффициент подобия ищется и таким способом. Krust­all [125K] 8 месяцев назад  Подобными фигурами называются фигуры, одинаковые по форме, но разные по величине. Треугольники подобны, если их углы равны, а стороны пропорциональны друг другу. Также есть три признака, которые позволяют определить сходство без выполнения всех условий. Первый признак состоит в том, что в подобных треугольниках два угла одного равны двум углам другого. Второй признак подобия треугольников состоит в том, что две стороны одного пропорциональны двум сторонам другого и углы между этими сторонами равны. Третий признак сходства — пропорциональность трех сторон одного по отношению к трем сторонам другого. Треугольники называются подобными, если они имеют равные углы и соответствующие стороны пропорциональны. Число k, равное отношению соответствующих сторон треугольников, называется коэффициентом подобия. Давайте вспомним, какие треугольники называются подобными. Треугольники считаются подобными, если у них: равны углы, пропорциональны соответственные стороны. Выделяют три признаки по добия треугольников: по трем сторонам, по двум сторонам и углу между ними, по двум углам. Коэффициент подобия треугольников равен отношению соответственных ( сходственных ) сторон этих треугольников. Вычислить этот коэффициент можно несколькими путями, в основе которых, по сути, лежит пропорциональность их сходственных сторон: 1.) Непосредственно как отношение сторон. 2.) Через периметры этих треугольников ( то есть через суммы длин их сторон ). 3.) Через площади этих фигур. 4.) Как отношение их биссектрис, высот или медиан. Серге­й Гории­нов [5.5K] 5 лет назад  Коэффициент подобия треугольников – это безразмерная величина, равная отношению соответствующих сторон подобных треугольников: К=a1/a2=b1/b2=c1/c2, где a1,b1,c1 – стороны первого подобного треугольника, а a2,b2,c2 – стороны второго подобного треугольника. Также существует коэффициент подобия площадей подобных треугольников, равный квадрату коэффициента подобия треугольника. Лара Изюми­нка [59.8K] 2 года назад  При изучении темы “Подобие треугольников” очень важно понимание , что такое коэффициент подобия траугольников. Итак, коэффициент подобия – это отношение сходственных сторон в подобных треугольниках. Сходственные стороны, это стороны, которые лежат против равных углов. Коэффициент подобия помогает найти площадь подобного треугольника, если известна площадь другого. Здесь пользуемся тем , что отношение площадей подобных треугольников равно квадрату коэффициента подобия. Также можно найти стороны одного подобного треугольника, если есть стороны другого и известен коэффициент подобия. Ьема изучается в 8 классе в курсе геометрии. Nasty­a Chuk [6.8K] 3 года назад  Актуальный вопрос на самом деле, поскольку он необходим для понимания различий между видами треугольников и их пропорциями.Предназн­ачение коэффициента подобия : показывает во сколько раз стороны нашего треугольника соответственно больше сторон другого треугольника и какую же часть составляют они от сходственных стороны.Коэффициент подобия обозначается как “к” и выражается всегда через некое соотношение 2-х или 3-х треугольников. Знаете ответ?