| Удельное электрическое сопротивление | |
|---|---|
 |
|
| Размерность |
СИ:L3MT-3I-2 СГС:T |
| Единицы измерения | |
| СИ | Ом·метр |
| СГС | с |
Уде́льное электри́ческое сопротивле́ние (удельное сопротивление) — физическая величина, характеризующая способность материала препятствовать прохождению электрического тока, выражается в Ом·метр. Удельное электрическое сопротивление принято обозначать греческой буквой ρ. Значение удельного сопротивления зависит от температуры в различных материалах по-разному: в проводниках, удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается. Величина, учитывающая изменение электрического сопротивления от температуры называется температурный коэффициент удельного сопротивления. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления, являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества.
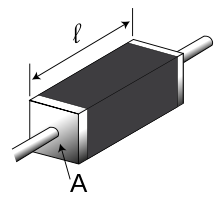
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле 
(при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется 
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Единицы измерения[править | править код]
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м[1]. Из соотношения 
следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10−6 от 1 Ом·м[1]. Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом[2]. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Зависимость от температуры[править | править код]
В проводниках удельное электрическое сопротивление увеличивается с увеличением температуры. Это объясняется тем, что с ростом температуры увеличивается интенсивность колебания атомов в узлах кристаллической решетки проводника, что препятствует движению свободных электронов[3].
В полупроводниках и диэлектриках удельное электрическое сопротивление уменьшается. Это объясняется тем, что с увеличением температуры увеличивается концентрация основных носителей заряда.
Величина, учитывающая изменение удельного электрического сопротивление от температуры называют температурным коэффициентом удельного сопротивления.
Обобщение понятия удельного сопротивления[править | править код]
Кусок резистивного материала с электрическими контактами на обоих концах
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля 
и плотность тока 
в данной точке 
. Указанная связь выражается законом Ома в дифференциальной форме:
Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент 
. В анизотропном веществе векторы плотности тока и напряжённости электрического поля в каждой данной точке вещества не сонаправлены; связь между ними выражается соотношением
В анизотропном, но однородном веществе тензор от координат не зависит.
Тензор симметричен, то есть для любых 
и 
выполняется 
.
Как и для всякого симметричного тензора, для можно выбрать
ортогональную систему декартовых координат, в которых матрица становится диагональной, то есть приобретает вид, при котором из девяти компонент отличными от нуля являются лишь три: 
, 
и 
. В этом случае, обозначив 
как 
, вместо предыдущей формулы получаем более простую
Величины называют главными значениями тензора удельного сопротивления.
Связь с удельной проводимостью[править | править код]
В изотропных материалах связь между удельным сопротивлением и удельной проводимостью 
выражается равенством
В случае анизотропных материалов связь между компонентами тензора удельного сопротивления и тензора удельной проводимости 
имеет более сложный характер. Действительно, закон Ома в дифференциальной форме для анизотропных материалов имеет вид:
Из этого равенства и приведённого ранее соотношения для 
следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
![rho _{{11}}={frac {1}{det(sigma )}}[sigma _{{22}}sigma _{{33}}-sigma _{{23}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/08befe7409fd1685d379b9d3045f8b7d88b62e44)
![rho _{{12}}={frac {1}{det(sigma )}}[sigma _{{33}}sigma _{{12}}-sigma _{{13}}sigma _{{32}}],](https://wikimedia.org/api/rest_v1/media/math/render/svg/023c28c36a33abc59ec81a040eeeee5d6040e007)
где 
— определитель матрицы, составленной из компонент тензора . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1, 2 и 3[4].
Удельное электрическое сопротивление некоторых веществ[править | править код]
Металлические монокристаллы[править | править код]
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C[5].
| Кристалл | ρ1=ρ2, 10−8 Ом·м | ρ3, 10−8 Ом·м |
|---|---|---|
| Олово | 9,9 | 14,3 |
| Висмут | 109 | 138 |
| Кадмий | 6,8 | 8,3 |
| Цинк | 5,91 | 6,13 |
| Теллур | 2,90·109 | 5,9·109 |
Металлы и сплавы, применяемые в электротехнике[править | править код]
Разброс значений обусловлен разной химической чистотой металлов, способов изготовления образцов, изученных разными учеными и непостоянством состава сплавов.
|
|
Значения даны при температуре t = 20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Другие вещества[править | править код]
| Вещество | ρ, Ом·мм²/м |
|---|---|
| Сжиженные углеводородные газы | 0,84⋅1010 |
Тонкие плёнки[править | править код]
Сопротивление тонких плоских плёнок (когда её толщина много меньше расстояния между контактами) принято называть «удельным сопротивлением на квадрат», 
Этот параметр удобен тем, что сопротивление квадратного куска проводящей плёнки не зависит от размеров этого квадрата, при приложении напряжения по противоположным сторонам квадрата. При этом сопротивление куска плёнки, если он имеет форму прямоугольника, не зависит от его линейных размеров, а только от отношения длины (измеренной вдоль линий тока) к его ширине L/W: 
где R — измеренное сопротивление. В общем случае, если форма образца отличается от прямоугольной, и поле в плёнке неоднородное, используют метод ван дер Пау.
См. также[править | править код]
- Электрическое сопротивление
- Сверхпроводимость
- Закон Ома
- Удельная проводимость
- Отрицательное сопротивление
- Импеданс
- Температурный коэффициент электрического сопротивления
Примечания[править | править код]
- ↑ 1 2 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 93. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Чертов А. Г. Единицы физических величин. — М.: «Высшая школа», 1977. — 287 с.
- ↑ Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд. — М.: Высшая школа, 1986. — 208 с.
- ↑ Давыдов А. С. Теория твёрдого тела. — М.: «Наука», 1976. — С. 191—192. — 646 с.
- ↑ Шувалов Л. А. и др. Физические свойства кристаллов // Современная кристаллография / Гл. ред. Б. К. Вайнштейн. — М.: «Наука», 1981. — Т. 4. — С. 317.
Литература[править | править код]
- Никулин Н. В., Назаров А. С. Радиоматериалы и радиокомпоненты. — 3-е изд., переработанное и дополненное. — М.: Высшая школа, 1986. — С. 6—7. — 208 с.
На этой странице представлен самый простой онлайн калькулятор расчета сопротивления проводника по простой математической формуле в зависимости от длины, площади поперечного сечения и удельного сопротивления проводника. С помощью этой программы вы в пару кликов сможете рассчитать сопротивление проводника.
Вы так же можете воспользоваться калькулятором для расчета сечения кабеля по мощности и току.
Формула для расчета сопротивления провода: R=(ρ*l)/S
Где:
- R – сопротивление в Омах,
- ρ – удельное сопротивление,
- l – длина в м,
- S – площадь поперечного сечения провода в мм2.
Калькулятор расчета сопротивления проводника.
как найти сопротивление проводника, зная массу, диаметр и плотность?
..::MEGAMOZG::..
Профи
(875),
на голосовании
11 лет назад
как найти сопротивление проводника, зная массу, диаметр и плотность?
Голосование за лучший ответ
Доктор
Гуру
(4502)
11 лет назад
Массу делишь на плотность = объем. Сечение: S=пD^2/4
V/S = длина пр-ка R=(L*p)/S p – удельное сопротивление материала пр-ка
Удельное сопротивление, формула.
Удельное сопротивление есть характеристика материала, вещества из которого сделан проводник.
Электрическое сопротивление проводника прямо пропорционально произведению удельного сопротивления материала из которого сделан проводник на его длинну, и обратно пропорционально его сечению.
Если
| R | электрическое сопротивление проводника, | Ом |
|---|---|---|
| ρ | удельное сопротивление материала проводника, | Ом·м |
| l | длина проводника, | Метр |
| A | сечение проводника, | Метр2 |
то
[R=frac{rho l}{A}]
Единица СИ удельного сопротивления
[ [rho]=Ом·м]
Удельное сопротивление ρ зависит от температуры.
Вычислить, найти электрическое сопротивление проводника по удельному сопротивлению по формуле (1).
Вычислить, найти электрическое сопротивление диэлектрика по удельному сопротивлению по формуле (1).
Удельное сопротивление |
стр. 601 |
|---|
Общие сведения
Упорядоченное движение носителей заряда в физическом теле называют электрическим током. Ими могут быть различные элементарные частицы. Например, в проводниках — электроны, электролитах — ионы. В состоянии покоя, то есть когда на тело не оказывается постороннее воздействие, движение носителей хаотичное. В результате происходит компенсирование зарядов, и ток не возникает. Если же к веществу приложить силу или деформировать его, направление движения частиц станет упорядоченным и возникнет электрический ток.
Все существующие вещества характеризуются физическими и химическими свойствами. Среди них и проводимость. Это электрическая величина, определяющая способность тела пропускать через себя ток. По своему строению все материалы делятся на 3 класса:
- проводники — вещества, не оказывающие сопротивление прохождению тока;
- полупроводники — тела, в которых величина проводимости зависит от чистоты материала, температуры и вида воздействующего излучения;
- диэлектрики — вещества, практически не проводящие электрический ток.
Величина, обратная проводимости, называется сопротивлением. Это параметр, который характеризует способность материала пропускать через себя электрический ток без потерь. Другими словами, для идеального тела количество электричества, поступившего и снятого с него, будет одинаковым.
За единицу измерения силы тока принят Ампер, показывающий, какое количество электричества проходит через поперечное сечение проводника за одну секунду: I = q / t = кулон / секунду = ампер.
Электрическое сопротивление тела зависит от природы носителей заряда и геометрии материала. Это скалярный параметр. При его расчёте используют понятие удельное сопротивление. Выражают его в омах, умноженных на метр, и обозначают греческой буквой р. По физическому смыслу величина является обратным параметром удельной проводимости.
С ней, кроме сопротивления и силы тока, тесно связано и напряжение. С физической точки зрения, это работа, которую выполняет электрическое поле при переносе единичного заряда из одной точки в другую. В Международной системе величин напряжение принято обозначать в вольтах: U = f2- f1, где f — значения потенциала заряда в точках.
Формула сопротивления
Ток обусловлен движением электронов. Классическая формула, используемая для расчёта его силы была выведена немецким физиком Омом. Он на опыте смог подтвердить зависимость между собой тока, сопротивления и напряжения. В математическом виде связь записывают в виде формулы: I = U /R.
Согласно закону Ома, сопротивление тела электрическому току прямо пропорционально его силе и обратно пропорционально напряжению: R = I / U. Это эмпирическая формула справедлива для любого участка цепи.
Подвижные носители при хаотичном движении ведут себя как молекулы газа, поэтому в первом приближении физики считают носителей зарядов своего рода электронным газом. Как было установлено эмпирически, плотность этого газа и строение кристаллической решётки зависят от рода проводника. Соответственно, проводимость, а значит и сопротивление, определяется также и родом вещества. В свою очередь, физическое тело характеризуется и геометрическими параметрами.
Влияние размеров полупроводника объясняется зависимостью от них поперечного сечения. При его уменьшении поток зарядов становится плотнее, степень взаимодействия между частицами возрастает. Полная формула сопротивления проводника с учётом поперечного сечения выглядит так: R = (p * l) / S. Из неё становится ясно, что проводимость прямо пропорциональна площади сечения и обратно пропорциональна длине проводника.
Удельное электрическое сопротивление для многих веществ было установлено во время исследований. Существуют таблицы, в которые занесены данные, измеренные при температуре 20 градусов Цельсия. Ими часто пользуются при решении различных задач, связанных с электричеством. Вот некоторые из них:
- олово — 9,9 * 10-8 Ом * мм2/м;
- медь — 0,01724 Ом * мм2/м;
- алюминий — 0,0262 Ом * мм 2/м;
- железо — 0,098 * Ом * мм2/м;
- золото — 0,023 Ом * мм2/м.
Для проводников характерно увеличение сопротивления при росте температуры. Это связано с колебаниями атомов. В то же время с ростом температуры проводимость в полупроводниках и диэлектриках возрастает из-за увеличения концентрации носителей заряда.
Удельное сопротивление для неоднородного материала можно вычислить по формуле: p = E / J. Где: E и J напряжённость и плотность тока в конкретной точке.
Нахождение параметра
Найти сопротивление — значит, рассчитать потери тока. Существует 2 принципиально разных подхода к расчёту. В одном случае он ведётся для электрической цепи, а в другой — для материала. Если во втором случае всё предельно понятно, используется одна формула, в которую подставляют размеры тела и табличное значение удельной проводимости, то для электрической цепи не так всё просто.
В цепи может встречаться 3 вида соединения элементов:
- Параллельное. При таком соединении цепь разветвляется, то есть появляются ветви, по которым течёт ток. Ветви могут пересекаться между собой.
- Последовательное. Схема соединения представляет единую цепь, в которой нет разветвлений.
- Смешанное. Состоит из комбинированного соединения, включающего комбинации из параллельного и последовательного подключения.
Вычисление сопротивления для каждого типа соединения имеет особенности. При последовательном включении общее значение определяется путём простого складывания: R = r1 + r2 +…+ rn. При параллельном же соединении полное сопротивление цепи будет меньше самого малого из сопротивлений ветвей. Для такого включения верна формула: 1 / R = 1 / r1 + 1 / r2 +…+ 1 / rn.
Принцип расчёта смешанного соединения построен на группировке электрической цепи по виду подключения элементов. Определение параметра выполняют поочерёдно. Сначала высчитывают сопротивление одного узла, включающего однотипное соединение, затем к результату добавляют следующий элемент. Эту операцию повторяют до тех пор, пока не останется один элемент.
В радиотехнике деталь, применяющуюся в качестве сопротивления, называют резистором. С его помощью обозначают и так называемый эквивалентный параметр, используемый при расчётах электрических цепей. Его вводят, если нужно определить, например, мощность источника тока, выходное напряжение.
Таким образом, чтобы правильно посчитать сопротивление, нужно учитывать несколько факторов. При этом нужно помнить о единой системе измерений. Следует придерживаться СИ. Все величины, используемые в формулах, должны подставляться в стандартных единицах измерения. Почти во всех таблицах значение удельного сопротивления даётся в мм2/м, что связано с измерением площади.
Примеры решения задач
Решение примеров позволяет лучше разобраться в теме. При этом не только быстрее запоминаются формулы, но и становится понятным, где можно использовать полученные знания. Существует ряд заданий для самостоятельной проработки. Вот некоторые из них:
- На катушку электромагнита намотан медный провод сечением 0,003 мм2 длиною 200 метров. Найти сопротивление и массу обмотки. Для решения задачи нужно воспользоваться справочником по электрофизике. Из него взять значение удельного сопротивления меди и её плотность. Согласно справочным данным: p = 1,7 * 10−8 Ом * м, а V = 8900 кг/м3. В первом действии нужно определить массу. Для этого выразить её из формулы f = m / V и подставить заданные значения: m = V * f = l * S * f = 2 * 10|2 м * 3 * 10-8 м2 8,9 * 103 кг/м3 = 53,4 грамма. Теперь можно определить искомое сопротивление по формуле: R = (f * l) / S = (0,017 (Ом * мм2) / м * 200 м) / 0,03 мм2 = 3,4 / 0,003 = 113 Ом.
- Нужно изготовить провод длиною 100 метров и сопротивлением 1 Ом. Определить, из какого материала вес изделия будет меньше: меди или алюминия. Нужно вычислить, чему будет равно отношение масс: MCu / MAl. Из справочника взять данные: fAl = 2700 кг/м3; fCu = 8900 кг/м3; pAl = 2,8 * 10−8 Ом/м; pCu = 1,7 10−8 Ом/м. Для решения нужно выразить массы через плотность, длину и площадь поперечного сечения: m = f *l * S. Длина одинаковая, значит, отношения масс примет вид: (fCu * SCu) / (fAl * SAl). Площадь поперечного сечения будет вычисляться из правила нахождения сопротивления. Конечная формула примет вид: MCu / Mal = (fCu * RCu) / (fAl * RAl) = (8900 * 1,7) / (2700 * 2,8) = 2. Изделие из алюминия будет весить в 2 раза меньше.
- Имеется электрическая цепь, подключённая к сети 120 В. Если к ней подключить 2 последовательных сопротивления ток будет равен 3 A, а если параллельно — 16 А. Найти сопротивление. Задача решается с помощью закона Ома и формул вычисления сопротивления цепи: Iпосл = U / (r1 + r2); Iпар = U * (r1 + r2) / r1 * r2. Из них можно выразить искомые величины: r1 + r2 = U /Iпосл и r1 * r2 = U2 / Iпар * Iпос. Выполнив вычисления, можно найти, что r1 = 30 Ом, r2 = 10 Ом.
Решение заданий по теме обычно не вызывает трудностей. Нужно лишь внимательно переводить единицы измерения, знать формулы и иметь радиофизический справочник.
