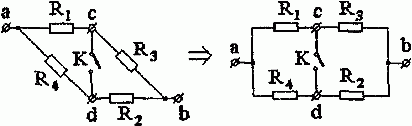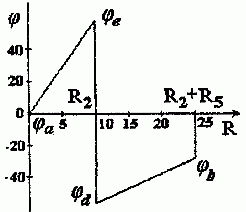Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
→
1.1 Методы анализа, основанные на законах Ома и Кирхгофа
1.1 Методы анализа, основанные на законах Ома и Кирхгофа
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
1.1 Методы анализа, основанные на законах Ома и законах Кирхгофа
Закон Ома устанавливает зависимость между напряжением и током на пассивной ветви, а также позволяет определить ток по известным потенциалам на концах ветви с источником напряжения.
Законы Кирхгофа применяют для нахождения токов в ветвях линейных и нелинейных схем при любом законе изменения во времени токов и напряжений.
Метод эквивалентных преобразований. При эквивалентных преобразований отдельные участки электрической цепи заменяются более простыми. Эквивалентность преобразования состоит в том, что токи и напряжения в непреобразованной части схемы не изменяются.
Последовательное упрощение схемы продолжается до ее преобразования в одноконтурную схему, после чего для расчета используется закон Ома.
Метод эквивалентных преобразований используется для нахождения внутреннего сопротивления эквивалентного генератора.
При помощи метода эквивалентных преобразований облегчают расчет расчет нелинейной цепи, упростив линейную часть цепи эквивалентными преобразованиями.
Принято пользоваться приведенным ниже алгоритмом метода законов Кирхгофа.
1. Произвольно выбирают положительные направления токов в ветвях и обозначают их на схеме.
2. Составляют уравнения по первому закону Кирхгофа: на одно уравнение меньше числа узлов (для последнего узла уравнение будет зависимым от предыдущих уравнений).
3. Выбирают независимые (главные) контуры и направление их обхода. Удобно для всех контуров выбрать одинаковое направление обхода.
4. Записывают уравнения по второму закону Кирхгофа для выбранных контуров.
5. Решая полученную систему уравнений, определяют искомые токи.
Решение задач на закон Ома и законы Кирхгофа
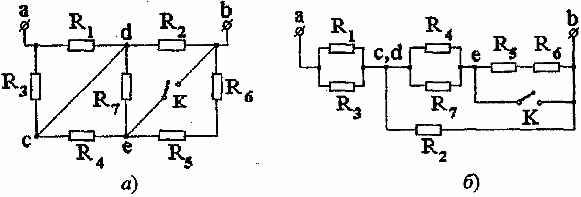
Задача 1.1. Определить эквивалентное сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К методом эквивалентных преобразований (рис. 1.1, a).
Рис. 1.1
Решение. Сохраняя топологию схемы, трансформируем ее к виду, удобному для анализа (отправная точка — потенциалы узлов c и d равны между собой).
Из рис. 1.1, б следует:
1. При разомкнутом ключе К
R ab = R 1 ⋅ R 3 R 1 + R 3 + ( R 47 + R 5 + R 6 )⋅ R 2 ( R 47 + R 5 + R 6 )+ R 2 .
2. При замкнутом ключе К
R 47 = R 1 ⋅ R 3 R 1 + R 3 + R 47 ⋅ R 2 R 47 + R 2 ,
где
R 47 = R 4 ⋅ R 7 R 4 + R 7 .
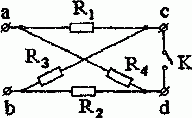
Задача 1.2. Определить методом эквивалентных преобразований сопротивление цепи между зажимами a и b при разомкнутом и замкнутом ключе К для схемы, изображенной на рис. 1.2.
Рис. 1.2
Решение. Совершим поворот части схемы относительно зажимов c и d. В результате получим (рис. 1.3):
Рис. 1.3
1. При разомкнутом ключе К
R ab = ( R 1 + R 3 )⋅ ( R 2 + R 4 ) ( R 1 + R 3 )+ ( R 2 + R 4 ) .
2. При замкнутом ключе К
R ab = R 1 ⋅ R 4 R 1 + R 4 + R 2 ⋅ R 3 R 2 + R 3 .
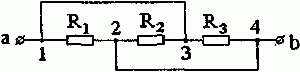
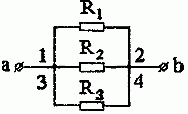
Задача 1.3. Найти сопротивление между зажимами a и b для схемы, изображенной на рис. 1.4.
Рис. 1.4
Решение. К точке 2 подходят условные «начало» сопротивления R2 и «концы» сопротивлений Rl и R3.
К точке 3 подходят «начала» сопротивлений R1 и R3 и «конец» сопротивления R2.
Но тогда, все «начала» сопротивлений и все их «концы» соединяются соответственно в одни точки. А значит, по определению, имеем параллельное соединение приемников (рис. 1.5).
Рис. 1.5
Таким образом, сопротивление между зажимами a и b:
R ab = 1 Y ab = 1 1 R 1 + 1 R 2 + 1 R 3 .
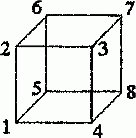
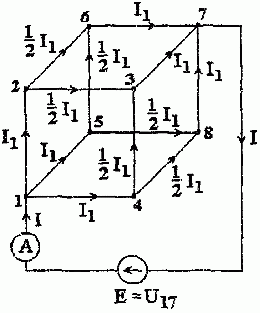
Задача 1.4. Найти сопротивление R13, R14, R17 между различными парами вершин куба, ребра которого имеют заданное сопротивление R (рис. 1.6).
Рис. 1.6
Решение. Задачу проще всего решить методом амперметра и вольтметра. Суть метода заключается в следующем. Если к фиксированным точкам схемы a и b подвести условно известное напряжение Uab и определить ток I во внешней цепи, то искомое сопротивление Rab = Uab/I. При этом напряжение Uab (показание вольтметра) в соответствии с законами Кирхгофа определяется как функция тока I (показание амперметра).
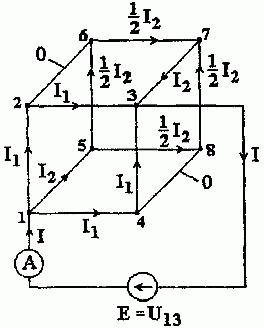
1. Расчетная схема для определения сопротивления R13 имеет вид, представленный на рис. 1.7.
Рис. 1.7
В силу симметрии потенциалы точек 2 и 6 (4 и 8) равны между собой. Поэтому токи в ребрах. 2 — 6 и 4 — 8 отсутствуют.
Перераспределение токов I1 и I2 легко находится из первого закона Кирхгофа и соответствует рисунку 1.7.
Соотношение между токами найдем из второго закона Кирхгофа:
U 14 = U 15 + U 58 + U 84 ; I 1 ⋅R= I 2 ⋅R+ 1 2 I 2 ⋅R+0= 3 2 I 2 ⋅R.
Откуда:
I 1 = 3 2 I 2 ; I 2 = 2 3 I 1 .
А значит, общий ток
I=2 I 1 + I 2 =2 I 1 + 2 3 I 1 = 8 3 I 1 .
Но
U 13 =I⋅ R 13 = 8 3 I 1 ⋅ R 13 = U 12 + U 23 =2 I 1 ⋅R.
Откуда, сокращая на I1, имеем 8/3·R13 = 2R. Или, что-то же, искомое R13 = 3/4·R.
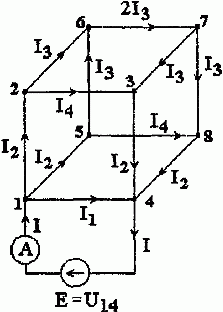
2. Расчетная схема для определения сопротивления R14 имеет вид, представленный на рис. 1.8.
Рис. 1.8
В силу симметрии токи в ребрах 1 — 2, 1 — 4, 2 — 3 и 4 — 3 равны между собой. А значит, в соответствии с первым законом Кирхгофа, токи в ребрах 2 — 6 и 4 — 8 отсутствуют.
Перераспределение неизвестных токов I1, I2, I3, I4 находится из первого закона Кирхгофа (и симметрии цепи) и соответствует рис. 1.8.
Поскольку падение напряжения
U 23 = U 26 + U 67 + U 73 ; I 4 ⋅R= I 3 ⋅R+2 I 3 ⋅R+ I 3 ⋅R=4 I 3 ⋅R,
то, сокращая на R, имеем:
I 4 =4 I 3
или
I 3 = 1 4 I 4 .
Ток
I 2 = I 3 + I 4 = 1 4 I 4 + I 4 = 5 4 I 4
или
I 4 = 4 5 I 2 .
Но
U 14 = U 15 + U 58 + U 84 ; I 1 ⋅R= I 2 ⋅R+ I 4 ⋅R+ I 2 ⋅R= I 2 ⋅R+ 5 4 I 2 ⋅R+ I 2 ⋅R= 14 5 I 2 ⋅R.
Откуда, сокращая на R, имеем:
I 1 = 14 5 I 2
или
I 2 = 5 14 I 1 .
Но
U 14 =I⋅ R 14 = ( I 1 +2 I 2 )⋅ R 14 = ( I 1 + 10 14 I 1 )⋅ R 14 = 24 14 I 1 ⋅ R 14 = I 1 ⋅R.
Или, что то же, искомое R14 = 14/24·R = 7/12·R.
3. Расчетная схема для определения сопротивления R17 имеет вид, представленный на рис. 1.9.
Рис. 1.9
В силу диагональной симметрии схемы полный ток I = 3I1.
Падение напряжения
U 17 = U 14 + U 43 + U 37 ; I⋅ R 17 = I 1 ⋅R+ 1 2 I 1 ⋅R+ I 1 ⋅R= 5 2 I 1 ⋅R.
Откуда искомое сопротивление R17 = 5/6·R.
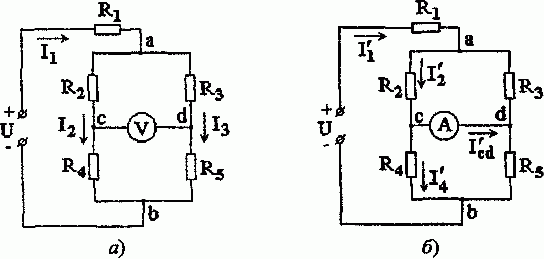
Задача 1.5. Определить методом эквивалентных преобразований токи в ветвях цепи (рис. 1 10, а) и показание вольтметра, включенного между точками c и d, считая, что его сопротивление во много раз превышает сопротивление каждого из элементов цепи.
Чему равно показание амперметра, включенного между точками c и d, сопротивление которого считать равным нулю?
Рис. 1.10
Сопротивления элементов цепи: R1 =10 Ом, R2 = R3 = R5 = 25 Ом и R4 = 50 Ом, а приложенное к ней напряжение U = 120 В.
Решение. Расчет показания вольтметра. Из условия вытекает, что его включение не оказывает влияния на распределение токов в цепи. Для расчета токов сначала определяем эквивалентное сопротивление всей цепи (рис. 1.10, а):
R= R 1 + ( R 2 + R 4 )⋅ ( R 3 + R 5 ) ( R 2 + R 4 )+ ( R 3 + R 5 ) =10+ 75⋅50 125 =40 Ом.
В неразветвленной части цепи протекает ток
I 1 = U R = 120 40 =3 A.
Токи, протекающие через сопротивления (R2 + R4) и (R3 + R5) можно найти различными способами.
1. В параллельных ветвях токи распределяются обратно пропорционально их сопротивлениям (формула разброса токов):
I 2 = I 1 ⋅ R 3 + R 5 ( R 2 + R 4 )+ ( R 3 + R 5 ) =3⋅ 50 125 =1,2 A; I 3 = I 1 ⋅ R 2 + R 4 ( R 2 + R 4 )+ ( R 3 + R 5 ) =3⋅ 75 125 =1,8 A.
2. Найдем напряжение на зажимах параллельных ветвей:
U ab = I 1 ⋅ ( R 2 + R 4 )⋅ ( R 3 + R 5 ) ( R 2 + R 4 )+ ( R 3 + R 5 ) =3⋅ 75⋅50 125 =90 B.
Токи в ветвях с сопротивлениями R2 + R4 и R3 + R5 равны:
I 2 = U ab R 2 + R 4 = 90 75 =1,2 A; I 3 = U ab R 3 + R 5 = 90 50 =1,8 A.
Напряжение на зажимах параллельных ветвей может быть найдено как разность между приложенным напряжением и падением напряжения на сопротивлении R1: Uab = U — R1·I1.
Найдем показание вольтметра, равное напряжению между точками с и d:
U V = U cd =− I 2 ⋅ R 2 + I 3 ⋅ R 3 =−1,2⋅25+1,8⋅25=15 B.
Наконец, вычислим ток, проходящий через амперметр; он равен току короткого замыкания I’cd (рис. 1.10, б). Для его нахождения вычислим токи:
I ′ 1 = U R 1 + R 2 ⋅ R 3 R 2 + R 3 + R 4 ⋅ R 5 R 4 + R 5 = 144 47 A; I ′ 2 = I ′ 1 ⋅ R 3 R 2 + R 3 = 72 47 A; I ′ 4 = I ′ 1 ⋅ R 5 R 4 + R 5 = 48 47 A.
Искомый ток, проходящий через амперметр,
I A = I ′ cd = I ′ 2 − I ′ 4 = 24 47 =0,51 A.
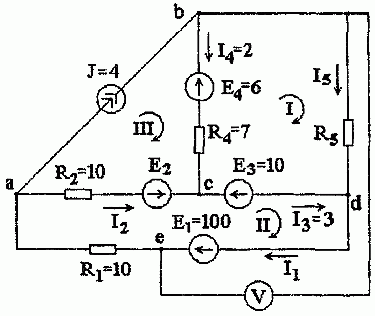
Задача 1.6. В схеме рис. 1.11 заданы сопротивления приемников, величины ЭДС и источника тока отдельных ветвей. Рассчитать неизвестные токи, ЭДС E2 и сопротивление R5, пользуясь законами Кирхгофа.
Рис. 1.11
Правильность решения проверить по балансу мощностей. Для наружного контура построить потенциальную диаграмму и определить показание вольтметра.
Решение
1. Всего в схеме пять ветвей, неизвестных токов I1, I2, I5 — три, неизвестных величин E2 и R5 — две, для нахождения которых составам три уравнения по первому закону Кирхгофа и два – по второму закону Кирхгофа:
для узла b: J= I 4 + I 5 ; для узла d: − I 5 − I 3 + I 1 =0; для контура I: I 5 R 5 − I 4 R 4 = E 3 + E 4 ; для контура II: I 1 R 1 + I 2 R 2 = E 1 + E 2 − E 3 .
Из первых трех уравнений находим токи:
I 5 =J− I 4 =4−2=2 A; I 1 = I 5 + I 3 =2+3=5 A; I 2 =−J+ I 1 =−4+5=1 A.
из четвертого уравнения
R 5 = E 3 + E 4 + I 4 ⋅ R 4 I 5 = 10+6+14 2 =15 Ом.
Величину E2 определяем из последнего уравнения:
E 2 = I 1 ⋅ R 1 + I 2 ⋅ R 2 − E 1 + E 3 =5⋅10+10⋅1−100+10=−30 B.
2. Для построения потенциальной диаграммы найдем потенциалы всех точек контура abcdea, приняв исходный потенциал точки a равным нулю:
φ e = φ a − I 1 ⋅ R 1 =0+5⋅10=50 B; φ d = φ e − E 1 =50−100=−50 B; φ b = φ d + I 5 ⋅ R 5 =−50+2⋅15=−20 B.
3. По найденным потенциалам строим потенциальную диаграмму, откладывая по оси ординат потенциалы точек, а по оси абсцисс — сопротивления участков (рис. 1.12).
Рис. 1.12
3. Из потенциальной диаграммы легко определить разность потенциалов между точками b и c Ubc = 70 В, что и будет показывать вольтметр.
4. Произведем проверку баланса мощностей:
P источников = E 1 ⋅ I 1 + E 2 ⋅ I 2 + E 3 ⋅ ( − I 3 )+ E 4 ⋅ ( − I 4 )+ U ba ⋅J; P потребителей = I 1 2 ⋅ R 1 + I 2 2 ⋅ R 2 + I 4 2 ⋅ R 4 + I 5 2 ⋅ R 5 .
В этом уравнении нам неизвестно напряжение на зажимах источника тока Uba, которое легко найти из потенциальной диаграммы: Uba = –20 В. С учетом этого
P источников =100⋅5+ ( −30 )⋅1+10⋅ ( −3 )+6⋅ ( −2 )+ ( −20 )⋅4=348 Вт; P потребителей = 5 2 ⋅10+ 1 2 ⋅10+ 3 2 ⋅0+ 2 2 ⋅7+ 2 2 ⋅15=348 Вт; P источников = P потребителей =348 Вт.
Закон Ома, законы Кирхгофа в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи

Законы Кирхгофа,
первый закон Кирхгофа,
второй закон Кирхгофа
Рассмотрим типовую задачу с ключом, который немного изменяет электрическую схему. Основной материал для повторения: формулы последовательного и параллельного подключения резисторов, закон Ома, выражение для мощности.
Задача:
Источник тока, два резистора и ключ включены в цепь, как показано на рисунке. При разомкнутом ключе на резисторе R₁ выделяется мощность P₁ = 2 Вт, а на резисторе R₂ — мощность P₂ = 1 Вт. Какая мощность будет выделяться на резисторе R₂ после замыкания ключа К? Внутренним сопротивлением источника пренебречь. Ответ дайте в ваттах.
Решение:
Схема с ключами всегда пугает учащихся. По началу кажется, что контуров такой цепи больше, чем на самом деле. Здесь нужно понимать, что разомкнутый ключ представляет собой обычный разрыв цепи. При этом даже не конденсатор, способный накапливать заряд и влиять на переходной процесс, а просто разрыв цепи. То есть ток туда не идет. Это и есть наш первый случай. В первой ситуации мы имеем два последовательных резистора, соединенных с ЭДС, при этом в цепи идет один ток, цепь состоит их одного контура.
Что меняется, когда мы замыкаем ключ К ? Ток начинает течь через меньшее сопротивление, то есть через провод с ключом. Это называется шунтированием резистора R₁. Ток через R₁ уже не течет, а обходит его через параллельный провод. Ток – существо ленивое, всегда идет в обход 🙂
Давайте я перерисую схему, чтобы было наглядно:
Как видите, схемы заметно упростились, что дает нам возможность приступить к решению задачи, расписывая основные законы электричества для двух разных случаев.
До замыкания ключа:
Имеем последовательное соединение двух резисторов. Выразим мощности, которые на них выделяются и которые изначально даны в условии.
Возьмем отношение этих мощностей, выразим через него отношение сопротивлений, которое нам понадобится в дальнейшем:
После замыкания ключа:
Шунтируется резистор R₁. Схема начинает работать только через резистор R₂. Выразим мощность, которая на нем выделяется.
Теперь рассмотрим отношение мощности, выделяемом на резисторе R₂ до замыкания ключа, к мощности, выделяемой на этом же резисторе R₂ после замыкания ключа. Отношения этих мощностей выражаются через отношение сопротивлений резисторов R₁/R₂, а это отношение соответственно выражается через отношение мощностей P₁/P₂, которое нам известно из условия (до замыкания ключа). Собираем всё вместе и получаем:
Ответ: на резисторе R₂ будет выделяться 9 Ватт после замыкания ключа.
Решение целиком:
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
Даю 25 баллов, если поможете Каково сопротивление цепи при разомкнутом и замкнутом ключе?
R1 = R4 = 600Ом, R2 = R3 = 1, 8 кОм.
Вы открыли страницу вопроса Даю 25 баллов, если поможете Каково сопротивление цепи при разомкнутом и замкнутом ключе?. Он относится к категории
Физика. Уровень сложности вопроса – для учащихся 5 – 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Физика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.
2) В случае, если цепь содержит непреобразованные источники напряжения и источники тока, то элементы матрицы узловых токов [Jy] рассчитывают следующим образом:
Jyk Jk Gk Ek ,
где Jk – алгебраическая сумма токов источника тока, подключенных к рассматриваемому узлу. Токи Jk записывают под знаком суммы со знаком плюс, если они направлены к k-му узлу и со знаком минус, если они направлены от k- го узла; GkEk – алгебраическая сумма произведений ЭДС ветвей, сходящихся в k-м узле, на проводимости этих ветвей. Слагаемое записывается со знаком плюс (минус), если ЭДС направлена к узлу (от узла).
1.7 Краткая характеристика методов расчета электрических цепей
Наиболее универсальным методом анализа и расчёта электрических цепей является метод, основанный на применении I и II – го законов Кирхгофа.
Первый закон применяют для описания баланса токов в узлах электрической цепи, согласно которому: “Алгебраическая сумма токов, сходящихся в узле электрической цепи, должна быть равна нулю”:
n
Ik 0. k 1
Если бы условие (3) не выполнялось, то в узлах электрической цепи происходило бы накопление электрических зарядов, что экспериментально не подтверждается.
Второй закон применяют для описания замкнутых (условно или, безусловно) контуров, согласно которому: “Алгебраическая сумма ЭДС, действующих в замкнутом контуре, должна уравновешиваться алгебраической суммой падений напряжений на элементах замкнутого контура”:
n m m
Ek Up IpRp. k 1 p 1 p 1
Оба закона Кирхгофа являются следствиями закона сохранения энергии применительно к электрическим цепям.
Метод наложения (суперпозиции) применяют для анализа и расчёта только линейных электрических цепей, содержащих несколько источников энергии. Здесь токи в ветвях определяются путем алгебраического суммирования “частичных” токов, получающихся в ветвях под воздействием каждой частичной ЭДС схемы в отдельности.
Наиболее эффективен метод наложения тогда, когда в цепи содержатся источники тока (с Rвн ) и источники ЭДС (с Rвн 0), так как при рассмотрении “частичных” режимов работы схемы (только с каким – то одним источником) – идеальные источники ЭДС закорачиваются (из-за Rвн 0), а ветви с ис-
21
точником тока обрываются (из-за Rвн ), что вызывает максимальное упрощение схемы в конкретном “частичном” режиме.
1.8 Потенциальная диаграмма
Второй закон Кирхгофа наглядно иллюстрируется с помощью потенциальной диаграммы (ПД). Если по оси абсцисс прямоугольной системы координат отложить сопротивления участков в той последовательности, в которой они включены в цепь, а по оси ординат – потенциалы соответствующих точек, то получится график распределения потенциала вдоль неразветвленной цепи. Пользуясь этим графиком, можно определить напряжение между двумя любыми точками цепи. Порядок построения потенциальной диаграммы (предварительно необходимо выполнить расчет электрической цепи) состоит в следующем:
1)Выбираем опорный узел и принимаем его потенциал равным нулю;
2)Задаем положительное направление обхода контура;
3)Если направление обхода контура и направление тока совпадают на участке цепи, то потенциал при прохождении через сопротивление уменьшается, при направлении обхода контура и противоположном направлении тока потенциал при прохождении через сопротивление увеличится;
4)Идеальный источник ЭДС вызывает скачкообразное изменение потенциала. Скачок потенциала положительный, если направление ЭДС совпадает по направлению с обходом контура и отрицательный, если направления обхода контура и ЭДС противоположны.
При построении ПД необходимо соблюдать следующие правила:
1)Если направление обхода выбранного замкнутого контура и направление тока на участке цепи совпадают, то потенциал будет уменьшаться при прохождении через сопротивление, на величину падения в нём напряжения;
2)Если направление обхода выбранного замкнутого контура и направление тока на участке цепи противоположны, то потенциал будет увеличиваться при прохождении через сопротивление, на величину падения в нём напряжения;
3)Идеальный источник ЭДС вызывает скачок потенциала на величину
ЭДС источника (т.к. его Rвн =0);
4)Скачок потенциала после источника ЭДС положительный, если направление ЭДС совпадает с направлением обхода и отрицательный, если направление ЭДС и направление обхода противоположны;
5)Источник ЭДС повышает потенциал в той точке, в которую направлена его стрелка.
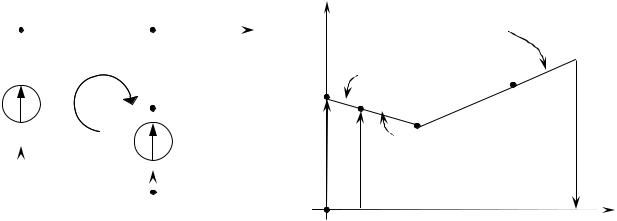
Для примера построим потенциальную диаграмму для контура “a – b – c – d – a” в схеме представленной на рис. 1.8.1.
Примем потенциал точки “а” равным нулю ( a) и найдём последовательно потенциалы точек “b”, “c”, “d”:
b = a + E1 – I1R01 ,
22
|
c = b – I1R1 = a + E1 – I1R01 + I1R1 , |
||||||||||||||||
|
d = c + I2R2 = a + E1 – I1R01 – I1R1 + I2R2 , |
||||||||||||||||
|
a = d – E2 = 0. |
||||||||||||||||
|
а затем построим потенциальную диаграмму (рис. 1.8.2). |
||||||||||||||||
|
b |
R1 |
c |
R3 |
I |
φ, В |
|||||||||||
|
3 |
ΔU2 = I1·R02 |
|||||||||||||||
|
E1 |
R2 |
ΔU1 = –I1·R01 |
d’ |
|||||||||||||
|
d |
b’ |
b |
||||||||||||||
|
R01 |
c |
|||||||||||||||
|
E2 |
E1 |
I2·R2 |
||||||||||||||
|
I1 |
–I1·R1 |
|||||||||||||||
|
R02 |
||||||||||||||||
|
I3 |
а |
|||||||||||||||
|
a |
||||||||||||||||
|
0 |
R01 |
|||||||||||||||

–E2
d R, Ом
Замечание: При построении ПД один из узлов схемы принимается за опорный и заземляется, то есть его потенциал обнуляется. При этом токи в ветвях не изменяются, так как их величина зависит от разности потенциалов, а не от абсолютной величины потенциала одного отдельно взятого узла схемы.
23
2 РАСЧЕТ ПРОСТЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА
2.1 Примеры решения задач цепей с источниками постоянного напряжения и тока
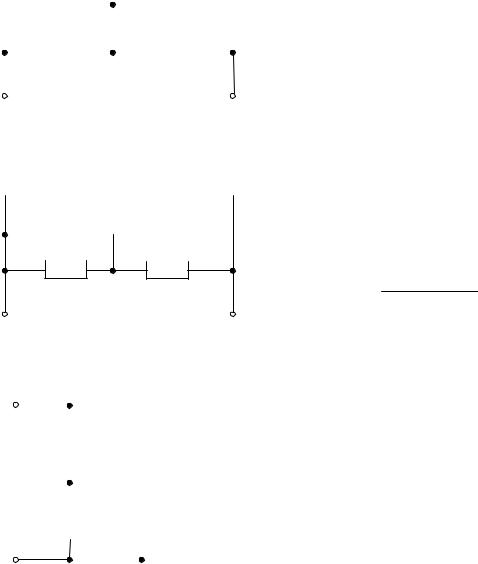
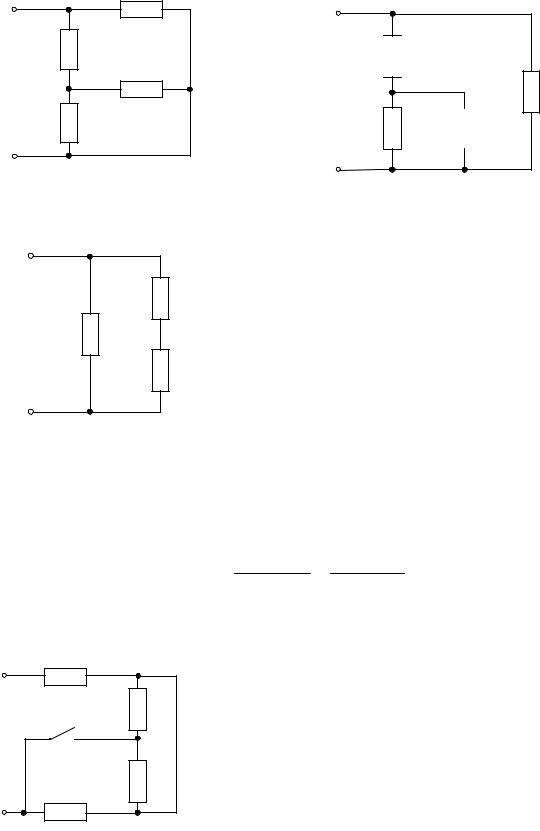
2.1.1 Найти эквивалентное сопротивление для цепей рис. 2.1.1 относительно зажимов a, b?
|
2R |
2R |
РЕШЕНИЕ: в схеме представленной на |
|||||||||||||||
|
рис. 2.1.1.а резисторы R и 2R попарно соеди- |
|||||||||||||||||
|
R |
R |
нены между собой параллельно: эквивалентное |
|||||||||||||||
|
сопротивление состоит из суммы этих двух со- |
|||||||||||||||||
|
единений: |
|||||||||||||||||
|
a |
b |
2RR |
2RR |
4 |
|||||||||||||
|
Rab |
R Ом. |
||||||||||||||||
|
Рис. 2.1.1.а |
2R R |
2R R |
3 |
||||||||||||||
|
R |
R |
РЕШЕНИЕ: в схеме представленной на |
|||||||||||||||
|
рис. 2.1.1.б перемычка закорачивает резистор |
|||||||||||||||||
|
4R, и он как бы исключается из схемы. Экви- |
|||||||||||||||||
|
валентное сопротивление состоит из парал- |
|||||||||||||||||
|
4R |
3R |
||||||||||||||||
|
лельного соединения резисторов 3R и (R+2R): |
|||||||||||||||||
R 2R 3R
Rab R 2R 3R 1,5R Ом.
Рис. 2.1.1.б
|
а |
РЕШЕНИЕ: в схеме представленной на |
||||||||||||||
|
рис. 2.1.1.в резисторы R1 и R2 соединены по- |
|||||||||||||||
|
R3 |
R1 |
следовательно: R12=R1+R2; резисторы R4 и R5 |
|||||||||||||
|
соединены параллельно, их общее сопротивле- |
|||||||||||||||
|
ние рассчитывается по формуле: |
|||||||||||||||
|
R5 |
R4 R2 |
R45 |
R4 R5 |
. |
|||||||||||
|
R4 R5 |
|||||||||||||||
|
b |
Эквивалентное сопротивление состоит из двух |
||||||||||||||
|
параллельно соединенных ветвей с резисто- |
|||||||||||||||
|
Рис. 2.1.1.в |
рами: R12 в одной ветви и последовательно со- |
||||||||||||||
|
единенных R3 и R45 в другой. Эквивалентное |
|||||||||||||||
|
сопротивление рассчитывается по формуле: |
|||||||||||||||
|
R12 R3 R45 |
|||||||||||||||
|
Rab |
. |
||||||||||||||
|
R12 R3 R45 |
24
25
2.1.2 Найти эквивалентное сопротивление цепи (рис. 2.1.2) относительно зажимов “a” и “b”, если: R1=600 Ом, R2=360 Ом, R3=400 Ом, R4=300 Ом.
а
R4
R2
R3
R1
b
Рис. 2.1.2
|
а |
|
|
R2 |
|
|
R4 |
|
|
b |
R13 |
|
Рис. 2.1.2.б |
а

R4
b
Рис. 2.1.2.а
РЕШЕНИЕ: Заданную схему можно представить в ином виде (рис. 2.1.2.а, рис. 2.1.2.б).
Резисторы R1 и R3 соединены параллельно, их сопротивление рассчитывается по формуле:
|
R13 |
R1 R3 |
600 400 |
240 Ом, |
||
|
R1 R3 |
600 400 |
||||
с резистором R2 сопротивление R13 соединено последовательно, то есть их общее сопротивление R123:
R123 R13 R2 240 360 600 Ом,
Эквивалентное сопротивление цепи Rab состоит из двух соединенных парал-
|
лельно резисторов R123 |
и R4: |
R123 R4 |
600 300 |
||
|
Rab |
R123 R4 |
600 300 200 Ом. |
|||
|
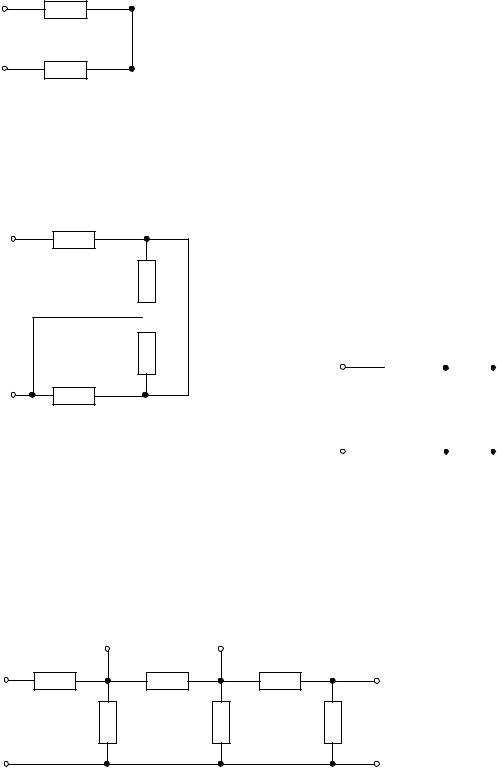
2.1.3 Чему равно сопротивление цепи (рис. 2.1.3) Rab при разомкнутом и |
|||||
|
замкнутом рубильнике? |
РЕШЕНИЕ: |
||||
|
а |
1 |
||||
|
R |
Решение данной задачи распадается на два от- |
||||
|
R |
дельных случая: |
||||
|
K |
1-й случай – ключ “К” разомкнут. Перемычка |
||||
|
2 |
|||||
|
между узлами 1 и 3 шунтирует два резистора, |
|||||
|
поэтому реальная схема имеет вид, представ- |
|||||
|
b |
R |
R |
ленный на рис. 2.1.3.а. Следовательно, эквива- |
||
|
лентное сопротивление состоит из двух после- |
|||||
|
3 |
|||||
|
Рис. 2.1.3 |
довательно соединенных резисторов: Rab=2R; |
||||
a R 1
b R
2
Рис. 2.1.3.а
а 1
R
R 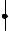
R
b R
3
Рис. 2.1.3.б
2-й случай – ключ “К” замкнут (рис. 2.3.1.б). Наличие в цепи двух перемычек приводит к тому, что три резистора между точками 1 и “b” включены параллельно между собой: каждый резистор одним полюсом подключен к узлу 1, что равносильно подключению к узлу 3, а вторым полюсом подключен к узлу “b”, что равносильно подключению к узлу 2.
В этом случае эквивалентное сопротивление преобразованной схемы представленной на рис. 2.1.3.в можно найти как:
|
Rab R |
1 |
R |
R |
4 |
R Ом. |
||||||||||||||||||
|
1 |
1 |
1 |
3 |
3 |
|||||||||||||||||||
|
R |
R |
R |
|||||||||||||||||||||
|
а |
R |
1 |
3 |
||||||||||||||||||||
|
R |
R |
R |
|||||||||||||||||||||
|
b |
|||||||||||||||||||||||
|
2 |
|||||||||||||||||||||||
|
Рис. 2.1.3.в |
2.1.4 Пусть требуется найти эквивалентное сопротивление цепи представленной на рис. 2.1.4 между различными зажимами “a” – “b”, “c” – “d”, “d”
– “f”, “a” – “f”, “e” – “f”, если: R1=6 Ом, R2=5 Ом, R3=15 Ом, R4=30 Ом, R5=3 Ом, R6=3 Ом.
|
а |
R1 |
c |
R2 |
d |
R5 |
e |
|
R3 |
R4 |
R6 |
||||
|
b |
f |
|||||
|
Рис. 2.1.4 |
РЕШЕНИЕ:
а) Для расчета сопротивления Rab между зажимами “а” и “b” представим схему в ином виде (рис. 2.1.4.а). Эта схема представляет собой лестничное соединение сопротивлений.
26
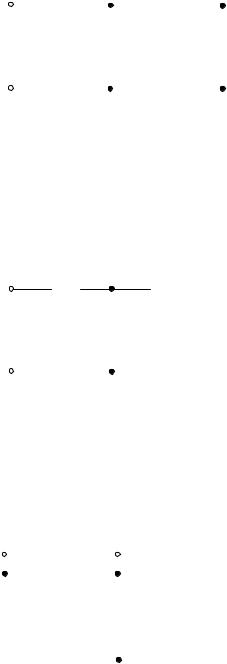
|
а |
R1 |
R2 |
R5 |
Резисторы R5 |
и R6 |
соединены по- |
||||||||||||||
|
следовательно и |
эквивалентное |
|||||||||||||||||||
|
сопротивление резисторов R5 и R6 |
||||||||||||||||||||
|
R5 |
R4 |
R6 |
найдем как: |
|||||||||||||||||
|
b |
R56 R5 R6 |
3 3 6 Ом. |
||||||||||||||||||
|
Рис. 2.1.4.а |
Сопротивление R56 соединено параллельно R4, поэтому их общее сопротивление найдем по формуле:
|
R456 |
R4 R56 |
30 6 |
5 Oм. |
|||||||||||||
|
R4 R56 |
||||||||||||||||
|
30 6 |
||||||||||||||||
|
а |
R1 |
R2 |
После этого преобразования схему мож- |
|||||||||||||
|
но свернуть и представить в виде (рис. |
||||||||||||||||
|
2.1.4.б). Резисторы R2 |
и R456 соединены |
|||||||||||||||
|
R3 |
R456 |
последовательно, тогда |
их общее сопро- |
|||||||||||||
|
b |
тивление R’ будет равно: |
|||||||||||||||
|
R R2 R456 5 5 10Oм. |
||||||||||||||||
|
Рис. 2.1.4.б |
||||||||||||||||
Полное эквивалентное сопротивление цепи Rab состоит из резистора R1, последовательно с которым соединены параллельно включенные резисторы R3 и R’:
|
Rab R1 |
||||||||||||||
|
c R2 |
d |
R5 |
||||||||||||
|
R3 |
R4 |
R6 |
||||||||||||
Рис. 2.1.4.в
|
R3R |
15 10 |
||
|
6 |
12 Oм; |
||
|
R3 R |
15 10 |
б) Для расчета сопротивления Rcd между зажимами “с” и “d” перечертим схему и представим в виде (рис. 2.1.4.в). Резистор R1 не следует учитывать, так как он подключен к разомкнутым зажимам “a” – “b”. Резисторы R5, R6 включены между собой последовательно, а с резистором R4 параллельно:
|
R456 |
R4 R5 R6 |
30 3 3 |
5 Oм, |
||
|
R4 R5 R6 |
|||||
|
30 3 3 |
с результирующим сопротивлением R456 последовательно соединен резистор R3 и их общее сопротивление R” будет равно: R”=R3+R456 =15+5=20 Ом, Эквивалентное сопротивление Rcd состоит из параллельно соединенных резисторов R2 и R”:
|
R |
2 R |
5 20 |
|||
|
Rcd |
4Oм. |
||||
|
R2 R |
|||||
|
5 20 |
27
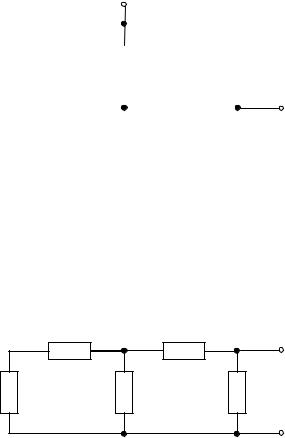
|
R2 |
d |
R5 |
в) Для расчета сопротивления Rdf |
ме- |
||||||||||||||
|
жду зажимами “d” и “f” представим |
||||||||||||||||||
|
схему в виде, как показано на |
рис. |
|||||||||||||||||
|
R3 |
R4 |
R6 |
2.1.4.г. |
|||||||||||||||
|
f |
Резистор R1 не будем учитывать, так |
|||||||||||||||||
|
как он подключен к разомкнутым за- |
||||||||||||||||||
|
Рис. 2.1.4.г |
жимам “a” и “b”. |
|||||||||||||||||
Эквивалентное сопротивление цепи между зажимами “d” – “f” состоит из трех параллельно соединенных ветвей: R2+R3; R4 и R5+R6. Поэтому найдем вначале сумму проводимостей 3-х параллельных ветвей:
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
См, откуда Rdf =4 Ом. |
|||||||
|
R2 R3 |
R5 R6 |
5 15 |
|||||||||||||
|
Rdf |
R4 |
30 3 3 4 |
|
R2 |
R5 |
e |
|
R3 |
R4 |
R6 |
|
f |
||
|
Рис. 2.1.4.д |
г) Для расчета сопротивления Ref между зажимами “e” и “f” рассчитаем схему, представленную (рис. 2.1.4.д). Резистор R1 так же не будем учитывать, т.к. он включен на разомкнутые зажи-
мы “a” и “b”.
Резисторы R2 и R3 соединены последовательно, то есть R23=R2+R3=5+15=20 Ом, а параллельно с ними соединен резистор R4; тогда их общее сопротивление
R234:
|
R234 |
R23 R4 |
20 30 |
12Oм, |
|||
|
R23 R4 |
20 30 |
|||||
последовательно с R234 соединен резистор R5: R2-5=R234 + R5=12 + 3 =15 Ом,
Эквивалентное сопротивление Ref состоит из параллельного соединения
|
R2-5 и R6: |
R2 5 R6 |
15 3 |
|||
|
Ref |
2,5Oм. |
||||
|
R2 5 R6 |
|||||
|
15 3 |
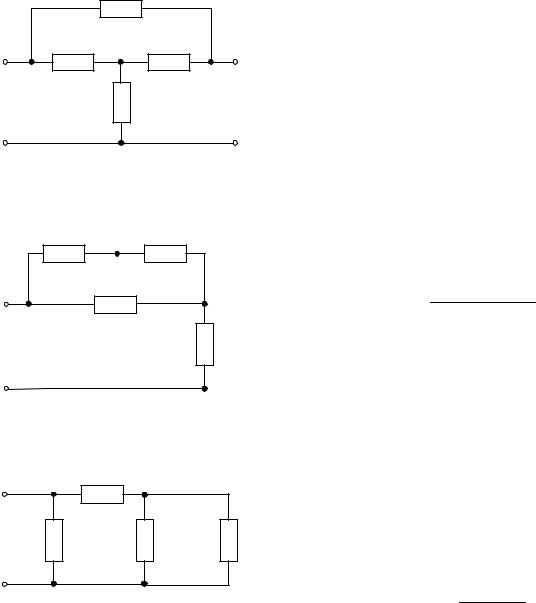
2.1.5 Пусть требуется найти сопротивление между зажимами “a” и “b” схемы представленной на рис. 2.1.5 в двух режимах:
1)при холостом ходе зажимов “c” и “d”;
2)коротком замыкании зажимов “c” и “d”, если: R1=16 Ом, R2=4 Ом, R3=4 Ом, R4=12 Ом.
28
|
R4 |
||||
|
а |
R1 |
e |
R2 |
c |
|
R3 |
||||
|
b |
d |
|||
|
f |
||||
|
Рис. 2.1.5 |
||||
|
R4 |
c |
R2 |
||
|
а |
R1 |
e |
||
|
b |
R3 |
|||
|
f |
||||
|
Рис. 2.1.5.а |
||||
|
а |
R1 |
e |
||
|
R4 |
R3 |
R2 |
||
|
b |
||||
|
c |
||||
|
Рис. 2.1.5.б |
РЕШЕНИЕ:
а) Зажимы “c” и “d” разомкнуты (режим холостого хода – хх). Схема для этого случая представлена на рис. 2.1.5.а. В этом режиме резисторы R4 и R2 соединены последовательно.
Результирующий резистор R42 = R4 + R2 соединен параллельно с резистором R1, тогда их общее сопротивление R’ найдем как:
|
R |
R42 R1 |
(12 4) 16 |
8Oм, |
|
|
R42 R1 |
||||
|
12 4 16 |
R’ оказывается соединен последовательно с R3 и эквивалентное сопротивление между зажимами а и b будет равно:
Rab R’ R3 (R4 R2)R1 R3 R4 R2 R1
8 4 12Oм.
б) Зажимы “c” и “d” закорочены. Для режима К.З. схема представлена на рис. 2.1.5.б. Здесь точки “c”, “d”, “f”, и “b” имеют одинаковые потенциалы, причем резистор R4 при коротком замыкании зажимов “c” и “d” оказывается включенным параллельно зажимам “а” и “b”. “Свернем” схему от конца к началу: резисторы R2 и R3 соединены параллельно между собой, их общее сопротивление R23 включено последовательно с R1:
R123 R1 R2 R3 .
R2 R3
Эквивалентное сопротивление схемы относительно зажимов “a” и “b” представляет параллельное соединение R4 и R123:
|
R4 |
(R1 |
R2 |
R3 |
) |
4 4 |
|||||||||||||||
|
R |
R123 |
12 (16 |
) |
|||||||||||||||||
|
R2 R3 |
||||||||||||||||||||
|
Rab |
4 |
4 4 |
7,2Oм. |
|||||||||||||||||
|
R4 |
R123 |
R4 |
R1 |
R |
2 R3 |
12 16 |
4 4 |
|||||||||||||
|
R2 R3 |
4 4 |
|||||||||||||||||||
2.1.6 Найти входное сопротивление цепи, представленной на рис. 2.1.6, при разомкнутом и замкнутом ключе, если: R1=40 Ом, R2=20 Ом, R3=10 Ом, R4=30 Ом, R5=40 Ом.
29
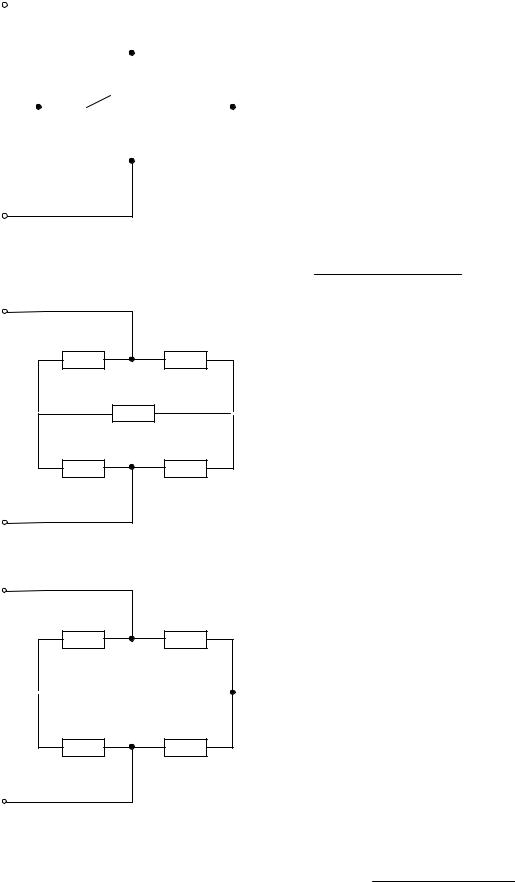
|
R3 |
R1 |
РЕШЕНИЕ: |
||||||||||
|
а) Пусть ключ “K” разомкнут (рис. 2.1.6). В |
||||||||||||
|
этом режиме входное сопротивление цепи оп- |
||||||||||||
|
а |
||||||||||||
|
K |
R5 |
ределяется параллельным соединением двух |
||||||||||
|
c |
d |
ветвей, в которые |
последовательно включены |
|||||||||
|
R4 |
резисторы R1 с R2 |
и R3 с R4. Найдем последова- |
||||||||||
|
R2 |
||||||||||||
|
b |
тельно включенные сопротивления: |
|||||||||||
|
R12 R1 R2, R34 R3 R4, |
||||||||||||
Рис. 2.1.6
R3 а R1
R5
c
R4 b R2
Рис. 2.1.6.a
R3 а R1
c
R4 b R2
Рис. 2.1.6.б
тогда, эквивалентное сопротивление схемы:
|
Rвх |
R12 R34 |
(R1 R2) (R3 R4) |
||
|
R12 R34 |
R1 R2 R3 R4 |
(40 20) (10 30) 24Oм. 40 20 30 10
б) Пусть ключ “К” замкнут (рис. 2.1.6.а). В этом случае резисторы схемы образуют два “треугольника” или две “звезды”. Так резисторы R1, R3, R5 и R2, R4, R5 соединены “треугольником”, а R1, R2, R5 и R3, R4, R5 – “звез-

1 способ:
Преобразуем “треугольник” R2, R4, R5 в эквивалентную “звезду” с сопротивлениями Rb, Rc, Rd. После преобразования схема принимает вид (рис. 2.1.6.б).
Сопротивления звезды:
|
Rb |
R2 R4 |
20 30 |
6Ом, |
|||||||||||||
|
R2 R4 R5 |
20 30 50 |
|||||||||||||||
|
d |
||||||||||||||||
|
R2 R5 |
20 |
50 |
||||||||||||||
|
Rd |
10 Ом, |
|||||||||||||||
|
R2 R4 R5 |
20 30 50 |
|||||||||||||||
|
Rc |
R4 R5 |
30 50 |
15 Ом. |
|||||||||||||
|
R2 R4 R5 |
20 30 50 |
|||||||||||||||
|
Входное сопротивление цепи Rвх: |
||||||||||||||||
|
R |
вх Rb |
(R3 Rc)(R1 Rd) |
||||||||||||||
|
R3 Rc R1 Rd |
6 (10 15) (40 10) 22,7 Oм. 10 15 40 10
30
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Сопротивление
Добавлено 25 сентября 2020 в 13:05
Схема из предыдущего раздела не очень практична. На самом деле, собирать ее (напрямую соединять полюсы источника напряжения с помощью только куска провода) может быть довольно опасно. Причина, по которой это опасно, заключается в том, что при таком коротком замыкании величина электрического тока может быть очень большой, а выделение энергии может быть очень значительным (обычно в виде тепла). Обычно на практике электрические цепи строятся таким образом, чтобы максимально безопасно использовать высвобождаемую энергию.
Ток, протекающий через нить накала лампы
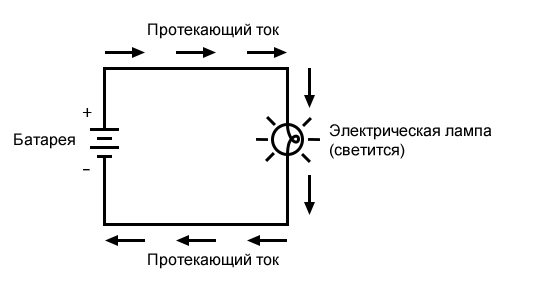
Одним из практических и популярных способов использования электрического тока является электрическое освещение. Самая простая форма электрической лампы – это крошечная металлическая «нить» внутри прозрачной стеклянной колбы, которая накаляется добела от тепловой энергии, когда через нее проходит достаточный электрический ток. Как и батарея, она имеет две проводящие точки подключения: одна для входа тока, а другая – для выхода. Схема электрической лампы, подключенной к источнику напряжения, выглядит примерно так:
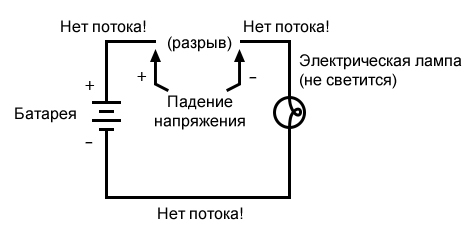
Когда ток проходит через тонкую металлическую нить накала лампы, он встречает большее противодействие движению, чем в обычном толстом куске провода. Это противодействие электрическому току зависит от типа материала, площади его поперечного сечения и температуры. Технически это противодействие известно как сопротивление (можно сказать, что проводники имеют низкое сопротивление, а диэлектрики – очень высокое сопротивление). Это сопротивление служит для ограничения величины тока, проходящего через цепь при заданном напряжении, подаваемом батареей, по сравнению с «коротким замыканием», когда у нас не было ничего, кроме провода, соединяющего один конец источника напряжения (батареи) с другим. Когда ток движется против противодействия сопротивления, возникает «трение». Как и в случае механического трения, трение, создаваемое током, протекающим через сопротивление, проявляется в виде тепла. Концентрированное сопротивление нити накала лампы приводит к тому, что на нити рассеивается относительно большое количество тепловой энергии. Этой тепловой энергии достаточно, чтобы нить накаливания стала раскаленной добела и начала светиться, в то время как провода, соединяющие лампу с батареей (которые имеют гораздо меньшее сопротивление), вряд ли станут хотя бы теплыми, проводя такую же величину тока. Как и в случае короткого замыкания, если целостность цепи нарушена в любой точке, ток прекращается по всей цепи. При установленной лампе, это означает, что она перестанет светиться:
Как и прежде, ток не течет, а в точках разрыва доступен весь потенциал (напряжение) батареи, ожидающий соединения, чтобы пересечь этот разрыв и позволить току снова течь. Это состояние известно как разомкнутая цепь, когда разрыв цепи предотвращает протекание тока повсюду. Всё, что требуется, чтобы «разомкнуть» цепь, – это один разрыв. После повторного соединения любых разрывов и восстановления непрерывности цепь называется замкнутой.
Основа для коммутации ламп
То, что мы видим здесь, является основой для включения и выключения ламп дистанционными выключателями. Поскольку любое нарушение непрерывности цепи приводит к прекращению протекания тока по всей цепи, то для управления протеканием тока в цепи мы можем использовать устройство, предназначенное для преднамеренного нарушения этой непрерывности (называемое ключом, или выключателем, переключателем и т.п.) и установленное в любом удобном месте, к которому мы можем провести провода:
Таким образом, выключатель, установленный на стене дома, может управлять лампой, установленной в длинном коридоре или даже в другой комнате, далеко от выключателя. Сам ключ состоит из пары проводящих контактов (обычно сделанных из какого-то металла), соединенных механическим рычажным приводом или кнопкой. Когда контакты соприкасаются друг с другом, устанавливается непрерывность цепи, и ток может течь от одного контакта к другому. Когда контакты разделены, течению тока от одного к другому препятствует воздушная изоляция между ними, и непрерывность цепи нарушается.
Выключатель ножевого типа
Возможно, лучший вид переключателя для иллюстрации принципа действия – это выключатель ножевого типа:
Ножевой переключатель – это не что иное, как токопроводящий рычаг, свободно поворачивающийся на шарнире, вступающий в физический контакт с одним или несколькими неподвижными контактами, которые также являются токопроводящими. Переключатель, показанный на приведенном выше рисунке, собран на фарфоровом основании (отличный изоляционный материал), с использованием меди (отличный проводник) для «лезвия» и контактов. Ручка сделана из пластика, чтобы изолировать руку оператора от токопроводящего лезвия переключателя при его открытии или закрытии. Ниже показан еще один тип переключателя, с двумя неподвижными контактами вместо одного:
Ножевой переключатель, показанный здесь, имеет одно «лезвие» и два неподвижных контакта, что означает, что он может включать или выключать более одной цепи. На данный момент это не так важно, чтобы просто понять основную идею того, что такое ключ, и как он работает. Ножевые переключатели отлично подходят для иллюстрации основного принципа работы ключа, но они представляют определенные проблемы безопасности при использовании в электрических цепях большой мощности. Открытые проводники переключателя делают очень возможным случайный контакт с цепью, а любая искра, которая может возникнуть между движущимся ножом и неподвижным контактом, может воспламенить любые находящиеся поблизости горючие материалы. В большинстве современных конструкций переключателей движущиеся проводники и контакты закрыты изолирующим кожухом, чтобы уменьшить эти опасности. Фотографии нескольких современных типов переключателей показывают, что механизмы переключения гораздо более скрыты, чем в конструкции ножевого выключателя:
Разомкнутые и замкнутые цепи
В соответствии с терминологией цепей «разомкнутая» и «замкнутая», переключатель, у которого контакт от одной клеммы подключения соединен с контактом другой клеммы (например, выключатель с лезвием, полностью касающимся неподвижного контакта), обеспечивает непрерывность протекания тока через себя и называется замкнутым переключателем. И наоборот, выключатель, который нарушает целостность цепи (например, выключатель с лезвием, не касающимся неподвижного контакта), не пропускает ток и называется разомкнутым выключателем.
Резюме
- Сопротивление – это мера противодействия электрическому току.
- Короткое замыкание – это электрическая цепь, которая практически не оказывает сопротивления току. Короткие замыкания опасны для источников питания высокого напряжения, так как возникающие высокие токи могут вызвать выделение большого количества тепловой энергии.
- Разомкнутая цепь – это цепь, в которой непрерывность была нарушена из-за прерывания пути прохождения тока.
- Замкнутая цепь – это замкнутая цепь с целой непрерывностью на всем протяжении.
- Устройство, предназначенное для размыкания или замыкания цепи в контролируемых условиях, называется ключом или переключателем.
- Термины «разомкнутый» и «замкнутый» относятся как к ключам, так и ко всем цепям. Разомкнутый ключ – это ключ, в котором есть разрыв: ток не может течь через него. Замкнутый ключ – это ключ, который обеспечивает непосредственный (с низким сопротивлением) путь прохождения тока.
Теги
ОбучениеСопротивлениеЭлектрический токЭлектрическое напряжениеЭлектричество