Как
видно из рис.6.5, полупроводниковый диод
является нелинейным элементом. Это
означает, что связь между приложенным
напряжением и током нелинейная, и закон
Ома для диода не выполняется. Сопротивление
диода зависит от приложенного напряжения.
В этой связи вводится понятие
дифференциального сопротивления

Зависимость
силы тока от напряжения, приложенного
к диоду, для диодов с плоским p-n переходом
достаточно хорошо описывается выражением
, (6.3)
где
Is
величина обратного тока насыщения; Rv
сопротивление того объема полупроводника,
который не участвует в образовании p-n
перехода; e
элементарный заряд; k
постоянная Больцмана; T
термодинамическая температура. Используя
выражение (6.3), дифференциальное
сопротивление диода наиболее просто
найти, преобразуя (6.2) следующим образом:

Простые
вычисления дают следующую формулу для
дифференциального сопротивления диода:
(6.5)
Величина
kT/e составляет примерно 25 мВ при комнатной
температуре. При относительно большом
токе I первым слагаемым в (6.5) можно
пренебречь, тогда
(6.6)
Следовательно,
начиная с некоторого напряжения,
сопротивление диода почти целиком
определяется сопротивлением объема
полупроводника Rv,
нелинейное сопротивление контакта
становится пренебрежимо малым, а ВАХ
близка к линейной. Это обстоятельство
будет использоваться далее для нахождения
Rv.
Описание экспериментальной установки
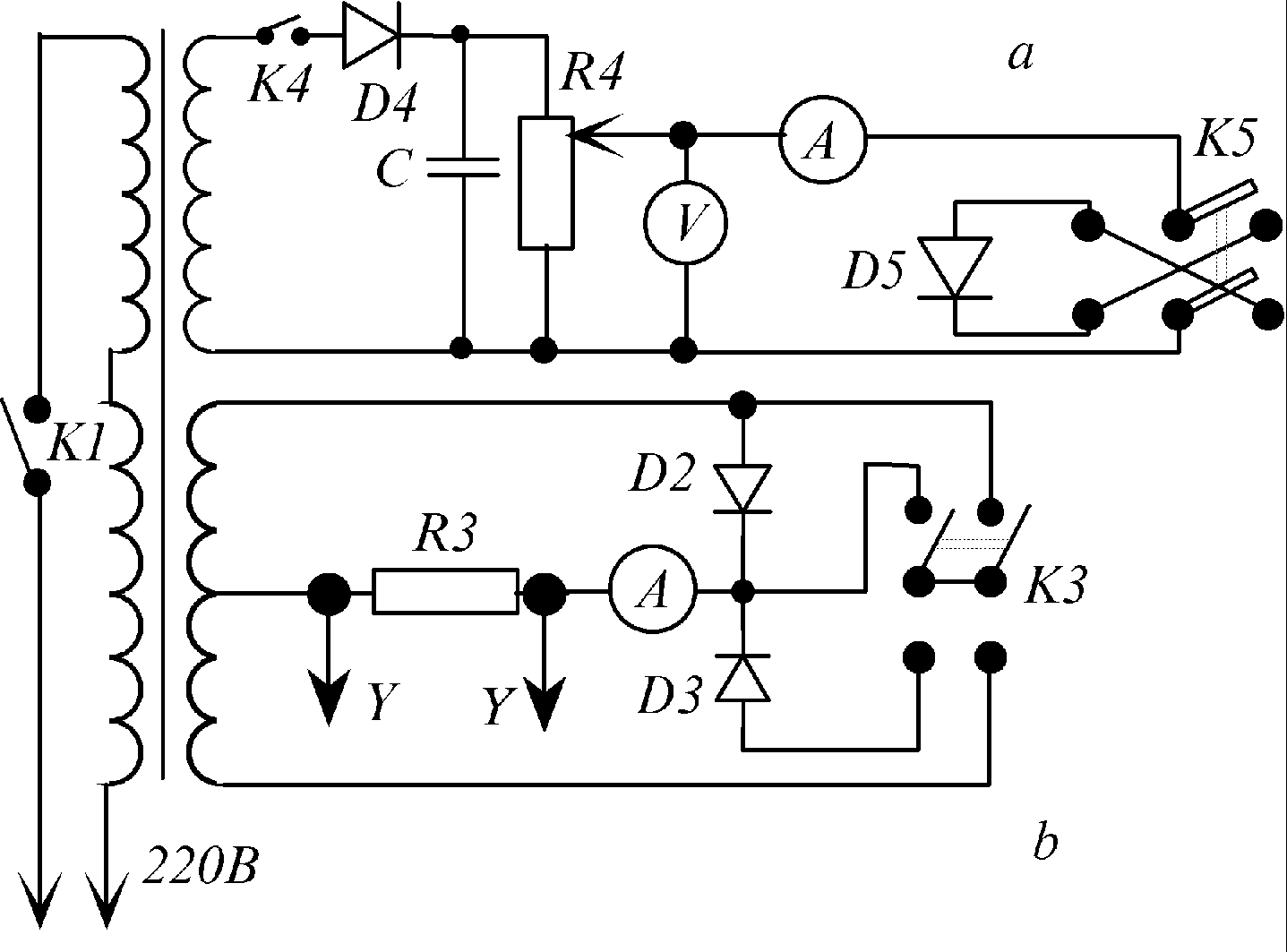
Схема
лабораторного макета для изучения
полупроводниковых выпрямителей показана
на рис. 6.6.
Рис.
6.6.
Все
два блока макета питаются от одного
трансформатора, включаемого в сеть
напряжением 220 В с помощью ключа K1.
Нижний на рис. 6.6. блок предназначен для
изучения одно- и двухполупериодного
выпрямления с помощью осциллографа,
верхний блок
для измерения вольт-амперных характеристик
диодов методом вольтметра-амперметра.
Буквой Y обозначены клеммы для подключения
усилителя осциллографа по входу Y.
Изучение полупроводниковых выпрямителей
проводится в три этапа.
1. Наблюдение одно- и двухполупериодного выпрямления
Схема
устройства для наблюдения выпрямляющих
свойств диодов показана на рис. 6.6,б. С
помощью ключа K3
закорачиваем диод D2
. В этом случае диод D3
не включен в цепь, на резисторе R3
будет синусоидальное напряжение, которое
наблюдается на экране осциллографа,
т.е. выпрямления нет. Амперметр, включенный
последовательно с резистором R3
,
не фиксирует переменный ток, так как в
макете применен прибор магнитоэлектрической
системы.
Если
ключ K3
поставить в среднее положение, то диод
D3
по-прежнему не включен в цепь. Но диод
D2
оказывается включенным в цепь и пропускает
ток только в одном направлении. Поэтому
на экране осциллографа наблюдается
пульсирующее напряжение одного знака,
имеет место однополупериодное выпрямление.
Амперметр при этом показывает некоторое
значение тока.
Если
ключом K3
включить в схему и диод D3,
то в один из полупериодов ток пропускается
диодом D2,
в следующий полупериод
диодом D3.
Ток через резистор R3
в обоих случаях течет в одном направлении,
на экране будет наблюдаться пульсирующее
напряжение одного знака с удвоенной
частотой. Возрастает в два раза и ток
через резистор R3.
Такое выпрямление называется
двухполупериодным.
Как по вольт-амперной характеристике определить дифференциальное сопротивление диода и сопротивление по постоянному току?
ФизикаПрограммированиеКомпьютерная техника
Константин Алышев
16 февраля 2021 · 661
Поскольку электрическое сопротивление диода зависит от величины и полярности приложенного напряжения, оно будет разным в каждой точке вольт-амперной характеристики (ВАХ) в отличие от резистора.
В общем случае дифференциальное сопротивление (Rдиф) – это производная напряжения, взятая по току.
Поскольку подобрать аналитическую функцию, соответствующую ВАХ бывает проблематично, определить Rдиф в заданной точке ВАХ можно приблизительно, взяв в окрестности этой точки два значения напряжения: U1 и U2; и соответствующие им значение тока I1 и I2.
Тогда Rдиф можно будет рассчитать по формуле:
Rдиф = (U2-U1)/(I2-I1).
Сопротивление по постоянному току определяется по приведенной формуле в точке, соответствующей величине заданного тока.
437
Комментировать ответ…Комментировать…
Сопротивление R = U/I, дифференциальное – это производная dU/dI
На графике сопротивление – котангенс секущей идущей из начала координат, а дифференциальное – котангенс касательной
443
Комментировать ответ…Комментировать…
Рпр – прямая
рассеиваемая мощность, значение мощности, рассеиваемой диодом при протекании
прямого тока;
Pср – средняя рассеиваемая мощность диода, среднее за
период значение мощности, рассеиваемой диодом при протекании прямого и
обратного тока;
Rдиф – дифференциальное сопротивление диода, отношение
малого приращения напряжения диода к малому приращению тока на нем при заданном
режиме
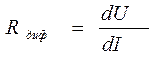
(1.1)
Rnp.д. – прямое сопротивление
диода по постоянному току, значение сопротивления диода, полученное как частное от деления постоянного прямого напряжения
на диоде и соответствующего прямого тока
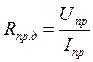
(1.2)
Rобр.д – обратное сопротивление диода; значение сопротивления
диода, полученное как частное от деления
постоянного обратного напряжения на диоде и соответствующего постоянного
обратного тока
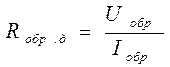
(1.3)
Максимально допустимые параметры определяют
границы эксплуатационных режимов, при которых диод может работать с заданной
вероятностью в течение установленного срока службы. К ним относятся:
максимально допустимое постоянное обратное напряжение Uобр.max;
максимально допустимый прямой ток Iпр.max,
максимально допустимый средний прямой ток Iпр.ср.max,
максимально допустимый средний выпрямленный токIвп.ср.max, максимально допустимая средняя рассеиваемая мощность
диода Рср.max.
Указанные параметры приводятся в
справочной литературе. Кроме того, их можно определить экспериментально и по
вольтамперным характеристикам.
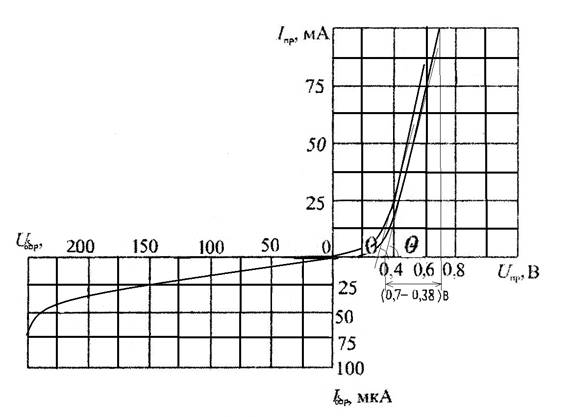
Задача 1.1 Рассчитать и сравнить Rдиф, Rпр.д для диода Д237Б при Iпр1= 75 мА.
Рисунок 1.2 – ВАХ диода Д237Б
Дифференциальное
сопротивление находим как котангенс угла наклона касательной, проведенной к
прямой ветви ВАХ в точке Iпр1= 75 мА (Rдиф
~ ctg Θ~)
(1.4)
Задача 1.2 Прямое сопротивление диода
находим как отношение постоянного напряжения на диоде Uпр=0,7В к
соответствующему постоянному току Iпр1=75мА на прямой
ветви ВАХ.
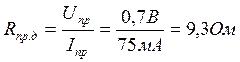
(1.5)
Видим, что Rдиф < Rпр.д . Кроме того, отметим, что значения данных параметров
зависят от заданного режима. Например, для этого же диода при Iпp2=25мА
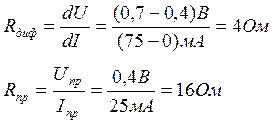
(1.6) , (1.7)
Задача 1.3 Рассчитать Rобр.д для диода
Д237 при Uобр = 150 В
и сравнить с рассчитанной величиной Rпр.д. На обратной ветви ВАХ Д237Б (рисунок 1.2) находим: Iобр = 25мкА при Uобр =150В. Следовательно,
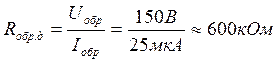
(1.8)
Видим,
что Rобр>>Rпр.д, что говорит об односторонней проводимости диода. Вывод об односторонней
проводимости можно сделать и непосредственно из анализа ВАХ: прямой ток Iпp~мА при Uпр <1B, в то время как Iобp ~ десятки мкА при Uобр~десятки вольт, т.е. прямой ток превышает обратный в
сотни- тысячи раз
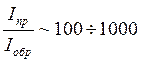
(1.9)
Задача
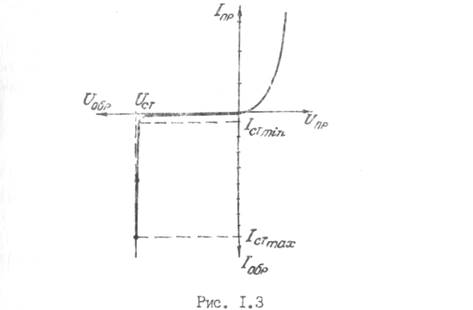
1.4 Стабилитроны и стабисторы предназначены для стабилизации уровня напряжения
при изменении протекающего через диод тока. У стабилитронов рабочим является
участок электрического пробоя вольтамперной характеристики в области обратных
напряжений рисунок 1.3.
На
этом участке напряжение на диоде остается практически постоянным при
значительном изменении тока протекающего через диод. Подобной характеристикой
обладают сплавные диоды с базой, изготовленной из низкоомного
(высоколегированного) материала. При этом образуется узкий p-n-переход, что создает, условия для возникновения электрического
пробоя при относительно низких обратных напряжениях (единицы – десятки вольт).
А именно такие напряжения нужны для питания многих транзисторных устройств. В
германиевых диодах электрический пробой быстро переходит в тепловой, поэтому в
качестве стабилитронов применяют кремниевые диоды, обладающие большей
устойчивостью в отношении теплового пробоя. У стабисторов рабочим служит прямой
участок вольтамперной характеристики рисунок 1.4. У двухсторонних (двуханодных)
стабилитронов имеется два встречно включенных p-n перехода, каждый
из которых является основным для противоположной полярности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Для начала стоит разобраться с понятием “дифференциальное сопротивление”. Я думаю, многие знают, что из себя представляет обычное “омическое” сопротивление и легко могут его найти, зная закон Ома:
I=U⁄R, (1)
где I ─ ток, протекающий в цепи, U ─ Напряжение на участке цепи, R ─ сопротивление участка цепи.
Благодаря этой формуле, мы легко вычисляем сопротивление и не паримся. Это справедливо к обычному резистору, сопротивление которого не меняется от приложенного тока и напряжения ( пока он не начнет гореть от перегрузки, но это уже другая история :)).
Если мы возьмем диод, приоткроем его определенным напряжением и начнем расчитывать его сопротивление по обычной формуле, исходя из полученных токов и напряжений, ничего путного из этого не получится, поскольку данная формула применима к линейным элементам (коим и является обычный резистор). Расчеты окажутся некорректными, поскольку диод имеет НЕЛИНЕЙНУЮ (экспоненциальную) вольт-амперную характеристику, график которой был приведен в этой статье, из которого видно, что при изменении протекающего тока, напряжение изменяется непропорционально.
Тут как раз на помощь приходит дифференциальное сопротивление, которое показывает, насколько изменяется это самое сопротивление при изменении тока или напряжения в нашем элементе. Оно имеет вид:
d(R)=|U2-U1|/|I2-I1|, (2)
где d(R) ─ дифференциальное сопротивление, U2-U1 ─ дифференциальное (разностное) напряжение на участке цепи, I2-I1 ─ дифференциальный (разностный) ток, протекающий в цепи.
Допустим, захотелось нам вычислить сопротивление диода. И тут есть,по крайней мере, два пути. Первый путь достаточно прост. Умные дяденьки, исходя из формулы вольт-амперной характеристики диода, вывели формулу, с помощью которой можно вычислить дифференциальное сопротивление диода, исходя из протекающего тока. Выглядит она таким образом:
d(R)=(k*T/e)/I, (3)
где k ─ постоянная Больцмана, T ─ абсолютная температура в Кельвинах, e ─ заряд электрона.
Далее, дяденьки пошли дальше и ввели величину теплового потенциала (ϕT), она равна:
ϕT=k*T/e (4)
При комнатной температуре (20…25°С), величина ϕT≈25 (мВ), а при другой температуре расчитать несложно, поскольку k и e ─ всем известные константы, а T ─ это собственно температура :).
Исходя из вышеописанного, формула 3 три приобретает вид:
Допустим, мы при комнатной температуре провели через диод ток величиной 1 милиампер. Расчитаем дифференциальное сопротивление диода по формуле 5:
Собственно говоря, на этом весь расчет и окончился :). Полученные результаты на 100% верны, если вольт-амперная характеристика нашего диода идеально экспоненциальная. Естественно, идеального ничего не бывает, поскольку на практике характеристика диода немного отличается от экспоненциальной, поэтому погрешность, конечно, есть. Это был первый путь.
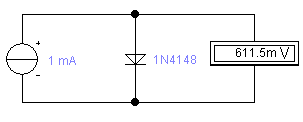
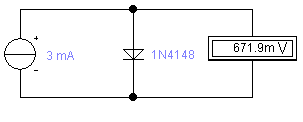
Второй путь ─ сугубо практический. Берем диод, пропускаем через него ток ,смотрим падение напряжения, записываем результаты. Далее, повышаем ток, смотрим падение напряжения, записываем результаты, после чего, расчитываем сопротивление с помощью формулы 2. Такой подход актуален, когда нужно прям очень точно расчитать сопротивление (мое мнение ─ на практике такая точность нахрен никому не нужна :)). Этим мы и займемся. В симуляторе выбираем диод, пропускаем через него ток 1 миллиампер смотрим падение напряжения при этом:
Напряжение составило 611,5 мВ. Повысим мы, допустим, ток в 3 раза (мне так захотелось). Что при этом получилось:
Падение напряжения составило 671,9 мВ. Ну что же, данные есть, осталось только подставить в формулу 2:
d(R)=(671,9-611,5)/(3-1)=30,2 Ом
Наше дифференциальное сопротивление составило 30,2 Ом. Вспомним, что с помощью первого метода расчета, оно составило 25 Ом. Какой расчет выбирать? Дело уже Ваше. Как правило, на практике, первого метода вполне достаточно.
В статье “Не так и сложен стабилитрон, хотя не так и прост” я не мало внимания уделил дифференциальному сопротивлению, но с точки зрения объяснения его влияния на работу стабилитрона. Однако оказалось, что нуждается в пояснении само понятие дифференциального сопротивления. Вот об этом и поговорим. Как и во всех статьях для начинающих, математики будет не много, а для понимания достаточно знаний в объеме средней школы.
Сопротивление, нелинейное сопротивление, проводимость
Что такое сопротивление изучают в курсе физики средней школы. Я не сомневаюсь, что это известно абсолютно всем. Как и закон Ома
R = U / I
С точки зрения математики, связь между напряжением, током и сопротивлением линейная. А на ВАХ (Вольт Амперная Характеристика) график этой зависимости прямая линия проходящая через начало координат.
Чем более вертикально проходит (для этой иллюстрации), тем меньше сопротивление. В данном случае
R1 < R2 < R3
Немного позже, уже при изучении переменного тока, школьники узнают о реактивном сопротивлении катушек индуктивности и конденсаторов. Их реактивное сопротивление зависит от частоты, но зависимость между током и напряжением остается по прежнему линейной.
При знакомстве с полупроводниками школьники сталкиваются с нелинейной зависимостью между током и напряжением для P-N перехода.
С точки зрения физики этот график тоже отображает сопротивление (зависимость между током и напряжением), но уже нелинейное. Нелинейной характеристикой обладает и электрический разряд в газах. Существуют и сопротивления зависящие от приложенного напряжения – варисторы. При этом нужно отметить, что термисторы и фоторезисторы не являются нелинейными сопротивлениями, так как величина их сопротивления зависит не от напряжения и тока (зависимость остается линейной), а от иных факторов, температуры и освещенности.
Да, я знаю про NTC и PTC термисторы. Но они не являются темой статьи.
Обратная к сопротивлению величина называется проводимостью.
G = I / U
Единицей проводимости является Сименс (См).
Аппроксимация
ВАХ не всегда являются графиками аналитических функций. Не редко это результат измерений и подобрать аналитическую функцию затруднительно. Или эта функция является слишком сложной.
Кроме того, параметры полупроводниковых приборов (да и вообще электронных компонентов) имеют естественный разброс, иногда довольно значительный. Поэтому точный график требуется далеко не всегда. Обычно нужна некая усредненная кривая, которая отражает типовой случай.
В таких случаях реальную кривую ВАХ делят на несколько частей и подбирают для каждой части функцию, которая является достаточно простой, но ее график может не полностью совпадать с реальностью, а давать некоторую (малую) погрешность. Это называется аппроксимацией.
Есть разные методы аппроксимации, но их изучение уведет нас далеко от темы статьи. Поэтому я остановлюсь на одном, наиболее простом методе – кусочно-линейной аппроксимации. Это замена сложной кривой отрезками прямых линий. Давайте посмотрим, как это будет выглядеть для нашего случая прямой ветви ВАХ диода
Здесь красным цветом показана реальная кривая, а отрезками черного цвета ее аппроксимация. Реальная кривая разделена точками (U1,0), (U2,I2), (U3,I3), (U4,I4) на части, которые и заменены отрезками прямых. Понятно, что чем короче эти отрезки, и чем их больше, тем точнее результат аппроксимации соответствует реальности.
Обратите внимание, что эти отрезки, хоть они и не проходят через начало координат, являются графиками постоянных сопротивлений. Тут нет никакого нарушения. Просто, хоть это и не очевидно, сопротивление на ВАХ соответствует углу между осью абсцисс и прямой линией зависимости между током и напряжением.
Если вы не очень уверены в своих знаниях математики, прочитайте статьи “Этюд о координатах” и “Сага о треугольниках“
На этот угол не влияет сдвиг графика относительно координатных осей. Просто при сдвиге катетом будет являться не ось координат, а отрезок параллельной ей прямой. Однако я понимаю, что преобразования координат и тригонометрия не вызывают восторга у многих. Поэтому я поступлю проще. При этом я опущу вспомогательные преобразования.
Давайте возьмем отрезок ограниченный точками (U2,I2) и (U3,I3). Разместим вспомогательную систему координат U’-0-I’ в начальной точке этого отрезка. В этой вспомогательной системе координат точка (U2,I2) станет началом координат, а точка (U3,I3) будет иметь координаты (U’3, I’3). Теперь хорошо видно, что отрезок действительно соответствует ВАХ линейного сопротивления.
Мы можем спокойно работать в этой вспомогательной системе координат. А если потребуется пересчитать координаты между основной и вспомогательной системами, то используются простейшие соотношения
U’3 = U3 – U2
I’3 = I3 – I2
Теперь мы очень близко подошли к понятию дифференциального сопротивления. Осталось сделать один простой шаг.
Дифференциальное сопротивление
По графику ВАХ можно узнать какому току какое напряжение соответствует, и наоборот, для любой точки. Это будут абсолютные значения тока и напряжения.
Но есть и другая задача, определить, насколько изменится ток при изменении напряжения. Для линейного сопротивления все просто, а для нелинейного мы можем воспользоваться ранее рассмотренной аппроксимацией. Для упрощения будем рассматривать случай, когда величина изменения полностью укладывается на одном отрезке кусочно-линейной аппроксимации. В противном случае просто придется разбивать диапазон изменений на несколько частей, что не повлияет на результат, но излишне усложнит пример.
Давайте посмотрим, как изменится ток при изменении напряжения от U2 до U3 нашего примера ВАХ диода. Достаточно очевидно, что
Иллюстрация кажется сложной? Не пугайтесь, на самом деле все просто. Изменение напряжения это разность двух отрезков по оси напряжений. Просто начала этих отрезков лежат в начале координат, что и позволяет нам записать привычное
ΔU = U3 – U2
В общем случае, напряжения могут отсчитываться не от нулевого уровня, а от некоторого U0. Напомню, что напряжение это разность потенциалов.
ΔU = (U3 – U0) – (U2 – U0) = U3 – U0 – U2 + U0 = U3 – U2
Зачем так сложно? Это не сложно, это иллюстрирует, что разность напряжений не зависит от точки отсчета. И для нас это важно. И именно это позволило нам так легко ввести вспомогательную систему координат.
Аналогично для тока. Величина изменения тока будет
ΔI = I3 – I2
В пределах нашего отрезка сопротивление будет постоянно и равно R23 (между точками 2 и 3).
ΔI = ΔU / R23
Обратите внимание, здесь здесь речь идет о сопротивлении между двумя точками. Это несколько отличается от просто сопротивления. На самом деле даже не важно, какая именно аппроксимация используется, и используется ли вообще.
Я уже говорил, что чем меньше аппроксимирующие отрезки, тем точнее результат аппроксимации. При длине отрезков стремящейся к нулю мы уже можем говорить не о сопротивлении между двумя точками, а о сопротивлении в данной точке, поскольку точки становятся неразличимыми. Причем совсем не обязательно точки на прямой, но и точки на кривой.
Вот это сопротивление в данной точке и называется дифференциальным сопротивлением
С математической точки зрения это производная от U по I. Я так много внимания уделил кучочно-линейной аппроксимации неспроста. В этом случае у нас дифференциальное сопротивление будет некоторой константой для каждой точки. Именно числовое значение и приводится в справочниках на электронные компоненты.
Графически, дифференциальное сопротивление это касательная к кривой ВАХ в данной точке. Помните, я приводил иллюстрацию, где сопротивление определялось как угол? Дифференциальное сопротивление как раз и определяет для заданной точки угол наклона касательной к оси абсцисс.
Приближенно можно рассчитать дифференциальное сопротивление так, как я показывал на примере R23. То есть, взяв две не очень далеко расположенные точки на графике ВАХ.
Точно так же, как проводимость является обратной величиной к сопротивлению, существует и дифференциальная проводимость, которая обратна дифференциальному сопротивлению.
По графику ВАХ можно найти соответствие тока и напряжения для любой точки. Дифференциальное же сопротивление позволяет определить величину изменения напряжения при изменении тока (и наоборот), а не абсолютные значения. Это самое важное отличие дифференциального сопротивления от просто сопротивления.
Заключение
Понятие дифференциального сопротивления может показаться сложным и непонятным, но на самом деле является довольно простым. Надеюсь, теперь у вас получилось во всем разобраться.
До новых встреч!