Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 января 2022 года; проверки требуют 6 правок.
| Электрическое сопротивление | |
|---|---|
 |
|
| Размерность |
L2MT −3I −2 (СИ); TL −1 (СГСЭ, гауссова система); LT −1 (СГСМ) |
| Единицы измерения | |
| СИ | Ом |
| СГСЭ | статом, с/см |
| СГСМ | абом, см/с |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
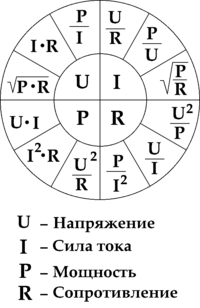
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойство проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему[1]
Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
где
- R — сопротивление, Ом (Ω);
- U — разность электрических потенциалов (напряжение) на концах проводника, Вольт (В);
- I — сила тока, протекающего между концами проводника под действием разности потенциалов, Ампер (А).
История[править | править код]
В 1826 г. Георг Ом экспериментальным путем открыл основной закон электрической цепи, научился вычислять сопротивление металлических проводников и вывел закон Ома. Таким образом, в первом периоде развития электротехники (1800 –1831 годы) были созданы предпосылки для ее развития, для последующих применений электрического тока.
Само понятие «сопротивление» появилось задолго до изысканий Георга Ома. Впервые этот термин применил и употребил русский ученый Василий Владимирович Петров. Он установил количественную зависимость силы тока от площади поперечного сечения проводника: он утверждал, что при использовании более толстой проволоки происходит «более сильное действие… и весьма скорое течение гальвани-вольтовской жидкости». Кроме того, Петров четко указал на то, что при увеличении сечения проводника (при употреблении одной и той же гальванической батареи) сила тока в нем возрастает.[2]
Единицы и размерности[править | править код]
Размерность электрического сопротивления в Международной системе величин: dim R = L2MT −3I −2. В Международной системе единиц (СИ), основанной на Международной системе величин, единицей сопротивления является ом (русское обозначение: Ом; международное: Ω). В системе СГС как таковой единица сопротивления не имеет специального названия, однако в её расширениях (СГСЭ, СГСМ и гауссова система единиц) используются[3]:
- статом (в СГСЭ и гауссовой системе, 1 statΩ = (109 c−2) с/см = 898 755 178 736,818 Ом (точно) ≈ 8,98755·1011 Ом, равен сопротивлению проводника, через который под напряжением 1 статвольт течёт ток 1 статампер);
- абом (в СГСМ, 1 abΩ = 1·10−9 Ом = 1 наноом, равен сопротивлению проводника, через который под напряжением 1 абвольт течёт ток 1 абампер).
Размерность сопротивления в СГСЭ и гауссовой системе равна TL−1 (то есть совпадает с размерностью обратной скорости, с/см), в СГСМ — LT−1 (то есть совпадает с размерностью скорости, см/с)[4].
Обратной величиной по отношению к сопротивлению является электропроводность, единицей измерения которой в системе СИ служит сименс (1 См = 1 Ом−1), в системе СГСЭ (и гауссовой) статсименс и в СГСМ — абсименс[5].
Физика явления[править | править код]
Высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока.
В других средах (полупроводниках, диэлектриках, электролитах, неполярных жидкостях, газах и т. д.) в зависимости от природы носителей заряда физическая причина сопротивления может быть иной. Линейная зависимость, выраженная законом Ома, соблюдается не во всех случаях.
Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он состоит.
Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле:
где ρ — удельное сопротивление вещества проводника, Ом·м, l — длина проводника, м, а S — площадь сечения, м².
Сопротивление однородного проводника также зависит от температуры.
Удельное сопротивление — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади сечения.
Сопротивление металлов снижается при понижении температуры; при температурах порядка нескольких кельвинов сопротивление большинства металлов и сплавов стремится или становится равным нулю (эффект сверхпроводимости). Напротив, сопротивление полупроводников и изоляторов при снижении температуры (в некотором диапазоне) растёт. Сопротивление также меняется по мере увеличения тока/напряжения, протекающего через проводник/полупроводник.
Зависимость сопротивления от материала, длины и площади поперечного сечения проводника[править | править код]
В металле подвижными носителями зарядов являются свободные электроны. Можно считать, что при своем хаотическом движении они ведут себя подобно молекулам газа. Поэтому в классической физике свободные электроны в металлах называют электронным газом и в первом приближении считают, что к нему применимы законы, установленные для идеального газа.
Плотность электронного газа и строение кристаллической решетки зависят от рода металла. Поэтому сопротивление проводника должно зависеть от рода его вещества. Кроме того, оно должно еще зависеть от длины проводника, площади его поперечного сечения и от температуры.
Влияние сечения проводника на его сопротивление объясняется тем, что при уменьшении сечения поток электронов в проводнике при одной и той же силе тока становится более плотным, поэтому и взаимодействие электронов с частицами вещества в проводнике становится сильнее.
Из формулы
видно, что сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Величину ρ, характеризующую зависимость сопротивления проводника от материала, из которого он сделан, и от внешних условий, называют удельным сопротивлением вещества. Удельное сопротивление различных веществ при расчетах берут из таблиц.
Величину, обратную удельному сопротивлению, называют удельной проводимостью вещества и обозначают σ.
Сопротивление тела человека[править | править код]
- Для расчёта опасной величины силы тока, протекающего через человека при попадании его под электрическое напряжение частотой 50 Герц (Гц), сопротивление тела человека условно принимается равным 1 кОм[6] . Эта величина имеет малое отношение к реальному сопротивлению человеческого тела. В реальности сопротивление человека не является омическим, так как эта величина, во-первых, нелинейна по отношению к приложенному напряжению, во-вторых, меняется во времени, в-третьих, гораздо меньше у человека, который волнуется и, следовательно, потеет и т. д.
- Серьёзные поражения тканей человека наблюдаются обычно при прохождении тока силой около 100 мА. Совершенно безопасным считается ток силой до 1 мА. Удельное сопротивление тела человека зависит от состояния кожных покровов. Сухая кожа обладает удельным сопротивлением порядка 10000 Ом·м, поэтому опасные токи могут быть достигнуты только при значительном напряжении. Однако при наличии сырости сопротивление тела человека резко снижается и безопасным может считаться напряжение только ниже 12 В. Удельное сопротивление крови 1 Ом·м при 50 Гц[7].
Метрологические аспекты[править | править код]
Приборы для измерения сопротивления[править | править код]
- Омметр
- Измерительный мост
- Амперметр и вольтметр (сопротивление находится по формуле)
Средства воспроизведения сопротивления[править | править код]
- Магазин сопротивлений — набор резисторов
- Катушки электрического сопротивления
Государственный эталон сопротивления[править | править код]
- ГЭТ 14-91 Государственный первичный эталон единицы электрического сопротивления. Институт-хранитель: ВНИИМ.
Статическое и динамическое сопротивление[править | править код]
В теории нелинейных цепей используются понятия статического и динамического сопротивлений. Статическим сопротивлением нелинейного элемента электрической цепи в заданной точке его ВАХ называют отношение напряжения на элементе к току в нем. Динамическим сопротивлением нелинейного элемента электрической цепи в заданной точке его ВАХ называют отношение бесконечно
малого приращения напряжения к соответствующему приращению тока.
См. также[править | править код]
- Сверхпроводимость
- Закон Ома
- Закон Барлоу
- Удельное электрическое сопротивление
- Электрическая проводимость
- Отрицательное сопротивление
- Внутреннее сопротивление
- Импеданс
- Волновое сопротивление
- Активное сопротивление
- Реактивное сопротивление
Примечания[править | править код]
- ↑ Электрическое сопротивление — статья из Большой советской энциклопедии.
- ↑ Василий Петров – основоположник отечественной электротехники // /infourok.ru.
- ↑ CRC Handbook of Chemistry and Physics, 92nd Edition. — Ed. William M. Haynes. — 2011. — ISBN 978-1-4398-5511-9
- ↑ Б. М. Яворский, А. А. Детлаф. — Справочник по физике для инженеров и студентов вузов. — М.: Наука, 1968. — 939 с.
- ↑ Иногда в англоязычной литературе сименс называют mho («перевёрнутое» название обратной единицы ohm), соответственно для СГСЭ и СГСМ — statmho (=statsiemens) и abmho (=absiemens).
- ↑ 1 кОм в модели, принятой в стандарте IEEE Std 80 Архивная копия от 23 августа 2011 на Wayback Machine
- ↑ Новиков С. Г. Действие электрического тока на человека. Московский энергетический институт. Дата обращения: 2013-25-04. Архивировано из оригинала 19 июня 2014 года.
Ссылки[править | править код]
- Таблица удельного сопротивления проводников
- Электрическое сопротивление проводников
Литература[править | править код]
- В. Г. Герасимов, Э. В. Кузнецов, О. В. Николаева. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.
Для изучения зависимости электрических параметров соберём электрическую цепь, изображённую на схеме (рис.(1)).
Состав схемы (по часовой стрелке по ходу электрического тока):
- источник электрического напряжения (тока);
- электрический ключ для размыкания;
- последовательно подключённый амперметр для измерения силы тока в цепи;
- сопротивление (спираль никелиновой проволоки);
- вольтметр, подключённый параллельно к сопротивлению.

Рис. (1). Первая схема электрической цепи
При замыкании цепи отметим показания приборов. Используя регулятор напряжения на источнике, изменим напряжение в два раза. При этом показания вольтметра и амперметра также изменятся в два раза. Продолжим увеличивать напряжение на источнике. Наблюдения показывают, что при увеличении напряжения в (3) раза, вольтметр покажет увеличение напряжения на спирали в три раза. Во столько же раз увеличится и сила тока.
Опыт показывает зависимость изменения силы тока от приложенного напряжения.
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника: (Ibacksim U).
Эту зависимость можно изобразить графически:
Рис. (2). График зависимости силы тока в проводнике от напряжения между концами этого проводника
При включении в электрическую цепь источника тока различных проводников и амперметров увидим, что для разных проводников показания амперметров различны, значит, сила тока для каждого проводника отличается.

Рис. (3). Электрическая схема с набором различных сопротивлений (AB), (CD), (EF)
Графики тоже будут отличаться.

Рис. (4). Графики зависимости силы тока от напряжения для сопротивлений (AB), (CD), (EF)
Вольтметр подключим поочерёдно к концам этих проводников. Увидим равные значения напряжения. Значение силы тока на участке цепи пропорционально разности потенциалов на его концах и зависит от рода вещества проводника. Отличие электрических параметров (U) и (I) связано с тем, что проводники имеют разное электрическое сопротивление.
Сопротивление проводника равно (1) Ом, если в проводнике при напряжении на концах (1) вольт протекает сила тока (1) ампер:
([R]=1) Ом;
(R=frac{U}{I});
Единицы измерения применяют с кратными приставками: миллиом (мОм), килоом (кОм), мегаом (МОм).
(1) мОм = (0,001) Ом;
(1) кОм = (1000) Ом;
(1) МОм = (1 000 000) Ом.
Почему существует сопротивление? Движению электронов под действием поля мешают ионы кристаллической решётки металла.
Электрический ток — направленное движение заряженных частиц.
В середине (XIX) века Джеймс Кларк Максвелл объединил исследования Вольта, Эрстеда, Ампера, Ома, Фарадея в классическую электродинамику. Учёные придерживались гипотезы, что электричество переносят положительные частицы. Все законы строились на этом предположении.
За направление электрического тока принимают движение положительно заряженных частиц.
(29) апреля (1897) года Джозеф Джон Томсон выступил на заседании Королевского общества с докладом о катодных лучах, что и считается датой открытия электрона.
Электронный ток — направленное движение электронов.
В металлах электрический ток переносится электронами. Положительные ионы, связанные узлами кристаллической решётки, перемещаться не могут. Электроны, перемещаясь между ионами, сталкиваются с ними, отскакивают обратно, что уменьшает общий поток электронов.
Электрическое сопротивление — физическая величина, отражающая свойство проводника препятствовать электронному току.
(R=frac{U}{I});
([R]=1~frac{В}{А}=1~Ом).
Чтобы узнать, как зависит сила тока в цепи от сопротивления, обратимся к опыту (рис.(4)).

Рис. (5). Электрическая цепь с аккумулятором
На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор.
- Напряжение (2) В на концах резисторов постоянно. Это подтверждают показания вольтметра, подключенного параллельно к резистору.
- Используются три постоянных резистора сопротивлениями (1), (2) и (4) Ом, которые подключаются в цепь поочерёдно.
- Сила тока в цепи измеряется амперметром, который подключен последовательно с резистором.
Таблица (1). Результаты опыта
| Напряжение на концах проводника, В | Сопротивление проводника, Ом | Сила тока в цепи, А |
|
(2) |
(1) |
(2) |
|
(2) |
(2) |
(1) |
|
(2) |
(4) |
(0,5) |
По опытным данным (табл.(1)) прослеживается закономерность, которую обнаружил ещё в (1827) году Георг Ом.
Сила тока в проводнике обратно пропорциональна сопротивлению проводника: (Ibacksim frac{1}{R}).
В честь этого ученого открытый им закон называют его именем — закон Ома для участка цепи.
Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи:
где I — сила тока, U — напряжение, R — сопротивление.
При изменяющемся сопротивлении и постоянном напряжении на участке зависимость силы тока от сопротивления будет гиперболической:

Рис. (6). График зависимости силы тока от сопротивления проводника
Определить сопротивление проводника можно несколькими способами:
1. при помощи амперметра и вольтметра;
2. при помощи омметра;
3. при помощи мультиметра, который эксплуатируется в режиме омметра.
Таблица (2). Способы измерения сопротивления
|
амперметр и вольтметр |
омметр |
мультиметр в режиме омметра |
|
Рис. 7. Амперметр и вольтметр |
Рис. 8. Омметр |
Рис. 9. Мультиметр |
|
|
|
|

Рис. 10. Обозначение омметра в цепи (или мультиметра в режиме измерения сопротивления)
Источники:
Рис. 2. График зависимости силы тока в проводнике от напряжения между концами этого проводника. © ЯКласс.
Рис. 4. Графики зависимости силы тока от напряжения для сопротивлений AB, CD, EF. © ЯКласс.
Рис. 6. График зависимости силы тока от сопротивления проводника. © ЯКласс.
Рис. 7. Старые советские измерительные приборы, Creative Commons Zero 1.0 License, https://openclipart.org/detail/205486/voltmeter-and-ammeter.
Рис. 8. Автор: Сергин Владимир Александрович – Собственный фотоснимок автора, Общественное достояние, https://commons.wikimedia.org/w/index.php?curid=4353228.
Рис. 9. Мультиметр. © ЯКласс.
Рис. 10. Указание авторства не требуется: 2021-06-07, бесплатно для коммерческого использования, https://clck.ru/VLDy3/.
По какой формуле можно найти сопротивление?
Анонимный вопрос
2 ноября 2018 · 61,6 K
Лучший ответ на 99.9% вопросов: “Поисковик в помощь”. · 2 нояб 2018
Самая простая формула для нахождения сопротивления – закон Ома для участка цепи.
R=U/I, где
R – сопротивление,
U – напряжение,
I – сила тока.
8,4 K
Комментировать ответ…Комментировать…
Рассчитайте сопротивление лампы накаливания в рабочем состоянии R и в выключенном состоянии R20 , а также токи в рабочем состоянии Iраб и в холодном состоянии I20 . Лампа мощностью 100 Вт включается в сеть напряжением 220 В. Температура нити лампы в холодном состоянии +200 С, в горячем – +30000 С. Материал нити – вольфрам. Его температурный коэффициент сопротивления – α=0,0045 1/К.
8,0 K
Комментировать ответ…Комментировать…
Сопротивление вычисляется по формуле (Закон Ома):
R = U/I
R — само сопротивление (Ом)
U — напряжение (Вольт)
I — сила тока (Ампер)
Т.е в системе СИ:
[R] = B/ A = Ом Читать далее
26,9 K
Комментировать ответ…Комментировать…
Закон Ома
Закон Ома — главный закон электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом. Вместе с экспертом разберем формулировку, формулу и задачи на закон Ома с решением

Физика — наука эмпирическая. Ее основные законы вытекают из практического опыта и частенько много лет не имеют теоретических обоснований. Именно так обстоит дело с главным законом электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом.
Электрические явления люди наблюдали сотни лет. Но никак не связывали между собой заряженность потертого янтаря и молнию. Только на исходе XVIII столетия электричество стали внимательно исследовать. В 1795 году Алессандро Вольта изобрел «вольтов столб», химическую батарею, и обнаружил появление тока в проводнике, соединяющем ее полюса. Сферы применения электричества стремительно множились, и появилась острая необходимость в расчетных формулах для инженеров. Эту задачу решали многие ученые, но первым сформулировал главную формулу электротехники именно Георг Ом. Он ввел в обиход понятие сопротивления и опытным путем установил зависимость между основными характеристиками электрической цепи.
Определение закона Ома простыми словами
Электрическая цепь состоит из двухполюсного источника напряжения, то есть батареи, аккумулятора или генератора. Если полюса источника соединить проводами, то по ним потечет электрический ток. Его величина определяется сопротивлением проводников. Наглядное представление этой зависимости — обыкновенный водопровод. Аналогом источника напряжения является насос или водонапорная башня, создающая давление в магистрали, количество воды, прошедшее по трубе, — подобие силы тока, а кран соответствует сопротивлению. Полностью открытый, он не ограничивает поток, по мере закручивания отверстие для воды уменьшается, пока не закроется совсем.
Закон Ома для участка цепи
Опытным путем исследователь установил взаимосвязь характеристик электрической цепи. Классическая формулировка закона Ома звучит так:
«Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению».
Формула закона Ома для участка цепи

В таком виде закон Ома приведен в школьных учебниках физики. Согласно этой простой формуле, для определения уровня тока в проводнике достаточно величину напряжения на его сторонах разделить на некий условно постоянный коэффициент, то есть на сопротивление. Почему «условно»? Потому что величина сопротивления может меняться в зависимости от температуры. Поэтому, кстати, лампы накаливания чаще всего перегорают при включении. Сопротивление холодной спирали ниже, чем нагретой, скачок тока при подаче напряжения вызывает ее резкое расширение и разрыв. Но если этот момент преодолен и нить накала уцелела, то ее сопротивление растет, и ток ограничивается. А при температуре жидкого гелия, например, сопротивление падает до нуля, наступает сверхпроводимость.
Закон Ома для замкнутой полной цепи
Предыдущая формулировка годится только для участка цепи, где отсутствует сам источник электродвижущей силы. В реальности ток течет по замкнутому контуру, где обязательно есть батарея или генератор, имеющий собственное внутреннее сопротивление. Поэтому формула закона Ома для полной цепи выглядит несколько сложнее
Формула закона Ома для замкнутой полной цепи

Применение закона Ома
Георг Ом дал в руки инженеров средство для решения задач, связанных с электрическими цепями. Тепловые и световые приборы, электродвигатели, генераторы, линии электропередач, кабели связи рассчитываются на основе этой простой формулы. Нет такой области электротехники, где она не находит применения. Даже в радиотехнике используется закон Ома, но в дифференциальной форме. «Все гениальное — просто», как считали Еврипид, Леонардо да Винчи, Наполеон Бонапарт и Альберт Эйнштейн, несомненные гении. Закон Ома целиком и полностью подтверждает эту истину.
Сила трения
Единицы измерения силы трения, от чего она зависит и какие виды существуют
подробнее

Задача на закон Ома с решением
Задача для участка электрической цепи
Электрочайник, включенный в сеть с напряжением 220 В, потребляет ток 1,1 А. Каково сопротивление электрочайника.
Дано:
U = 220 В
I = 1,1 А
Решение:
Согласно закону Ома для участка цепи:
R=U/I=220/1,1=200 Ом
Ответ: R = 200 Ом.
Задача для полной замкнутой цепи
Источник постоянного тока с ЭДС E = 24 В и внутренним сопротивлением r = 1,5 Ом замкнут на внешнее сопротивление R = 11 Ом. Определить силу тока в цепи.
Дано:
Е=24 В, r=1,5 Ом, R = 11 Ом
Решение:
По закону Ома для замкнутой цепи: I = E/(R + r) = 24/(11+1,5) = 1,92 А.
Ответ: I=1, 92 А.
Популярные вопросы и ответы
Отвечает Николай Герасимов, старший преподаватель физики в Домашней школе «ИнтернетУрок».
Сколько всего законов Ома в физике?
Существует два закона Ома: закон Ома для участка цепи и закон Ома для полной (замкнутой) цепи. Первый связывает сопротивление участка, силу тока в нём и разность потенциалов (напряжение) на его концах. Кроме того, в нем отражено наличие в цепи источника тока.
Второй учитывает и потребителей электрического тока (электрические лампы, обогреватели, телевизоры и так далее), и его источники (генераторы, батарейки, аккумуляторы). Дело в том, что любой источник тока обладает внутренним сопротивление, которое влияет на силу тока. Именно это и учитывается в законе Ома для полной (замкнутой) цепи.
При каких условиях выполняется закон Ома?
Согласно закону Ома, существует линейная зависимость между силой тока в участке цепи и напряжением на его концах. Он отлично выполняется для металлических проводников при любых напряжениях, а вот для тока в вакууме, газе, растворах или расплавах электролитов, полупроводниках линейная зависимость нарушается, и применять закон Ома в том виде, в котором его изучают в школьном курсе, уже нельзя.
Для чего нужен закон Ома?
Трудно переоценить значимость этого закона. Он позволил производить расчет электрических цепей, без которых практически невозможно представить жизнь современного человека, так как они лежат в основе любого электроприбора, начиная от обычной лампы накаливания и заканчивая самыми современными компьютерами.
В каком классе проходят закон Ома?
В школьном курсе ученики впервые знакомятся с электрическими явлениями и законом Ома для участка цепи в 8 классе. Более подробно о причинах возникновения электрического тока и его источниках ученики знакомятся в курсе старшей школы (10 или 11 класс, в зависимости от программы). Здесь же ученики впервые встречаются и с законом Ома для полной (замкнутой) цепи.
Расчет сопротивления проводника


4.6
Средняя оценка: 4.6
Всего получено оценок: 119.
4.6
Средняя оценка: 4.6
Всего получено оценок: 119.
Сопротивление проводника ограничивает величину тока в электрической цепи. Чем больше величина сопротивление, тем меньше ток. Расчет сопротивления проводника можно произвести двумя способами: первый способ заключается в использовании формулы закона Ома, а второй вариант расчета подразумевает знание геометрических размеров проводника и удельного сопротивления вещества, из которого он сделан.
Почему проводник “сопротивляется”?
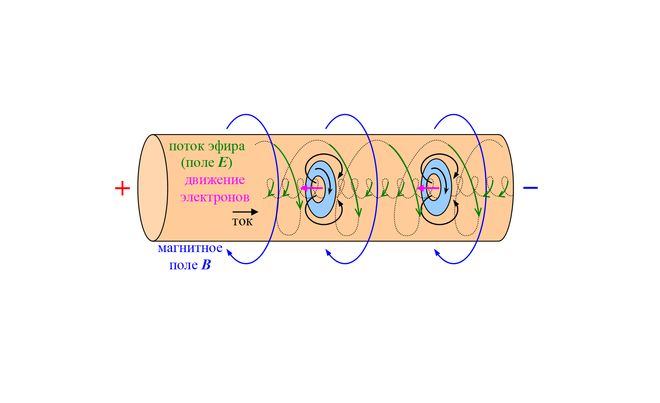
Напряжение U, поданное на концы проводника, создает внутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем самым электрический ток цепи.
В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию. Масса атома превосходит массу электрона в тысячи раз, поэтому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).
Таким образом возникает сопротивление протеканию (нарастанию) тока.
Расчет сопротивления с помощью закона Ома
Немецкий физик Георг Ом в 1826 г. обнаружил, что отношение напряжения U между концами металлического проводника, являющегося участком электрической цепи, к силе тока I есть величина постоянная:
$ R={U over I}=const $ (1),
где:
U — напряжение, В;
I — сила тока, А;
R — сопротивление, Ом.
Эту величину стали называть электрическим сопротивлением. Пользуясь этой формулой, можно экспериментально определить величину неизвестного сопротивления.
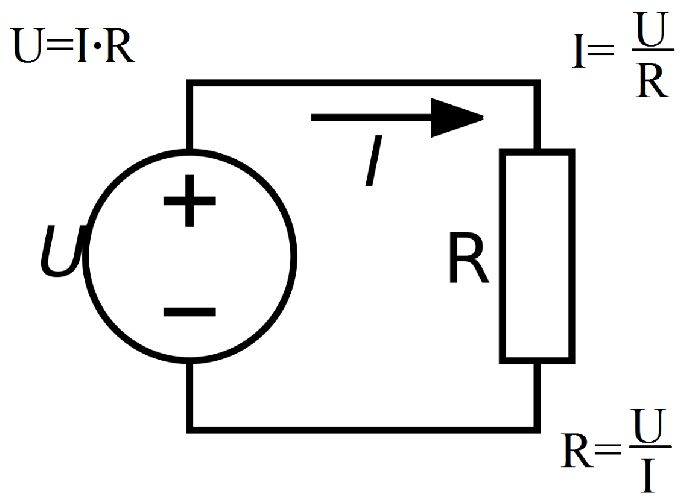
Для этого амперметром измеряется величина электрического тока через сопротивление, а вольтметром — напряжение на участке цепи. Далее, применяя формулу (1), вычисляется значение R.
Единица измерения названа в честь Георга Ома. Электрическим сопротивлением 1 Ом обладает участок цепи, на котором при силе тока 1 А напряжение равно 1 В:
$$ 1 Ом = { 1 Вover 1 A} $$
Расчет с помощью удельного сопротивления
Расчет сопротивления проводника можно произвести без измерения величин напряжения и тока. Но для этого необходимо знать дополнительную информацию о проводнике.
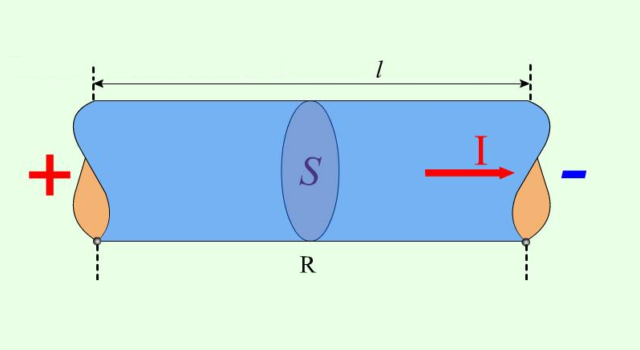
Георг Ом и другие исследователи опытным путем определили, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S. Эту закономерность можно описать формулой расчета сопротивления проводника:
$ R = ρ *{ Lover S} $ (2)
Коэффициент ρ был назван удельным сопротивлением. Эта физическая величина отражает особенности конкретного вещества, которые зависят от плотности вещества, кристаллической структуры, строения атомов и других внутренних параметров. Расчет удельного сопротивления проводника производить каждый раз необязательно, так как для большинства веществ удельные сопротивления измерены и сведены в справочные таблицы, которые можно найти в бумажных справочниках или в их интернет-версиях.
Но если такая необходимость возникнет, то из формулы (2) можно получить следующую формулу (3), и по ней рассчитать ρ:
$ ρ = R*{ Sover L } $ (3)
Серебро имеет одно из самых низких значений ρ, равное $ 0,016 {Ом*мм^2over м} $. Этим объясняется использование такого довольно дорогого металла для пайки особенно важных радиодеталей (микросхем, микропроцессоров, электронных плат), которые должны как можно меньше нагреваться в процессе работы.

Что мы узнали?
Итак, мы узнали, что расчет сопротивления проводника можно произвести двумя способами. Первый расчет проводится с помощью формулы закона Ома после измерения величин напряжения и тока. Для второго расчета необходима информация о геометрических размерах проводника и его удельном сопротивлении.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 119.
А какая ваша оценка?





