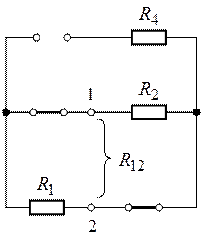
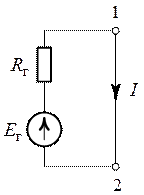
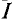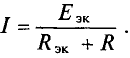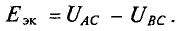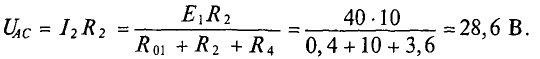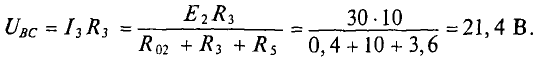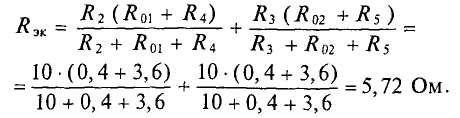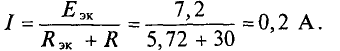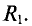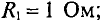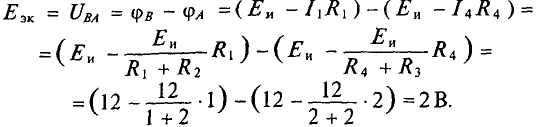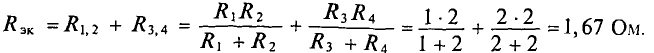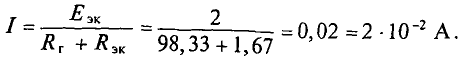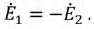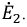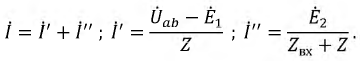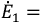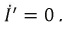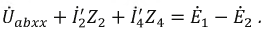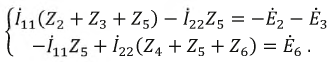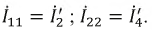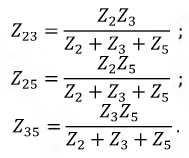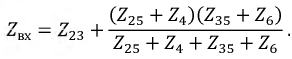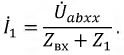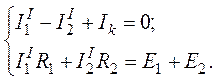Метод эквивалентного генератора:
Метод эквивалентного генератора рационально применять в случае необходимости определения тока (напряжения, мощностн и др.) только одной ветви сложной электрической цепи.
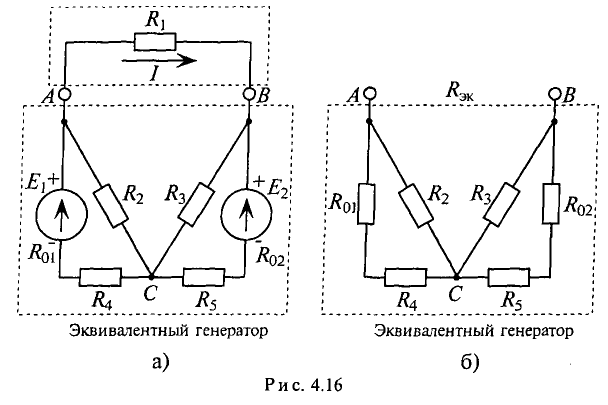
Для этой цели разбивают сложную электрическую цепь на две части — на сопротивление R, ток которого
Активным этот двухполюсник называют потому, что в нем имеется источник ЭДС. Этот активный двухполюсник обладает определенной ЭДС
Ток в резисторе с сопротивлением R определяют по закону Ома
Таким образом, определение тока 
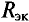
Величина ЭДС 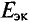
Внутреннее сопротивление эквивалентного генератора 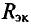
Практически для определения внутреннего сопротивления эквивалентного генератора измеряют амперметром ток между точки А и В работающего двухполюсника при коротком замыкании так как сопротивление амперметра настолько мало, что им можно пренебречь. Тогда
где 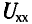
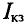
Такой метод практического определения внутреннего сопротивления эквивалентного генератора 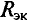
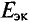
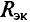
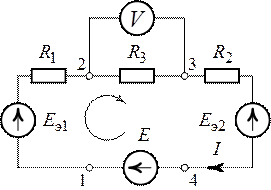
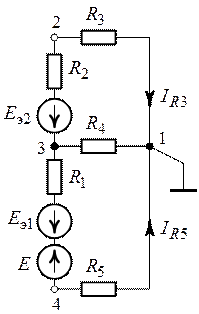
Пример 4.12
Определить ток в сопротивлении 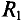
Решение
Для определения тока 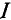
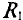
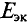
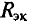
Знак «минус» обусловлен тем, что источники в схеме включены встречно и потенциал в точке А больше потенциала в точке В, так как 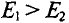
Напряжение
Напряжение
Следовательно, 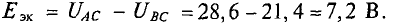
Искомый ток
Такой же ток получен в примере 4.6 на сопротивлении
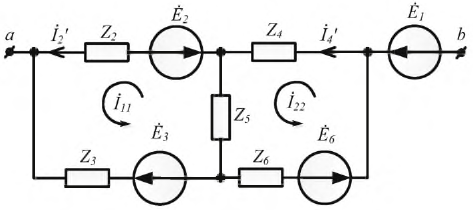
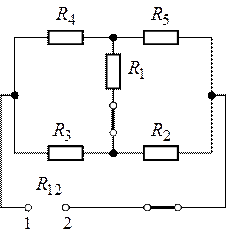
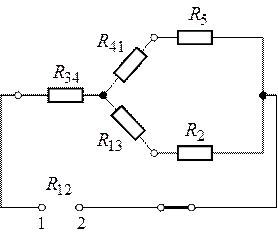
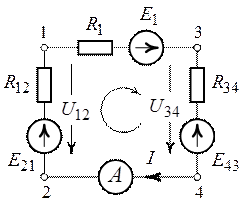
Пример 4.13
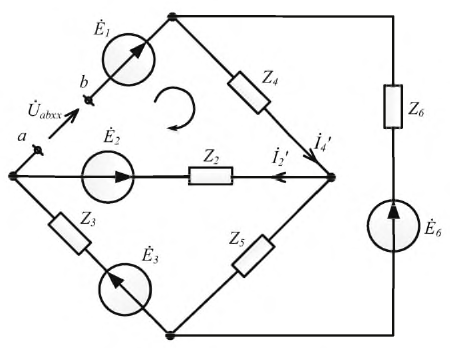
В схеме рис. 4.17а сопротивления плеч моста равны
Сопротивление гальванометра Rr = 98,33 Ом, ЭДС источника 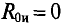
Решение
Для определения тока в цепи гальванометра 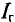
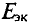
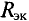
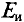
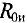
Для определения ЭДС эквивалентного генератора 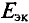
Тогда
При замене источника ЭДС 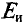
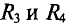
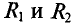
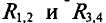
Тогда ток в ветви с гальванометром, который направлен из точки В в точку А, т. е. из точки с большим потенциалом в точку с наименьшим потенциалом (рис. 4.17а), будет равен
Метод эквивалентного генератора (активного двухполюсника)
Все методы, рассмотренные ранее, предполагали расчет токов одновременно во всех ветвях цепи. Однако в ряде случаев бывает необходимым контролировать ток в одной отдельно взятой ветви. В этом случае применяют для расчета метод эквивалентного генератора.
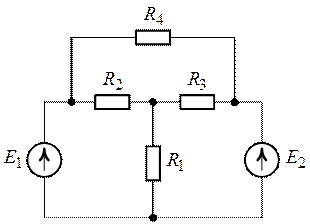
Пусть дана некоторая электрическая цепь, которую заменим активным двухполюсником (рис. 3.10), оставив только ветвь 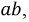
Сначала, введем в ветвь 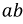
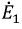
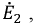
Затем, используя принцип наложения, данную цепь представим суммой двух цепей. В первой оставим все источники активного двухполюсника и источник ЭДС 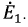
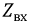
Рис. 3.10. Преобразование исходного двухполюсника в сумму двух цепей
На основании принципа наложения ток ветви
Поскольку 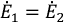
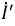
Напряжение на зажимах источника в режиме холостого хода численно равно его ЭДС. Тогда активный двухполюсник с источником 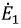
Рис. 3.11. Схема замещения активного двухполюсника
В этой схеме ЭДС 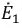
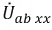
Таким образом, ток в ветви
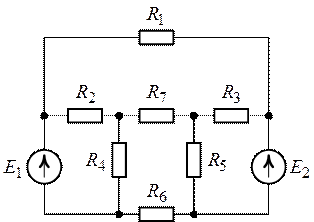
Пусть дана цепь (рис. 3.12), в которой необходимо рассчитать ток 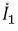
Рис. 3.12. Исходная цепь
Последовательность расчета:
1. Разомкнем ветвь с сопротивлением 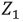
2. Зададим положительное направление 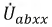
3. Токи 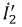
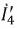
Тогда
4. Определим эквивалентное сопротивление пассивного двухполюсника. Для этого мысленно закоротим все источники ЭДС исходной цепи, оставляя в схеме для реальных источников их внутренние сопротивления.
В образовавшейся схеме пассивного двухполюсника невозможно определить эквивалентное сопротивление относительно зажимов 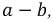
Преобразуем, например, «треугольник» сопротивлений 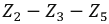
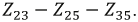
Рис. 3.14. Схема пассивного двухполюсника
Сопротивления этой схемы будут:
Входное сопротивление цепи 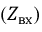
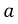
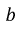
Окончательно имеем:
- Теоремы теории цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Метод свертывания электрической цепи
- Метод преобразования схем электрических цепей
- Параллельное соединение генераторов
- Метод узловых и контурных уравнений
Продолжаем решать задачи по основам электротехники(ТОЭ). В сегодняшней статье будет метод, по которому задают больше всего вопросов. Это понятно, поскольку этот метод является, на мой взгляд, самым сложным методом расчета сложных электрических цепей постоянного тока.
В свое время и я его понял далеко не сразу. Поэтому рассмотрим каждый пункт подробно. Начнём с того, что необходимо знать и понимать для успешного решения этим методом.
1) Закон Ома. Без него не только этот метод, но и многие другие задачи не решаются.
2) Правила последовательного и параллельного соединения резисторов.
3) Хотя бы один любой метод расчета сложных цепей, то есть по Кирхгофу, контурными токами, узловыми потенциалами и так далее.
4) И, самое важное, для этого метода – это умение строить потенциальную диаграмму. Именно потенциальную, а не векторную. Потому что векторная диаграмма строится для цепей переменного тока, а мы рассматриваем цепь постоянного тока. Строить мы конечно потенциальную диаграмму тут не будем. Но чтобы её построить, необходимо знать два основных правила, которые нужны и в методе эквивалентного генератора.
Первое правило: ток течет через резистор всегда от большего потенциала к меньшему.
Второе правило: у ЭДС “+” всегда больше “-“.
Давайте перейдем к решению задачи. На конкретном примере всегда понятнее.
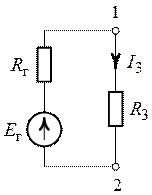
Имеется данная схема цепи. Даны ЭДС и сопротивления резисторов. Требуется найти ток I3 методом эквивалентного генератора.
Поскольку нужно найти ток I3, который протекает по третьей ветви, нам нужно обеспечить холостой ход, сделав обрыв той части цепи, по которой протекает интересующий нас ток. То есть делаем обрыв третьей ветви. Это ветвь подключена между точками “c” и “d”. Сами точки мы не трогаем, а лишь убираем только ветвь.
В точках “c” и “d” узлов нет, поскольку там сходятся только по две ветви. А узел – это место соединения трех и более ветвей.
Наша цель – определить две величины:
1) Напряжение Ucd между точками “c” и “d”, оно же ЭДС эквивалентного генератора(Еэг). И, поскольку, мы обеспечили холостой ход, оборвав третью ветвь, все токи и напряжения будем указываем на схеме с индексом “х”, при коротком замыкании указывают кз.
2) Сопротивление эквивалентного генератора rэг, оно же сопротивление между точками “c” и “d”. А определить это сопротивление нам поможет правило последовательного и параллельного соединения резисторов.
В первом случае, когда мы ищем напряжение Ucd(оно же Еэг), применим один любой метод расчета сложных электрических цепей.
Сложной считается цепь, если в ней два и более источников энергии.
В данном случае два источника. Давайте для начала найдём, каким будет напряжение между точками “c” и “d”. Воспользуемся методом контурных токов.
Получили два неизвестных контурных тока. В цепи, в общем случае, три ветви и два узла. Поскольку две неизвестные, значит составим два уравнения и из этих уравнений найдём контурные токи I11 и I22.
Напряжение Ucd снимается с точек “c” и “d”, а между ними включены резисторы r2 и r4. Нам остается найти напряжение на этих элементах. Их сопротивления известны. Найдем токи I4 и I2, умножим эти токи на сопротивления, получим напряжения.
Контурные токи мы уже нашли. Тогда токи ветвей:
I2x=-I22=0.3333 A; I4x=-I11=0.2222 A;
Напряжения на резисторах r4 и r2:
U4x=I4x*r4=0.2222*4=0.8888 B; U2x=I2x*r2=0.3333*2=0.6666 B;
Так как оба тока направлены в одну и ту же сторону, тогда
Ucdx=U2x+U4x=0.6666+0.8888=1.5554 B;
А теперь самое главное в этом методе. Почему именно взяли U2 + U4? Почему не -U2-U4? А здесь нужно воспользоваться правилом, что ток течет от большего потенциала к меньшему и стрелкой под напряжением Ucdx мы указали, что φс больше чем φd. А так как нам нужно найти ЭДС эквивалентного генератора, давайте представим именно эту часть схемы отдельно.
Предположим, что φc больше чем φd и стрелкой под напряжением укажем направление от большего потенциала к меньшему.
Заменим напряжение Ucd на Eэг. Еэг будет направлен от “d” к “c”(минусом на “d”, а плюсом на “c”, потому что “плюс” у ЭДС всегда больше чем “минус”).
Запишем второй закон Кирхгофа:
I4x*r4+I2x*r2=-Еэг
В данном случае ЭДС эквивалентного генератора Еэг получится отрицательным. Можно в принципе оставить как есть, это ошибкой не будет. Но если мы на данном этапе поменяем направление ЭДС эквивалентного генератора на этой схеме, тогда мы получим положительное значение ЭДС эквивалентного генератора. Или оставляем как есть. Как поступить – без разницы. Давай поменяем направление.
Тогда I4x*r4+I2x*r2=Еэг; Еэг=U4x+U2x=0.8888+0.6666=1.5554 B;
Это говорит о том, что потенциал в точке “d” большие чем в точке “с”. Это и так изначально было понятно cудя по тому, как мы направили токи. А ток течет от большего потенциала к меньшему, т. е. мы изначально указали точки от “d” к “e” и от “e” к “c” и эти токи получились положительными. Значит мы их верно расставили.
С ЭДС эквивалентного генератора мы разобрались, осталось посчитать сопротивление эквивалентного генератора (сопротивление между точками “c” и “d”). Для этого мы должны исключить все источники энергии и оставить только резисторы.
Когда исключаем ЭДС, на его месте остается короткое замыкание (это в случае если источник напряжения идеальный и его внутреннее сопротивление равно нулю). Если имеется какое-то внутреннее сопротивление, то оно остается в ветви, это нужно учитывать. Если в схеме цепи есть источник тока, то после его исключения на его месте остается обрыв, поскольку его внутреннее сопротивление бесконечно большое. А после исключения источника тока, его внутреннее сопротивление остается в схеме, и так как оно бесконечно большое, это равносильно обрыву.
В схеме, изображенной на рисунке 9, применяя правила последовательного и параллельного соединения резисторов:
r4 и r5 включены параллельно;
r1 и r2 включены параллельно;
r45 и r12 включены последовательно;
Численные значения r45, r12 и rэг рассчитаны на рисунке 9.
Осталось изобразить последнюю схему, в которой будет протекать ток I3.
Ток получился отрицательным, значит на самом деле он течет не вправо, а влево от “d” к “c”. Это и понятно, поскольку, как мы ранее выяснили, φd больше чем φc, и, повторюсь, ток течет от большего потенциала к меньшему.
Таким образом решаются задачи методом эквивалентного генератора.
Если понравилась статья, подписывайтесь на канал и не пропускайте новые публикации.
Читайте также:
1. Как электроэнергия передается от электростанций до наших домов;
2. Что такое электрический ток – простыми словами;
Страницы работы
Содержание работы
6.
МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
(ЭКВИВАЛЕНТНОГО
ИСТОЧНИКА)
Целесообразность использования данного метода
становится очевидной, в случае если расчет электрической цепи ограничен в определении
тока только одной ветви. В этом случае вся цепь относительно ветви с
интересующим током заменяется эквивалентной схемой. Таким образом, основной
расчет сводится к определению двух параметров эквивалентной схемы – ЭДС и
сопротивления эквивалентного генератора.
Задача 6.1.
Для схемы цепи (рис. 6.1) методом эквивалентного
генератора найти ток ветви с сопротивлением ,
если ,
,
,
,
,
,
.
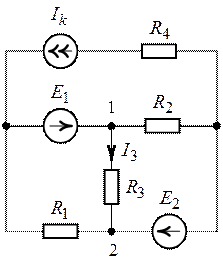
Рис. 6.1. Рис.
6.2.
Решение.
1. Выделим ветвь с сопротивлением и обозначим
ток (рис.6.1) .
2. Всю цепь, рис. 6.1, относительно ветви с
сопротивлением , представим эквивалентным
генератором с источником ЭДС равным и сопротивлением
(рис. 6.2).
Согласно схеме (рис. 6.2) интересующий ток в ветви
определиться как
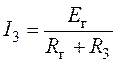
т.е.
решение задачи сводится к определению двух параметров эквивалентного генератора
и
.
3. Найдем ЭДС генератора. По определению равно напряжению
между узловыми точками 1 и 2
разомкнутой ветви с сопротивлением (рис. 6.3).
Рис. 6.3.
Рис. 6.4.
Для этого в схеме (рис. 6.3) определим токи и
. На
основании законов Кирхгофа получим систему:
Из системы найдем
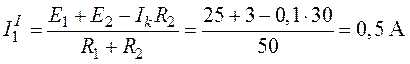
.
На основании второго закона Кирхгофа для указанного в
схеме (рис. 6.3) направления обхода контура получим
.
4. Найдем сопротивление генератора. По определению равно входному сопротивлению
между узловыми точками 1 и 2 разомкнутой
ветви с (рис. 6.3). Расчет сопротивления
производим при закороченных источниках
ЭДС ,
и
разомкнутом источнике тока , рис. 6.4.
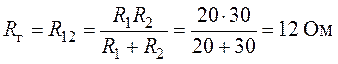
5. Окончательно определяем ток :
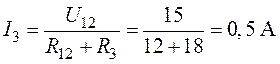
Задача 6.2.
Определить методом эквивалентного генератора ток в
ветви с источником ЭДС (рис. 6.5). Дано:
,
,
,
,
,
,
.
Рис. 6.5. Рис.
6.6.
Решение
1. Обозначим ток в
ветви с источником ЭДС (рис. 6.5).
2. Применив теорему об эквивалентном генераторе, ток в
ветви, имеющей нулевое сопротивление согласно схеме (рис. 6.6):
3. Найдем ЭДС генератора. Разомкнем ветвь с источником
(рис.6.7) и найдем напряжение
между точками 1 и 2.
Предварительно выполним расчет токов и
в
схеме (рис. 6.7).
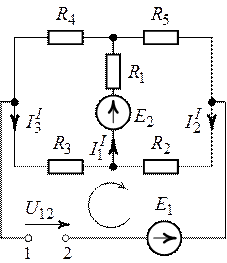
Рис. 6.7.
Рис. 6.8.
Ток в
неразветвленной части схемы
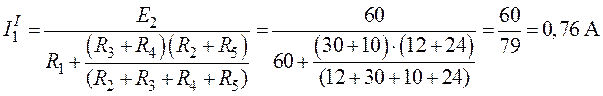
Токи и
в разветвленной части схемы:
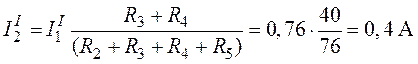
.
На основании второго закона Кирхгофа для обозначенного
на схеме (рис. 6.7) контура запишем:
,
откуда
.
4. Найдем сопротивление генератора , которое равно входному
сопротивлению между точками 1 и 2 (рис.
6.8) (при замкнутых источниках ЭДС ,
).
Преобразуем треугольник сопротивлений ,
и
(рис.6.8) в эквивалентную звезду
(рис. 6.9).
Рис. 6.9.
Величины сопротивлений эквивалентной звезды (рис. 6.9):
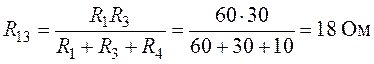
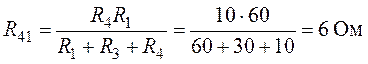
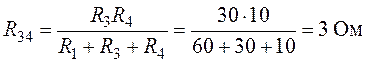
Согласно выполненным преобразованиям окончательно
получим (рис. 6.9):
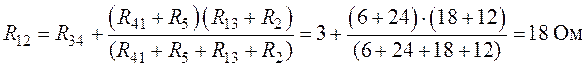
5. Ток в ветви с источником определится
как
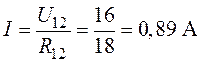
Задачи для самостоятельного решения
Задача 6.3. Методом
эквивалентного генератора для схемы (рис. 6.10) определить ток в ветви с
сопротивлением . Дано
,
,
,
,
,
.
О т в е т: (
,
).
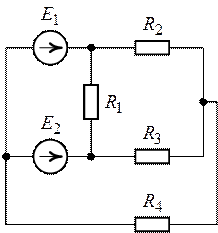
Рис. 6.10.
Рис. 6.11.
Задача 6.4. Для
цепи (рис. 6.11) методом эквивалентного генератора определить ток в ветви с
сопротивление , если
,
,
,
,
.
О т в е т: (
,
)
Задача 6.5. Определить
обозначенный в схеме (рис. 6.12) ток по методу эквивалентного генератора, если ,
,
,
,
,
,
,
.
О т в е т: (
,
)
Задача 6.6. Для
схемы (рис. 6.13) методом эквивалентного генератора определить обозначенный в
ветви ток, если ,
,
,
,
,
.
О т в е т: (
,
)
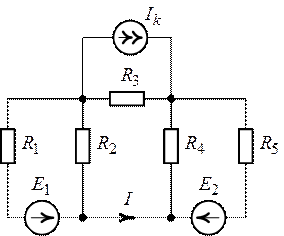
Рис. 6.12.
Рис. 6.13.
Задача 6.6. Рассчитать
обозначенный в схеме (рис. 6.14) ток, используя метод эквивалентного
генератора, если ,
,
,
,
,
.
О т в е т: (
,
)
Задача 6.4. Для
цепи (рис. 6.15) методом эквивалентного генератора определить ток в ветви с
сопротивление , если
,
,
,
,
,
,
,
,
.
О т в е т: (
,
)
Рис. 6.14.
Рис. 6.15.
7. ПРИМЕНЕНИЕ ЭКВИВАЛЕНТНЫХ ПРЕОБРАЗОВАНИЙ ПРИ
РАСЧЕТАХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Расчет сложных электрических цепей можно упростить
путем различных эквивалентных преобразований активных участков схем содержащих
ветви с идеальными источниками ЭДС и тока. В частях схемы не затронутых
преобразованиями должно выполняться условие неизменности напряжений и токов
ветвей. Упрощение расчета сводится, как правило, к уменьшению числа ветвей или
узлов схемы и, в конечном счете, к сокращению расчетных уравнений.
Задача 7.1.
Для цепи (рис.7.1) требуется определить показание
вольтметра, если ,
,
,
,
.
Внутреннее сопротивление вольтметра принять .
Рис. 7.1. Рис.
7.2.
Решение.
1. Преобразуем источники тока и
(рис. 7.1) в эквивалентные источники
ЭДС ,
(рис.
7.2).
2. Значения ЭДС эквивалентных источников:
;
.
3. Ток, протекающий в контуре (рис. 7.2) найдем на
основании второго закона Кирхгофа
,
откуда
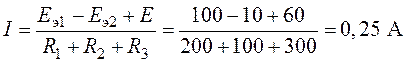
4. Показание вольтметра установленного
в схеме будет соответствовать напряжению на
сопротивлении :
.
Задача 7.2.
Методом узловых потенциалов определить токи в ветвях с
сопротивлениями и
схемы
(рис. 7.3) , если ,
,
,
,
,
,
.
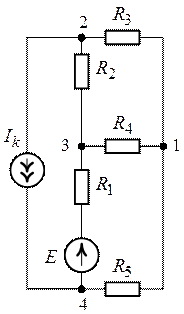
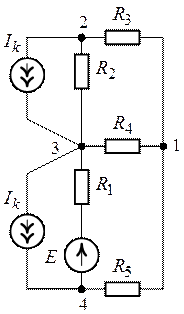
Рис. 7.3. Рис. 7.4. Рис.
7.5.
Решение.
1. Чтобы уменьшить число узлов расчетной схемы и
упростить расчет преобразуем источник тока в
эквивалентные источники ЭДС.
Включая в узле 3 два равных и противоположно
направленных источника тока , получим
эквивалентную схему (рис. 7.4).
После преобразования источников тока в эквивалентные
источники ЭДС получим эквивалентную схеме (рис.7.3) схему представленную на
рис. 7.5.
2. Значения ЭДС эквивалентных источников:
;
.
3. Расчет токов преобразованной схемы (рис. 7.5)
выполним методом двух узлов. Потенциал узловой точки 1 принимаем равным нулю (). Напряжение между узлами 3 и 1
найдем как
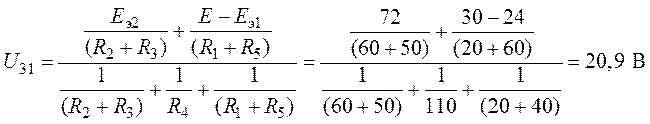
4. Интересующие в схеме токи
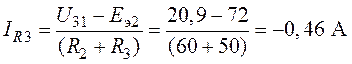
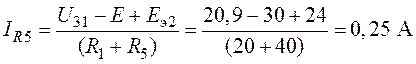
Задача 7.3.
Определить показание амперметра для схемы рис. 7.6, если
,
,
,
,
,
,
,
,
,
.
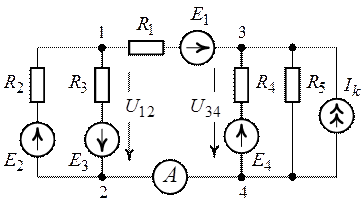
Рис. 7.6. Рис.
7.7.
Решение.
1. Для упрощения расчета воспользуемся
преобразованиями активных участков схем с параллельными ветвями одной
эквивалентной.
2. Эквивалентная ЭДС и
эквивалентное сопротивление двух параллельных
ветвей левой части схемы (рис. 7.6):
Похожие материалы
- Вопросы для защиты отчета по лабораторной работы № 1
- Применение метода наложения к расчету электрических цепей с двумя и более источниками энергии. Метод узловых потенциалов (узловых напряжений) (главы 3-5 учебного пособия “Теоретические основы электротехники в примерах и задачах”)
- Расчет простых цепей при постоянных токах и напряжениях. Расчет сложных цепей с помощью прямого применения законов Кирхгофа (главы 1-2 учебного пособия “Теоретические основы электротехники в примерах и задачах”)
Информация о работе
Активное r и реактивные X сопротивления складываются не арифметически, а геометрически. Их сумма равна гипотенузе треугольника, катеты которого активное и реактивное сопротивления. Реактивное сопротивление в генераторе также, как и аиктвное, препятствует прохождению тока. На нем также происходит падение напряжения (но со сдвигом фазы). Отличие реактивного сопротивления от активного в том, что на реактивном сопротивлении не теряется мощность. При большом внутреннем активном сопротивлении генератора падает КПД. А большое реактивное сопротивление даже полезно в определенных случаях. Оно несколько стабилизирует выходное напряжение при изменении нагрузки и ограничивает ток короткого замыкания.
Для расчета надо иметь данные для двух частот вращения генератора.
Ток, протекающий в цепи при первой частоте вращения равен:
Ток, протекающий при второй, более высокой частоте вращения:
Из этих двух уравнений несложно найти X1 и r
В формулах n1 и n2 – первая и вторая частота вращения генератора. Можно подставлять в об/мин или об/с. Важно, чтобы в одной формуле единицы были одинаковы.
Индуктивное сопротивление X рассчитано для первой, нижней, частоты вращения. Для любой другой частоты вращения его легко пересчитать
В качестве примера рассчитаем внутренние сопротивления двух генераторов. ВГБЖ и ГЗОЗВ.
При скорости вращения 120 об/мин E1 = 23 В, U1 = 19,5 В, I1 = 2,75 А.
При скорости вращения 500 об/мин E2 = 95 В, U2 = 71 В, I2 = 9 А.
Величина реактивного сопротивления при 120 об/мин.

Если E2, U2, I2 подставить для частоты в 300 и 400 об/мин, то значение X120 получатся 1,51 и 1,57 Ом. Среднее значение 1,56 Ом. Точность получается очень хорошая. Но для скорости вращения в 180 об/мин расчет дает отрицательное значение под корнем. На кривой тока видно, что при 180 об/мин точка смещена вверх от плавного хода кривой. Погрешность при измерении характеристик оказалась слишком большой. Для надежного расчета точки надо брать далеко друг от друга по оси скорости вращения.
Посчитать внутреннее активное сопротивление генератора не получается. Сопротивление нагрузки на графиках указано 14 Ом. Но если разделить напряжение на ток, то при 120 и 500 об/мин получится: 19,5/2,75 = 7,1 Ом. 71/9 = 7,9 Ом. Сопротивление нагрузки указано ошибочно. Скорее всего, генератор испытывался под нагрузкой 7 Ом. Повышение величины нагрузочного сопротивления с ростом оборотов связано с тем, что либо сопротивление раскалилось и возросло от нагрева или же сопротивление намотано в катушку и на высоких частотах приобретает заметную индуктивную составляющую. Можно принять сопротивление нагрузки равным 7,5 Ом, тогда внутреннее активное сопротивление генератора равно

С учетом неопределенности сопротивления нагрузки, внутреннее сопротивление лежит в пределах 0,32 – 1,12 Ом.
Индуктивное сопротивление при 500 об/мин, а такие обороты реальны для ветряка, возрастает до 1,56*500/120 = 6,5 Ом и заметно влияет на величину тока в нагрузке. Поэтому его необходимо учитывать при расчетах. Иначе ошибка может быть значительна. Внутреннее активное сопротивление генератора имеет малую величину, и даже такая большая погрешность в его определении мало скажется на величине тока в нагрузке.
На этом графике не показаны кривые тока. Но ток легко вычислить, разделив напряжение на нагрузке, на сопротивление. При сопротивлении наргузки 10 Ом и оборотах 360 и 2000 об/мин получится


Реактивное сопротивление на высоких оборотах у этого генератора будет тоже большим. Этот генератор высокооборотистый. Номинальные обороты около 6000 об/мин. При 2000 об/мин. X2000 = 1,74*2000/360 = 9,7 Ом. При 6000 об/мин. X6000 = 1,74*6000/360 = 29 Ом
Электрика, альтернативная энергия,электрооборудование, внутреннее сопротивление генератора
Источник
Расчёт генератора
Синхронной машиной (СМ) называется двухобмоточная электрическая машина переменного тока, одна из обмоток которой присоединена к электрической сети с постоянной частотой, а вторая – возбуждается постоянным током.
Конструктивное исполнение статора синхронной машины может быть различным в зависимости от назначения и габаритов машины. Так, в многополюсных машинах большой мощности при наружном диаметре сердечника статора более 900 мм пластины сердечника делают из отдельных сегментов, которые при сборке образуют цилиндр сердечника статора. Корпуса статоров крупногабаритных машин делают разъемными, что необходимо для удобства транспортировки и монтажа этих машин.
Роторы синхронных машин могут иметь две принципиально различающиеся конструкции: явнополюсную и неявнополюсную.
У синхронного генератора (IP23) на якоре имеются обмотки, на которые подается электрический ток. Изменяя его величину, можно влиять на магнитное поле, а следовательно, и на напряжение на выходе статорных обмоток. Роль регулятора прекрасно исполняет простейшая электрическая схема с обратной связью по току и напряжению. Благодаря этому способность синхронного генератора «проглатывать» кратковременные перегрузки высока и ограничена лишь омическим (активным) сопротивлением его обмоток, т.е. легче переносят пусковые нагрузки.
Однако у такой схемы есть и недостатки. Прежде всего, ток приходится подавать на вращающийся ротор, для чего традиционно используют щеточный узел. Работая с довольно большими (особенно во время перегрузок) токами, щетки перегреваются и частично «выгорают». Это приводит к плохому их прилеганию к коллектору, к повышению омического сопротивления и к дальнейшему перегреву узла. Кроме того, подвижный контакт неизбежно искрит, а значит, становиться источником радиопомех. И самый основной недостаток низкая степень защиты от внешних воздействий таких как: пыль, грязь, вода, т. к. синхронный генератор охлаждается «протягивая» через себя воздух, соответственно все что находится в воздухе может попадать в генератор.
Если генератор щёточный, чтобы избежать преждевременного износа, рекомендуется время от времени контролировать состояние щеточного узла и при необходимости очищать либо менять щетки. Кстати, после их заменены, желательно дать им время «приработаться» к коллектору, а уж за тем нагружать станцию «по полной программе».
Многие современные синхронные генераторы снабжены безщеточными системами возбуждения тока на катушках ротора (их еще называют brash-less). Они лишены вышеуказанных недостатков связанных с щёточным узлом, а потому предпочтительнее.
· для трёхфазных синхронных генераторов допустимый перекос фаз 33%
· коэффициент нелинейных искажений 13–25% (в зависимости от производителя).
1. Данные для проектирования
| Назначение | Двигатель |
| Номинальный режим работы | Продолжительный |
| Номинальная отдаваемая мощность Р2 , кВт | 200 |
| Количество фаз статора m1 | 3 |
| Способ соединения фаз статора | Звезда |
| Частота напряжения f, Гц | 50 |
| Коэффициент мощности cos φ | 0,8 |
| Номинальное линейное напряжение Uл , В | 400 |
| Частота вращения n1 , об/мин | 1000 |
| Способ возбуждения | От спец. обмотки |
| Степень защиты от внешних воздействий | IP23 |
| Способ охлаждения | IC01 |
| Исполнение по способу монтажа | IM1001 |
| Климатические условия и категория размещения | У2 |
2. Магнитная цепь машины. Размеры, конфигурация, материалы
Принимаем изоляцию класса нагревостойкости F
Количество пар полюсов (9.1)
Индуктивное сопротивление рассеяния обмотки статора (рисунок 11.1)
Коэффициент мощности нагрузки (11.1)
кн =
Предварительное значение КПД (рисунок 11.2)
2.2 Главные размеры
Высота оси вращения (таблица 11.1)
Допустимое расстояние от корпуса до опорной поверхности (таблица 9.2)
Наружный диаметр корпуса (1.27)
Максимально допустимый наружный диаметр сердечника статора (таблица 9.2)
Выбираемый диаметр сердечника статора (§ 11.3)
Внутренний диаметр сердечника статора (§ 11.3)
Предварительное значение линейной нагрузки статора (рис. 11.3)
Предварительное значение магнитной индукции в воздушном зазоре и номинальном режиме (рисунок 11.4)
В’б =0,79 Тл.
Предварительное значение максимальной магнитной индукции в воздушном зазоре машины при х.х. (11.3)
В’б0 =В’б /кн =0,79/1,076=0,85 Тл.
Полюсное деление статора (1.5)

Индуктивное сопротивление машины по продольной оси (рис. 11.5)
Индуктивное сопротивление реакции якоря по продольной оси (11.4)
Коэффициент, учитывающий наличие зазоров в стыке полюса и сердечника ротора или полюсного наконечника и полюса (§ 11.3)
Расчетная величина воздушного зазора между полюсным наконечником и сердечником статора (11.2)

Уточненная величина воздушного зазора (§ 11.3)
Форма зазора эксцентричная по рисунку 11.8
Отношение максимальной величины зазора к минимальной (§ 11.3)
Воздушный зазор по оси полюса (11.13)
Воздушный зазор под краем полюсного наконечника (11.14)
Коэффициент полюсной дуги действительный (§ 11.3)
α=0,73–3,33∙10 -5 ∙Dн1 =0,73–3,33∙10 -5 ∙660=0,7.
Коэффициент полюсной дуги расчетный (рисунок 11.9)
2.3 Сердечник статора
Марка стали 2312, изолировка листов лакировка, толщина стали 0,5 мм.
Коэффициент заполнения сердечника статора сталью (§ 9.3)
Коэффициент формы поля возбуждения (рисунок 11.9)
Обмоточный коэффициент (§ 9.3)
Расчетная длина сердечника статора (1.31)
2.3.5 Конструктивная длина сердечника статора (§ 11.3)
Отношение конструктивной длины к внутреннему диаметру сердечника статора (9.2)
Проверка по условию λ 2.4 Сердечник ротора
Марка стали Ст3, толщина листов 1,5 мм, листы без изоляции, коэффициент заполнения стали кс =0,98.
Длина сердечник ротора (11.20)
2.5 Сердечник полюса и полюсный наконечник
Марка стали Ст3, толщина листов 1,5 мм, листы без изоляции, коэффициент заполнения кс =0,98.
Длина шихтованного сердечника полюса (11.19)
Магнитная индукция в основании сердечника полюса (§ 11.3)
Предварительное значение магнитного потока (9.14)
Ширина дуги полюсного наконечника (11.25)
Радиус очертания полюсного наконечника при эксцентричном воздушном зазоре (11.26)

Ширина полюсного наконечника (11.28)
Высота полюсного наконечника (§ 11.3)
Высота полюсного наконечника по оси полюса для машин с эксцентричным зазором (11.29)
hн.п =h’н.п +Rн.п – 
Поправочный коэффициент (11.24)
Предварительное значение коэффициента магнитного рассеяния полюсов (11.22)
σ’=1+кσ 35б/τ 2 =1+66∙35∙2/271,2 2 =1,06.
Ширина сердечника полюса (11.21)
Высота выступа у основания сердечника (11.32)
Предварительный внутренний диаметр сердечника ротора (11.33)
D’2 =dв =кв 
Высота спинки ротора (11.34)
Расчетная высота спинки ротора с учетом прохождения части магнитного потока по валу (11.35)
Магнитная индукция в спинке ротора (11.36)
Вс2 = 
3.1 Принимаем двухслойную петлевую обмотку с жесткими секциями из провода марки ПЭТВП, укладываемую в прямоугольные полуоткрытые пазы
3.2 Коэффициент распределения (9.9)
кр1 = 
3.3 Укорочение шага (§ 9.3)
3.5 Укорочение шага обмотки статора по пазам (11.37)
3.6 Коэффициент укорочения (9.12)
3.7 Обмоточный коэффициент (9.13)
3.8 Предварительное количество витков в обмотке фазы (9.15)
w’1 = 
3.9 Количество параллельных ветвей обмотки статора (§ 9.3)
3.10 Предварительное количество эффективных проводников в пазу (9.16)
N’п1 = 
3.11 Уточненное количество витков (9.17)
3.12 Количество эффективных проводников в пазу (§ 11.4)
3.13 Количество параллельных ветвей фазы дополнительной обмотк и
3.14 Количество витков дополнительной обмотки статора (11.38)
3.15 Уточненное значение магнитного потока (9.18)
3.16 Уточненное значение индукции в воздушном зазоре (9.19)
3.17 Предварительное значение номинального фазного тока (9.20)

3.18 Уточненная линейная нагрузка статора (9.21)
Полученное значение А1 не отличается от предварительно принятого А’1 =425 А/см более чем на 10%.
3.19 Среднее значение магнитной индукции в спинке статора (т. 9.13)
3.20 Обмотка статора с прямоугольными полуоткрытыми пазами (таблица 9.16)
3.21 Зубцовое деление статора в наиболее узком месте (9.46)
t1 min = 
3.22 Предельная ширина зубца в наиболее узком месте (9.47)
b’з1 min = 
3.23 Предварительная ширина полуокрытого паза в штампе (9.48)
3.24 Высота спинки статора (9.24)
hc 1 = 
3.26 Изоляция обмотки статора (приложение 28)
3.27 Двусторонняя толщина корпусной изоляции (§ 9.4)
3.28 Высота шлица (§ 9.4)
3.30 Припуск на сборку сердечника по ширине (§ 9.4)
3.31 Припуск на сборку сердечника по высоте (§ 9.4)
3.32 Количество эффективных проводников по ширине паза (§ 9.4)
3.33 Допустимая ширина эффективного проводника с витковой изоляцией (9.50)
3.34 Количество эффективных проводников по высоте паза (9.52)
3.35 Допустимая высота эффективного проводника (11.49)
3.36 Площадь эффективного проводника (9.53)
3.37 Количество элементарных проводов в эффективном (§ 9.4)
3.38 Меньший размер неизолированного элементарного провода (9. 54)
где Δи =0,15 мм – двухсторонняя толщина изоляции провода (приложение 3).
3.39 Больший размер неизолированного элементарного провода (9.55)
3.40 Размеры провода (приложение 2)
3.41 Размер по ширине паза в штампе (9.57)
3.42 Уточненная ширина зубца в наиболее узкой части (9.85)
3.43 Уточненная магнитная индукция в узкой части зубца статора (9.59)
3.44 Размер основной обмотки статора (11.50)
где со.в =2 – количество элементарных проводников основной обмотки в одном эффективном по высоте пазе.
3.45 Изоляция обмотки статора (приложение 30)
3.46 Размер дополнительной обмотки статора (11.51)
где сд.в =2 – количество элементарных проводников дополнительной обмотки в одном эффективном по высоте пазе.
3.47 Уточненная высота паза статора в штампе (11.52)
3.48 Среднее зубцовое деление статора (9.40)
3.49 Средняя ширина катушки обмотки статора (9.41)
3.50 Средняя длина одной лобовой части обмотки (9.60)
3.51 Средняя длина витка обмотки (9.43)
3.52 Длина вылета лобовой части обмотки (9.63)
3.53 Плотность тока в обмотке статора (9.39)
(А1 J1 ) доп=2750 > 2742 А 2 /см∙мм 2 .
4. Демпферная (пусковая) обмотка
Суммарная площадь поперечного сечения меди обмотки статора, приходящейся на одно полюсное деление (11.53)
Зубцовое деление полюсного наконечника ротора (§ 11.5)
Предварительное количество стержней демпферной обмотки на один полюс (11.54)
Предварительный диаметр стержня демпферной обмотки (11.55)
d’с =1,13 
Диаметр и сечение стержня (§ (11.5)
Определяем отношение (§ 11.5)
Минимальная ширина крайнего зубца полюсного наконечника
Уточненное значение зубцового деления полюсного наконечника (11.56)
Диаметр круглой части паза полюсного наконечника (11.57)
Размеры шлица паза демпферной обмотки (§ 11.5)
Предварительная длина стержня демпферной обмотки (11.58)
Площадь поперечного сечения (11.59)
Высота короткозамыкающих сегментов (§ 11.5)
Ширина короткозамыкающих сегментов (§ 11.5)
Определяем размеры и сечение короткозамыкающих сегментов.
5. Расчет магнитной цепи
Расчетная площадь поперечного сечения воздушного зазора (11.60)
Уточненное значение магнитной индукции в воздушном зазоре (11.61)
Коэффициент, учитывающий увеличение магнитного зазора, вследствие зубчатого строения статора (9.116)
кб1 = 
Коэффициент, учитывающий увеличение магнитного зазора, вследствие зубчатого строения ротора (9.117)
кб2 =1+ 
Общий коэффициент воздушного зазора (9.120)
МДС для воздушного зазора (9.121)
Зубцовое деление на 1/3 высоты зубца (9.122)
Расчетная площадь поперечного сечения зубцов статора (11.64)
Sз1(1/3) = 
Магнитная индукция в зубце статора (11.65)
Вз1(1/3) =Ф∙10 6 /Sз1(1/3) =38,3∙10 3 /(30,89∙10 3 )=1,24 Тл.
Напряженность магнитного поля (приложение 9)
Средняя длина пути магнитного потока (9.124)
Расчетная площадь поперечного сечения спинки статора (11.66)
Расчетная магнитная индукция (11.67)
Напряженность магнитного поля (приложение (12)
Средняя длина пути магнитного потока (9.166)
МДС для спинки статора (11.68)
5.4 Зубцы полюсного наконечника
Магнитная индукция в зубцах полюсного наконечника (11.69)
Вз2 = 
Напряженность магнитного поля в зубцах полюсного наконечника.
Средняя длина пути магнитного потока в зубцах полюсного наконечника (11.70)
МДС для зубцов полюсного наконечника (11.71)
Величина выступа полюсного наконечника (11.72)
Высота широких полюсных наконечников (11.83)
Расстояние между боковыми поверхностями смежных полюсных наконечников (11.84)
Коэффициент магнитной проводимости потока рассеяния (11.85)
Длина пути магнитного потока (11.87)
Коэффициент магнитной проводимости потока рассеяния по сердечникам полюсов (11.88)
Коэффициент магнитной проводимости потока рассеяния по торцам полюсов (11.89)
Коэффициент магнитной проводимости потока рассеяния полюсов (11.90)
МДС для статора и воздушного зазора (11.91)
Магнитный поток рассеяния полюсов (11.92)
Коэффициент рассеяния магнитного потока (11.93)
Расчетная площадь поперечного сечения сердечника полюса (11.94)
Магнитный поток в сердечнике полюса (11.95)
Магнитная индукция в сердечнике полюса (11.96)
Напряженность магнитного поля в сердечнике полюса.
Длина пути магнитного потока в полюсе (11.87)
Расчетная площадь поперечного сечения спинки ротора (11.105)
Среднее значение индукции в спинке ротора (11.106)
Напряженность магнитного поля в спинке ротора (приложение 21)
Средняя длина пути магнитного потока в спинке ротора (11.107)
МДС для спинки ротора (9.170)
5.7 Воздушный зазор в стыке полюса
МДС для зазора в стыке между сердечником полюса и полюсным наконечником (11.109)
Суммарная МДС для полюса и спинки ротора (11.170)
5.8 Общие параметры магнитной цепи
Суммарная МДС магнитной цепи (11.111)
Коэффициент насыщения (11.112)
6. Активное и индуктивное сопротивление обмотки статора для установившегося режима
Активное сопротивление обмотки фазы (9.178)
r1 = 
Активное сопротивление в относительных единицах (9.179)
r1* =r1 I1 /U1 =0,01∙360,8∙ 
Проверка правильности определения r1* (9.180)
r1* = 
Активное сопротивление демпферной обмотки (9.178)
rд = 
Коэффициенты, учитывающие укорочение шага (9.181, 9.182)
Коэффициент проводимости рассеяния (9.187)
λп1 =
Коэффициент проводимости дифференциального рассеяния (11.118)
λд1 = 
Коэффициент проводимости рассеяния лобовых частей обмотки (9.191)
λл1 =0,34 
Коэффициент зубцовой зоны статора (11.120)
квб = 
Коэффициент, учитывающий влияние открытия пазов статора на магнитную проницаемость рассеяния между коронками зубцов (§ 11.7)
Коэффициент проводимости рассеяния между коронками зубцов (11.119)
Суммарный коэффициент магнитной проводимости потока рассеяния обмотки статора (11.121)
Индуктивное сопротивление обмотки статора (9.193)
Индуктивное сопротивление обмотки фазы статора (9.194)
хσ* =х1 ∙I1 /U1 =0,0558∙360,8∙ 
Проверка правильности определения х1* (9.195)
хσ* = 
7. Расчет магнитной цепи при нагрузке
Строим частичные характеристики намагничивания Ф=f(Fбзс ), Фσ =f(Fбзс ), Фп =f(Fп2 ) (о.е.).
Строим векторные диаграммы Блонделя по следующим исходным данным: U1=1; I1=1; cosφ=0,8; φ=36,87 

Рисунок 5 – Диаграмма Блонделя
ЭДС, индуктированная магнитным потоком воздушного зазора
МДС для воздушного зазора
МДС для магнитной цепи воздушного зазора и статора
Предварительный коэффициент насыщения магнитной цепи статора
Поправочные коэффициенты, учитывающие насыщение магнитной цепи
Коэффициенты реакции якоря
Коэффициент формы поля реакции якоря
Амплитуда МДС обмотки статора (11.125)
Амплитуда МДС обмотки статора в относительных единицах (11.127)
Fф* = 
Поперечная составляющая МДС реакции якоря, с учетом насыщения, отнесенная к обмотке возбуждения (11.128)
ЭДС обмотки статора, обусловленная действием МДС
Направление вектора ЭДС Еб d , определяемое построением вектора Еaq /cosψ
Продольная МДС реакции якоря с учетом влияния поперечного поля (11.130)
Продольная составляющая ЭДС
Результирующая МДС по продольной оси (11.131)
Магнитный поток рассеяния
Результирующий магнитный поток (11.132)
МДС, необходимая для создания магнитного потока
МДС обмотки возбуждения при нагрузке (11.133)
МДС обмотки возбуждения при нагрузке (11.134)
Напряжение дополнительной обмотки (1.135)
Предварительная средняя длина витка обмотки возбуждения (11.136)
Предварительная площадь поперечного сечения проводника обмотки возбуждения (11.173)
S’= 
Предварительное количество витков одной полюсной катушки (11.138)
w’п = 
Расстояние между катушками смежных полюсов (11.139)
ак = 
По таблице 10–14 принимаем изолированный медный провод марки ПСД (класс нагревостойкости изоляции F) прямоугольного сечения с двусторонней толщиной изоляции 0,27х0,48 мм, катушка многослойная.
Размеры проводника без изоляции:
Размеры проводника с изоляцией
Площадь поперечного сечения проводника (приложение 2)
Предварительное наибольшее количество витков в одном слое
Предварительное количество слоев обмотки по ширине полюсной катушки
Выбираем Nш =16 слоев обмотки по ширине полюсной катушки
Уточненное наибольшее количество витков в одном слое (рис 11.22)
Уточненное количество витков одной полюсной катушки (рис. 11.22)
Размер полюсной катушки по ширине
Размер полюсной катушки по высоте (11.150)
Средняя длина витка катушки (11.144)
Ток возбуждения при номинальной нагрузке (11.153)
Количество параллельных ветвей в цепи обмотки возбуждения (§ 11.9)
Уточненная плотность тока в обмотке возбуждения (11.154)
Общая длина всех витков обмотки возбуждения (11.155)
Массам меди обмотки возбуждения (11.156)
Сопротивление обмотки возбуждения при температуре 20˚ С (11.157)
Максимальный ток возбуждения (11.158)
Коэффициент запаса возбуждения (11.159)
Номинальная мощность возбуждения (11.160)
Рисунок 6 – Эскиз полюса ротора
9. Параметры обмоток и постоянные времени. Сопротивления обмоток статора при установившемся режиме
9.1 Сопротивления обмоток статора при установившемся режиме
Коэффициент продольной реакции якоря (таблица 11.4)

Коэффициент насыщения при Е=0,5
кнас(0,5) = 
МДС для воздушного зазора
Индуктивное сопротивление продольной реакции якоря (11.162)
хad * = 
Коэффициент поперечного реакции якоря (таблица 11.4)
Индуктивное сопротивление поперечной реакции якоря (11.163)
хaq * = 
Синхронное индуктивное сопротивление по продольной оси (11.164)
Синхронное индуктивное сопротивление по поперечной оси (11.165)
9.2 Сопротивление обмотки возбуждения
Активное сопротивление обмотки возбуждения, приведенное к обмотке статора (11.166)

Коэффициент магнитной проводимости потоков рассеяния обмотки возбуждения (11.167)
Индуктивное сопротивление обмотки возбуждения (11.168)
хп* =1,27кad хad * (1+ 

Индуктивное сопротивление рассеяния обмотки возбуждения (11.169)
9.3 Сопротивления пусковой обмотки
Относительное зубцовое деление демпферной обмотки (11.170)
Коэффициент распределения демпферной обмотки (11.171)
кр2 = 
Коэффициент магнитной проводимости потока рассеяния по зубцам полюсного наконечника (11.172)
Коэффициент магнитной проводимости пазового рассеяния полюсов (11.173)
λd п =(0,785- 
Коэффициенты (рисунок 11.23)
Коэффициент магнитной проводимости рассеяния лобовых частей демпферной обмотки по продольной оси (11.174)
Коэффициент магнитной проводимости рассеяния лобовых частей демпферной обмотки по поперечной оси (11.175)
Коэффициент магнитной проводимости рассеяния демпферной обмотки по продольной оси (11.176)
λд d = 
Коэффициент магнитной проводимости рассеяния демпферной обмотки по поперечной оси (11.177)
λд q = 
Индуктивной сопротивление полной демпферной обмотки по продольной оси (11.178)
хд d * = 
Индуктивной сопротивление полной демпферной обмотки по поперечной оси (11.179)
хд q * = 
Активное сопротивление стержней демпферной обмотки по продольной оси (11.181)
rcd * = 

где μ0 =4π∙10 -7 Гн/м – магнитная проницаемость воздуха.
Активное сопротивление стержней демпферной обмотки по поперечной оси (11.182)
Активное сопротивление короткозамыкающих колец демпферной обмотки по продольной оси (11.183)
rkd * = 

Активное сопротивление короткозамыкающих колец демпферной обмотки по поперечной оси (11.184)
Активное сопротивление полной демпферной обмотки по продольной оси (11.185)
Активное сопротивление полной демпферной обмотки по поперечной оси (11.186)
9.4 Переходные и сверхпереходные сопротивления обмотки статора
Переходное индуктивное сопротивление обмотки статора по продольной оси (11.188)
x’d * =xσ * + 
Переходное индуктивное сопротивление обмотки статора по поперечной оси (11.189)
Сверхпереходное индуктивное сопротивление обмотки статора по продольной оси (11.190)
x»d * =xσ * = 
Сверхпереходное индуктивное сопротивление обмотки статора по поперечной оси (11.191)
x»q * =xσ * + 
9.5 Сопротивления для токов обратной и нулевой последовательности
Индуктивное сопротивление обмотки статора для токов обратной последовательности при работе машины на малое внешнее сопротивление (11.194)
х2* = 
Индуктивное сопротивление обмотки статора для токов обратной последовательности при большом внешнем индуктивном сопротивлении (11.195)
Индуктивное сопротивление двухслойной обмотки статора для токов нулевой последовательности (11.196)
Активное сопротивление обмотки фазы статора для тока нулевой последовательности при рабочей температуре (11.197)
9.6 Постоянные времени обмоток
Обмотка возбуждения при разомкнутых обмотках статора и демпферной (11.198)
Обмотка возбуждения при замкнутых обмотках статора и демпферной (11.199)
Демпферная обмотка при разомкнутых обмотках статора и возбуждения по продольной оси (11.200)
Tд d 0 = 
Демпферная обмотка при разомкнутых обмотках статора и возбуждения по поперечной оси (11.201)
Tд q 0 = 
Демпферная обмотка по продольной оси при разомкнутой обмотке возбуждения (11.202)
T»d 0 = 
Демпферная обмотка по продольной оси при короткозамкнутых обмотке возбуждения и статора (11.203)
Демпферная обмотка по поперечной оси при короткозамкнутой обмотке статора (11.204)
Обмотка статора при короткозамкнутых обмотках ротора (11.205)
Зубцовое деление статора в максимальном сечении зубца (9.128)
Расчетная масса стали зубцов статора (9.260)
Магнитные потери в зубцах статора (9.251)
Масса стали спинки статора (9.261)
Магнитные потери в спинке статора (9.254)
Амплитуда колебаний индукции (11.206)
Среднее значение удельных поверхностных потерь (11.207)
Поверхностные потери машины (11.208)
Суммарные магнитные потери (11.213)
Потери в обмотке статора (11.209)
Рм1 =m1 I 2 1 r1 mт +m1 (I’пн / 
=3∙360,8 2 ∙0,0138∙1,38+3 (61,4/ 
Потери на возбуждение синхронной машины при питании от дополнительной обмотки статора (11.214)
Добавочные потери в обмотке статора и стали магнитопровода при нагрузке (11.216)
Потери на трение в подшипниках и на вентиляцию (11.210)
Р’мх =Рт.п +Рвен =8 ( 



Потери на трение щеток о контактные кольца (11.212)
Механические потери (11.217)
КПД при номинальной нагрузке (11.219)
11.1 Изменение напряжения генератора


=3ּ1,48 [360,8 2 ∙0,0138+(61,4/ 
где m’т =1,48 – коэффициент для класса нагревостойкости изоляции В (§ 5.1).
Потери на возбуждение синхронной машины при питании от дополнительной обмотки статора
Условная внутренняя поверхность охлаждения активной части статора (9.379)
Условный периметр поперечного сечения (9.381)
Условная поверхность охлаждения пазов (9.382)
Условная поверхность охлаждения лобовых частей обмотки (9.383)
Условная поверхность охлаждения двигателей с охлаждающими ребрами на станине (9.384)
Удельный тепловой поток от потерь в активной части обмотки и от потерь в стали, отнесенных к внутренней поверхности охлаждения активной части статора (9.386)
рп1 = 
где к=0,76 – коэффициент (таблица 9.25).
Удельный тепловой поток от потерь в активной части обмотки и от потерь в стали, отнесенных к поверхности охлаждения пазов (9.387)
ри.п1 = 
Удельный тепловой поток от потерь в активной части обмотки и от потерь в стали, отнесенных к поверхности охлаждения лобовых частей обмотки (9.388)
рл1 = 
Окружная скорость ротора (9.389)
v2 = 
Превышение температуры внутренней поверхности активной части статора над температурой воздуха внутри машины (9.390)
Δtп1 = 
где α1 =17,5ּ10 -5 Вт/мм 2 ּград – коэффициент теплоотдачи поверхности статора.
Односторонняя толщина изоляции в пазу статора (§ 9.13)
Перепад температуры в изоляции паза и катушек из круглых проводов (9.392)
Δtи.п1 = 
Превышение температуры наружной поверхности лобовых частей обмотки над температурой воздуха внутри двигателя (9.393)
Перепад температуры в изоляции лобовых частей катушек из круглых проводов (9.395)
Δtи.л1 =рл1 

Среднее превышение температуры обмотки над температурой воздуха внутри двигателя (9.396)
Δt’1 =(Δtп1 +Δtи.п1 ) 



Потери в двигателе, передаваемые воздуху внутри машины (9.397)
Р’Σ =к(Р’м1 



Среднее превышение температуры воздуха внутри двигателя над температурой наружного воздуха (9.399)
Δtв = 
Среднее превышение температуры обмотки над температурой наружного воздуха (9.400)
Условная поверхность охлаждения многослойных катушек из изолированных проводов (11.249)
Удельный тепловой поток от потерь в обмотке, отнесенных к поверхности охлаждения обмотки (11.250)
Коэффициент теплоотдачи катушки (§ 11.13)
αТ =(3+0,42∙26,9)∙10 -5 =14,3∙10 -5 Вт/(мм 2 ˚С).
Превышение температуры наружной поверхности охлаждения обмотки (11.251)
Перепад температуры в наружной и внутренней изоляции многослойных катушек из изолированных проводов
Δtип = рп 

Среднее превышение температуры обмотки над температурой воздуха внутри машины (11.253)
Среднее превышение температуры обмотки над температурой охлаждающего воздуха (11.254)
12.3 Вентиляционный расчет
Необходимый расход воздуха (5.28)
Vв = 
V’в =к1 (Dн2 /100) 2 ּ10 -2 =3,5 (514,2/100) 2 ּ10 -2 =0,93 м 3 /с;
где к1 =3,5 
Н=7,85 (n1 /1000) 2 (Dн2 /100) 2 =7,85 (1000/1000) 2 (514,2/100) 2 =208 Па.
13. Масса и динамический момент инерции
Масса стали сердечника статора (11.255)
Масса стали полюсов (11.256)
Масса стали сердечника ротора (11.257)
Суммарная масса активной стали статора и ротора (11.258)
Масса меди обмотки статора (11.259)
Масса меди демпферной обмотки (11.260)
Суммарная масса меди (11.261)
Суммарная масса изоляции (11.262)
Масса конструкционных материалов (11.264)
13.2 Динамический момент инерции ротора
Радиус инерции полюсов с катушками (11.266)
Rп.ср =0,5 [(0,5D 2 1 +(0.85÷0.96) (0.5D2 +hc 2 ) 2 ]∙10 6 =0.5 [(0.5∙518,2 2 +0.85 (0.5∙140+42) 2 ]∙10 -6 =0.072 м.
Динамический момент инерции полюсов с катушками (11.267)
Динамический момент инерции сердечника ротора (11.268)
mв =15∙10 -6 ℓ1 D 2 2 =15∙10 -6 ∙300∙140 2 =88,2 кг.
Динамический момент инерции вала (11.270)
Jв =0,5mв (0,5D2 ) 2 10 -6 =0,5∙88,2 (0,5∙140) 2 ∙10 -6 =0.22 кг/м 2 .
Суммарный динамический момент инерции ротора (11.271)
1. Антонов М.В. Технология производства электрических машин. – М.: Энергоатомиздат, 1993. -590 с.
2. Анурьев В.И. Справочник конструктора-машиностроителя. — М.; Машиностроение. 1978
3. Гольдберг О.Д. Проектирование электрических машин – М.: Высшая школа, 2001
4. Копылов И.П. Проектирование электрических машин – М.: Высшая школа, 2002
5. Электротехнический справочник – Под ред. Орлова И.Н. – М.; Энергоатомиздат 1986
6. Проектирование синхронных машин средней мощности: Методические указания к выполнению курсового проекта по дисциплине «Инженерное проектирование и САПР электромагнитных устройств и электромеханических преобразователей» / Уфимск. гос. авиац. техн. ун-т; Сост. Н.Л. Бабикова. — Уфа, 2008. – 38 с.
Источник
➤ Adblock
detector
Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Имеем источник ЭДС
Давайте вспомним, что такое ЭДС. ЭДС — это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе «спрятано» сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой «r «.
Выглядит все это в аккумуляторе примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка — это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что
Далее
Закон Ома для полной цепи
Итак, последнее выражение носит название «закон Ома для полной цепи»
где
Е — ЭДС источника питания, В
R — сопротивление всех внешних элементов в цепи, Ом
I — сила ток в цепи, А
r — внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на «ближний» свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр — силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r
Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.