Сопротивление
параллельного контура при резонансе
чисто активное; напряжение на контуре
и ток в неразветвленной части цепи
совпадают по фазе. Реальный контур
отбирает от питающего генератора
некоторое количество энергии, которое
превращается в тепло на активном
сопротивлении R
(сопротивлении потерь)
контура. На основании закона сохранения
энергии мощность, отдаваемая генератором,
и мощность, расходуемая на тепло в
активном сопротивлении контура, равны.
Мощность, отдаваемая
генератором, определяется выражением
![]()
где![]() –ток в неразветвленной
–ток в неразветвленной
части цепи при резонансе;
![]() –сопротивление
–сопротивление
контура при резонансе.
Мощность,
расходуемая в активном сопротивлении
R,
равна
![]() ,
,
где
![]() –ток внутри контура
–ток внутри контура
при резонансе (![]() ).
).
R
–активное сопротивление,
учитывающее потери энергии вкатушке.
Если
напряжение на зажимах генератора
![]() ,
,
то
![]()
и
![]() .
.
Имея
в виду последние два выражения, приравняем
мощности
![]() и
и![]() :
:
![]() .
.
Отсюда
![]() ,
,
или
![]() .
.
Так
как
![]() ,
,
то ,
,
где
![]() – резонансное сопротивление
– резонансное сопротивление
контура в омах;
L
–индуктивность
контура в генри;
С –емкость контура в фарадах;
R
– активное сопротивление
в омах.
Резонансное
сопротивление параллельного контура
зависит от величины активного сопротивления
потерь R
и от соотношения
величин L
и С,
т. е. от волнового сопротивления контура.
Чем больше R,
тем больше энергии расходуется в нем
на тепло и тем больше энергии (большая
мощность) поступает от генератора в
контур. Следовательно, чем больше
сопротивление потерь R,
тем больше ток
![]() в общей части цепи. Но по величине тока
в общей части цепи. Но по величине тока
можно судить о величине сопротивления
контура: чем больше ток, тем меньше
сопротивление. Поэтому чем больше
сопротивление потерь, тем меньше
сопротивление параллельного контура
при резонансе. В отсутствиеR
![]() .
.
3.2. Зависимость сопротивления параллельного контура от частоты
Пусть частота
генератора, питающего параллельный
контур, изменяется в широких пределах.
При повышении частоты генератора
емкостное сопротивление конденсатора
уменьшается:
![]() ,
,
а индуктивное
сопротивление увеличивается:
![]() .
.
При
этом ток в емкостной ветви увеличивается,
а в индуктивной уменьшается. При частоте
ниже резонансной в общей цепи преобладает
индуктивный ток и контур ведет себя как
индуктивное сопротивление. При частоте
генератора, равной собственной частоте
контура , емкостной и индуктивный токи
равны по величине и реактивный ток в
общей части цепи равен нулю (состояние
резонанса). Сопротивление контура имеет
чисто активный характер и значительную
величину, определяемую формулой
![]() .
.
При частоте выше
резонансной в общей цепи преобладает
емкостной ток и контур ведет себя как
емкостное сопротивление.
Чем
больше частота генератора отличается
от собственной (резонансной) частоты
контура, тем больше различаются токи![]() и
и![]() ,
,
тем больше реактивный ток в общей части
цепи и меньше реактивное сопротивление
контура. Исходя из этих рассуждений,
можно показать зависимость сопротивления
параллельного контура от частоты
питающего генератора (рис.14).

Рис.14.
Зависимость
сопротивления параллельного контура
от частоты генератора
При
изменении частоты генератора изменяется
фазовый сдвиг между напряжением
генератора и током
![]() ,
,
идущим через контур. Если частота
генератора значительно ниже собственной
(резонансной) частоты контура, то
сопротивление контура можно считать
чисто индуктивным, т.к. реактивный ток
в общей цепи во много раз больше активного.
Угол фазового сдвига между напряжением
генератора и током
![]() при этом близок к
при этом близок к![]() .
.
По мере повышения частоты генератора
реактивная составляющая тока в общей
цепи и фазовый угол уменьшаются. При
резонансе сопротивление контура является
чисто активным и фазовый сдвиг между
напряжением генератора и током
![]()
равен нулю. Если частота генератора
превышает резонансную частоту контура,
то сопротивление контура состоит из
активной и емкостной составляющих. По
мере повышения частоты генератора
соотношение между активной и реактивной
составляющими изменяется и угол фазового
сдвига между напряжением генератора и
током
![]()
приближается к![]() .
.
Кривая, показывающая
зависимость угла фазового сдвига между
напряжением генератора и током через
контур, называется фазо-частотной
характеристикой параллельногоконтура(рис.15).

Рис.15.
Фазо-частотная характеристика
параллельного контура
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В прошлой статье мы с вами рассмотрели последовательный колебательный контур, так как все участвующие в нем радиоэлементы соединялись последовательно. В этой же статье мы рассмотрим параллельный колебательный контур, в котором катушка и конденсатор соединяются параллельно.
Параллельный колебательный контур
Идеальный колебательный контур
На схеме идеальный колебательный контур выглядит вот так:
где

L — индуктивность, Генри
С — емкость, Фарад
Реальный колебательный контур
В реальности у нас катушка обладает приличным сопротивлением потерь, так как намотана из провода, да и конденсатор тоже имеет некоторое сопротивление потерь. Потери в емкости очень малы и ими обычно пренебрегают. Поэтому оставим только одно сопротивление потерь катушки R. Тогда схема реального колебательного контура примет вот такой вид:
где
R — это сопротивление потерь контура, Ом
L — индуктивность, Генри
С — емкость, Фарад
Принцип работы параллельного колебательного контура
Давайте подцепим к генератору частоты реальный параллельный колебательный контур
Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.
Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.
Реактивное сопротивление катушки выражается по формуле

а конденсатора по формуле

Более подробно про это можно прочитать в этой статье.
Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки XL и конденсатора XC уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.
Резонанс параллельного колебательного контура
Очень интересное свойство параллельного колебательного контура заключается в том, что при ХL = ХС у нас колебательный контур войдет в резонанс. При резонансе колебательный контур начнет оказывать большее сопротивление переменному электрическому току. Еще часто это сопротивление называют резонансным сопротивлением контура и оно выражается формулой:

где
Rрез — это сопротивление контура на резонансной частоте
L — собственно сама индуктивность катушки
C — собственно сама емкость конденсатора
R — сопротивление потерь катушки
Формула резонанса
Для параллельного колебательного контура также работает формула Томсона для резонансной частоты как и для последовательного колебательного контура:

где
F — это резонансная частота контура, Герцы
L — индуктивность катушки, Генри
С — емкость конденсатора, Фарады
Как найти резонанс параллельного колебательного контура на практике
Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.
Итак, реальная схема этого контура будет вот такая:
Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:
На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.
Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура Rкон.
Упрощенная схема будет выглядеть вот так:
Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление Rкон будет максимальным, вследствие чего у нас на этом сопротивлении «упадет» бОльшее напряжение.
У нас есть калькулятор резисторов по цветам. Самый крутой подборник.
Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.
200 Герц.

Как вы видите, на колебательном контуре «падает» малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление Rкон
Добавляем частоту. 11,4 Килогерца

Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.
Добавляем еще частоту. 50 Килогерц

Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.
723 Килогерца

Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше.
И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре. Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам.

Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:

Снова добавляем частоту и видим, что напряжение стало еще меньше:

Что происходит на резонансной частоте в параллельном колебательном контуре
Давайте более подробно рассмотрим эту осциллограмму, когда у нас было максимальное напряжение с контура.

Что здесь у нас произошло?
Так как на этой частоте был всплеск напряжения, следовательно, на этой частоте параллельный колебательный контур имел самое высокое сопротивление Rкон. На этой частоте ХL = ХС. Потом с ростом частоты сопротивление контура снова упало. Это и есть то самое резонансное сопротивление контура, которое выражается формулой:

Резонанс токов
Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:
Чему будет равняться резонансный ток Iрез ? Считаем по закону Ома:
Iрез = Uген /Rрез , где Rрез = L/CR.
Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток Iкон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.
Добротность параллельного колебательного контура
Кстати, этот контурный ток будет намного больше, чем ток, который проходит через контур. И знаете во сколько раз? Правильно, в Q раз. Q — это и есть добротность! В параллельном колебательном контуре она показывает во сколько раз сила тока в контуре Iкон больше сила тока в общей цепи Iрез
Или формулой:

Если сюда еще прилепить сопротивление потерь, то формула примет вот такой вид:
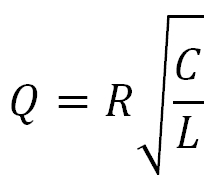
где
Q — добротность
R — сопротивление потерь на катушке, Ом
С — емкость, Ф
L — индуктивность, Гн
Применение параллельного колебательного контура
Параллельный колебательный контур применяется в радиоприемном оборудовании, где надо выделить частоту какой-либо станции. Также с помощью колебательного контура можно построить различные резонансные фильтры.
Также смотрите видео:
Содержание:
Частотные методы анализа электрических цепей:
Частотные характеристики являются компонентами комплексных функций цепи.
Комплексная функция цепи (КФЦ)
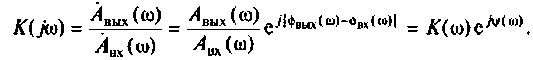
Амплитудно-частотная характеристика (АЧХ)
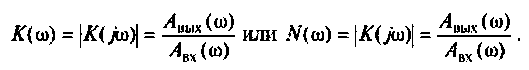
Фазочастотная характеристика (ФЧХ)
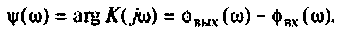
Амплитудно-фазовая частотная характеристика (АФЧХ) (комплексная функция цепи)
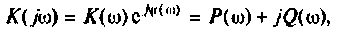
где 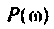 — вещественная частотная характеристика (ВЧХ);
— вещественная частотная характеристика (ВЧХ); 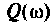 — мнимая частотная характеристика (МЧХ).
— мнимая частотная характеристика (МЧХ).
Комплексные функции простых цепей можно рассчитать непосредственно по закону Ома.
На рис.4.1 показаны АЧХ и ФЧХ, а на рис.4.2 — АФЧХ простейшей интегрирующей цепи (апериодического звена). По АЧХ определяют полосу пропускания
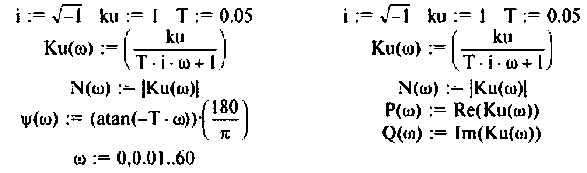
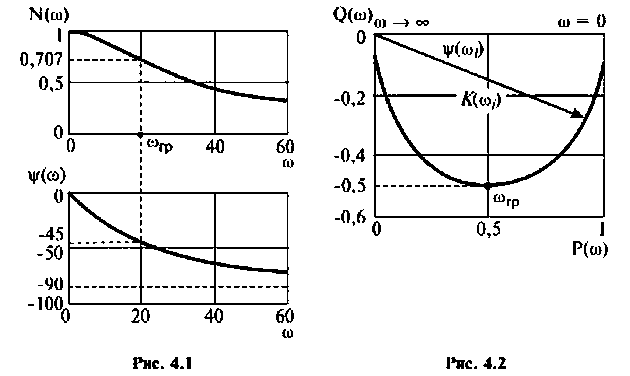
Полосой пропускания П называется диапазон частот, на границах которого мощность сигнала уменьшается в 2 раза, а амплитуда (действующее значение) напряжения (тока) — в 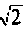 раз по сравнению с максимальными значениями.
раз по сравнению с максимальными значениями.
Полоса пропускания может измеряться в радианах в секунду 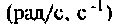 или в герцах (Гц).
или в герцах (Гц).
Например, для простой интегрирующей цепи полоса пропускания (см. рис. 4.1)
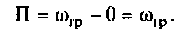
Для сложных цепей КФЦ рассчитывают по MKT или МУН. В табл. 4.1 приведены соотношения для расчета КФЦ, выраженные через определитель и алгебраические дополнения матрицы контурных сопротивлений и узловых проводимостей.
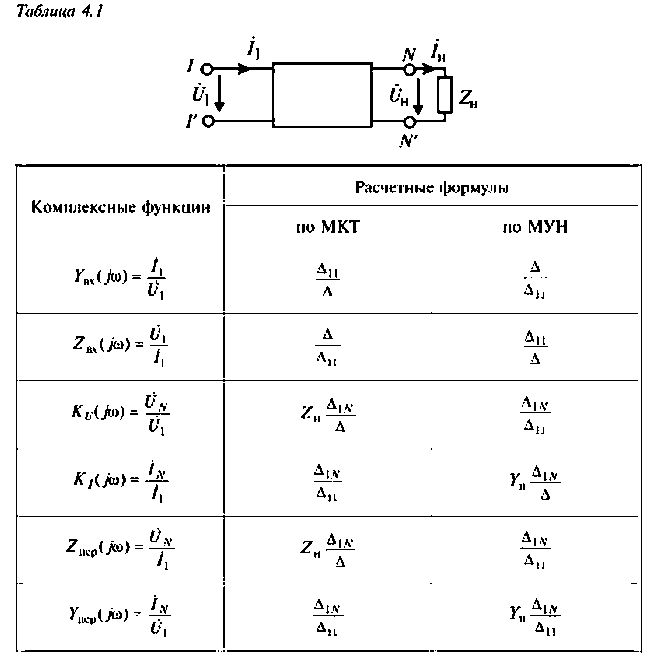
Частотные характеристики цепей с одним реактивным элементом
Примеры решения типовых задач:
Пример 4.2.1.
Определить комплексный коэффициент передачи по напряжению для дифференцирующего RC-контура (рис.4.3, а), рассчитать и построить графики АЧХ и ФЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.3, б).
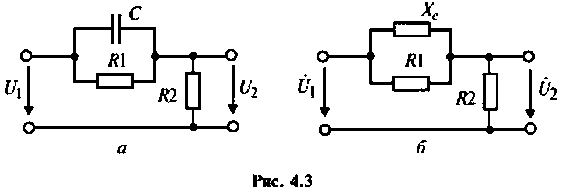
2. Определим комплексное напряжение на выходе цепи в виде
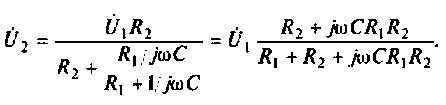
Преобразуем полученное выражение, вынеся зa скобки в числителе и знаменателе члены, не содержащие 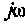 . После преобразований получим
. После преобразований получим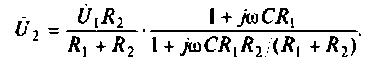
Следовательно.
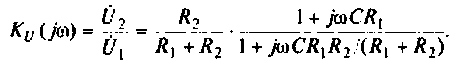
Введем обозначения:
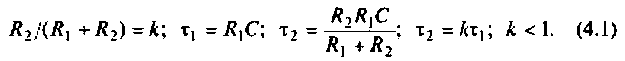
Величина 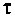 называется постоянной времени цепи и измеряется в секундах. Величина
называется постоянной времени цепи и измеряется в секундах. Величина 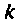 имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте
имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте 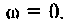
С учетом принятых обозначений
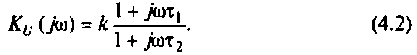
Для получения аналитических выражений АЧХ и ФЧХ запишем комплексную функцию в показательной форме.
Так как выражение (4.2) есть отношение двух полиномов, то удобно числитель и знаменатель записать отдельно в показательной форме, а затем разделить:
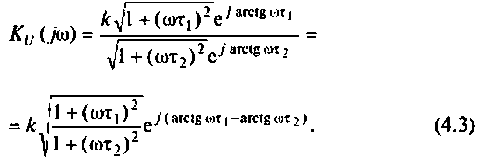
3. Из (4.3) запишем АЧХ и ФЧХ соответственно:
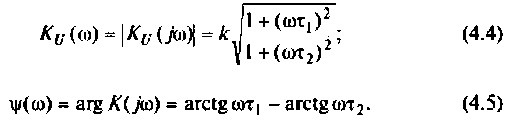
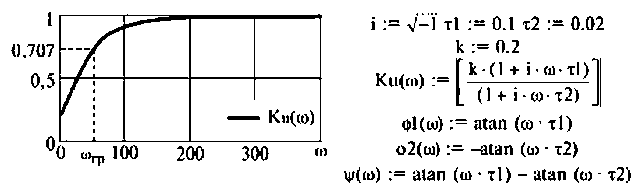
4. Построим график АЧХ и ФЧХ качественно по двум точкам. Для этого рассчитаем значения 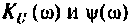 для крайних значений частот:
для крайних значений частот:
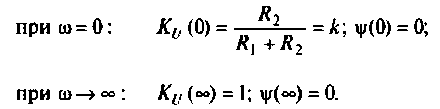
График АЧХ 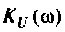 (рис. 4.4, а) является кривой, монотонно возрастающей от значения
(рис. 4.4, а) является кривой, монотонно возрастающей от значения 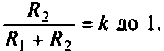
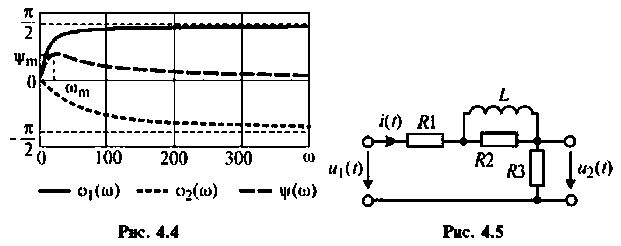
График функции ФЧХ 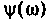 можно построить качественно как сумму двух графиков (рис. 4.4). Из рис. 4.4,б видно, что оба слагаемых монотонно увеличиваются: первое от нуля до +90° и вносит опережение по фазе. Второе до -90° и вносит отставание по фазе. Но первое слагаемое растет быстрее, так как
можно построить качественно как сумму двух графиков (рис. 4.4). Из рис. 4.4,б видно, что оба слагаемых монотонно увеличиваются: первое от нуля до +90° и вносит опережение по фазе. Второе до -90° и вносит отставание по фазе. Но первое слагаемое растет быстрее, так как 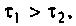 что следует из формулы (4.1). Поэтому функция
что следует из формулы (4.1). Поэтому функция 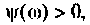 следовательно, дифференцирующий RС-контур вносит опережение по фазе.
следовательно, дифференцирующий RС-контур вносит опережение по фазе.
Исследуя функцию (4.5) на экстремум, можно показать, что она имеет максимум на частоте
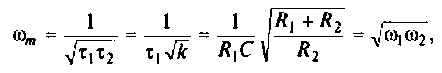
где 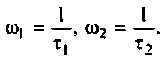
Подставляя 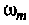 в (4.5), получим
в (4.5), получим
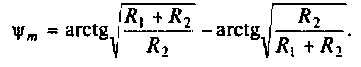
Графики АЧХ и ФЧХ изображены на рис. 4.4.
Пример 4.2.2.
Для электрической цепи, изображенной на рис. 4.5, определить АЧХ 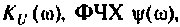 граничную частоту полосы пропускания. Рассчитать АЧХ, ФЧХ и построить графики, если параметры цепи:
граничную частоту полосы пропускания. Рассчитать АЧХ, ФЧХ и построить графики, если параметры цепи: 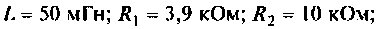
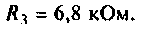
Решение
1. Найдем комплексную функцию К(; (/ш) но формуле делителя напряжения
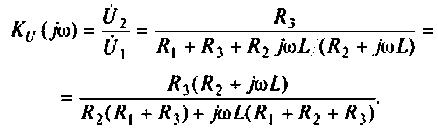
Преобразуем полученное выражение к виду
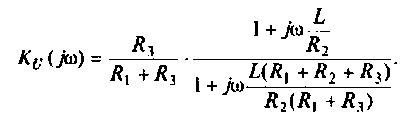
Обозначим:
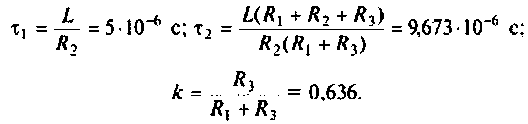
Следовательно,
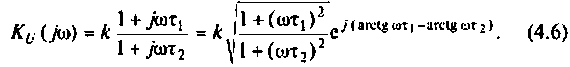
Отсюда: АЧХ
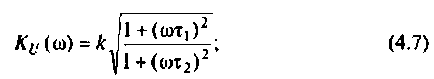
ФЧХ
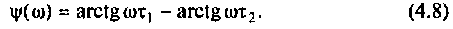
2. Рассчитаем граничную частоту. По определению
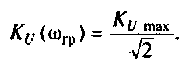
Из (4.7) найдем
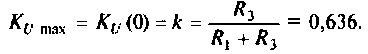
Следовательно,
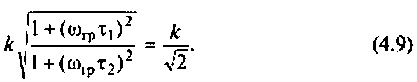
Из уравнения (4.9) получаем, что
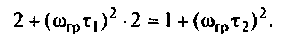
Отсюда 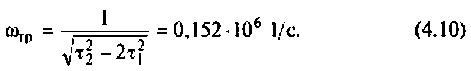
3. Построим график функций.
Вычислим значения (4.7) и (4.8) для частот с дискретностью 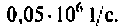
Графики и таблицы выполним в среде Mathcad (рис. 4.6).
Пример 4.2.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.7, а), используя метод контурных токов. Построить в среде Mathcad график АЧХ, определить полосу пропускания.
Параметры цепи: 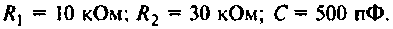
Решение
1. Представим цепь комплексной схемой замещения (рис. 4.7, б). Данная цепь имеет два независимых контура. Ток 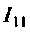 в первом контуре замыкается через источник, который на схеме не изображен. Направления контурных токов выбираем одинаковыми.
в первом контуре замыкается через источник, который на схеме не изображен. Направления контурных токов выбираем одинаковыми.
2.Составим матрицы контурных сопротивлений для двух независимых контуров
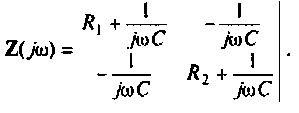
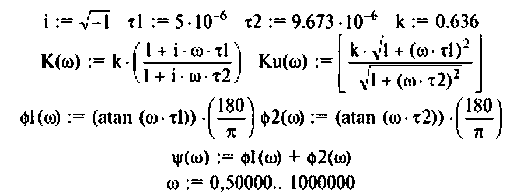
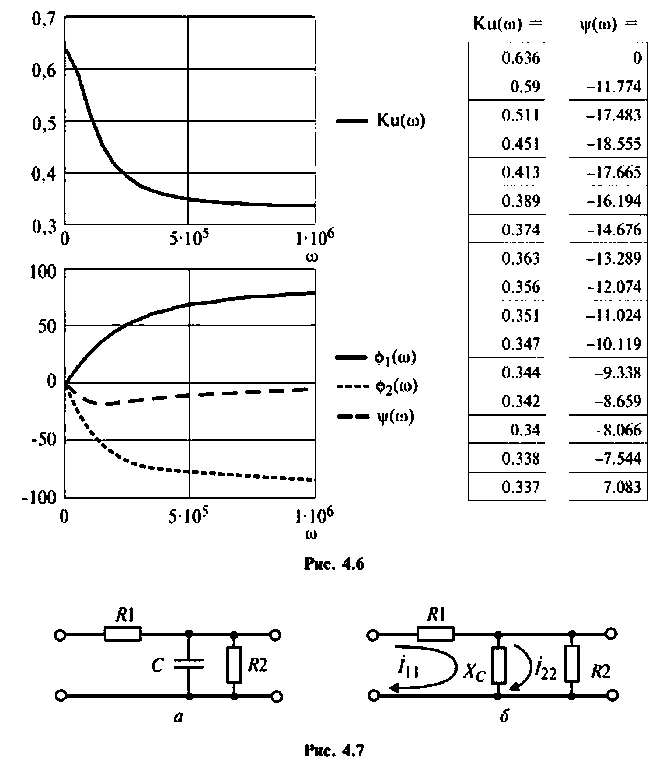
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
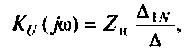
где сопротивление нагрузки равно 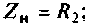
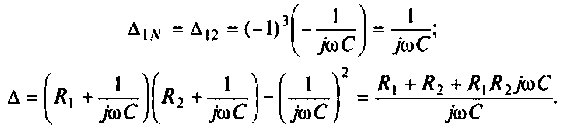
Подставляя найденные выражения, получаем
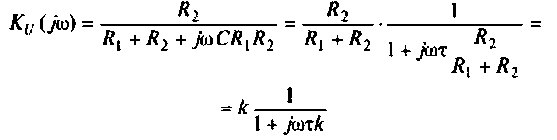
или 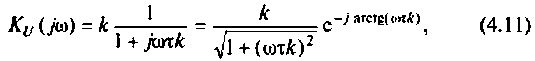
где 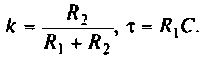
4. Рассчитаем 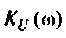 для крайних значений частоты
для крайних значений частоты 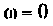 и
и 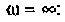
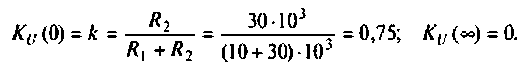
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 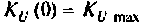
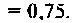 С ростом частоты емкостное сопротивление уменьшается. Если
С ростом частоты емкостное сопротивление уменьшается. Если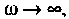 то
то 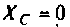 и шунтирует сопротивление
и шунтирует сопротивление 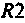 . При этом
. При этом
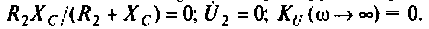 = 0.
= 0.
По полученным выражениям строим график АЧХ (рис. 4.8) и среде Mathcad.
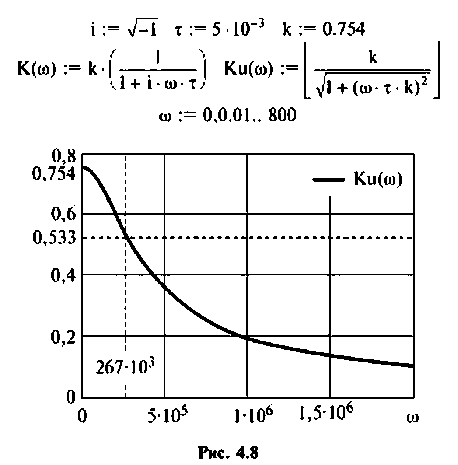
5. Определяем полосу пропускания. По определению
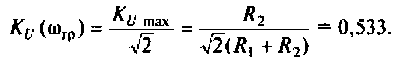
Поэтому из (4.11) имеем
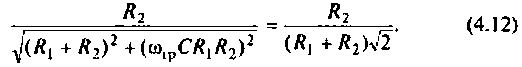
После преобразований уравнения (4.12) получаем
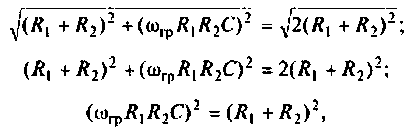
откуда
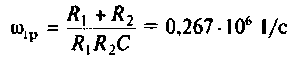
или
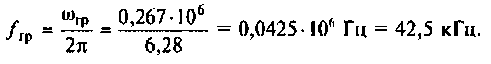
Следовательно, цепь имеет полосу пропускания
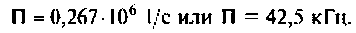
На рис. 4.8 указана граничная частота 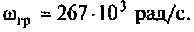
Данная цепь представляет собой фильтр нижних частот с полосой пропускания 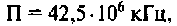 сигналы на частотах
сигналы на частотах  проходят с большим затуханием.
проходят с большим затуханием.
Пример 4.2.4.
Найти комплексную передаточную проводимость 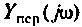 для цепи, изображенной на рис. 4.9, а методом узловых напряжений.
для цепи, изображенной на рис. 4.9, а методом узловых напряжений.
Параметры цепи: 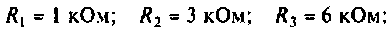
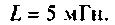
Определить АЧХ и ФЧХ, построить их графики в среде Mathcad.
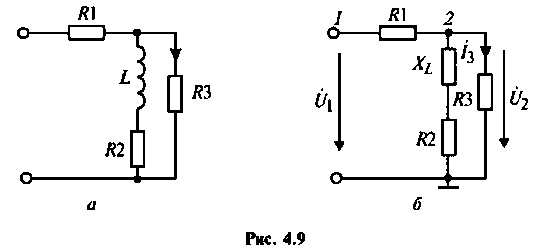
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.9, б). Схема имеет два независимых узла. В данном случае 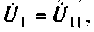
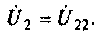
2. Составим матрицу узловых проводимостей. При определении собственной проводимости узлов необходимо помнить, что собственная проводимость ветви, состоящей из последовательно включенных пассивных элементов, находится из соотношения 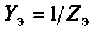 , где
, где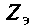 — эквивалентное сопротивление ветви. Как найти проводимость ветви с последовательно включенными
— эквивалентное сопротивление ветви. Как найти проводимость ветви с последовательно включенными 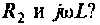
В начале рассчитывают комплексное сопротивление этой ветви, 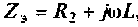 , а затем комплексную проводимость
, а затем комплексную проводимость
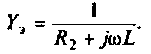
Составим матрицу проводимостей цепи 1 2
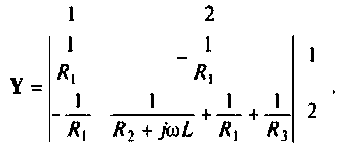
Как видим, общие проводимости узлов взяты со знаком минус, так как узловые напряжения 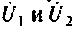 направлены одинаково, к базисному yзлy.
направлены одинаково, к базисному yзлy.
3.Определим комплексную передаточную проводимость по соотношению, приведенному в табл. 4.1
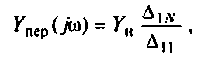
где 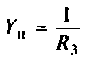 -комплексная проводимость ветви, по которой протекает ток
-комплексная проводимость ветви, по которой протекает ток 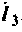 ,так как по определению
,так как по определению
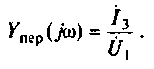
Найдем алгебраические дополнения:
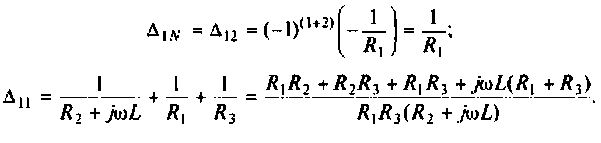
После подстановки найденных значений получим
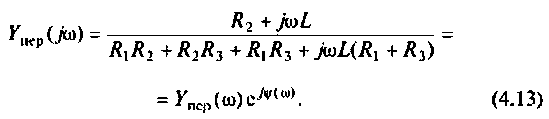
Для определении АЧХ и ФЧХ запишем выражения для модуля и аргумента 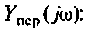
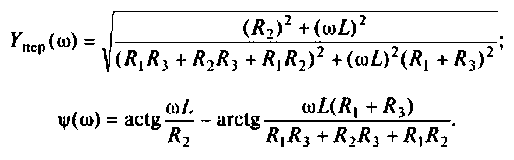
4. Рассчитаем значения 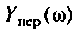 на частотах
на частотах 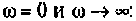
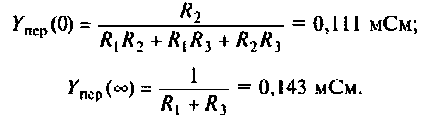
Примечание. Эти значения можно найти без вывода аналитического выражения для 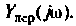 Для этого достаточно воспользоваться эквивалентными схемами цепи на рассматриваемых частотах.
Для этого достаточно воспользоваться эквивалентными схемами цепи на рассматриваемых частотах.
Учитывая, что 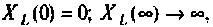 получим две схемы, показанные на рис. 4.10. а, б, соответственно.
получим две схемы, показанные на рис. 4.10. а, б, соответственно.
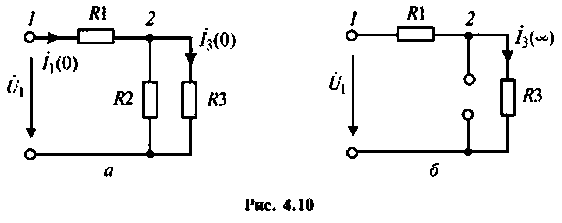
Для первой схемы:
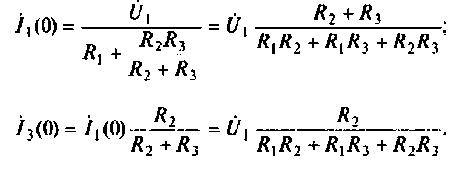
Следовательно,
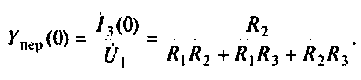
Аналогично для второй схемы получим
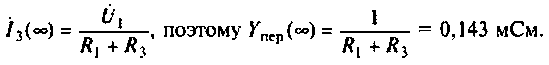
При расчете сложных схем такой прием можно применять для проверки правильности полученного аналитического выражения КФЦ.
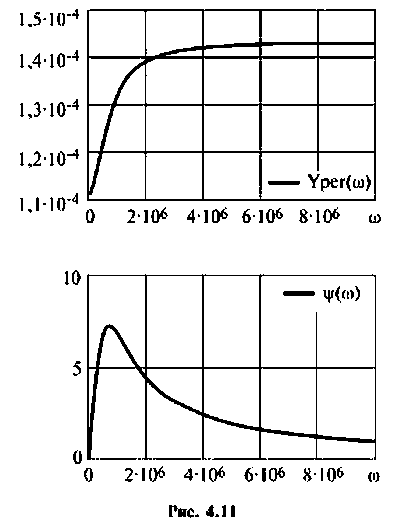
Из (4.13) видно, что функция наметен монотонной, но для качественного построения графика АЧХ (рис. 4.11) необходимо воспользоваться ПЭВМ, например построить функцию в среде Mathcad.
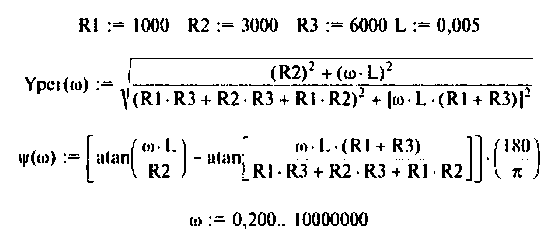
Пример 4.2.5.
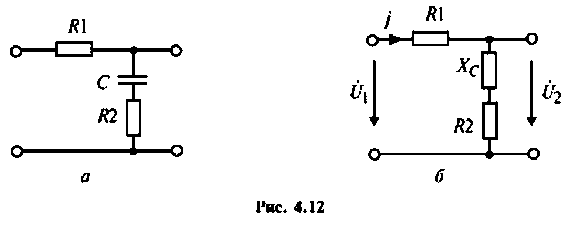
Для интегрирующего RС-контура (рис.4.12,а) определить комплексный коэффициент передачи по напряжению, рассчитать АЧХ, ФЧХ, ВЧХ, МЧХ. Построить графики АЧХ, ФЧХ. АФЧХ, если
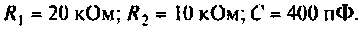
Решение
1. Составим комплексную схему замещения цепи (рис. 4.12, б).
2. Определим 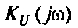 из соотношения
из соотношения 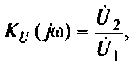 где
где
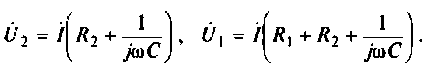
Следовательно.
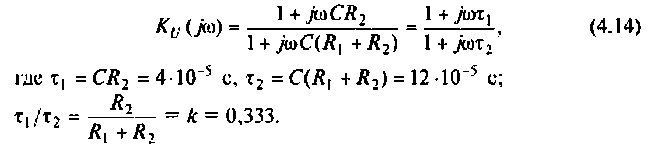
3. Для нахождения АЧХ и ФЧХ комплексную функцию 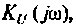 представленную в виде отношения двух полиномов мнимой частоты
представленную в виде отношения двух полиномов мнимой частоты 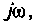 записывают в показательной форме
записывают в показательной форме
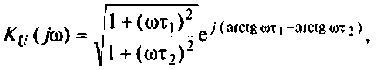
Найдем модуль (АЧХ) и аргумент (ФЧХ) комплексной функции;
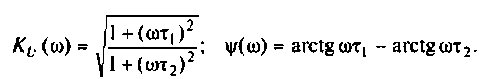
Для определения вещественной и мнимой частотных характеристик запишем КФЦ в алгебраической форме. Для этого умножим и разделим (4.14) на комплексно-сопряженный знаменатель:
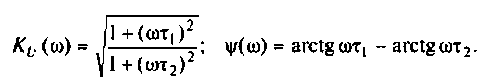
4. Для приближенного построения графиков АЧХ, ФЧХ. АФХ найдем значения 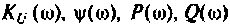 для трех значений частот:
для трех значений частот: 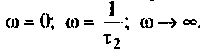 Результаты расчетов для удобства построения графиков сведем в табл. 4.2.
Результаты расчетов для удобства построения графиков сведем в табл. 4.2.

Для более точного и наглядного представления графиков воспользуемся ПЭВМ и математической средой Mathcad.
Графики характеристик приведены на рис. 4.13.
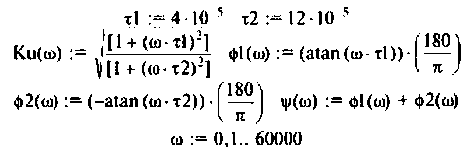
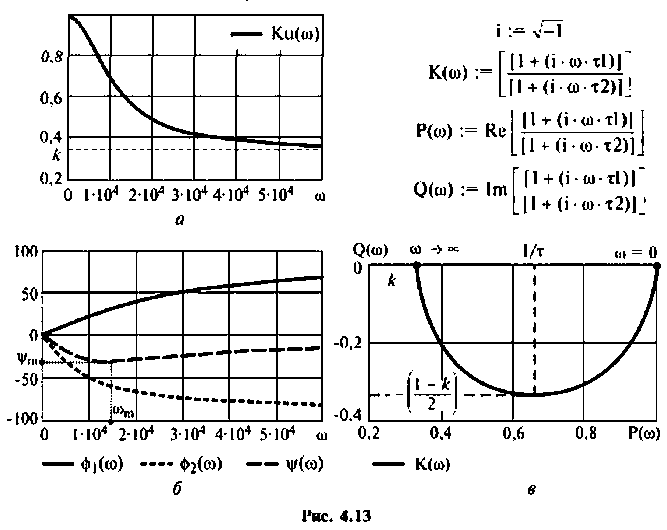
АЧХ представляет монотонно убывающую функцию (рис. 4.13, а).
ФЧХ принимает отрицательные значения, т.е. контур вносит фазовое отставание, а на частоте  ФЧХ имеет экстремум (рис.4.13, б). Найдем из соотношения
ФЧХ имеет экстремум (рис.4.13, б). Найдем из соотношения
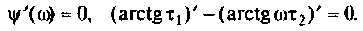
Взяв производную, получим
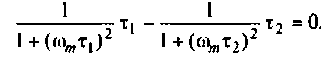
Решая полученное уравнение относительно  , найдем
, найдем
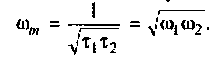
Подставляя  в выражение
в выражение 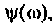 определим максимальное значение фазовой частотной характеристики.
определим максимальное значение фазовой частотной характеристики.
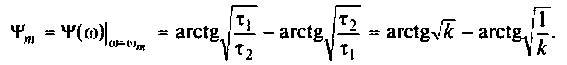
АФХ (рис. 4.13, в) представляет собой полуокружность, расположенную в 4-м квадрате. Центр окружности находится на оси 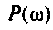 в точке с абсциссой, равной
в точке с абсциссой, равной
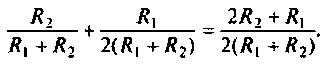
Радиус окружности нетрудно определить из соотношения:
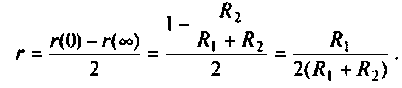
МЧХ:
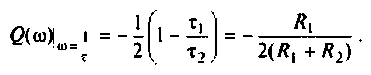
Отрицательное значение 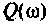 свидетельствует о том, что
свидетельствует о том, что
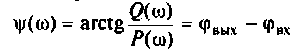 принимает отрицательное значения, т.е. интегрирующий контур вносит запаздывание по фазе.
принимает отрицательное значения, т.е. интегрирующий контур вносит запаздывание по фазе.
5. Проверка расчетов АЧХ. Воспользуемся эквивалентными схемами цепи для частот 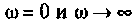 (рис. 4.14).
(рис. 4.14).
На частоте 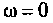 цепь разомкнута (рис. 4.14, а), поэтому
цепь разомкнута (рис. 4.14, а), поэтому
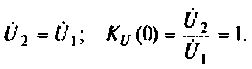
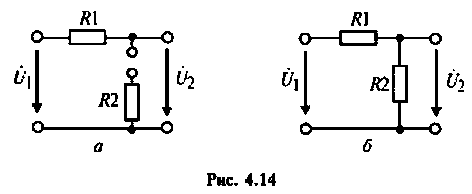
При 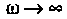 схема представляет собой резистивный делитель напряжения (рис. 4.14, б) с коэффициентом передачи
схема представляет собой резистивный делитель напряжения (рис. 4.14, б) с коэффициентом передачи
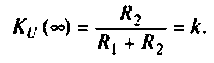
Подставляя эти значения частот в аналитическое выражение (4.14) для 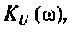 получаем
получаем
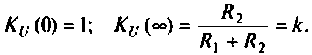
Следовательно, расчет АЧХ выполнен верно.
Частотные характеристики последовательного колебательного контура
Основные теоретические сведения:
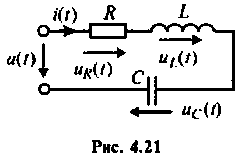
В последовательном колебательном контуре (рис. 4.21) возникает резонанс напряжений, если выполняется условие
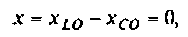
т. е. 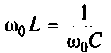
Резонансная частота
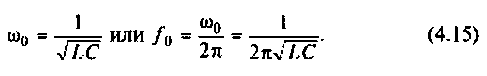
Волновое сопротивление контура 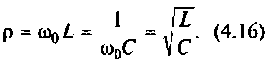
Сопротивление контура при резонансе 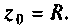
Собственная добротность контура 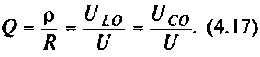
Добротность нагруженного контура 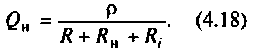
Затухание контура 
Абсолютная расстройка 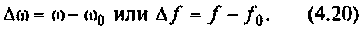
Относительная расстройка 
Обобщенная расстройка
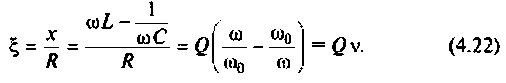
Фактор расстройки: 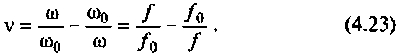
Абсолютная полоса пропускания (рис. 4.22)
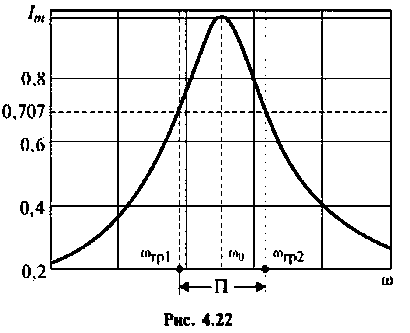
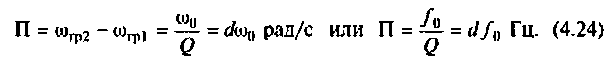
Относительная полоса пропускания

Для нагруженного контура:
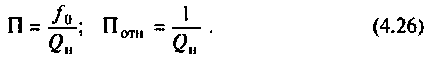
Комплексные коэффициенты передачи по напряжению:
на активном сопротивлении
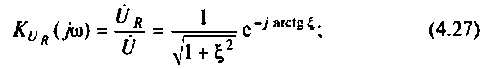
на индуктивности
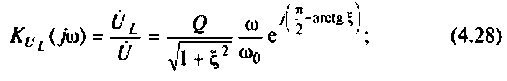
на емкости
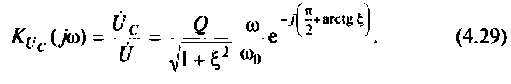
Примеры решения типовых задач:
Пример 4.3.1.
Последовательный колебательный контур (рис. 4.23) подключен к источнику напряжению. Контур настроен в резонанс.
Параметры цепи: 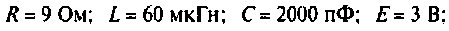
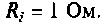
Определить резонансную частоту, волновое сопротивление. добротность и полосу пропускания, ток и напряжения на элементах контура.
Построить АЧХ и ФЧХ по напряжению на конденсаторе в среде Mathcad.
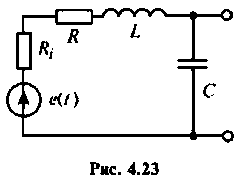
Решение
1. Определяем резонансную частоту контура
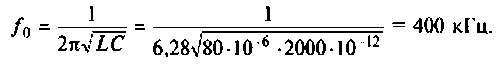
2. Находим волновое сопротивление контура
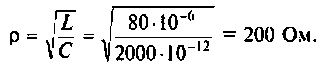
3. Вычисляем добротность нагруженного контура
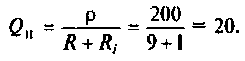
4. Определяем полосу пропускания
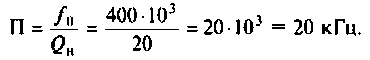
5. Рассчитываем ток и напряжения на элементах контура при резонансе
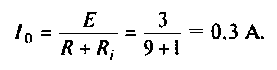
Напряжение на R равно
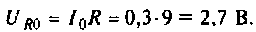
Напряжения на реактивных элементах
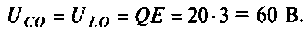
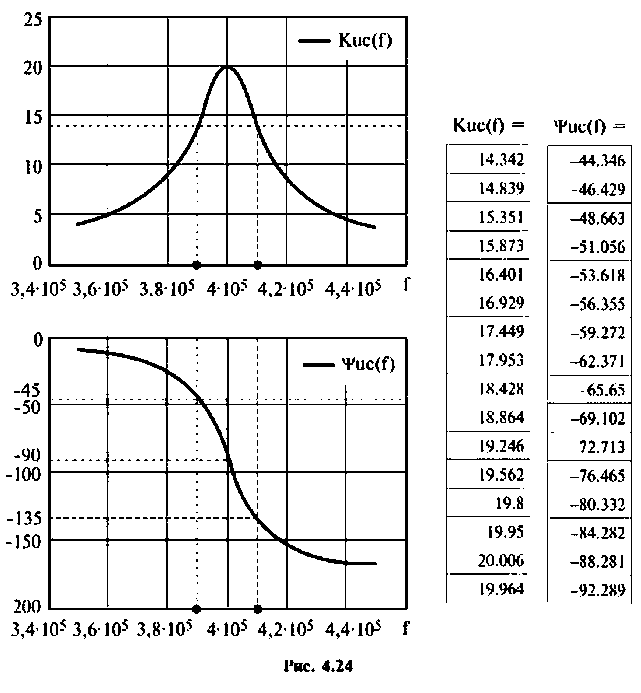
6. Рассчитаем АЧХ и ФЧХ комплексного коэффициента передачи напряжения с емкости.
Учитывая (4.22), из (4.29) получим:
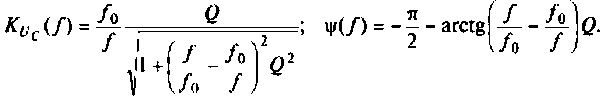
Для построения графиков АЧХ и ФЧХ, выполнения расчетов используем среду Mathcad. АЧХ, ФЧХ в виде графиков и таблиц приведены на рис. 4.24.
Следует заметить, что максимум А11Х достигается на частоте
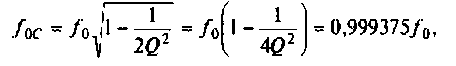
т.е. при 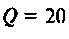 смещение максимума мало, тогда
смещение максимума мало, тогда 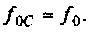
Задача 4.3.2.
К последовательному колебательному контуру (рис. 4.25) с параметрами 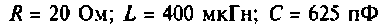 подключена нагрузка
подключена нагрузка 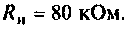
Определить собственную добротность и добротность нагруженного контура, полосу пропускания нагруженного и ненагруженного контура.
Решение
1. Рассчитаем вторичные параметры ненагруженного контура:
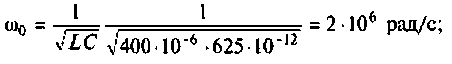
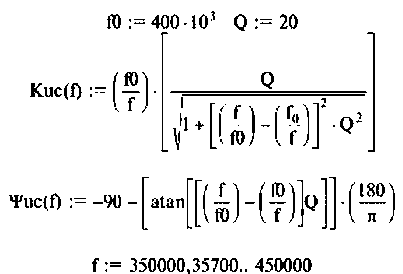
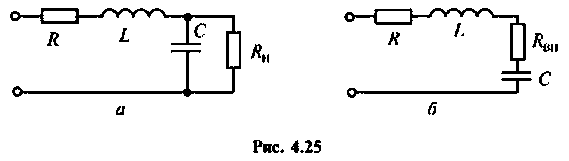
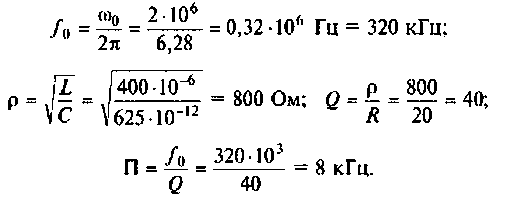
2.Определим вторичные параметры наруженного контура. Так как сопротивление нагрузки активное, причем 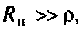 то согласно (4.15) и (4.16) резонансная частота и волновое сопротивление не изменяются.
то согласно (4.15) и (4.16) резонансная частота и волновое сопротивление не изменяются.
Для определения добротности рассчитаем сопротивление 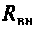 , вносимое в контур за счет нагрузки, и построим эквивалентную схему нагруженного контура (рис. 4.25, б). Так как
, вносимое в контур за счет нагрузки, и построим эквивалентную схему нагруженного контура (рис. 4.25, б). Так как 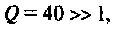 то
то
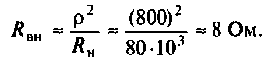
Следовательно,
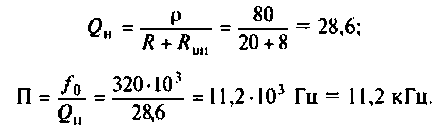
Вывод. Подключение нагрузки ухудшает добротность контура, что приводит к расширению полосы пропускания.
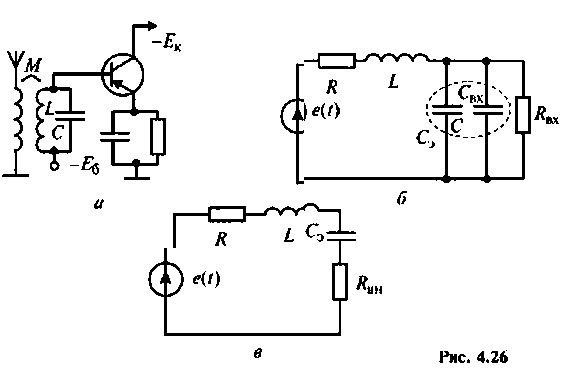
Пример 4.3.3.
На рис. 4.26, а изображена входная цепь приемника, а на рис. 4.26, б — ее эквивалентная схема. Известны входное сопротивление и входная емкость транзистора входного каскада УВЧ:  . На резонансной частоте антенна наводит в контуре ЭДС
. На резонансной частоте антенна наводит в контуре ЭДС 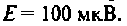 Емкость конденсатора
Емкость конденсатора 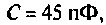 катушка индуктивности имеет
катушка индуктивности имеет 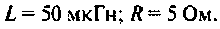
Определить абсолютную полосу пропускания и ток в контуре на резонансной частоте.
Решение
1. Определяем эквивалентную емкость контура
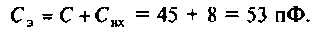
2. Рассчитываем резонансную частоту контура
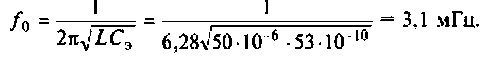
3. Находим волновое сопротивление и сопротивление, вносимое в контур за счет транзистора усилителя (рис. 4.26, в):
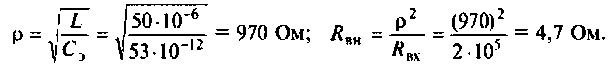
4. Определяем добротность нагруженного контура
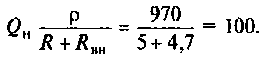
5. Рассчитаем абсолютную полосу пропускания нагруженного контура
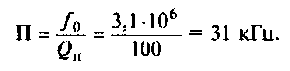
6. Находим ток в контуре
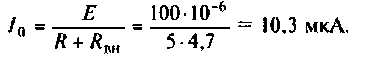
Пример 4.3.4.
Рассчитать емкость последовательного колебательного контура, если резонансная частота контура 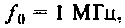 полоса пропускания
полоса пропускания 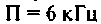 при сопротивлении потерь 0,5 Ом.
при сопротивлении потерь 0,5 Ом.
Построить АЧХ и ФЧХ комплексного коэффициента передачи напряжения с индуктивности в среде Mаthcad.
Решение
1. Определим требуемую добротность контура
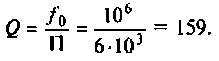
2. Рассчитаем емкость конденсатора. Из формулы 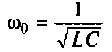 найдем
найдем
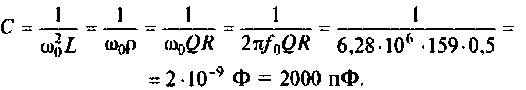
3. Рассчитаем АЧХ и ФЧХ.
Воспользуемся комплексным коэффициентом передачи напряжения с индуктивности по формуле (4.28). Учитывая 4.22), запишем:
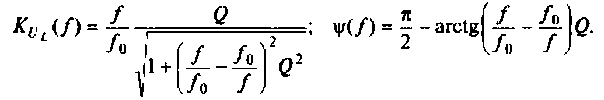
Вычислим значения функций на частотах:
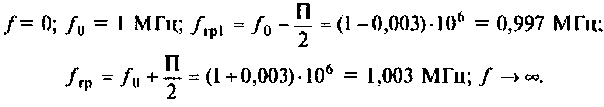
Определим частоту, при которой АЧХ имеет максимум
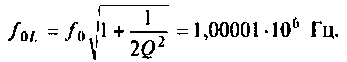
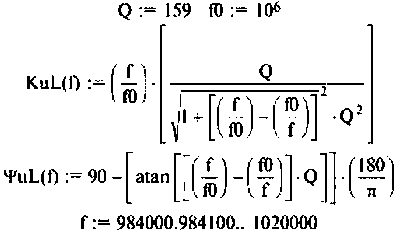
Смещением частоты  можно пренебречь.
можно пренебречь.
Результаты расчетов АЧХ и ФЧХ б графическом и табличном видах приведены на рис. 4.27.
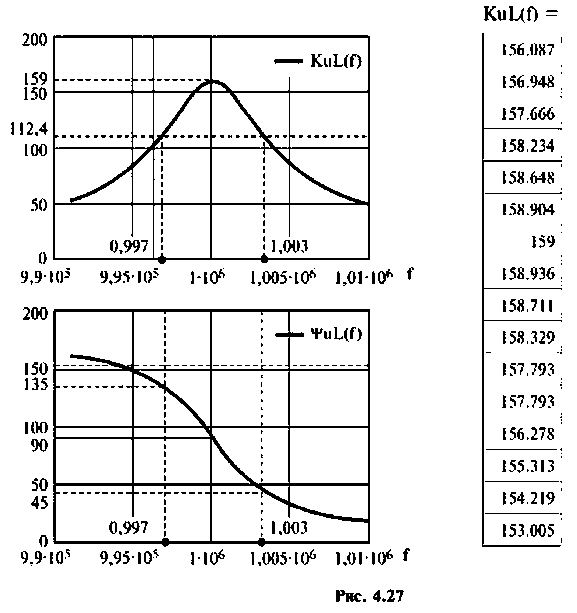
Частотные характеристики параллельного колебательного контура
Основные теоретические сведения:
Параллельный колебательный контур образуется путем параллельного соединения катушки индуктивности и конденсатора. Оба элемента, кроме основного эффекта (запасания энергии), имеют потери энергии. В расчетной схеме (рис. 4.29, а) тепловые потери в элементах учтены включением условных сопротивлений 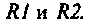
где резонансная частота колебаний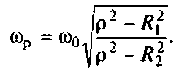
Для реального контура 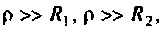 поэтому при расчете можно полагать, что
поэтому при расчете можно полагать, что
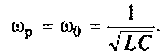
При резонансе сопротивление контура является активным, поэтому ток 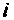 в цепи и напряжение
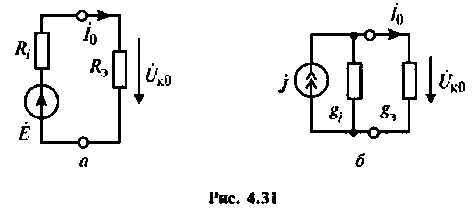
в цепи и напряжение 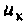 в контуре синфазны. Эквивалентные схемы цепи в режиме резонанса токов показаны на рис. 4.31, а, б.
в контуре синфазны. Эквивалентные схемы цепи в режиме резонанса токов показаны на рис. 4.31, а, б.
Сопротивление параллельного колебательного контура при резонансе максимально и равно (без учета внешней цепи)
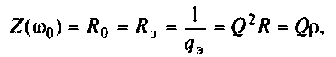
где 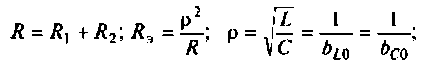
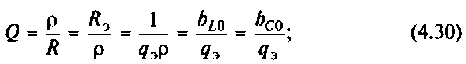
Добротность 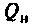 нагруженного контура меньше собственной добротности
нагруженного контура меньше собственной добротности 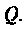 Ее можно выразить через сопротивления элементов цепи
Ее можно выразить через сопротивления элементов цепи
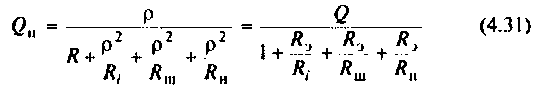
или через их проводимости
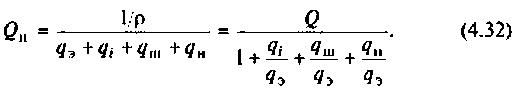
Важными параметрами цепи при резонансе являются токи в ветвях и напряжение на контуре. Ток в обшей ветви (ток источника) при резонансе минимален и равен (см. рис. 4.31)
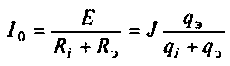
При этом напряжение на контуре максимально и равно
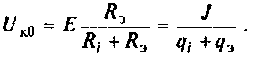
Токи в индуктивности и в емкости при резонансе равны по значению и противоположны по направлению. Они образуют замкнутый ток в контуре, равный
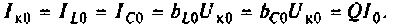
Частотные свойства параллельного колебательного контура обычно оценивают по нормированной АЧХ
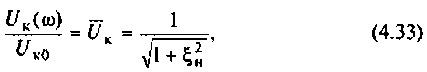
где 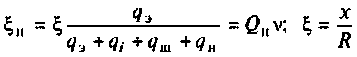 -обобщенная расстройка контура без учета внешних цепей;
-обобщенная расстройка контура без учета внешних цепей; 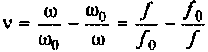 — фактор расстройки.
— фактор расстройки.
Параллельный контур, показанный на рис. 4.29, имеет по одной реактивности в ветвях. Такой контур называется простым или контуром I вида. Для уменьшения шунтирующего действия внешних цепей часто применяют сложные параллельные контуры.
На рис. 4.32, а, б, в показаны контуры II, (III и IV) видов, соответственно.
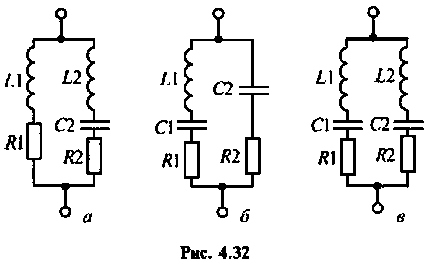
Главной особенностью этих контуров является то, что их резонансное сопротивление меньше резонансного сопротивления простого контура с такими же параметрами.
Сопротивление контуров (рис.4.32) при резонансе рассчитывается по формулам, соответственно:
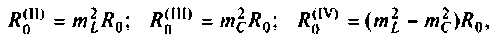
где 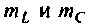 — коэффициенты включения:
— коэффициенты включения:
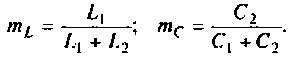
Примеры решения типовых задач:
Пример 4.4.1.
Параллельный контур (см. рис. 4.29, а) подключен к источнику с параметрами 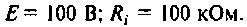 Контур настроен в резонанс на длину волны, равную 1000 м.
Контур настроен в резонанс на длину волны, равную 1000 м.
Параметры катушки индуктивности: 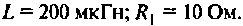
Определить действующие значения тока в контуре, тока на входе цепи и напряжения на контуре при резонансе, абсолютную и относительную полосы пропускания контура, добавочное сопротивление необходимое для расширения полосы пропускания в 2 раза.
Решение
1. Определим резонансную частоту колебания
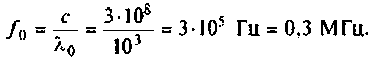
2. Рассчитаем волновое сопротивление
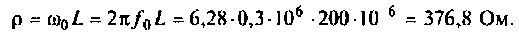
3. Определим сопротивление контура при резонансе
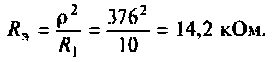
4. Найдем действующее значение тока на входе контура (см. рис. 4.31, а) при резонансе
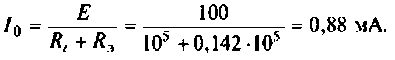
5. Определим соответственную добротность контура
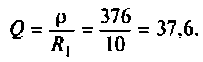
6. Найдем ток в контуре и напряжение на нем:
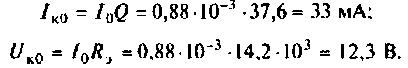
7. Определим добротность нагруженного контура
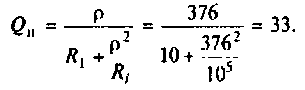
8. Рассчитаем абсолютную и относительную полосы пропускания:
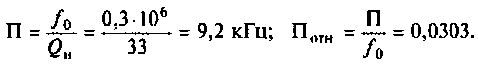
9. Определяем добавочное cопротивление 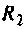 из (4.31)
из (4.31)
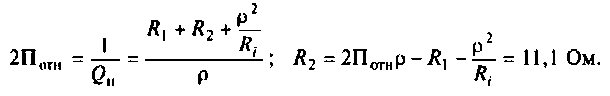
Пример 4.4.2.
Рассчитать полосу пропускания колебательного контура (см. рис. 4.30, а).
Дано: 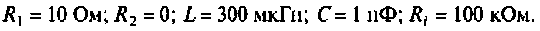
Определить сопротивление 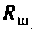 шунта, необходимого для расширения полосы пропускания до 10 кГц.
шунта, необходимого для расширения полосы пропускания до 10 кГц.
Решение
1. Рассчитаем волновое сопротивление и резонансную частоту контура:
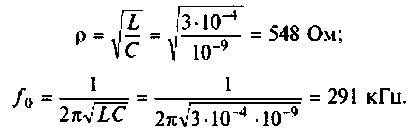
2.Рассчитаем добротность цепи без шунта. Воспользуемся трехветвевой эквивалентной схемой цепи и соотношением (4.32). Найдем проводимость элементов схемы:
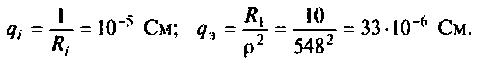
Тогда
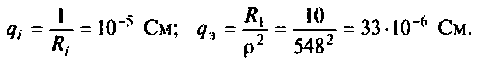
3. Определим полосу пропускания
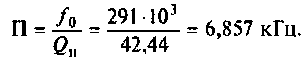
4. Найдем сопротивление шунта, необходимою для расширения полосы до 10 кГц,
В этом случае добротность цепи должна быть равна
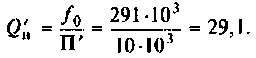
Тогда из (4.32) получаем
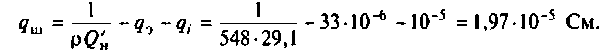
Следовательно, сопротивление шунта должно быть равно
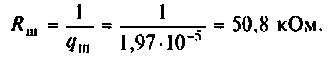
Пример 4.4.3.
Параллельный колебательный контур с параметрами: 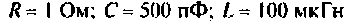 подключен к источнику
подключен к источнику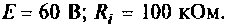
Определить собственную добротность контура, добротность нагруженного контура, абсолютную полосу пропускания и граничные частоты полосы пропускания. Построить резонансную кривую по напряжению на ЭВМ.
Решение
1. Определим волновое сопротивление контура
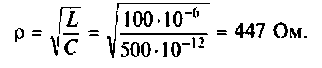
2. Рассчитаем собственную добротность контура
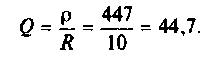
3. Найдем сопротивление контура при резонансе
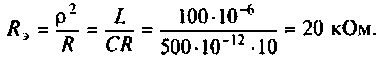
4. Определим добротность нагруженного контура по формуле (4.31)
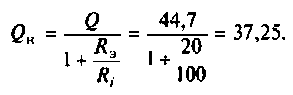
5. Рассчитаем резонансную частоту
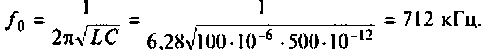
6. Найдем полосу пропускания
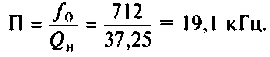
7. Определим граничные частоты полосы пропускания:
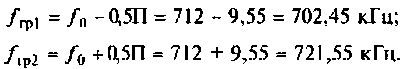
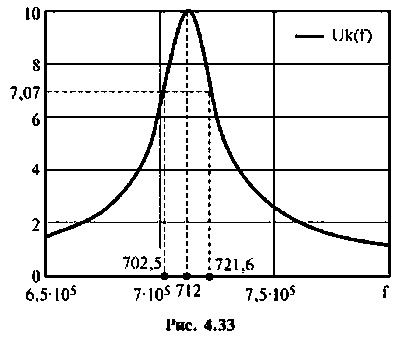
8. Построим резонансную характеристику контура но напряжению. Из выражения (4.33) запишем
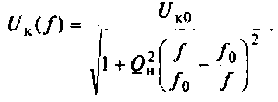
Напряжение па контуре при резонансе
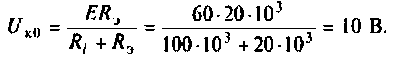
Для построения резонансной характеристики задаемся характерными значениями частот: 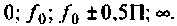 Результаты расчетов в графическом виде представлены на рис. 4.33.
Результаты расчетов в графическом виде представлены на рис. 4.33.
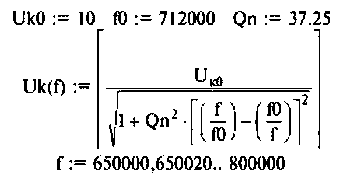
Пример 4.4.4.
Определить резонансную частоту, эквивалентное сопротивление при резонансе и добротность сложного контура (рис. 4.32, а), подключенного к источнику напряжения.
Дано: 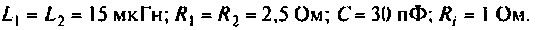
Решение
1. Определим резонансную частоту и сопротивление параллельного контура при резонансе:
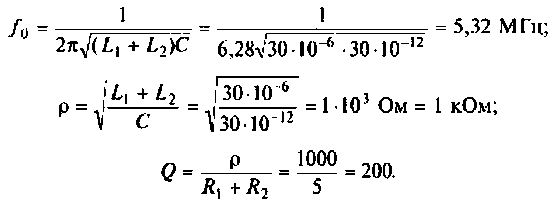
Сопротивление контура при резонансе
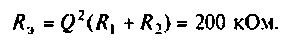
2. Рассчитаем эквивалентное сопротивление сложного контура II вида
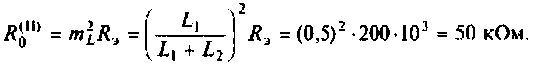
3. Найдем добротность нагруженного контура II вида
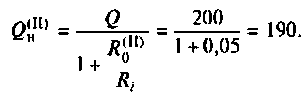
Сравним значения 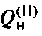 с добротностью простого нагруженного контура
с добротностью простого нагруженного контура
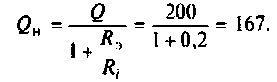
Вывод. За счет неполного включения индуктивности 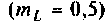 уменьшилось шунтирующее действие источника. Поэтому добротность сложного контура больше, чем простого с теми же параметрами элементов.
уменьшилось шунтирующее действие источника. Поэтому добротность сложного контура больше, чем простого с теми же параметрами элементов.
Частотные характеристики связанных колебательных контуров
Основные теоретические сведения:
С целью повышения коэффициента прямоугольности АЧХ контуров применяют связанные контуры последовательного и параллельного питания (рис. 4.37, а, б).
Частотные характеристики связанных контуров рассмотрим на примере системы из двух контуров.
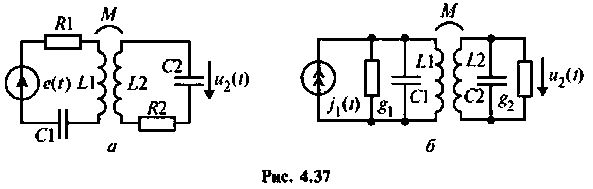
Эквивалентные схемы связанных контуров
Во всех случаях систему связанных контуров можно представить в виде Т- или П-образной эквивалентной схемы (рис. 4.38).
Количественной характеристикой связи является сопротивление связи 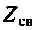 в Т-образной эквивалентной схеме (рис. 4.38,а) или проводимость связи
в Т-образной эквивалентной схеме (рис. 4.38,а) или проводимость связи 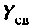 в П-образной эквивалентной схеме (рис. 4.38, б).
в П-образной эквивалентной схеме (рис. 4.38, б).
Удобным параметром для оценки связи является коэффициент связи
В случае реактивной связи для Т-образной схемы
Для П-образной схемы
где — сопротивление (проводимость) связи;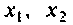
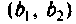 — сопротивления (проводимости) контуров, однотипные элементу связи. Для анализа связанных контуров удобно применять схемы, приведенные к первичному (рис. 4.39, а) или ко вторичному (рис. 4.39, б) контуру.
— сопротивления (проводимости) контуров, однотипные элементу связи. Для анализа связанных контуров удобно применять схемы, приведенные к первичному (рис. 4.39, а) или ко вторичному (рис. 4.39, б) контуру.
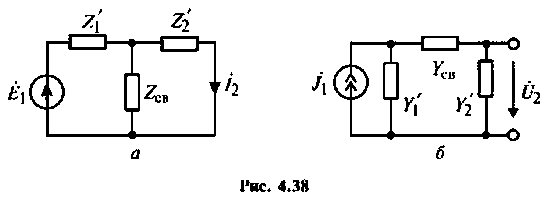
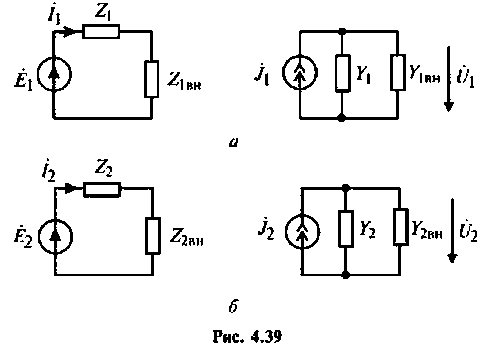
Для этого используют понятия вносимого сопротивления 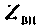 и вносимой проводимости
и вносимой проводимости 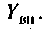 Эти схемы представляют собой одиночные последовательные (параллельные) контуры с параметрами:
Эти схемы представляют собой одиночные последовательные (параллельные) контуры с параметрами:
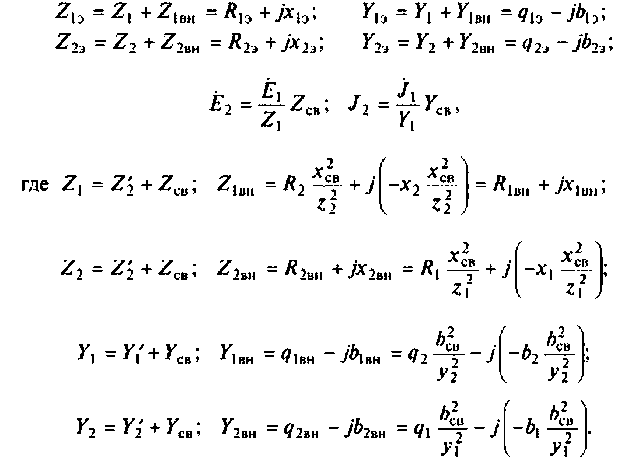
Резонансы в связанных контурах:
При настройке контуров в резонанс добиваются максимального тока (напряжения) во вторичном контуре.
Настройка связанных контуров может производиться различными способами, поэтому различают шесть резонансов. В табл. 4.3, 4.4 приведены виды и условия резонансов, способы настройки и соотношения для токов (напряжений) в связанных контурах последовательного (параллельного) питания.


Резонансные характеристики связанных контуров:
Для двух неидентичных связанных контуров: последовательного питания
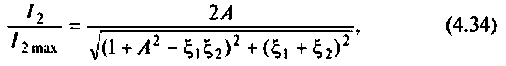
где 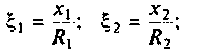
параллельного питания:
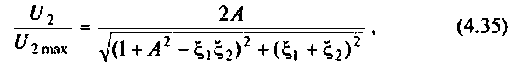
где 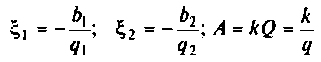 — параметр связи.
— параметр связи.
Если контуры идентичны, то обобщенная расстройка 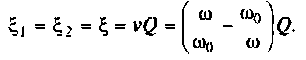
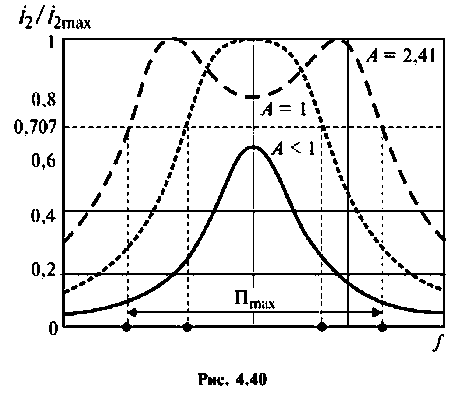
На рис. 4.40 приведены резонансные характеристики при различных факторах связи.
Относительная полоса пропускания:
а) связь слабая 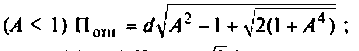
б) связь критическая 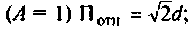
в) связь сильная 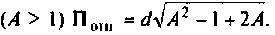
При 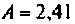 достигается максимально возможная полоса пропускания
достигается максимально возможная полоса пропускания 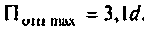
Примеры решения типовых задач:
Пример 4.5.1.
В системе двух индуктивно связанных контуров (см. рис.4.37,а) известны следующие параметры: коэффициент связи
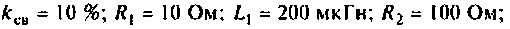
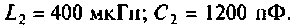
Определить емкость 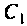 при которой в системе наступает первый частный резонанс, если частота источника равна 500 кГц.
при которой в системе наступает первый частный резонанс, если частота источника равна 500 кГц.
Решение
Емкость конденсатора 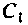 определим но реактивному сопротивлению первого контура:
определим но реактивному сопротивлению первого контура:
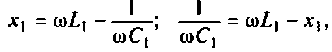
отсюда
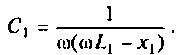
Определим реактивное сопротивление 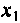 , первого контура из условия первого частного резонанса (см. табл. 4.3)
, первого контура из условия первого частного резонанса (см. табл. 4.3)
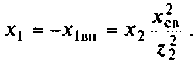
Peaктивное сопротивление второго контура
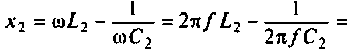
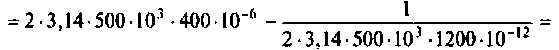
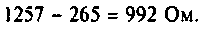
Рассчитаем полное сопротивление второго контура
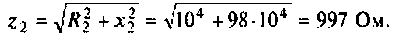
Определим сопротивление связи контуров
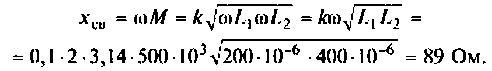
Следовательно
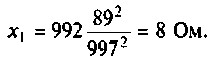
Находим емкость первого контура
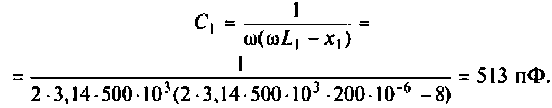
Пример 4.5.2.
Рассчитать емкости связанных контуров (см. рис. 4.37,а) и оптимальное сопротивление связи, если система настроена и полный резонанс. Определить токи, мощности в контурах при этом режиме, а также КПД системы.
Дано: 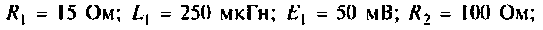
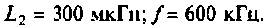
Решение
1. Определим емкость конденсатора 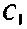 , полагая, что
, полагая, что
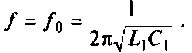
Отсюда
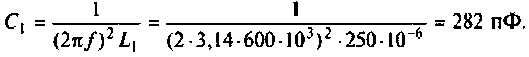
2. Сопротивление оптимальной связи при полном резонансе
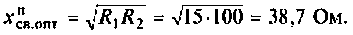
3. Рассчитаем токи в первом и втором контурах при полном резонансе
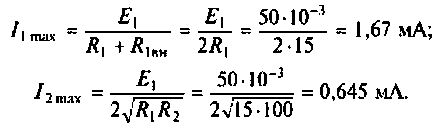
4. Определим активные мощности в первом и втором контурах и КПД связанных контуров:
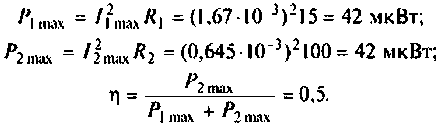
Пример 4.5.3.
На рис. 4.37, а показана система из двух идентичных связанных контуров с параметрами: 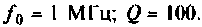 Рассчитать полосы пропускания одиночного контура и связанных контуров при различной связи:
Рассчитать полосы пропускания одиночного контура и связанных контуров при различной связи: 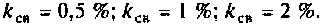
Решение
1. Определим полосу пропускания одиночного контура
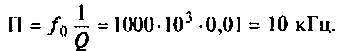
2. Рассчитаем полосу пропускания системы связанных контуров:
1) определим параметр связи для 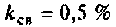
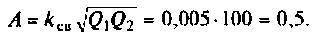
Таким образом при 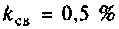 связь меньше критической
связь меньше критической 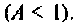 При этом относительная полоса пропускания
При этом относительная полоса пропускания
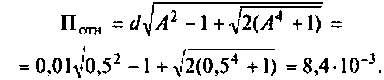
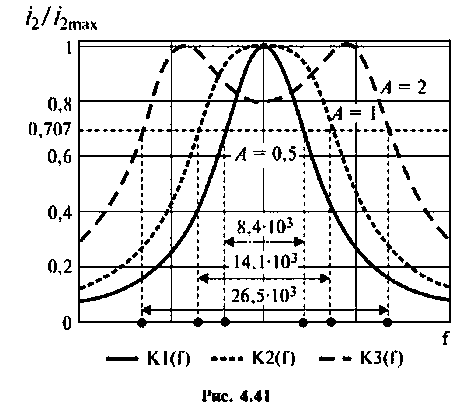
Абсолютная полоса пропускания (рис. 4.41, резонансная кривая А = 0,5)
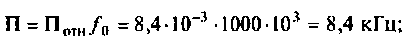
2) при 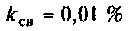 параметр связи
параметр связи 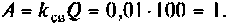 Таким образом, коэффициент связи является оптимальным, а связь критическая, система настроена в полный резонанс. Полоса пропускания в этом случае
Таким образом, коэффициент связи является оптимальным, а связь критическая, система настроена в полный резонанс. Полоса пропускания в этом случае
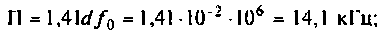
3) если 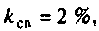 то параметр связи
то параметр связи 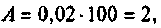 следовательно, связь больше критической.
следовательно, связь больше критической.
Рассчитаем полосу пропускания для этого случая.
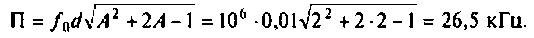
Вид резонансных кривых по току и полоса пропускания для критической и сильной связи показаны на рис. 4.41, кривые А = 1 и А = 2.

Пример 4.5.4.
Антенный контур (см. рис. 4.37,б) индуктивно связан с входным контуром усилителя высокой частоты. Оба контура настроены в резонанс на частоту 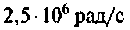 принимаемого сигнала. В антенном контуре наводится
принимаемого сигнала. В антенном контуре наводится 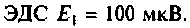
Дано: 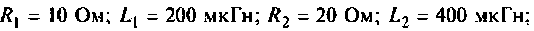
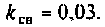
Входное сопротивление УВЧ считать бесконечно большим.
Определить емкости и добротности контуров, их взаимную индуктивность, а также ток и напряжение на емкости во вторичном контуре.
Решение
1.Емкости контуров определим из формулы резонансной частоты. Емкость конденсатора первого контура
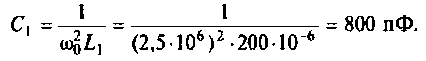
Емкость конденсатора второго контура
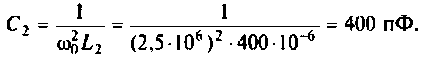
2. Рассчитаем волновое сопротивление контуров:
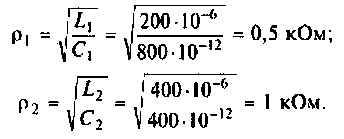
3. Рассчитаем добротности контуров и параметр связи:
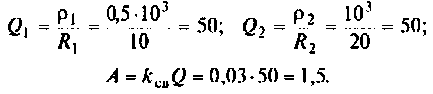
4. Определим взаимную индуктивность двух связанных контуров
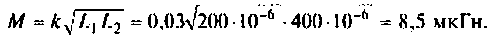
5. Рассчитаем ток во вторичном контуре. Известно (см. табл. 4.3), что при полном резонансе 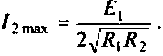
Тогда, учитывая, что контуры настроены в резонанс, то из (4.34) получаем
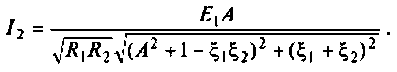
Оба контура по условию настроены в резонанс, поэтому расстройки равны нулю:
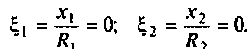
С учетом этого рассчитаем ток во втором контуре
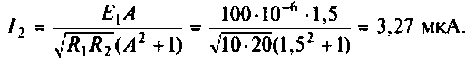
6. Найдем напряжение на конденсаторе вторичного контура
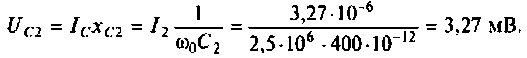
Пример 4.5.5.
На рис. 4.42 приведена схема одного каскада УПЧ радиоприемника, в котором избирательность обеспечивается двумя связанными контурами с емкостной связью. Оба контура настроены в резонанс на промежуточную частоту 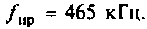
Эквивалентная схема этого каскада (рис. 4.43) имеет следующие параметры: 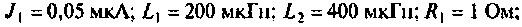
Определить емкости и добротности контуров, емкость связи, напряжение на емкости во вторичном контуре, а также полосу пропускания каскада УПЧ.
Решение
1. Из формулы резонансной частоты найдем емкость первого контура. С учетом влияния выходной емкости транзистора 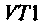 и емкости монтажа получаем
и емкости монтажа получаем
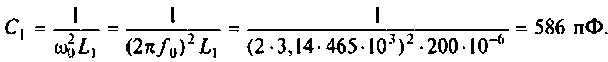
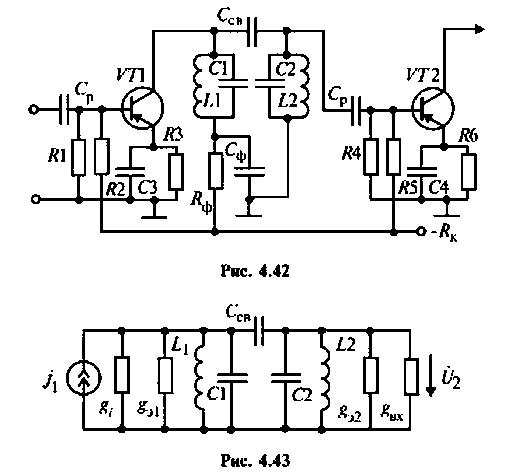
Емкость второго контура с учетом влияния входной емкости транзистора 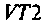 и емкости монтажа
и емкости монтажа
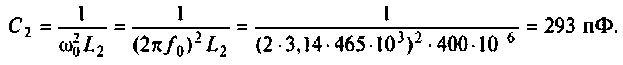
2. Определим емкость связи
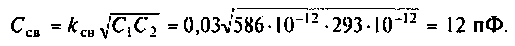
3. Рассчитаем добротности нагруженных контуров при отсутствии связи между ними. Для расчета воспользуемся формулой (4.31)
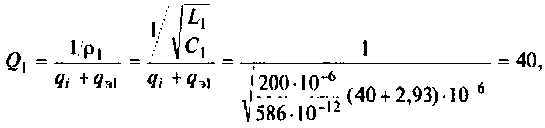
где
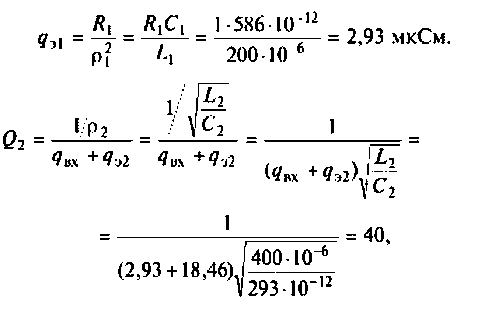
где
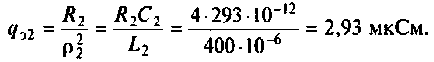
4. Рассчитаем параметр связи 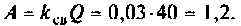
5. Рассчитаем напряжение на втором контуре. Известно (см. табл. 4.4), что при полном резонансе
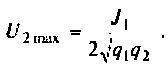
Тогда, учитывая, что контуры настроены в резонанс 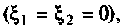 из (4.35) получаем
из (4.35) получаем
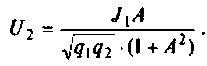
Найдем проводимость контуров
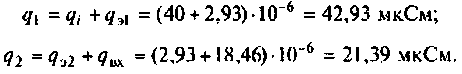
Тогда
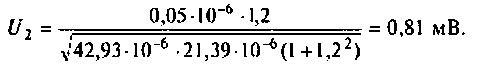
6. Рассчитаем полосу пропускания каскадов УПЧ. учитывая, что А = 1,2.
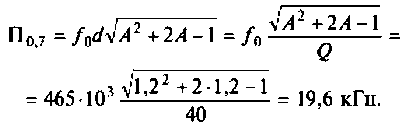
Частотные методы расчета и построения переходных и установившихся процессов в электрических цепях
Основные теоретические сведения:
Зная частотную характеристику электрической цепи 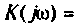
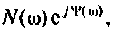 можно определить ее выходную величину при подаче на вход синусоидального (гармонического) сигнала. Действительно, если на вход цепи подано синусоидальное напряжение комплексное изображение которого
можно определить ее выходную величину при подаче на вход синусоидального (гармонического) сигнала. Действительно, если на вход цепи подано синусоидальное напряжение комплексное изображение которого 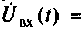
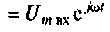 то в установившемся режиме комплексное изображение выходного напряжения
то в установившемся режиме комплексное изображение выходного напряжения
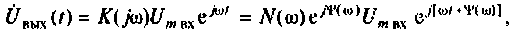
где 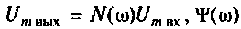 амплитуда и сдвиг по фазе выходных колебаний соответственно.
амплитуда и сдвиг по фазе выходных колебаний соответственно.
С помощью частотной характеристики электрической цели можно не только определить выходную величину цепи в установившемся режиме при гармоническом входном воздействии, но и найти реакцию цепи в переходном процессе на произвольное воздействие 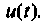 . Действительно, представляя это воздействие в зависимости от того, является оно периодической или непериодической функцией, в виде ряда или интеграла Фурье, т.е. в виде бесконечной суммы гармонических колебаний. По частотной характеристике можно определить реакцию электрической цепи на каждое из этих элементарных колебаний, а затем, просуммировав все реакции, найти результирующую реакцию в виде суммы или интеграла [4].
. Действительно, представляя это воздействие в зависимости от того, является оно периодической или непериодической функцией, в виде ряда или интеграла Фурье, т.е. в виде бесконечной суммы гармонических колебаний. По частотной характеристике можно определить реакцию электрической цепи на каждое из этих элементарных колебаний, а затем, просуммировав все реакции, найти результирующую реакцию в виде суммы или интеграла [4].
Найдем реакцию цепи на единичную ступенчатую функцию (т.е. найдем переходную функцию цепи), используя ее частотную характеристику. Как известно, интеграл Фурье для единичной ступенчатой функции имеет вид
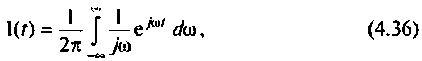
т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида 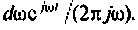
Каждому из этих колебаний соответствует выходное колебание 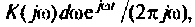 а реакция системы на единичную ступенчатую функцию выражается интегралом
а реакция системы на единичную ступенчатую функцию выражается интегралом
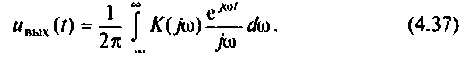
Представляя 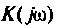 в алгебраической форме
в алгебраической форме 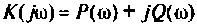 и преобразуя выражение (4.37), получаем следующую формулу для переходной функции |4, 6|:
и преобразуя выражение (4.37), получаем следующую формулу для переходной функции |4, 6|:
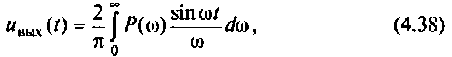
где 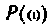 — вещественная частотная характеристика (ВЧХ) КФ электрической цепи. Полученное выражение связывает ВЧХ КПФ цепи с ее переходной функцией. Таким образом, при частотном методе анализа косвенной характеристикой переходной функции является вещественная частотная характеристика КФ электрической цепи.
— вещественная частотная характеристика (ВЧХ) КФ электрической цепи. Полученное выражение связывает ВЧХ КПФ цепи с ее переходной функцией. Таким образом, при частотном методе анализа косвенной характеристикой переходной функции является вещественная частотная характеристика КФ электрической цепи.
Построение переходной функции с помощью вещественной частотной характеристики методами численного интегрирования:
Выражение (4.38) позволяет вычислить переходную функцию ЭЦ и определить качество переходного процесса. Однако интегрирование этого выражения аналитическими методами — задача весьма трудоемкая, а чаще всего просто практически невыполнимая. С применением современных ЭВМ и методов численного интегрирования (метод прямоугольников, трапеций, метод Симпсона и др.) эта задача существенно упрощается, ее решение сводится к составлению программы для ПЭВМ. В инженерной практике интегрирование достаточно осуществлять в области существенных частот от 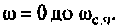 В области частот
В области частот  влияние ВЧХ
влияние ВЧХ 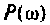 на переходную функцию (4.38) мало и им можно пренебречь. В dtom случае используют модифицированное выражение от (4.38) [4]
на переходную функцию (4.38) мало и им можно пренебречь. В dtom случае используют модифицированное выражение от (4.38) [4]
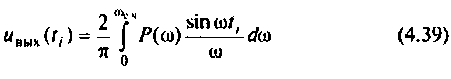
В результате интегрирования получают совокупность значений 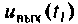 переходной функции системы и исследуемом интервале времени и строят график переходной функции, по которой определяют показатели качества переходного процесса.
переходной функции системы и исследуемом интервале времени и строят график переходной функции, по которой определяют показатели качества переходного процесса.
В качестве примера построения алгоритма численного интегрирования рассмотрим интегрирование с точки зрения простоты вычислений и точности результата. Сущность метода заключается в следующем. Пусть необходимо вычислить определенный интеграл
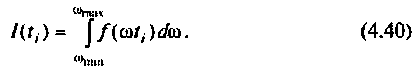
Вид подынтегральной функции, соответствующей выражению
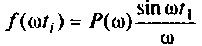
при фиксированном времени 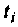 приведен на рис. 4.47, кривая
приведен на рис. 4.47, кривая 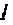 для t = 10 с, кривая 2 для
для t = 10 с, кривая 2 для 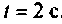 , а кривая 3 изображает ВЧХ электрической цепи. Функция
, а кривая 3 изображает ВЧХ электрической цепи. Функция 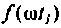 представляет функцию
представляет функцию 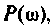 модулированную «замечательным» синусом. Известно, что интеграл (4.40) численно равен площади под кривой функции
модулированную «замечательным» синусом. Известно, что интеграл (4.40) численно равен площади под кривой функции 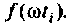 Если интервал аргумента
Если интервал аргумента 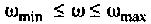 разбить на
разбить на 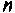 равных частей, то длина одного интервала будет равна
равных частей, то длина одного интервала будет равна 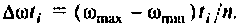 Площадь под кривой можно аппроксимировать суммой площадей прямоугольных трапеций с основаниями
Площадь под кривой можно аппроксимировать суммой площадей прямоугольных трапеций с основаниями 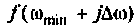
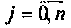 и высотой
и высотой  Тогда интеграл (4.40) можно представить как сумму площадей прямоугольных трапеций:
Тогда интеграл (4.40) можно представить как сумму площадей прямоугольных трапеций:
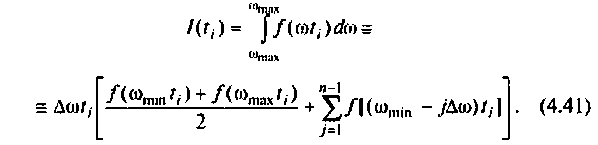
Очевидно, что погрешность численного интегрирования зависит и от выбора числа интервалов 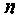 разбиения аргумента
разбиения аргумента 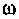 при конкретном времени
при конкретном времени 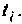 При увеличении времени , как видно из рис. 4.47, период подынтегральной функции уменьшается. Следовательно, необходимо увеличивать число интервалов, которое определился выражением
При увеличении времени , как видно из рис. 4.47, период подынтегральной функции уменьшается. Следовательно, необходимо увеличивать число интервалов, которое определился выражением

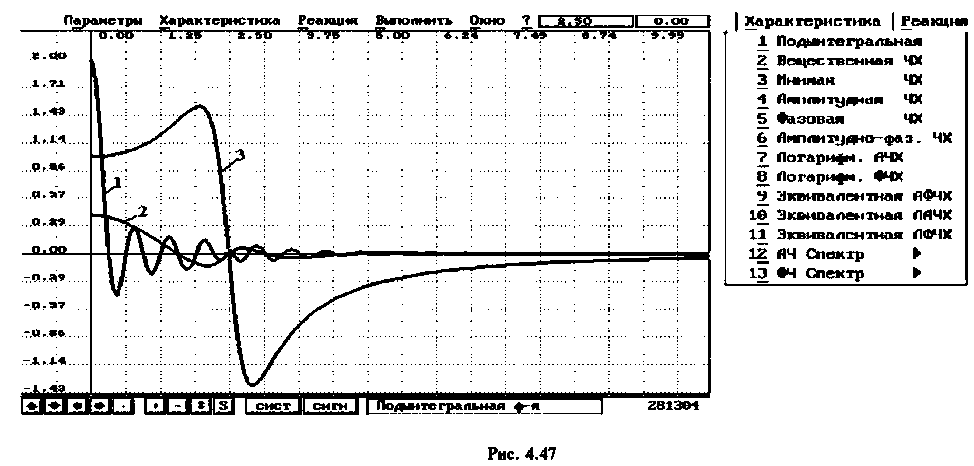
При этом одно полное колебание подынтегральной функции представляется не менее чем шестнадцатью трапециями.
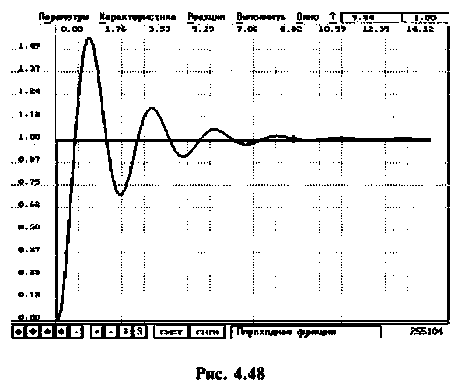
В качестве примера для построения переходной функции возьмем электрическую цепь, ВЧХ которой была построена и приведена на рис. 4.47 (кривая 3). На рис. 4.48 приведена переходная функция этой сложной электрической цепи.
Переходная функция на рис. 4.48 получена с помощью пакета ПП «Сигнал» [5].
Для вычисления интеграла (4.39) необходимо определить значение частоты для верхнего предела интегрирования 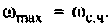 Это значение легко может быть определено из кривой вещественной частотной характеристики (ВЧХ) КФ электрической цепи. В качестве примера возьмем простую интегрирующую цепь (см. рис. 4.1), КФ которой имеет вид
Это значение легко может быть определено из кривой вещественной частотной характеристики (ВЧХ) КФ электрической цепи. В качестве примера возьмем простую интегрирующую цепь (см. рис. 4.1), КФ которой имеет вид
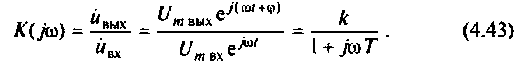
Алгебраическая форма КФ
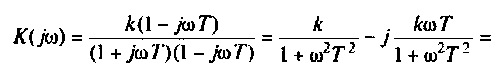
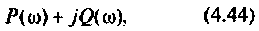
где 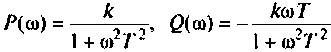 — вещественная и мнимая части КФ. Построим кривую
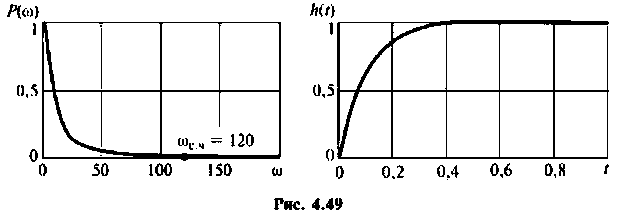
— вещественная и мнимая части КФ. Построим кривую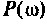 (рис. 4.49) в среде Mathcad, если
(рис. 4.49) в среде Mathcad, если 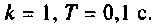 .
.
Из графика ВЧХ видно, что при 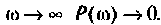 Влияние ВЧХ в области больших частот на переходную функцию несущественно, поэтому за частоту
Влияние ВЧХ в области больших частот на переходную функцию несущественно, поэтому за частоту 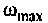 можно принять частоту, при которой ВЧХ принимает значение
можно принять частоту, при которой ВЧХ принимает значение 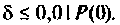 Эту частоту принято называть «существенной частотой» и обозначать
Эту частоту принято называть «существенной частотой» и обозначать 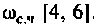 . В нашем примере
. В нашем примере 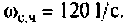 Переходная функция, вычисленная по выражению (4.39), приведена на рис. 4.49.
Переходная функция, вычисленная по выражению (4.39), приведена на рис. 4.49.
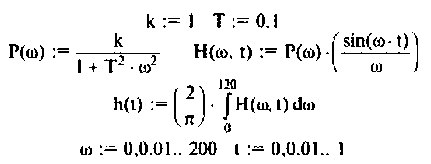
Для случая электрических цепей с дифференцирующими свойствами может оказаться, что при 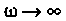 ВЧХ КФ этой цепи
ВЧХ КФ этой цепи 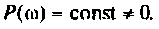 Тогда для расчета переходной функции необходимо использовать мнимую частотную характеристику (МЧХ) в соответствии с выражением
Тогда для расчета переходной функции необходимо использовать мнимую частотную характеристику (МЧХ) в соответствии с выражением
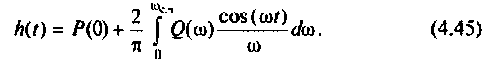
Приведенный пример наглядно показывает, что использование частотных характеристик для построения временных характеристик с помощью ЭВМ существенно расширяет возможности частотных методов анализа электрических цепей.
Спектральный метод расчета и построения выходных величин электрических цепей при сложных входных воздействиях:
Применение частотных методов при анализе и синтезе электрических цепей с требуемыми динамическими характеристиками и использованием ЭВМ позволяет не только строить переходные характеристики, но и строить реакцию цепи на любые детерминированные воздействия, оценивать их в установившихся режимах.
Математической основой частотных методов анализа электрических цепей и систем автоматического управления является обратное преобразование Фурье, позволяющее получать изображение выходного сигнала системы y(t) с помощью вещественной и мнимой частотных характеристик систем. В свою очередь, по вещественной или мнимой частотным характеристикам можно построить переходный процесс выходной величины и оценить реакцию цепи в переходном и установившемся режимах.
Как известно, реакция системы определяется по формуле обратного преобразования Фурье [4]
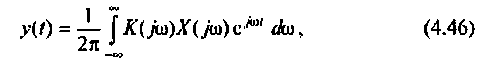
где 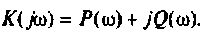
После соответствующих преобразований выражение (4.46) примет вид:
I) для ступенчатой входной функции 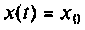 спектром
спектром 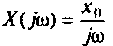
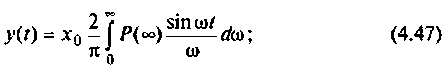
2) для линейной входной функции 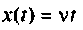 со спектром
со спектром 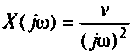
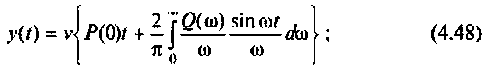
y{t) = vP(0)t+±l
2 r0(
Л» И
(4.48)
О)
3) для параболической входной функции 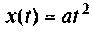 со спектром
со спектром 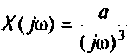
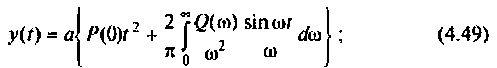
4) для полиномиального воздействия вида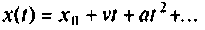
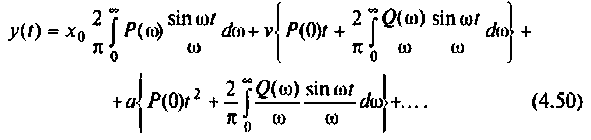
Применение ЭВМ и численных методов интегрирования позволяет отказаться от графических и табличных методов построения переходных и других необходимых функций в электрических цепях.
Примеры решения типовых задач:
Пример 4.6.1.
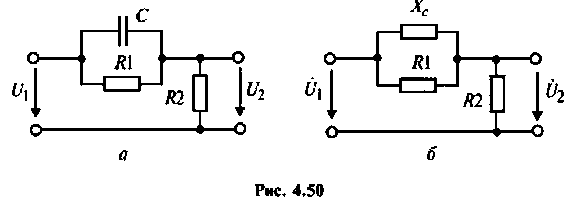
Определить комплексный коэффициент передачи по напряжению для дифференцирующего 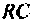 -контура (рис. 4.50,а), рассчитать и построить переходную функцию контура с помощью ВЧХ.
-контура (рис. 4.50,а), рассчитать и построить переходную функцию контура с помощью ВЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.50, б).
2. Определим комплексное напряжение на выходе цепи в виде
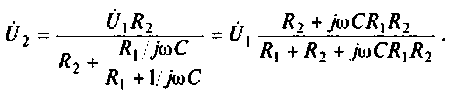
Преобразуем полученное выражение, вынеся за скобки в числителе и знаменателе члены, не содержащие 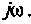 После преобразований получим
После преобразований получим
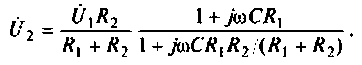
Следовательно
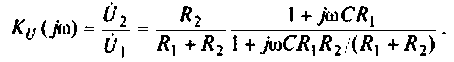
Введем обозначения:
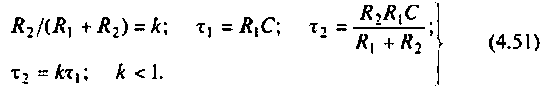
Величина 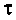 называется постоянной времени цепи и измеряется в секундах. Величина k имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте
называется постоянной времени цепи и измеряется в секундах. Величина k имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте 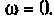 С учетом принятых обозначений
С учетом принятых обозначений
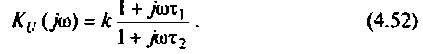
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
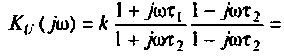
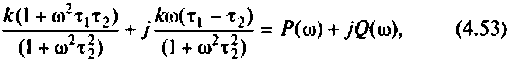
где 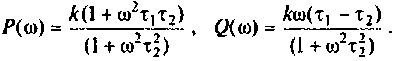
Примем: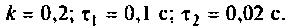
Для определения частоты 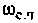 в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.51).
в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.51).
Из частотных характеристик КПФ принимаем 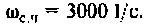 Для построения переходной функции воспользуемся выражением (4.45). Построение проведем также в среде Mathcad.
Для построения переходной функции воспользуемся выражением (4.45). Построение проведем также в среде Mathcad.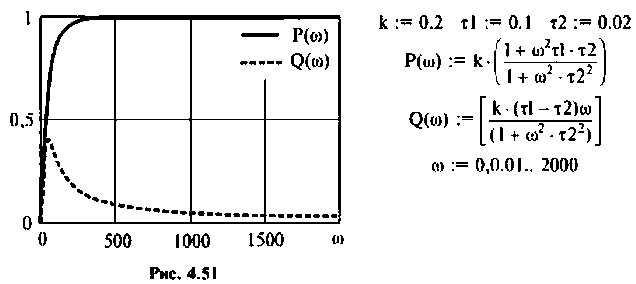
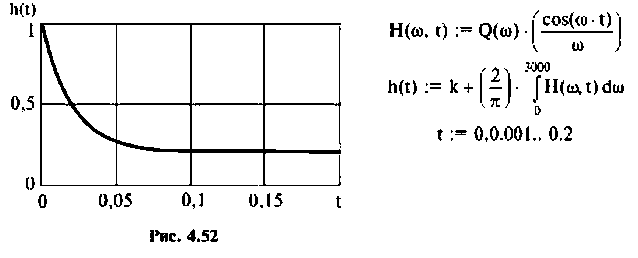
Переходная функция, показанная на рис.4.52, соответствует дифференцирую щему фазоопережающему контуру, который широко применяется в электронных и радиотехнических устройствах, системах автоматического управления.
Пример 4.6.2.
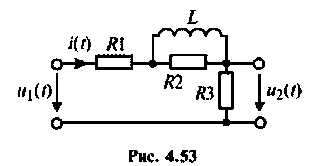
Для электрической цепи, изображенной на рис, 4.53, определить КПФ 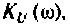 построить ВЧХ
построить ВЧХ 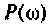 и МЧХ
и МЧХ 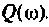 . Рассчитать и построить график переходной функции. Параметры цепи:
. Рассчитать и построить график переходной функции. Параметры цепи: 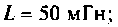
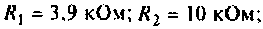
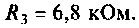
Решение
1. Найдем комплексную функцию 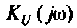 по формуле делителя напряжения
по формуле делителя напряжения
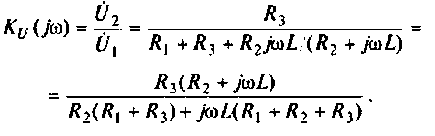
Преобразуем полученное выражение к виду
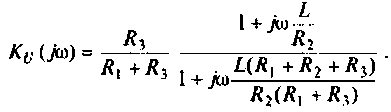
Обозначим:
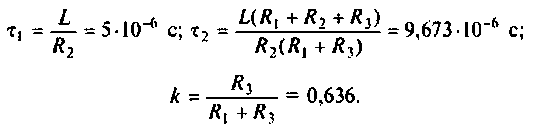
Следовательно,
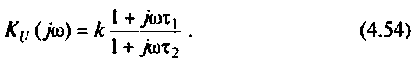
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
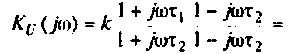
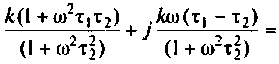
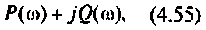
где 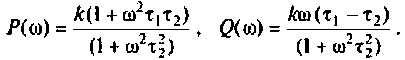
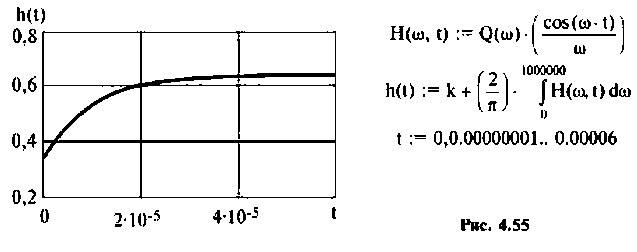
Для определения частоты 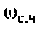 в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.54).
в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.54).
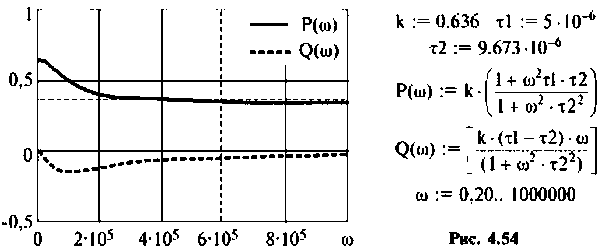
По виду ВЧХ и МЧХ определяем, что для построения переходной функции необходимо применить МЧХ. Примем из графика МЧХ 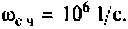 Переходная функция и программа для ее вычисления и построения приведена на рис. 4.55.
Переходная функция и программа для ее вычисления и построения приведена на рис. 4.55.
Из рис. 4.55 видно, что переходная функция соответствует интегрирующему контуру.
Пример 4.6.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.56, а), используя метод контурных токов. Построить в среде Mathcad графики АЧХ, ВЧХ, МЧХ. Рассчитать и построить эпюру входного и выходного напряжения, если на вход цепи поступает напряжение вида 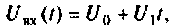 где
где 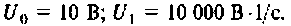
Параметры цепи: 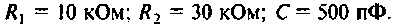
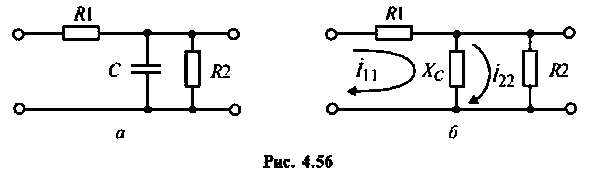
Решение
1.Представим цепь комплексной схемой замещения (рис. 4.56, б). Данная цепь имеет два независимых контура. Ток 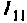 в первом контуре замыкается через источник, который на схеме не изображен. Направление контурных тиков выбираем одинаковым.
в первом контуре замыкается через источник, который на схеме не изображен. Направление контурных тиков выбираем одинаковым.
2.Составим матрицы контурных сопротивлений для двух независимых контуров
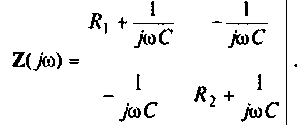
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
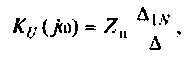
где сопротивление нагрузки 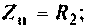
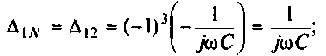
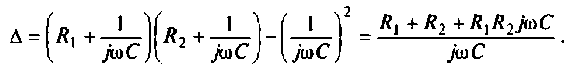
Подставляя найденные выражения, получаем
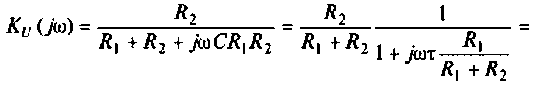
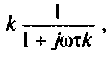
т.е. 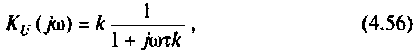
где 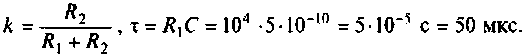
4. Рассчитаем 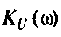 для крайних значений частоты
для крайних значений частоты 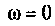 и
и 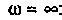
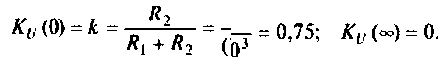
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 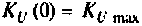 = = 0,75. С ростом частоты емкостное сопротивление уменьшается. Если
= = 0,75. С ростом частоты емкостное сопротивление уменьшается. Если 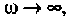 то
то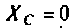 и шунтирует сопротивление
и шунтирует сопротивление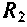 . При этом
. При этом
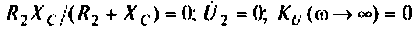
5.Определим выражения для АЧХ, ВЧХ, МЧХ. Представим КГ1Ф (4.55) в алгебраической форме
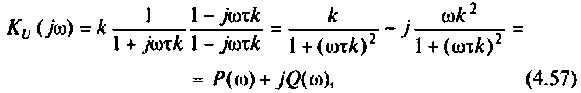
где 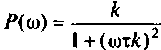 вещественная частотная характеристика:
вещественная частотная характеристика:
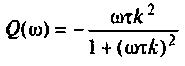 — мнимая частотная характеристика.
— мнимая частотная характеристика.
Амплитудно-частотную характеристику запишем в виде
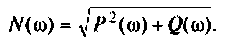
6. В среде Mathcad построим частотные характеристики и определим 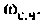
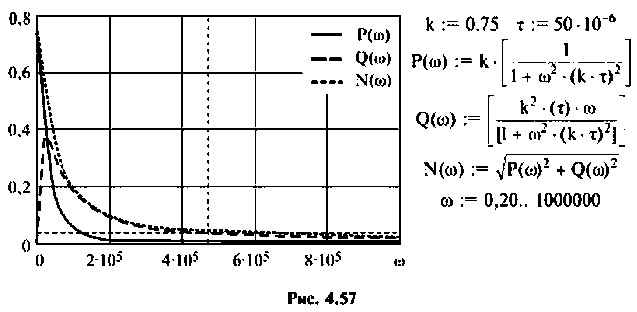
По ВЧХ на рис. 4.57 определяем, что существенная частота 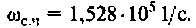
7. Построим переходную функцию электрической цепи, которая представлена на рис. 4.58.
Переходная функция электрической цепи соответствует апериодическому звену.
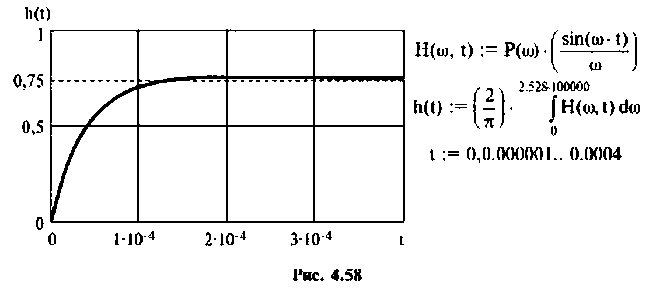
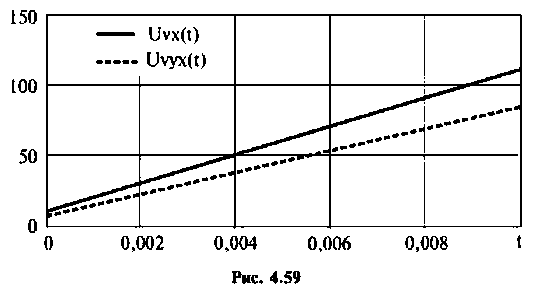
8. Построим реакцию электрической цепи на напряжение, изменяющееся но линейному закону (рис. 4.59).
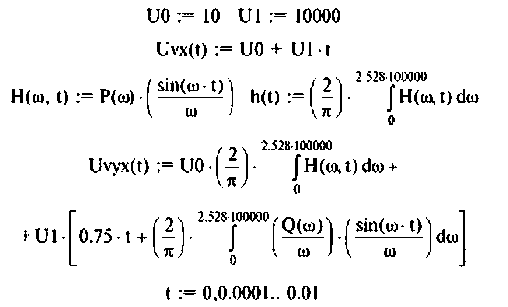
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
Колебательный контур является типичным представителем резонансных колебательных систем, играющих важную роль в большинстве разделов физики — в механике это различного типа маятники и звуковые резонаторы (струны, мембраны, трубы, свистки, органы), в электродинамике — колебательные контуры, закрытые и открытые резонаторы с распределенными параметрами, в оптике — лазерные резонаторы, эталоны Фабри — Перо и т.д. Принципы описания всех колебательных систем настолько общи, что теория колебаний стала самостоятельным разделом физики. Поэтому изучение параметров, свойств и характеристик колебательного контура полезно рассматривать как общее введение в мир резонансных колебательных систем.
В теории колебаний выделяются два класса явлений — явления в линейных и нелинейных колебательных системах. Линейными называются такие системы, параметры которых не зависят от амплитуды колебаний. Например, для маятников это означает такие малые колебания, при которых упругость пружин и стержней не зависит от амплитуды колебания, а натяжение нити подвеса определяется только гравитационными силами. Для электрических колебательных контуров независимыми от амплитуды токов и напряжений должны оставаться такие величины, как индуктивность $L$, емкость $C$ и сопротивление $R$.
Резонансные системы имеют два важных свойства.
-
Свойство избирательно реагировать на внешние источники сигналов, выделяя только те из них, частоты которых совпадают с собственной частотой колебательной системы.
-
Свойство запасать энергию колебаний, возбужденных внешним источником, поддерживая колебания в течение определенного времени после выключения внешнего источника.
Колебательный контур характеризуется двумя основными параметрами: частотой собственных (резонансных) колебаний $omega _{0} $ и добротностью $Q$, характеризующей отношение мощности энергии собственного колебания к мощности потерь за период.

На рис. 18 приведены примеры «параллелей» электрических и механических колебательных систем. В электрических резонаторах происходит периодический переход электрической энергии, запасенной в конденсаторе $(W_Э =frac 12 CU^2),$ в магнитную энергию катушки индуктивности $(W_M =frac 12 LI^2)$ и обратно. В маятниках происходит аналогичный циклический переход энергии из потенциальной (поднятого груза или сжатой пружины) в кинетическую и обратно.
Свободные колебания происходят в замкнутой цепи без вынуждающей силы (рис. 19,а).

Согласно второму закону Кирхгофа для такой цепи можно написать:
$$
Rcdot I+U_{C} =-Lcdot frac{dI}{dt}.
$$
Выражая $U_{C} $ через заряд $q$, получим уравнение
$$
Rcdot I+Lcdot frac{dI}{dt} +frac{q}{C} =0 mbox{ (СИ). }
$$
Дифференцируя по времени и учитывая равенство $I=frac{dq}{dt} $, получаем
$$
Lfrac{d^{2} I}{dt^{2} } +Rfrac{dI}{dt} +frac{I}{C} =0 mbox{ (СИ). }
$$
Разделив на $L$ и вводя обозначения
$delta =frac{R}{2cdot L} $ и $omega _{0}^{2} =frac{1}{LC} $,
получим общее уравнение для свободных колебаний линейной резонансной системы:
$$
I”+2delta , I’+omega _{0}^{2} I=0,
$$
где параметр $delta $ называется затухание, а параметр $omega _{0} $ — собственная частота, или частота свободных колебаний. Оно решается подстановкой $I=Acdot e^{iomega , t} $, которая приводит к характеристическому уравнению
$$
-omega ^{2} +2iomega , delta +omega _{0}^{2} =0,
$$
с решением
$$
lambda , _{1,2} =i, delta pm sqrt{omega _{0}^{2} -delta ^{2} } .
$$
Общее решение имеет две составляющие
$$
I=Acdot e^{iomega _{1} , t} +Bcdot e^{iomega _{2} , t} .
$$
Константы $A$ и $B$ определяются начальными данными задачи, например, зарядом $q_{0} $ или напряжением на конденсаторе $U_{0} $. Характер начальных данных определяется конкретной физической системой.
Частный пример схемы для возбуждения свободных колебаний в колебательном контуре приведен на рис. 19,б. Конденсатор $C$ заряжается от батареи до напряжения $U_{0} $ (положение «а» переключателя), а затем переключается в точку «б». Свободные колебания будут представлять собой циклический переход энергии электрического поля (в конденсаторе) в энергию магнитного поля (в индуктивности) и обратно.
Подставив найденные значения $A$ и $B$, получим общее решение для свободных колебаний в контуре
$$
I=ifrac{U_{0} }{Lsqrt{omega _{0}^{2} -delta ^{2} } } e^{-delta , t} frac{e^{isqrt{omega _{0}^{2} -delta ^{2} } , t} -e^{-isqrt{omega _{0}^{2} -delta ^{2} } , t} }{2} .
$$
Если бы колебательный контур состоял только из идеальных (без потерь) реактивных элементов (индуктивности $L$ и емкости $C$), то переход энергии из электрической в магнитную и обратно совершался бы без потерь, а в контуре существовали бы незатухающие свободные колебания с собственной частотой $omega _{0} =2pi , f=sqrt{frac{1}{LC}}.$
Наличие в схеме активного элемента $R$ приводит к тому, что часть энергии за каждый период переходит в тепло и колебания затухают с некоторой постоянной времени $tau $. Роль частоты в уравнении теперь играет величина $omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } $, зависящая от отношения реактивной мощности к потерям на активном сопротивлении $R$. При этом вовсе не обязательно в схему должен быть включен отдельный резистор. В его качестве может выступать, например, омическое сопротивление провода, которым намотана катушка индуктивности, а также сопротивление утечки изоляторов конденсатора. Кроме того, часть энергии колебаний может излучаться контуром в окружающее пространство в виде электромагнитной волны. На этом основано действие так называемых связанных контуров: если вблизи данного колебательного контура расположен другой, то в нем «наводятся» (возникают) колебания за счет того, что часть энергии трансформируется из первого контура во второй. Передача энергии совершается переменным электромагнитным полем, возникающим вокруг первого контура.
Если затухание мало, т. е. $delta <omega _{0} $, то мы получаем уравнение слабо затухающих колебаний в виде
$$
I=-frac{U_{0} }{Lomega _{p} } e^{-delta , t} sin omega _{p} t=-I_{0} e^{-delta , t} sin omega _{p} t.
$$
При этом резонансная частота приближается к частоте собственных колебаний:
$$
omega _{p} =sqrt{omega _{0}^{2} -delta ^{2} } approx omega _{0} left(1-frac{1}{2} frac{delta ^{2} }{omega _{0}^{2} } right).
$$
Таким образом, при малом затухании резонансная частота практически совпадает с собственной, однако колебания при этом не являются гармоническими. Для гармонических колебаний должно соблюдаться условие $Ileft(tright)=Ileft(t+Tright)$, где $T$ — период колебания. В нашем случае $Ileft(tright)ne Ileft(t+Tright)$, и о периоде можно говорить лишь как о времени, через которое повторяются нули функции (рис. 20). Именно в этом смысле мы будем ниже использовать термин «период колебаний».

Введем понятия добротности $Q$ и логарифмического декремента затухания $gamma $ контура. Из отношение амплитуд $n$–того и $(n + k)$–го колебаний равно
$I_{n} I_{n+k}^{-1} = e^{kdelta T}$, где $T=2, pi omega ^{-1} $ — период колебания («повторения нулей»). Логарифмическим декрементом затухания $gamma $ называется величина
$$
gamma =delta , T=frac{1}{k} ln frac{I_{n} }{I_{n+k} } =ln frac{I_{n} }{I_{n+1} } .
$$
Из уравнения для тока видно, что величина $delta $ обратно пропорциональна времени, за которое амплитуда колебаний уменьшается в $e$ раз. Из последнего уравнения следует, что декремент затухания $gamma $ показывает уменьшение амплитуды за период колебания:
$$
gamma =delta , T=frac{2; pi , delta }{omega } .
$$
С логарифмическим коэффициентом затухания однозначно связан другой, более распространенный параметр, характеризующий колебательную систему, добротность $Q$.
Добротность контура $Q$ определяется соотношением
$$
Q=frac{omega _{0} L}{R} =frac{1}{omega _{0} CR} =frac{rho }{R},
$$
где $rho =sqrt{frac LC} $ (СИ).
Физический смысл добротности заключается в отношении запасенной в контуре энергии к энергии потерь за период колебания
$$
Q=omega cdot frac{W_0}{Delta W},
$$
откуда можно найти связь добротности с другими параметрами контура
$$
Q=frac{pi }{gamma } =frac{pi }{delta , T} =frac{omega }{2, delta } =omega frac{L}{R} mbox{ (СИ).}
$$
Экспериментально добротность определяется по резонансной кривой как отношение резонансной частоты $omega _{p} $ к полосе частот $2cdot Delta omega $, определяемой на уровне $U_{1,2} =pm frac{U_p}{sqrt{2}}$:
$$
Q=frac{omega _{з}}{2cdot Delta omega } =frac{f_{з}}{2cdot Delta f} ,
$$
где $U_{p} $ — амплитуда колебания на резонансной частоте контура. Величина $rho =sqrt{frac LC}$ называется характеристическим (волновым) сопротивлением контура.
При большом затухании, т.е. при $delta >omega _{0} $, величина $omega _{0}^{2} -delta ^{2} $ отрицательна, корень из нее мнимый. Такой случай называется апериодическим процессом. Общее решение, аналогичное, полученному ранее, будет иметь вид
$$
I=-frac{U_{0} }{Lsqrt{(delta ^{2} -omega _{0}^{2} )} } e^{-delta , , t} mbox{sh}sqrt{(delta ^{2} -omega _{0}^{2} )} , t.
$$
График этой функции приведен на рис. 21.

Критическим условием, при котором затухающие колебания переходят в апериодический процесс, является условие $delta =omega _{0} $. В этом случае решение общего уравнения имеет вид
$$
I=-frac{U_{0} }{omega L} (omega t)e^{-delta , t} , =-frac{U_{0} }{L} t, e^{-delta , t} .
$$
Остается добавить, что аналогичные параметры могут быть введены для любой резонансной колебательной системы независимо от ее физической природы (механические, термодинамические, электромагнитные, оптические, аэро– и гидродинамические системы).
Колебательный контур, рассмотренный в предыдущем разделе, представлял собой замкнутую электрическую цепь, в которой совершаются свободные колебания.
В случае вынужденных колебаний мы должны подводить к контуру электрическую энергию от внешнего источника (генератора). Есть много способов для подключения источника внешней энергии к контуру, которые сводятся к той или иной комбинации двух основных: в разрыв цепи контура (рис. 22, а) или параллельно емкостной и индуктивной ветвям контура (рис. 22,б).

В зависимости от способа включения различают соответственно последовательный (рис. 22,а) и параллельный (рис. 22,б) колебательные контуры. Они предъявляют разные требования к согласованию с генератором и нагрузкой. Поэтому нужно отличать собственные параметры контура от параметров нагруженного контура, получаемые с учетом влияния генератора и «нагрузки» (входного сопротивления той цепи, в которую включен контур). В параллельном контуре (рис. 22,б) возникает резонанс токов. Для его поддержания в качестве вынуждающей силы необходимо применение генератора стабильного тока. В последовательном контуре (рис. 22,а) имеет место резонанс напряжений, и для его поддержания должен применяться внешний генератор стабильного напряжения.
Закон Кирхгофа, позволяющий исследовать процессы в контуре (рис. 22,а) в зависимости от частоты, записывается в виде
$$
U=U_{R} +U_{L} +U_{C} =IR+iI(omega L-frac{1}{omega C} )=Icdot Z.
$$
Контур представляет для генератора некоторое комплексное сопротивление
$$
Z=R_L +icdot (omega L-frac{1}{omega C} ),
$$
$$
left|Zright| = sqrt{R_L^2 +(omega L-frac{1}{omega C})^2}, mbox{tg}varphi =frac{omega L-frac{1}{omega C} }{R_L}
$$
где $left|Zright|$ — модуль комплексного сопротивления; $R_{L}$ — омическое сопротивление катушки индуктивности; $varphi $ — сдвиг фазы между активным и реактивным сопротивлениями, равный сдвигу фазы между током $I$ в цепи и входным напряжением $U$.
Из последнего выражения видно, что сопротивление цепи будет минимально и равно активному сопротивлению $R_{L} $ на некоторой частоте $omega _{0} $, определяемой условием
$$
omega _0 L=frac{1}{omega _0 C} , mbox{ где } omega _{0} =frac{1}{sqrt{LC}} mbox{ (СИ).}
$$
Таким образом, на резонансной частоте сопротивление контура минимально, чисто активно, а ток в цепи совпадает по фазе с входным напряжением (напряжением генератора). Фактически это и есть определение резонанса в последовательном колебательном контуре.
Для практических целей представляет интерес исследовать поведение напряжений на реактивных элементах контура в зависимости от частоты генератора и определить его добротность $Q$.
Поскольку фазы $U_{L} $ и $U_{C} $ независимо от частоты всегда сдвинуты относительно тока $I$ на $+$ и $-90^{circ}$ соответственно, то достаточно исследовать зависимость от частоты их модулей. Это можно сделать исходя из уравнений
$$
U_{R} =IR, U_{L} =Iomega L, U_{C} =frac{I}{omega C}, I=frac{U}{Z} .
$$
Для примера раскроем уравнения для $I$ и $U_{L} $. Используя введенное для свободных колебаний понятие добротности $Q=left(omega _{0} RCright)^{-1}$, получим следующее выражение для тока в последовательном контуре:
$$
I=frac{U}{sqrt{R^{2} +(omega L-frac{1}{omega C} )^{2} } } =frac{U}{R} frac{1}{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$
Тогда напряжение на индуктивности будет равно
$$
U_{L} =omega LI=Ufrac{Qfrac{omega }{omega _{0} } }{sqrt{1+Q^{2} (frac{omega }{omega _{0} } -frac{omega _{0} }{omega } )^{2} } } .
$$
Аналогичное уравнение можно получить для напряжения на $C$. При $omega =omega _{0} $ напряжения на $L$ и $C$ будут равны $U_{L0} =U_{C0} =Qcdot U$, т.е. в $Q$ раз больше напряжения вынуждающей эдс.
На самом деле максимумы напряжения на элементах $L$ и $C$ несколько выше и смещены от резонансной частоты и выражаются следующими соотношениями:
$$
omega _{Lmax } =omega _{0} sqrt{frac{2}{2-frac{R^{2} C}{L} } } =omega _{0} sqrt{frac{2}{2-left(frac{1}{Q} right)^{2} } } , omega _{Cmax } =frac{omega _{0}^{2} }{omega _{L} } .
$$
При добротности контура $Q ge 10$ сдвиг частот максимумов $U_{L} $ и $U_{C} $ относительно резонансной частоты $omega _{0} $ не превышает 1% и экспериментально резонансную частоту и добротность можно определять по резонансной кривой любого из напряжений $U_{L} $ и $U_{C} $. Напряжение на реактивных элементах $U_{L} $ и $U_{C} $ при $omega =omega _{0} $ в $Q$ раз больше, чем входное напряжение $U$, поэтому резонанс в последовательном контуре называется резонансом напряжений.
Важно отметить, что для нашего анализа существенно, что само входное напряжение $U$ от частоты не зависит. В противном случае все параметры зависели бы не только от самого контура, но и от параметров источника сигнала. Как было показано в предыдущем параграфе, для этого выходное сопротивление генератора должно быть много меньше $R$.
Схема подключения параллельного контура представлена на рис. 21,б. Из–за комплексного характера нагрузки ток генератора является комплексной величиной. Поэтому модуль тока $I$ может оказаться меньше не только суммы модулей токов индуктивной и емкостной ветвей контура, но и каждого из них в отдельности. Именно это и происходит при резонансе в параллельном контуре: токи в индуктивной и емкостной ветвях контура в $Q$ раз больше, чем ток, потребляемый от генератора тока. Поэтому резонанс в параллельном контуре называется резонансом токов.
Комплексное сопротивление параллельного контура равно
$$
Z=frac{Z_{1} Z_{2} }{Z_{1} +Z_{2} } =
frac{(R_{L} +iomega L)(iomega C)^{-1}}{R_{L} +i(omega L-(omega C)^{-1} )} approx
frac{LC^{-1}}{R_{L} +i(omega L-(omega C)^{-1})} .
$$
Мы пренебрегли величиной $R_{L} $ в числителе, поскольку она в $Q$ раз меньше индуктивного сопротивления, но этого нельзя делать в знаменателе, поскольку при резонансе величина в скобках стремится к нулю.
Условие резонанса для параллельного контура то же, что и для последовательного — равенство реактивных сопротивлений ветвей с $L$ и $C$:
$$
omega _{0} L=frac{1}{omega _{0} C}, mbox{ где } omega _{0} =frac{1}{sqrt{LC} } mbox{ (СИ). }
$$
Таким образом, при резонансе сопротивление контура становится чисто активным и равным
$$
R_{э} =frac{L}{ C R_{L} } =frac{rho ^{2} }{R_{L} } ,
$$
где — $rho =sqrt{frac LC} $ волновое сопротивление контура.
Сопротивление $R_{э} $ отдельного физического эквивалента в контуре не имеет, а является комбинацией волнового сопротивления $rho $ и сопротивления потерь $R_{L} $. Поэтому оно не составляет отдельной ветви параллельного контура и не ответвляет в себя ток. Следовательно, «переносить» его куда–либо или к чему–нибудь «подсоединять» (например, к внутреннему сопротивлению источника тока) бессмысленно. На схеме это просто условное обозначение того факта, что на резонансной частоте параллельный колебательный контур представляет для внешнего генератора некоторое чисто активное сопротивление величиной $R_{э} $, а в формулах символическая запись определенной комбинации $rho $ и $R_{L} $, даваемой последней формулой.
Добротность параллельного контура
$$
Q=frac{omega _{0} L}{R_{L} } =frac{1}{R_{L} omega _{0} C} =frac{R_{э} }{rho } =R_{э} sqrt{frac{C}{L} } .
$$
Собственные параметры параллельного контура, т.е. резонансная частота $omega _{0} $ и добротность $Q$ будут такими же, как и в последовательном контуре при тех же $C$, $L$ и $R_{L}.$
