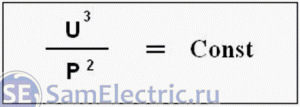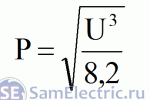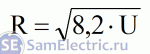Лучший ответ
Chelovek
Искусственный Интеллект
(392001)
5 лет назад
Используем две формулы:
P=UI и I=U/R
получается
R = U^2/P
R = 230х230/60=881,7 ом
Остальные ответы
Ron Jeremy
Мыслитель
(9821)
5 лет назад
U^2/P=R
snake
Просветленный
(29086)
5 лет назад
U в квадрате дели на P
Юлия БучневаУченик (216)
5 лет назад
Спасибо большое
snake
Просветленный
(29086)
удачи
Nik Vas
Искусственный Интеллект
(265570)
5 лет назад
Только помни, сопротивление холодной и горячей лампы сильно отличаются.
val
Просветленный
(33691)
5 лет назад
сопротивление раскалённой (!) нити
ELEktrocool
Оракул
(99125)
5 лет назад
3,83 ом
Ник Ник
Искусственный Интеллект
(178391)
5 лет назад
P=U x I
Аркаша
Высший разум
(539694)
5 лет назад
При работе около 880 Ом. В холодном состоянии раз в 10 меньше (что нибудь около 60-80 Ом)
По какой формуле можно найти сопротивление?
Анонимный вопрос
2 ноября 2018 · 61,6 K
Лучший ответ на 99.9% вопросов: “Поисковик в помощь”. · 2 нояб 2018
Самая простая формула для нахождения сопротивления – закон Ома для участка цепи.
R=U/I, где
R – сопротивление,
U – напряжение,
I – сила тока.
8,5 K
Комментировать ответ…Комментировать…
Рассчитайте сопротивление лампы накаливания в рабочем состоянии R и в выключенном состоянии R20 , а также токи в рабочем состоянии Iраб и в холодном состоянии I20 . Лампа мощностью 100 Вт включается в сеть напряжением 220 В. Температура нити лампы в холодном состоянии +200 С, в горячем – +30000 С. Материал нити – вольфрам. Его температурный коэффициент сопротивления – α=0,0045 1/К.
8,0 K
Комментировать ответ…Комментировать…
Сопротивление вычисляется по формуле (Закон Ома):
R = U/I
R — само сопротивление (Ом)
U — напряжение (Вольт)
I — сила тока (Ампер)
Т.е в системе СИ:
[R] = B/ A = Ом Читать далее
26,9 K
Комментировать ответ…Комментировать…
Решил
я
как-то
проверить
закон
Ома.
Применительно
к
лампе
накаливания.
Измерил
сопротивление
лампочки
Лисма
230
В
60
Вт,
оно
оказалось
равным
59
Ом.
Я
было
удивился,
но
потом
вспомнил
слово,
которое
всё
объясняло
–
бареттер.
Дело
в
том,
что
сопротивление
вольфрамовой
нити
лампы
накаливания
сильно
зависит
от
температуры
(следствие
протекания
тока).
В
моем
случае,
если
это
бы
был
не
вольфрам,
а
обычный
резистор,
его
рассеиваемая
мощность
при
напряжении
230
Вольт
была
бы
P
=
U2/R
=
896.
Почти
900
Ватт!
Кстати,
именно
поэтому
производители
датчиков
с
транзисторным
выходом
рекомендуют
соблюдать
осторожность
при
подключении
датчиков.
Как
же
измерить
рабочее
сопротивление
нити
лампы
накаливания?
А
никак.
Его
можно
только
определить
косвенным
путем,
из
закона
знаменитого
Ома.
(Строго
говоря,
все
омметры
используют
тот
же
закон
–
прикладывают
напряжение
и
меряют
ток).
И
мультиметром
тут
не
обойдешься.
Используя
косвенный
метод
и
лампочку
Лисма
24
В
с
мощностью
40
Вт,
я
составил
вот
такую
табличку:
Зависимость
сопротивления
нити
лампы
накаливания
от
напряжения
| Напряжение | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|
% напряжения |
8.3 | 16.7 | 25.0 | 33.3 | 41.7 | 50.0 | 58.3 | 66.7 |
| Ток | 0.55 | 0.7 | 0.84 | 0.97 | 1.08 | 1.19 | 1.29 | 1.38 |
| Сопротивление | 3.6 | 5.7 | 7.1 | 8.2 | 9.3 | 10.1 | 10.9 | 11.6 |
| Мощность | 1.1 | 2.8 | 5.04 | 7.76 | 10.8 | 14.28 | 18.06 | 22.08 |
(продолжение таблицы)
| Напряжение | 18 | 20 | 22 |
24 |
26 | 28 | 30 | 32 |
|
% напряжения |
75.0 | 83.3 | 91.7 |
100.0 |
108.3 | 116.7 | 125.0 | 133.3 |
| Ток | 1.47 | 1.55 | 1.63 |
1.7 |
1.77 | 1.84 | 1.92 | 2 |
| Сопротивление | 12.2 | 12.9 | 13.5 |
14.1 |
14.7 | 15.2 | 15.6 | 16.0 |
| Мощность | 26.46 | 31 | 35.86 |
40.8 |
46.02 | 51.52 | 57.6 | 64 |
(Номинальные параметры выделены)
Как
видно
из
таблицы,
зависимость
сопротивления
лампочки
от
напряжения
нелинейная.
Это
может
проиллюстрировать
график,
приведенный
ниже.
Рабочая
точка
на
графике
выделена.
Сопротивление
нити
лампы
накаливания
в
зависимости
от
напряжения
Кстати,
сопротивление
подопытной
лампочки,
измеренное
с
помощью
цифрового
мультиметра
–
около
1
Ома.
Предел
измерения
–
200
Ом,
при
этом
выходное
напряжение
вольтметра
–
0,5
В.
Эти
данные
также
укладываются
в
полученные
ранее.
Зависимость
мощности
от
напряжения:
Зависимость
мощности
от
напряжения
Для
ламп
на
напряжение
230
В
на
основании
экспериментальных
данных
была
составлена
вот
такая
табличка:
|
Мощность лампочки, Вт |
25 | 40 | 60 | 75 | 100 |
|
R холодной нити,Ом |
150 | 90-100 | 60-65 | 45-50 | 37-40 |
|
R горячей нити, |
1930 | 1200 | 805 | 650 | 490 |
| Rгор./Rхол. | 12 | 12 | 13 | 13 | 12 |
Из
этой
таблицы
видно,
что
сопротивление
нити
лампы
накаливания
в
холодном
и
горячем
состоянии
отличается
в
12-13
раз.
А
это
значит,
что
во
столько
же
раз
увеличивается
потребляемая
мощность
в
первоначальный
момент.
Стоит
отметить,
что
сопротивление
в
холодном
состоянии
измерялось
мультиметром
на
пределе
200
Ом
при
выходном
напряжении
мультиметра
0,5
В.
При
измерении
сопротивления
на
пределе
2000
Ом
(выходное
напряжение
2
В)
показания
сопротивления
увеличиваются
более
чем
в
полтора
раза,
что
опять
же
укладывается
в
идею
статьи.
“Горячее”
сопротивление
измерялось
косвенным
методом.
UPD:
Сопротивление
нити
накаливания
люминесцентных
ламп
Дополнение
к
статье,
чтобы
получился
ещё
более
полный
материал.
Лампы
с
цоколем
Т8,
сопротивление
спирали
в
зависимости
от
мощности
:
10
Вт
–
8,0…8,2
Ом
15
Вт
–
3,3…3,5
Ом
18
Вт
–
2,7…2,8
Ом
36
Вт
–
2,5
Ом.
Сопротивление
измерялось
цифровым
омметром
на
пределе
200
Ом.
Формула
мощности
и
напряжения
Обновление
статьи
от
января
2018.
У
меня
на
блоге
появилась
статья
автора
Станислава
Матросова,
который
развил
тему
сопротивления
спирали
лампочки
с
теоретической
стороны.
Он
вывел
формулу,
согласно
которой:
Для
любой
лампы
накаливания
существует
параметр,
стабильный
в
широком
диапазоне
электрических
режимов. Этим
параметром
является
отношение
куба
напряжения
к
квадрату
мощности:
Я
решил
на
основе
данных,
полученных
в
статье,
посчитать
эту
величину
в
Экселе.
Вот
что
у
меня
получилось:
|
U |
P |
U^3 |
P^2 |
Const |
| 2 | 1,1 | 8 | 1,21 | 6,61157 |
| 4 | 2,8 | 64 | 7,84 | 8,163265 |
| 6 | 5,04 | 216 | 25,4016 | 8,503401 |
| 8 | 7,76 | 512 | 60,2176 | 8,502498 |
| 10 | 10,8 | 1000 | 116,64 | 8,573388 |
| 12 | 14,28 | 1728 | 203,9184 | 8,473978 |
| 14 | 18,06 | 2744 | 326,1636 | 8,412956 |
| 16 | 22,08 | 4096 | 487,5264 | 8,401596 |
| 18 | 26,46 | 5832 | 700,1316 | 8,329863 |
| 20 | 31 | 8000 | 961 | 8,324662 |
| 22 | 35,86 | 10648 | 1285,94 | 8,280327 |
| 24 | 40,8 | 13824 | 1664,64 | 8,304498 |
| 26 | 46,02 | 17576 | 2117,84 | 8,29902 |
| 28 | 51,52 | 21952 | 2654,31 | 8,270321 |
| 30 | 57,6 | 27000 | 3317,76 | 8,138021 |
| 32 | 64 | 32768 | 4096 | 8 |
Действительно,
константа,
которая
с
некоторой
погрешностью
во
всём
диапазоне
равна
8,2±0,2.
Её
размерность
–
“Вольт
в
кубе
на
Ватт
в
квадрате”.
Константа
для
расчета
лампы
накаливания
=
8,2
Низкое
значение
константы
в
начале
диапазона
объяснено
автором
в
приведенной
по
ссылке
статье.
Теперь,
зная
значение
этой
константы
(8,2),
можем
записать
формулу
зависимости
мощности
от
напряжения
лампочки
накаливания
40Вт
24В:
Зависимость
мощности
лампочки
накаливания
от
напряжения
Формула
для
сопротивления
Но
вернёмся
к
теме
статьи.
Проверим
вывод
Станислава
Матросова
о
том,
что
сопротивление
лампочки
пропорционально
корню
из
напряжения.
Из
предыдущих
выводов
можно
вывести
формулу
для
конкретной
лампочки
40Вт
24В:
Зависимость
сопротивления
от
напряжения,
формула
для
лампы
накаливания
Теперь
проверим,
как
эта
формула
соотносится
с
полученными
мною
экспериментальным
данным
(см.
таблицу
в
начале
статьи).
Составим
такую
таблицу:
|
1. Напря- жение, |
2. Норм. напр. |
3. Сопрот., Ом |
4. Норм. сопрот. |
5. Корень из напряж. |
6. Корень из Х из |
| 2 | 0,08 | 3,6 | 0,26 | 0,29 | 4,04 |
| 4 | 0,17 | 5,7 | 0,40 | 0,41 | 5,72 |
| 6 | 0,25 | 7,1 | 0,50 | 0,50 | 7,01 |
| 8 | 0,33 | 8,2 | 0,58 | 0,58 | 8,09 |
| 10 | 0,42 | 9,3 | 0,66 | 0,65 | 9,04 |
| 12 | 0,50 | 10,1 | 0,72 | 0,71 | 9,91 |
| 14 | 0,58 | 10,9 | 0,77 | 0,76 | 10,70 |
| 16 | 0,67 | 11,6 | 0,82 | 0,82 | 11,44 |
| 18 | 0,75 | 12,2 | 0,87 | 0,87 | 12,13 |
| 20 | 0,83 | 12,9 | 0,91 | 0,91 | 12,79 |
| 22 | 0,92 | 13,5 | 0,96 | 0,96 | 13,41 |
| 24 | 1,00 | 14,1 | 1,00 | 1,00 | 14,01 |
| 26 | 1,08 | 14,7 | 1,04 | 1,04 | 14,58 |
| 28 | 1,17 | 15,2 | 1,08 | 1,08 | 15,13 |
| 30 | 1,25 | 15,6 | 1,11 | 1,12 | 15,66 |
| 32 | 1,33 | 16 | 1,13 | 1,15 | 16,18 |
Таблица
требует
пояснений.
Чтобы
была
соблюдена
размерность,
я
нормировал
экспериментально
заданное
напряжение
(столбец
2)
и
рассчитанное
сопротивление
(столбец
4).
Колонка
5
–
это
корень
из
нормированного
напряжения,
и
видно,
что
значения
этой
колонки
отлично
совпадают
с
колонкой
4!
Но
давайте
вернемся
в
реальному
сопротивлению,
и
рассчитаем
его
по
приведенной
выше
формуле
(Зависимость
сопротивления
от
напряжения).
Это
–
6-я
колонка.
Хорошо
видно,
что
расчет
по
формуле
практически
идеально
совпадает
с
расчетом
из
экспериментальных
данных!
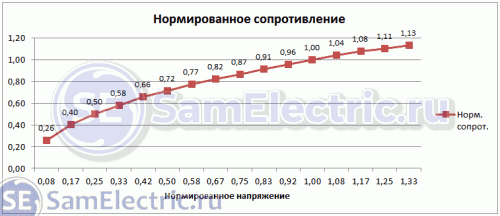
Зависимость
сопротивления
от
напряжения.
Квадратичная
зависимость.
Кто
хочет
проверить
мои
расчеты,
прикладываю
файл: •
Файл
с
расчетами
и
графиками
/
Файл
с
расчетами
и
графиками
к
статье
про
лампу
накаливания,
xlsx,
19.51
kB,
скачан:
1064
раз./
Всё,
учебник
физики
можно
переписывать!
😉
Кому
интересно
–
задачкапро
последовательное
подключение
двух
лампочек.
Понравилось?
Поставьте
оценку,
и
почитайте
другие
статьи
блога!
Загрузка…
Внимание!
Автор
блога
не
гарантирует,
что
всё
написанное
на
этой
странице
–
истина.
За
ваши
действия
и
за
вашу
безопасность
ответственны
только
вы!
Решил я как-то проверить закон Ома. Применительно к лампе накаливания. Измерил сопротивление лампочки Лисма 230 В 60 Вт, оно оказалось равным 59 Ом. Это в несколько раз больше заявленной мощности! Я было удивился, но потом вспомнил слово, которое всё объясняло – бареттер.
Дело в том, что сопротивление вольфрамовой нити лампы накаливания сильно зависит от температуры (следствие протекания тока). В моем случае, если это бы был не вольфрам, а обычный резистор, его рассеиваемая мощность при напряжении 230 Вольт была бы P = U2/R = 896. Почти 900 Ватт!
Кстати, именно поэтому производители датчиков с транзисторным выходом рекомендуют соблюдать осторожность при подключении датчиков.
Как же измерить рабочее сопротивление нити лампы накаливания? А никак. Его можно только определить косвенным путем, из закона знаменитого Ома. (Строго говоря, все омметры используют тот же закон – прикладывают напряжение и меряют ток). И мультиметром тут не обойдешься.
Используя косвенный метод и лампочку Лисма 24 В с мощностью 40 Вт, я составил вот такую табличку:
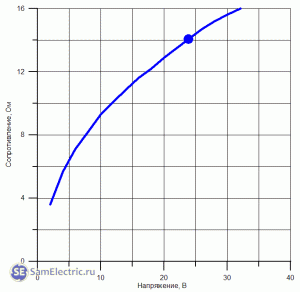
Зависимость сопротивления нити лампы накаливания от напряжения
(Номинальные параметры выделены)
Как видно из таблицы, зависимость сопротивления лампочки от напряжения нелинейная. Это может проиллюстрировать график, приведенный ниже. Рабочая точка на графике выделена.
Кстати, сопротивление подопытной лампочки, измеренное с помощью цифрового мультиметра – около 1 Ома. Предел измерения – 200 Ом, при этом выходное напряжение вольтметра – 0,5 В. Эти данные также укладываются в полученные ранее.
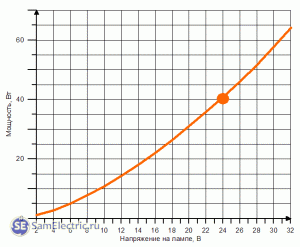
Зависимость мощности от напряжения:
Для ламп на напряжение 230 В на основании экспериментальных данных была составлена вот такая табличка:
Из этой таблицы видно, что сопротивление нити лампы накаливания в холодном и горячем состоянии отличается в 12-13 раз. А это значит, что во столько же раз увеличивается потребляемая мощность в первоначальный момент.
Можно говорить о пусковом токе для ламп накаливания.
Стоит отметить, что сопротивление в холодном состоянии измерялось мультиметром на пределе 200 Ом при выходном напряжении мультиметра 0,5 В. При измерении сопротивления на пределе 2000 Ом (выходное напряжение 2 В) показания сопротивления увеличиваются более чем в полтора раза, что опять же укладывается в идею статьи.
“Горячее” сопротивление измерялось косвенным методом.
Сопротивление нити накаливания люминесцентных ламп
Дополнение к статье, чтобы получился ещё более полный материал.
Лампы с цоколем Т8, сопротивление спирали в зависимости от мощности :
10 Вт – 8,0…8,2 Ом
15 Вт – 3,3…3,5 Ом
18 Вт – 2,7…2,8 Ом
36 Вт – 2,5 Ом.
Сопротивление измерялось цифровым омметром на пределе 200 Ом.
Формула мощности и напряжения
Обновление статьи. У меня на блоге появилась статья автора Станислава Матросова, который развил тему сопротивления спирали лампочки с теоретической стороны. Он вывел формулу, согласно которой:
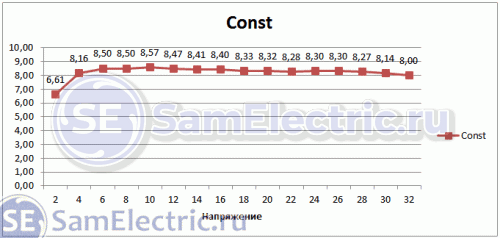
Я решил на основе данных, полученных в статье, посчитать эту величину в Экселе. Вот что у меня получилось:
Действительно, константа, которая с некоторой погрешностью во всём диапазоне равна 8,2±0,2. Её размерность – “Вольт в кубе на Ватт в квадрате”.
Низкое значение константы в начале диапазона объяснено автором в приведенной по ссылке статье.
Теперь, зная значение этой константы (8,2), можем записать формулу зависимости мощности от напряжения лампочки накаливания 40Вт 24В:
Формула для сопротивления
Но вернёмся к теме статьи. Проверим вывод Станислава Матросова о том, что сопротивление лампочки пропорционально корню из напряжения. Из предыдущих выводов можно вывести формулу для конкретной лампочки 40Вт 24В:
Теперь проверим, как эта формула соотносится с полученными мною экспериментальным данным (см. таблицу в начале статьи). Составим такую таблицу:
Таблица требует пояснений. Чтобы была соблюдена размерность, я нормировал экспериментально заданное напряжение (столбец 2) и рассчитанное сопротивление (столбец 4).
Колонка 5 – это корень из нормированного напряжения, и видно, что значения этой колонки отлично совпадают с колонкой 4!
Но давайте вернемся в реальному сопротивлению, и рассчитаем его по приведенной выше формуле (Зависимость сопротивления от напряжения). Это – 6-я колонка. Хорошо видно, что расчет по формуле практически идеально совпадает с расчетом из экспериментальных данных!
Кто хочет проверить мои расчеты, прикладываю файл: • Файл с расчетами и графиками / Файл с расчетами и графиками к статье про лампу накаливания, xlsx, 19.51 kB, скачан: 430 раз./
Всё, учебник физики можно переписывать! 😉
Кому интересно – задачка про последовательное подключение двух лампочек.
Оригинал статьи.
Если интересны темы канала, заходите также на мой сайт – https://samelectric.ru/ и в группу ВК – https://vk.com/samelectric
Не забываем подписываться и ставить лайки, впереди много интересного!
Обращение к хейтерам: за оскорбление Автора и Читателей канала – отправляю в баню.
Перейти к содержимому
Для лампы накаливания мощностью сто пятьдесят ват и напряжением двести двадцать вольт необходимо определить величину сопротивления вольфрамовой нити накаливания при температуре двадцать пять градусов Цельсия. Известно, что температура накала нити лампы составляет две тысячи пятьсот градусов Цельсия. Температурный коэффициент сопротивления вольфрама 5,1×10-3град-1.
Дано: U=220 В; Р=150 Вт; t°1=25°C; t°2=2500°C; α=5,1×10-3град-1
Найти: R1-?
Решение
Запишем формулы для расчета величины сопротивления нити накаливания при комнатной и рабочей температуре


где R1 — сопротивление нити накаливания при температуре 25 градусов Цельсия;
R2 — сопротивление нити накаливания при температуре 2500 градусов Цельсия.


Сопротивление нити накаливания при рабочей температуре определим из формулы

Итоговая формула для расчета величины сопротивления нити накаливания при температуре 25 градусов Цельсия принимает вид

Ответ: сопротивление вольфрамовой нити накаливания электрической лампы при температуре двадцать пять градусов Цельсия составляет двадцать шесть целых пять десятых Ом.