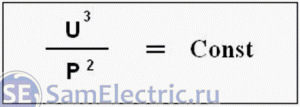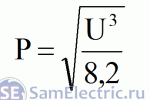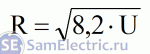Лучший ответ
Chelovek
Искусственный Интеллект
(392001)
5 лет назад
Используем две формулы:
P=UI и I=U/R
получается
R = U^2/P
R = 230х230/60=881,7 ом
Остальные ответы
Ron Jeremy
Мыслитель
(9821)
5 лет назад
U^2/P=R
snake
Просветленный
(29086)
5 лет назад
U в квадрате дели на P
Юлия БучневаУченик (216)
5 лет назад
Спасибо большое
snake
Просветленный
(29086)
удачи
Nik Vas
Искусственный Интеллект
(265570)
5 лет назад
Только помни, сопротивление холодной и горячей лампы сильно отличаются.
val
Просветленный
(33691)
5 лет назад
сопротивление раскалённой (!) нити
ELEktrocool
Оракул
(99125)
5 лет назад
3,83 ом
Ник Ник
Искусственный Интеллект
(178391)
5 лет назад
P=U x I
Аркаша
Высший разум
(539694)
5 лет назад
При работе около 880 Ом. В холодном состоянии раз в 10 меньше (что нибудь около 60-80 Ом)
Решил я как-то проверить закон Ома. Применительно к лампе накаливания. Измерил сопротивление лампочки Лисма 230 В 60 Вт, оно оказалось равным 59 Ом. Это в несколько раз больше заявленной мощности! Я было удивился, но потом вспомнил слово, которое всё объясняло – бареттер.
Дело в том, что сопротивление вольфрамовой нити лампы накаливания сильно зависит от температуры (следствие протекания тока). В моем случае, если это бы был не вольфрам, а обычный резистор, его рассеиваемая мощность при напряжении 230 Вольт была бы P = U2/R = 896. Почти 900 Ватт!
Кстати, именно поэтому производители датчиков с транзисторным выходом рекомендуют соблюдать осторожность при подключении датчиков.
Как же измерить рабочее сопротивление нити лампы накаливания? А никак. Его можно только определить косвенным путем, из закона знаменитого Ома. (Строго говоря, все омметры используют тот же закон – прикладывают напряжение и меряют ток). И мультиметром тут не обойдешься.
Используя косвенный метод и лампочку Лисма 24 В с мощностью 40 Вт, я составил вот такую табличку:
Зависимость сопротивления нити лампы накаливания от напряжения
(Номинальные параметры выделены)
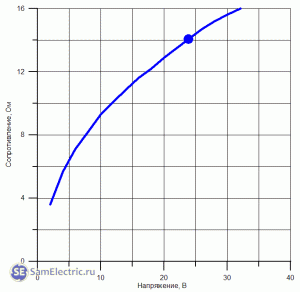
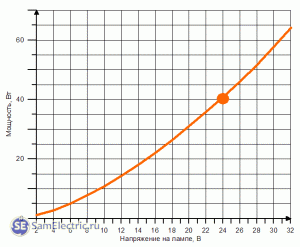
Как видно из таблицы, зависимость сопротивления лампочки от напряжения нелинейная. Это может проиллюстрировать график, приведенный ниже. Рабочая точка на графике выделена.
Кстати, сопротивление подопытной лампочки, измеренное с помощью цифрового мультиметра – около 1 Ома. Предел измерения – 200 Ом, при этом выходное напряжение вольтметра – 0,5 В. Эти данные также укладываются в полученные ранее.
Зависимость мощности от напряжения:
Для ламп на напряжение 230 В на основании экспериментальных данных была составлена вот такая табличка:
Из этой таблицы видно, что сопротивление нити лампы накаливания в холодном и горячем состоянии отличается в 12-13 раз. А это значит, что во столько же раз увеличивается потребляемая мощность в первоначальный момент.
Можно говорить о пусковом токе для ламп накаливания.
Стоит отметить, что сопротивление в холодном состоянии измерялось мультиметром на пределе 200 Ом при выходном напряжении мультиметра 0,5 В. При измерении сопротивления на пределе 2000 Ом (выходное напряжение 2 В) показания сопротивления увеличиваются более чем в полтора раза, что опять же укладывается в идею статьи.
“Горячее” сопротивление измерялось косвенным методом.
Сопротивление нити накаливания люминесцентных ламп
Дополнение к статье, чтобы получился ещё более полный материал.
Лампы с цоколем Т8, сопротивление спирали в зависимости от мощности :
10 Вт – 8,0…8,2 Ом
15 Вт – 3,3…3,5 Ом
18 Вт – 2,7…2,8 Ом
36 Вт – 2,5 Ом.
Сопротивление измерялось цифровым омметром на пределе 200 Ом.
Формула мощности и напряжения
Обновление статьи. У меня на блоге появилась статья автора Станислава Матросова, который развил тему сопротивления спирали лампочки с теоретической стороны. Он вывел формулу, согласно которой:
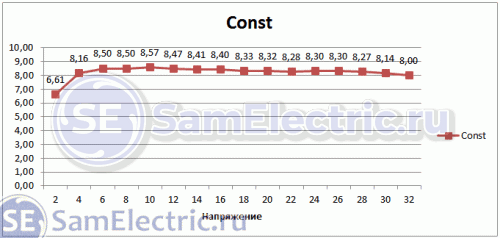
Я решил на основе данных, полученных в статье, посчитать эту величину в Экселе. Вот что у меня получилось:
Действительно, константа, которая с некоторой погрешностью во всём диапазоне равна 8,2±0,2. Её размерность – “Вольт в кубе на Ватт в квадрате”.
Низкое значение константы в начале диапазона объяснено автором в приведенной по ссылке статье.
Теперь, зная значение этой константы (8,2), можем записать формулу зависимости мощности от напряжения лампочки накаливания 40Вт 24В:
Формула для сопротивления
Но вернёмся к теме статьи. Проверим вывод Станислава Матросова о том, что сопротивление лампочки пропорционально корню из напряжения. Из предыдущих выводов можно вывести формулу для конкретной лампочки 40Вт 24В:
Теперь проверим, как эта формула соотносится с полученными мною экспериментальным данным (см. таблицу в начале статьи). Составим такую таблицу:
Таблица требует пояснений. Чтобы была соблюдена размерность, я нормировал экспериментально заданное напряжение (столбец 2) и рассчитанное сопротивление (столбец 4).
Колонка 5 – это корень из нормированного напряжения, и видно, что значения этой колонки отлично совпадают с колонкой 4!
Но давайте вернемся в реальному сопротивлению, и рассчитаем его по приведенной выше формуле (Зависимость сопротивления от напряжения). Это – 6-я колонка. Хорошо видно, что расчет по формуле практически идеально совпадает с расчетом из экспериментальных данных!
Кто хочет проверить мои расчеты, прикладываю файл: • Файл с расчетами и графиками / Файл с расчетами и графиками к статье про лампу накаливания, xlsx, 19.51 kB, скачан: 430 раз./
Всё, учебник физики можно переписывать! 😉
Кому интересно – задачка про последовательное подключение двух лампочек.
Оригинал статьи.
Если интересны темы канала, заходите также на мой сайт – https://samelectric.ru/ и в группу ВК – https://vk.com/samelectric
Не забываем подписываться и ставить лайки, впереди много интересного!
Обращение к хейтерам: за оскорбление Автора и Читателей канала – отправляю в баню.
По какой формуле можно найти сопротивление?
Анонимный вопрос
2 ноября 2018 · 61,6 K
Лучший ответ на 99.9% вопросов: “Поисковик в помощь”. · 2 нояб 2018
Самая простая формула для нахождения сопротивления – закон Ома для участка цепи.
R=U/I, где
R – сопротивление,
U – напряжение,
I – сила тока.
8,5 K
Комментировать ответ…Комментировать…
Рассчитайте сопротивление лампы накаливания в рабочем состоянии R и в выключенном состоянии R20 , а также токи в рабочем состоянии Iраб и в холодном состоянии I20 . Лампа мощностью 100 Вт включается в сеть напряжением 220 В. Температура нити лампы в холодном состоянии +200 С, в горячем – +30000 С. Материал нити – вольфрам. Его температурный коэффициент сопротивления – α=0,0045 1/К.
8,0 K
Комментировать ответ…Комментировать…
Сопротивление вычисляется по формуле (Закон Ома):
R = U/I
R — само сопротивление (Ом)
U — напряжение (Вольт)
I — сила тока (Ампер)
Т.е в системе СИ:
[R] = B/ A = Ом Читать далее
26,9 K
Комментировать ответ…Комментировать…
Разработка схемы и расчет осложняется еще одним обстоятельством. Ни один производитель не может определить точные параметры для каждого диода, поэтому они определяют среднее напряжение при оптимальном уровне электрического тока для выпускаемой партии. Это означает, что для определения точных значений при проектировании схем и расчете формул лучше всего использовать мультиметр.
Как рассчитать сопротивление лампочки?
Светодиоды пришли на смену традиционным системам освещения – лампам накаливания и энергосберегающим лампам. Чтобы светодиод работал правильно и не перегорал, его нельзя подключать непосредственно к электросети. Идея заключается в том, что он имеет низкое внутреннее сопротивление, поэтому если вы подключите его напрямую, ток будет высоким, и он сгорит. Вы можете ограничить ток с помощью резисторов. Однако необходимо выбрать правильный резистор для светодиода. Для этого производятся специальные расчеты.
Из этой таблицы видно, что сопротивление нити накала лампы накаливания в холодном и горячем состоянии отличается в 12-13 раз. Это означает, что потребляемая мощность в начальный момент времени увеличивается в тот же фактор.
Зависимость сопротивления нити накала лампы накаливания от напряжения
| Напряжение | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| % напряжения | 8.3 | 16.7 | 25.0 | 33.3 | 41.7 | 50.0 | 58.3 | 66.7 |
| Текущая сторона | 0.55 | 0.7 | 0.84 | 0.97 | 1.08 | 1.19 | 1.29 | 1.38 |
| Сопротивление | 3.6 | 5.7 | 7.1 | 8.2 | 9.3 | 10.1 | 10.9 | 11.6 |
| Мощность | 1.1 | 2.8 | 5.04 | 7.76 | 10.8 | 14.28 | 18.06 | 22.08 |
| Напряжение | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| % напряжения | 75.0 | 83.3 | 91.7 | 100.0 | 108.3 | 116.7 | 125.0 | 133.3 |
| Текущая страница | 1.47 | 1.55 | 1.63 | 1.7 | 1.77 | 1.84 | 1.92 | 2 |
| Сопротивление | 12.2 | 12.9 | 13.5 | 14.1 | 14.7 | 15.2 | 15.6 | 16.0 |
| Мощность | 26.46 | 31 | 35.86 | 40.8 | 46.02 | 51.52 | 57.6 | 64 |
Как видно из таблицы, зависимость сопротивления лампочки от напряжения нелинейна. Это можно проиллюстрировать на графике ниже. Рабочая точка на графике выделяется.
Сопротивление нити накала лампы накаливания в зависимости от напряжения
Кстати, сопротивление тестовой лампочки, измеренное цифровым мультиметром, составляет около 1 Ом. Предел измерения составляет 200 Ом, выходное напряжение вольтметра – 0,5 В. Эти данные также находятся в пределах, полученных ранее.
Зависимость мощности от напряжения:
Зависимость мощности от напряжения
Для ламп 230 В следующая таблица основана на экспериментальных данных:
| Мощность лампочки, W |
25 | 40 | 60 | 75 | 100 |
| R холодной нити накаливания, Ом | 150 | 90-100 | 60-65 | 45-50 | 37-40 |
| R hot нить накала, Ом |
1930 | 1200 | 805 | 650 | 490 |
| R gore./Rhool. | 12 | 12 | 13 | 13 | 12 |
Из этой таблицы видно, что сопротивление холодной и горячей нити накала лампочки отличается в 12-13 раз. Это означает, что потребляемая мощность в начальный момент времени увеличивается в такой же раз.
Следует отметить, что сопротивление в холодном состоянии измерялось мультиметром на пределе 200 Ом при выходном напряжении мультиметра 0,5 В. При измерении сопротивления на пределе 2000 Ом (выходное напряжение 2 В) показания сопротивления увеличиваются более чем в полтора раза, что опять же соответствует идее статьи.
“Горячее” сопротивление измерялось косвенным методом.
Получаем значение 100 Ом для резистора. Найдите рассеиваемую мощность для него (отнимите ток от Imax):
Онлайн-калькулятор сопротивления
Задача усложняется, если необходимо подключить более одного диода.
Чтобы вам было проще самостоятельно выполнять расчеты, мы подготовили онлайн-калькулятор для расчета сопротивления резисторов. Если вы подключаете несколько светодиодов, вам придется выбирать между параллельным и последовательным соединением между ними. И для этих схем нужны дополнительные расчеты для источника питания. Эти данные можно легко найти в Интернете, но мы рекомендуем использовать наш калькулятор.
Вам необходимо знать:
- Напряжение источника питания.
- Вольтамперная характеристика диода.
- Токовая характеристика диода.
- Количество диодов.
Вам также нужно будет выбрать параллельное или последовательное подключение. Мы рекомендуем изучить различия между соединениями в подготовленных ниже разделах.
Это свойство металлов позволяет создавать простые и относительно дешевые лампы накаливания без сложных пускорегулирующих аппаратов, необходимых в светодиодных и люминесцентных светильниках.
Полезная информация для начинающих электриков
Как использовать закон Ома на практике
Почти два столетия назад, в далеком 1827 году, Георг Ом распознал взаимосвязь между фундаментальными характеристиками электричества.
Он изучил и опубликовал данные о влиянии сопротивления участка цепи на величину тока, создаваемого напряжением. Удобно представить это с помощью изображения.
Любая работа всегда создается рабочим электрическим током. Он вращает ротор электродвигателя, заставляет светиться лампочку, сваривает или режет металлы и делает другие вещи.
Поэтому ему должны быть созданы оптимальные условия: значение электрического тока должно поддерживаться на номинальном уровне. Это зависит от:
- значение напряжения, приложенного к цепи;
- сопротивление среды, через которую протекает ток.
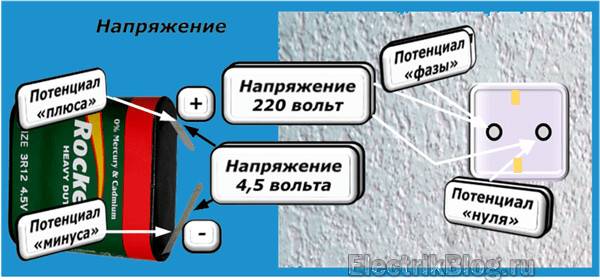
Здесь напряжение, как разность потенциалов приложенной энергии, является силой, которая создает электрический ток.
Если нет напряжения, то из-за отсутствия тока в подключенной электрической цепи не может быть совершена полезная работа. Такая ситуация часто возникает, когда кабель питания сломан, перетерт или перегорел.
С другой стороны, сопротивление решает противоположную проблему для напряжения. При очень высоком значении он ограничивает ток так, что он не может совершить никакой работы. Этот режим работы используется для хороших диэлектриков.
Примеры из реальной жизни
Между контактами образуется воздушный зазор. Это отличный изолятор, который препятствует прохождению тока через светильник.
Ток короткого замыкания может пережечь провода, что приведет к пожару в квартире. Поэтому из таких ситуаций есть только один выход: использование защитных устройств, способных как можно быстрее отключить напряжение питания.
В случае бытовой сети эту функцию выполняют автоматические выключатели или предохранители, работу которых я рассмотрю в других статьях.
При использовании резистора важно помнить, что сам по себе он не вечен: имея запас, чтобы выдержать приложенную энергию, он может износиться, выйти из строя и перегореть.
По этой причине в сопротивление вводится понятие диссипативной мощности, которая надежно рассеивается во внешнюю среду. Если тепловая энергия, создаваемая протекающим током, превысит это значение, резистор сгорит.
Что такое участок цепи
Рассмотрим простейшую электрическую цепь, состоящую из батареи, лампочки и нескольких проводов. В нем циркулирует электрический ток.
Показанная схема, или полная цепь, состоит из двух контуров:
- Внутренний источник напряжения.
- Внешняя область: лампочка с подключенными проводами.
Эти процессы, происходящие внутри аккумулятора, интересуют нас в основном как когнитивные процессы. Мы можем сделать их только хуже, если используем их неправильно.
Например, мы не можем контролировать электроэнергию, которая поступает в наш дом из трансформаторной подстанции. Мы просто используем его. Автоматические выключатели, УЗО, реле, разрядники или ограничители перенапряжения и другие современные модули защиты защищают нас от неисправностей и аварийных ситуаций.
Внешняя цепь, подключенная к источнику напряжения, является той частью цепи, в которой, используя закон Ома, мы совершаем полезную для себя работу.
Как использовать треугольник закона Ома
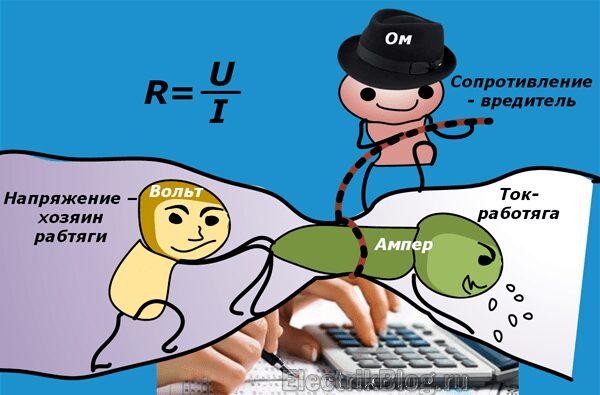
Простой мнемонический принцип представлен тремя частями треугольника. Это облегчает запоминание взаимосвязи между током, сопротивлением и напряжением.
Напряжение всегда находится на самом верху. Ток и сопротивление находятся внизу. Когда мы вычисляем одно значение из двух других, мы выводим его из треугольника и выполняем арифметическую операцию: деление или умножение.
Руководство для начинающих электриков
Треугольник закона Ома легко запомнить, но он не позволяет учитывать потребляемую мощность электроприбора. Этот четвертый параметр, важный для каждого домашнего электрика, всегда должен быть принят во внимание. .
Все бытовые электроприборы показывают потребляемую мощность в ваттах или киловаттах. Его формулу вместе с предыдущими значениями можно прочитать на рисунке ниже.
Этот справочник электрика позволит вам произвести простые расчеты в голове или на бумаге. Формулы из него встроены в алгоритм, по которому работает мой онлайн-калькулятор закона Ома.
Я предлагаю вам провести те же расчеты, используя оба метода, и сравнить результаты. Если вы обнаружили несоответствия, пожалуйста, укажите их в комментариях. Это будет вашей помощью для моего проекта.
Я постарался кратко и просто изложить принципы закона Ома в применении к домашней работе. Я считаю это достаточным и не рассматриваю закон Ома для полной цепи в его обычной форме, комплексные числа или что-то еще.
Однако если вы хотите получить видеоурок по этой теме, воспользуйтесь уроком владельца Физика – Закон Ома.
Возможно, у вас остались вопросы о том, как работает калькулятор? Ответьте на них, и я отвечу. Используйте раздел комментариев.
Наконец, я напоминаю вам, что сейчас самое время поделиться этим материалом со своими друзьями в социальных сетях и подписаться на рассылку. Это позволит вам быть в курсе новых статей.
<t^circ>_1)” />,
<t^circ>_2)” />,
Задача 40: Определение сопротивления нити накала электрической лампы
Для лампы накаливания мощностью сто пятьдесят ватт и напряжением двести двадцать вольт определите сопротивление вольфрамовой нити при температуре двадцать пять градусов Цельсия. Известно, что температура нити лампы составляет две тысячи пятьсот градусов Цельсия. Температурный коэффициент сопротивления вольфрама составляет 5,1×10 -3 град -1 .
Напишем формулы для расчета сопротивления нити накала при комнатной и рабочей температуре


где R1 – Сопротивление нити накала при 25 градусах Цельсия;
R2 – сопротивление нити накала при температуре 2500 градусов Цельсия.


Сопротивление нити накала при рабочей температуре определяется по формуле

Формула для расчета сопротивления нити накала при температуре 25 градусов Цельсия имеет вид

Ответ: сопротивление вольфрамовой нити электрической лампы при температуре двадцать пять градусов Цельсия составляет двадцать шесть целых пять ом.
Из этой таблицы видно, что сопротивление нити накала лампы накаливания в холодном и горячем состоянии отличается в 12-13 раз. Это означает, что потребляемая мощность в начальный момент времени увеличивается в тот же фактор.
Каково сопротивление лампочки?
Однажды я решил проверить закон Ома. Я применил его к лампочке. Я измерил сопротивление лампы Лисма 230В 60Вт и оно составило 59 Ом. Он в несколько раз мощнее, чем заявлено! Я удивился, но потом вспомнил слово, которое все объяснило. бареттер
Дело в том, что сопротивление вольфрамовой нити лампы накаливания сильно зависит от температуры (следствие протекания тока). В моем случае, если бы это был не вольфрам, а обычный резистор, его рассеиваемая мощность при 230 В была бы P = U2/R = 896. Почти 900 ватт!
Кстати, именно поэтому производители датчиков с транзисторным выходом рекомендуют соблюдать осторожность при их подключении.
Как же измерить рабочее сопротивление нити накала? Ты не можешь. Вы можете определить его только косвенно, основываясь на знаменитом законе Ома. (Строго говоря, все омметры используют один и тот же закон – прикладывают напряжение и измеряют ток). Без мультиметра тоже не обойтись.
Используя косвенный метод и лампочку Лисма 24 В мощностью 40 Вт, я составил следующую таблицу:
Зависимость сопротивления нити накала лампы накаливания от напряжения
(Номинальные значения отмечены).
Как видно из таблицы, зависимость сопротивления лампочки от напряжения нелинейная. Это можно проиллюстрировать на графике ниже. Рабочая точка на графике выделяется.
Сопротивление нити накала лампы накаливания в зависимости от напряжения
Кстати, сопротивление тестовой лампочки, измеренное цифровым мультиметром, составляет около 1 Ом. Предел измерения составляет 200 Ом, выходное напряжение вольтметра – 0,5 В. Эти данные также находятся в пределах, полученных ранее.
Зависимость мощности от напряжения:
Зависимость мощности от напряжения
Для ламп на 230 В эта таблица составлена на основе экспериментальных данных:
Сила и сопротивление
Из этой таблицы видно, что сопротивление нити накала холодной и горячей лампочки отличается в 12-13 раз. Это означает, что потребление энергии при включении увеличивается в 12 раз.
Можно говорить о пусковом токе для ламп накаливания.
Стоит отметить, что холодное сопротивление было измерено мультиметром на пределе 200 Ом при выходном напряжении мультиметра 0,5 В. При измерении сопротивления на пределе 2000 Ом (выходное напряжение 2 В) показания сопротивления увеличиваются более чем в полтора раза, что опять же соответствует идее статьи.
“Горячее” сопротивление измерялось косвенным методом.
Сопротивление нити накала лампы накаливания
Дополнение к статье, чтобы сделать ее еще более полной.
Лампы с цоколем T8, сопротивление нити накала зависит от мощности:
Сопротивление измеряется цифровым омметром на пределе 200 Ом.
Формула для мощности и напряжения
Обновление статьи. У меня в блоге есть статья автора Станислава Матросова, который разработал тему сопротивления катушки лампы накаливания с теоретической стороны. Он вывел формулу, согласно которой:
Для каждой лампы существует параметр, который стабилен в широком диапазоне электрических условий. Этот параметр представляет собой отношение куба напряжения к квадрату мощности:
Я решил рассчитать это значение в Excel, используя данные из статьи. Вот что я получил:
Действительно, константа, которая с некоторой погрешностью по всему диапазону равна 8,2±0,2. Ее размерность – “вольт на куб на ватт в квадрате”.
Расчетная постоянная для лампочки = 8,2
Низкое значение константы в начале диапазона объясняется автором в статье по ссылке.
Теперь, зная значение этой константы (8.2), мы можем написать формулу зависимости мощности от напряжения для лампы накаливания 40 Вт 24 В:
Зависимость мощности лампы накаливания от напряжения
Формула сопротивления
Но давайте вернемся к теме статьи. Проверим вывод Станислава Матросова о том, что сопротивление лампочки пропорционально корню из напряжения. Исходя из предыдущих рассуждений, можно вывести формулу для конкретной лампы накаливания 40 Вт 24 В:
Зависимость сопротивления от напряжения, формула для электрической лампочки
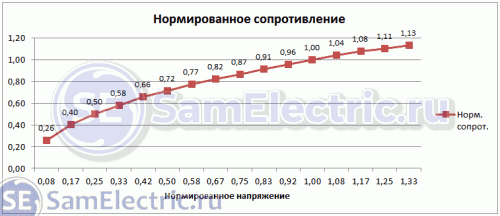
Давайте теперь проверим, как эта формула соотносится с полученными мной экспериментальными данными (см. таблицу в начале статьи). Давайте создадим такую таблицу:
Таблица требует пояснений. Для сохранения размерности я нормализовал экспериментально определенное напряжение (колонка 2) и рассчитанное сопротивление (колонка 4).
Столбец 5 – это корень из нормализованного напряжения, и вы можете видеть, что значения этого столбца идеально совпадают со столбцом 4!
Но давайте вернемся к фактическому сопротивлению и рассчитаем его по приведенной выше формуле (зависимость сопротивление/напряжение). Это столбец 6. Вы можете ясно видеть, что расчет по формуле почти идеально совпадает с расчетом по экспериментальным данным!
Зависимость сопротивления от напряжения. Квадратичная зависимость.
Кто хочет проверить мои расчеты, прилагаю файл: •Файл с расчетами и графиками
/ Файл с расчетами и графиками для статьи о лампочках, xlsx, 19.51 kB, скачан: 430 раз
</t^circ></t^circ>
- 5 причин, почему лампочки часто перегорают в вашей квартире и что делать?.
- Основные параметры выпрямительных диодов; Школа для инженеров-электриков: Электротехника и электроника.
- Правильное переключение светодиодов; STC ORBITA.
- Полупроводниковые диоды.
- Обратный ток. Что такое возвратный ток?.
- Важен ли для вас индикатор уведомлений?.
- Основы электроники. Урок 4: Расчет резистора для светодиода.
Решил
я
как-то
проверить
закон
Ома.
Применительно
к
лампе
накаливания.
Измерил
сопротивление
лампочки
Лисма
230
В
60
Вт,
оно
оказалось
равным
59
Ом.
Я
было
удивился,
но
потом
вспомнил
слово,
которое
всё
объясняло
–
бареттер.
Дело
в
том,
что
сопротивление
вольфрамовой
нити
лампы
накаливания
сильно
зависит
от
температуры
(следствие
протекания
тока).
В
моем
случае,
если
это
бы
был
не
вольфрам,
а
обычный
резистор,
его
рассеиваемая
мощность
при
напряжении
230
Вольт
была
бы
P
=
U2/R
=
896.
Почти
900
Ватт!
Кстати,
именно
поэтому
производители
датчиков
с
транзисторным
выходом
рекомендуют
соблюдать
осторожность
при
подключении
датчиков.
Как
же
измерить
рабочее
сопротивление
нити
лампы
накаливания?
А
никак.
Его
можно
только
определить
косвенным
путем,
из
закона
знаменитого
Ома.
(Строго
говоря,
все
омметры
используют
тот
же
закон
–
прикладывают
напряжение
и
меряют
ток).
И
мультиметром
тут
не
обойдешься.
Используя
косвенный
метод
и
лампочку
Лисма
24
В
с
мощностью
40
Вт,
я
составил
вот
такую
табличку:
Зависимость
сопротивления
нити
лампы
накаливания
от
напряжения
| Напряжение | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|
% напряжения |
8.3 | 16.7 | 25.0 | 33.3 | 41.7 | 50.0 | 58.3 | 66.7 |
| Ток | 0.55 | 0.7 | 0.84 | 0.97 | 1.08 | 1.19 | 1.29 | 1.38 |
| Сопротивление | 3.6 | 5.7 | 7.1 | 8.2 | 9.3 | 10.1 | 10.9 | 11.6 |
| Мощность | 1.1 | 2.8 | 5.04 | 7.76 | 10.8 | 14.28 | 18.06 | 22.08 |
(продолжение таблицы)
| Напряжение | 18 | 20 | 22 |
24 |
26 | 28 | 30 | 32 |
|
% напряжения |
75.0 | 83.3 | 91.7 |
100.0 |
108.3 | 116.7 | 125.0 | 133.3 |
| Ток | 1.47 | 1.55 | 1.63 |
1.7 |
1.77 | 1.84 | 1.92 | 2 |
| Сопротивление | 12.2 | 12.9 | 13.5 |
14.1 |
14.7 | 15.2 | 15.6 | 16.0 |
| Мощность | 26.46 | 31 | 35.86 |
40.8 |
46.02 | 51.52 | 57.6 | 64 |
(Номинальные параметры выделены)
Как
видно
из
таблицы,
зависимость
сопротивления
лампочки
от
напряжения
нелинейная.
Это
может
проиллюстрировать
график,
приведенный
ниже.
Рабочая
точка
на
графике
выделена.
Сопротивление
нити
лампы
накаливания
в
зависимости
от
напряжения
Кстати,
сопротивление
подопытной
лампочки,
измеренное
с
помощью
цифрового
мультиметра
–
около
1
Ома.
Предел
измерения
–
200
Ом,
при
этом
выходное
напряжение
вольтметра
–
0,5
В.
Эти
данные
также
укладываются
в
полученные
ранее.
Зависимость
мощности
от
напряжения:
Зависимость
мощности
от
напряжения
Для
ламп
на
напряжение
230
В
на
основании
экспериментальных
данных
была
составлена
вот
такая
табличка:
|
Мощность лампочки, Вт |
25 | 40 | 60 | 75 | 100 |
|
R холодной нити,Ом |
150 | 90-100 | 60-65 | 45-50 | 37-40 |
|
R горячей нити, |
1930 | 1200 | 805 | 650 | 490 |
| Rгор./Rхол. | 12 | 12 | 13 | 13 | 12 |
Из
этой
таблицы
видно,
что
сопротивление
нити
лампы
накаливания
в
холодном
и
горячем
состоянии
отличается
в
12-13
раз.
А
это
значит,
что
во
столько
же
раз
увеличивается
потребляемая
мощность
в
первоначальный
момент.
Стоит
отметить,
что
сопротивление
в
холодном
состоянии
измерялось
мультиметром
на
пределе
200
Ом
при
выходном
напряжении
мультиметра
0,5
В.
При
измерении
сопротивления
на
пределе
2000
Ом
(выходное
напряжение
2
В)
показания
сопротивления
увеличиваются
более
чем
в
полтора
раза,
что
опять
же
укладывается
в
идею
статьи.
“Горячее”
сопротивление
измерялось
косвенным
методом.
UPD:
Сопротивление
нити
накаливания
люминесцентных
ламп
Дополнение
к
статье,
чтобы
получился
ещё
более
полный
материал.
Лампы
с
цоколем
Т8,
сопротивление
спирали
в
зависимости
от
мощности
:
10
Вт
–
8,0…8,2
Ом
15
Вт
–
3,3…3,5
Ом
18
Вт
–
2,7…2,8
Ом
36
Вт
–
2,5
Ом.
Сопротивление
измерялось
цифровым
омметром
на
пределе
200
Ом.
Формула
мощности
и
напряжения
Обновление
статьи
от
января
2018.
У
меня
на
блоге
появилась
статья
автора
Станислава
Матросова,
который
развил
тему
сопротивления
спирали
лампочки
с
теоретической
стороны.
Он
вывел
формулу,
согласно
которой:
Для
любой
лампы
накаливания
существует
параметр,
стабильный
в
широком
диапазоне
электрических
режимов. Этим
параметром
является
отношение
куба
напряжения
к
квадрату
мощности:
Я
решил
на
основе
данных,
полученных
в
статье,
посчитать
эту
величину
в
Экселе.
Вот
что
у
меня
получилось:
|
U |
P |
U^3 |
P^2 |
Const |
| 2 | 1,1 | 8 | 1,21 | 6,61157 |
| 4 | 2,8 | 64 | 7,84 | 8,163265 |
| 6 | 5,04 | 216 | 25,4016 | 8,503401 |
| 8 | 7,76 | 512 | 60,2176 | 8,502498 |
| 10 | 10,8 | 1000 | 116,64 | 8,573388 |
| 12 | 14,28 | 1728 | 203,9184 | 8,473978 |
| 14 | 18,06 | 2744 | 326,1636 | 8,412956 |
| 16 | 22,08 | 4096 | 487,5264 | 8,401596 |
| 18 | 26,46 | 5832 | 700,1316 | 8,329863 |
| 20 | 31 | 8000 | 961 | 8,324662 |
| 22 | 35,86 | 10648 | 1285,94 | 8,280327 |
| 24 | 40,8 | 13824 | 1664,64 | 8,304498 |
| 26 | 46,02 | 17576 | 2117,84 | 8,29902 |
| 28 | 51,52 | 21952 | 2654,31 | 8,270321 |
| 30 | 57,6 | 27000 | 3317,76 | 8,138021 |
| 32 | 64 | 32768 | 4096 | 8 |
Действительно,
константа,
которая
с
некоторой
погрешностью
во
всём
диапазоне
равна
8,2±0,2.
Её
размерность
–
“Вольт
в
кубе
на
Ватт
в
квадрате”.
Константа
для
расчета
лампы
накаливания
=
8,2
Низкое
значение
константы
в
начале
диапазона
объяснено
автором
в
приведенной
по
ссылке
статье.
Теперь,
зная
значение
этой
константы
(8,2),
можем
записать
формулу
зависимости
мощности
от
напряжения
лампочки
накаливания
40Вт
24В:
Зависимость
мощности
лампочки
накаливания
от
напряжения
Формула
для
сопротивления
Но
вернёмся
к
теме
статьи.
Проверим
вывод
Станислава
Матросова
о
том,
что
сопротивление
лампочки
пропорционально
корню
из
напряжения.
Из
предыдущих
выводов
можно
вывести
формулу
для
конкретной
лампочки
40Вт
24В:
Зависимость
сопротивления
от
напряжения,
формула
для
лампы
накаливания
Теперь
проверим,
как
эта
формула
соотносится
с
полученными
мною
экспериментальным
данным
(см.
таблицу
в
начале
статьи).
Составим
такую
таблицу:
|
1. Напря- жение, |
2. Норм. напр. |
3. Сопрот., Ом |
4. Норм. сопрот. |
5. Корень из напряж. |
6. Корень из Х из |
| 2 | 0,08 | 3,6 | 0,26 | 0,29 | 4,04 |
| 4 | 0,17 | 5,7 | 0,40 | 0,41 | 5,72 |
| 6 | 0,25 | 7,1 | 0,50 | 0,50 | 7,01 |
| 8 | 0,33 | 8,2 | 0,58 | 0,58 | 8,09 |
| 10 | 0,42 | 9,3 | 0,66 | 0,65 | 9,04 |
| 12 | 0,50 | 10,1 | 0,72 | 0,71 | 9,91 |
| 14 | 0,58 | 10,9 | 0,77 | 0,76 | 10,70 |
| 16 | 0,67 | 11,6 | 0,82 | 0,82 | 11,44 |
| 18 | 0,75 | 12,2 | 0,87 | 0,87 | 12,13 |
| 20 | 0,83 | 12,9 | 0,91 | 0,91 | 12,79 |
| 22 | 0,92 | 13,5 | 0,96 | 0,96 | 13,41 |
| 24 | 1,00 | 14,1 | 1,00 | 1,00 | 14,01 |
| 26 | 1,08 | 14,7 | 1,04 | 1,04 | 14,58 |
| 28 | 1,17 | 15,2 | 1,08 | 1,08 | 15,13 |
| 30 | 1,25 | 15,6 | 1,11 | 1,12 | 15,66 |
| 32 | 1,33 | 16 | 1,13 | 1,15 | 16,18 |
Таблица
требует
пояснений.
Чтобы
была
соблюдена
размерность,
я
нормировал
экспериментально
заданное
напряжение
(столбец
2)
и
рассчитанное
сопротивление
(столбец
4).
Колонка
5
–
это
корень
из
нормированного
напряжения,
и
видно,
что
значения
этой
колонки
отлично
совпадают
с
колонкой
4!
Но
давайте
вернемся
в
реальному
сопротивлению,
и
рассчитаем
его
по
приведенной
выше
формуле
(Зависимость
сопротивления
от
напряжения).
Это
–
6-я
колонка.
Хорошо
видно,
что
расчет
по
формуле
практически
идеально
совпадает
с
расчетом
из
экспериментальных
данных!
Зависимость
сопротивления
от
напряжения.
Квадратичная
зависимость.
Кто
хочет
проверить
мои
расчеты,
прикладываю
файл: •
Файл
с
расчетами
и
графиками
/
Файл
с
расчетами
и
графиками
к
статье
про
лампу
накаливания,
xlsx,
19.51
kB,
скачан:
1064
раз./
Всё,
учебник
физики
можно
переписывать!
😉
Кому
интересно
–
задачкапро
последовательное
подключение
двух
лампочек.
Понравилось?
Поставьте
оценку,
и
почитайте
другие
статьи
блога!
Загрузка…
Внимание!
Автор
блога
не
гарантирует,
что
всё
написанное
на
этой
странице
–
истина.
За
ваши
действия
и
за
вашу
безопасность
ответственны
только
вы!