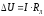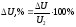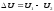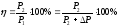Как найти сопротивление линий электропередачи??
Владимир Кузин
Знаток
(418),
закрыт
11 лет назад
Лучший ответ
гена ткаченко
Ученик
(160)
11 лет назад
так я прокоментировал—сопротивление равно напряжение делить на ток//
Источник: школа 10 класс
Остальные ответы
Ol_Tim
Искусственный Интеллект
(148575)
11 лет назад
У каждого провода есть удельное сопротивление на погонный метр, а дальше всё просто – умножить удельное сопротивление на длину линии.
Похожие вопросы
Схема замещения линии электропередачи — это представление линии электропередачи в виде математической модели для исследования различных режимов работы электрической сети.
Содержание
- 1 Общие положения
- 2 Воздушная линия электропередачи
- 3 Кабельная линия электропередачи
- 4 Схема замещения с сосредоточенными параметрами
- 5 Литература
- 6 Использованные источники
Общие положения
Активное сопротивление проводов и кабелей определяется материалом токоведущих жил, их сечением и частотой электрического тока. Для большинства расчётных задач зависимостью активного сопротивления провода от частоты переменного тока пренебрегают, вследствие низкой частоты тока в электрической сети (в России 50 Гц). Эта зависимость обусловлена наличием скин эффекта.
Активное сопротивление проводников электрического тока изменяется при их нагреве или охлаждении. При этом температура проводников изменяется при изменении величины протекающего электрического тока (более подробно можно ознакомиться здесь). Вследствие этого величины удельных активных сопротивлений являются переменными величинами, и определение их по справочным таблицам позволяет получить лишь приближённую оценку их величины. Зачастую этого приближения вполне достаточно, так как оно лежит в пределах точности задания других параметров электрической сети.
Магнитное поле, возникающее вокруг и внутри проводников, определяет их индуктивное сопротивление. Электродвижущая сила (э.д.с.), соответствующая индуктивному сопротивлению наводится в каждом проводнике линии электропередачи от проводов всех фаз. Поэтому её величина, а следовательно, и величина пропорционального её индуктивного сопротивления зависят от взаимного расположения проводов. Если это расположение обеспечивает одинаковое потокосцепление каждого провода, то наводимые в проводах э.д.с. становятся равными, а индуктивные сопротивления фазных проводов линии электропередачи одинаковыми. Такое равенство имеет место при расположении фазных проводов по вершинам равностороннего треугольника.
Индуктивные сопротивления фазных проводов линии электропередачи, у которой провода расположены горизонтально, по всей длине, отличаются друг от друга. Чтобы избежать появления нежелательной нессиметрии фазных значений сопротивлений, а следовательно токов и напряжений, применяют транспозицию проводов.
В большинстве случаев можно принять, что активное и реактивное сопротивление, активная и ёмкостная проводимости равномерно распределены по всей её длине. Для линий электропередач небольшой длины (при частоте 50 Гц границей можно считать длину 300 км) распределёность параметров можно не учитывать и можно использовать более простое представление в виде схемы замещения с сосредоточенными параметрами. Обычно в расчётах режимов работы энергосистем применяется П-образная схема замещения линии электропередач с сосредоточенными параметрами.
Воздушная линия электропередачи
Расчеты параметров приведены для одной цепи ЛЭП.
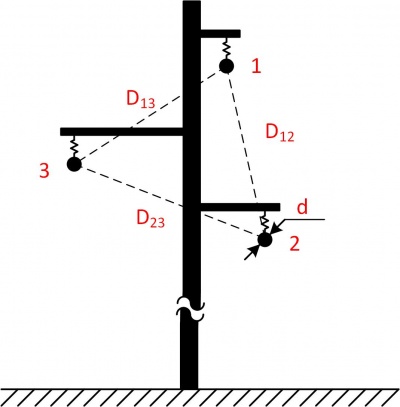
Рисунок — Пример треугольного расположения фазных проводов без расщепления на одноцепной опоре.
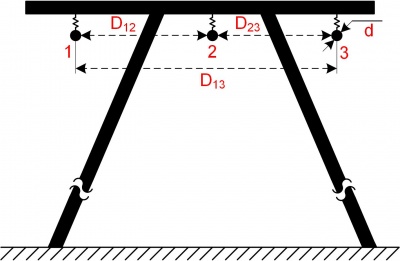
Рисунок — Пример горизонтального расположения фазных проводов без расщепления на одноцепной опоре.
Величина активного сопротивления воздушной линии электропередачи влияет на нагрев проводов, при протекании по ним электрического тока. Для сталеалюминиевых проводов, являющихся наиболее часто используемыми для воздушных ЛЭП, активное сопротивление определяется главным образом алюминиевой частью. Это обусловлено эффектом вытеснения переменного тока к поверхности проводника (скин-эфффект). Активное сопротивление в первую очередь зависит от материала, из которого изготовлен проводник, его длины и сечения. При расчётах режимов работы энергосистемы активное сопротивление принято измерять в [Ом]:
- [math]displaystyle
R = rho frac{L}{F},
[/math]
где [math]displaystyle rho[/math] — удельное активное сопротивление проводника [[math]displaystyle frac{text{Ом} cdot text{мм}^2}{text{км}} [/math]]; [math]L[/math] — длина проводника [км]; [math]F[/math] — площадь поперечного сечения проводника [[math]displaystyle text{мм}^2 [/math]].
Для сталеалюминиевых проводов (обозначение марки провода — АС), выполненных в виде стального многопроволочного сердечника и многопроволочной алюминиевой оболочки, из-за поверхностного эффекта и разницы в удельных сопротивлениях стали и алюминия практически весь ток протекает по алюминиевым проводникам. Если учесть также, что ток протекает по отдельным проводникам, навитым вокруг сердечника и имеющим длину на 3—4 % больше длины провода, то расчётное удельное сопротивление сталеалюминиевого провода, отнесенное к единице его длины, составит [math]displaystyle rho = 31,5 frac{text{Ом} cdot text{мм}^2}{text{км}}[/math].
Обычно в справочных материалах приводится удельное (погонное) сопротивление линии электропередачи [math]displaystyle R_0[/math] [Ом/км] для стандартных сечений, тогда результирующее сопротивление одного провода определяется как,
- [math]displaystyle
R = R_0 cdot L.
[/math]
Справочные значения приводятся для температуры окружающей среды 20°С. Активное сопротивление зависит от температуры, но при расчётах эта зависимость учитывается не всегда.
Индуктивное сопротивление воздушной ЛЭП определяется индуктивностью фаз ЛЭП по отношению к земле и взаимоиндукцией между фазами и, следовательно, зависит от взаимного расположения фаз, расстояния между фазами и диаметра провода.
Для устранения разницы в величине индуктивного сопротивления фаз (крайних и средней) производится транспозиция проводов.
Расположение проводов воздушной линии электропередачи на опоре может быть горизонтальным или треугольным.
Удельное индуктивное сопротивление фазы одноцепной транспонированной линии подсчитывается с учётом взаимоиндукции фаз по соотношению:
- [math]displaystyle
X_0 =0,1445 cdot lg frac{D_text{ср}}{r_{text{э}}} + frac{0,0157}{m}text{ }frac{text{Ом}}{text{км}}.
[/math]
где [math]displaystyle D_text{ср}[/math] — среднегеометрическое расстояние между фазами [м]; [math]displaystyle r_{text{э}}[/math] — эквивалентный радиус фазы, если нет расщепления то [math]displaystyle r_{text{э}}=r[/math] [м]; [math]r[/math] – радиус провода фазы [м]; [math]m[/math] — число проводов в фазе, если нет расщепления то [math]displaystyle m=1[/math] [шт.];
- [math]displaystyle
D_text{ср} =sqrt[3]{D_{1,2}D_{1,3}D_{2,3}};
[/math]
- [math]displaystyle
r_{text{э}} =sqrt[m]{r prod^m_{i=2}a_{1i} },
[/math]
где [math]displaystyle a_i[/math] — расстояние между первым и [math]displaystyle i[/math]-м проводом в фазе [м]; [math]displaystyle r = frac{d}{2}[/math] — радиус фазного проводника.
| Класс напряжения, кВ | 35 | 110 | 150 | 220 | 330 | 500 | 750 |
|---|---|---|---|---|---|---|---|
| Среднее геометрическое расстояние, м | 3,5 | 5,0 | 6,5 | 8,0 | 11,0 | 14,0 | 19,5 |
Удельная активная проводимость воздушной линии (характеризующая потери на корону крайне малый ток утечки через изоляторы) определяется по соотношению:
- [math]displaystyle
G_0 = frac{Delta P_{к.0}}{U^2_text{ном}},
[/math]
Эквивалентная активная проводимость определяется следующим образом:
- [math]displaystyle
G = G_0 cdot L.
[/math]
Для воздушных линий погонные потери активной мощности на корону существенно зависят от погодных условий и напряжения, поэтому активная погонная проводимость является переменным и нелинейным параметром. В большинстве случаев более целесообразно непосредственно учитывать для линии электропередачи в виде дополнительной нагрузки по концам линии (узлы 1 и 2) [math]displaystyle P_1=P_2=frac{Delta P_{к.0}}{2}[/math] или в виде активной проводимости на землю [math]displaystyle frac{G}{2} [/math].
Коронирование проводов приводит:
- к снижению КПД передачи электрической энергии;
- к усиленному окислению поверхности проводов;
- к появлению радиопомех.
Ёмкостная проводимость линии определяется токами смещения за счёт электростатического поля линии (между фазами и по отношению к земле). Эта проводимость создает так называемый зарядный, или ёмкостный, ток, вектор которого опережает на 90° вектор напряжения линии. Величина удельной ёмкостной проводимости
- [math]displaystyle
B_0 = frac{7,58}{lg frac{D_text{ср}}{r_{text{э}} }} cdot 10^{-6} [frac{text{См}}{text{км}}].
[/math]
Эквивалентная ёмкостная проводимость:
- [math]displaystyle
B = B_0 cdot L.
[/math]
Ёмкостная проводимость воздушных линий электропередачи слабо зависит от конструктивных особенностей ЛЭП и имеет значение от [math]2,55 cdot 10^{-6}[/math] до [math]2,80 cdot 10^{-6}[/math] [См/км] для ВЛ 110—220 кВ и от [math]displaystyle 3,4 cdot 10^{-6}[/math] до [math]displaystyle 4,2 cdot 10^{-6}[/math] [См/км] для ВЛ 330—750 кВ. Значения удельных проводимостей приводятся в справочной литературе[1].
Кабельная линия электропередачи
Кабельные линии электропередач в расчётах представляют такой же П-образной схемой замещения, что и воздушные линии. Удельные продольные активные и реактивные сопротивления определяются по справочным таблицам так же как и для воздушных линий.
Особенностью кабельных линий электропередач является близкое расположение фаз (по сравнению с воздушными линиями), что приводит к снижению удельного индуктивного сопротивления и увеличению удельной ёмкостной проводимости.
Для кабельных линий электропередачи напряжением 110 кВ и выше необходимо учитывать потери в изоляции кабеля. Они определяются по формуле:
- [math]
G = B cdot operatorname{tg} delta.
[/math]
Параметр [math]operatorname{tg} delta[/math] называется тангенс диэлектрчиеских потерь и определяется по данным завода изготовителя кабеля. Обычно находится в пределах от 0,003 до 0,006.
Схема замещения с сосредоточенными параметрами
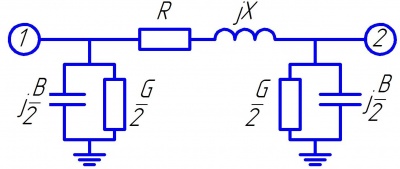
Рисунок — Полная П-образная схема замещения линии электропередачи. Цифрами 1 и 2 показаны узлы начала и конца линии электропередачи.
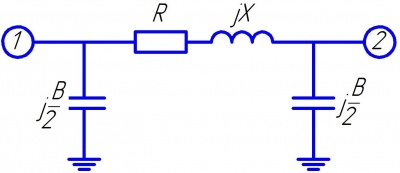
Рисунок — П-образная схема замещения линии электропередачи, только с ёмкостной проводимостью. Цифрами 1 и 2 показаны узлы начала и конца линии электропередачи.
Рисунок — П-образная схема замещения линии электропередачи, без учёта шунтов. Цифрами 1 и 2 показаны узлы начала и конца линии электропередачи.
При расчёте режима работы электрической сети воздушная трехфазная линия переменного тока напряжением до 500 кВ и длиной до 300 км может быть представлена схемой замещения с сосредоточенными параметрами П-образного вида. В случае превышения длины линии электропередачи 300 км необходимо изменить схему замещения одним из трёх способов:
- Разделить её на сегменты длиной менее 300 км.
- Представить линию волновыми параметрами.
- При длинах от 300 до 500 км можно использовать поправочные коэффициенты, значение которых при малых длинах близко к единице:
- [math]displaystyle K_R = 1 – frac{L^2}{3} X_0 B_0 [/math];
- [math]displaystyle K_X = 1 – frac{L^2}{6} X_0 B_0 (1 – frac{R^2_0}{X^2_0}) [/math];
- [math]displaystyle K_C = frac{3 + K_R}{2(1+K_R)}[/math].
В зависимости от класснапряжения воздушной ЛЭП можно использовать различные схемы замещения:
- 220 кВ и выше. Полная схема замещения с активным и ёмкостным шунтом.
- от 35 кВ до 220 кВ. Сокращённая схема замещения только с ёмкостным шунтом.
- до 35 кВ. Схема замещения без шунтов.
Для расчёта режимов электрической сети, как правило, используется П-образная схема замещения сети, параметры схемы замещения вычисляются для одной фазы. При расчётах режима удобно схемы замещения представлять в виде, представленном на рисунке.
Полное продольное сопротивление и проводимости (шунты узлов 1 и 2) схемы замещения имеют вид
- [math]displaystyle
Z = R +jX;
[/math]
- [math]displaystyle
Y_1 = Y_2 = frac{G}{2}+jfrac{B}{2}.
[/math]
Зачастую при расчётах установившихся режимов активная проводимость ЛЭП не учитывается, так как принятые меры борьбы с короной достаточно эффективны и, следовательно, потери на корону достаточно малы. Для воздушных линий классом напряжения менее 220 кВ потери на коронирование можно не учитывать, так как это существенно не скажется на полученной оценке параметров установившегося режима.
В случае исследования режимов воздушных линий напряжением менее 35 кВ можно не учитывать также ёмкостные шунты. В этом случае, схема замещения будет содержать только продольное сопротивление [math]Z[/math].
Литература
- Электрические системы. Электрические сети. / Под ред. д.т. н. В. А. Веникова. М.: Высшая школа — 1971.
Использованные источники
- ↑ 1,0 1,1 Справочник по проектированию электроэнергетических систем. Третье издание, переработанное и дополненное. Под редакцией С. С. Рокотяна, И. М. Шапиро. Авторы В. В. Ершевич, А. Н. Зейлигер, Г. А. Илларионов, Л. Я. Рудых, Д. Л. Файбисович, Р. М. Фришберг, Л. Д. Хабачев. И. М. Шапиро. М.: Энергоатомиздат, 1985
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное
государственное бюджетное учреждение
высшего
профессионального образования
РОСТОВСКИЙ
ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Дорожно-транспортный
институт
Кафедра
«Электротехника и автоматика»
ОТЧЁТ
ПО
ЛАБОРАТОРНОЙ РАБОТЕ №2
Исследование
работы двухпроводной линии
электропередачи
Выполнил
студент гр. ТЛ-304 Сопнева Е. С.
Принял
Мелихов О. О.
Дата
___________________
Ростов-на-Дону
2015
г.
Лабораторная
работа №2
Исследование
работы двухпроводной линии
электропередачи
Цель
работы:
-
Познакомиться с основными электротехническими
параметрами, характеризующими работу
линии электропередачи (ЛЭП). -
Исследовать работу линии в режиме
холостого хода и нагрузки. -
Исследовать влияние тока нагрузки на
потерю напряжения и мощности, а так же
КПД линии.
Основные теоретические положения
Передача и распределение электрической
энергии осуществляется в большинстве
случаев с помощью воздушных и кабельных
линий электропередачи. Однолинейная,
принципиальная схема производства,
передачи и распределения электроэнергии
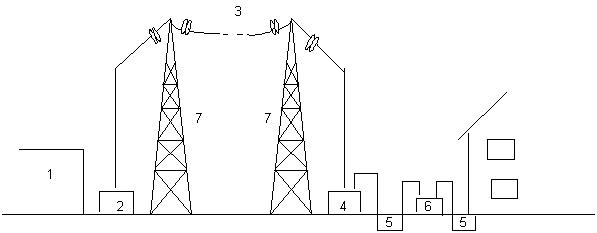
показана на рис. 1.
На строительных площадках получили
широкое распространение воздушные
линии (ВЛ) вследствие возможности
простого изменения трассы в ходе
строительных работ, их меньшей стоимости
(по сравнению с кабельными), простоты
обнаружения мест повреждения, а также
удобства ремонта.
U=10 кВ U=110
кВ U=10 кВ
U=0,4кВ
Рис.1.
Принципиальная схема производства,
передачи и распределения электроэнергии:
-
генератор электростанции;
-
повышающий трансформатор;
-
воздушная ЛЭП;
-
районная подстанция;
-
кабельные линии;
-
понижающий трансформатор;
-
опоры ЛЭП.
В условиях предприятии стройиндустрии,
как и вообще промышленных предприятий,
а также в жилых районах и на стройплощадках,
распределение электроэнергии
осуществляется и кабельными линиями
(КЛ), которые отличаются высокой
надежностью электроснабжения. Они не
подвержены влиянию ветра и гололеда,
не загромождают, подобно ВЛ, улицы ropoда
и территории предприятий
При передаче
электроэнергии от электростанции к
потребителю, т.е. при прохождении по
проводам электрического тока, в ЛЭП
возникает потеря напряжения, под которой
понимают разность напряжений в начале
U1 и в конце U2
линии:
(1)
Потеря напряжения может быть определена
и таким образом
(2)
где I
– величина тока в линии передачи;
R – сопротивление
проводов линии.
Необходимо отметить, что потеря напряжения
в ЛЭП ухудшает работу электроприемников.
Так, при уменьшении напряжения на 10%
от
номинального, световой поток ламп
снижается на 30%. Поскольку вращающий
момент на валy асинхронных двигателей
пропорционален квадрату напряжения на
его зажимах, то он значительно уменьшается
при снижении питающего напряжения. А
это отрицательно сказывается на работе
производственных механизмов.
ГОСТом нормируются допустимые отклонения
напряжения в проц.:
а) на зажимах приборов рабочего освещения,
в т.ч. и прожекторного, от ‑2,5 до +5 % от
номинального;
б) не электродвигателях от -5 до +10% от
номинального;
в) на зажимах остальных приемников
электрической энергии в пределах 5%
от номинального.
В связи с этим потерю напряжения, при
расчетах выражают часто
не в вольтах,
а в процентах
(3)
Прохождение электрического тока по
проводам линий электропередач приводит
к необратимому преобразованию
электрической энергии в тепловую, т.е.
к их бесполезному нагреву. Этот нагрев
происходит за счет потерь мощности Р
в проводах
(4)
которые можно определить и так:

Мощность Р1 (затраченная)
подается на вход линии передачи
от
генератора и может быть определена из
соотношения
(6)
Мощность Р2 (полезная) снимается
с выхода линии и передается
потребителям.
Её величину рассчитывают, используя
выражение
(7)
Отношение этих мощностей называют
коэффициентом полезного
действия :

(8)
который характеризует экономичность
работы линии электропередачи. Современные
ЛЭП обеспечивают передачу электрической
энергии с =95÷98 %.
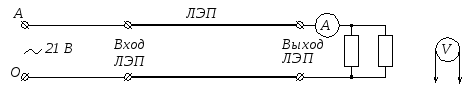
Схема
лабораторной установки
Таблица
измерений и расчетов
|
№ |
Измерено |
Вычислено |
||||||||
|
U1 |
U2 |
I |
|
Rл |
P1 |
P2 |
|
|
RН |
|
|
В |
В |
А |
В |
Ом |
Вт |
Вт |
Вт |
% |
Ом |
|
|
1 |
50,00 |
113,64 |
22,00 |
0,00 |
22,00 |
0,00 |
0,00 |
50,00 |
113,64 |
22,00 |
|
2 |
25,00 |
75,76 |
16,50 |
8,25 |
8,25 |
50,00 |
75,76 |
25,00 |
75,76 |
16,50 |
|
3 |
20,00 |
74,07 |
13,50 |
8,10 |
5,40 |
60,00 |
111,11 |
20,00 |
74,07 |
13,50 |
|
4 |
17,00 |
77,27 |
11,00 |
7,26 |
3,74 |
66,00 |
150,00 |
17,00 |
77,27 |
11,00 |
|
5 |
22,00 |
115,79 |
9,50 |
5,32 |
4,18 |
56,00 |
147,37 |
22,00 |
115,79 |
9,50 |
|
6 |
18,00 |
112,50 |
8,00 |
5,12 |
2,88 |
64,00 |
200,00 |
18,00 |
112,50 |
8,00 |
|
7 |
0,00 |
– |
0,00 |
0,00 |
0,00 |
– |
– |
0,00 |
– |
0,00 |
Величина
эквивалентных сопротивлений потребителей:
По данным измерений и расчётов строим
графики: U2 = f(I);
= f(I);

f(I);

f(I).
Выводы:
В этой
лабораторной работе были практически
изучены основные, электротехнические
параметры, характеризующие работу ЛЭП,
в режиме нагрузки и холостого хода,
влияние тока на потерю напряжения,
мощности, а так же КПД линии.
Потеря
напряжения возникает при прохождении
тока по ЛЭП (разность напряжений на
входе и выходе) и определяется по
формулам:
КПД
линии – это отношение затраченной
мощности, характеризующей экономичность
работы ЛЭП. Наиболее удачными были опыты
1, 5 и 6, т.к. в них
= 113,64%, 115,79%
и 112,50% соответственно; они были наиболее
экономичны, т.к. передавалось наибольшее
количество электроэнергии. КПД
определяется:
Сопротивление
ЛЭП можно найти как отношение потери
напряжения в ЛЭП на силу тока в ЛЭП:
В
результате проведенных опытов построены
графические зависимости, отражающие
ход лабораторной работы.
При
увеличении тока 1:
а)
увеличивается потеря напряжений Д11 и
потеря мощности ДР;
б)
уменьшается напряжение в конце ЛЭП 112
и КПД.
Контрольные
вопросы и задания.
-
Основные режимы
работы линии электропередачи.
Режим холостого
хода (I=0,

U2=U1);
режим короткого замыкания (Rн=0,
I=

U2=0),
когда всё входное напряжение гасится
на сопротивлении линии Rл.
-
Каким напряжением
выгодно передавать заданную мощность
(высоким или низким) и почему? -
Что такое потеря
напряжения в линии? Как её можно
определить?
Потеря напряжения
– разность напряжений в начале U1
и в конце U2
линии.

или

где I
– величина тока в линии передачи; R
– сопротивление проводов линии.
-
0т чего зависит
потеря мощности в ЛЭП?
Потеря активной
мощности в линии зависит и от передаваемой
реактивной мощности.
-
Что такое коэффициент
полезного действия линии и как он
определяется?
Отношение
затраченной и полезной мощностей
называют коэффициентом полезного
действия
.
-
Как найти
сопротивление линии электропередачи?
Сопротивление
ЛЭП можно найти как отношение потери
напряжения в ЛЭП на силу тока в ЛЭП:
-
Какие отклонения
напряжения на зажимах электроприемников
допускаются ГОСТом?
ГОСТом
нормируются допустимые отклонения
напряжения в проц.:
а)
на зажимах приборов рабочего освещения,
в т.ч. и прожекторного, от ‑2,5 до +5 % от
номинального;
б)
не электродвигателях от -5 до +10% от
номинального;
в)
на зажимах остальных приемников
электрической энергии в пределах 5%
от номинального.
-
Расскажите о цели,
порядке выполнения лабораторной работы.
Цель работы:
Познакомиться с основными электротехническими
параметрами, характеризующими работу
линии электропередачи (ЛЭП).
Ход работы:
-
Исследовать работу
линии в режиме холостого хода и нагрузки. -
Исследовать
влияние тока нагрузки на потерю
напряжения и мощности, а так же КПД
линии.
-
Как определить
сопротивление потребителей?
Величина эквивалентных
сопротивлений потребителей:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Активное сопротивление проводов и кабелей из цветных металлов определяется по одной из следующих формул:
где r — расчетное удельное сопротивление провода или жилы кабеля, ом⋅мм2/м;
g — расчетная удельная проводимость провода или жилы кабеля, м/ом⋅мм2;
F — номинальное сечение провода или кабеля, мм2.
Значения удельного сопротивления и удельной проводимости для медных проводов и кабелей:
для алюминиевых проводов и кабелей
| Таблица 5-1 Активные сопротивления проводов и кабелей, ом/км | |||
|---|---|---|---|
| Сечение провода, мм кв. | Медные провода и кабели | Алюминиевые провода и кабели | Сталеалюминиевые провода |
| 1 | 18,9 | – | – |
| 1.5 | 12,6 | – | – |
| 2,5 | 7,55 | 12,6 | – |
| 4 | 4,65 | 7,90 | – |
| 6 | 3,06 | 5,26 | – |
| 10 | 1,84 | 3,16 | 3,12 |
| 16 | 1,20 | 1,98 | 2,06 |
| 25 | 0,74 | 1,28 | 1,38 |
| 35 | 0,54 | 0,92 | 0,85 |
| 50 | 0,39 | 0,64 | 0,65 |
| 70 | 0,28 | 0,46 | 0,46 |
| 95 | 0,20 | 0,34 | 0,33 |
| 120 | 0,158 | 0,27 | 0,27 |
| 150 | 0,123 | 0,21 | 0,21 |
| 185 | 0,103 | 0,17 | 0,17 |
| 240 | 0,078 | 0,132 | 0,132 |
| 300 | 0,062 | 0,106 | 0,107 |
| 400 | 0,047 | 0,08 | 0,08 |
Индуктивное сопротивление трехфазной линии с проводами из цветных металлов при частоте переменного тока 50 Гц определяется по формуле
где d — внешний диаметр провода, мм;
D — среднее геометрическое расстояние между проводами линии, вычисляемое по формуле
где D — расстояния между проводами у каждой пары проводов трехфазной линии, мм.
Активные сопротивления 1 км провода или жилы кабеля приведены в табл. 5-1, индуктивные сопротивления 1 км линии — в табл. 5-2 и 5-4.
Для стальных проводов активное и внутреннее индуктивное сопротивления зависят от протекающего по проводу переменного тока. Общее индуктивное сопротивление воздушной линии, выполненной стальными проводами, определяется как сумма внешнего х’ и внутреннего х» индуктивных сопротивлений:
х=х’+х», ом/км (5-5)
| Таблица 5-2 Индуктивные сопротивления воздушных лм/км | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Среднее геометрическое расстояние между проводами, мм | Сечение проводов, мм2 | ||||||||||
| 6 | 10 | 16 | 25 | 35 | 50 | 70 | 95 | 120 | 150 | 185 | |
| Медные провода | |||||||||||
| 400 | 0,371 | 0,355 | 0,333 | 0,319 | 0,308 | 0,297 | 0,283 | 0,274 | – | – | – |
| 600 | 0,397 | 0,381 | 0,358 | 0,345 | 0,336 | 0,325 | 0,309 | 0,300 | 0,292 | 0,287 | 0,280 |
| 800 | 0,413 | 0,399 | 0,377 | 0,363 | 0,352 | 0,341 | 0,327 | 0,318 | 0,310 | 0,305 | 0,298 |
| 1000 | 0,429 | 0,413 | 0,391 | 0,377 | 0,366 | 0,355 | 0,341 | 0,332 | 0,324 | 0,319 | 0,313 |
| 1250 | 0,443 | 0,427 | 0,405 | 0,391 | 0,380 | 0,369 | 0,355 | 0,346 | 0,338 | 0,333 | 0,327 |
| 1500 | – | 0,438 | 0,416 | 0,402 | 0,391 | 0,380 | 0,366 | 0,357 | 0,349 | 0,344 | 0,338 |
| 2000 | – | 0,457 | 0,435 | 0,421 | 0,410 | 0,398 | 0,385 | 0,376 | 0,368 | 0,363 | 0,357 |
| 2500 | – | – | 0,449 | 0,435 | 0,424 | 0,413 | 0,399 | 0,390 | 0,382 | 0,377 | 0,371 |
| 3000 | – | – | 0,460 | 0,445 | 0,435 | 0,423 | 0,410 | 0,401 | 0,393 | 0,388 | 0,382 |
| Алюминиевые провода | |||||||||||
| 600 | – | – | 0,358 | 0,345 | 0,336 | 0,325 | 0,315 | 0,303 | 0,297 | 0,288 | 0,279 |
| 800 | – | – | 0,377 | 0,363 | 0,352 | 0,341 | 0,331 | 0,319 | 0,313 | 0,305 | 0,298 |
| 1000 | – | – | 0,391 | 0,377 | 0,366 | 0,355 | 0,345 | 0,334 | 0,327 | 0,319 | 0,311 |
| 1250 | – | – | 0,405 | 0,391 | 0,380 | 0,369 | 0,359 | 0,347 | 0,341 | 0,333 | 0,328 |
| 1500 | – | – | – | 0,402 | 0,391 | 0,380 | 0,370 | 0,358 | 0,352 | 0,344 | 0,339 |
| 2000 | – | – | – | 0,421 | 0.410 | 0,398 | 0,388 | 0,377 | 0,371 | 0,363 | 0,355 |
| Сталеалюминиевые провода | |||||||||||
| 2000 | – | – | – | – | 0,403 | 0,392 | 0,382 | 0,371 | 0,365 | 0,358 | – |
| 2500 | – | – | – | – | 0,417 | 0,405 | 0,396 | 0,385 | 0,379 | 0,272 | – |
| 3000 | – | – | – | – | 0,429 | 0,413 | 0,403 | 0,397 | 0,391 | 0,384 | 0,377 |
| Таблица 5-4 Индуктивные сопротивления трехжильных кабелей и изолированных проводов, проложенных на роликах и изоляторах, ом/км | ||||||
|---|---|---|---|---|---|---|
| Сечение, мм кв. | Трехжильные кабели с медными жилами | Изолированные провода | ||||
| до 1 кв | 3 кв | 6 кв | 10 кв | на роликах | на изоляторах | |
| 1,5 | – | – | – | 0,28 | 0,32 | |
| 2,5 | – | – | – | – | 0,26 | 0,30 |
| 4 | 0,095 | 0,111 | – | – | 0,25 | 0,29 |
| 6 | 0,090 | 0,104 | – | – | 0,23 | 0,28 |
| 10 | 0,073 | 0,0825 | 0,11 | 0,122 | 0,22 | 0,26 |
| 16 | 0,0675 | 0,0757 | 0,102 | 0,113 | 0,22 | 0,24 |
| 25 | 0,0662 | 0,0714 | 0,091 | 0,099 | 0,20 | 0,24 |
| 35 | 0,0637 | 0,0688 | 0,087 | 0,095 | 0,19 | 0,24 |
| 50 | 0,0625 | 0,0670 | 0,083 | 0,09 | 0,19 | 0,23 |
| 70 | 0,0612 | 0,0650 | 0,08 | 0,086 | 0,19 | 0,23 |
| 95 | 0,0602 | 0,0636 | 0,078 | 0,083 | 0,18 | 0,23 |
| 120 | 0,0602 | 0,0626 | 0,076 | 0,081 | 0,18 | 0,22 |
| 150 | 0,0596 | 0,0610 | 0,074 | 0,079 | – | – |
| 185 | 0,0596 | 0,0605 | 0,073 | 0,077 | – | – |
| 240 | 0,0587 | 0,0595 | 0,071 | 0,075 | – | – |
| Таблица 5-6 Активные (омические) и индуктивные сопротивления шин прямоугольного сечения из алюминия и меди | |||||
|---|---|---|---|---|---|
| Размеры шин, мм | Активное (омическое) сопротивление при температуре шины +30° С, ом/км | Индуктивное сопротивление при расстоянии между центрами шин 250 мм, ом/км | |||
| Алюминиевые шины | Медные шины | ||||
| при постоянном токе | при переменном токе | при постоянном токе | при переменном токе | ||
| 25X3 | 0,410 | 0,413 | 0,248 | 0,263 | 0,253 |
| 30X4 | 0,256 | 0,269 | 0,156 | 0,175 | 0,240 |
| 40X4 | 0,192 | 0,211 | 0,117 | 0,138 | 0,224 |
| 40X5 | 0,154 | 0,173 | 0,0935 | 0,112 | 0,222 |
| 50X5 | 0,123 | 0,140 | 0,0749 | 0,0913 | 0,210 |
| 50X6 | 0,102 | 0,119 | 0,0624 | 0,0780 | 0,208 |
| 60X6 | 0,0855 | 0,102 | 0,0520 | 0,0671 | 0,198 |
| 80X6 | 0,0640 | 0,0772 | 0,0390 | 0,0507 | 0,182 |
| 100X6 | 0,0510 | 0,0635 | 0,0312 | 0,0411 | 0,169 |
| 60X8 | 0,0640 | 0,0772 | 0,0390 | 0,0507 | 0,196 |
| 80X8 | 0,0481 | 0,0595 | 0,0293 | 0,0395 | 0,179 |
| 100X8 | 0,0385 | 0,0488 | 0,0234 | 0,0321 | 0,168 |
| 120X8 | 0,0320 | 0,0410 | 0,0195 | 0,0271 | 0,156 |
| 80X10 | 0,0385 | 0,0495 | 0,0234 | 0,0323 | 0,179 |
| 100X10 | 0,0308 | 0,0398 | 0,0187 | 0,0260 | 0,165 |
| 120X10 | 0,0255 | 0,0331 | 0,0156 | 0,0218 | 0,156 |
Индуктивное сопротивление воздушных линий напряжением до 10 кВ с медными и алюминиевыми проводами колеблется в пределах: х0=0,35-0,4 Ом/км.
Активное сопротивление голых алюминиевых проводов в зависимости от сечения определяется:
25 мм2 — 1,28 Ом/км.
35 мм2 — 0,9.2 Ом/км.
50 мм2 — 0,64 Ом/км.
70 мм2 — 0,46 Ом/км.
а активное сопротивление медных проводов составляет при сечении:
10 мм2 — 1,84 Ом/км.
16 мм2 — 1,2 Ом/км.
25 мм2 — 0,74 Ом/км.
Для воздушных линий с проводами сечения до 16 мм2 можно не учитывать влияния их индуктивного сопротивления, так как в данном случае определяющей является величина активного сопротивления.
Для кабельных линий напряжения до 10 кВ величина х0 составляет 0,07—0,08 Ом/км. По сравнению с активным сопротивлением это весьма малая величина, поэтому при расчетах ею пренебрегают.
Величина r0 с некоторым приближением может быть определена как
r0=017,5/S Ом/км для медных проводов и r0=28/S Ом/км, для алюминиевых проводов.
Из предыдущего изложения следует, что при расчете проводов на допустимую потерю напряжения нужно пользоваться следующими формулами:
в линиях постоянного и однофазного переменного тока:
ΔU%=200Il/γSUN
или
ΔU%=200Il/γSU2N%,
где I — расчетный ток нагрузки, А;
Р — расчетная мощность, Вт;
l — длина линии, м;
UN — номинальное напряжение сети, В;
S — сечение провода, мм2;
γ — удельная проводимость материала линии, м/[Ом*мм2].
Если от сети питается несколько приемников, то формула (смотрите формулу выше) приобретает вид:
ΔU%=200ΣPl/γSU2N%,
где ΣPl — сумма моментов нагрузки в Вт*м (Р — расчетная мощность, Вт, а l — длина линии, м, до соответствующей нагрузки);
в линиях трехфазной системы токов (в тех случаях, когда индуктивным сопротивлением ЛЭП можно пренебречь):
где Р — расчетная мощность, Вт;
UN — номинальное значение линейного напряжения, В;
l — длина линии, км;
r0 — активное сопротивление 1 км провода, Ом/км.
в линиях трехфазной системы токов при учете влияния индуктивного сопротивления проводов:
или
где S — расчетная нагрузка равная Рр/cosφ, ВА;
UN — напряжение, В;
cosφ — коэффициент мощности нагрузки соответствующий ему sin φ.
Сравнивая сечения, полученные из расчетов на нагрев,механическую прочность и допустимую потерю напряжения, выбирают большее.
Формулу (ΔU%=√3100Il/UN (r0 соsφ + x0 sin φ)) можно записать в ином виде, если Р и Q заданы в кВт и квар:
По полученным формулам можно определить потери напряжения в линии, если известны сечения проводов. Поэтому при расчете новых линий необходимо выбирать сечения проводов по условиям допустимого нагрева (а там, где это имеет смысл, например, если линия напряжения выше 1 кВ, при постоянном электроснабжении — по экономической плотности тока), а затем проверить выбранные сечения по допустимой потере напряжения. Если потери напряжения ори выбранных сечениях превосходят допустимые, то следует увеличить сечения проводов и повторить расчет.
«Электроснабжение строительно-монтажных работ», Г.Н. Глушков