Индуктивное сопротивление катушки
Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.
Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.
Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.
При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.

Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.
Индуктивное сопротивление обозначается буквой XL и измеряется в омах.
Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле
XL=2π• f •L
где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн
Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:
XL=ω•L
Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.
Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Калькулятор индуктивного сопротивления катушки
При подключении катушки индуктивности в цепь переменного тока, под действием изменяющегося напряжения на обмотке,
происходят изменения этого тока с определенной частотой. Эти изменения вызывают генерацию магнитного поля, которое
периодический возрастает или убывает. В результате в катушке индуцируется встречное напряжение (ЭДС самоиндукции),
препятствующее изменениям тока. Величина ЭДС самоиндукции прямо пропорциональна скорости изменения тока.
Противодействие протеканию тока получило название индуктивного сопротивления XL.

XL — сопротивление, Ом;
f — частота, Гц;
I — индуктивность, Гн.
Электрическое сопротивление катушки индуктивности — это отношение действующих значений
напряжения и тока. Оно прямо пропорционально индуктивности и частоте изменения тока.
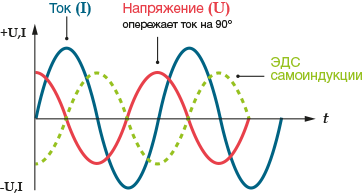
Фазы кривых тока и напряжения на катушке индуктивности смещены на 90 градусов,
при этом ток отстает от напряжения.
Расчет индуктивного сопротивления
Для расчета введите значение индуктивности расчетной катушки и частоту переменного тока
В калькуляторе активное сопротивление обмотки катушки принято как пренебрежимо малая величина по сравнению
с ее индуктивным сопротивлением.
Калькулятор вычисления действующих значений тока или напряжения на катушке индуктивности.
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Для школьников.
В предыдущих статьях рассмотрены цепи переменного тока, содержащие только активное сопротивление и содержащие только емкостное сопротивление.
Сейчас рассмотрим случай, когда в цепи переменного тока находится только катушка индуктивности (индуктивное сопротивление), а активным и емкостным сопротивлениями цепи можно пренебречь.
Начнём с опыта, позволяющего понять, когда появляется и от чего зависит индуктивное сопротивление в цепи переменного тока.
Две маленькие одинаковые электрические лампочки подключались к источникам одинакового напряжения. Но одна (правая) подключалась к источнику постоянного тока (аккумуляторной батарее), а другая (левая) – к источнику переменного тока.
Лампочки светили одинаково, так как количество выделяющегося тепла не зависит от того, какой ток протекает по нитям лампочек (постоянный или переменный).
Затем к лампочкам последовательно подключили катушки индуктивности, сделанные из толстой медной проволоки, содержащей большое число витков. Внутри катушек находятся железные сердечники.
Катушками индуктивности называются катушки, имеющие большую индуктивность и малое активное сопротивление (изготовлены из толстой проволоки). Часто активным сопротивлением такой катушки можно пренебречь.
Опыт показал, что в случае постоянного тока лампочка горит ярко, а в случае переменного тока она светит тускло. Как это объяснить?
В случае постоянного тока лампочка горит ярко, потому что сопротивление катушки мало.
Но почему катушка индуктивности очень сильно ослабляет переменный ток? Продолжаем рассматривать опыт.
Если из катушки (рис. б) постепенно вытягивать железный сердечник, то нить лампочки будет накаляться всё сильнее. При полном вытягивании сердечника лампочка будет светить довольно ярко. Убрав железный сердечник, во много раз уменьшили индуктивность катушки, значит дело в индуктивности.
Так как сила переменного тока быстро меняется, то в катушке возникает ЭДС самоиндукции.
В цепи только с индуктивным сопротивлением приложенное к цепи напряжение в каждый момент времени равно и противоположно ЭДС самоиндукции.
ЭДС самоиндукции по правилу Ленца направлена так, что стремится препятствовать изменению тока, то есть оказывает току сопротивление. Чем больше индуктивность катушки, тем большая ЭДС самоиндукции в ней возникает, тем больше индуктивное сопротивление. Индуктивное сопротивление зависит ещё от частоты тока, чем больше частота, тем больше это сопротивление.
При нарастании тока ЭДС самоиндукции препятствует этому нарастанию, поэтому ток позже достигает максимума, чем в отсутствие самоиндукции.
При убывании тока ЭДС самоиндукции стремится поддерживать ток. Поэтому нулевые значения тока достигаются в более поздний момент, чем в отсутствие самоиндукции.
Таким образом, при наличие индуктивности ток отстаёт по фазе от тока в отсутствие индуктивности, а следовательно, отстаёт по фазе от своего напряжения.
Можно сказать так: из-за явления самоиндукции ток в катушке индуктивности не может меняться скачком и отстаёт от напряжения.
Чем больше частота тока, тем больше будет ЭДС самоиндукции, стремящейся противодействовать изменению тока и тем больше будет сопротивление переменному току.
Индуктивное сопротивление находится по формуле, которая получена теоретически и подтверждена опытом:
Напряжение на индуктивном сопротивлении (индуктивное напряжение) :
Ток в цепи, содержащей только индуктивность, равен отношению напряжения на зажимах источника к индуктивному сопротивлению цепи:
В цепи, содержащей только индуктивное сопротивление, напряжение опережает ток на четверть Т/4 периода (или ток отстаёт от напряжения на четверть периода):
Из рисунка видно, когда ток ещё только проходит через нулевое положение, напряжение уже проходит через максимум, то есть мгновенные значения напряжения и тока меняются согласно уравнениям:
Разность фаз между током и напряжением, равная “пи” пополам, величина отрицательная.
На следующем рисунке показано, как меняются во времени мгновенные значения тока, напряжения и мощности в цепи переменного тока, содержащей только индуктивное сопротивление:
Мгновенные значения мощности находятся через произведение мгновенных значений напряжения и тока, уравнения для которых записаны выше.
Видим, что мгновенная мощность в цепи, обладающей только индуктивностью, изменяется по синусоидальному закону с двойной частотой и имеет равные по модулю положительные и отрицательные значения.
В первую и третью части периода, когда ток в цепи растёт, мощность имеет положительное значение. В эти части периода магнитное поле вокруг электрической цепи усиливается за счёт энергии источника.
Убыванию тока соответствует отрицательное значение мощности. В эти части периода (второй и четвёртый) магнитное поле ослабевает, его энергия идёт обратно к источнику тока.
Таким образом, в цепи, содержащей только катушку индуктивности, происходит периодическая перекачка энергии от источника в энергию магнитного поля катушки индуктивности и возвращение её источнику.
Положительные и отрицательные значения мощности по модулю равны, поэтому средняя мощность за период в такой цепи равна нулю.
Эта мощность не расходуется во внешней части цепи, поэтому называется реактивной индуктивной мощностью:
Она образуется при работе электроприборов (трансформаторов, двигателей, электромагнитов и др., обладающих большой индуктивностью.)
Реактивная мощность в промышленных электрических цепях увеличивает нагрузку на провода и снижает коэффициент мощности цепи, поэтому реактивную нагрузку в электрической цепи на предприятиях снижают (об этом будет сказано в последующих статьях.)
Пример.
Катушка с индуктивностью 0,01 Гн включена в цепь переменного тока напряжением 120 В и частотой 50 Гц. Определить силу тока в катушке, индуктивное напряжение в ней и её реактивную мощность, если активным сопротивлением катушки можно пренебречь.
Используем формулы:
Ответ: 38,2 А; 120 В; 1460 Вт.
Из полученного ответа видим, что всё приложенное к катушке напряжение является индуктивным.
Итак, присутствие индуктивности в цепи переменного тока приводит к сдвигу фаз между током и напряжением в сети (колебания тока отстают от колебаний напряжения).
Емкостная мощность не совершает механической работы, не нагревает проводники.
Катушка индуктивности лишь периодически накапливает энергию магнитного поля и возвращает её обратно источнику тока.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Предыдущая запись : Конденсатор в цепи переменного тока. Емкостное сопротивление.
Следующая запись: Занятие 71. Последовательное соединение сопротивлений. Резонанс напряжений.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58 .
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .
Что такое активное сопротивление катушки
Содержание
- 1 Катушка
- 2 Конструкция и разновидности
- 3 Принцип работы
- 4 Индуктивность
- 5 Активное сопротивление
- 6 Постоянный ток
- 7 Переменный ток
- 8 Замер сопротивления и формула расчета
- 9 Заключение
- 10 Видео по теме
Одной из наиболее важных радиотехнических деталей является катушка индуктивности. Статья раскроет тему, что такое активное сопротивление катушки. Также будет дана информация о назначении и принципе действия этого элемента, приведена формула расчета сопротивления.
Катушка
Катушка индуктивности представляет собой металлический или ферритный сердечник, на который намотано несколько витков медного провода. Элемент обладает следующими свойствами:
- За счет индуктивности ограничивается скорость изменения токов.
- С увеличением частоты тока катушка способна увеличить свое сопротивление (скин-эффект).
- Создает магнитное поле.
- Увеличивает и накапливает напряжение.
- Создает сдвиг фаз переменного тока.
- Пропорционально скорости движения тока создает ЭДС самоиндукции.

Все эти свойства находят применение при разработке радиоприемных устройств, генераторов частоты, тестеров, магнитометров и других видов сложного оборудования.
Конструкция и разновидности
Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
- Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
- Тороидальная. В такой катушке соленоид выполнен в форме «тора».
- Многослойный тип, имеет несколько рядов обмотки.
- Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
- Универсальная, может совмещать сразу несколько вариантов обмотки.

Независимо от конструкции, все катушки работают по одному и тому же принципу.
Принцип работы
Катушка индуктивности работает только при прохождении электрического тока через набор витков обмотки. При подключении элемента к электрической цепи, по витку начинает двигаться ток. За счет взаимодействия провода с металлическим сердечником создается магнитный поток. Поток полностью пропорционален индуктивности катушки и величине тока. Величину магнитного потока можно рассчитать по следующей формуле: Ф=L×I.
Элементами формулы являются:
- «Ф» — величина магнитного потока.
- «L» — индукция.
- «I» — величина тока.

Количество витков влияет на величину ЭДС самоиндукции. Витки взаимодействуют не только с сердечником, но и между собой, что приводит к увеличению ЭДС.
В цепи переменного напряжения, величина ЭДС способна спровоцировать разность фаз напряжения и тока вплоть до 90 градусов.
Индуктивность
Индуктивностью катушки является способность к накапливанию электричества. Этот параметр зависит от:
- Числа витков.
- Сечения и длины провода.
- Конструктивных особенностей детали.
- От материала, длины, диаметра и формы сердечника.
- От расстояния между витками.
- Наличия экрана.
В радиоэлектронике не принято указывать значение индуктивности. Производители маркируют детали числом витков и указывают тип сердечника.
Активное сопротивление
Катушка индуктивности, не подключенная к электрической цепи, имеет только активное сопротивление.

Оно создается медным проводом и зависит от его длины, сечения. Активное сопротивление способно нарастать только после подключения в цепь. В этом случае процессы, протекающие внутри элемента, зависят от типа тока.
Постоянный ток
В подключенной к постоянному току катушке индуктивности создается магнитное поле. Его величина зависит от числа витков на сердечнике. При этом, ЭДС самоиндукции возникает при движении магнитного потока, который в зависимости от своей силы и скорости, выталкивает часть напряжения на поверхность обмотки.

За счет образования ЭДС, возникает эффект занижения нарастания тока в этой цепи. Ток, имея определенную силу, не способен нарасти мгновенно, так как на него действует сопротивление катушки. Постепенно преодолевая ограничение, ток плавно нарастает и достигает нормальных значений. Скорость такого переходного процесса рассчитывается с использованием следующих значений:
- «L» — индуктивность, генри;
- «R» — сопротивление электрической цепи, ом. Берется значение всей схемы с катушкой;
- «t» — время переходного процесса, сек.
Формула расчета выглядит следующим образом: t=L/R. В этой формуле также используется число витков элемента. Например, t=5×0.7/70=0.05 секунд, где 5 — число витков.
Для катушек индуктивности с первичной и вторичной обмоткой, ЭДС индуктивности протекает немного иным способом. Это различие создается за счет разницы сечений витков. В такой детали ЭДС не препятствует увеличению напряжения, а направляется вместе с прерванным током в одном направлении.
В трансформаторах первичная обмотка создает эффект сильного увеличения напряжения на контактах выхода. Этого удается достичь за счет изменения силы тока на первичной обмотке. Учитывая мгновенно изменение силы тока (одномоментное размыкание), во вторичной обмотке наводится импульс э.д.с амплитудой в десятки киловольт. Примером такого явления является катушка зажигания автомобиля. Ее магнитное поле позволяет достичь напряжения в тысячи вольт, несмотря на то, что сама она работает от аккумулятора с напряжением 12 вольт.
Переменный ток
Переменный ток сильно отличается от постоянного. Поэтому и его влияние на катушку индуктивности так же будет сильно отличаться. Помимо активного сопротивления, катушка подключенная к источнику переменному току, обладает еще и индуктивным.

Активное сопротивление не подключенной в цепь катушки зависит только от марки провода, его длины и сечения. При замере сопротивления отключенной от цепи катушки, тестер покажет только способность самого провода сопротивляться прохождению тока. По своей сути, активное сопротивление этого элемента будет равно 0 + подключенный резистор. При таком соотношении, катушка с ее 0 сопротивлением является идеальной. Для более точного измерения сопротивления в состоянии покоя, важно чтобы деталь была полностью отключена от цепи. При замере на схеме, сопротивление будет увеличено за счет параметров других радиодеталей.

Индуктивное сопротивление возникает только после подключения катушки в цепь переменного тока. Оно зависит от частоты тока и числа витков. Индуктивное сопротивление можно определить, используя простую формулу: XL=2×π×f×L. В данном выражении:
- «XL» — индуктивное сопротивление.
- «π» — число «пи», равное 3.14.
- «f» — частотная характеристика тока.
- «L» — индуктивность.
При прохождении переменного тока по виткам катушки, создается эффект вытеснения магнитными потоками доли токов. Это свойство схоже с влиянием постоянного тока. Главное отличие заложено в боковом вытеснении. Магнитное поле каждого витка оказывает давление на поле последующего витка. Таким образом происходит увеличение активного сопротивления.
Данный эффект увеличивается в зависимости от сечения провода, его проводимости и температуры. Эффект близости, сильно влияющий на увеличение активного сопротивления, снижают за счет подбора сечения обмоточного провода. Снижение эффекта близости недопустимо за счет увеличения расстояния между витками. Такой подход влияет на реактивное сопротивление и мощность магнитного поля.

В итоге активное сопротивление при подключении катушки к источнику переменного тока обладает следующими свойствами:
- Взаимодействует с параметрами индуктивного сопротивления.
- Способно занижать скорость магнитного потока.
- Создает сдвиг фаз напряжения и тока.
- При работе в условиях больших токов, активное сопротивление катушки увеличивает температуру самого компонента и всей цепи в целом. Нагрев часто происходит по причине непрочных контактов, неправильно подобранного сечения проводов на выходе и сильной нагрузки в общей сети.
В электротехнике существует ряд разновидностей экранированных катушек индуктивности. Такие экран часто делают из стали или алюминия. Они необходимы для снижения воздействия магнитного поля на ближайшие элементы схемы. У экранов есть и обратная функция. С помощью них катушка защищает себя от воздействия смежных компонентов схемы. Таким образом производители могут уменьшить определенную часть помех. Воздействие магнитного поля неэкранированной катушки можно услышать, например, если поднести элемент к включенному радиоприемнику. У экрана есть и один существенный недостаток. Он сильно увеличивает активное сопротивление самой детали.
Замер сопротивления и формула расчета
Замерить активное сопротивление катушки индуктивности можно только в обесточенном виде. Делается это при помощи мультиметра.
- Мультиметр надо перевести в режим омметра.
- Красный измерительный щуп соединить с первым выходом катушки.
- Черный измерительный щуп соединить со вторым выходом.
- Прибор покажет только активное сопротивление обмотки.

При помощи тестера можно определить только целостность витков. Если элемент включен в цепь под напряжением, то величину сопротивления находят за счет простого вычисления по формуле: Z=U/I.
Для расчета по этой формуле, при помощи тестера определяют сначала величину тока (I) и напряжения (U). Активное сопротивление измеряется в Омах.
Зная формулу расчета активного и индуктивного сопротивления, полное сопротивление элемента может быть найдено с помощью формулы:
Z= 2×(R×R+XL×XL)
В этом выражении R является активным сопротивлением, а XL — индуктивным.
Заключение
Расчет активного сопротивления катушки несет в себе большую практическую пользу. Радиолюбители и инженеры могут определить наименьший коэффициент сопротивляемости элемента, что помогает настроить частотные характеристики электронной аппаратуры.
Видео по теме
Включить звук
Так как самоиндукция
препятствует всякому резкому изменению
силы тока в цепи, то, следовательно, она
представляет собой для переменного
тока особого рода сопротивление,
называемое индуктивным
сопротивлением.
Чисто индуктивное
сопротивление отличается
от обычного
(омического)
сопротивления
тем, что
при прохождении через него переменного
тока в нем не происходит потери мощности.
Под чисто
индуктивным
сопротивлением мы
понимаем сопротивление, оказываемое
переменному току катушкой, проводник
которой не обладает вовсе омическим
сопротивлением. В действительности же
всякая катушка обладает некоторым
омическим сопротивлением. Но если это
сопротивление невелико по сравнению с
индуктивным сопротивлением, то им можно
пренебречь.
При этом наблюдается
следующее явление: в течение одной
четверти периода, когда ток возрастает,
магнитное поле потребляет энергию из
цепи, а в течение следующей четверти
периода, когда ток убывает, возвращает
ее в цепь. Следовательно, в среднем за
период в индуктивном сопротивлении
мощность не затрачивается. Поэтому
индуктивное сопротивление называется
реактивным (прежде его неправильно
называли безваттным).
Индуктивное сопротивление
одной и той же катушки будет различным
для токов различных частот. Чем выше
частота переменного тока, тем большую
роль играет индуктивность и тем больше
будет индуктивное сопротивление данной
катушки. Наоборот, чем ниже частота
тока, тем индуктивное сопротивление
катушки меньше. При частоте, равной нулю
(установившийся постоянный ток),
индуктивное сопротивление тоже равно
нулю.
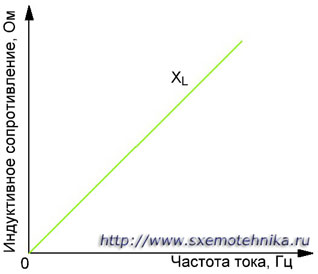
Рисунок 2 – Зависимость
индуктивного сопротивления катушки от
частоты переменного тока.
Реактивное
сопротивление катушки возрастает с
увеличением частоты тока.
Индуктивное сопротивление
обозначается буквой XL и
измеряется в Омах.
Подсчет индуктивного
сопротивления катушки для переменного
тока данной частоты производится по
формуле
XL
=
2π f L,
где XL —
индуктивное сопротивление в Ом;
f—частота
переменного тока в Гц;
L
— индуктивность катушки в Гн
Как известно, величину 2πf
называют угловой частотой и обозначают
буквой ω (омега). Поэтому приведенная
выше формула может быть представлена
так
XL
=
ωL.
Отсюда следует, что для
постоянного тока (ω
= 0) индуктивное сопротивление равно
нулю. Поэтому, когда, нужно пропустить
по какой-либо цепи постоянный ток,
задержав в то же время переменный, то в
цепь включают последовательно катушку
индуктивности.
Для преграждения пути токам
низких звуковых частот ставят катушки
с железным сердечником, так называемые
дроссели низкой частоты, а для более
высоких радиочастот — без железного
сердечника, которые носят название
дросселей высокой частоты.
2.3 Электрические модели
реальных катушек индуктивности
Характеристики идеальной
катушки индуктивности будут соответствовать
индуктивному элементу схемы замещения.
Реальные катушки индуктивности намотаны
из провода, имеющего ненулевое удельное
сопротивление, таким образом, чем больше
витков содержит катушка, тем будет выше
её активное сопротивление, которое,
обычно, необходимо учитывать во всём
диапазоне частот Следует отметить, что
на постоянном токе индуктивная
составляющая катушки будет равна нулю,
и в качестве схемы замещения можно
использовать один резистивный элемент
(рисунок 3а). С ростом частоты возрастёт
индуктивное сопротивление катушки,
поэтому в схеме замещения появляется
индуктивность (рисунок 3б). Еще на более
высоких частотах начинает проявляться
влияние межвитковой ёмкости (витки
выполнены из изолированного провода,
таким образом два соседних можно
рассматривать как конденсатор)
(рисунок 3в).
На сверхвысоких частотах резко возрастает
роль индуктивности и ёмкости выводов
катушки индуктивности.

а ––
на постоянном токе; б ––
на низких частотах; в ––
на высоких частотах;
Rк ––
активное сопротивление катушки; Cп ––
паразитная межвитковая ёмкость
Рисунок 3 – Схема
замещения катушки индуктивности
2.4 Параметры элементов
схемы замещения на низких частотах
2.4.1 Индуктивность катушки
Согласно ГОСТ Р 52002-2003 и ГОСТ 20715-75
предусмотрены следующие термины и
определения индуктивности.
Собственная индуктивность
![]()
– это скалярная величина, равная отношению
потокосцепления самоиндукции
![]()
элемента электрической цепи к
электрическому току
![]()
в нем
![]()
.
Это понятие относится к одной катушке
индуктивности или одному ее элементу,
которые является одновременно источником
магнитного поля и ее приемником.
Взаимная
индуктивность
![]()
– скалярная величина, равная отношению
потокосцепления взаимной индукции
одного элемента
![]()
электрической цепи к току
![]()
в
другом элементе, обусловливающему это
потокосцепление
![]()
.
Это понятие относится как минимум к
двум катушкам индуктивности или к двум
элементам одной катушки, одни из которых
являются одновременно источником
магнитного поля, а другой – ее приемником
и наоборот.
Начальная индуктивность катушки –
значение индуктивности, определенное
при условии отсутствия влияния собственной
емкости, изменения начальной проницаемости
сердечника и собственной индуктивности.
Начальная индуктивность – это собственная
индуктивность идеальной катушки.
Индуктивность, максимально приближенная
к начальной индуктивности определяется
на низкой частоте, где практически
отсутствует влияние собственной
емкости.
Эффективная индуктивность катушки –
значение индуктивности, определенное
с учетом влияния собственной емкости,
собственной индуктивности и изменения
начальной проницаемости сердечника.
В настоящее время частично катушки
индуктивности также как резисторы и
конденсаторы можно отнести к изделиям
общего применения. Они производятся на
специализированных предприятиях и
предназначены для продажи. Однако много
катушек проектируют и производят те
предприятия, в изделиях которых
предполагается их эксплуатация. То есть
такие катушки являются изделиями
частного применения.
Для катушек обоих типов существует
понятие номинальной индуктивности.
Номинальная индуктивность – значение
индуктивности, являющееся исходной для
отсчета отклонений.
Номинальные индуктивности для катушек
общего применения регламентируется
обычно рядами Е6 и Е12 с допусками 1 %, 2
%, 5 %, 10 %, 20 % и 30 %.
Номинальные индуктивности и допуски
для катушек частного применения
определяются результатами электрического
расчета, представленным в
техническом задании на разработку
катушки и регламентируются
стандартами предприятий или техническими
условиями на конкретную аппаратуру.
На практике под индуктивностью катушки
обычно имеют ввиду собственную
индуктивность. В РЭА применяются катушки
с индуктивностью от долей микрогенри
(контурные высокочастотные) до десятков
генри (дроссели фильтров выпрямителей).
Контурные катушки по величине индуктивности
изготовляются с точностью от 0,2 до 0,5%,
а для других катушек индуктивности
допустима точность до 30 %.
Индуктивность катушки пропорциональна
линейным размерам обмотки катушки,
магнитной проницаемости сердечника,
квадрату числа витков намотки и
соотношению размеров экрана и обмотки.
В зависимости от вида и типа обмотки
существуют различные аналитические
или графические алгоритмы расчета ее
параметров.
Из теоретической электротехники
известно следующее выражение для
индуктивности
длинного соленоида круглого сечения
![]()
(предполагается
![]()
=
1)
![]()
,
где
![]()
–
магнитная постоянная;
![]()
– относительная магнитная проницаемость
материала;
![]()
– число витков
![]()
– длина магнитной силовой линии. Это
выражение дает достаточно точный (до
2%) результат лишь для соленоидов,
длина которых от 20 до 30 раз больше
диаметра, со сплошной намоткой проводом,
имеющим бесконечно тонкую изоляцию.
В реальных соленоидах (катушках)
длина обычно соизмерима с диаметром.
Благодаря этому магнитное поле у концов
катушки искривляется, крайние витки
сцепляются с меньшим числом магнитных
силовых линий и фактическая индуктивность
оказывается меньше расчетной.
Точный учет этого явления приводит к
громоздким, неудобным для практики
выражениям. Поэтому для простоты в
расчетные формулы вводят поправочные
коэффициенты, величина которых
зависит от отношения
![]()
.
Наиболее удобной является следующая
формула
![]()
,
где
— индуктивность, мкГн;
![]()
—диаметр
катушки, см. Значения поправочных
коэффициентов
![]()
для однослойных катушек определяются
из графиков
= f(
).
Соседние файлы в папке ЛР МиКЭС 2020
- #
- #
- #
- #
- #
- #
- #
- #
- #
