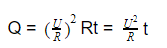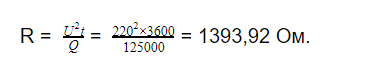Как найти сопротивление по формуле закона джоуля

Как найти сопротивление по формуле закона джоуля

Закон Джоуля-Ленца описывает тепловое действие электрического тока и находит широкое применение в электротехнике. В сегодняшней статье разберем несколько задач на закон Джоуля-Ленца.

Лень решать задачи? Зайдите на наш телеграм-канал: там найдется много интересного для всех учащихся. А если вы решили обратиться к нам за помощью, не упустите выгоду и обязательно прочекайте приятные скидки и акции на нашем втором канале.

Закон Джоуля-Ленца: задачи с решением

Для решения любой физической задачи существует алгоритм: сначала записываются все известные данные, затем определяются величины, которые нужно найти. Подробнее о решении физических задач читайте в нашей памятке для студентов. Также советуем держать под рукой формулы, это существенно облегчит процесс решения.

Кстати, если вы интересуетесь задачами на закон Джоуля-Ленца, вам также может быть полезно ознакомиться с задачами на мощность тока.

Задача на закон Джоуля-Ленца №1

Условие

Какое количество теплоты выделяет за 5 минут нагреватель электрочайника, если его сопротивление равно 30 Ом, а сила тока в цепи 1,5 А?

Решение

Это простейшая задача на закон Джоуля-Ленца для участка цепи. Запишем сам закон:

Q=I2Rt

Подставив значения из условия в формулу, найдем:

Q=1,52·30·300=20250 Дж

Ответ: 20,25 кДж.

Задача на закон Джоуля-Ленца №2

Условие

Какое количество теплоты выделит за 40 минут спираль электроплитки, если сила тока в цепи 3 А, а напряжение 220 В?

Решение

Эта также простейшая задача на закон Джоуля-Ленца, но, в отличие от первой задачи, при ее решении используется другая формулировка закона. Сначала запишем закон Джоуля-Ленца:

Q=I2Rt

Теперь перепишем его с учетом закона Ома:

I=URR=UIQ=I2UIt=IUt

Осталось подставить значения и вычислить:

Q=3·220·2400=1,584 МДж

Ответ: 1,584 МДж.

Задача на закон Джоуля-Ленца №3

Условие

Сколько минут ток шел по проводнику сопротивлением 25 Ом, если при силе тока 1 А проводник вылелил 6 кДж теплоты.

Решение

Запишем закон Джоуля-Ленца и выразим время:

Q=I2Rtt=QI2R

Найдем:

t=600012·25=240 c=4 мин

Ответ: 4 минуты.

При расчетах не забывайте переводить все величины из условия в систему СИ.

Задача на закон Джоуля-Ленца №4

Условие

Электрическая плитка при силе тока 4 А за 20 минут потребляет 1000 кДж энергии. Рассчитайте сопротивление плитки.

Решение

Выразим сопротивление из закона Джоуля-Ленца:

Q=I2RtR=QI2t

Подставим значения и вычислим:

R=1000·10316·1200=52 Ом

Ответ: 52 Ом.

Задача на закон Джоуля-Ленца №5

Условие

По проводнику с сопротивлением 6 Ом пропускали постоянный ток в течение 9 c. Какое количество теплоты выделилось в проводнике за это время, если через его сечение прошел заряд 3 Кл?

Решение

Заряд можно определить, зная время и силу тока. А зная заряд и врямя, за которое он прошел по проводнику, найдем силу тока:

I=qt

Запишем закон Джоуля-Ленца для количества теплоты:

Q=I2RtQ=q2t2Rt=q2Rt

Подставим значения и вычислим:

Q=32·69=6 Дж

Ответ: 6 Дж.

Вопросы на закон Джоуля-Ленца

Вопрос 1. Как звучит закон Джоуля-Ленца?

Ответ. Закон Джоуля-Ленца гласит:

Количество теплоты, выделившейся в проводнике при прохождении по нему электрического тока, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока.

Q=I2Rt

Вопрос 2. Почему проводник с током нагревается?

Ответ. При прохождении тока по проводнику положительные ионы в узлах кристаллических решеток проводника за счет энергии тока начинают сильнее колебаться. Это сопровождается увеличением внутренней энергии проводника, т.е. его нагреванием. При этом энергия тока выделяется в виде теплоты, которую называют джоулевым теплом.

Вопрос 3. Как был открыт закон Джоуля-Ленца?

Ответ.  По спирали, помещенной в калориметр с водой, пропускали электрический ток. Через некоторое время вода нагревалась. По температуре воды можно было вычислить количество выделившейся теплоты. Эмпирическим путем было доказано, что при прохождении тока по проводнику, обладающему определенным сопротивлением, в течение времени током совершается работа, проявляющаяся в виде выделившейся теплоты.

Английский физик Джеймс Джоуль и русский физик Эмилий Ленц изучали зависимость количества выделяемой теплоты от силы тока одновременно. Они пришли к одному и тому же выводу независимо друг от друга.

Вопрос 4. Как еще можно записать закон Джоуля-Ленца?

Ответ. Воспользовавшись законом Ома для участа цепи, закон Джоуля-Ленца можно переписать следующим образом:

Q=UIt=U2Rt

Вопрос 5. Каково практическое применение закона Джоуля-Ленца?

Ответ. Закон Джоуля-Ленца находит широкое применение на практике:

  1. На нем основан принцип действия многих нагревательных приборов (чайник, электроплитка, фен, утюг, паяльник и т.д).
  2. На принципе закона Джоуля-Ленца основана контактная сварка, где создание неразъемного сварного соединения достигается путем нагрева металла за счет проходящего через него электрического тока и пластической деформации свариваемых деталей путем сжатия. Электродуговая сварка также использует закон Джоуля-Ленца.
  3. Расчеты на основе закона Джоуля-Ленца позволяют стабилизировать и минимизировать тепловые потери в линиях электропередач.

Нужна помощь в решении задач и выполнении других заданий по учебе? Обращайтесь в профессиональный сервис для учащихся в любое время.

Источник

2.4. Закон Ома. Электрическое сопротивление. Закон Джоуля – Ленца

Как отмечалось выше, для поддержания постоянного тока в проводнике, т. е. движения электронов с постоянной скоростью, необходимо непрерывное действие сил электрического поля на носители заряда. Это означает, что электроны в проводниках движутся «с трением», иначе говоря, проводники обладают электрическим сопротивлением.

Если состояние проводника остаётся неизменным (не изменяется его температура и т. д.), то для каждого проводника существует однозначная зависимость между напряжением `U` на концах проводника и силой `I` тока в нём `I=f(U)`. Она называется вольтамперной характеристикой данного проводника.

Для многих проводников эта зависимость особенно проста – линейная: сила тока прямо пропорциональна приложенному напряжению, т. е.

где `R` – электрическое сопротивление проводника (постоянная при неизменных условиях величина).

Этот закон носит название закона Ома. Немецкий физик Г. Ом в 1827 г. в результате серии экспериментов установил, что для широкого класса проводников сила `I` электрического тока в проводнике пропорциональна напряжению `U` на концах проводника.

Сопротивление `R` проводника зависит от рода вещества проводника, от его размеров и формы, а также от состояния проводника.

Единицей сопротивления в СИ является один Ом (Ом). За один Ом принимается сопротивление такого проводника, в котором при напряжении между его концами один вольт течёт постоянный ток силой один ампер: `1`Ом`=1`В`//1`A.

Вытекающее из закона Ома (8) соотношение

можно рассматривать и как определение сопротивления по приведённой формуле.

Г. Ом установил, что для проводников  $$ R$$ не зависит от $$ U.$$ 

В технических приложениях для описания процессов в электрических цепях часто используется понятие  вольтамперной характеристики. Для проводников, подчиняющихся закону Ома (8), графиком зависимости силы `I` тока в проводнике от напряжения `U` на нём будет прямая линия, проходящая через начало координат (см. рис. 1). При этом говорят, что проводник имеет линейную вольтамперную характеристику.

В то же время для полупроводников, электронных ламп, диодов, транзисторов зависимость `I=f(U)` носит сложный характер, и такие элементы называют нелинейными (или неомическими). Для таких элементов величина `R`, вычисленная по формуле `R=U/I`, зависит от `U`. В частности, при измерении вольтамперной характеристики лампочки накаливания с вольфрамовой нитью мы обнаружим, что она имеет вид, схематически показанный на рис. 2. Искривление вольтамперной характеристики связано с нагревом нити и увеличением сопротивления нити накала с ростом температуры. В некоторых устройствах, таких как диод, сопротивление зависит от направления тока.

Обсудим вопрос о тепловыделении в проводнике. С учётом закона Ома (8) формула (7) для мощности тепловыделения принимает вид:

Другими словами, если через резистор `R` протекает постоянный ток силой `I`, то за `t` секунд в резисторе выделяется количество теплоты, равное

`Q_(“тепл”)=P*t=U^2/R*t=I^2*R*t`.                               (11)

Соотношения (10), (11) являются математическим выражением закона, открытого в XIX веке практически одновременно и независимо английским физиком Д. Джоулем и русским физиком Э.Х. Ленцем.

Обратим внимание, что полученный закон является прямым следствием закона сохранения энергии в применении к движению электрических зарядов под действием сил электрического поля.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 октября 2021 года; проверки требуют 4 правки.

Закон Джоуля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем[1].

Определения[править | править код]

В словесной формулировке звучит следующим образом[2]:

Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока на величину напряженности электрического поля.

Математически может быть выражен в следующей форме:

{displaystyle w={vec {j}}cdot {vec {E}}=sigma E^{2},}

где w — мощность выделения тепла в единице объёма, vec j — плотность электрического тока, vec E — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах[3]:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка.

В интегральной форме этот закон имеет вид

{displaystyle dQ=I^{2}Rdt,}
{displaystyle Q=int limits _{t_{1}}^{t_{2}}I^{2}Rdt,}

где dQ — количество теплоты, выделяемое за промежуток времени dt, I — сила тока, R — сопротивление, Q — полное количество теплоты, выделенное за промежуток времени от t_{1} до t_{2}. В случае постоянных силы тока и сопротивления:

{displaystyle Q=I^{2}Rt.}

Применяя закон Ома, можно получить следующие эквивалентные формулы:

{displaystyle Q=U^{2}t/R =IUt.}

Практическое значение[править | править код]

Снижение потерь энергии[править | править код]

При передаче электроэнергии тепловое действие тока в проводах является нежелательным, поскольку ведёт к потерям энергии. Подводящие провода и нагрузка соединены последовательно — значит, ток в сети I на проводах и нагрузке одинаков. Мощность нагрузки и сопротивление проводов не должны зависеть от выбора напряжения источника. Выделяемая на проводах и на нагрузке мощность определяется следующими формулами

{displaystyle Q_{w}=R_{w}cdot I^{2},}
{displaystyle Q_{c}=U_{c}cdot I.}

Откуда следует, что {displaystyle Q_{w}=R_{w}cdot Q_{c}^{2}/U_{c}^{2}}. Так как в каждом конкретном случае мощность нагрузки и сопротивление проводов остаются неизменными и выражение {displaystyle R_{w}cdot Q_{c}^{2}} является константой, то тепло, выделяемое на проводе, обратно пропорционально квадрату напряжения на потребителе. Повышая напряжение, мы снижаем тепловые потери в проводах. Это, однако, снижает электробезопасность линий электропередачи.

Выбор проводов для цепей[править | править код]

Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при выборе проводов, предназначенных для сборки электрических цепей, достаточно следовать принятым нормативным документам, которые регламентируют выбор сечения проводников.

По этой причине для передачи необходимой мощности через современные магистральные воздушные линии электропередач, их проектируют под сверхвысокое напряжение (до 1150 кВ), чтобы обеспечить сверхнизкие токи в ЛЭП.

Электронагревательные приборы[править | править код]

Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.

За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.

Плавкие предохранители[править | править код]

Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.

См. также[править | править код]

  • Закон Ома

Примечания[править | править код]

  1. ↑ Джоуля — Ленца закон // Дебитор — Евкалипт. — М. : Советская энциклопедия, 1972. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 8).
  2. ↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 186. — 688 с.
  3. ↑ Сивухин Д. В. Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 197—198. — 688 с.
Источник

Закон Джоуля-Ленца

На чтение 3 мин Просмотров 93 Опубликовано 20.10.2021

Содержание

  1. Закон Джоуля-Ленца
  2. Уравнение Джоуля-Ленца
  3. Практическое применение
  4. Примеры задач
  5. Задача 1
  6. Задача 2

Закон Джоуля-Ленца

  • Теперь представим, что сечение проводника увеличилось. Конечно, столкновений частиц будет меньше, а значит — выделится меньше тепла. Вспоминаем, что удельное сопротивление проводника обратно пропорционально его сечению. Чем меньше сечение материала, тем выше его сопротивление и тем сильнее он нагревается. Вот мы и описали тепловое действие тока в соответствии с законом Джоуля-Ленца.

    Уравнение Джоуля-Ленца

    Посмотрим, как данный закон выражается в математическом виде. Допустим, на некоем участке цепи проходит электрический ток и вызывает нагревание проводника. Если на этом участке нет каких-либо механических процессов или химических реакций, требующих энергозатрат, выделенная проводником теплота Q равна работе тока A.

    Q = A

    Поскольку А = IUt, где I — сила тока, U — напряжение, а t — время, Q = IUt.

    Теперь вспомним, что напряжение можно выразить через сопротивление и силу тока U = IR. Подставим это в формулу:

    Q = IUt = I(IR)t = I2Rt

    Q = I2Rt

    Мы выразили количество теплоты в проводнике через сопротивление — эта формула для закона Джоуля-Ленца называется интегральной.

    Но бывает так, что сила электрического тока неизвестна, зато есть информация о напряжении на участке цепи. В таком случае нужно использовать закон Ома:

    I = U/R

    Исходя из этого, закон Джоуля-Ленца можно записать в виде дифференциальной формулы:

    Напомним, что такое уравнение, как и предыдущее, верно только в том случае, когда вся работа электрического тока уходит на выделение тепла и нет других потребителей энергии.

    При расчетах используют следующие единицы измерения:

    • количество тепла Q— в джоулях (Дж),

    • силу тока I — в амперах (А),

    • сопротивление R — в омах (Ом),

    • время t — в секундах (с).

    Практическое применение

    Применение на практике закона Джоуля-Ленца заключается в том, что тепловым действием электрического тока можно управлять, подбирая проводники с нужным сопротивлением. К примеру, для электрических нагревательных приборов, которые должны выделять максимум тепла, выбирают проводники с высоким сопротивлением.

    Низкое сопротивление, напротив, позволяет проводнику практически не нагреваться при прохождении тока. Поэтому на промышленных предприятиях с усиленными требованиями к пожаробезопасности для прокладки линий электропередач используется медный кабель. Удельное сопротивление меди сечением 1 мм2 равно 0,0175 Ом, в то время как у алюминия оно составляет 0,0271 Ом. Медь практически не нагревается, чем снижает риск возгораний.

    Примеры задач

    Задача 1

    Электроплита подключена к сети с напряжением 220 В. Какое количество тепла выделит ее нагревательный элемент за 50 минут, если известно, что сила тока в цепи составляет 10 А.

    Решение:

    Дано:

    I = 10 A,

    t = 50 мин = 3000 с,

    U = 220 В.

    Для того, чтобы рассчитать количество тепла, в данном случае подойдет интегральная формула Джоуля-Ленца Q = I2Rt, однако мы не знаем, чему равно сопротивление R. Однако согласно закону Ома R = U/I.

    Вычислим сопротивление: R = U/I = 220/10 = 22 Ом.

    Подставим имеющиеся данные в формулу:

    Q = I2Rt = 102 × 22 × 3000 = 6 600 000 Дж = 6,6 МДж.

    Ответ: плита выделит 6,6 мегаджоулей тепла.

    Задача 2

    Для обогрева дома требуется, чтобы отопительный прибор выделял 125 кДж тепла в час. Напряжение в электрической сети составляет 220 В. Каким должно быть электрическое сопротивление проводника, чтобы обеспечить данную теплоотдачу?

    Решение:

    Дано:

    Q = 125 Дж = 125 000 Дж,

    U = 220 В,

    t = 1 ч = 3600 с.

    В данном случае подойдет уравнение

    Ответ: сопротивление проводника 1393,92 Ом.

Источник

Добавить комментарий