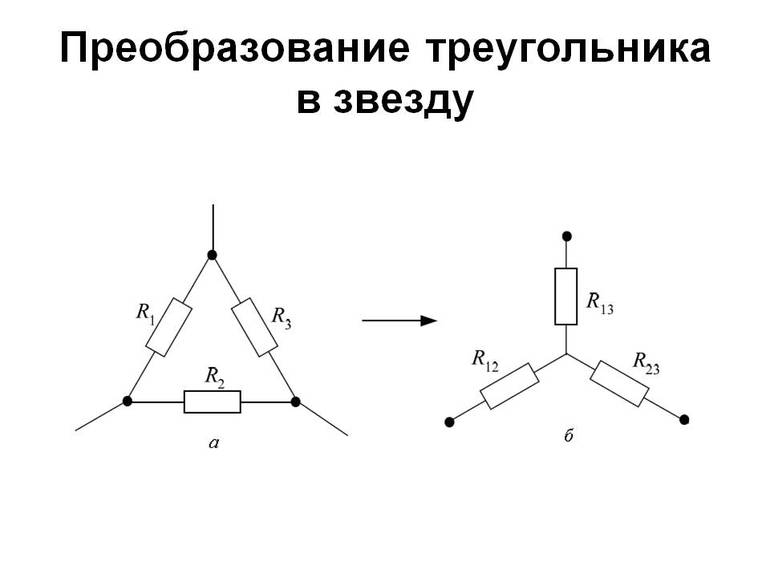
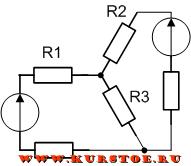
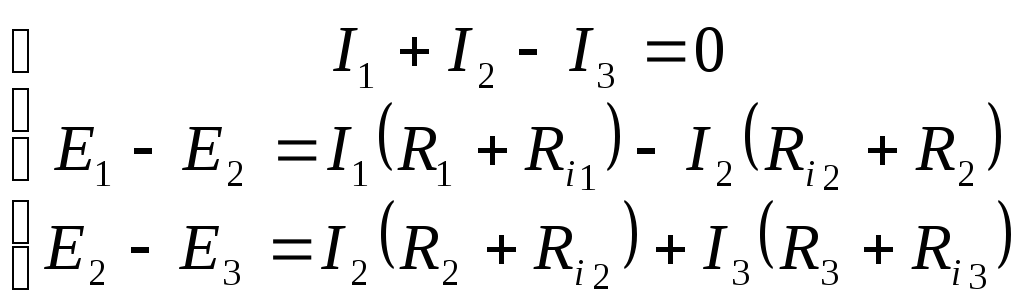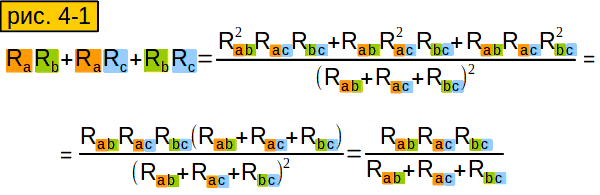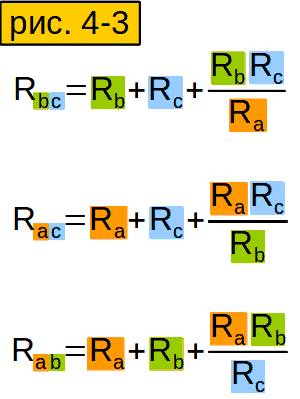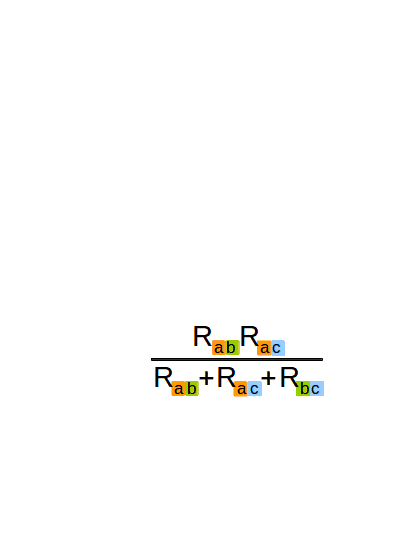Треугольник в звезду
Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядным путем преобразования электрических схем одного вида в схемы другого вида. Одним из способов является эквивалентное преобразование треугольника в звезду. В этом методе выполняется преобразование пассивной части электрической цепи, т.е. приемников электрической энергии.
Определение соединения сопротивлений треугольником
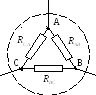
Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.
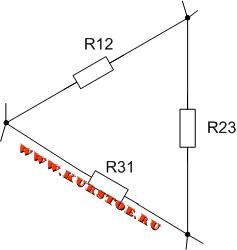
Соединение, при котором три сопротивления, находящиеся в пассивных ветвях, соединены между собою попарно и образуют замкнутый контур – называется треугольником.
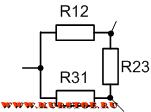
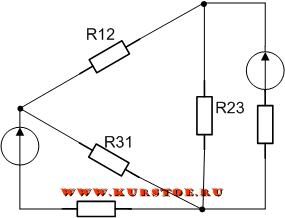
Обычно в курсе электротехники принято элементы рисовать только горизонтально и вертикально. На следующем рисунке так же представлено соединение треугольником.
Определение соединения сопротивлений звездой
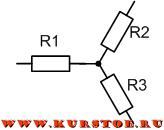
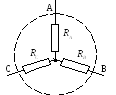
Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой.
Причина преобразования треугольника в звезду
При расчете электрической цепи бывают случаи, когда нет ни последовательных, ни параллельных соединений сопротивлений. В этом случае можно попробовать отыскать соединение сопротивлений треугольником и выполнить экивалентное преобразование треугольника в звезду.
Если в электрической цепи нашли соединение сопротивлений треугольником, то в узлы соединения сопротивлений подставляем концы лучей соединения сопротивлений в виде звезды.
Далее убираем (удаляем первоначальное) соединение треугольником. В результате получается эквивалентное соединение звездой.
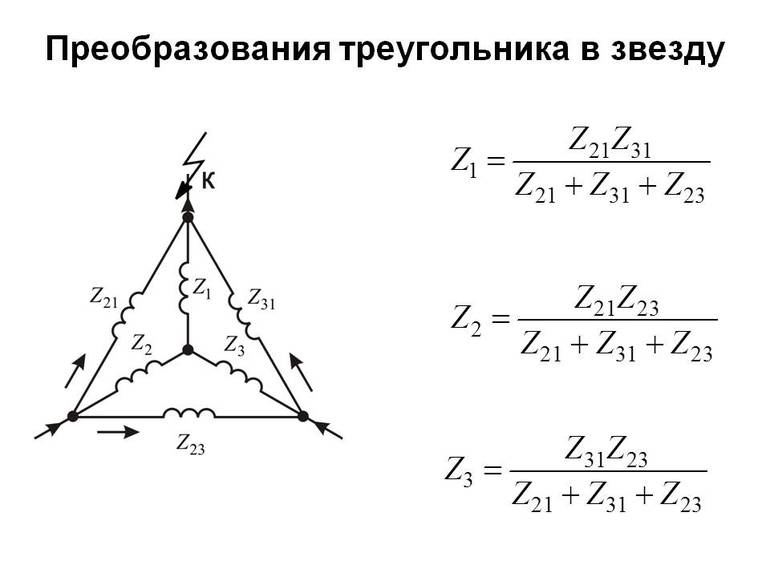
Формулы для расчета преобразования треугольника в звезду
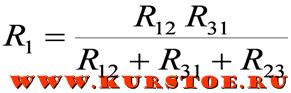
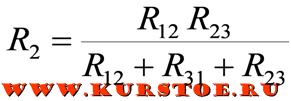
Пример преобразования
Для электрической цепи необходимо выполнить преобразование треуголькника R12 – R23 – R31 в звезду.
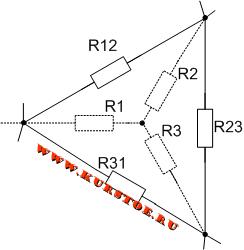
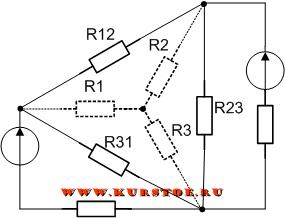
Добавляем к узлам подключения сопротивлений треугольником концы лучей подключения сопротивлений звездой.
Удаляем соединение сопротивлений треугольником. В результате остается подключение сопротивлений звездой. По формулам рассчитываются значения сопротивлений R1, R2, R3.
Преобразование треугольника в звезду – методы, формулы и примеры
Общие сведения
Электрическая цепь предназначена для обеспечения протекания по ней токов определённой величины. Она содержит источники и приёмники энергии, которые соединены проводниками. При изображении радиоэлементов используют их графические обозначения. Электрические же соединения обозначают прямыми линиями. Замкнутые проводники образовывают контуры. В их состав входят узлы (точки контакта трёх и более линий) и ветви (соединители).
Существует 2 способа обеспечения контакта между элементами:
- параллельный — при таком включении в цепи не будет ни одного узла;
- последовательный — входящие в цепь эквиваленты присоединены к одной точке, связанной или не имеющей контакта с другой.
В основе преобразований лежит приведение схемы к упрощённому виду без изменения величины тока или напряжения. Для этого выделяют один контур и заменяют его эквивалентным сопротивлением. При последовательном соединении импеданс просто складывают, а вот при параллельном используют формулу: 1/R = 1/R1 + 1/R2 +…1/Rn.
Таким образом, путем замены пары элементов одним, схема последовательно упрощается до тех пор, пока в ней не окажется один резистор. А уже по его величине и рассчитывают ток цепи. Но в некоторых случаях существуют соединения, которые не поддаются методу упрощения. Если внимательно посмотреть на такую цепь, можно увидеть подключение, похожее на треугольник. В таком случае невозможно определить, какие элементы параллельные, а какие последовательные.
Чтобы найти эквивалентное сопротивление таких сложных соединений, используют преобразование треугольника в равнозначную звезду. По сути, при треугольном подключении 3 элемента образуют замкнутый контур. При этом между каждой парой резисторов имеется узел. Связь же звездой образуется при получении трёх лучевого соединения, в котором каждый элемент цепи подсоединён одним концом к общему узлу, а другой стороной контакта к остальной части схемы.
Преобразование в физике выполняют по строго установленным формулам.
Если его выполнить правильно, значения потенциалов в одноимённых точках треугольника и звёзды, а также подводящиеся к этим узлам токи, останутся одинаковыми. Это значит, что вся оставшаяся часть схемы «не заметит» выполненной замены.
Переход треугольник — звезда
Чтобы преобразовать треугольник в звезду, нужно применять особый подход. Закон Ома для такого случая применить невозможно, поэтому упрощения выполняют, руководствуясь правилами Киргофа. Их 2. Первое гласит, что в узле токи компенсируют друг друга, то есть их алгебраическая сумма равняется нулю. Второе же сообщает, что если сложить электродвижущую силу в любом замкнутом контуре цепи, она будет равна алгебраической сумме падений потенциала на импедансе этой части схемы.
В соответствии с этими законами, можно утверждать, что в узлах электрического заряда нет. Он не расходуется и не собирается. В количественном виде первое утверждение записывают так: I1 = I2 + I3, где с левой стороны стоит значение тока втекающего, а справа вытекающих. Второй закон описывается выражением: E1 — Е2 = -UR1 — UR2 или E1 = Е2 — UR1 — UR2.
Опираясь на эти правила, можно выполнить перевод схемы.
Сделать это удобно, руководствуясь следующим алгоритмом:
- Пусть имеется контур, образованный из резисторов Ra1, Rb1, Rc1, соединённых треугольником.
- Сумму всех сопротивлений можно обозначить символом RΔ. Её можно будет найти, сложив все импедансы: RΔ = Ra1 + Rb1 + Rc1.
- Для получения равенства с неизвестными нужно сделать перестановку в соотношении. Выражение примет вид: Ra2 + (RΔs)Rb2 + (RΔs)Rc2 = Ra1 * Rb1 + Rb1 * Rc1.
- Из эквивалентных уравнений можно вывести ещё 2 формулы, описывающие оставшиеся пары контактов. Беря во внимание симметрию, можно получить: Ra2 + (0)Rb2 + (RΔs)Rc2 = Ra1 * Rс1 + Rb1 * Rc1 и Ra2 + (RΔs)Rb2 + (0)Rc2 = Ra1 * Rc1 + Ra1 * Rb1.
- Нужно выполнить сложение последних двух уравнений, а после, отняв первое, получить равенство: 2 (RΔs) * Ra2 = 2 * Ra1 * Rc1. Отсюда: Ra2 = Ra1 * Rc1 / RΔs.
- По аналогии можно найти и оставшиеся эквиваленты: Rb2 = Ra1 * Rb1 / RΔs и Rc2 = Rc1 * Rb1 / RΔs.
Конечно же, при решении задачи о переводе из одного вида подключения в другое никто не расписывает промежуточные вычисления, а используют сразу конечную формулу: Rk = Rk1 * Rk2 / RΔs, где: Rk — сопротивление, подключённое к контакту в уже трансформированной схеме, а Rk1 и Rk2 — резисторы, стоящие в контуре типа треугольник.
Таким образом, сопротивление, соединённое с каждым узлом при переходе, можно найти из перемножения сопротивлений, подключённых к соответствующей точке в цепи, подключённой треугольником, и дальнейшему их делению на сумму всех резисторов в неизменном контуре.
Обратное преобразование
Чтобы получить нужную формулу, следует вести ряд обозначений. Токи, подходящие к узлам, можно обозначить как I1, I2, I3. Преобразование должно выполняться таким образом, чтобы при замене контура величины других токов и потенциалов не изменялись. Для этого следует выразить упорядоченное движение зарядов через напряжение точек и проводимость.
В соответствии с первым правилом Кирхгофа, можно записать: I1 + I2 + I3 = 0. Равенство можно изменить так: (f1 — f0) * p1 + (f2 — f0) * p1 + (f2 — f0) * p1 = 0, где: f — потенциал в точке. В выражении легко выполнить простые преобразования и найти f0. Оно будет равно: f0 = (f1p1 + f2p2 + f3p3) / (p1 + p2 + p3). Полученную формулу возможно использовать для вывода тока. Для I1 будет верным уравнение: I1 = (f1 — f0) * p1 = (f1 * (p2 + p3) — f2 * p2 — f3p3) * p / (p1 + p2 + p3).
Движение заряда удобно обозначать не буквами, а цифрами. Например, число 12 будет показывать, что рассматривается связь первого и второго узла. Таким образом, в треугольнике I1 = I12 — I31 = (f1 — f2) * p12 — (f3 — f1) * p13 = f1* (p12 + p13) — f3p13 -f 2p12.
Учитывая, что ток I1 в схеме треугольник и звезда одинаков, при этом величины потенциалов не влияют на его значение, коэффициенты, стоящие возле f в правой и левой части, будут равны. Тогда можно записать следующие равенства: p12 = p1 * p2 / (p1 + p2 + p3); p13 = p1 * p3 / (p1 + p2 + p3); p23 = p2 * p2 / (p1 + p2 + p3). Как раз по этим формулам и возможно рассчитать проводимость треугольника через звезду.
Зная проводимость, можно определить импеданс, так как это величина обратна сопротивлению. Вывод формулы будет иметь следующий вид: R12 = (1/r1 + 1/r2 + 1/r3) / 1/r1 * r2. Для дальнейших расчётов многочлен (1/r1 + 1/r2 + 1/r3) удобно заменить одной буквой, например, s. Тогда: R12 = s / r3; R23 = s / r1; R13 = s / r2. Подставив последние выражения в формулу для нахождения s, можно будет получить отношение: m = (r12 * r23 * r31) / (r12 + r23 + r31).
Формулы для нахождения эквивалента при переходе примут вид:
- R1 = (r12 * r31) / y;
- R2 = (r23 * r12) / y;
- R3 = (r13 * r23) / y.
Где: y = r12 + r23 + r31. Полезность преобразования в треугольник позволяет привести схему к набору простых последовательных соединений. Подключение двигателей по этой схеме позволяет добиться наибольшей отдачи мощности, например, при модернизации промышленных электросетей.
Решение примера
При знании формул решение задач на преобразование треугольника в звезду или обратно обычно не доставляет проблем. Нужно просто внимательно следить за подставляемыми величинами. Но перед тем как приступить непосредственно к расчёту эквивалентной схемы, следует оценить необходимость выполнения такого действия. Некоторые элементы могут быть соединены последовательно или параллельно, поэтому нужно будет начать с простых преобразований, а уже позже переходить к звезде или треугольнику.
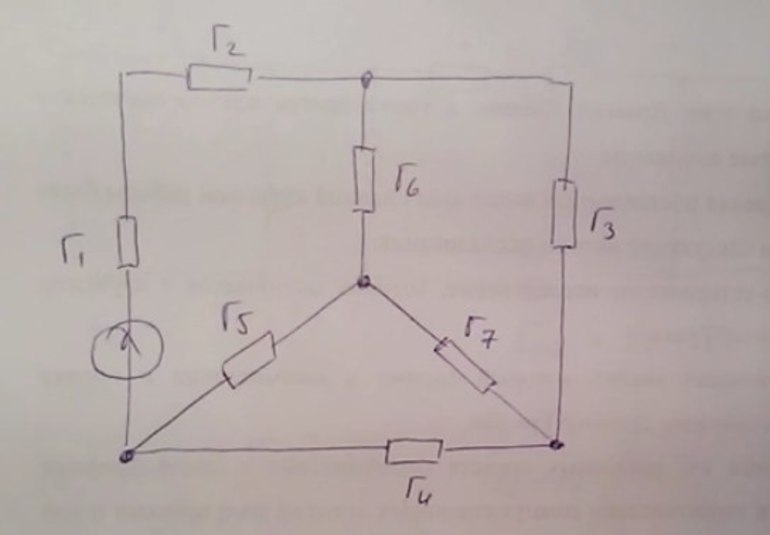
Вот пример задания. Имеется трёхфазная цепь. Посчитать её эквивалентное сопротивление. Известно, что схема подключена к источнику напряжения 220 вольт, сопротивление: R1 = 10 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 50 Ом, R6 = 60 Ом, R7 = 70 Ом.
В этой схеме сопротивления R1 и R2 соединены последовательно. Что же касается остальных элементов, сказать, какой тип подключения у них по отношению друг к другу, нельзя. Но зато видно, что контур, состоящий из R5, R7, R4, является треугольником, то есть задача состоит в превращении его в эквивалентную трёхлучевую звезду.
Новые элементы можно обозначить как R57, R45, R47. Чтобы найти номиналы новых сопротивлений, нужно воспользоваться эквивалентными формулами. R57 = (R5 * R7) / R5 + R4 + R7 = 50 * 70 / 50 + 40 + 70 = 3500 / 160 = 21,8 Ом; R45 = (R4 * R5) / R5 + R4 + R7 = 40 * 50 / 50 + 40 + 70 = 2000 / 160 = 12,5 Ом; R47 = (R4 * R7) / R5 + R4 + R7 = 40 * 70 / 50 + 40 + 70 = 2800 / 160 = 17,5 Ом.
Теперь эквивалентный контур можно подставить в схему вместо треугольника. В результате цепь будет состоять из трёх последовательно соединённых резисторов R1, R2 и R45. Общий импеданс для них будет равен: Rx = R1 + R2 + R45 = 10 + 20 + 17,5 = 47,5 Ом. Аналогично можно вычислить параметр и для второго контура: Ry = R6 + R57 = 60 + 21,8 = 81,8 Ом. Останется найти сопротивление ветви, включающую R3 и R47, Rz = R3 + R47 = 30 + 17,5 = 47,5 Ом.
Теперь схема принимает довольно простой вид. Контур состоит из трёх включённых параллельно относительно друг друга резисторов Rx, Ry, Rz. Если использовать формулу нахождения эквивалента для такого типа включения, результирующее первое сопротивление будет равно: Rоб = Ry * Rz / (Ry + Rz) = 81,8 * 47,5 / (81,8 + 47,5) = 3885,5 / 129,3 = 30,05 Ом. Теперь схема уже стала одноконтурной и содержит соединение, которое будет называться последовательным.
Таким образом, эквивалентное сопротивление для схемы будет составлять: Rx + R об = 30,05 + 47,5 = 77,55 Ом. Задача решена.
Сопротивление при соединении треугольником
Преобразования треугольник-звезда и звезда-треугольник
Во многих схемах можно встретить такие конфигурации компонентов, в которых невозможно выделить последовательные или параллельные цепи. К этим конфигурациям относятся соединения компонентов в виде звезды (Y) и треугольника (Δ):
Очень часто, в ходе анализа электрических цепей, оказывается полезным преобразовать треугольник в звезду или, наоборот, звезду в треугольник. Практически, чаще возникает необходимость преобразования треугольника в звезду. Если при замене одной из этих схем другой не изменяются потенциалы одноименных точек и подтекающие к ним токи, то во внешней цепи также не произойдет никаких изменений. Иными словами, эквивалентные Δ и Y цепи ведут себя одинаково.
Существует несколько уравнений, используемых для преобразования одной цепи в другую:
Δ и Y цепи очень часто встречаются в 3-фазных сетях переменного тока, но там они, как правило, сбалансированы (все резисторы равны по значению) и преобразование одной цепи в другую не требует таких сложных расчетов. Тогда возникает вопрос: где мы сможем использовать эти уравнения?
Использовать их можно в несбалансированных мостовых схемах:
Анализ данной схемы при помощи Метода Токов Ветвей или Метода Контурных Токов довольно сложен. Теорема Миллмана и Теорема Наложения здесь тоже не помощники, так как в схеме имеется только один источник питания. Можно было бы использовать теорему Тевенина или Нортона, выбрав в качестве нагрузки резистор R3, но и здесь у нас вряд ли что-нибудь получится.
Помочь в этой ситуации нам сможет преобразование треугольник – звезда. Итак, давайте выберем конфигурацию резисторов R1, R2 и R3, представляющих собой треугольник (Rab, Rac и Rbc соответственно), и преобразуем ее в звезду:
После преобразования схема примет следующий вид:
В результате преобразования у нас получилась простая последовательно-параллельная цепь. Если мы правильно выполним расчеты, то напряжения между точками А, В и С преобразованной схемы будут аналогичны напряжениям между этими же точками исходной схемы, и мы сможем вернуть их обратно.
Сопротивления резисторов R4 и R5 остаются неизменными: 18 и 12 Ом соответственно. Применив к схеме последовательно-параллельный анализ, мы получим следующие значения:
Теперь, используя значения напряжений из приведенной выше таблицы, нам нужно рассчитать напряжения между точками А, В и С. Для этого мы применим обычную математическую операцию сложения (или вычитания для напряжения между точками В и С):
Переносим эти напряжения в исходную схему (между точками А, В и С):
Напряжение на резисторах R4 и R5 останется таким же, каким оно было в преобразованной схеме.
К данному моменту у нас есть все необходимые данные для определения токов через резисторы (используем для этой цели Закон Ома I = U / R):
Моделирование при помощи программы PSPICE подтвердит наши расчеты:
[spoiler title=”источники:”]
http://nauka.club/matematika/geometriya/preobrazovani%D0%B5-treugolnika-v-zvezdu.html
http://www.radiomexanik.spb.ru/9.-analiz-tsepey-postoyannogo-toka/14.-preobrazovaniya-treugolnik-zvezda-i-zvezda-treugolnik.html
[/spoiler]
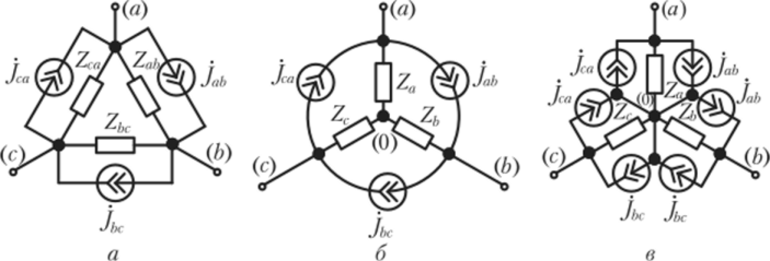
Если имеется 3 сопротивления, образующих
3 узла, то такое сопротивление составляет
пассивный треугольник, а если
имеется только один узел, то сопротивления
составляютпассивную звезду.
пассивный треугольник
пассивная звезда
Эти схемы можно эквивалентно заменить
одна другой, если все токи в ветвях не
подвергнутся преобразованию (то есть
то, что за пределами штриховой линии
не изменится). Из этих предпосылок
получим следующие формулы
преобразования:

звезду):
Сопротивление луча эквивалентной
звезды равно произведению сопротивлений
сторон треугольника, примыкающих к той
же вершине, что и луч звезды, делённое
на сумму всех сопротивлений сторон
треугольника:

Сопротивление стороны треугольника
равно сумме сопротивлений лучей звезды,
примыкающих к тем же вершинам, что и
сторона треугольника, плюс произведение
этих сопротивлений, делённое на
сопротивление третьего луча звезды:
Преобразование треугольника в звезду
применяется в мостовых схемах,
которые представляют собой 4 резистора,
соединённых четырёхугольником, в одну
диагональ которого ставится источник,
во вторую — измерительные приборы.
Найти входное сопротивление таких схем
без предварительного преобразования
невозможно.
Задача
Д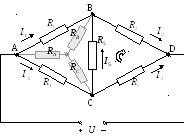
Найти все токи и направить их.
В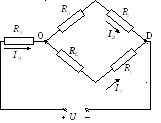
преобразование треугольника ABC в
эквивалентную звезду:
Рассчитаем входное сопротивление и
ток:
Найдём напряжение на разветвлённом
участке OD и токи в его ветвях:
В первоначальной схеме направим токи,
ток
направим произвольно.
Для треугольника, который не заменяли,
составляем уравнение по второму закону
Кирхгофа:
Чтобы найти токи
и
,
составляем уравнения по первому закону
Кирхгофа для узлов B и C:
B:
С:
Вопрос 19. Первый закон Кирхгофа, узловые уравнения. Второй закон Кирхгофа, контурные уравнения.
Узел— точка, в которой сходятся
не менее 3-х токов.
Ветвь— участок цепи, по которому
течёт один и тот же ток.
Контур— любой замкнутый путь в
схеме.
Первый закон Кирхгофа
Для любого узла сумма токов, приходящих
к узлу, равна сумме токов, отходящих от
узла.
Для любого узла электрической цепи
алгебраическая сумма токов равна нулю.
Ток, который притекает к узлу, берётся
со знаком “+”, который оттекает — со
знаком “–”.
Второй закон Кирхгофа
Для любого замкнутого контура
алгебраическая сумма ЭДС равна
алгебраической сумме падений напряжений
на участках этого контура.
Порядок составления контурных
уравнений:
-
Выбираем произвольное направление
тока ветвей. -
Если в схеме n узлов, то составляем n –
1 уравнение по первому закону Кирхгофа. -
Выбираем произвольное направление
обхода контура. -
Если направление обхода и ЭДС совпадают,
то она входит в уравнение со знаком
“+”, если нет — со знаком “–”. -
Если ток ветви и направление обхода
совпадают, то падение напряжения входит
в уравнение со знаком “+”, если нет —
со знаком “–”. -
Если при расчёте получился отрицательный
ток, значит его направление противоположно
выбранному.
Задача
С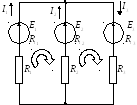
контурные уравнения для решения сложной
электрической цепи.
Соседние файлы в предмете Теория электрических цепей
- #
- #
- #
- #
- #
- #
- #

4 инструмента крутого Кирхгофщика
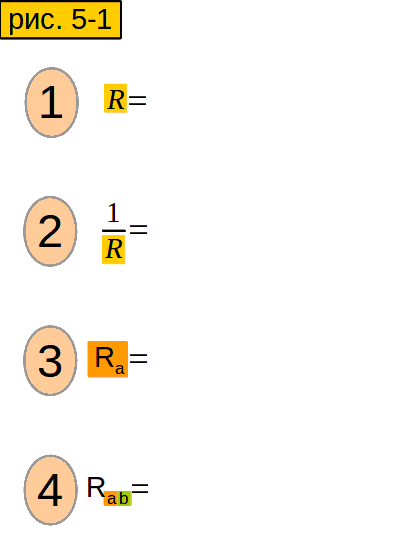
Внимание! Чтобы увидеть ответы на вопросы, кликните по ним. Кликать надо по тексту, а не по пустому месту. Чтобы сменить картинку, кликните по кнопке. Если ответ на вопрос вам не ясен, советую хорошо подумать, прежде чем смотреть ответ.
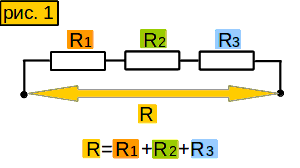
Инструмент 1. Вычисление сопротивления цепи из нескольких последовательно соединённых сопротивлений
Просто, как ….. Сложил все эти сопротивления и получил сопротивление цепи.
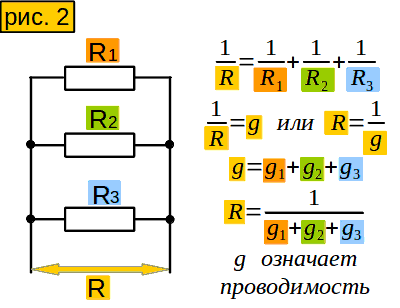
Инструмент 2. Вычисление сопротивления участка из нескольких параллельно соединённых сопротивлений
Рассмотрим участок с двумя параллельными одинаковыми сопротивлениями. Сопротивление его в два раза меньше, чем каждого сопротивления. Если сопротивлений три, сопротивление участка будет в три раза меньше.
Какую тут можно провести аналогию?
Несколько одинаковых дырок. Через них протечёт воды в столько раз больше, чем через одну дырку, сколько дырок имеется.
А как быть, если сопротивления не одинаковые? Есть такое понятие – проводимость. Оно означает величину, обратную сопротивлению. (рисунок 2)
Так если сопротивление больше, то проводимость что?
меньше
Чтобы вычислить проводимость нашего участка, надо сложить проводимости сопротивлений. Потом можно легко найти сопротивление участка.
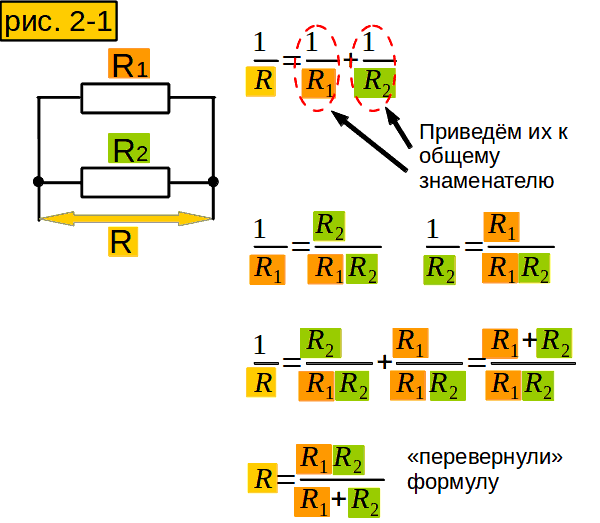
А нельзя ли вычислить сопротивление участка, не преобразуя сопротивления в проводимости, а потом обратно? Можно. Пусть у нас участок из двух параллельно соединённых сопротивлений (рис. 2-1). Проводимость его равна сумме проводимостей сопротивлений (1 строчка). Приведём проводимости сопротивлений к общему знаменателю (2 строчка). Сложим их и получим суммарную проводимость (3 строчка). “Переворачиваем” формулу (4 строчка) и получаем формулу для участка из двух параллельно соединённых сопротивлений. А если сопротивлений не два, а больше?
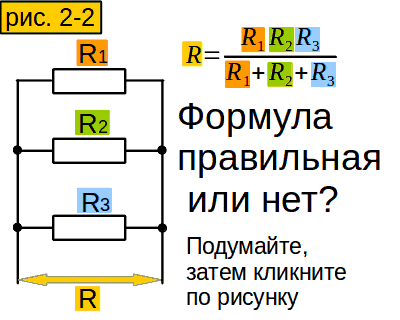

Сформулируйте своими словами формулу сопротивления участка из нескольких параллельных сопротивлений, чтобы лучше её запомнить.
Надо умножить все сопротивления, и разделить на сумму произведений этих сопротивлений, но в каждом этом произведнии одного сопротивления не хватает. Вы, может быть, и получше сформулируете.
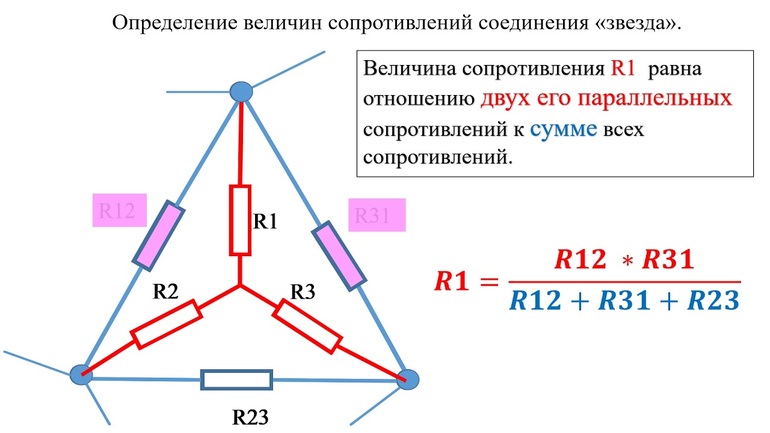
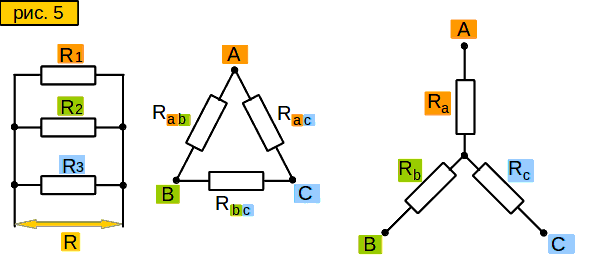
Инструмент 3. Преобразование “треугольника” в “звезду”
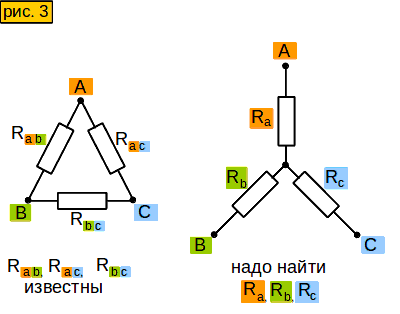
Пусть у нас в схеме есть вот такой участок цепи – “треугольник” (рис. 3, слева). Нам надо заменить его участком вот такого вида – “звездой” (рис. 3, справа), но чтобы сопротивления между сторонами “звезды” были такими же, как между соответствующими лучами “треугольника”. Зачем это нужно? Позже узнаете.
Смотрим на “звезду” на рис. 3. Допустим, мы знаем сопротивления между точками
A и B, то есть (Ra+Rb);
A и C, то есть (Ra+Rc);
B и C, то есть (Rb+Rc).
Чему будут равны сопротивления Ra, Rb, Rc ?
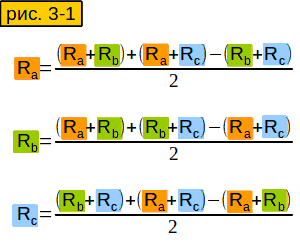
Зная все сопротивления между концами лучей “звезды”, мы можем вычислить сопротивление каждого отдельного луча.
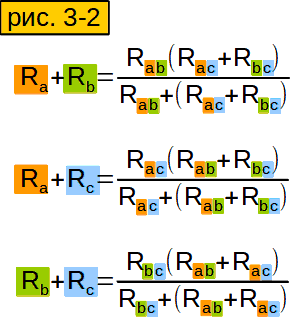
Теперь будем вычислять сопротивления между точками A, B, и C (звезды) через сопротивления треугольника, которые нам известны (рис. 3-2). Для начала вычислим сопротивление между точками A и B звезды (рис. 3-2 верхняя строчка). В нашем треугольнике мы имеем два параллельно включённых сопротивления – Rab и (Rac+Rbc). Вычислять их общее сопротивление мы умеем (ответы на вопросы 3 и 4). Вычисляем сопротивления между точками A и C, B и C (2 и 3 строчки). Обратите внимание, что во всех формулах знаменатель одинаковый.
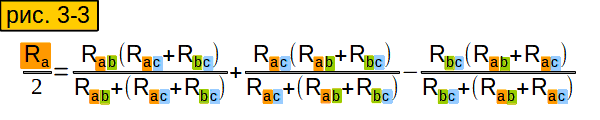
Теперь можно вычислить сопротивление отдельного луча (рис. 3-3). Формула получилась очень громоздкая, но мы её хорошенько подсократим.
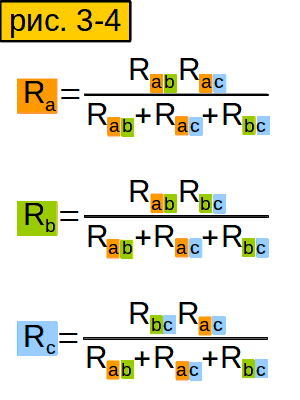
И получим вот такую стройную и изящную формулу (рис. 3-4, верхняя строчка). Аналогично вычисляем сопротивления других лучей звезды.
Сформулируйте своими словами формулу из рисунка 3-4, чтобы лучше её запомнить.
Чтобы найти сопротивление луча “звезды”, надо умножить сопротивления сторон “треугольника”, которые “прилегают” (“имеют ту же букву”), и разделить на сумму сопротивлений всех сторон “треугольника”.
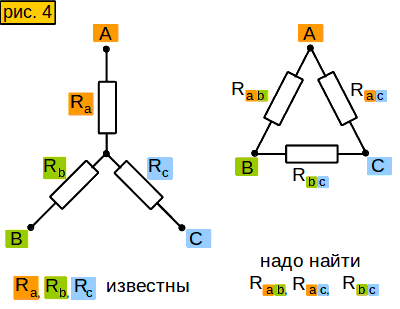
Инструмент 4. Преобразование “звезды” в “треугольник”
Иногда полезно делать обратное преобразование – “звезды” в “треугольник”. Нельзя ли вычислить сопротивление стороны “треугольника” через сопротивления эквивалентной “звезды”, используя формулы, которые мы уже вывели? Можно. Смотрим рисунок 3-4. Проделаем с формулами этого рисунка следующий трюк: попарно их перемножим и результаты сложим (смотрим рис. 4-1).
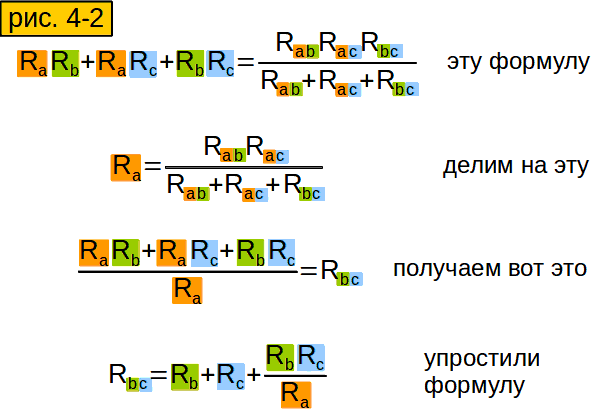
Затем результат разделим на верхнюю формулу рисунка 3-4. Получится у нас вот что: рисунок 4-2, третья сверху формула. Маленько её подсократим и получим нижнюю формулу.
Как раз то, что нам надо!
Сопротивления других сторон “треугольника” выводятся аналогично (рисунок 4-3).
Сформулируйте своими словами формулу из рисунка 4-3, чтобы лучше её запомнить.
Чтобы найти сопротивление стороны “треугольника”, надо сложить сопротивления соответствующих сторон “звезды” (у которых “те же буквы”), и ещё прибавить произведение тех же сторон “звезды”, делёное на оставшуюся сторону.
Зубрилка
об ошибках сообщайте по адресу obuchmat@mail.ru
Продолжение следует
На домашнюю страницу
Расчет и исследование сложных электрических цепей во многих случаях можно значительно облегчить и сделать более наглядным путем преобразования электрических схем одного вида в схемы другого вида. Одним из способов является эквивалентное преобразование треугольника в звезду. В этом методе выполняется преобразование пассивной части электрической цепи, т.е. приемников электрической энергии.
Определение соединения сопротивлений треугольником
Если три сопротивления соединены так, что образуют собою стороны треугольника, то такое соединение сопротивлений называют треугольником сопротивлений.
Соединение, при котором три сопротивления, находящиеся в пассивных ветвях, соединены между собою попарно и образуют замкнутый контур – называется треугольником.
Обычно в курсе электротехники принято элементы рисовать только горизонтально и вертикально. На следующем рисунке так же представлено соединение треугольником.
Определение соединения сопротивлений звездой
Если соединение трех сопротивлений имеет общий узел и имеет внешний вид трехлучевой звезды, то такое соединение сопротивлений называется звездой.
Причина преобразования треугольника в звезду
При расчете электрической цепи бывают случаи, когда нет ни последовательных, ни параллельных соединений сопротивлений. В этом случае можно попробовать отыскать соединение сопротивлений треугольником и выполнить экивалентное преобразование треугольника в звезду.
Если в электрической цепи нашли соединение сопротивлений треугольником, то в узлы соединения сопротивлений подставляем концы лучей соединения сопротивлений в виде звезды.
Далее убираем (удаляем первоначальное) соединение треугольником. В результате получается эквивалентное соединение звездой.
Формулы для расчета преобразования треугольника в звезду
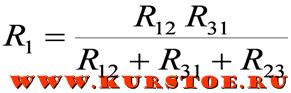
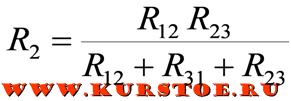
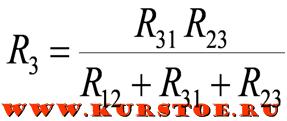
Пример преобразования
Для электрической цепи необходимо выполнить преобразование треуголькника R12 – R23 – R31 в звезду.
Добавляем к узлам подключения сопротивлений треугольником концы лучей подключения сопротивлений звездой.
Удаляем соединение сопротивлений треугольником. В результате остается подключение сопротивлений звездой. По формулам рассчитываются значения сопротивлений R1, R2, R3.
Рассмотрим схему приведенную на рисунке 1:
Рисунок 1 – Исходная схема
Допустим необходимо найти сопротивление схемы относительно точек A и B. Заданы сопротивления резисторов: R1=20, R2=20, R3=10, R4=20, R5=8, R6=4, R7=4. Преобразуем треугольник сопротивлений R1, R2, R3 в звезду сопротивлений R12, R23, R13:
Рисунок 2 – Схема с преобразованным в звезду треугольником
Сопротивления R12, R13, R23 найдены по формулам 1-3:
Чтобы найти сопротивление луча звезды надо произведение сопротивлений прилегающих к нему сторон треугольника разделить на сумму сопротивлений всех сторон треугольника.
Преобразуем последовательное соединение резисторов R13 и R6 в резистор R136 и аналогично преобразуем последовательное соединение резисторов R23 и R7 в резистор R237:
Рисунок 3 – Схема3
Сопротивления резисторов R136 и R237 найдены по формулам 4 и 5:
Преобразуем параллельное соединение резисторов R136 и R237 в резистор R136IIR237:
Рисунок 4 – Схема4
Найдем R136IIR237 по формуле 6:
Далее преобразуем схему 4 к виду:
Рисунок 5 – Схема5
Найдем сопротивление которое стоит справа:
Теперь, заменой параллельного соединения резисторов, в схеме на рисунке 5, одним резистором Rэ, находится эквивалентное сопротивление всей схемы:
Найдем Rэ:
Преобразование треугольника R1, R2, R3 в звезду R12, R23, R13 упростило расчёт эквивалентного сопротивления схемы относительно точек А и B в данном примере.