Расчет сопротивления проводника


4.6
Средняя оценка: 4.6
Всего получено оценок: 118.
4.6
Средняя оценка: 4.6
Всего получено оценок: 118.
Сопротивление проводника ограничивает величину тока в электрической цепи. Чем больше величина сопротивление, тем меньше ток. Расчет сопротивления проводника можно произвести двумя способами: первый способ заключается в использовании формулы закона Ома, а второй вариант расчета подразумевает знание геометрических размеров проводника и удельного сопротивления вещества, из которого он сделан.
Почему проводник “сопротивляется”?
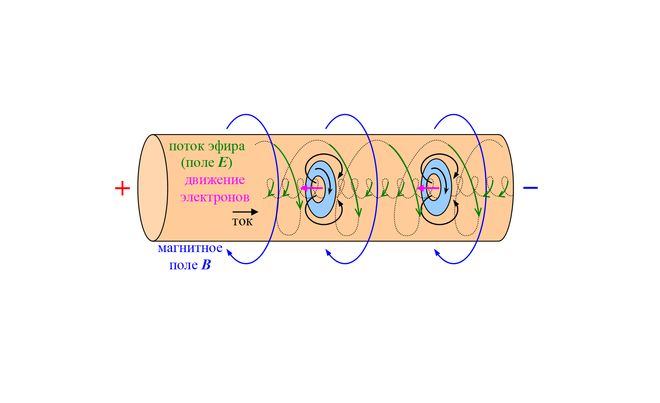
Напряжение U, поданное на концы проводника, создает внутри него электрическое поле, которое приводит в движение свободные электроны вещества. Электроны, получив дополнительную кинетическую энергию, начинают двигаться упорядоченно в одном направлении, создавая тем самым электрический ток цепи.
В процессе движения электроны сталкиваются с нейтральными и заряженными атомами, из которых стоит проводник, теряют энергию. Масса атома превосходит массу электрона в тысячи раз, поэтому их столкновение приводит к изменению направления движения электронов и потере скорости (“торможению”).
Таким образом возникает сопротивление протеканию (нарастанию) тока.
Расчет сопротивления с помощью закона Ома
Немецкий физик Георг Ом в 1826 г. обнаружил, что отношение напряжения U между концами металлического проводника, являющегося участком электрической цепи, к силе тока I есть величина постоянная:
$ R={U over I}=const $ (1),
где:
U — напряжение, В;
I — сила тока, А;
R — сопротивление, Ом.
Эту величину стали называть электрическим сопротивлением. Пользуясь этой формулой, можно экспериментально определить величину неизвестного сопротивления.
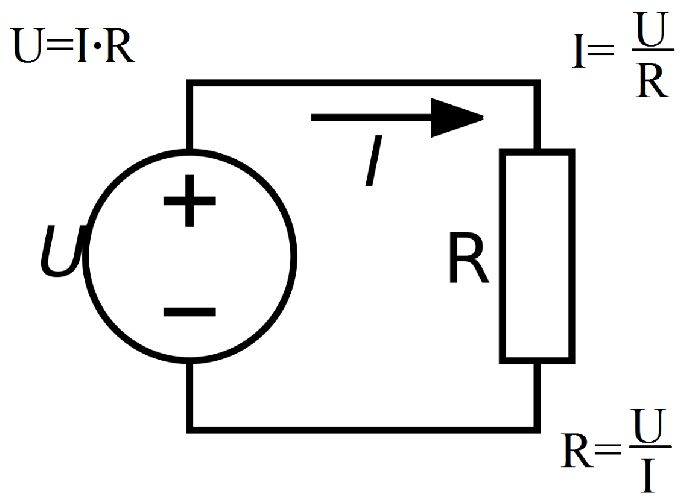
Для этого амперметром измеряется величина электрического тока через сопротивление, а вольтметром — напряжение на участке цепи. Далее, применяя формулу (1), вычисляется значение R.
Единица измерения названа в честь Георга Ома. Электрическим сопротивлением 1 Ом обладает участок цепи, на котором при силе тока 1 А напряжение равно 1 В:
$$ 1 Ом = { 1 Вover 1 A} $$
Расчет с помощью удельного сопротивления
Расчет сопротивления проводника можно произвести без измерения величин напряжения и тока. Но для этого необходимо знать дополнительную информацию о проводнике.
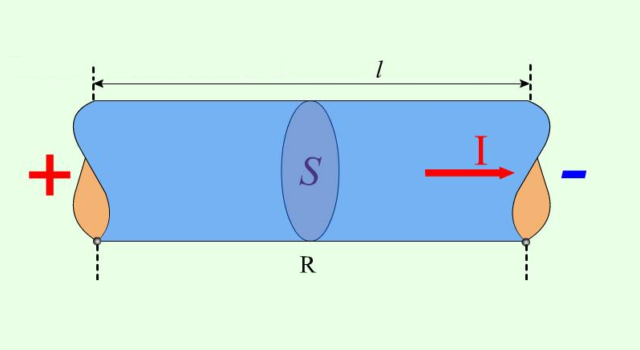
Георг Ом и другие исследователи опытным путем определили, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S. Эту закономерность можно описать формулой расчета сопротивления проводника:
$ R = ρ *{ Lover S} $ (2)
Коэффициент ρ был назван удельным сопротивлением. Эта физическая величина отражает особенности конкретного вещества, которые зависят от плотности вещества, кристаллической структуры, строения атомов и других внутренних параметров. Расчет удельного сопротивления проводника производить каждый раз необязательно, так как для большинства веществ удельные сопротивления измерены и сведены в справочные таблицы, которые можно найти в бумажных справочниках или в их интернет-версиях.
Но если такая необходимость возникнет, то из формулы (2) можно получить следующую формулу (3), и по ней рассчитать ρ:
$ ρ = R*{ Sover L } $ (3)
Серебро имеет одно из самых низких значений ρ, равное $ 0,016 {Ом*мм^2over м} $. Этим объясняется использование такого довольно дорогого металла для пайки особенно важных радиодеталей (микросхем, микропроцессоров, электронных плат), которые должны как можно меньше нагреваться в процессе работы.

Что мы узнали?
Итак, мы узнали, что расчет сопротивления проводника можно произвести двумя способами. Первый расчет проводится с помощью формулы закона Ома после измерения величин напряжения и тока. Для второго расчета необходима информация о геометрических размерах проводника и его удельном сопротивлении.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 118.
А какая ваша оценка?

Общие сведения

Упорядоченное движение носителей заряда в физическом теле называют электрическим током. Ими могут быть различные элементарные частицы. Например, в проводниках — электроны, электролитах — ионы. В состоянии покоя, то есть когда на тело не оказывается постороннее воздействие, движение носителей хаотичное. В результате происходит компенсирование зарядов, и ток не возникает. Если же к веществу приложить силу или деформировать его, направление движения частиц станет упорядоченным и возникнет электрический ток.
Все существующие вещества характеризуются физическими и химическими свойствами. Среди них и проводимость. Это электрическая величина, определяющая способность тела пропускать через себя ток. По своему строению все материалы делятся на 3 класса:
- проводники — вещества, не оказывающие сопротивление прохождению тока;
- полупроводники — тела, в которых величина проводимости зависит от чистоты материала, температуры и вида воздействующего излучения;
- диэлектрики — вещества, практически не проводящие электрический ток.
Величина, обратная проводимости, называется сопротивлением. Это параметр, который характеризует способность материала пропускать через себя электрический ток без потерь. Другими словами, для идеального тела количество электричества, поступившего и снятого с него, будет одинаковым.
За единицу измерения силы тока принят Ампер, показывающий, какое количество электричества проходит через поперечное сечение проводника за одну секунду: I = q / t = кулон / секунду = ампер.

Электрическое сопротивление тела зависит от природы носителей заряда и геометрии материала. Это скалярный параметр. При его расчёте используют понятие удельное сопротивление. Выражают его в омах, умноженных на метр, и обозначают греческой буквой р. По физическому смыслу величина является обратным параметром удельной проводимости.
С ней, кроме сопротивления и силы тока, тесно связано и напряжение. С физической точки зрения, это работа, которую выполняет электрическое поле при переносе единичного заряда из одной точки в другую. В Международной системе величин напряжение принято обозначать в вольтах: U = f2- f1, где f — значения потенциала заряда в точках.
Формула сопротивления
Ток обусловлен движением электронов. Классическая формула, используемая для расчёта его силы была выведена немецким физиком Омом. Он на опыте смог подтвердить зависимость между собой тока, сопротивления и напряжения. В математическом виде связь записывают в виде формулы: I = U /R.
Согласно закону Ома, сопротивление тела электрическому току прямо пропорционально его силе и обратно пропорционально напряжению: R = I / U. Это эмпирическая формула справедлива для любого участка цепи.

Подвижные носители при хаотичном движении ведут себя как молекулы газа, поэтому в первом приближении физики считают носителей зарядов своего рода электронным газом. Как было установлено эмпирически, плотность этого газа и строение кристаллической решётки зависят от рода проводника. Соответственно, проводимость, а значит и сопротивление, определяется также и родом вещества. В свою очередь, физическое тело характеризуется и геометрическими параметрами.
Влияние размеров полупроводника объясняется зависимостью от них поперечного сечения. При его уменьшении поток зарядов становится плотнее, степень взаимодействия между частицами возрастает. Полная формула сопротивления проводника с учётом поперечного сечения выглядит так: R = (p * l) / S. Из неё становится ясно, что проводимость прямо пропорциональна площади сечения и обратно пропорциональна длине проводника.
Удельное электрическое сопротивление для многих веществ было установлено во время исследований. Существуют таблицы, в которые занесены данные, измеренные при температуре 20 градусов Цельсия. Ими часто пользуются при решении различных задач, связанных с электричеством. Вот некоторые из них:
- олово — 9,9 * 10-8 Ом * мм2/м;
- медь — 0,01724 Ом * мм2/м;
- алюминий — 0,0262 Ом * мм 2/м;
- железо — 0,098 * Ом * мм2/м;
- золото — 0,023 Ом * мм2/м.

Для проводников характерно увеличение сопротивления при росте температуры. Это связано с колебаниями атомов. В то же время с ростом температуры проводимость в полупроводниках и диэлектриках возрастает из-за увеличения концентрации носителей заряда.
Удельное сопротивление для неоднородного материала можно вычислить по формуле: p = E / J. Где: E и J напряжённость и плотность тока в конкретной точке.
Нахождение параметра
Найти сопротивление — значит, рассчитать потери тока. Существует 2 принципиально разных подхода к расчёту. В одном случае он ведётся для электрической цепи, а в другой — для материала. Если во втором случае всё предельно понятно, используется одна формула, в которую подставляют размеры тела и табличное значение удельной проводимости, то для электрической цепи не так всё просто.
В цепи может встречаться 3 вида соединения элементов:
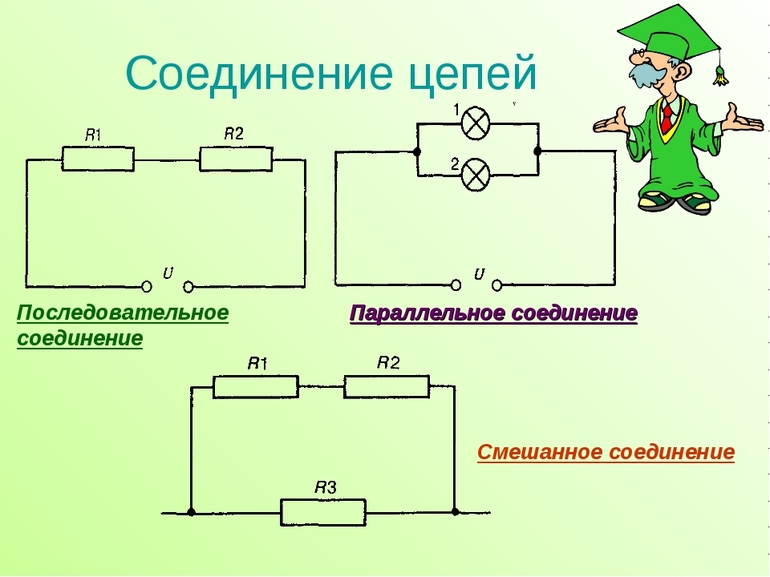
- Параллельное. При таком соединении цепь разветвляется, то есть появляются ветви, по которым течёт ток. Ветви могут пересекаться между собой.
- Последовательное. Схема соединения представляет единую цепь, в которой нет разветвлений.
- Смешанное. Состоит из комбинированного соединения, включающего комбинации из параллельного и последовательного подключения.
Вычисление сопротивления для каждого типа соединения имеет особенности. При последовательном включении общее значение определяется путём простого складывания: R = r1 + r2 +…+ rn. При параллельном же соединении полное сопротивление цепи будет меньше самого малого из сопротивлений ветвей. Для такого включения верна формула: 1 / R = 1 / r1 + 1 / r2 +…+ 1 / rn.
Принцип расчёта смешанного соединения построен на группировке электрической цепи по виду подключения элементов. Определение параметра выполняют поочерёдно. Сначала высчитывают сопротивление одного узла, включающего однотипное соединение, затем к результату добавляют следующий элемент. Эту операцию повторяют до тех пор, пока не останется один элемент.
В радиотехнике деталь, применяющуюся в качестве сопротивления, называют резистором. С его помощью обозначают и так называемый эквивалентный параметр, используемый при расчётах электрических цепей. Его вводят, если нужно определить, например, мощность источника тока, выходное напряжение.
Таким образом, чтобы правильно посчитать сопротивление, нужно учитывать несколько факторов. При этом нужно помнить о единой системе измерений. Следует придерживаться СИ. Все величины, используемые в формулах, должны подставляться в стандартных единицах измерения. Почти во всех таблицах значение удельного сопротивления даётся в мм2/м, что связано с измерением площади.
Примеры решения задач
Решение примеров позволяет лучше разобраться в теме. При этом не только быстрее запоминаются формулы, но и становится понятным, где можно использовать полученные знания. Существует ряд заданий для самостоятельной проработки. Вот некоторые из них:

- На катушку электромагнита намотан медный провод сечением 0,003 мм2 длиною 200 метров. Найти сопротивление и массу обмотки. Для решения задачи нужно воспользоваться справочником по электрофизике. Из него взять значение удельного сопротивления меди и её плотность. Согласно справочным данным: p = 1,7 * 10−8 Ом * м, а V = 8900 кг/м3. В первом действии нужно определить массу. Для этого выразить её из формулы f = m / V и подставить заданные значения: m = V * f = l * S * f = 2 * 10|2 м * 3 * 10-8 м2 8,9 * 103 кг/м3 = 53,4 грамма. Теперь можно определить искомое сопротивление по формуле: R = (f * l) / S = (0,017 (Ом * мм2) / м * 200 м) / 0,03 мм2 = 3,4 / 0,003 = 113 Ом.
- Нужно изготовить провод длиною 100 метров и сопротивлением 1 Ом. Определить, из какого материала вес изделия будет меньше: меди или алюминия. Нужно вычислить, чему будет равно отношение масс: MCu / MAl. Из справочника взять данные: fAl = 2700 кг/м3; fCu = 8900 кг/м3; pAl = 2,8 * 10−8 Ом/м; pCu = 1,7 10−8 Ом/м. Для решения нужно выразить массы через плотность, длину и площадь поперечного сечения: m = f *l * S. Длина одинаковая, значит, отношения масс примет вид: (fCu * SCu) / (fAl * SAl). Площадь поперечного сечения будет вычисляться из правила нахождения сопротивления. Конечная формула примет вид: MCu / Mal = (fCu * RCu) / (fAl * RAl) = (8900 * 1,7) / (2700 * 2,8) = 2. Изделие из алюминия будет весить в 2 раза меньше.
- Имеется электрическая цепь, подключённая к сети 120 В. Если к ней подключить 2 последовательных сопротивления ток будет равен 3 A, а если параллельно — 16 А. Найти сопротивление. Задача решается с помощью закона Ома и формул вычисления сопротивления цепи: Iпосл = U / (r1 + r2); Iпар = U * (r1 + r2) / r1 * r2. Из них можно выразить искомые величины: r1 + r2 = U /Iпосл и r1 * r2 = U2 / Iпар * Iпос. Выполнив вычисления, можно найти, что r1 = 30 Ом, r2 = 10 Ом.
Решение заданий по теме обычно не вызывает трудностей. Нужно лишь внимательно переводить единицы измерения, знать формулы и иметь радиофизический справочник.
Расчёт сопротивления проводника. Удельное сопротивление вещества
План урока
- Сопротивление проводника. Удельное сопротивление вещества
- Примеры решения задач
Цели урока
- Знать: как зависит сопротивление проводника от его длины, площади поперечного сечения и материала; физический смысл удельного электрического сопротивления; формулу для расчета сопротивления проводника
- Уметь: рассчитывать электрическое сопротивление проводника; выражать из формулы для расчета сопротивления проводника неизвестные величины
Разминка
- Как сила тока зависит от сопротивления?
- Какой проводник будет обладать большим сопротивлением: имеющий большую длину или меньшую?
- Будут ли одинаковы сопротивления двух проводников одинаковых размеров, но изготовленных из разных материалов?
Сопротивление проводника. Удельное сопротивление вещества
Мы уже знаем, что сила тока обратно пропорциональна сопротивлению проводника, а сопротивление зависит от геометрических размеров и материала проводника. Рассмотрим подробнее, как зависит сопротивление от длины проводника и площади его поперечного сечения.
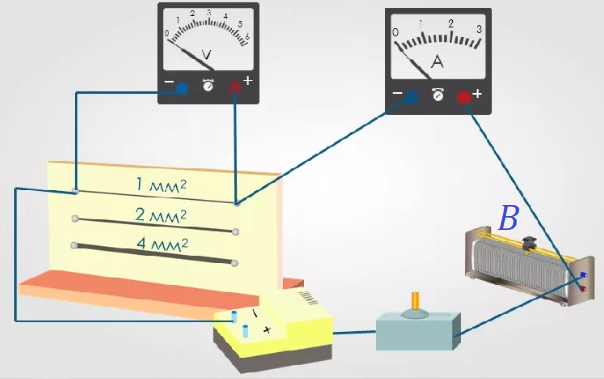
Рис. 1. Схема установки для определения зависимости сопротивления от длины проводника и площади его поперечного сечения
Соберем установку, состоящую из источника тока, резистора В, ключа, амперметра, вольтметра и трех проволочных проводников (рис. 1).
Используемые проводники изготовлены из одинакового материала, имеют одинаковую длину, но разную толщину – разную площадь поперечного сечения S.
Поэтапно включая в цепь каждый из проволочных резисторов и снимая показания амперметра, можно увидеть, что наибольшее значение силы тока будет отмечено при включении проводника наибольшего поперечного сечения, наименьшее – при включении проводника наименьшей толщины. Получается, что проводник с наибольшей площадью поперечного сечения обладает наименьшим сопротивлением.
Это легко объяснить, если вспомнить, что электроны при прохождении через проводник сталкиваются с положительными ионами в узлах кристаллической решетки. Чем больше площадь поперечного сечения, тем больше электронов смогут пройти через это сечение в единицу времени. Таким образом, чем больше площадь поперечного сечения проводника S, тем меньше его сопротивление.
Сопротивление проводника R обратно пропорционально площади его поперечного сечения S.
Для определения зависимости сопротивления проводника от его длины воспользуемся резистором В. В верхней части резистора расположен ползунок, который позволяет изменять длину той части проводника, по которой протекает ток.
Изменяя длину рабочей части резистора, можно убедиться, что при увеличении ее длины сила тока в цепи уменьшается и наоборот: при уменьшении длины рабочей части проводника сила тока растет. Значит, сопротивление проводника увеличивается вместе с увеличением его длины. Зависимость сопротивления проводника от его длины применяется в таких приборах, как реостаты, для регулирования силы тока в цепи.
Сопротивление проводника R прямо пропорционально его длине l.
Резистор, сопротивление которого можно при необходимости изменять, получил название
реостат
.

Рис. 2. Реостат и его условное обозначение в электрической цепи
Данную зависимость также легко объяснить с точки зрения внутреннего строения проводника: чем длиннее проводник, тем с большим количество положительных ионов придется столкнуться электронам при движении через него, тем сильнее снизится их скорость.
Простейший реостат представляет собой проволоку из материала с большим удельным сопротивлением, намотанную, например, на керамический цилиндр. Стоит обратить внимание на то, что сила тока, текущего через реостат, не должна превышать наибольшее допустимое для него значение, в противном случае реостат перегорит.
Сопротивление проводника определяется не только его геометрическими параметрами, но и внутренним строением. Так как все вещества имеют разное внутреннее строение, все металлы будут иметь разную способность проводить электричество.
Физическая величина, учитывающая проводимость вещества, из которого изготовлен проводник, называется удельное сопротивление проводника ρ.
Удельное сопротивление проводника ρ
– это сопротивление проводника, имеющего длину 1 метр и площадь поперечного сечения 1 мм2.
Исходя из определения удельного сопротивления проводника становится ясно, что для расчета сопротивления всего проводника R необходимо удельное сопротивление умножить на его длину l и разделить на площадь поперечного сечения S:
R=ρlS,
где R [Ом] – сопротивление проводника;
ρ [Ом ∙ мм2/м] – удельное сопротивление проводника;
l [м] – длина проводника;
S [мм2] – площадь поперечного сечения проводника.
Обратите внимание, что удельное сопротивление в связи с малыми значениями площади поперечного сечения проводников S удобно рассчитывать на площадь, измеряемую в мм2. При решении задач значение площади S обязательно должно быть выражено в квадратных миллиметрах. В системе СИ размерность удельного сопротивления будет равна Ом ∙ м, поэтому при использовании табличных значений или при решении задач внимательно следите за размерностью удельного сопротивления.
В таблице 1 приведены значения удельных сопротивлений некоторых веществ.
Таблица 1. Удельное электрическое сопротивление некоторых веществ при нормальных условиях
|
Вещество |
ρ, Ом ∙ мм2/м |
Вещество |
ρ, Ом ∙ мм2/м |
|
Серебро |
0,016 |
Манганин |
0,44 |
|
Медь |
0,017 |
Константан |
0,5 |
|
Золото |
0,024 |
Ртуть |
0,96 |
|
Алюминий |
0,028 |
Нихром |
1,1 |
|
Вольфрам |
0,055 |
Фехраль |
1,3 |
|
Железо |
0,1 |
Фарфор |
1012 |
|
Свинец |
0,21 |
Никелин |
0,43 |
Примеры решения задач
Пример 1
Определите длину железного провода площадью поперечного сечения 0,05 мм2, если сопротивление такого проводника равно 30 Ом.
Решение
Из таблицы 1 находим удельное сопротивление железа: ρ= 0,1 Ом ∙ мм2/м.
Из формулы для расчета сопротивления всего проводника выражаем искомую длину:
l=R·Sρ=30·0,050,1=15 м.
Ответ: 15 м.
Пример 2
Найти напряжение на серебряном проводнике длиной 8 м и площадью поперечного сечения 0,25 мм2, если сила тока в цепи равна 5 А.
Решение
Из таблицы 1 находим удельное сопротивление серебра:
ρ = 0,016 Ом ∙ мм2/м.
По формуле находим сопротивление проводника:
R=ρlS=0,01680,25=0,512 Ом.
Из закона Ома находим напряжение:
U=I·R=5·0,512=2,56 В.
Ответ: 2,56 В.
Итоги
Удельное сопротивление проводника ρ
– это сопротивление проводника, имеющего длину 1 метр и площадь поперечного сечения 1 мм2;- Сопротивление проводника прямо пропорционально удельному электрического сопротивлению и длине проводника, но обратно пропорционально площади его поперечного сечения: R=ρlS.
Упражнение 1
1. Во сколько раз изменится электрическое сопротивление проводника, если площадь его поперечного сечения уменьшить в 4 раза, а длину уменьшить в 2 раза?
2. Определите сопротивление медного провода длиной 10 м и площадью поперечного сечения 0,2 мм2.
3. Найдите силу тока, протекающего через алюминиевый проводник длиной 5 м и площадью поперечного сечения 0,14 мм2. Напряжение на концах проводника 200 В.
Контрольные вопросы
1. По какой формуле рассчитывается электрическое сопротивление проводника?
2. Что такое удельное электрическое сопротивление?
3. Как изменится сила тока в цепи, если увеличить длину проводника?
Ответы
Упражнение 1
1. Увеличится в 2 раза.
2. 0,85 Ом.
3. 200 А.
Закон Ома для участка цепи связывает три величины: $I = frac{U}{R}$. Эти величины: сила тока, напряжение и сопротивление. Сила тока в проводнике и напряжение на его концах могут изменяться. Они прямо пропорциональны друг другу. Также вы знаете, что сила тока в проводнике и сопротивление связаны между собой обратной пропорциональностью.
Но дело в том, что электрическое сопротивление — величина в законе Ома постоянная. При изменениях силы тока или напряжениях она не изменяется. Сопротивление зависит исключительно от свойств проводника.
На данном уроке мы рассмотрим, от каких именно свойств проводника зависит его сопротивление, введем понятие «удельное сопротивление» и сравним его значения для разных веществ.
Опыты по установлению величин, от которых зависит сопротивление
Причина электрического сопротивления кроется во взаимодействии электронов с ионами кристаллической решетки металла. Логично предположить, что сопротивление будет зависеть от рода вещества, из которого он состоит. Также мы предположим, что есть некоторая зависимость от длины проводника и площади его поперечного сечения.
Теперь давайте проведем опыты, которые подтвердят или опровергнут наши предположения.
Соберем электрическую цепь из источника тока, ключа, амперметра и реостата. Реостат — это прибор, который позволит нам изменять силу тока в цепи. Подробнее о нем вы узнаете в отдельном уроке.
В эту цепь мы будем поочередно подключать различные проводники. К ним же параллельно подсоединим вольтметр (рисунок 1).
Какие проводники мы будем подключать в цепь?
Вариантов может быть огромное множество. Мы рассмотрим следующие:
- Никелиновые проволоки одинаковой толщины (с одинаковой площадью поперечных сечений), но разной длины
- Такие же никелиновые проволоки, но теперь одинаковой длины и разной толщины (с различной площадью поперечных сечений)
- Никелиновую и нихромовую проволоки одинаковой длины и толщины
Каждый раз мы будем фиксировать значения силы тока в цепи, показанные амперметром. Вольтметр даст нам значения напряжения на концах каждого проводника.
Далее, используя закон Ома для участка цепи, мы сможем рассчитать сопротивление каждого проводника по формуле $I = frac{U}{R}$.
Результаты опытов
Какие выводы мы сможем сделать после всех расчетов?
- Из двух никелиновых проволок с одинаковой толщиной большее сопротивление имеет более длинная проволока
- Большее сопротивление имеет та никелиновая проволока, у которой поперечное сечение меньше. При этом длина проволок была одинаковой
- Никелиновая и нихромовая проволоки имеют разное сопротивление при одинаковых размерах
Зависимость сопротивления проводника от его размеров и вещества, из которого он состоит
Как зависит сопротивление проводника от его длины и от площади поперечного сечения?
Подобные опыты впервые проводил уже известный нам Георг Ом. Именно он установил следующие зависимости.
Сопротивление прямо пропорционально длине проводника, обратно пропорционально площади его поперечного сечения и зависит от вещества проводника.
Удельное сопротивление
Если с длиной и толщиной проводника все просто и понятно, то что с веществом, из которого он состоит? Как учесть эту зависимость значения сопротивления? Для этого нужно вычислить удельное сопротивление вещества (проводника).
Что называется удельным сопротивлением проводника?
Удельное сопротивление — это физическая величина, которая определяет сопротивление проводника из данного вещества длиной $1 space м$ и площадью поперечного сечения $1 space м^2$.
Обозначается удельное сопротивление буквой $rho$.
Не путать с плотностью вещества! Обращайте внимание на единицы измерения, чтобы не запутаться. Плотность в СИ измеряется в $frac{кг}{м^3}$, а про единицу измерения удельного сопротивления мы поговорим чуть ниже.
По какой формуле можно рассчитывать сопротивление проводников?
Используя новую величину, теперь мы можем вычислить сопротивление любого проводника.
$R = frac{rho l}{S}$,
где $rho$ — удельное сопротивление проводника, $l$ — длина проводника, $S$ — площадь его поперечного сечения.
Из этой формулы для расчетов мы можем выразить и другие величины:
$l = frac{RS}{rho}$,
$S = frac{rho l}{R}$,
$rho = frac{RS}{l}$.
Единица удельного сопротивления
Чтобы определить единицу измерения удельного сопротивления обратимся к формуле $rho = frac{RS}{l}$.
Единица сопротивления — $1 space Ом$, площади поперечного сечения — $1 space м^2$, длины — $1 space м$.
Подставим все это в формулу:
$[rho] = frac{1 space Ом cdot 1 space м^2}{1 space м} = 1 space Ом cdot м$.
Площадь поперечного сечения проводника обычно небольшая, поэтому ее удобно выражать в $мм^2$. Поэтому часто удельное сопротивление проводника измеряют в $frac{1 space Ом cdot 1 space мм^2}{1 space м}$.
Значения удельных сопротивлений некоторых веществ
В таблице 1 приведены значения удельных сопротивлений некоторых веществ.
| Вещество | $rho$, $frac{Ом cdot мм^2}{м}$ | Вещество | $rho$, $frac{Ом cdot мм^2}{м}$ |
| Серебро | $0.016$ | Манганин (сплав) | $0.43$ |
| Медь | $0.017$ | Константан (сплав) | $0.50$ |
| Золото | $0.024$ | Ртуть | $0.96$ |
| Алюминий | $0.028$ | Нихром (сплав) | $1.1$ |
| Вольфрам | $0.055$ | Фехраль (сплав) | $1.3$ |
| Железо | $0.10$ | Графит | $13$ |
| Свинец | $0.21$ | Фарфор | $10^{19}$ |
| Никелин (сплав) | $0.40$ | Эбонит | $10^{20}$ |
Обратите внимание, что эти значения актуальны при температуре $20 space degree C$.
Удельное сопротивление вещества зависит от температуры.
Опыты показали, что при определенной температуре для каждого вещества диэлектрик может стать проводником (полупроводник). Также экспериментально доказано, что с повышением температуры удельное сопротивление металлов увеличивается.
Использование веществ для изготовления проводников и изолятов
У каких веществ самые большие значения удельного сопротивления? Конечно, у диэлектриков. Например, эбонит и фарфор практически не проводят электрический ток. Поэтому их и используют в качестве изоляторов.
Самое меньшее удельное сопротивление имеют чистые металлы. Серебро и медь — лучшие проводники электричества.
Из каких веществ изготавливают проводники, применяемые на практике? Чаще всего для проводки электрических цепей используют медные, алюминиевые и железные провода.
В таблице 1 вы также могли обратить внимание на значения удельных сопротивлений для сплавов нескольких веществ. Они имеют достаточно большие значения. Зачем? Обычно их используют для изготовления приборов, которым необходимо для нормального функционирования иметь большое сопротивление, но все-таки пропускать ток.
Для изучения зависимости электрических параметров соберём электрическую цепь, изображённую на схеме (рис.(1)).
Состав схемы (по часовой стрелке по ходу электрического тока):
- источник электрического напряжения (тока);
- электрический ключ для размыкания;
- последовательно подключённый амперметр для измерения силы тока в цепи;
- сопротивление (спираль никелиновой проволоки);
- вольтметр, подключённый параллельно к сопротивлению.

Рис. (1). Первая схема электрической цепи
При замыкании цепи отметим показания приборов. Используя регулятор напряжения на источнике, изменим напряжение в два раза. При этом показания вольтметра и амперметра также изменятся в два раза. Продолжим увеличивать напряжение на источнике. Наблюдения показывают, что при увеличении напряжения в (3) раза, вольтметр покажет увеличение напряжения на спирали в три раза. Во столько же раз увеличится и сила тока.
Опыт показывает зависимость изменения силы тока от приложенного напряжения.
Сила тока в проводнике прямо пропорциональна напряжению на концах проводника: (Ibacksim U).
Эту зависимость можно изобразить графически:
Рис. (2). График зависимости силы тока в проводнике от напряжения между концами этого проводника
При включении в электрическую цепь источника тока различных проводников и амперметров увидим, что для разных проводников показания амперметров различны, значит, сила тока для каждого проводника отличается.

Рис. (3). Электрическая схема с набором различных сопротивлений (AB), (CD), (EF)
Графики тоже будут отличаться.

Рис. (4). Графики зависимости силы тока от напряжения для сопротивлений (AB), (CD), (EF)
Вольтметр подключим поочерёдно к концам этих проводников. Увидим равные значения напряжения. Значение силы тока на участке цепи пропорционально разности потенциалов на его концах и зависит от рода вещества проводника. Отличие электрических параметров (U) и (I) связано с тем, что проводники имеют разное электрическое сопротивление.
Сопротивление проводника равно (1) Ом, если в проводнике при напряжении на концах (1) вольт протекает сила тока (1) ампер:
([R]=1) Ом;
(R=frac{U}{I});
Единицы измерения применяют с кратными приставками: миллиом (мОм), килоом (кОм), мегаом (МОм).
(1) мОм = (0,001) Ом;
(1) кОм = (1000) Ом;
(1) МОм = (1 000 000) Ом.
Почему существует сопротивление? Движению электронов под действием поля мешают ионы кристаллической решётки металла.
Электрический ток — направленное движение заряженных частиц.
В середине (XIX) века Джеймс Кларк Максвелл объединил исследования Вольта, Эрстеда, Ампера, Ома, Фарадея в классическую электродинамику. Учёные придерживались гипотезы, что электричество переносят положительные частицы. Все законы строились на этом предположении.
За направление электрического тока принимают движение положительно заряженных частиц.
(29) апреля (1897) года Джозеф Джон Томсон выступил на заседании Королевского общества с докладом о катодных лучах, что и считается датой открытия электрона.
Электронный ток — направленное движение электронов.
В металлах электрический ток переносится электронами. Положительные ионы, связанные узлами кристаллической решётки, перемещаться не могут. Электроны, перемещаясь между ионами, сталкиваются с ними, отскакивают обратно, что уменьшает общий поток электронов.
Электрическое сопротивление — физическая величина, отражающая свойство проводника препятствовать электронному току.
(R=frac{U}{I});
([R]=1~frac{В}{А}=1~Ом).
Чтобы узнать, как зависит сила тока в цепи от сопротивления, обратимся к опыту (рис.(4)).

Рис. (5). Электрическая цепь с аккумулятором
На рисунке изображена электрическая цепь, источником тока в которой является аккумулятор.
- Напряжение (2) В на концах резисторов постоянно. Это подтверждают показания вольтметра, подключенного параллельно к резистору.
- Используются три постоянных резистора сопротивлениями (1), (2) и (4) Ом, которые подключаются в цепь поочерёдно.
- Сила тока в цепи измеряется амперметром, который подключен последовательно с резистором.
Таблица (1). Результаты опыта
| Напряжение на концах проводника, В | Сопротивление проводника, Ом | Сила тока в цепи, А |
|
(2) |
(1) |
(2) |
|
(2) |
(2) |
(1) |
|
(2) |
(4) |
(0,5) |
По опытным данным (табл.(1)) прослеживается закономерность, которую обнаружил ещё в (1827) году Георг Ом.
Сила тока в проводнике обратно пропорциональна сопротивлению проводника: (Ibacksim frac{1}{R}).
В честь этого ученого открытый им закон называют его именем — закон Ома для участка цепи.
Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению участка цепи:
где I — сила тока, U — напряжение, R — сопротивление.
При изменяющемся сопротивлении и постоянном напряжении на участке зависимость силы тока от сопротивления будет гиперболической:

Рис. (6). График зависимости силы тока от сопротивления проводника
Определить сопротивление проводника можно несколькими способами:
1. при помощи амперметра и вольтметра;
2. при помощи омметра;
3. при помощи мультиметра, который эксплуатируется в режиме омметра.
Таблица (2). Способы измерения сопротивления
|
амперметр и вольтметр |
омметр |
мультиметр в режиме омметра |
|
Рис. 7. Амперметр и вольтметр |
Рис. 8. Омметр |
Рис. 9. Мультиметр |
|
|
|
|

Рис. 10. Обозначение омметра в цепи (или мультиметра в режиме измерения сопротивления)
Источники:
Рис. 2. График зависимости силы тока в проводнике от напряжения между концами этого проводника. © ЯКласс.
Рис. 4. Графики зависимости силы тока от напряжения для сопротивлений AB, CD, EF. © ЯКласс.
Рис. 6. График зависимости силы тока от сопротивления проводника. © ЯКласс.
Рис. 7. Старые советские измерительные приборы, Creative Commons Zero 1.0 License, https://openclipart.org/detail/205486/voltmeter-and-ammeter.
Рис. 8. Автор: Сергин Владимир Александрович – Собственный фотоснимок автора, Общественное достояние, https://commons.wikimedia.org/w/index.php?curid=4353228.
Рис. 9. Мультиметр. © ЯКласс.
Рис. 10. Указание авторства не требуется: 2021-06-07, бесплатно для коммерческого использования, https://clck.ru/VLDy3/.



