Как найти сопротивление проводника примеры

Задачи на Сопротивление проводников с решениями

Формулы, используемые на уроках «Задачи на сопротивление проводников»:

Название величины	Обозначение	Единица измерения	Формула
Сила тока	I	А	I = U / R
Напряжение	U	В	U = IR
Сопротивление	R	Ом	R = U/I
Длина проводника	l	м	l = RS / p
Площадь поперечного сечения проводника	S	мм2	S = pl / R
Удельное сопротивление вещества	p	Ом • мм2 /м Ом • м	p = RS / l
Сопротивление проводника	R	Ом	R = pl / S

Площадь поперечного сечения измеряют в мм², поэтому в справочниках значения удельного сопротивления проводника приводятся не только в единицах СИ Ом • м, но в Ом • мм² / м.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

---

Задача № 1.
 Длина алюминиевого провода 500 м, площадь его поперечного сечения 4 мм² , Чему равно сопротивление провода?

---

Задача № 2.
 Медный провод с площадью поперечного сечения 0,85 мм² обладает сопротивлением 4 Ом. Какова длина провода?

---

Задача № 3.
 Длина серебряного провода 0,6 м, а сопротивление 0,015 Ом. Определите площадь поперечного сечения провода.

---

Задача № 4.
 Жила алюминиевого провода, используемого для электропроводки, имеет площадь поперечного сечения 2 мм². Какой площадью поперечного сечения должен обладать никелиновый провод, чтобы длина и сопротивление линии не изменились?

---

Задача № 5.
 Площади поперечных сечений стальных проволок с одинаковыми длинами равны 0,05 и 1 мм². Какая из них обладает меньшим сопротивлением; во сколько раз?

---

Задача № 6.
 Сопротивление проволоки длиной 1 км равно 5,6 Ом. Определите напряжение на каждом участке проволоки длиной 100 м, если сила тока в ней 7 мА.

---

Задача № 7.
 Имеются два однородных проводника, однако первый в 8 раз длиннее второго, который имеет вдвое большую площадь поперечного сечения. Какой из проводников обладает большим сопротивлением; во сколько раз?

---

Задача № 8.
 Шнур, употребляемый для подводки тока к телефону, для гибкости делают из многих тонких медных проволок. Рассчитайте сопротивление такого провода длиной 3 м, состоящего из 20 проволок площадью поперечного сечения 0,05 мм² каждая.

---

Задача № 9.
 Определите силу тока, проходящего через реостат, изготовленный из никелиновой проволоки длиной 50 м и площадью поперечного сечения 1 мм², если напряжение на зажимах реостата равно 45 В.

---

Задача № 10.
Сопротивление проволоки, у которой площадь поперечного сечения 0,1 мм², равно 180 Ом. Какой площади поперечного сечения надо взять проволоку той же длины и из того же материала, чтобы получить сопротивление 36 Ом?

---

Краткая теория для решения
Задачи на Сопротивление проводников.

Таблица удельного электрического сопротивления
некоторых веществ при 20 °С.

---

Это конспект по теме «ЗАДАЧИ на Сопротивление проводников». Выберите дальнейшие действия:

• Перейти к теме: ЗАДАЧИ на Последовательное соединение проводников
• Посмотреть конспект по теме Электрическое сопротивление
• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Общие сведения

Упорядоченное движение носителей заряда в физическом теле называют электрическим током. Ими могут быть различные элементарные частицы. Например, в проводниках — электроны, электролитах — ионы. В состоянии покоя, то есть когда на тело не оказывается постороннее воздействие, движение носителей хаотичное. В результате происходит компенсирование зарядов, и ток не возникает. Если же к веществу приложить силу или деформировать его, направление движения частиц станет упорядоченным и возникнет электрический ток.

Все существующие вещества характеризуются физическими и химическими свойствами. Среди них и проводимость. Это электрическая величина, определяющая способность тела пропускать через себя ток. По своему строению все материалы делятся на 3 класса:

• проводники — вещества, не оказывающие сопротивление прохождению тока;
• полупроводники — тела, в которых величина проводимости зависит от чистоты материала, температуры и вида воздействующего излучения;
• диэлектрики — вещества, практически не проводящие электрический ток.

Величина, обратная проводимости, называется сопротивлением. Это параметр, который характеризует способность материала пропускать через себя электрический ток без потерь. Другими словами, для идеального тела количество электричества, поступившего и снятого с него, будет одинаковым.

За единицу измерения силы тока принят Ампер, показывающий, какое количество электричества проходит через поперечное сечение проводника за одну секунду: I = q / t = кулон / секунду = ампер.

Электрическое сопротивление тела зависит от природы носителей заряда и геометрии материала. Это скалярный параметр. При его расчёте используют понятие удельное сопротивление. Выражают его в омах, умноженных на метр, и обозначают греческой буквой р. По физическому смыслу величина является обратным параметром удельной проводимости.

С ней, кроме сопротивления и силы тока, тесно связано и напряжение. С физической точки зрения, это работа, которую выполняет электрическое поле при переносе единичного заряда из одной точки в другую. В Международной системе величин напряжение принято обозначать в вольтах: U = f2- f1, где f — значения потенциала заряда в точках.

Формула сопротивления

Ток обусловлен движением электронов. Классическая формула, используемая для расчёта его силы была выведена немецким физиком Омом. Он на опыте смог подтвердить зависимость между собой тока, сопротивления и напряжения. В математическом виде связь записывают в виде формулы: I = U /R.

Согласно закону Ома, сопротивление тела электрическому току прямо пропорционально его силе и обратно пропорционально напряжению: R = I / U. Это эмпирическая формула справедлива для любого участка цепи.

Подвижные носители при хаотичном движении ведут себя как молекулы газа, поэтому в первом приближении физики считают носителей зарядов своего рода электронным газом. Как было установлено эмпирически, плотность этого газа и строение кристаллической решётки зависят от рода проводника. Соответственно, проводимость, а значит и сопротивление, определяется также и родом вещества. В свою очередь, физическое тело характеризуется и геометрическими параметрами.

Влияние размеров полупроводника объясняется зависимостью от них поперечного сечения. При его уменьшении поток зарядов становится плотнее, степень взаимодействия между частицами возрастает. Полная формула сопротивления проводника с учётом поперечного сечения выглядит так: R = (p * l) / S. Из неё становится ясно, что проводимость прямо пропорциональна площади сечения и обратно пропорциональна длине проводника.

Удельное электрическое сопротивление для многих веществ было установлено во время исследований. Существуют таблицы, в которые занесены данные, измеренные при температуре 20 градусов Цельсия. Ими часто пользуются при решении различных задач, связанных с электричеством. Вот некоторые из них:

• олово — 9,9 * 10^-8 Ом * мм²/м;
• медь — 0,01724 Ом * мм²/м;
• алюминий — 0,0262 Ом * мм ²/м;
• железо — 0,098 * Ом * мм²/м;
• золото — 0,023 Ом * мм²/м.

Для проводников характерно увеличение сопротивления при росте температуры. Это связано с колебаниями атомов. В то же время с ростом температуры проводимость в полупроводниках и диэлектриках возрастает из-за увеличения концентрации носителей заряда.

Удельное сопротивление для неоднородного материала можно вычислить по формуле: p = E / J. Где: E и J напряжённость и плотность тока в конкретной точке.

Нахождение параметра

Найти сопротивление — значит, рассчитать потери тока. Существует 2 принципиально разных подхода к расчёту. В одном случае он ведётся для электрической цепи, а в другой — для материала. Если во втором случае всё предельно понятно, используется одна формула, в которую подставляют размеры тела и табличное значение удельной проводимости, то для электрической цепи не так всё просто.

В цепи может встречаться 3 вида соединения элементов:

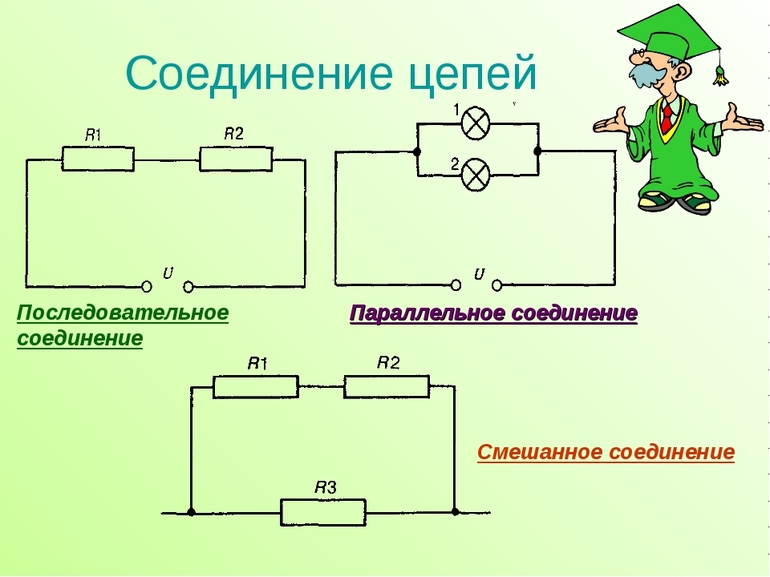
1. Параллельное. При таком соединении цепь разветвляется, то есть появляются ветви, по которым течёт ток. Ветви могут пересекаться между собой.
2. Последовательное. Схема соединения представляет единую цепь, в которой нет разветвлений.
3. Смешанное. Состоит из комбинированного соединения, включающего комбинации из параллельного и последовательного подключения.

Вычисление сопротивления для каждого типа соединения имеет особенности. При последовательном включении общее значение определяется путём простого складывания: R = r1 + r2 +…+ rn. При параллельном же соединении полное сопротивление цепи будет меньше самого малого из сопротивлений ветвей. Для такого включения верна формула: 1 / R = 1 / r1 + 1 / r2 +…+ 1 / rn.

Принцип расчёта смешанного соединения построен на группировке электрической цепи по виду подключения элементов. Определение параметра выполняют поочерёдно. Сначала высчитывают сопротивление одного узла, включающего однотипное соединение, затем к результату добавляют следующий элемент. Эту операцию повторяют до тех пор, пока не останется один элемент.

В радиотехнике деталь, применяющуюся в качестве сопротивления, называют резистором. С его помощью обозначают и так называемый эквивалентный параметр, используемый при расчётах электрических цепей. Его вводят, если нужно определить, например, мощность источника тока, выходное напряжение.

Таким образом, чтобы правильно посчитать сопротивление, нужно учитывать несколько факторов. При этом нужно помнить о единой системе измерений. Следует придерживаться СИ. Все величины, используемые в формулах, должны подставляться в стандартных единицах измерения. Почти во всех таблицах значение удельного сопротивления даётся в мм²/м, что связано с измерением площади.

Примеры решения задач

Решение примеров позволяет лучше разобраться в теме. При этом не только быстрее запоминаются формулы, но и становится понятным, где можно использовать полученные знания. Существует ряд заданий для самостоятельной проработки. Вот некоторые из них:

1. На катушку электромагнита намотан медный провод сечением 0,003 мм² длиною 200 метров. Найти сопротивление и массу обмотки. Для решения задачи нужно воспользоваться справочником по электрофизике. Из него взять значение удельного сопротивления меди и её плотность. Согласно справочным данным: p = 1,7 * 10−8 Ом * м, а V = 8900 кг/м3. В первом действии нужно определить массу. Для этого выразить её из формулы f = m / V и подставить заданные значения: m = V * f = l * S * f = 2 * 10|² м * 3 * 10^-8 м² 8,9 * 10³ кг/м³ = 53,4 грамма. Теперь можно определить искомое сопротивление по формуле: R = (f * l) / S = (0,017 (Ом * мм²) / м * 200 м) / 0,03 мм² = 3,4 / 0,003 = 113 Ом.
2. Нужно изготовить провод длиною 100 метров и сопротивлением 1 Ом. Определить, из какого материала вес изделия будет меньше: меди или алюминия. Нужно вычислить, чему будет равно отношение масс: MCu / MAl. Из справочника взять данные: fAl = 2700 кг/м3; fCu = 8900 кг/м3; pAl = 2,8 * 10−8 Ом/м; pCu = 1,7 10−8 Ом/м. Для решения нужно выразить массы через плотность, длину и площадь поперечного сечения: m = f *l * S. Длина одинаковая, значит, отношения масс примет вид: (fCu * SCu) / (fAl * SAl). Площадь поперечного сечения будет вычисляться из правила нахождения сопротивления. Конечная формула примет вид: MCu / Mal = (fCu * RCu) / (fAl * RAl) = (8900 * 1,7) / (2700 * 2,8) = 2. Изделие из алюминия будет весить в 2 раза меньше.
3. Имеется электрическая цепь, подключённая к сети 120 В. Если к ней подключить 2 последовательных сопротивления ток будет равен 3 A, а если параллельно — 16 А. Найти сопротивление. Задача решается с помощью закона Ома и формул вычисления сопротивления цепи: Iпосл = U / (r1 + r2); Iпар = U * (r1 + r2) / r1 * r2. Из них можно выразить искомые величины: r1 + r2 = U /Iпосл и r1 * r2 = U2 / Iпар * Iпос. Выполнив вычисления, можно найти, что r1 = 30 Ом, r2 = 10 Ом.

Решение заданий по теме обычно не вызывает трудностей. Нужно лишь внимательно переводить единицы измерения, знать формулы и иметь радиофизический справочник.

Сила тока в цепи определяется электрическим зарядом, проходящим через поперечное сечение проводника за единицу времени: $I = frac{q}{t}$.

Электрическое напряжение — это еще одна физическая величина, характеризующая электрическое поле. Она равна отношению работы тока на данном участке к электрическому заряду, прошедшему по этому участку: $U = frac{A}{q}$.

Электрическое сопротивление — величина, зависящая от свойств проводника. На значение сопротивления не влияет ни значение силы тока в проводнике, ни значение напряжения на его концах. Его можно рассчитать по формуле $R = frac{rho l}{S}$, где $rho$ — удельное сопротивление проводника,  $l$ — длина проводника, $S$ — площадь его поперечного сечения. Значение удельного сопротивления для определенного вещества можно посмотреть в таблице 1 в уроке «Расчет сопротивления проводника. Удельное сопротивление».

Эти три физические величины (силу тока, напряжение и сопротивление) связывает между собой закон Ома для участка цепи: $I = frac{U}{R}$. Сила тока в проводнике прямо пропорциональна напряжению на его концах и обратно пропорциональна его сопротивлению.

В данном уроке вы научитесь использовать эти знания для решения задач. Мы рассмотрим несколько примеров, а затем перейдем к упражнениям и их подробным решениям.

Пример задачи №1

Длина медного провода, использованного в осветительной сети, $100 space м$, площадь поперечного сечения его $2 space мм^2$. Чему равно сопротивление такого провода?

Для того, чтобы рассчитать сопротивление такого проводника, нам понадобится значение его удельного сопротивления. Удельное сопротивление меди равно $0.017 frac{Ом cdot мм^2}{м}$. Так как эта величина нам дана именно в этих единицах измерения, мы не будем переводить в СИ значение площади поперечного сечения, выраженное в $мм^2$.

Теперь мы можем записать условие задачи и решить ее.

Дано:
$l = 100 space м$
$S = 2 space мм^2$
$rho = 0.017 frac{Ом cdot мм^2}{м}$

$R — ?$

Решение:

Формула для расчета сопротивления проводника:
$R = frac{rho l}{S}$.

Рассчитаем его:
$R = frac{0.017 frac{Ом cdot мм^2}{м} cdot 100 space м}{2 space мм^2} = frac{1.7 space Ом}{2} = 0.85 space Ом$.

Ответ: $R = 0.85 space Ом$.

Пример задачи №2

Никелиновая проволока длиной $120 space м$ и площадью поперечного сечения $0.5 space мм^2$ включена в цепь с напряжением $127 space В$. Определить силу тока в проволоке.

Табличное значение удельного сопротивления никелина равно $0.4 frac{Ом cdot мм^2}{м}$.

Перейдем к записи условия задачи и ее решению.

Дано:
$l = 120 space м$
$S = 0.5 space мм^2$
$U = 127 space В$
$rho = 0.4 frac{Ом cdot мм^2}{м}$

$I — ?$

Решение:

Силу тока мы можем рассчитать, используя формулу закона Ома для участка цепи:
$I = frac{U}{R}$.

Но мы не знаем значения сопротивления проводника. Его мы тоже можем вычислить:
$R = frac{rho cdot l}{S}$,
$R = frac{0.4 frac{Ом cdot мм^2}{м} cdot 120 space м}{0.5 space мм^2} = frac{48 space Ом}{0.5} = 96 space Ом$.

Теперь мы можем рассчитать силу тока:
$I = frac{127 space В}{96 space Ом} approx 1.3 space А$.

Ответ: $I approx 1.3 space А$.

Пример задачи №3

Манганиновая проволока длиной $8 space м$ и площадью поперечного сечения $0.8 space мм^2$ включена в цепь аккумулятора. Сила тока в цепи $0.3 space А$. Определить напряжение на полюсах аккумулятора.

Табличное значение удельного сопротивления манганина равно $0.43 frac{Ом cdot мм^2}{м}$.

Запишем условие задачи и решим ее.

Дано:
$l = 8 space м$
$S = 0.8 space мм^2$
$I = 0.3 space А$
$rho = 0.43 frac{Ом cdot мм^2}{м}$

$U — ?$

Решение:

Если в условии задачи сказано, что проводник включен в цепь аккумулятора, это означает, что напряжение на полюсах аккумулятора будет равно напряжению на концах проволоки.

Почему? Взгляните на такую электрическую цепь (рисунок 1). Она состоит только из проводника и аккумулятора.

Если мы захотим измерить напряжение на полюсах аккумулятора c помощью вольтметра, то параллельно подключим его в эту цепь (рисунок 2). А если захотим измерить напряжение на концах проводника? Мы подключим вольтметр точно так же. Получается, что вольтметр подключен параллельно одновременно и к источнику тока, и к проводнику. Поэтому напряжение на концах проводника — это то же самое напряжение на полюсах аккумулятора.

Запишем закон Ома:
$I = frac{U}{R}$.

Выразим из него напряжение, которое нужно найти:
$U = IR$.

Сопротивление проводника рассчитаем по формуле $R = frac{rho cdot l}{S}$.
$R = frac{0.43 frac{Ом cdot мм^2}{м} cdot 8 space м}{0.8 space мм^2} = frac{3.44 space Ом}{0.8} = 4.3 space Ом$.

Теперь мы можем рассчитать напряжение:
$U = 0.3 space А cdot 4.3 space Ом = 1.29 space В approx 1.3 space В$.

Ответ: $U approx 1.3 space В$.

Упражнения

Обратите внимание, что если материал проводников один и тот же, то одинаковы и значения удельных сопротивлений $rho$ для этих проводников.

$frac{R_2}{R_1} — ?$

Показать решение и ответ

Скрыть

Для решения этой задачи нам понадобятся табличные значения удельного сопротивления для веществ, из которых изготовлены проволоки. Удельное сопротивление алюминия — $0.028 frac{Ом cdot мм^2}{м}$, никелина — $0.4 frac{Ом cdot мм^2}{м}$, константана — $0.5 frac{Ом cdot мм^2}{м}$.

Обратите внимание на единицы измерения удельных сопротивлений, длин и площадей проводников. Для корректных расчетов длину каждой проволоки мы переведем в СИ (в $м^2$). Площади поперечных сечений должны быть выражены в $мм^2$. Для третьего задания переведем $см^2$ в $см^2$.

$R_1 — ?$
$R_2 — ?$
$R_3 — ?$

Показать решение и ответ

Скрыть

Удельное сопротивление нихрома равно $1.1 frac{Ом cdot мм^2}{м}$.

Дано:
$l = 13.75 space м$
$S = 0.1 space мм^2$
$U = 220 space В$
$rho = 1.1 frac{Ом cdot мм^2}{м}$

$I — ?$

Показать решение и ответ

Скрыть

Для решения задачи нам понадобится значение удельного сопротивления. Для железа оно равна $0.1 frac{Ом cdot мм^2}{м}$.

$U — ?$

Показать решение и ответ

Скрыть

Физика — наука эмпирическая. Ее основные законы вытекают из практического опыта и частенько много лет не имеют теоретических обоснований. Именно так обстоит дело с главным законом электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом.

Электрические явления люди наблюдали сотни лет. Но никак не связывали между собой заряженность потертого янтаря и молнию. Только на исходе XVIII столетия электричество стали внимательно исследовать. В 1795 году Алессандро Вольта изобрел «вольтов столб», химическую батарею, и обнаружил появление тока в проводнике, соединяющем ее полюса. Сферы применения электричества стремительно множились, и появилась острая необходимость в расчетных формулах для инженеров. Эту задачу решали многие ученые, но первым сформулировал главную формулу электротехники именно Георг Ом. Он ввел в обиход понятие сопротивления и опытным путем установил зависимость между основными характеристиками электрической цепи.

Определение закона Ома простыми словами

Электрическая цепь состоит из двухполюсного источника напряжения, то есть батареи, аккумулятора или генератора. Если полюса источника соединить проводами, то по ним потечет электрический ток. Его величина определяется сопротивлением проводников. Наглядное представление этой зависимости — обыкновенный водопровод. Аналогом источника напряжения является насос или водонапорная башня, создающая давление в магистрали, количество воды, прошедшее по трубе, — подобие силы тока, а кран соответствует сопротивлению. Полностью открытый, он не ограничивает поток, по мере закручивания отверстие для воды уменьшается, пока не закроется совсем.

Закон Ома для участка цепи

Опытным путем исследователь установил взаимосвязь характеристик электрической цепи. Классическая формулировка закона Ома звучит так:

«Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению».

Формула закона Ома для участка цепи

В таком виде закон Ома приведен в школьных учебниках физики. Согласно этой простой формуле, для определения уровня тока в проводнике достаточно величину напряжения на его сторонах разделить на некий условно постоянный коэффициент, то есть на сопротивление. Почему «условно»? Потому что величина сопротивления может меняться в зависимости от температуры. Поэтому, кстати, лампы накаливания чаще всего перегорают при включении. Сопротивление холодной спирали ниже, чем нагретой, скачок тока при подаче напряжения вызывает ее резкое расширение и разрыв. Но если этот момент преодолен и нить накала уцелела, то ее сопротивление растет, и ток ограничивается. А при температуре жидкого гелия, например, сопротивление падает до нуля, наступает сверхпроводимость.

Закон Ома для замкнутой полной цепи

Предыдущая формулировка годится только для участка цепи, где отсутствует сам источник электродвижущей силы. В реальности ток течет по замкнутому контуру, где обязательно есть батарея или генератор, имеющий собственное внутреннее сопротивление. Поэтому формула закона Ома для полной цепи выглядит несколько сложнее

Формула закона Ома для замкнутой полной цепи

Применение закона Ома

Георг Ом дал в руки инженеров средство для решения задач, связанных с электрическими цепями. Тепловые и световые приборы, электродвигатели, генераторы, линии электропередач, кабели связи рассчитываются на основе этой простой формулы. Нет такой области электротехники, где она не находит применения. Даже в радиотехнике используется закон Ома, но в дифференциальной форме. «Все гениальное — просто», как считали Еврипид, Леонардо да Винчи, Наполеон Бонапарт и Альберт Эйнштейн, несомненные гении. Закон Ома целиком и полностью подтверждает эту истину.

Задача на закон Ома с решением

Задача для участка электрической цепи

Электрочайник, включенный в сеть с напряжением 220 В, потребляет ток 1,1 А. Каково сопротивление электрочайника.

Дано:
U = 220 В
I = 1,1 А

Решение:
Согласно закону Ома для участка цепи:
R=U/I=220/1,1=200 Ом

Ответ: R = 200 Ом.

Задача для полной замкнутой цепи

Источник постоянного тока с ЭДС E = 24 В и внутренним сопротивлением r = 1,5 Ом замкнут на внешнее сопротивление R = 11 Ом. Определить силу тока в цепи.

Дано:
Е=24 В, r=1,5 Ом, R = 11 Ом

Решение:
По закону Ома для замкнутой цепи: I = E/(R + r) = 24/(11+1,5) = 1,92 А.

Ответ: I=1, 92 А.

Популярные вопросы и ответы

Отвечает Николай Герасимов, старший преподаватель физики в Домашней школе «ИнтернетУрок».

Сопротивление в проводниках возникает из-за
взаимодействия электронов с ионами кристаллической решетки. Если вдуматься, то
можно заметить, что чем длиннее проводник, тем больше такое взаимодействие.

Также, логично предположить, что чем толще
проводник, тем больший поток электронов может пройти через поперечное сечение.

И, конечно, мы знаем, что разные вещества по-разному
проводят ток. Исходя из этих знаний, мы можем установить следующее:

Чем длиннее проводник, тем больше его
сопротивление.

Чем толще проводник, тем меньше его
сопротивление.

Сопротивления проводников одинаковой длины
и толщины могут быть различны, в зависимости от вещества.

Ну а как именно зависит сопротивление проводника от
его размеров, можно узнать только с помощью опытов. Мы уже немного знакомы с
методикой проведения подобных экспериментов: нам нужно провести некоторые
измерения, и, построив график, установить зависимость сопротивления от тех или
иных величин. Данные опыты были проведены Георгом Омом.

Подключим проводник к источнику тока и, с помощью
амперметра и вольтметра, измерим силу тока и напряжение. Мы используем, так
называемый, мультиметр — современный прибор, который выполняет функции
амперметра и вольтметра, в зависимости от настроек. Но, тем не менее, мы
по-прежнему должны следовать правилам: когда мы хотим измерить силу тока,
мультиметр подключается последовательно. На мультиметре есть переключатель
между режимами измерения той или иной величины. Также, когда мы хотим измерить
напряжение, мультиметр подключается параллельно. Используя закон Ома, мы можем
вычислить сопротивление данного проводника.

Подобным способом, мы можем вычислить сопротивление
проводников разной длины, но той же толщины, сделанных из того же материала.
Проведя несколько измерений, выясним, что сопротивление проводника
увеличивается ровно во столько раз, во сколько увеличивается его длина.

В таблице с данными можно увидеть незначительные
несоответствия. Однако, мелкие погрешности в измерениях, при проведении любого
опыта, неизбежны. Тем не менее, закономерность очевидна: сопротивление
проводника прямо пропорционально длине проводника. Это подтверждается и
графиком, который является прямой линией.

Проведем несколько иной опыт: сравним сопротивления
проводников из того же материала, одинаковой длины, но разной толщины.
Поскольку роль играет не сама толщина, а площадь поперечного сечения
проводника, то мы попытаемся выяснять, как зависит сопротивление именно от
этого параметра.

Полученные данные показывают, что на этот раз сопротивление
проводника обратно пропорционально площади поперечного сечения проводника.
Наш график зависимости сопротивления от поперечного сечения имеет форму ветви
гиперболы.

Как вы уже, наверное, догадались, удельное
сопротивление проводников из того или иного материала тоже вычисляется
экспериментальным путём. На этот раз, все проводники имеют одну и ту же длину и
толщину, но состоят из разного вещества.

Удельное сопротивление проводника — это
сопротивление проводника из данного вещества с площадью поперечного сечения 1 м²
и длиной 1 м. В таблице даны значения удельного
сопротивления для некоторых веществ.  

Однако, площадь поперечного сечения проводника удобнее
измерять в квадратных миллиметрах, поскольку это больше соответствует размерам
реальных проводников.

Итак, исходя из наших опытов, сопротивление
проводника прямо пропорционально длине проводника, обратно пропорционально
площади поперечного сечения и зависит от вещества:

Из формулы мы можем выразить удельное сопротивление и
определить его единицы измерения:

Упражнения.

Задача 1. Железный
провод длиной 250 м имеет площадь поперечного сечения 2 мм². Найдите
сопротивление данного провода.

Задача 2. Какое
напряжение должно быть на эбонитовом диске толщиной 1 мм, чтобы через него
прошел ток в 1 мкА? Диаметр диска составляет 1 см.

Мы видим, что даже для того, чтобы через эбонит прошел
очень маленький ток, нужно просто огромное напряжение. Такое напряжение создать
практически невозможно. Даже в современных ускорителях частиц достигалось
напряжение не больше нескольких ТВ. Поэтому, можно сказать, что мы не можем
провести ток через эбонит. Этого следовало ожидать, поскольку удельное
сопротивление эбонита огромно, и он является непроводником.

Задача 3. На
рисунке показан график зависимости силы тока на участке цепи от неизвестной
величины. Можете ли вы определить, что это за величина?

Итак, давайте вспомним, от чего вообще может зависеть
сила тока. В первую очередь, сила тока — это количество заряда, прошедшего
через поперечное сечение за единицу времени. Из формулы видно, что сила тока
находится в линейной зависимости от количества заряда в единицу времени, а на
рисунке мы видим график функции, который показывает нелинейную зависимость. Мы
знаем, что график функции, описывающий любую линейную зависимость, будет
являться прямой. Из формулы, описывающей закон Ома, мы видим, что сила тока
прямо пропорциональна напряжению. Значит, неизвестная величина не является ни
количеством заряда, ни напряжением. Сила тока обратно пропорциональна
сопротивлению. Однако, мы уже знаем, что график функции зависимости силы тока
от сопротивления представляет собой ветвь гиперболы, а на рисунке мы видим
другой график.

Тогда следует заметить, что сила тока зависит от
величин, которые, в свою очередь, зависят от других величин. Напряжение связано
с работой по переносу заряда, но эта зависимость тоже линейная. Рассмотрим, от чего
зависит сопротивление: от удельного сопротивления, от длины проводника и от
площади поперечного сечения. Удельное сопротивление для каждого проводника —
есть величина постоянная. Сопротивление находится в линейной зависимости от
длины проводника, длина проводника — это независимая величина. Остается площадь
поперечного сечения. Как раз-таки, она зависит не от радиуса, а от квадрата
радиуса проводника, что приводит нас к нелинейной зависимости. Если мы
преобразуем формулу, по которой вычисляется сила тока в проводнике, то увидим,
что сила тока прямо пропорциональна квадрату радиуса проводника. Это
единственная величина, которая могла привести к построению графика квадратичной
функции. Действительно, если мы внимательно изучим график, то убедимся, что это
парабола. Следует заметить, что это может быть график зависимости силы тока не
от радиуса, а от диаметра. Однако, для того, чтобы это проверить, нам нужна
дополнительная информация. Тем не менее, мы с уверенностью можем сказать, что
это график зависимости силы тока либо от радиуса, либо от диаметра проводника
(по форме эти два графика ничем не отличаются — существуют лишь числовые
отличия).