
На этой странице представлен самый простой онлайн калькулятор расчета сопротивления проводника по простой математической формуле в зависимости от длины, площади поперечного сечения и удельного сопротивления проводника. С помощью этой программы вы в пару кликов сможете рассчитать сопротивление проводника.
Вы так же можете воспользоваться калькулятором для расчета сечения кабеля по мощности и току.
Формула для расчета сопротивления провода: R=(ρ*l)/S
Где:
- R – сопротивление в Омах,
- ρ – удельное сопротивление,
- l – длина в м,
- S – площадь поперечного сечения провода в мм2.
Калькулятор расчета сопротивления проводника.
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ, длиной l и площадью поперечного сечения S может быть рассчитано по формуле:
где R — сопротивление, Ом; ρ — удельное сопротивление, (Ом•мм2)/м; l — длина провода, м; s — площадь сечения провода, мм2.
При этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника.
Если известен диаметр провода d, то площадь его сечения равна:
Для расчета сопротивления проводника можно воспользоваться онлайн калькулятором, выберите из списка металл или сплав проводника, укажите диаметр и длину проводника.
Все расчеты верны при температуре проводника +20 °C. Сопротивления сплавов зависят от их химического состава и могут варьироваться. Для чистых веществ колебания численных значений удельного сопротивления обусловлены различными методами механической и термической обработки, например, отжигом проволоки после волочения.
Для определения длины провода известного диаметра из данного материала, необходимой для получения нужного сопротивления, пользуются формулой:
Расчет сопротивления проводов на сайте rcl-radio.ru
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 января 2022 года; проверки требуют 6 правок.
| Электрическое сопротивление | |
|---|---|
 |
|
| Размерность |
L2MT −3I −2 (СИ); TL −1 (СГСЭ, гауссова система); LT −1 (СГСМ) |
| Единицы измерения | |
| СИ | Ом |
| СГСЭ | статом, с/см |
| СГСМ | абом, см/с |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
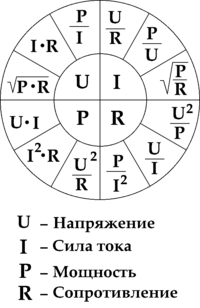
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойство проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему[1]
Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
где
- R — сопротивление, Ом (Ω);
- U — разность электрических потенциалов (напряжение) на концах проводника, Вольт (В);
- I — сила тока, протекающего между концами проводника под действием разности потенциалов, Ампер (А).
История[править | править код]
В 1826 г. Георг Ом экспериментальным путем открыл основной закон электрической цепи, научился вычислять сопротивление металлических проводников и вывел закон Ома. Таким образом, в первом периоде развития электротехники (1800 –1831 годы) были созданы предпосылки для ее развития, для последующих применений электрического тока.
Само понятие «сопротивление» появилось задолго до изысканий Георга Ома. Впервые этот термин применил и употребил русский ученый Василий Владимирович Петров. Он установил количественную зависимость силы тока от площади поперечного сечения проводника: он утверждал, что при использовании более толстой проволоки происходит «более сильное действие… и весьма скорое течение гальвани-вольтовской жидкости». Кроме того, Петров четко указал на то, что при увеличении сечения проводника (при употреблении одной и той же гальванической батареи) сила тока в нем возрастает.[2]
Единицы и размерности[править | править код]
Размерность электрического сопротивления в Международной системе величин: dim R = L2MT −3I −2. В Международной системе единиц (СИ), основанной на Международной системе величин, единицей сопротивления является ом (русское обозначение: Ом; международное: Ω). В системе СГС как таковой единица сопротивления не имеет специального названия, однако в её расширениях (СГСЭ, СГСМ и гауссова система единиц) используются[3]:
- статом (в СГСЭ и гауссовой системе, 1 statΩ = (109 c−2) с/см = 898 755 178 736,818 Ом (точно) ≈ 8,98755·1011 Ом, равен сопротивлению проводника, через который под напряжением 1 статвольт течёт ток 1 статампер);
- абом (в СГСМ, 1 abΩ = 1·10−9 Ом = 1 наноом, равен сопротивлению проводника, через который под напряжением 1 абвольт течёт ток 1 абампер).
Размерность сопротивления в СГСЭ и гауссовой системе равна TL−1 (то есть совпадает с размерностью обратной скорости, с/см), в СГСМ — LT−1 (то есть совпадает с размерностью скорости, см/с)[4].
Обратной величиной по отношению к сопротивлению является электропроводность, единицей измерения которой в системе СИ служит сименс (1 См = 1 Ом−1), в системе СГСЭ (и гауссовой) статсименс и в СГСМ — абсименс[5].
Физика явления[править | править код]
Высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока.
В других средах (полупроводниках, диэлектриках, электролитах, неполярных жидкостях, газах и т. д.) в зависимости от природы носителей заряда физическая причина сопротивления может быть иной. Линейная зависимость, выраженная законом Ома, соблюдается не во всех случаях.
Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он состоит.
Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле:
где ρ — удельное сопротивление вещества проводника, Ом·м, l — длина проводника, м, а S — площадь сечения, м².
Сопротивление однородного проводника также зависит от температуры.
Удельное сопротивление — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади сечения.
Сопротивление металлов снижается при понижении температуры; при температурах порядка нескольких кельвинов сопротивление большинства металлов и сплавов стремится или становится равным нулю (эффект сверхпроводимости). Напротив, сопротивление полупроводников и изоляторов при снижении температуры (в некотором диапазоне) растёт. Сопротивление также меняется по мере увеличения тока/напряжения, протекающего через проводник/полупроводник.
Зависимость сопротивления от материала, длины и площади поперечного сечения проводника[править | править код]
В металле подвижными носителями зарядов являются свободные электроны. Можно считать, что при своем хаотическом движении они ведут себя подобно молекулам газа. Поэтому в классической физике свободные электроны в металлах называют электронным газом и в первом приближении считают, что к нему применимы законы, установленные для идеального газа.
Плотность электронного газа и строение кристаллической решетки зависят от рода металла. Поэтому сопротивление проводника должно зависеть от рода его вещества. Кроме того, оно должно еще зависеть от длины проводника, площади его поперечного сечения и от температуры.
Влияние сечения проводника на его сопротивление объясняется тем, что при уменьшении сечения поток электронов в проводнике при одной и той же силе тока становится более плотным, поэтому и взаимодействие электронов с частицами вещества в проводнике становится сильнее.
Из формулы
видно, что сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Величину ρ, характеризующую зависимость сопротивления проводника от материала, из которого он сделан, и от внешних условий, называют удельным сопротивлением вещества. Удельное сопротивление различных веществ при расчетах берут из таблиц.
Величину, обратную удельному сопротивлению, называют удельной проводимостью вещества и обозначают σ.
Сопротивление тела человека[править | править код]
- Для расчёта опасной величины силы тока, протекающего через человека при попадании его под электрическое напряжение частотой 50 Герц (Гц), сопротивление тела человека условно принимается равным 1 кОм[6] . Эта величина имеет малое отношение к реальному сопротивлению человеческого тела. В реальности сопротивление человека не является омическим, так как эта величина, во-первых, нелинейна по отношению к приложенному напряжению, во-вторых, меняется во времени, в-третьих, гораздо меньше у человека, который волнуется и, следовательно, потеет и т. д.
- Серьёзные поражения тканей человека наблюдаются обычно при прохождении тока силой около 100 мА. Совершенно безопасным считается ток силой до 1 мА. Удельное сопротивление тела человека зависит от состояния кожных покровов. Сухая кожа обладает удельным сопротивлением порядка 10000 Ом·м, поэтому опасные токи могут быть достигнуты только при значительном напряжении. Однако при наличии сырости сопротивление тела человека резко снижается и безопасным может считаться напряжение только ниже 12 В. Удельное сопротивление крови 1 Ом·м при 50 Гц[7].
Метрологические аспекты[править | править код]
Приборы для измерения сопротивления[править | править код]
- Омметр
- Измерительный мост
- Амперметр и вольтметр (сопротивление находится по формуле)
Средства воспроизведения сопротивления[править | править код]
- Магазин сопротивлений — набор резисторов
- Катушки электрического сопротивления
Государственный эталон сопротивления[править | править код]
- ГЭТ 14-91 Государственный первичный эталон единицы электрического сопротивления. Институт-хранитель: ВНИИМ.
Статическое и динамическое сопротивление[править | править код]
В теории нелинейных цепей используются понятия статического и динамического сопротивлений. Статическим сопротивлением нелинейного элемента электрической цепи в заданной точке его ВАХ называют отношение напряжения на элементе к току в нем. Динамическим сопротивлением нелинейного элемента электрической цепи в заданной точке его ВАХ называют отношение бесконечно
малого приращения напряжения к соответствующему приращению тока.
См. также[править | править код]
- Сверхпроводимость
- Закон Ома
- Закон Барлоу
- Удельное электрическое сопротивление
- Электрическая проводимость
- Отрицательное сопротивление
- Внутреннее сопротивление
- Импеданс
- Волновое сопротивление
- Активное сопротивление
- Реактивное сопротивление
Примечания[править | править код]
- ↑ Электрическое сопротивление — статья из Большой советской энциклопедии.
- ↑ Василий Петров – основоположник отечественной электротехники // /infourok.ru.
- ↑ CRC Handbook of Chemistry and Physics, 92nd Edition. — Ed. William M. Haynes. — 2011. — ISBN 978-1-4398-5511-9
- ↑ Б. М. Яворский, А. А. Детлаф. — Справочник по физике для инженеров и студентов вузов. — М.: Наука, 1968. — 939 с.
- ↑ Иногда в англоязычной литературе сименс называют mho («перевёрнутое» название обратной единицы ohm), соответственно для СГСЭ и СГСМ — statmho (=statsiemens) и abmho (=absiemens).
- ↑ 1 кОм в модели, принятой в стандарте IEEE Std 80 Архивная копия от 23 августа 2011 на Wayback Machine
- ↑ Новиков С. Г. Действие электрического тока на человека. Московский энергетический институт. Дата обращения: 2013-25-04. Архивировано из оригинала 19 июня 2014 года.
Ссылки[править | править код]
- Таблица удельного сопротивления проводников
- Электрическое сопротивление проводников
Литература[править | править код]
- В. Г. Герасимов, Э. В. Кузнецов, О. В. Николаева. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.
В своей работе электрик часто сталкивается с вычислением различных величин и преобразований. Так для корректного подбора кабеля приходится подбирать нужное сечение. Логика выбора сечения основана на зависимости сопротивления от длины линии и площади сечения проводника. В этой статье мы рассмотрим, как выполняется расчет сопротивления провода по его геометрическим размерам.
- Формула для расчета
- Удельное сопротивление
- Расчет по диаметру
- Обязательны ли расчеты?
Формула для расчета
Любые вычисления начинаются с формулы. Основной формулой для расчета сопротивления проводника является:
R=(ρ*l)/S
Где R – сопротивление в Омах, ρ – удельное сопротивление, l – длина в м, S – площадь поперечного сечения провода в мм2.
Эта формула подходит для расчета сопротивления провода по сечению и длине. Из неё следует, что в зависимости от длины изменяется сопротивление, чем длиннее – тем больше. И от площади сечения – наоборот, чем толще провод (большое сечение), тем меньше сопротивление. Однако непонятной остаётся величина, обозначенная буквой ρ (Ро).
Удельное сопротивление
Удельное сопротивление – это табличная величина, для каждого металла она своя. Она нужна для расчета и зависит от кристаллической решетки металла и структуры атомов.
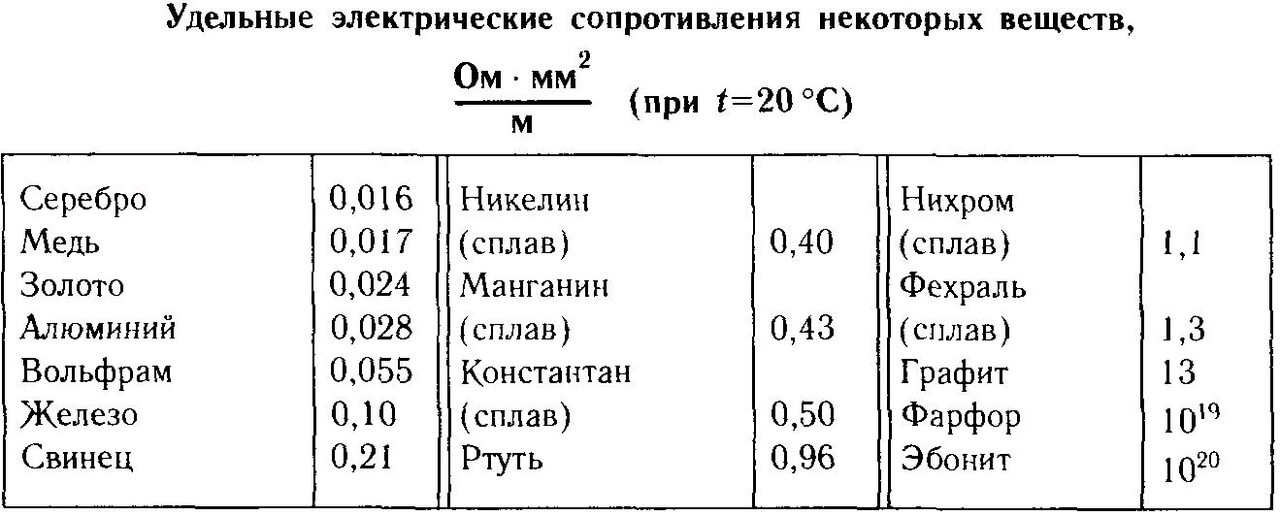
Из таблицы видно, что самое меньшее сопротивление у серебра, для медного кабеля оно равняется 0,017 Ом*мм2/м. Такая размерность говорит нам, сколько приходится Ом при сечении в 1 миллиметр квадратный и длине в 1 метр.
Кстати, серебряное покрытие используется в контактах коммутационных аппаратов, автоматических выключателей, реле и прочего. Это снижает переходное контактное сопротивление, повышает срок службы и уменьшает нагрев контактов. При этом в контактах измерительной и точной аппаратуры используют позолоченные контакты из-за того, что они слабо окисляются или вообще не окисляются.
У алюминия, который часто использовался в электропроводке раньше, сопротивление в 1,8 раза больше чем у меди, равняется 2,82*10-8 Ом*мм2/м. Чем больше сопротивление проводника, тем сильнее он греется. Поэтому при одинаковом сечении алюминиевый кабель может передать меньший ток, чем медный, это и стало основной причиной почему все современные электрики используют медную электропроводку. У нихрома, который используется в нагревательных приборах оно в 100 раз больше чем у меди 1,1*10-6 Ом*мм2/м.
Расчет по диаметру
На практике часто бывает так, что площадь поперечного сечения жилы не известна. Без этого значения ничего рассчитать не получится. Чтобы узнать её, нужно измерить диаметр. Если жила тонка, можно взять гвоздь или любой другой стержень, намотать на него 10 витков провода, обычной линейкой измерить длину получившейся спирали и разделить на 10, так вы узнаете диаметр.
Ну, или просто замерить штангенциркулем. Расчет сечения выполняется по формуле:
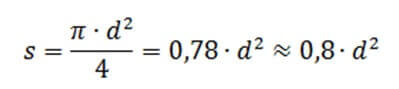
Обязательны ли расчеты?
Как мы уже сказали, сечение провода выбирают исходя из предполагаемого тока и сопротивления металла, из которого изготовлены жилы. Логика выбора заключается в следующем: сечение подбирают таким способом, чтобы сопротивление при заданной длине не приводило к значительным просадкам напряжения. Чтобы не проводить ряд расчетов, для коротких линий (до 10-20 метров) есть достаточно точные таблицы:
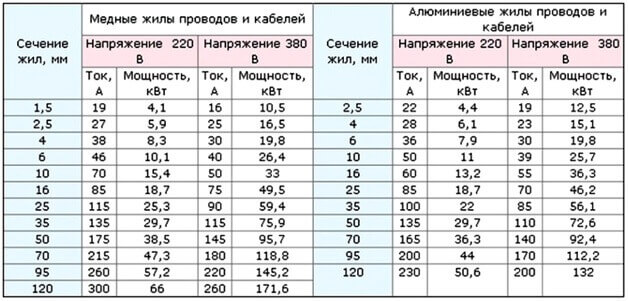
В этой таблице указаны типовые значения сечения медных и алюминиевых жил и номинальные токи через них. Для удобства указана мощность нагрузки, которую выдержит эта линия. Обратите внимание на разницу в токах и мощности при напряжении 380В, естественно, что это предполагается трёхфазная электросеть.
Напоследок рекомендуем просмотреть видео, на котором подробно рассказывается, как рассчитать сечение проводника, а также предоставлены примеры расчетных работ:
Расчет сопротивления провода сводится к использованию пары формул, при этом вы можете скачать готовые калькуляторы из Плэй Маркета для своего смартфона, например, «Electrodroid» или «Мобильный электрик». Эти знания пригодятся для расчетов нагревательных приборов, кабельных линий, предохранителей и даже популярных на сегодняшний день спиралей для электронных сигарет.
Материалы по теме:
- Программы для расчета сечения кабеля
- Как зависит сопротивление проводника от температуры
- Закон Ома простыми словами
Расчет сопротивления проводника — онлайн калькулятор, формула

Расчет сопротивления проводника — неотъемлемый этап при проектировании и анализе электрической цепи. Если обратится к понятным примером, то провода, обеспечивающие электроэнергией наши дома, в зависимости от длинны, сечения и материала обладают сопротивлением. Сопротивление проводника ограничивает величину тока в электрической цепи. Чем больше величина сопротивление, тем меньше ток. Провода, как правило, не обладают большим сопротивлением, способным значительно снизить силу тока. Но, так как проводник — это по сути последовательно соединенный резистор, то от его сопротивления зависит падение напряжения в цепи.
С помощью калькулятора расчета сопротивления проводника вы можете в онлайн режиме определить как сопротивление по длине, так и длину по сопротивлению. Также в обзоре приведена методика расчета с примерами.
Калькулятор сопротивления проводника
Особенность данного калькулятора в том, что вы можете производить как расчет сопротивления проводника по известной длине, так и длину по известному сопротивлению. После выбора соответствующего расчета необходимо указать:
- Материал.
- Температуру. По умолчанию 20 °C.
- Площадь или диаметр поперечного сечения проводника. Если вы заполните оба поля, то калькулятор будет считать по наибольшему значению. То есть, если указанная площадь будет больше площади, рассчитанной по введенному диаметру, калькулятор будет считать просто по площади. Такое разделение удобно для проводников с произвольным сечением (не круг).
- Длину или сопротивление (зависит от конкретного расчета)
Нажав на кнопку «Расчет» вы получите результат. Для очистки формы и нового расчета воспользуйтесь кнопкой «Очистить».
Расчет сопротивления провода
Сопротивление проводника рассчитывается по следующей формуле:
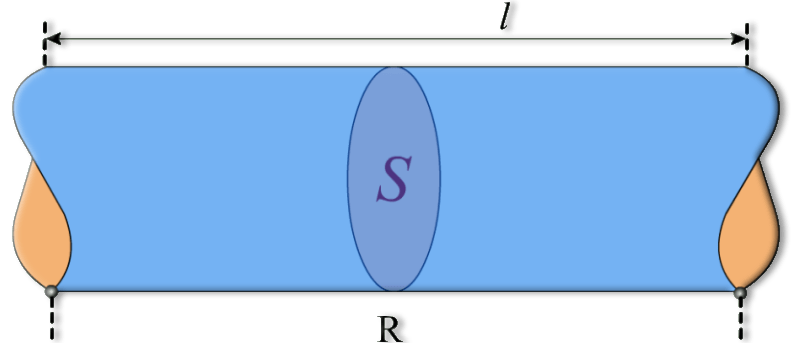 |
R = ρ×(l/S) |
| Где: R — электрическое сопротивление проводника (Ом); ρ — удельное сопротивление проводника (Ом·м);l — длина проводника (м);S — площадь сечения проводника (м²). |
Воспользуемся данной формулой и рассмотрим несколько примеров расчета сопротивления проводника:
- Определить сопротивление 200 м железной проволоки сечением 5 мм². R = ρ×(l/S) = 0,13×(200/5) = 5,2 Ом.
- Вычислить сопротивление 2 км алюминиевого проводника сечением 2,5 мм². R = ρ×(l/S) = 0,03×(2000/2,5) = 24 Ом.
-
Для радиоприемника необходимо намотать сопротивление в 30 Ом из
никелиновой проволоки сечением 0,21 мм². Определить необходимую длину
проволоки. Преобразуем формулу для определения длинны проводника. l = R×(S/ρ) = 30×(0,21/0,42) = 15 м.
-
Определить сечение 20 м нихромовой проволоки, если сопротивление
ее равно 25 Ом. Преобразуем формулу для определения площади сечения проводника. S = ρ×(l/R) = 1,1×(20/25) = 0,88 мм².
-
Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16
Ом. Определить удельное сопротивление проводника. Преобразуем формулу для определения удельного электрического сопротивления проводника. ρ = R×(S/l) = 16×(0,5/40) = 0,2 Ом·мм²/м.
В приведенных примерах не указаны удельные сопротивления проводников. Они брались из приведенных ниже таблиц. Причем, так как сечения у нас были в миллиметрах, то удельное сопротивление для простоты расчетов бралось из второй таблицы (Ом·мм²/м).
Удельное сопротивление проводников (электрическое)
Удельное электрическое сопротивление (удельное сопротивление) — это физическая величина, характеризующая способность материала препятствовать прохождению электрического тока, выражается в Ом·метр. Значение удельного сопротивления зависит от температуры. В проводниках удельное электрическое сопротивление с повышением температуры возрастает, а в полупроводниках и диэлектриках — наоборот, уменьшается.
Из соотношения ρ = R×(S/l) следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².
Для характеристики удельного сопротивления также применяется единица Ом·мм²/м. То есть единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм², изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм².
Таблица показателей удельного сопротивления материалов (Ом·м):
| Материал | Удельное сопротивление, ρ при 20 °C (Ом·м) |
| Латунь | ∼0.6 — 0.9 x 10-7 |
| Серебро | 1.59×10−8 |
| Медь | 1.68×10−8 |
| Обожженная медь | 1.72×10−8 |
| Золото | 2.44×10−8 |
| Алюминий | 2.65×10−8 |
| Вольфрам | 5.60×10−8 |
| Цинк | 5.90×10−8 |
| Кобальт | 6.24×10−8 |
| Никель | 6.99×10−8 |
| Рутений | 7.10×10−8 |
| Литий | 9.28×10−8 |
| Железо | 9.70×10−8 |
| Платина | 1.06×10−7 |
| Олово | 1.09×10−7 |
| Тантал | 1.3×10−7 |
| Галлий | 1.40×10−7 |
| Ниобий | 1.40×10−7 |
| Углеродистая сталь (1010) | 1.43×10−7 |
| Свинец | 2.20×10−7 |
| Титан | 4.20×10−7 |
| Электротехническая сталь | 4.60×10−7 |
| Манганин (сплав) | 4.82×10−7 |
| Константан (сплав) | 4.90×10−7 |
| Нержавеющая сталь | 6.90×10−7 |
| Ртуть | 9.80×10−7 |
| Марганец | 1.44×10−6 |
| Нихром (сплав) | 1.10×10−6 |
| Углерод (аморфный) | 5×10−4 — 8×10−4 |
| Углерод (графит) параллельно-базальная плоскость | 2.5×10−6 — 5.0×10−6 |
| Углерод (графит) перпендикулярно-базальная плоскость | 3×10−3 |
| Германий | 4.6×10−1 |
| Морская вода | 2.1×10−1 |
| Вода в плавательном бассейне | 3.3×10−1 — 4.0×10−1 |
| Питьевая вода | 2×101 — 2×103 |
| Кремний | 2.3×103 |
| Древесина (влажная) | 103 — 104 |
| Деионизированная вода | 1.8×105 |
| Стекло | 1011 — 1015 |
| Углерод (алмаз) | 1012 |
| Твердая резина | 1013 |
| Воздух | 109 — 1015 |
| Древесина (сухая) | 1014 — 1016 |
| Сера | 1015 |
| Плавленый кварц | 7.5×1017 |
Таблица удельных сопротивлений проводников (Ом·мм²/м):
| Материал проводника | Удельное сопротивление, ρ (Ом·мм²/м) |
| Серебро | 0,015 |
| Медь | 0,0175 |
| Золото | 0,023 |
| Латунь | 0,025 — 0,108 |
| Алюминий | 0,028 |
| Натрий | 0,047 |
| Иридий | 0,0474 |
| Вольфрам | 0,05 |
| Цинк | 0,054 |
| Молибден | 0,059 |
| Никель | 0,087 |
| Бронза | 0,095 — 0,1 |
| Железо | 0,1 |
| Сталь | 0,103 — 0,137 |
| Олово | 0,12 |
| Свинец | 0,22 |
| Никелин | 0,42 |
| Манганин | 0,43 — 0,51 |
| Константан | 0,5 |
| Титан | 0,6 |
| Ртуть | 0,94 |
| Нихром | 1,05 — 1,4 |
| Фехраль | 1,15 — 1,35 |
| Висмут | 1,2 |
| Хромаль | 1,3 — 1,5 |
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм² обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления, нужно взять 7,7 м такого проводника. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки с площадью поперечного сечения 1 мм². 1 м медного проводника сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такого проводника.


