Какие есть формулы для вычисления сопротивления резистора
Содержание
- 1 Что такое резистор
- 2 Сопротивление резистора
- 3 Последовательная цепь источника и сопротивлений
- 4 Параллельная схема элементов
- 5 Расчет смешанного соединения элементов схемы
- 6 Мощность рассеивания
- 7 Параметры резисторов
- 8 Определение параметров по маркировке и схеме
- 9 Видео по теме
Сопротивление направленному движению электронов (электрическому току) в проводах электроснабжения чаще всего провоцирует потери. Они зависят от площади сечения (S), длины (L), удельного сопротивления вещества провода (ρ). Однако, сопротивление послужило созданию самого распространенного элемента в электронике — резистора.

Что такое резистор
Деталь электрической или электронной схемы, сопротивляющаяся прохождению электрического тока, называется резистор (от латинского resisto — сопротивляюсь). Падение или изменение напряжения на этом элементе используется в схемотехнике для получения нужных процессов управления автоматикой или преобразования электричества в свет, тепло, звук или движение.
Наиболее удобно классифицировать резисторы по следующим признакам:
- назначение. Для различных сфер используют элементы с
общими свойствами или специфическими по частоте тока, точности изготовления или ограничения по напряжению;
- способ управления сопротивлением. Постоянные резисторы в определенном диапазоне напряжения и тока не меняют сопротивление. У переменных можно менять вручную данный параметр с целью управления процессами. Подстроечные используются для корректировки режимов при наладке и после ремонта;
- материал рабочей части резистора. Металлы, их окислы и сплавы, графитовые или композитные смеси;
- вид резистивных тел. Проволока, фольга или ленты из метала, напыление пленки на керамику, интегрированные каналы в микросхеме;
- способ размещения. Резисторы могут быть впаяны в электронную плату, устанавливаться отдельно на панели управления или закладываться при создании микросхемы внутри изделия;
- характер изменения падения напряжения на элементе от внешних условий (ВАХ). Вольт-амперная характеристика в рабочем диапазоне резистора может быть линейной или нелинейной.
Нелинейная ВАХ отражает изменение сопротивления компонента от внешних условий. Такие резисторы служат датчиками напряжения (варисторы), магнитного поля (магниторезисторы), уровня освещенности (фоторезисторы), перепада температуры (терморезисторы), изменения деформации (тензорезисторы).

Сопротивление резистора
У тех, кто только начинает изучать азы электротехники, часто возникает вопрос, а чем отличается резистор от сопротивления. Разница в том, что резистор является пассивным элементом электроцепи, а сопротивление — это характеристика данного элемента, которую можно рассчитать, определить по маркировке или измерить. Но зачастую сопротивление используется в качестве синонима слова «резистор».
Рассчитать внутреннее сопротивление резистора в сети постоянного тока помогает формула закона Ома для элемента цепи:

Эту формулу применяют также для расчета активного сопротивления в сети переменного тока, но используют действующий ток через элемент. Он равен постоянному току, при котором выделяется на резисторе столько же теплоты, сколько за одинаковое время при прохождении импульсного или синусоидального тока различной частоты.
Суммарное электрическое сопротивление в сетях переменного тока вычисляется при учете активной и реактивной составляющей участка цепи. Любой вид сопротивления измеряется в омах.
Одинокий резистор в схеме часто используется как ограничитель тока. На электронных платах этих элементов много. Друг с другом они соединяются в различных комбинациях: последовательно, параллельно или по смешанной системе.
Последовательная цепь источника и сопротивлений
В замкнутом контуре из последовательно соединенных резисторов и батареи ток в разных точках цепи имеет одинаковое значение. Показание вольтметра на отдельном резисторе будет отражать произведение его внутреннего сопротивления на ток в контуре. Суммарные показания вольтметров будут равны напряжению источника, а для определения общего сопротивления резисторов надо сложить сопротивления всех элементов.
Последовательную цепочку сопротивлений часто используют как делитель напряжения в маломощных измерительных или задающих ступенчатое управление параметрами устройствах. Сопротивление нагрузки Rн, подключенной параллельно R1 вместо вольтметра, должно быть немного больше, чтобы делитель работал стабильно.

Параллельная схема элементов
При параллельном соединении на каждом элементе присутствует напряжение источника, общий ток равен сумме токов резисторов. Расчет сопротивления участка цепи осуществляется по формуле R = (R1 • R2) / (R1 + R2).
Отличие параллельного соединения от последовательного заключается в том, что каждый резистор получает напряжение, которое равно напряжению источника, а общее сопротивление участка меньше меньшего из его составляющих.

Расчет смешанного соединения элементов схемы
Перед тем как рассчитать общее сопротивление схемы, состоящей из параллельных и последовательных участков, используют методы упрощения. На каждом шаге упрощенные эквивалентные схемы можно посчитать по уже известным формулам. Полученный в результате резистор будет обладать общим сопротивлением исходной схемы.

Мощность рассеивания
Для надежной работы электрической схемы нужно знать и сопротивление резистора, и мощность рассеивания, формула для вычисления последней имеет вид:

Правильно подобранный элемент схемы должен рассеять мощность Р (Вт) не разрушаясь и не нагревая другие детали.
Параметры резисторов
Выбор резисторов происходит чаще всего по следующим основным параметрам:
- номинальному сопротивлению. Подбирается или подгоняется ближайшее к расчетному;
- допуску — характеристика, отражающая точность при изготовлении номинального сопротивления. Она составляет 5–20%;
- номинальной мощности рассеивания. Наибольшая величина рассеянного тепла без изменения характеристик меньше номинала элемента;
- предельному рабочему напряжению. Приложенное к выводам резистора наибольшее напряжение, которое не разрушает его;
- температурный коэффициент. Показывает, как изменится сопротивление резистора при колебании на один градус температуры среды.
Для переменных резисторов учитывают ряд дополнительных характеристик:
- износоустойчивость — число циклов;
- функцию изменения сопротивления (линейная, логарифмическая, обратнологарифмическая);
- уровень шума при движении ползунка.
Определение параметров по маркировке и схеме
Некоторые из параметров наносятся непосредственно на резисторы, например, сопротивление и допуск. Раньше для информации о них использовали буквы и цифры. Номинальное сопротивление резисторов имеет диапазон от 0.01 Ом до 1 ГОм. Цифры в маркировке обозначают номинал, а буквы — множитель. Конкретная величина получается умножением или делением цифр.

Буквенно-цифровая маркировка предполагает использование букв Е и R для сопротивлений до 99 Ом, выше — К, а уровень мегаомов обозначается буквой М. В зависимости от того, какую позицию занимает буква в цифровом коде, определяются целые числа или дробные. Узнать, какому множителю соответствует определенная буква, поможет специальная таблица, которую можно найти в любом справочном пособии.

Элементы с цифро-буквенной маркировкой сейчас можно найти преимущественно в старой аппаратуре. В ходе ее ремонта часто приходится менять резисторы, поэтому необходимо уметь расшифровывать такое обозначение.

Сейчас в угоду минимизации отказались от буквенно-цифровых обозначений. На поверхность резисторов наносится маркировка кольцами или точками разных цветов. Чтобы определить по полоскам сопротивление резистора, следует начинать со смещенной к одному из выводов или самой широкой цветной полоски.
Набор цветов первых трех колец при 5 и 6-полосной раскраске означает шифр сопротивления резистора, цвет четвертого кольца обозначает определенное значение множителя для него. Цвет пятого кольца показывает точность изготовления резистора. При шестиполосной окраске цвет последнего кольца обозначает изменение сопротивления (процент) при перепаде температуры окружающей среды на 1 градус. Четырех и пятиполосная раскраска его не имеет.
При четырехполосной маркировке сопротивление резисторов определяется по цветам первых двух. Цвет третьей полосы — это множитель для точного определения сопротивления. Последняя полоса своей расцветкой говорит о допуске в процентах от номинала.

На электрической схеме резистор изображается в виде прямоугольника с размерами 4×10 мм. Рядом с изображением указывается буква R и цифра, обозначающая порядковый номер элемента на схеме, например, R1. Указывается также номинальное сопротивление. Как определить его по буквенно-цифровой маркировке, было рассказано выше.
Мощность рассеивания указывается на графическом изображении специальными метками, если этот параметр меньше 1 ватта. Как узнать мощность по ним подскажет таблица, приведенная ниже.

Если мощность рассеивания выше одного ватта, то внутри прямоугольника ставят римскую цифру. Например, V используется для мощности величиной 5 Вт, Х — 10 Вт и т. п.
Бывают случаи, когда нет возможности воспользоваться маркировкой, например, если она повреждена или стерта. В таком случае нужно знать, как измерить сопротивление специальным прибором. Это может быть омметр или мультиметр. Они мало чем отличаются, но последний является многофункциональным прибором. Принцип измерений основывается на законе Ома. Перед тем как проверить резистор, следует выставить рабочий режим и диапазон измеряемого сопротивления.

Алгоритм по измерению сопротивления используется такой:

Резистор является довольно простым элементом и по своему устройству, и по принципу работы. Поэтому его сопротивление определяется также довольно просто. Еще больше облегчают задачу онлайн-калькуляторы. Ими можно воспользоваться, если возникает необходимость рассчитывать сопротивление многих элементов, для соединения которых применяются разные способы, а также для расшифровки маркировки в виде цветных полос.
Видео по теме
На чтение 7 мин. Просмотров 3.8k. Опубликовано 13.05.2020
В чем измеряется сопротивление резистора
Чтобы ответить на вопрос в чем измеряется сопротивление резистора, нужно обратиться к стандартизации и наукам об измерениях. Международная и общепринятая схема цветовых кодов резисторов была разработана много лет назад как простой и быстрый способ определения омического значения резистора независимо от его размера или состояния. Он состоит из набора отдельных цветных колец или полос в спектральном порядке, представляющих каждую цифру значения резисторов. Сила сопротивления определеяет качество резистора.
Цветовая маркировка резистора всегда считывается по одной полосе за раз, начиная слева направо, с большей полосой допуска ширины, ориентированной на правую сторону, что указывает на ее допуск. Путем сопоставления цвета первой полосы с соответствующим номером в столбце цифр цветовой диаграммы под первой цифрой идентифицируется, и это представляет первую цифру значения сопротивления.
Опять же, сопоставляя цвет второй полосы с соответствующим номером в столбце цифр цветовой диаграммы, мы получаем вторую цифру значения сопротивления и так далее. Затем цветовой код резистора читается слева направо, как показано ниже:

Это система маркировки. Резисторы бывают разных размеров и значений сопротивления, а чтобы вычислить нужный, и существуют формулы расчета. Резисторы изготавливаются по определенной стандартной сетке, которая подходит для большинства целей. Чтобы не быть голословными, нужно приложить цветовую таблицу.
Вместо последовательных значений сопротивления от 1 Ом (базовая единица измерений) и выше, определенные значения резисторов существуют в определенных пределах допуска. Допуск резистора представляет собой максимальную разницу между его фактическим значением и требуемым значением и обычно выражается как зависимость положительного или отрицательного значения в процентах. Например, резистор с допуском 1 кОм ± 20% может иметь максимальное и минимальное значение сопротивления:
Максимальное значение сопротивления
- 1 кОм или 1000 Ом + 20% = 1200 Ом
Минимальное значение сопротивления
- 1 кОм или 1000 Ом — 20% = 800 Ом
От чего зависит сопротивление резистора
Температура и последовательность включения — два главных фактора, которые определяют сопротивление в цепи. Но помимо этих показателей есть и допуски. Как же измерять? В большинстве электрических или электронных цепей большой 20% -ный допуск на один и тот же резистор, как правило, не является проблемой, но если для высокоточных цепей, таких как фильтры, генераторы или усилители и т. д., требуются резисторы с малым допуском, то необходимо использовать резистор с правильным допуском. Так как резистор с допуском 20% обычно не может использоваться для замены типа допуска 2% или даже 1%.
Цветовой код пяти- и шестиполосного резистора чаще всего ассоциируется с высокопрецизионными типами пленок 1% и 2%, в то время как универсальные садовые разновидности 5% и 10% общего назначения обычно используют четырехполосный цветовой код резистора. Резисторы имеют различные допуски, но наиболее распространенными являются E12 и E24 .
Е12 серия поставляется в двенадцати значений сопротивления за десятилетие (А десятилетие , представляющее кратные 10, то есть 10, 100, 1000 и т.д.), в то время как Е24 серия приходит в двадцать четыре значений за десятилетие и E96 серии девяносто шесть значений за десятилетие. Серия E192 с очень высокой точностью теперь доступна с допусками до ± 0,1%, что дает массивные 192 значения отдельных резисторов за десятилетие.

Как зависит от температуры
Чем выше температура, тем выше сопротивление. Это связано с быстрой скоростью движения атомов внутри твердого тела. Обратное явление — сверхпроводимость при низких температурах. Опять же, не забываем про погрешность.
От других параметров
Если резистор подключен в сложную цепь с множеством преобразующих, защитных, трансформирующих, компрессирующих устройств, то он будет иметь другое, отличное от стандартного, сопротивление, так как часть напряжения все равно будет проходить через него в нескомпрессированном виде, что не позволит ему отработать как следует. Чтобы более точно узнать удельный ток и сопротивление, показатель, полученный в расчетах, нужно уменьшить или увеличить на заданную величину.
Как найти сопротивление резистора в цепи
Система цветового кода резистора хороша, но нам нужно понять, как ее применять, чтобы получить правильное значение резистора. «Левая» или наиболее значимая цветная полоса — это полоса, ближайшая к соединительному выводу, полосы с цветовой кодировкой читаются слева направо следующим образом:
Цифра, цифра, множитель = цвет, цвет х 10 цветов в омах (Ω)
Например, резистор имеет следующие схемы маркировки;
Желтый Фиолетовый Красный = 4 7 2 = 4 7 x 10 2 = 4700 Ом или 4 кОм Ом.
Типичные допуски на резисторы для пленочных резисторов варьируются от 1% до 10%, в то время как для углеродных резисторов допуски составляют до 20%. Резисторы с допусками ниже 2% называются прецизионными, а резисторы с более низким допуском более дорогими. Само напряжение играет малую роль.
Большинство пятиполосных резисторов являются прецизионными резисторами с допусками 1% или 2%, в то время как большинство четырехполосных резисторов имеют допуски 5%, 10% и 20%. Цветовой код, используемый для обозначения номинального допуска резистора, имеет вид:
Коричневый = 1%, красный = 2%, золото = 5%, серебро = 10%
При параллельном соединении
Как находить сопротивление при параллельном соединении? По формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + … + (1 / Rn).
При последовательном соединении
Общее сопротивление цепи при последовательном соединении в электрической цепи равно сумме сопротивлений отдельных проводников (или отдельных участков цепи): R = R 1 + R 2.
Могут ли быть погрешности и какие
Если резистор не имеет четвертой полосы допусков, тогда допуск по умолчанию будет обозначаться 20% . Остальной ток будет рассеиваться.
Иногда проще запомнить цветовой код резистора, используя короткие, легко запоминающиеся предложения в форме выражений, рифм и фраз, называемых акростихами , в которых есть отдельное слово в предложении для представления каждого из десяти + двух цветов.
Полученная мнемоника сопоставляет первую букву каждого слова каждому цвету, который составляет цветовой код резисторов в порядке возрастания величины, и есть много разных мнемонических фраз, которые можно использовать. Однако эти высказывания часто бывают очень грубыми, но тем не менее эффективными для запоминания цветов резисторов, но все же помогают определить сопротивление.
Таблица погрешнойстей для более точного определения сопротивления
| Коды допусков для резисторов (±) |
| B = 0,1% |
| С = 0,25% |
| D = 0,5% |
| F = 1% |
| G = 2% |
| J = 5% |
| К = 10% |
| М = 20% |
Кроме того, при чтении этих письменных кодов соблюдайте осторожность, чтобы не перепутать букву сопротивления k для килограммов с буквой допуска K для допуска 10% или буквой сопротивления M для мегаом с буквой допуска M для допуска 20%.
Как использовать на практике
Существует множество различных типов резисторов, которые можно использовать как в электрических, так и в электронных цепях для управления током или для падения напряжения различными способами. Но для того, чтобы сделать это, реальный резистор должен иметь некоторую форму «резистивного» или «резистивного» значения. Резисторы доступны в диапазоне различных значений сопротивления от долей Ом ( Ом ) до миллионов Ом.
Очевидно, что было бы нецелесообразно иметь в наличии резисторов каждого возможного значения , например, 1 Ом , 2 Ом , 3Ω , 4Ω и т.д., потому что буквально десятки сотен тысяч, если не десятки миллионов различных резисторов должны существовать , чтобы покрыть все возможные значения. Вместо этого резисторы изготавливаются в так называемых «предпочтительных значениях», а их значения сопротивления печатаются на корпусе цветными чернилами.
Значение сопротивления, допуск и номинальная мощность обычно печатаются на корпусе резистора в виде цифр или букв, когда корпус резистора достаточно большой, чтобы считывать отпечаток, например, большие силовые резисторы. Но когда резистор маленький, такой как углеродный или пленочный тип на 1/4 Вт, эти характеристики должны быть показаны другим способом, так как отпечаток будет слишком маленьким для чтения. Подача большого напряжения нагреет краску и расплавит надписи.
Таким образом, чтобы преодолеть это, маленькие резисторы используют цветные окрашенные полосы, чтобы указать как их значение сопротивления, так и их допуск с физическим размером резистора, указывающим его номинальную мощность. Эти цветные окрашенные полосы производят систему идентификации, обычно известную как цветовой код резисторов.

Содержание материала
- Закон Ома
- Видео
- Реостат
- Пример расчета
- Параметры резисторного элемента
- Делитель напряжения
- Зависимость сопротивления
- Электрические величины
- Ток, протекающий в цепи параллельно соединенных резисторах
- Смешанное соединение резисторов
- Мощность резисторов
Закон Ома
Закон Ома позволяет на заданном участке цепи определить одну из величин: силу тока I, напряжение U, сопротивление R, если известны две остальные:

Для обозначения напряжения наряду с символом U используется V.
Видео
Реостат
Есть такие выключатели, которые крутишь, а они делают свет ярче-тусклее. В такой выключатель спрятан резистор с переменным сопротивлением — реостат.

Стрелка сверху — это ползунок. По сути, он отсекает ту часть резистора, которая находится от него справа. То есть, если мы двигаем ползунок вправо — мы увеличиваем длину резистора, а значит и сопротивление. И наоборот — двигаем влево и уменьшаем.
По формуле сопротивления это очень хорошо видно, так как длина проводника находится в числителе:
Пример расчета
Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Параметры резисторного элемента
Сопротивление тока: формула
При нанесении на схемы графического обозначения элемента сопротивления на нём указывается некоторые из его параметров.

Графическое обозначение резистора на схемах
К главным параметрам и элементарным характеристикам относятся:
- номинальное значение сопротивления;
- температурный коэффициент;
- максимальная рассеиваемая мощность;
- допустимое рабочее напряжение;
- коэффициент шума;
- относительное отклонение от номинала;
- устойчивость элемента к высокой температуре и влажности.
На чертежах и схемах резистор обозначается буквой R, с нанесением его порядкового номера.
Делитель напряжения
Наиболее применяемые готовые блоки питания рассчитаны на выходные напряжения: 9, 12 или 24 вольта. В то же время большинство электронных схем и устройств использует напряжение питания в интервале от 3 до 5 В. В этом случае возникает потребность снизить величину Uпит до необходимого значения. Сделать это можно, используя делитель напряжения, который имеет много вариантов исполнения. Самый простой – делитель на резисторах.

Схема делителя, выполненного на резисторах
Мощность резистора
Подобные делители напряжения применяются исключительно в маломощных контурах. Это обусловлено их низким КПД. Часть мощности блока питания рассеивается на делителе, превращаясь в тепло. Эти потери тем больше, чем больше нужно уменьшить исходное напряжение. Подключение нагрузки параллельно одному плечу требует того, чтобы Rн было намного больше резистора, установленного в этом плече. Иначе делитель будет выдавать нестабильное питание.
При такой схеме напряжение по плечам делителя распределяется согласно полученным соотношениям между R1 и R2. Величина сопротивлений при этом роли не играет. Но следует помнить, что при низких значениях R1 и R2 увеличивается и мощность на нагрузке, и величина потерь на нагревание элементов.
Внимание! Перед тем, как вычислять точные параметры, нужно помнить, как подобрать резисторы. При их равном значении напряжение на выходе делится пополам. Если равенство не соблюдается, снимать поделенное напряжение нужно с элемента, имеющего больший номинал.

Пример схемы делителей на резисторах с малыми и большими значениями
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
 Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Вам это будет интересно Прибор для электрика: тестер напряжения
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (закон Ома для участка цепи).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны. Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Правило Кирхгофа гласит: «Общий ток, входящий в цепь равен току выходящему из цепи».
Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Смешанное соединение резисторов
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:

Давайте рассчитаем общее сопротивление. Начнем с резисторов R_1 и R_2 — они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:
Теперь у нас образовались две группы последовательно соединенных резисторов:

- R_{1-2} и R_3
- R_4 и R_5
Заменим эти две группы двумя резисторами, сопротивление которых равно:

Как видите, схема стала уже совсем простой. Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5} одним резистором R_{1-2-3-4-5}:
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:

Общее сопротивление цепи получилось равным:
Таким вот образом достаточно большая схема свелась к банальнейшему последовательному соединению двух резисторов. Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление — для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте 🤝
 Переменные и подстроечные резисторы. Реостат.
Переменные и подстроечные резисторы. Реостат. Добротность и энергия катушки индуктивности.…
Добротность и энергия катушки индуктивности.… Маркировка конденсаторов. Расчет общей…
Маркировка конденсаторов. Расчет общей… Постоянный резистор. Номиналы и цветовая…
Постоянный резистор. Номиналы и цветовая…
Мощность резисторов
Резисторы помимо сопротивления обладают ещё характеристикой мощности. Она определяет нагрузку, которую способен выдержать резистор. Среди обычных керамических резисторов наиболее распространены показатели 0.25 Вт, 0.5 Вт и 1 Вт. Для расчёта нагрузки, действующей на резистор, используйте формулу:

При превышении допустимой нагрузки, резистор будет греться и его срок службы может сильно сократиться. При сильном превышении — резистор может начать плавиться и вызвать воспламенение. Будьте осторожны!
Теги
Загрузить PDF
Загрузить PDF
Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.
-

1
Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.
-

2
Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь.[1]
Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.- Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.
-

3
Вычислите сопротивление по известной силе тока и напряжению. Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.
- Сила тока в любых частях последовательной цепи одна и та же.[2]
Поэтому можно использовать известное значение силы тока на любом участке последовательной цепи. - Общее напряжение равно напряжению источника тока. Оно не равно напряжению на каком-либо элементе цепи.[3]
- Сила тока в любых частях последовательной цепи одна и та же.[2]
-

4
Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.
- Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: RO = 12 В / 8 А = 1,5 Ом.
Реклама
-

1
Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
- Если цепь включает элементы, расположенные до или после разветвления, или если на одной ветви два и более элементов, перейдите к третьему разделу этой статьи (такая цепь является комбинированной).
-

2
Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления:
, где R1 – сопротивление первой ветви, R2 – сопротивление второй ветви и так далее до последней ветви Rn.
-

3
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.[4]
Поэтому достаточно знать значение напряжение на любой ветви цепи. Общее напряжение также равно напряжению источника тока. - В параллельной цепи сила тока на каждой ветви разная. Поэтому необходимо знать значение общей силы тока, чтобы найти общее сопротивление.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи.[4]
-

4
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.
- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: RO = 9 В / 3 А = 3 Ом.
-

5
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.[5]
Реклама
- В реальной жизни это означает, что резистор неисправен или шунтирован (замкнут); в этом случае большая сила тока может повредить другие элементы цепи.[5]
-

1
Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
-

2
Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи:
.
-

3
Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
-

4
Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно:
Ом.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно:
-

5
Воспользуйтесь законом Ома, чтобы найти неизвестные величины. Если сопротивление каждого элемента цепи не известно, попытайтесь вычислить его. Вычислить сопротивление по известной силе тока и напряжению можно по закону Ома: R = V/I.
Реклама
-

1
Запомните формулы, включающие мощность. Электрическая мощность – это величина, которая характеризует скорость преобразования электроэнергии и скорость ее передачи (например, к лампочке).[6]
Общая мощность цепи равна произведению общего напряжения на общую силу тока. Формула: P = VI.[7]
- Запомните: чтобы вычислить общее сопротивления, нужно знать общую мощность. Значение мощности на одном элементе цепи для этих целей не подходит.
-

2
Вычислите сопротивление по известным значениям мощности и силы тока. В этом случае можно объединить две формулы, чтобы найти сопротивление.
- P = VI (мощность = напряжение х сила тока)
- Закон Ома: V = IR.
- В первую формулу вместо V подставьте произведение IR: P = (IR)I = I2R.
- Обособьте переменную R: R = P / I2.
- Сила тока в любых частях последовательной цепи одна и та же. Это не так в параллельной цепи.
-

3
Вычислите сопротивление по известным значениям мощности и напряжения. В этом случае можно объединить две формулы, чтобы найти сопротивление. Учитывайте общее напряжение в цепи, которое равно напряжению источника тока.
- P = VI
- Перепишите закон Ома так: I = V/R
- В первой формуле замените I на V/R: P = V(V/R) = V2/R.
- Обособьте переменную R: R = V2/P.
- В параллельной цепи напряжение на одной ветви равно общему напряжению в цепи. Это не так в последовательной цепи, где общее напряжение не равно напряжению на одном элементе цепи.
Реклама
Советы
- Мощность измеряется в ваттах (Вт).
- Напряжение измеряется в вольтах (В).
- Сила тока измеряется в амперах (А) или в миллиамперах (мА). 1 мА =
A = 0,001 А.
- В приведенных формулах переменная Р – это мгновенная мощность, то есть мощность в определенный момент времени. Если цепь подключена к источнику переменного тока, мощность постоянно меняется. Поэтому для цепей с источником переменного тока специалисты вычисляют среднюю мощность; для этого используется формула: PСР = VIcosθ, где cosθ – это коэффициент мощности цепи.[8]
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 407 658 раз.
Была ли эта статья полезной?
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях, будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
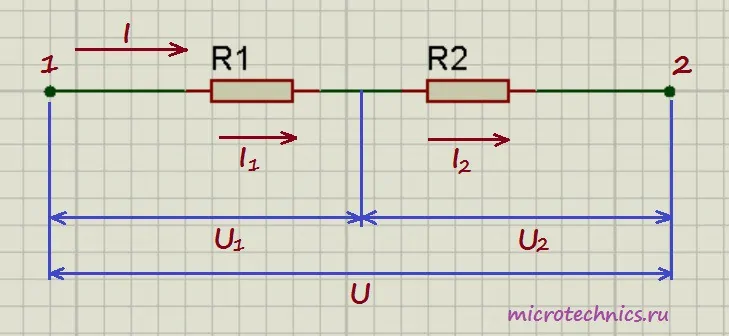
Здесь у нас классический случай последовательного соединения – два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
Тогда для вычисления общего напряжения можно использовать следующее выражение:
U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)
Но для общего напряжения также справедлив закон Ома:
Здесь R_0 – это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников.
Например, для следующей цепи:
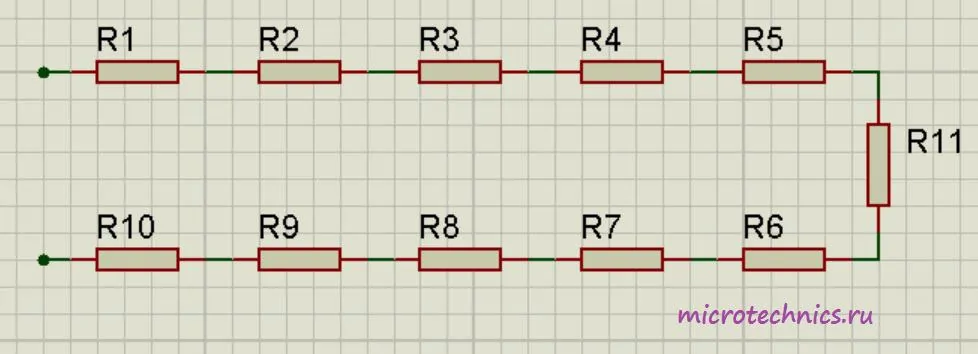
Общее сопротивление будет равно:
R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_{10}
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление, будет работать в любом случае. А если при последовательном соединении все сопротивления равны (R_1 = R_2 = … = R), то общее сопротивление цепи составит:
В данной формуле n равно количеству элементов. С последовательным соединением резисторов разобрались, логичным образом переходим к параллельному.
Параллельное соединение резисторов.
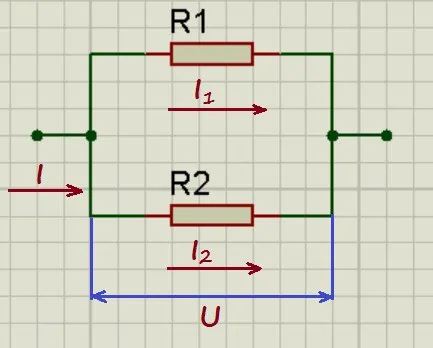
При параллельном соединении напряжения на проводниках равны:
А для токов справедливо следующее выражение:
То есть общий ток разветвляется на две составляющие, а его значение равно сумме всех составляющих. По закону Ома:
I_1 = frac{U_1}{R_1} = frac{U}{R_1}
I_2 = frac{U_2}{R_2} = frac{U}{R_2}
Подставим эти выражения в формулу общего тока:
I = frac{U}{R_1} + frac{U}{R_2} = Umedspace (frac{1}{R1} + frac{1}{R2})
А по закону Ома:
Приравниваем эти выражения и получаем формулу для общего сопротивления цепи:
frac{1}{R_0} = frac{1}{R_1} + frac{1}{R_2}
Данную формулу можно записать и несколько иначе:
R_0 = frac{R_1R_2}{R_1 + R_2}
Таким образом, при параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Аналогичная ситуация будет наблюдаться и при большем количестве проводников, соединенных параллельно:
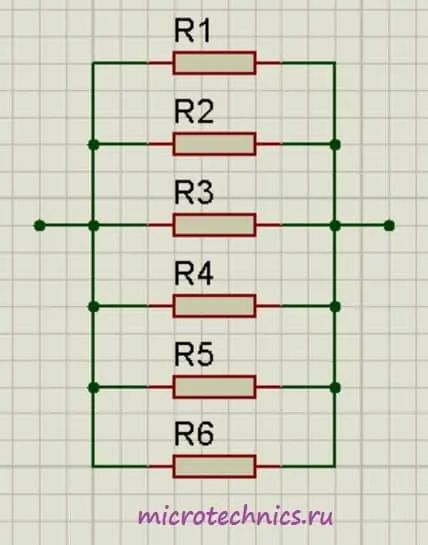
frac{1}{R_0} = frac{1}{R_1} + frac{1}{R_2} + frac{1}{R_3} + frac{1}{R_4} + frac{1}{R_5} + frac{1}{R_6}
Смешанное соединение резисторов.
Помимо параллельного и последовательного соединений резисторов существует еще смешанное соединение. Из названия уже понятно, что при таком соединении в цепи присутствуют резисторы, соединенные как параллельно, так и последовательно. Вот пример такой цепи:
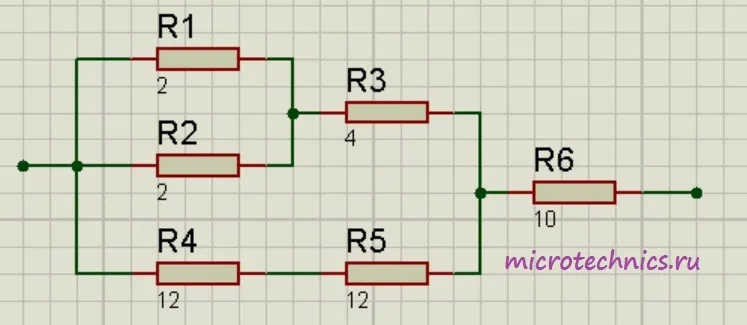
Давайте рассчитаем общее сопротивление. Начнем с резисторов R_1 и R_2 – они соединены параллельно. Мы можем рассчитать общее сопротивление для этих резисторов и заменить их в схеме одним единственным резистором R_{1-2}:
R_{1-2} = frac{R1cdot R2}{R1 + R2} = 1
Теперь у нас образовались две группы последовательно соединенных резисторов:
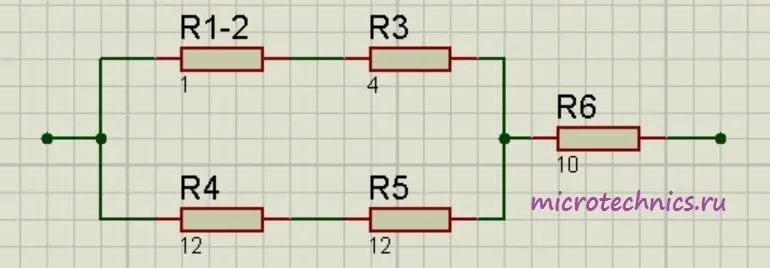
- R_{1-2} и R_3
- R_4 и R_5
Заменим эти две группы двумя резисторами, сопротивление которых равно:
R_{1-2-3} = R_{1-2} + R_3 = 5
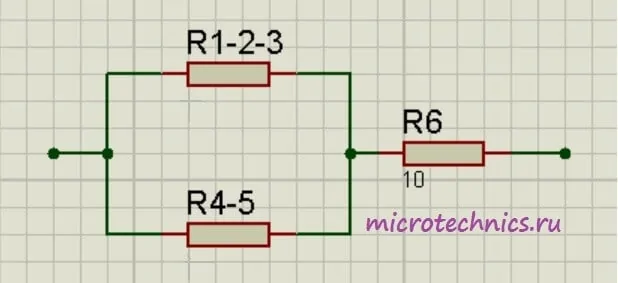
Как видите, схема стала уже совсем простой. Заменим группу параллельно соединенных резисторов R_{1-2-3} и R_{4-5} одним резистором R_{1-2-3-4-5}:
R_{1-2-3-4-5}enspace = frac{R_{1-2-3}medspacecdot R_{4-5}}{R_{1-2-3} + R_{4-5}} = frac{5cdot24}{5 + 24} = 4.14
И в итоге у нас на схеме осталось только два резистора соединенных последовательно:
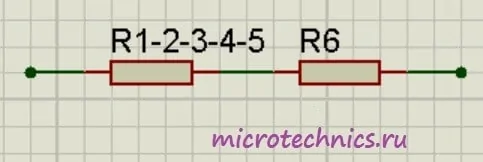
Общее сопротивление цепи получилось равным:
R_0 = R_{1-2-3-4-5}medspace +medspace R_6 = 4.14 + 10 = 14.14
Таким вот образом достаточно большая схема свелась к банальнейшему последовательному соединению двух резисторов. Тут стоит отметить, что некоторые схемы невозможно так просто преобразовать и определить общее сопротивление – для таких схем нужно использовать правила Кирхгофа, о которых мы обязательно поговорим в будущих статьях. А сегодняшняя статья на этом подошла к концу, до скорых встреч на нашем сайте 🤝
