Содержание
- Соединение резисторов
- Как правильно соединять резисторы?
- Последовательное соединение резисторов.
- Параллельное соединение резисторов.
- Что ещё нужно учитывать при соединении резисторов?
- Как найти сопротивление резисторов при замкнутом ключе
- Сопротивление
- Ток, протекающий через нить накала лампы
- Основа для коммутации ламп
- Выключатель ножевого типа
- Разомкнутые и замкнутые цепи
Соединение резисторов
Как правильно соединять резисторы?

О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:

На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.

Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:

Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:

Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Источник
Как найти сопротивление резисторов при замкнутом ключе
На сколько изменится сопротивление участка цепи АВ, изображенного на рисунке, если ключ К разомкнуть? Сопротивление каждого резистора равно 4 Ом. (Ответ дайте в омах. Если сопротивление увеличится, изменение считайте положительным, если уменьшится — отрицательным.)
До размыкания ключа резисторы, изображенные на рисунке вертикально, закорочены, схема представляет собой просто резистор R.
Если разомкнуть ключ, «вертикальные» резисторы перестанут быть закороченным и схема станет представлять собой последовательное соединение резистора R с двумя параллельно соединенными резисторами R. Следовательно, сопротивление участка цепи после размыкания ключа будет равно
Таким образом, сопротивление участка цепи увеличится на 2 Ом.
Добрый день! Вопрос, наверное, слегка не в тему, но что значит вертикально закорочены? И как определить, как пойдет тот при замыкании или размыкании ключа?
«Вертикальные» — в данном контексте является просто указанием на резисторы, нарисованные на схеме вертикально.
Две точки называют закороченными, если они соединены проводником с пренебрежимо малым сопротивлением, коим является соединительный провод. Такие точки оказываются под одинаковым потенциалом.
Посмотрите комментарий к задаче 1411
На фотографии — электрическая цепь. Показания вольтметра даны в вольтах. Чему будут равны показания вольтметра, если его подключить параллельно резистору 2 Ом? (Ответ дайте в вольтах. Вольтметр считать идеальным.)
Согласно закону Ома, сила тока, сопротивление проводника и напряжение между его концами связаны соотношением Поскольку резистор 1 Ом и резистор 2 Ом подключены последовательно, сила тока, текущего через них, совпадает. Следовательно, идеальный вольтметр, подключенный параллельно к резистору 2 Ом, покажет напряжение
На рисунке показан участок цепи постоянного тока. Каково сопротивление этого участка, если ?
Участок представляет собой последовательное соединение резистора r и двух параллельно соединенных резисторов 3r. Следовательно, сопротивление этого участка равно
На фотографии — электрическая цепь. Показания включенного в цепь амперметра даны в амперах. Какое напряжение покажет идеальный вольтметр, если его подключить параллельно резистору 3 Ом? (Ответ дайте в вольтах.)
Согласно закону Ома, сила тока, сопротивление проводника и напряжение между его концами связаны соотношением Все резисторы подключены последовательно, а значит, через них всех течет одинаковый ток силой 0,8 A. Таким образом, идеальный вольтметр, подключенный параллельно к резистору 3 Ом, покажет напряжение
На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно Чему равно полное сопротивление участка при замкнутом ключе К?
После замыкания ключа правая половина схемы окажется закороченной, получившаяся схема будет эквивалента двум подключенным параллельно резисторам.
Полное сопротивление участка при замкнутом ключе равно
Не учитывается третий резистор потому что ток идет по пути наименьшего сопротивления?
Начну с совета: «Раз и навсегда забудьте эту фразу про то, что ток течет по пути наименьшего сопротивления». Она иногда приводит людей к очень странным выводам, так что от нее больше вреда, чем пользы. А что стоит помнить? Это законы о токах и напряжениях при параллельном и последовательном соединениях. Если у Вас есть два параллельно соединенных проводника, то ток между ними делится таким образом, чтобы напряжения на них совпадали. По закону Ома получается, что чем меньше одно сопротивление, чем другое, тем большая часть тока через него потечет. Если оба сопротивления отличны от нуля, то через них обоих течет ток. В нашем же случае (после замыкания ключа) получается, что сверху есть какое-то ненулевое сопротивление, а снизу идет просто соединительный провод, сопротивлением которого всегда пренебрегают. По законам для параллельного соединения:
.
При этом сумма и
должна давать полный, конечный по величине ток в цепи. Единственная возможность для того, чтобы эти уравнения выполнялись: потребовать, чтобы
. То есть, если есть закороченный участок, то его можно смело выкидывать из рассмотрения, ток туда не пойдет. В других случаях, ток всегда как-то распределяется. Например, если бы в левой части схемы были не одинаковые сопротивления, то ток пошел бы не «по пути наименьшего сопротивления», а через оба из них.
P.S. Возможно, я немного переусердствовал, и зря Вас обвинил, может Вы и так все правильно для себя трактовали, в этом случае прошу извинить меня, но у меня просто был опыт общения с людьми, которые реально путались из-за этой фразы.
Спасибо за расшифровку, теперь понимаю! Вы не переусердствовали, все отлично объяснили. Спасибо, еще раз!
Источник
Сопротивление
Схема из предыдущего раздела не очень практична. На самом деле, собирать ее (напрямую соединять полюсы источника напряжения с помощью только куска провода) может быть довольно опасно. Причина, по которой это опасно, заключается в том, что при таком коротком замыкании величина электрического тока может быть очень большой, а выделение энергии может быть очень значительным (обычно в виде тепла). Обычно на практике электрические цепи строятся таким образом, чтобы максимально безопасно использовать высвобождаемую энергию.
Ток, протекающий через нить накала лампы
Одним из практических и популярных способов использования электрического тока является электрическое освещение. Самая простая форма электрической лампы – это крошечная металлическая «нить» внутри прозрачной стеклянной колбы, которая накаляется добела от тепловой энергии, когда через нее проходит достаточный электрический ток. Как и батарея, она имеет две проводящие точки подключения: одна для входа тока, а другая – для выхода. Схема электрической лампы, подключенной к источнику напряжения, выглядит примерно так:
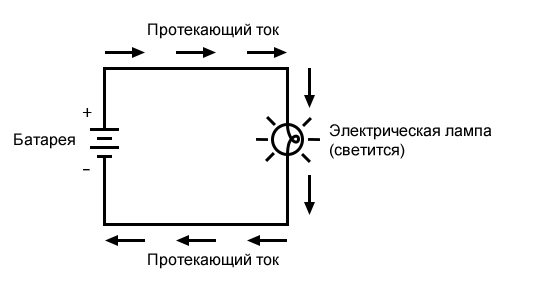 Рисунок 1 – Ток через лампу
Рисунок 1 – Ток через лампу
Когда ток проходит через тонкую металлическую нить накала лампы, он встречает большее противодействие движению, чем в обычном толстом куске провода. Это противодействие электрическому току зависит от типа материала, площади его поперечного сечения и температуры. Технически это противодействие известно как сопротивление (можно сказать, что проводники имеют низкое сопротивление, а диэлектрики – очень высокое сопротивление). Это сопротивление служит для ограничения величины тока, проходящего через цепь при заданном напряжении, подаваемом батареей, по сравнению с «коротким замыканием», когда у нас не было ничего, кроме провода, соединяющего один конец источника напряжения (батареи) с другим. Когда ток движется против противодействия сопротивления, возникает «трение». Как и в случае механического трения, трение, создаваемое током, протекающим через сопротивление, проявляется в виде тепла. Концентрированное сопротивление нити накала лампы приводит к тому, что на нити рассеивается относительно большое количество тепловой энергии. Этой тепловой энергии достаточно, чтобы нить накаливания стала раскаленной добела и начала светиться, в то время как провода, соединяющие лампу с батареей (которые имеют гораздо меньшее сопротивление), вряд ли станут хотя бы теплыми, проводя такую же величину тока. Как и в случае короткого замыкания, если целостность цепи нарушена в любой точке, ток прекращается по всей цепи. При установленной лампе, это означает, что она перестанет светиться:
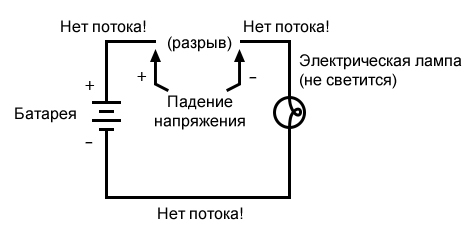 Рисунок 2 – Ток через лампу не течет
Рисунок 2 – Ток через лампу не течет
Как и прежде, ток не течет, а в точках разрыва доступен весь потенциал (напряжение) батареи, ожидающий соединения, чтобы пересечь этот разрыв и позволить току снова течь. Это состояние известно как разомкнутая цепь, когда разрыв цепи предотвращает протекание тока повсюду. Всё, что требуется, чтобы «разомкнуть» цепь, – это один разрыв. После повторного соединения любых разрывов и восстановления непрерывности цепь называется замкнутой.
Основа для коммутации ламп
То, что мы видим здесь, является основой для включения и выключения ламп дистанционными выключателями. Поскольку любое нарушение непрерывности цепи приводит к прекращению протекания тока по всей цепи, то для управления протеканием тока в цепи мы можем использовать устройство, предназначенное для преднамеренного нарушения этой непрерывности (называемое ключом, или выключателем, переключателем и т.п.) и установленное в любом удобном месте, к которому мы можем провести провода:
 Рисунок 3 – Добавление ключа в цепь из батареи и лампы
Рисунок 3 – Добавление ключа в цепь из батареи и лампы
Таким образом, выключатель, установленный на стене дома, может управлять лампой, установленной в длинном коридоре или даже в другой комнате, далеко от выключателя. Сам ключ состоит из пары проводящих контактов (обычно сделанных из какого-то металла), соединенных механическим рычажным приводом или кнопкой. Когда контакты соприкасаются друг с другом, устанавливается непрерывность цепи, и ток может течь от одного контакта к другому. Когда контакты разделены, течению тока от одного к другому препятствует воздушная изоляция между ними, и непрерывность цепи нарушается.
Выключатель ножевого типа
Возможно, лучший вид переключателя для иллюстрации принципа действия — это выключатель ножевого типа:
 Рисунок 4 – Выключатель ножевого типа
Рисунок 4 – Выключатель ножевого типа
Ножевой переключатель – это не что иное, как токопроводящий рычаг, свободно поворачивающийся на шарнире, вступающий в физический контакт с одним или несколькими неподвижными контактами, которые также являются токопроводящими. Переключатель, показанный на приведенном выше рисунке, собран на фарфоровом основании (отличный изоляционный материал), с использованием меди (отличный проводник) для «лезвия» и контактов. Ручка сделана из пластика, чтобы изолировать руку оператора от токопроводящего лезвия переключателя при его открытии или закрытии. Ниже показан еще один тип переключателя, с двумя неподвижными контактами вместо одного:
 Рисунок 5 – Переключатель ножевого типа с 3-мя контактами
Рисунок 5 – Переключатель ножевого типа с 3-мя контактами
Ножевой переключатель, показанный здесь, имеет одно «лезвие» и два неподвижных контакта, что означает, что он может включать или выключать более одной цепи. На данный момент это не так важно, чтобы просто понять основную идею того, что такое ключ, и как он работает. Ножевые переключатели отлично подходят для иллюстрации основного принципа работы ключа, но они представляют определенные проблемы безопасности при использовании в электрических цепях большой мощности. Открытые проводники переключателя делают очень возможным случайный контакт с цепью, а любая искра, которая может возникнуть между движущимся ножом и неподвижным контактом, может воспламенить любые находящиеся поблизости горючие материалы. В большинстве современных конструкций переключателей движущиеся проводники и контакты закрыты изолирующим кожухом, чтобы уменьшить эти опасности. Фотографии нескольких современных типов переключателей показывают, что механизмы переключения гораздо более скрыты, чем в конструкции ножевого выключателя:
 Рисунок 6 – Сравнение размеров переключателей
Рисунок 6 – Сравнение размеров переключателей
Разомкнутые и замкнутые цепи
В соответствии с терминологией цепей «разомкнутая» и «замкнутая», переключатель, у которого контакт от одной клеммы подключения соединен с контактом другой клеммы (например, выключатель с лезвием, полностью касающимся неподвижного контакта), обеспечивает непрерывность протекания тока через себя и называется замкнутым переключателем. И наоборот, выключатель, который нарушает целостность цепи (например, выключатель с лезвием, не касающимся неподвижного контакта), не пропускает ток и называется разомкнутым выключателем.
Источник
Рассмотрим типовую задачу с ключом, который немного изменяет электрическую схему. Основной материал для повторения: формулы последовательного и параллельного подключения резисторов, закон Ома, выражение для мощности.
Задача:
Источник тока, два резистора и ключ включены в цепь, как показано на рисунке. При разомкнутом ключе на резисторе R₁ выделяется мощность P₁ = 2 Вт, а на резисторе R₂ — мощность P₂ = 1 Вт. Какая мощность будет выделяться на резисторе R₂ после замыкания ключа К? Внутренним сопротивлением источника пренебречь. Ответ дайте в ваттах.
Решение:
Схема с ключами всегда пугает учащихся. По началу кажется, что контуров такой цепи больше, чем на самом деле. Здесь нужно понимать, что разомкнутый ключ представляет собой обычный разрыв цепи. При этом даже не конденсатор, способный накапливать заряд и влиять на переходной процесс, а просто разрыв цепи. То есть ток туда не идет. Это и есть наш первый случай. В первой ситуации мы имеем два последовательных резистора, соединенных с ЭДС, при этом в цепи идет один ток, цепь состоит их одного контура.
Что меняется, когда мы замыкаем ключ К ? Ток начинает течь через меньшее сопротивление, то есть через провод с ключом. Это называется шунтированием резистора R₁. Ток через R₁ уже не течет, а обходит его через параллельный провод. Ток – существо ленивое, всегда идет в обход 🙂
Давайте я перерисую схему, чтобы было наглядно:
Как видите, схемы заметно упростились, что дает нам возможность приступить к решению задачи, расписывая основные законы электричества для двух разных случаев.
До замыкания ключа:
Имеем последовательное соединение двух резисторов. Выразим мощности, которые на них выделяются и которые изначально даны в условии.
Возьмем отношение этих мощностей, выразим через него отношение сопротивлений, которое нам понадобится в дальнейшем:
После замыкания ключа:
Шунтируется резистор R₁. Схема начинает работать только через резистор R₂. Выразим мощность, которая на нем выделяется.
Теперь рассмотрим отношение мощности, выделяемом на резисторе R₂ до замыкания ключа, к мощности, выделяемой на этом же резисторе R₂ после замыкания ключа. Отношения этих мощностей выражаются через отношение сопротивлений резисторов R₁/R₂, а это отношение соответственно выражается через отношение мощностей P₁/P₂, которое нам известно из условия (до замыкания ключа). Собираем всё вместе и получаем:
Ответ: на резисторе R₂ будет выделяться 9 Ватт после замыкания ключа.
Решение целиком:
Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в VK
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Различные электрические цепи
На рисунке показан участок цепи постоянного тока. Каково сопротивление этого участка, если (r) = 2 Ом? (Ответ дайте в омах.) 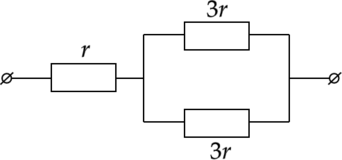
При параллельном соединении проводников сопротивление участка цепи равно: [dfrac{1}{R} = dfrac{1}{3r}+dfrac{1}{3r} = dfrac{2}{3r} ; ; ; Rightarrow ; ; ; R = dfrac{3r}{2}] Общее сопротивление цепи при последовательном соединении резистора с сопротивлением (r) и участка цепи с сопротивлением (dfrac{3r}{2}) равно: [R_{text{общ}}=r+dfrac{3r}{2}= 5 text{ Ом}]
Ответ: 5
На фотографии — электрическая цепь. Показания вольтметра даны в вольтах. Чему будут равны показания вольтметра, если его подключить параллельно резистору 2 Ом? Вольтметр считать идеальным. (Ответ дайте в вольтах.) 
Согласно закону Ома сила тока равна: [I=dfrac{U_1}{R_1}=dfrac{0,6text{ В}}{1text{ Ом}}=0,6 text{ А}] Так как все резисторы соединены последовательно, то сила тока, протекающего через каждый резистор, будет одинкова для первого и второго случая.
Тогда напряжение в цепи во втором случае равно: [U_2=IR_2=0,6text{ А}cdot2text{ Ом}=1,2 text{ В}]
Ответ: 1,2
На участке цепи, изображенном на рисунке, сопротивление каждого из резисторов равно (R) = 1 Ом. Чему равно полное сопротивление участка при замкнутом ключе К? (Ответ дайте в омах.) 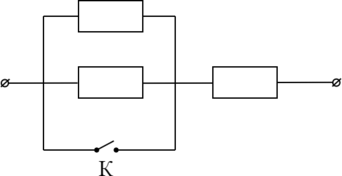
При замыкании ключа К два параллельно соединенных резисторов выпадают из цепи.
Полное сопротивление равно: [R_{text{общ}}=R=1 text{ Ом}]
Ответ: 1
Какая мощность выделяется в резисторе (R_2), включённом в электрическую цепь, схема которой изображена на рисунке? (R_1) = 3 Ом, (R_2) = 2 Ом, (R_3) = 1 Ом, ЭДС источника 5 В, внутреннее сопротивление источника пренебрежимо мало. (Ответ дайте в ваттах.) 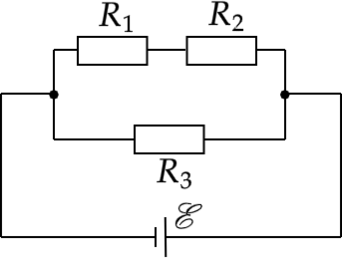
Общее сопротивление цепи равно: [R_{text{общ}}=dfrac{(R_1+R_2)R_3}{(R_1+R_2)+R_3}=dfrac{5}{6} text{ Ом}] Из закона Ома для полной цепи: [I=dfrac{varepsilon}{R_{text{общ}}+r}= dfrac{5text{ В}}{dfrac{5}{6}text{ Ом}} =6 text{ А}] где (I) — сила тока, (varepsilon) — ЭДС источника, (r) = 0.
При параллельном соединении ток распределяется обратно пропорционально сопротивлениям.
Ток, протекающий через 1 и 2 резистор (I_1) = (I_2) = 1 А, через 3 резистор (I_3) = 5 А.
Тогда мощность на втором резисторе равна: [P_2=I_2^2R_2= (1text{ А})^2 cdot 2text{ Ом} = 2 text{ Вт}]
Ответ: 2
Каждый из резисторов в схеме, изображённой на рисунке, имеет сопротивление 150 Ом. Каким будет сопротивление участка цепи, если ключ К замкнуть? (Ответ дайте в омах.) 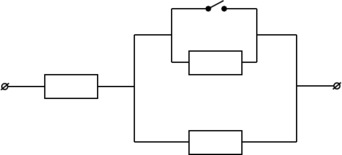
При замыкании ключа К два параллельно соединенных резисторов выпадают из цепи.
Полное сопротивление в цепи равно: [R_{text{общ}}=R=150 text{ Ом}]
Ответ: 150
На участке цепи, изображённом на рисунке, сопротивление каждого из резисторов равно (R) = 1 Ом. Чему равно полное сопротивление участка при замкнутом ключе К? (Ответ дайте в омах.) 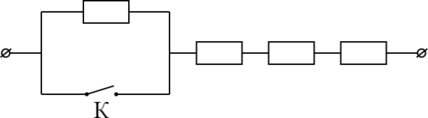
При замыкании ключа К через первый резистор ток не течет.
Тогда полное сопротивление равно сопротивлению на участке цепи, состоящем из трех последовательно соединенных резисторов: [R_{text{общ}}=3R=3 text{ Ом}]
Ответ: 3
Два резистора включены в электрическую цепь параллельно, как показано на рисунке. Значения силы тока в резисторах (I_1) = 0,8 А, (I_2) = 0,2 А. Чему равно отношение сопротивлений резисторов (dfrac{R_1}{R_2}) ? 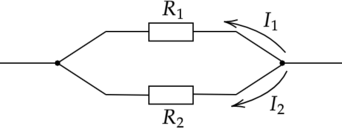
При параллельном соединении напряжения на обоих резисторах одинаковы: (U_1) = (U_2).
Исходя из закона Ома: [I_1R_1=I_2R_2] [dfrac{R_1}{R_2}=dfrac{I_2}{I_1}=dfrac{0,2text{ А}}{0,8text{ А}}=0,25]
Ответ: 0,25

УСТАЛ? Просто отдохни
ПОМОГИТЕ ПОЖАЛУЙСТА СРОЧНО ОЧЕНЬ!!! Найти общее сопротивление, если ключ замкнуть. ПОЖАЛУЙСТА!!!
Знаток
(496),
на голосовании
7 лет назад
Голосование за лучший ответ
Шкипер
Просветленный
(29178)
7 лет назад
Все просто. цепь состоит из двух участков. 1й Участок, где три резистора: резисторы соединены параллельно, значит ищем общее сопротивление для проводников соединенных параллельно.
1й и 2й участки соединены последовательно, значит их общее сопротивление находим как для последовательного соединения.
Даю 25 баллов, если поможете Каково сопротивление цепи при разомкнутом и замкнутом ключе?
R1 = R4 = 600Ом, R2 = R3 = 1, 8 кОм.
Вы открыли страницу вопроса Даю 25 баллов, если поможете Каково сопротивление цепи при разомкнутом и замкнутом ключе?. Он относится к категории
Физика. Уровень сложности вопроса – для учащихся 5 – 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Физика,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.
