поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,939 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
2016-09-08
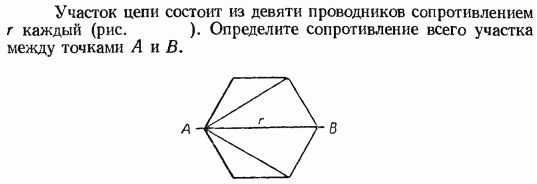
Найти сопротивление электрической цепи между точками $A$ и $B$ (см. рисунок). Сопротивление стороны большого шестиугольника равно $R$, сопротивление стороны малого шестиугольника равно $R/2$, сопротивление каждого внутреннего проводника, заключённого между шестиугольниками, равно $R/2$, а сопротивление каждого проводника, находящегося внутри малого шестиугольника, равно $R/4$.
Решение:
В схеме электрической цепи, изображённой на первом рисунке, точки $E_{1}, E_{2}$2 и центр схемы имеют, в силу её симметрии, одинаковые потенциалы. При их соединении проводником с нулевым сопротивлением токи в цепи и её сопротивление не меняются, а полученная при таком преобразовании схема совпадает со схемой, приведённой в условии.
Будем поэтому рассчитывать сопротивление эквивалентной электрической цепи, схема которой изображена на первом рисунке. В ней пары точек $A_{1}$ и $A_{2}, B_{1}$ и $B_{2}, C_{1}$ и $C_{2}, D_{1}$ и $D_{2}$ также в силу симметрии имеют попарно одинаковые потенциалы. Соединяя их, получаем следующую эквивалентную схему, изображённую на втором рисунке; здесь учтено, что сопротивление двух параллельно соединённых одинаковых резисторов вдвое меньше сопротивления каждого из них.
В схеме на втором рисунке, как следует из соображений симметрии, пары точек $A_{12}$ и $F, B_{12}$ и $G$ имеют одинаковые потенциалы; соединяя их, получаем электрическую цепь, схема которой изображена на третьем рисунке. Её сопротивление легко рассчитывается по формулам последовательного и параллельного соединения резисторов: оно равно $frac{13R}{20}$.
Помогите решить задачу по физике
МНД
Знаток
(332),
закрыт
7 лет назад
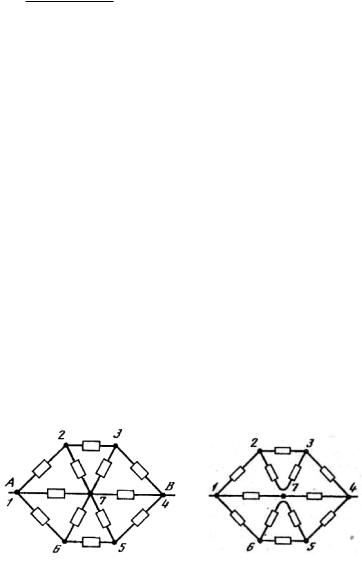
Определить сопротивление проволочного каркаса в виде правильного шестиугольника с диагоналями, спаяными в центре. Каркас включён в сеть точками А и В. Соротивление стороны шестиугольника – R.
Добавил:
Вуз:
Предмет:
Файл:
Скачиваний:
0
Добавлен:
30.04.2022
Размер:
1.12 Mб
Скачать

u и u – подвижность соответственно положительных и отрицательных ионов.
Плотность тока насыщения
jнас qn0 d ,
|
где n0 – |
число пар ионов, создаваемых ионизатором в |
|||||
|
единице объёма в единицу времени; |
||||||
|
d |
– |
расстояние между электродами [ n N |
, где |
|||
|
0 |
V t |
|||||
|
N – |
число пар ионов, создаваемых ионизатором за время |
|||||
|
t в пространстве между электродами; V – |
объём этого |
|||||
|
пространства]. |
||||||
|
1. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ |
||||||
|
Задача 1.1. Какой заряд |
пройдет |
по проводни- |
||||
|
ку, если |
в течение t 10,0 с сила |
тока уменьшилась от |
I0 10,0 А до I = 5,00 А? Рассмотреть два случая: 1) сила
тока уменьшилась равномерно; 2) сопротивление проводника равномерно возрастало в течение указанного промежутка времени, а разность потенциалов на концах проводника поддерживалась постоянной.
Решение.
1) Величина заряда dq , проходящего через поперечное сечение проводника за время dt , связана с силой тока
соотношением I dqdt .
Если в эту формулу вместо элементарных величин dq и dt подставить конечные значения q и t, то получим среднее значение силы тока I ср за время t, т. е. Iср q
11

Отсюда искомый заряд
q Iср t .
Поскольку сила тока в цепи изменялась равномерно, т. е. являлась линейной функцией времени, в качестве среднего значения I ср можно взять среднее арифметиче-
ское между начальным и конечным значениями силы тока за время t. Следовательно,
2) Теперь равномерно изменяется не сила тока, а сопротивление R. Это значит, что величина R является линейной функцией времени, т. е.
где R0 и R – соответственно начальное и конечное сопро-
тивления проводника;
k – постоянная величина, выражающая скорость изменения сопротивления.
Тогда по закону Ома для однородного участка цепи получим
|
I |
1 2 |
1 |
2 . |
(3) |
|
|
R |
R |
kt |
|||
|
0 |
Видим, что в этом случае зависимость силы тока от времени не является линейной, поэтому соотношение (1) здесь неприменимо. Однако при любой зависимости силы тока от времени можно записать
dq I dt .
12

Отсюда полный заряд, проходящий через поперечное сечение проводника за время t, выразится интегралом
|
t |
||||||||||||||||||||
|
q Idt . |
(4) |
|||||||||||||||||||
|
0 |
||||||||||||||||||||
|
Подставив в (4) вместо силы тока её значение по |
||||||||||||||||||||
|
формуле (3), выполним интегрирование: |
||||||||||||||||||||
|
t |
2 |
2 |
R |
kt |
||||||||||||||||
|
q |
1 |
dt |
1 |
ln |
0 |
. |
||||||||||||||
|
0 |
R kt |
k |
R |
|||||||||||||||||
|
0 |
0 |
|||||||||||||||||||
|
Преобразовав этот результат с учётом формулы (2) и |
||||||||||||||||||||
|
соотношений R 1 |
2 / I , |
R0 |
1 2 |
/ I0 , найдём |
||||||||||||||||
|
q 1 2 t |
ln |
R |
I0 I t |
ln |
I0 |
. |
(5) |
|||||||||||||
|
I |
||||||||||||||||||||
|
R R |
R |
I |
0 |
I |
||||||||||||||||
|
0 |
0 |
Подставив в формулу (5) числовые значения, получим q = 69 Кл.
Задача 1.2. Определить плотность тока в медной проволоке длиной l = 10 м, если разность потенциалов на её концах 1 2 12 В.
Решение.
Плотность тока, определяемую формулой j dSdI ,
найдём, выразив силу тока I по закону Ома для однородно-
го участка цепи. Тогда с учётом R Sl получим
I 1 2 S / l .
13

|
Отсюда плотность тока |
|||
|
j |
dI |
1 2 . |
(1) |
|
dS |
l |
||
|
К этому результату можно прийти, применив закон |
|||
|
Ома в дифференциальной форме |
|||
|
j E , |
(2) |
предварительно выразив напряжённость электрического поля внутри однородного проводника через разность потенциалов на концах проводника и его длину:
E 1 2 
|
Подставив |
это значение |
Е в (2) и учитывая, что |
||
|
1 , снова получим ответ (1). |
||||
|
Взяв из справочных таблиц значение удельного со- |
||||
|
противления меди 1,7 10 8 |
Ом м и выполнив вычис- |
|||
|
ление по формуле (1), найдём |
||||
|
j 7 107 |
A м2 . |
|||
|
Задача 1.3. Два гальванических элемента, имеющих |
||||
|
э.д.с. 1 |
1,5 В, |
2 1,6 В |
и |
внутреннее сопротивление |
|
r1 0,60 |
Ом, r2 |
0,40 Ом, |
соединены разноимёнными по- |
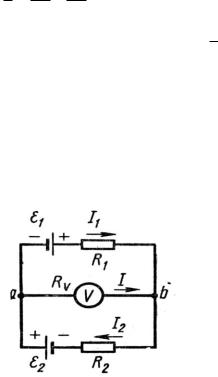
люсами (рис. 1.1). Пренебрегая сопротивлением соединительных проводов, определить разность потенциалов на зажимах элементов (между точками
a и b).
Решение.
Точки a и b являются концами двух участков цепи: a 1b и a 2b .
Оба эти участка содержат э.д.с. и, следовательно, являются участками
неоднородной цепи. Применим закон Ома в виде
I1 2 . Так как обе э.д.с. имеют положительные
R
знаки при обходе цепи по часовой стрелке, ток по цепи будет течь в том же направлении. Тогда для участка a 1b получим
|
I a b 1 / r1 . |
(1) |
|
Далее есть два пути решения задачи. Во-первых, |
|
|
можно применить закон Ома для участка a 2b : |
|
|
I a b 2 / r2 . |
(2) |
|
Во-вторых, можно воспользоваться законом Ома для |
|
|
замкнутой цепи: |
|
|
I 1 2 / r1 r2 . |
(3) |
|
Взяв любые два уравнения из (1), (2), (3) и исключив |
|
из них силу тока I, найдём |
||||||||
|
2 r1 |
1r2 |
0,4 В. |
||||||
|
a |
b |
r1 |
r2 |
|||||
Задача 1.4. Найти сопротивление шестиугольника, изображённого на рис. 1.2, если он включён в цепь между точками А и В. Сопротивление каждого проводника схемы равно R.
15
Решение. Вследствие симметрии очевидно, что ток в проводнике 1-7 равен току в проводнике 7-4, ток в 2-7 равен току в 7-3, ток в 6-7 равен току в 7-5 (см. рис. 1.2). Поэтому распределение токов и, следовательно, сопротивление шестиугольника не изменится, если отсоединить проводники 2-7, 7-3, 6-7 и 7-5 от центра (рис. 1.3). Сопротивление же этой схемы, которая эквивалентна исходной, легко вычислить. Сопротивление верхней части схемы равно 8R/3. Таково же сопротивление нижней части.
Полное сопротивление r найдётся из соотношения
1r 21R 86R , отсюда
r 54 R .
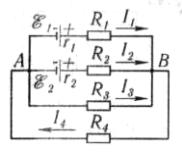
Задача 1.5. Элементы цепи, схема которой изображена на (рис. 1.4), имеют следующие значения: 1 1,50 В,
2 1,60 В, R1 1,00 кОм, R2 2,00 кОм. Определить показания вольтметра, если его сопротивление Rv 2,00 кОм.
Сопротивлением источников напряжения и соединительных проводов пренебречь.
Решение. Здесь требуется найти разность потенциалов между точками a и b, которую измеряет вольтметр, подключённый к этим точкам. Имеется разветвлённая цепь, по трём участкам которой текут, вообще говоря, разные токи: I1, I2, I (см. рис. 1.4). Задачу можно решить двумя способами, ис-
Рис. 1.4
16
пользуя правила Кирхгофа и закон Ома для неоднородного участка цепи. Рассмотрим оба способа.
1. Искомая разность потенциалов по закону Ома рав-
|
на |
||
|
a b |
IRV . |
(1) |
|
Чтобы определить силу тока I |
в цепи вольтметра, |
применим правила Кирхгофа. Обозначив на рис. 1.4 направление всех токов (для тока I делаем это лишь предположительно), согласно первому правилу Кирхгофа запишем для узла a:
Для составления остальных двух независимых уравнений воспользуемся вторым правилом Кирхгофа. Предварительно выбрав направление обхода замкнутых контуров, например по часовой стрелке, и учитывая правило знаков,
|
получим соответственно для контуров aR1ba и abR2a: |
|||||||||
|
I1R1 – IRV = 1, |
(3) |
||||||||
|
I2R2 + IRV = 2. |
(4) |
||||||||
|
Решив систему трёх уравнений (2), (3), (4) с тремя |
|||||||||
|
неизвестными I1, I2, I относительно тока I, |
найдём |
||||||||
|
I |
2 R1 1R2 |
(5) |
|||||||
|
R R (R R )R . |
|||||||||
|
1 2 |
1 2 |
v |
|||||||
|
Подставив это значение I в (1) и произведения вычис- |
|||||||||
|
ления, получим |
|||||||||
|
a b |
(2 R1 |
1R2 )Rv |
0,35Â. |
(6) |
|||||
|
R1R2 |
(R1 R2 )Rv |
||||||||
Знак « » в ответе означает, что b a и в действительности ток в цепи вольтметра имеет направление, про-
17
тивоположное тому, что мы предположили, т. е. от точки b
кточке а.
2.Применим закон Ома для неоднородного участка
цепи поочерёдно к трём участкам: aR1b, aR2b, aRvb. Тогда, учитывая правило знаков, запишем соответственно три уравнения:
|
I a b 1 ; |
I |
2 |
a b 2 ; I a b . |
|||
|
1 |
R1 |
R2 |
RV |
|||
|
Подставим эти значения сил токов в уравнение (2) |
||||||
|
a b 2 a b 1 |
a b 0. |
|||||
|
R2 |
R1 |
Rv |
||||
|
Решив это уравнение относительно величины a b , |
||||||
|
найдём ответ, совпадающий с формулой (6). |
||||||
|
Задача 1.6. Источники тока с электродвижущими |
||||||
|
силами 1 |
и 2 включены в цепь, как показано на рис. 1.5. |
|||||
|
Определить силы токов, |
текущих в сопротивлениях R1 |
и |
||||
|
R2 , если |
1 10В и |
2 |
4В , а |
R1 R4 2 Ом |
и |
R2 R3 4 Ом. Сопротивлениями источников тока пренебречь.
Рис. 1.5
18
Решение. Силы токов в разветвлённой цепи определяют с помощью законов Кирхгофа. Чтобы найти значения силы токов, следует составить четыре уравнения.
Выберем направления токов, как они показаны на рис. 1.5, и условимся обходить контуры по часовой стрелке.
|
Рассматриваемая |
в задаче схема имеет два узла: |
|
А и В. Но составлять |
уравнение по первому закону |
Кирхгофа следует только для одного узла, так как уравнение, составленное для второго узла, будет следствием первого уравнения.
При составлении уравнений по первому закону Кирхгофа необходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком плюс; ток, отходящий от узла, – со знаком минус.
По первому закону Кирхгофа для узла В имеем
I1 I2 I3 I4 0 .
Недостающие три уравнения получим по второму закону Кирхгофа. Число независимых уравнений, которые могут быть составлены по второму закону Кирхгофа, также меньше числа контуров (в нашем случае контуров шесть, а независимых уравнений три). Чтобы найти необходимое число независимых уравнений, следует придерживаться правила: выбирать контуры таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь, не участвовавшая ни в одном из ранее использованных контуров.
При составлении уравнений по второму закону Кирхгофа необходимо соблюдать следующее правило знаков:
а) если ток по направлению совпадает с выбранным направлением обхода контуров, то соответствующее произведение IR входит в уравнение со знаком плюс, в проти-
19
воположном случае произведение IR входит в уравнение со знаком минус;
б) если э.д.с. повышает потенциал в направлении обхода контура, т. е. если при обходе контура приходится идти от минуса к плюсу внутри источника, то соответствующая э.д.с. входит в уравнение со знаком плюс, в противном случае – со знаком минус.
По второму закону Кирхгофа имеем соответственно для контуров AR1BR2 A; AR1BR3 A; AR3BR4 A :
|
I1R1 – I2R2 = 1 – 2; |
(1) |
|
I1R1 – I3R3 = 1; |
(2) |
|
I3 R3 I 4 R4 0. |
(3) |
Подставив в равенства (1) – (3) значения сопротивлений и ЭДС, получим систему уравнений:
I1 I2 I3 I4 0;
2I1 4I2 6;
2I1 4I3 10;
4I3 2I 4 0.
Поскольку нужно найти только два тока, то удобно воспользоваться методом определителей (детерминантов). С этой целью перепишем уравнения ещё раз в следующем виде:
I1 I2 I3 I4 0;
2I1 4I2 0 0 6;
2I1 0 4I3 0 10;
0 0 4I3 2I4 0.
20
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Физика,
вопрос задал JastDrey,
7 лет назад
Приложения:
Ответы на вопрос
Рассчитаем сначала RΣ1.
RΣ1 – это два последовательно соединенных резистора и один – параллельно:
1/RΣ1=1/2R+1/К Тогда RΣ1 =2R/3
Схема упростилась, теперь найдем сопротивление последовательно соединенных RΣ1 и R. Это 5R/3.
Наконец, у нас есть параллельное соединение из трех резисторов: два – по 5R/3 и один – R.
Найдем RΣ2, по формуле: 1/RΣ2 = 1/5R/3+1/5R/3+1/R.
Получаем RΣ2 = 5R/11
Вроде так. Вроде все верно сосчитала…
Приложения:
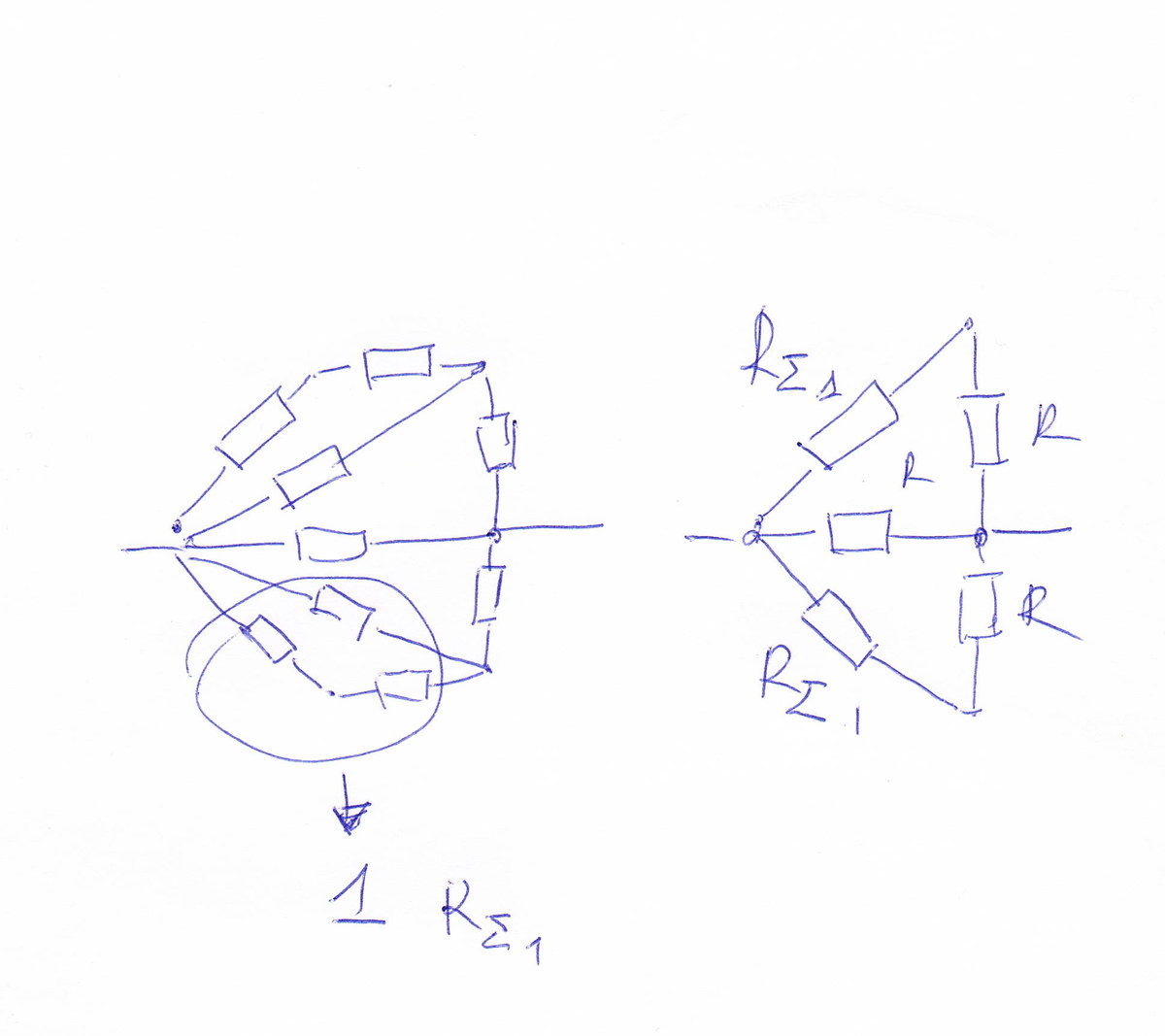
В первом расчете вылезло K вместо R, исправь!
Новые вопросы




